Optimal Sensor Placement for Reliable Virtual Sensing Using Modal Expansion and Information Theory
Abstract
1. Introduction
2. Bayesian Virtual Sensing Using the Modal Expansion Method
2.1. Modal Expansion for Virtual Sensing
2.2. Bayesian Virtual Sensing
3. Optimal Sensor Placement Formulation
3.1. Expected Utility Using Information Gain
3.2. Optimal Sensor Placement
4. Model Prediction Error Formulation
5. Implementation
6. Applications
6.1. Strain Predictions Using Strain Observations
6.1.1. Model/Prediction Errors, Measurement Error and Prior Distribution
6.1.2. FSSP and BSSP Algorithms
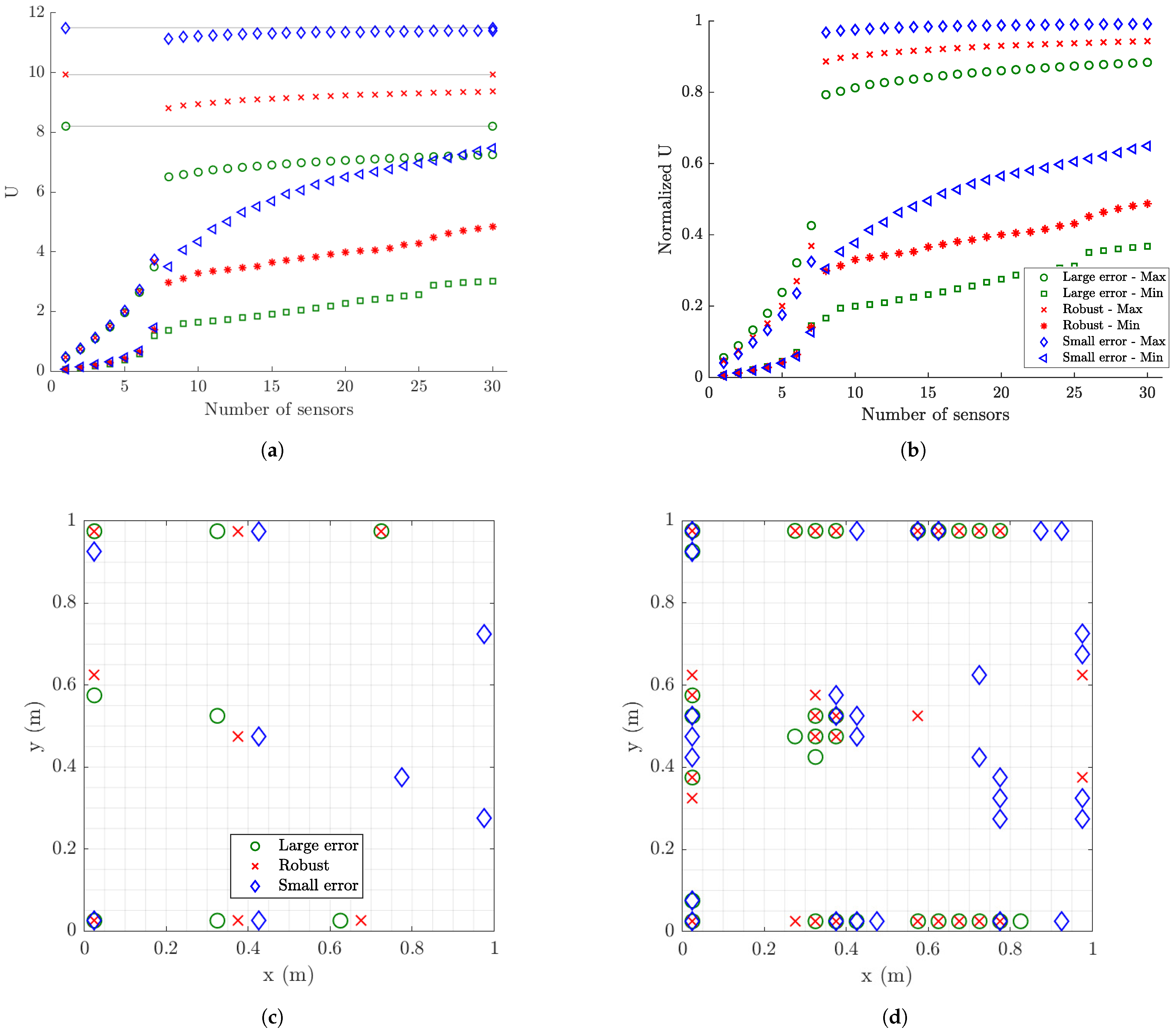
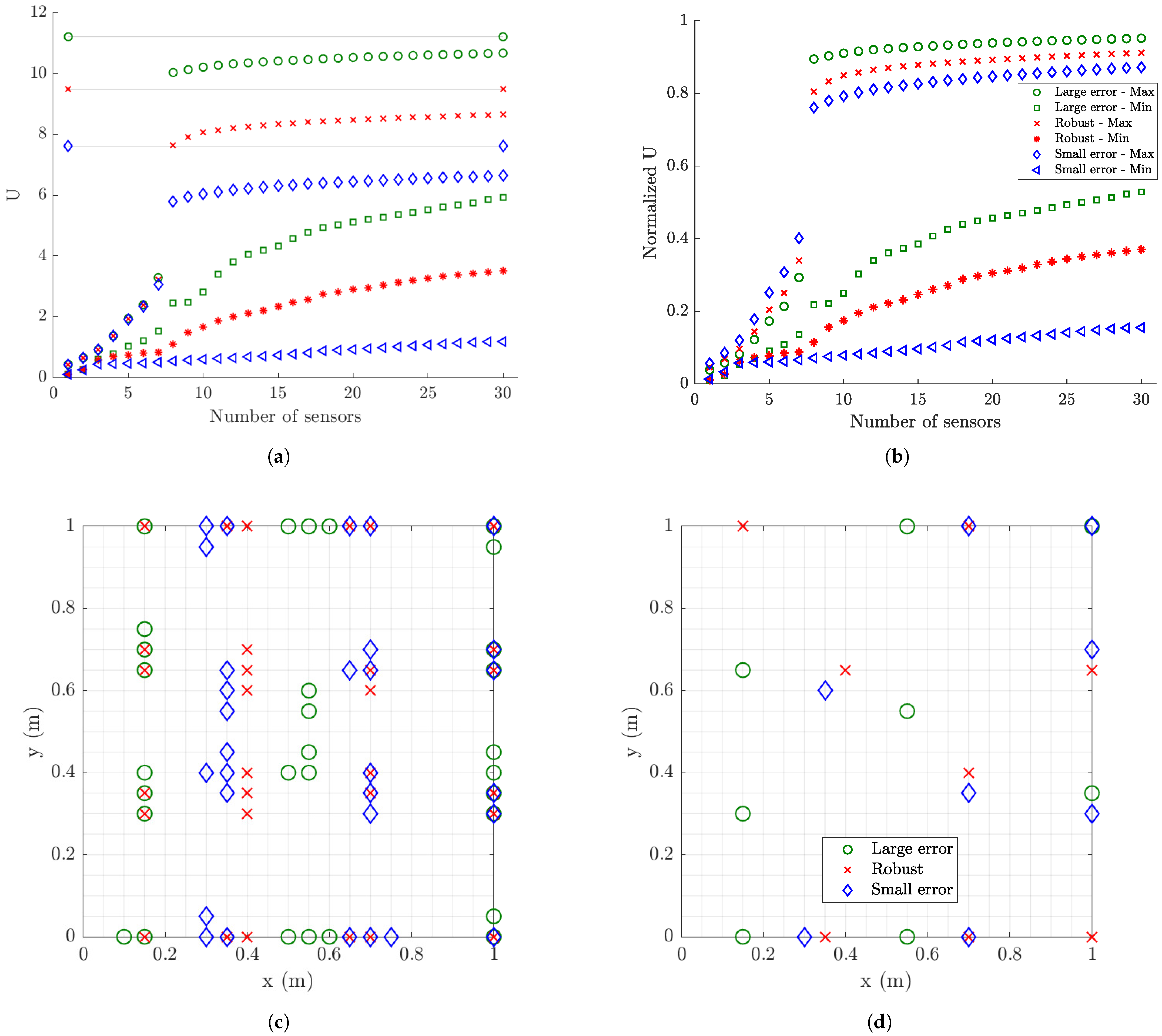
6.1.3. Information Gain versus Number of Sensors
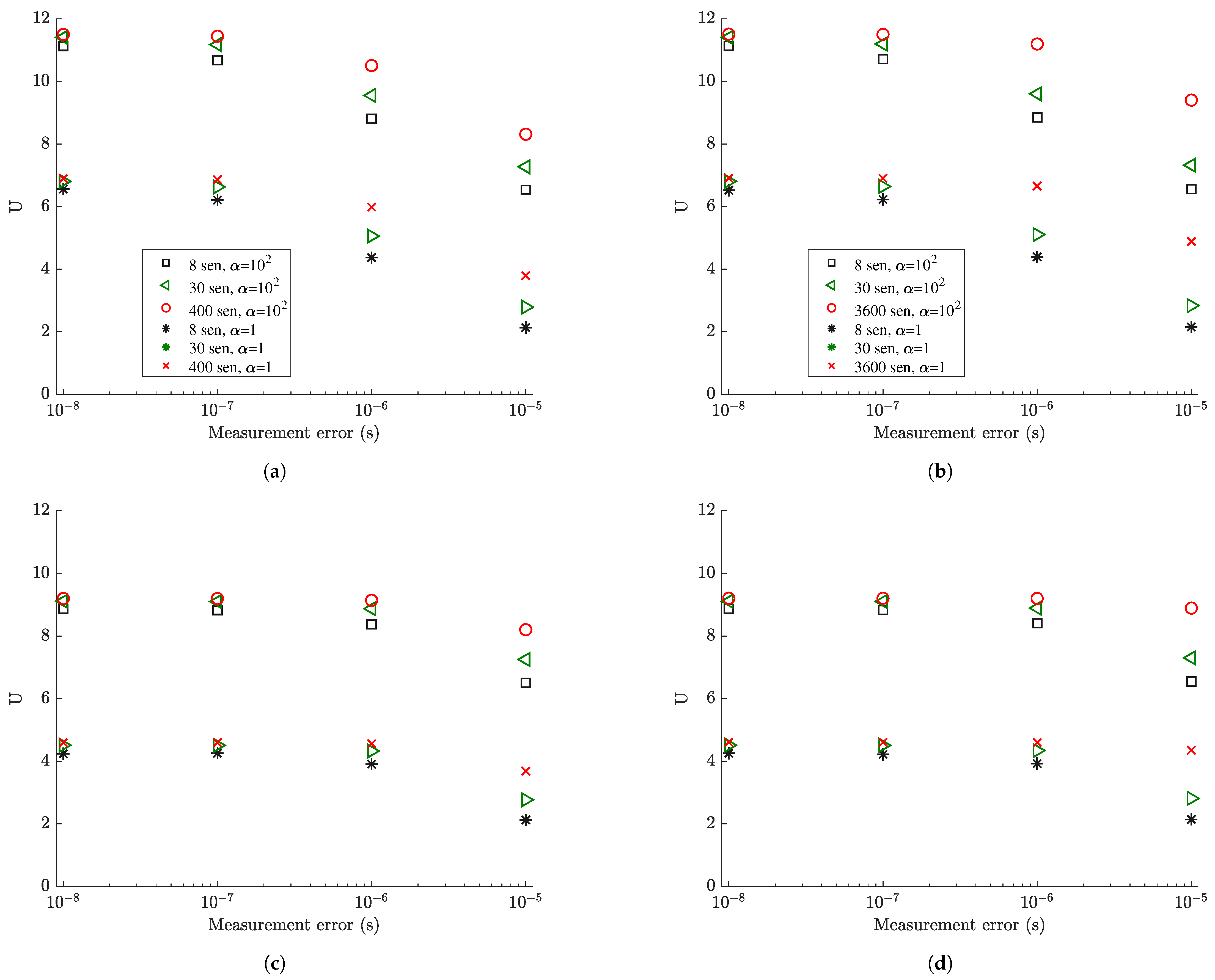
6.1.4. Information Gain versus Measurement Error
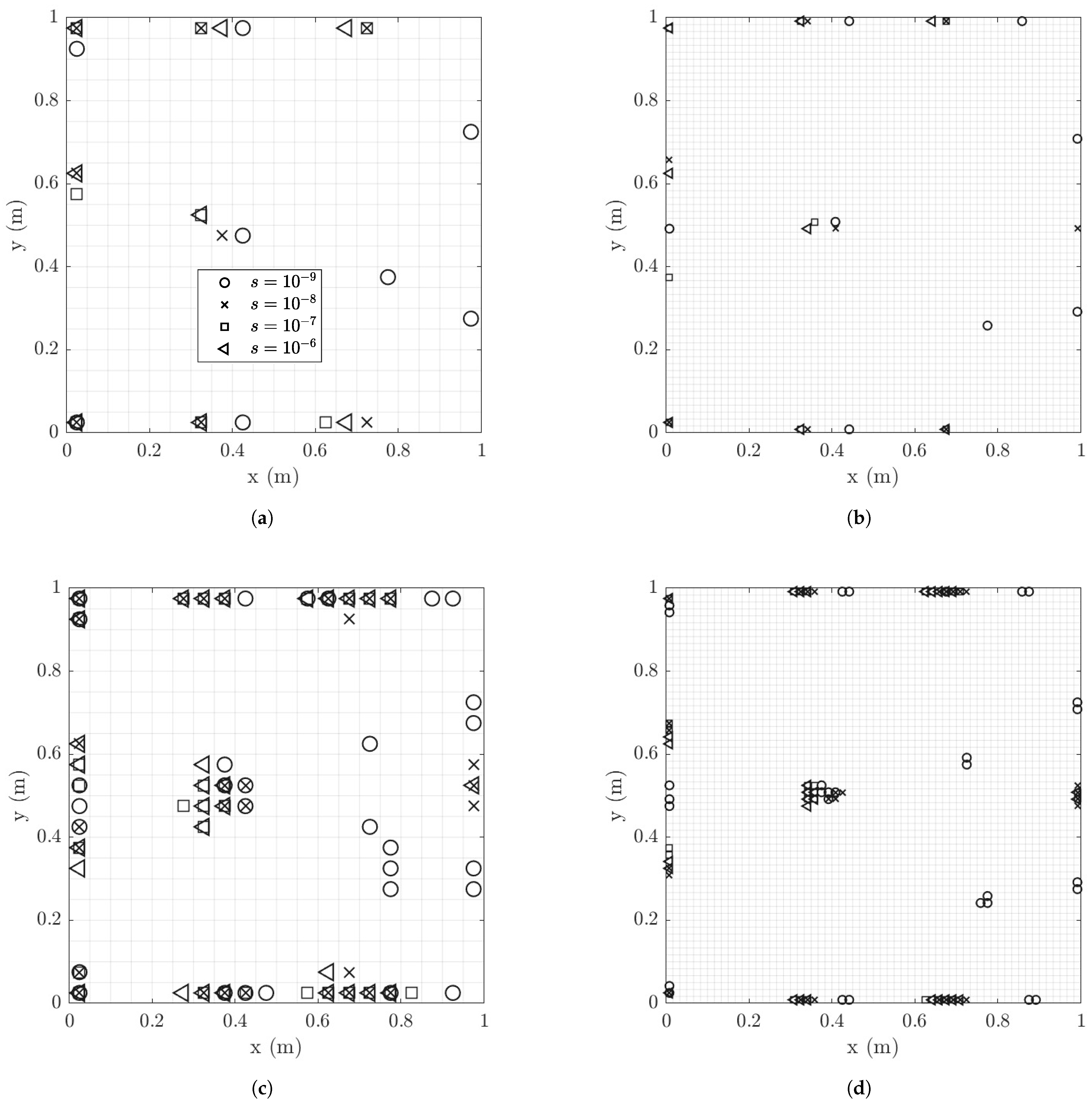
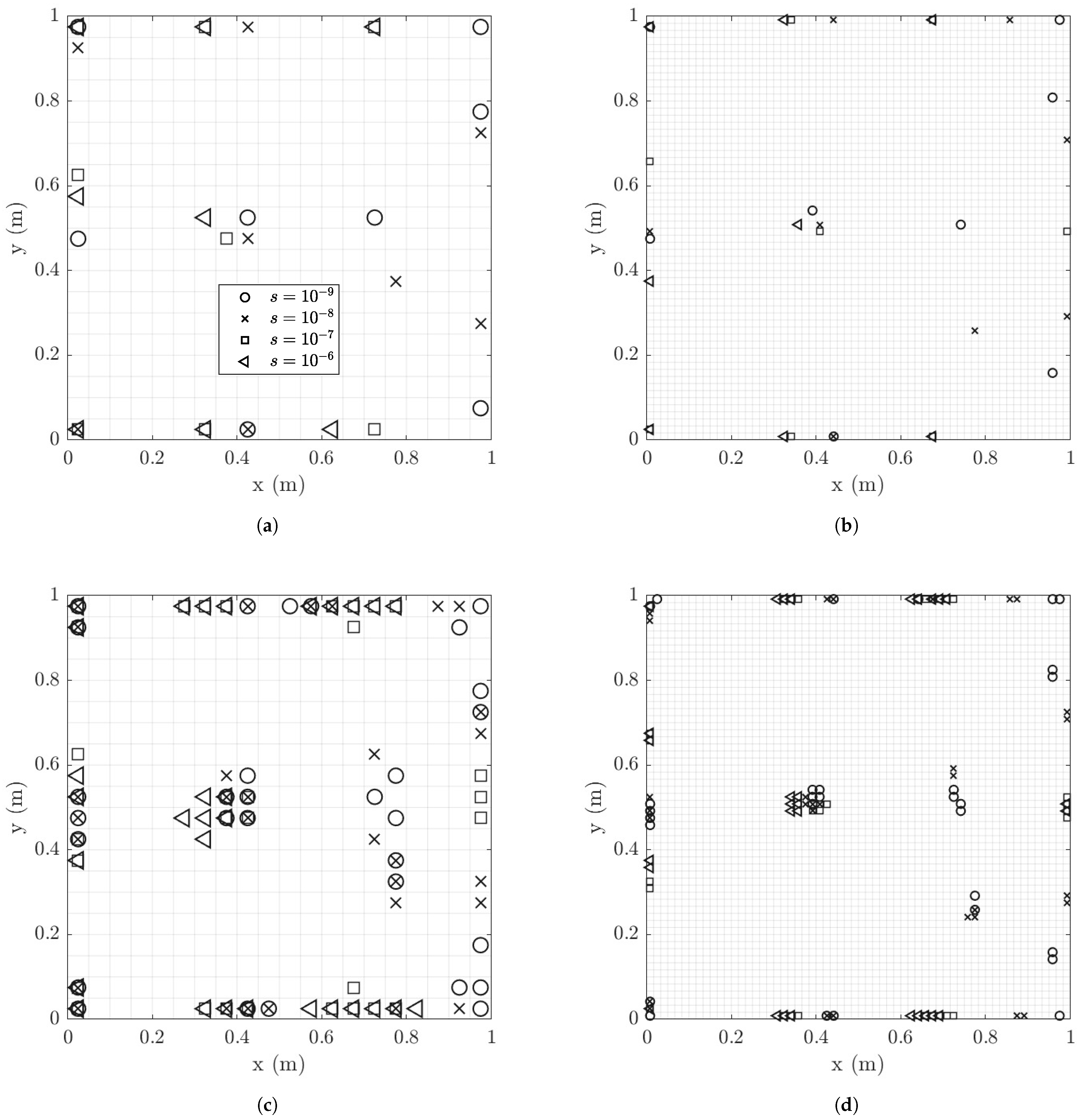
6.1.5. Optimal Locations of Strain Sensors
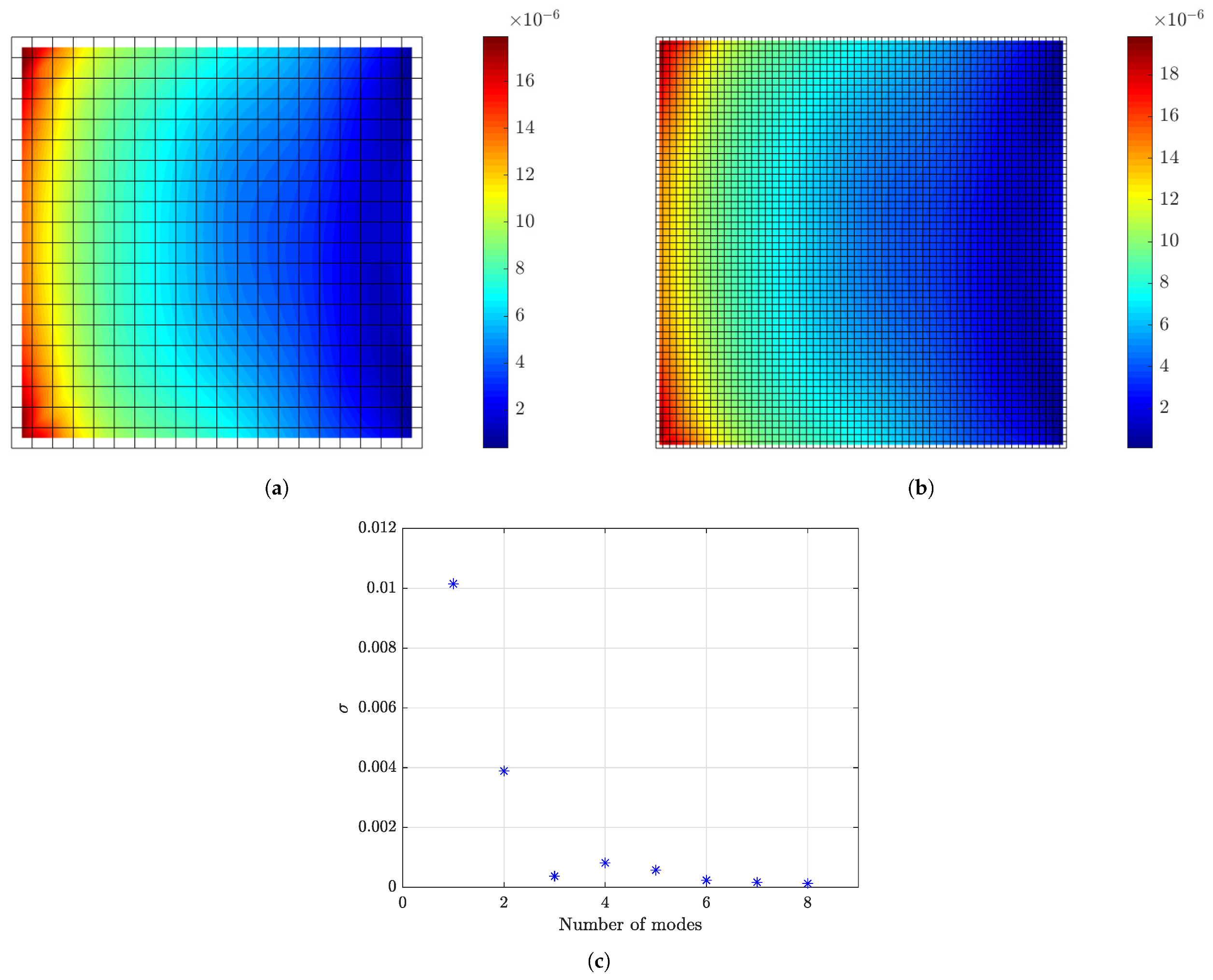
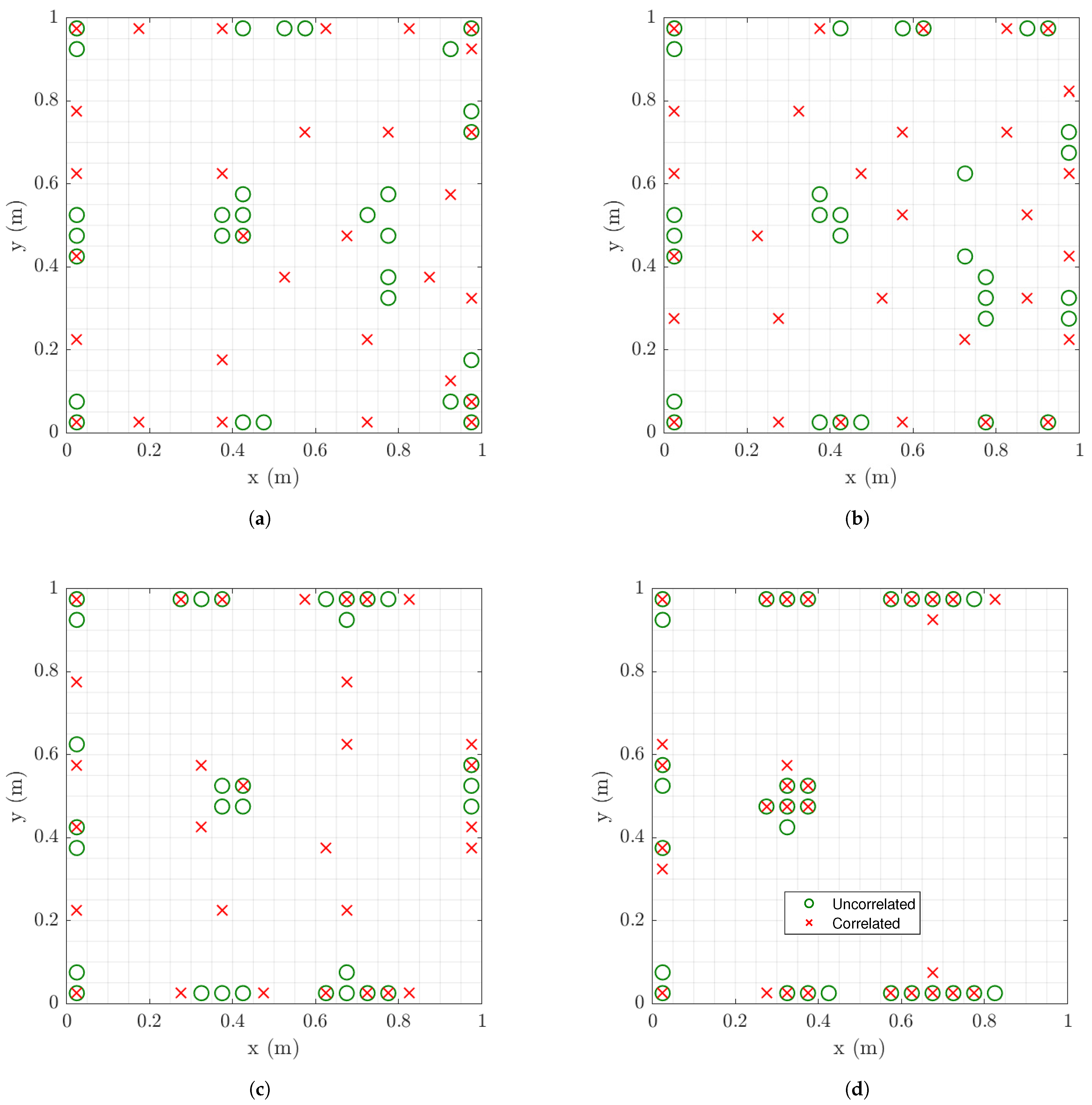
6.1.6. Effect of Spatial Correlation of Model Error
6.1.7. Effectiveness of Optimal Sensor Configuration for Response Predictions
6.1.8. Robustness to Model/Prediction and Measurement Error Uncertainties
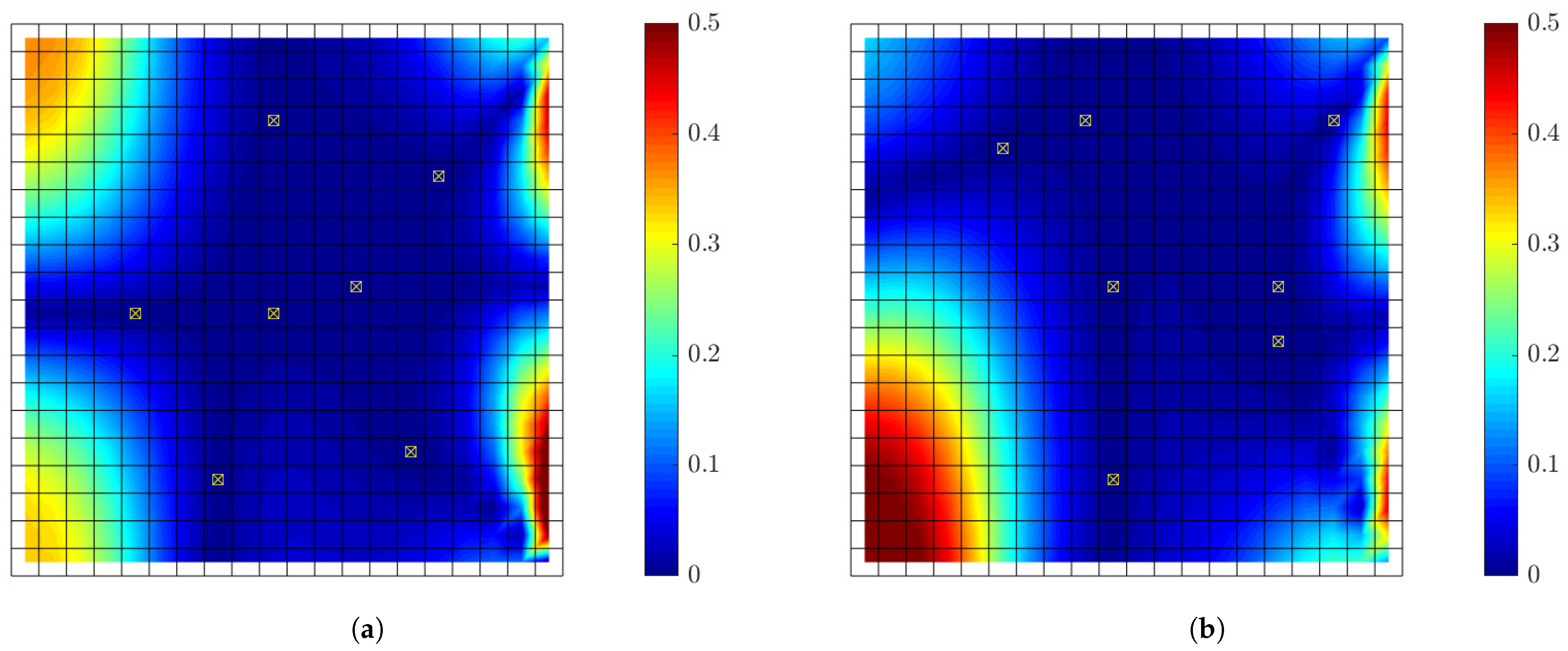
6.2. Strain Predictions Using Displacement Observations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| OSP | Optimal sensor placement |
| QoI | Quantities of interest |
| KL-div | Kullback-Leibler divergence |
| DOF | Degrees of freedom |
| FSSP | Forward sequential sensor placement |
| BSSP | Backward sequential sensor placement |
| SSP | Sequential sensor placement |
| CMA-ES | Covariance matrix adaptation evolution strategy |
| FIM | Fisher information matrix |
Nomenclature
| structural model parameters | |
| number of response locations | |
| excitation vector | |
| number of excitation | |
| D | the available data |
| vector of response time history data | |
| number of sensors | |
| sensor configuration vector | |
| vector of predicted responses | |
| vector of modal coordinates | |
| m | number of modal coordinates |
| n | number of model degree of freedoms |
| L | observation matrix that maps the displacements at all n model DOF to the measured QoI indicated by the sensor location vector |
| displacement mode shape matrix | |
| a multi-variable zero-mean Gaussian noise term for measurement and model errors | |
| covariance matrix of | |
| r-th modal frequency | |
| diagonal matrix of the squares of the modal frequencies | |
| r-th modal damping ratio | |
| Z | diagonal matrix with diagonal elements equal to , |
| M | a matrix of zeros and ones associating the independent excitations in the vector to the DOF of the structural model |
| mode shape matrix of predicted QoI | |
| a zero-mean prediction error term for model error | |
| covariance matrix of | |
| posterior PDF of the modal vector parameter given , and | |
| prior PDF of given | |
| likelihood function of observing the data | |
| posterior covariance matrix of the | |
| posterior covariance matrix of the | |
| covariance matrix of the assigned prior distribution for | |
| weight that quantifies the importance of the i-th QoI | |
| U | expected utility function |
| prior information entropy | |
| posterior information entropy | |
| ratio between and | |
| Difference between prior and posterior information entropy for a sensor configuration | |
| number of all possible sensor positions | |
| number of function evaluations required by FSSP | |
| number of function evaluations required by BSSP | |
| measurement error term in | |
| model error term in | |
| covariance matrix of | |
| covariance matrix of | |
| level of model error in | |
| level of model error in | |
| s | level of model error in |
| R | the correlation matrix |
| a constant that quantifies the extent of the uncertainty in the prior distribution | |
| A,B,C,D | state-space matrices |
| covariance of the state vector | |
| variance of the discrete white noise excitation | |
| parameter quantifying the uncertainty in and | |
| parameter quantifying the uncertainty in s |
Appendix A. Proof of Equation (18)
Appendix B. Properties of Information Gain (Utility Function)
Appendix B.1. Effect of Modelling and Measurement Errors
Appendix B.2. Utility Versus Number of Sensors
References
- Hjelm, H.P.; Brincker, R.; Graugaard-Jensen, J.; Munch, K. Determination of stress histories in structures by natural input modal analysis. In Proceedings of the 23rd International Modal Analysis Conference, Orlando, FL, USA, 31 January–3 February 2005; pp. 838–844. [Google Scholar]
- Pingle, P.; Avitabile, P. Full-field dynamic stress/strain from limited sets of measured data. Sound Vib. 2011, 2, 187–200. [Google Scholar] [CrossRef]
- Baqersad, J.; Bharadwaj, K.; Poozesh, P. Modal expansion using strain mode shapes. In Shock & Vibration, Aircraft/Aerospace, Energy Harvesting, Acoustics & Optics; Springer: New York, NY, USA, 2017; Volume 9, pp. 219–226. [Google Scholar] [CrossRef]
- Avitabile, P.; Harvey, E.; Ruddock, J. Comparison of full field strain distributions to predicted strain distributions from limited sets of measured data for SHM applications. Key Eng. Mater. 2013, 569–570, 1140–1147. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Fritzen, C.P.; Kraemer, P.; Ntotsios, E. Fatigue predictions in entire body of metallic structures from a limited number of vibration sensors using Kalman filtering. Struct. Control Health Monit. 2011, 18, 554–573. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Lourens, E.M.; Lombaert, G.; De Roeck, G.; Liu, K. Prediction of fatigue damage accumulation in metallic structures by the estimation of strains from operational vibrations. In Life-Cycle and Sustainability of Civil Infrastructure Systems, Proceedings of the 3rd International Symposium on Life-Cycle Civil Engineering, Vienna, Austria, 3–6 October 2012; IALCCE; CRC Press: Boca Raton, FL, USA, 2012; pp. 304–310. [Google Scholar]
- Maes, K.; Iliopoulos, A.; Weijtjens, W.; Devriendt, C.; Lombaert, G. Dynamic strain estimation for fatigue assessment of an offshore monopile wind turbine using filtering and modal expansion algorithms. Mech. Syst. Signal Process. 2016, 76, 592–611. [Google Scholar] [CrossRef]
- Iliopoulos, A.; Shirzadeh, R.; Weijtjens, W.; Guillaume, P.; Hemelrijck, D.V.; Devriendt, C. A modal decomposition and expansion approach for prediction of dynamic responses on a monopile offshore wind turbine using a limited number of vibration sensors. Mech. Syst. Signal Process. 2016, 68, 84–104. [Google Scholar] [CrossRef]
- Nabiyan, M.; Ebrahimian, H.; Moaveni, B.; Khoshnoudian, F. Structural identification for dynamic strain estimation in wind turbine towers. In Proceedings of the 36th International Modal Analysis Conference (IMAC), Orlando, FL, USA, 28–31 January 2019; Springer: Cham, Switzerland, 2019; pp. 239–245. [Google Scholar] [CrossRef]
- Nabiyan, M.S.; Khoshnoudian, F.; Moaveni, B.; Ebrahimian, H. Mechanics-based model updating for identification and virtual sensing of an offshore wind turbine using sparse measurements. Struct. Control Health Monit. 2021, 28, e2647. [Google Scholar] [CrossRef]
- Henkel, M.; Häfele, J.; Weijtjens, W.; Devriendt, C.; Gebhardt, C.G.; Rolfes, R. Strain estimation for offshore wind turbines with jacket substructures using dual-band modal expansion. Mar. Struct. 2020, 71, 102731. [Google Scholar] [CrossRef]
- Ren, P.; Zhou, Z. Strain estimation of truss structures based on augmented Kalman filtering and modal expansion. Adv. Mech. Eng. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Chen, Y.; Joffre, D.; Avitabile, P. Underwater dynamic response at limited points expanded to full-field strain response. J. Vib. Acoust. Trans. ASME 2018, 140, 1–9. [Google Scholar] [CrossRef]
- Vettori, S.; Di Lorenzo, E.; Peeters, B.; Chatzi, E. Kalman-based coupled response-input estimation during environmental tests on the box assembly with removable component structure. In Proceedings of the 11th International Conference on Structural Dynamics, Athens, Greece, 23–26 November 2020; pp. 3878–3885. [Google Scholar] [CrossRef]
- Vettori, S.; Lorenzo, E.D.; Cumbo, R.; Musella, U.; Tamarozzi, T.; Peeters, B.; Chatzi, E. Kalman-Based virtual sensing for improvement of service response replication in environmental tests. In Proceedings of the 38th International Modal Analysis Conference (IMAC), Houston, TX, USA, 10–13 February 2020; pp. 93–106. [Google Scholar] [CrossRef]
- Iliopoulos, A.; Weijtjens, W.; Van Hemelrijck, D.; Devriendt, C. Fatigue assessment of offshore wind turbines on monopile foundations using multi-band modal expansion. Wind Energy 2017, 20, 1463–1479. [Google Scholar] [CrossRef]
- Giagopoulos, D.; Arailopoulos, A.; Dertimanis, V.; Papadimitriou, C.; Chatzi, E.; Grompanopoulos, K. Computational framework for online estimation of fatigue damage using vibration measurements from a limited number of sensors. Procedia Eng. 2017, 199, 1906–1911. [Google Scholar] [CrossRef]
- Tchemodanova, S.P.; Tatsis, K.; Dertimanis, V.; Chatzi, E.; Sanayei, M. Remaining fatigue life prediction of a roller coaster subjected to multiaxial nonproportional loading using limited measured strain locations. In Structures Congress 2019: Bridges, Nonbuilding and Special Structures, and Nonstructural Components; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 112–121. [Google Scholar] [CrossRef]
- Tarpø, M.; Nabuco, B.; Georgakis, C.; Brincker, R. Expansion of experimental mode shape from operational modal analysis and virtual sensing for fatigue analysis using the modal expansion method. Int. J. Fatigue 2020, 130, 105280. [Google Scholar] [CrossRef]
- Maes, K.; Lombaert, G. Fatigue monitoring of railway bridges by means of virtual sensing. In Proceedings of the Belgian and Dutch National Groups of IABSE— Young Engineers Colloquium 2019 (YEC2019), Eindhoven, The Netherlands, 15–16 March 2019; pp. 24–25. [Google Scholar]
- Giagopoulos, D.; Arailopoulos, A.; Dertimanis, V.; Papadimitriou, C.; Chatzi, E.; Grompanopoulos, K. Structural health monitoring and fatigue damage estimation using vibration measurements and finite element model updating. Struct. Health Monit. 2019, 18, 1189–1206. [Google Scholar] [CrossRef]
- Foss, G.C.; Haugse, E. Using modal test results to develop strain to displacement transformations. In Proceedings of the 13th International Modal Analysis Conference (IMAC), Nashville, TN, USA, 13–16 February 1995; Volume 2460, pp. 112–118. [Google Scholar]
- Rapp, S.; Kang, L.H.; Han, J.H.; Mueller, U.C.; Baier, H. Displacement field estimation for a two-dimensional structure using fiber Bragg grating sensors. Smart Mater. Struct. 2009, 18, 025006. [Google Scholar] [CrossRef]
- Glaser, R.; Caccese, V.; Shahinpoor, M. Shape monitoring of a beam structure from measured strain or curvature. Exp. Mech. 2012, 52, 591–606. [Google Scholar] [CrossRef]
- Bang, H.J.; Ko, S.W.; Jang, M.S.; Kim, H.I. Shape estimation and health monitoring of wind turbine tower using a FBG sensor array. In Proceedings of the International Instrumentation and Measurement Technology Conference Proceedings (2012 IEEE I2MTC), Graz, Austria, 13–16 May 2012; Number 3. pp. 496–500. [Google Scholar] [CrossRef]
- Wang, Z.C.; Geng, D.; Ren, W.X.; Liu, H.T. Strain modes based dynamic displacement estimation of beam structures with strain sensors. Smart Mater. Struct. 2014, 23, 125045. [Google Scholar] [CrossRef]
- Kim, H.I.; Han, J.H.; Bang, H.J. Real-time deformed shape estimation of a wind turbine blade using distributed fiber Bragg grating sensors. Wind Energy 2014, 17, 1455–1467. [Google Scholar] [CrossRef]
- Fu, G.; Untaroiu, A.; O’Brien, W. An approach to approximate the full strain field of turbofan blades during operation. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition Volume 7C: Structures and Dynamics, Oslo, Norway, 11–15 June 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Johns, W.; Davis, L.; Jankauski, M. Reconstructing full-field flapping wing dynamics from sparse measurements. Bioinspir. Biomim. 2021, 16, 016005. [Google Scholar] [CrossRef]
- Park, J.W.; Sim, S.H.; Jung, H.J. Displacement estimation using multimetric data fusion. IEEE/ASME Trans. Mechatron. 2013, 18, 1675–1682. [Google Scholar] [CrossRef]
- Papadioti, D.C. Management of Uncertainties in Structural Response and Reliability Simulations Using Measured Data. Ph.D. Thesis, University of Thessaly, Volos, Greece, 2015. [Google Scholar]
- Giagopoulos, D.; Arailopoulos, A.; Azam, S.E.; Papadimitriou, C.; Chatzi, E.; Grompanopoulos, K. Dynamic response estimation and fatigue prediction in a linear substructure of a complex mechanical assembly. In Proceedings of the 8th European Workshop on Structural Health Monitoring (EWSHM), Bilbao, Spain, 5–8 July 2016; Volume 2, pp. 890–899. [Google Scholar]
- Tarpø, M.; Friis, T.; Nabuco, B.; Amador, S.; Katsanos, E.; Brincker, R. Operational modal analysis based stress estimation in friction systems. In Nonlinear Dynamics; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2019; Volume 1, pp. 143–153. [Google Scholar] [CrossRef]
- Tatsis, K.E.; Dertimanis, V.K.; Papadimitriou, C.; Lourens, E.; Chatzi, E.N. A general substructure-based framework for input-state estimation using limited output measurements. Mech. Syst. Signal Process. 2021, 150, 107223. [Google Scholar] [CrossRef]
- Zhang, X.H.; Xu, Y.L.; Zhu, S.; Zhan, S. Dual-type sensor placement for multi-scale response reconstruction. Mechatronics 2014, 24, 376–384. [Google Scholar] [CrossRef]
- Argyris, C.; Papadimitriou, C.; Panetsos, P. Bayesian optimal sensor placement for modal identification of civil infrastructures. J. Smart Cities 2017, 2, 69–86. [Google Scholar] [CrossRef]
- Kullaa, J. Bayesian virtual sensing for full-field dynamic response estimation. Procedia Eng. 2017, 199, 2126–2131. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Argyris, C. Bayesian optimal experimental design for parameter estimation and response predictions in complex dynamical systems. Procedia Eng. 2017, 199, 972–977. [Google Scholar] [CrossRef]
- Kullaa, J. Bayesian virtual sensing in structural dynamics. Mech. Syst. Signal Process. 2019, 115, 497–513. [Google Scholar] [CrossRef]
- Kullaa, J. Structural health monitoring using a large sensor network and Bayesian virtual sensors. In Proceedings of the 1st International Conference on Advances in Signal Processing and Artificial Intelligence, Barcelona, Spain, 20–22 March 2019; IFSA Publishing: Barcelona, Spain, 2019; pp. 20–22. [Google Scholar]
- Kullaa, J. Robust damage detection using Bayesian virtual sensors. Mech. Syst. Signal Process. 2020, 135, 106384. [Google Scholar] [CrossRef]
- Kullaa, J. Robust damage detection in the time domain using Bayesian virtual sensing with noise reduction and environmental effect elimination capabilities. J. Sound Vib. 2020, 473, 115232. [Google Scholar] [CrossRef]
- Ercan, T.; Sedehi, O.; Papadimitriou, C.; Katafygiotis, L.S. Robust optimal sensor placement for response reconstruction using output only vibration measurements. In Proceedings of the 29th European Safety and Reliability Conference, (ESREL), Hannover, Germany, 22–26 September 2019; Research Publishing Services: Singapore, 2019; pp. 1270–1276. [Google Scholar] [CrossRef]
- Argyris, C.; Papadimitriou, C.; Samaey, G.; Lombaert, G. A unified sampling-based framework for optimal sensor placement considering parameter and prediction inference. Mech. Syst. Signal Process. 2021, 161, 107950. [Google Scholar] [CrossRef]
- Barthorpe, R.J.; Worden, K. Emerging trends in optimal structural health monitoring system design: From sensor placement to system evaluation. J. Sens. Actuator Netw. 2020, 9, 31. [Google Scholar] [CrossRef]
- Shah, P.C.; Udwadia, F.E. A methodology for optimal sensor locations for identification of dynamic systems. J. Appl. Mech. 1978, 45, 188–196. [Google Scholar] [CrossRef]
- Udwadia, F.E. Methodology for optimum sensor locations for parameter identification in dynamic systems. J. Eng. Mech. 1994, 120, 368–390. [Google Scholar] [CrossRef]
- Kirkegaard, P.H.; Brincker, R. On the optimal location of sensors for parametric identification of linear structural systems. Mech. Syst. Signal Process. 1994, 8, 639–647. [Google Scholar] [CrossRef]
- Ucinski, D. Optimal sensor location for parameter estimation of distributed processes. Int. J. Control 2000, 73, 1235–1248. [Google Scholar] [CrossRef]
- Qureshi, Z.H.; Ng, T.S.; Goodwin, G.C. Optimum experimental design for identification of distributed parameter systems. Int. J. Control 1980, 31, 21–29. [Google Scholar] [CrossRef]
- Kammer, D.C. Sensor placement for on-orbit modal identification and correlation of large space structures. J. Guid. Control. Dyn. 1991, 14, 251–259. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Beck, J.L.; Au, S.K. Entropy-based optimal sensor location for structural model updating. JVC J. Vib. Control 2000, 6, 781–800. [Google Scholar] [CrossRef]
- Yuen, K.V.; Katafygiotis, L.S.; Papadimitriou, C.; Mickleborough, N.C. Optimal sensor placement methodology for identification with unmeasured excitation. J. Dyn. Syst. Meas. Control. Trans. ASME 2001, 123, 677–686. [Google Scholar] [CrossRef]
- Papadimitriou, C. Optimal sensor placement methodology for parametric identification of structural systems. J. Sound Vib. 2004, 278, 923–947. [Google Scholar] [CrossRef]
- Robert-Nicoud, Y.; Raphael, B.; Smith, I.F. Configuration of measurement systems using Shannon’s entropy function. Comput. Struct. 2005, 83, 599–612. [Google Scholar] [CrossRef]
- Yuen, K.V.; Kuok, S.C. Efficient Bayesian sensor placement algorithm for structural identification: A general approach for multi-type sensory systems. Earthq. Eng. Struct. Dyn. 2015, 44, 757–774. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Lombaert, G. The effect of prediction error correlation on optimal sensor placement in structural dynamics. Mech. Syst. Signal Process. 2012, 28, 105–127. [Google Scholar] [CrossRef]
- Bertola, N.J.; Pai, S.G.S.; Smith, I.F.C. A methodology to design measurement systems when multiple model classes are plausible. J. Civ. Struct. Health Monit. 2021, 11, 1–22. [Google Scholar] [CrossRef]
- Stephan, C. Sensor placement for modal identification. Mech. Syst. Signal Process. 2012, 27, 461–470. [Google Scholar] [CrossRef]
- Ye, S.Q.; Ni, Y.Q. Information entropy based algorithm of sensor placement optimization for structural damage detection. Smart Struct. Syst. 2012, 10, 443–458. [Google Scholar] [CrossRef]
- Chow, H.M.; Lam, H.F.; Yin, T.; Au, S.K. Optimal sensor configuration of a typical transmission tower for the purpose of structural model updating. Struct. Control Health Monit. 2011, 18, 305–320. [Google Scholar] [CrossRef]
- Yin, T.; Lam, H.F.; Chow, H.M. A Bayesian probabilistic approach for crack characterization in plate structures. Comput. Aided Civ. Infrastruct. Eng. 2010, 25, 375–386. [Google Scholar] [CrossRef]
- Yin, T.; Yuen, K.V.; Lam, H.F.; Zhu, H.P. Entropy-based optimal sensor placement for model identification of periodic structures endowed with bolted joints. Comput. Aided Civ. Infrastruct. Eng. 2017, 32, 1007–1024. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Astroza, R.; Conte, J.P.; Bitmead, R.R. Information-theoretic approach for identifiability assessment of nonlinear structural finite-element models. J. Eng. Mech. 2019, 145, 04019039. [Google Scholar] [CrossRef]
- Bertola, N.J.; Papadopoulou, M.; Vernay, D.; Smith, I.F. Optimal multi-type sensor placement for structural identification by static-load testing. Sensors 2017, 17, 2904. [Google Scholar] [CrossRef]
- Papadopoulou, M.; Raphael, B.; Smith, I.F.; Sekhar, C. Hierarchical sensor placement using joint entropy and the effect of modeling error. Entropy 2014, 16, 5078–5101. [Google Scholar] [CrossRef]
- Huan, X.; Marzouk, Y.M. Simulation-based optimal Bayesian experimental design for nonlinear systems. J. Comput. Phys. 2013, 232, 288–317. [Google Scholar] [CrossRef]
- Lindley, D.V. On a measure of the information provided by an experiment. Ann. Math. Stat. 1956, 27, 986–1005. [Google Scholar] [CrossRef]
- Chaloner, K.; Verdinelli, I. Bayesian experimental design: A review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Bhattacharyya, P.; Beck, J. Exploiting convexification for Bayesian optimal sensor placement by maximization of mutual information. Struct. Control Health Monit. 2020, 27, 1–18. [Google Scholar] [CrossRef]
- Argyris, C. Bayesian Uncertainty Quantification and Optimal Experimental Design in Data Driven Simulations of Engineering Systems. Ph.D. Thesis, University of Thessaly, Volos, Greece, 2010. [Google Scholar]
- Malings, C.; Pozzi, M. Value of information for spatially distributed systems: Application to sensor placement. Reliab. Eng. Syst. Saf. 2016, 154, 219–233. [Google Scholar] [CrossRef]
- Cantero-Chinchilla, S.; Chiachío, J.; Chiachío, M.; Chronopoulos, D.; Jones, A. Optimal sensor configuration for ultrasonic guided-wave inspection based on value of information. Mech. Syst. Signal Process. 2020, 135, 106377. [Google Scholar] [CrossRef]
- Malings, C.; Pozzi, M. Submodularity issues in value-of-information-based sensor placement. Reliab. Eng. Syst. Saf. 2019, 183, 93–103. [Google Scholar] [CrossRef]
- Pasquier, R.; Goulet, J.A.; Smith, I.F. Measurement system design for civil infrastructure using expected utility. Adv. Eng. Inform. 2017, 32, 40–51. [Google Scholar] [CrossRef]
- Li, B.; Der Kiureghian, A. Robust optimal sensor placement for operational modal analysis based on maximum expected utility. Mech. Syst. Signal Process. 2016, 75, 155–175. [Google Scholar] [CrossRef]
- Leyder, C.; Chatzi, E.; Frangi, A.; Lombaert, G. Comparison of optimal sensor placement algorithms via implementation on an innovative timber structure. In Life-Cycle of Engineering Systems: Emphasis on Sustainable Civil Infrastructure; Bakker, J., Frangopol, D.M., van Breugel, K., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 260–267. [Google Scholar] [CrossRef]
- Green, P.L.; Cross, E.J.; Worden, K. Bayesian system identification of dynamical systems using highly informative training data. Mech. Syst. Signal Process. 2015, 56, 109–122. [Google Scholar] [CrossRef]
- Leyder, C.; Ntertimanis, V.; Chatzi, E.; Frangi, A. Optimal sensor placement for the modal identification of an innovative timber structure. In Proceedings of the 1st International Conference on Uncertainty Quantification in Computational Sciences and Engineering (UNCECOMP), Crete Island, Greece, 25–27 May 2015; pp. 467–476. [Google Scholar] [CrossRef]
- Capellari, G.; Chatzi, E.; Mariani, S. Structural health monitoring sensor network optimization through Bayesian experimental design. ASCE ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2018, 4, 04018016. [Google Scholar] [CrossRef]
- Capellari, G.; Chatzi, E.; Mariani, S. Cost–benefit optimization of structural health monitoring sensor networks. Sensors 2018, 18, 2174. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Haralampidis, Y.; Sobczyk, K. Optimal experimental design in stochastic structural dynamics. Probabilistic Eng. Mech. 2005, 20, 67–78. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Ryan, K.J. Estimating Expected Information Gains for Experimental Designs with Application to the Random Fatigue-Limit Model. J. Comput. Graph. Stat. 2003, 12, 585–603. [Google Scholar] [CrossRef]
- Gerstner, T.; Griebel, M. Numerical integration using sparse grids. Numer. Algorithms 1998, 18, 209–232. [Google Scholar] [CrossRef]
- Heiss, F.; Winschel, V. Likelihood approximation by numerical integration on sparse grids. J. Econom. 2008, 144, 62–80. [Google Scholar] [CrossRef]
- Hofmeister, B.; Bruns, M.; Rolfes, R. Finite element model updating using deterministic optimisation: A global pattern search approach. Eng. Struct. 2019, 195, 373–381. [Google Scholar] [CrossRef]
- Girardi, M.; Padovani, C.; Pellegrini, D.; Robol, L. A finite element model updating method based on global optimization. Mech. Syst. Signal Process. 2021, 152, 107372. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Worden, K.; Staszewski, W.J. Impact location and quantification on a composite panel using neural networks and a genetic algorithm. Strain 2000, 36, 61–68. [Google Scholar] [CrossRef]
- Abdullah, M.M.; Richardson, A.; Hanif, J. Placement of sensors/actuators on civil structures using genetic algorithms. Earthq. Eng. Struct. Dyn. 2001, 30, 1167–1184. [Google Scholar] [CrossRef]
- Yao, L.; Sethares, W.A.; Kammer, D.C. Sensor placement for on-orbit modal identification via a genetic algorithm. AIAA J. 1993, 31, 1922–1928. [Google Scholar] [CrossRef]
- Bianconi, F.; Salachoris, G.P.; Clementi, F.; Lenci, S. A genetic algorithm procedure for the automatic updating of fem based on ambient vibration tests. Sensors 2020, 20, 3315. [Google Scholar] [CrossRef] [PubMed]
- Papadimitriou, D.I.; Papadimitriou, C. Optimal Sensor Placement for the Estimation of Turbulence Model Parameters in CFD. Int. J. Uncertain. Quantif. 2015, 5, 545–568. [Google Scholar] [CrossRef]






| Natural Frequency (Hz) | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | Mode 7 | Mode 8 |
|---|---|---|---|---|---|---|---|---|
| Coarse mesh | 0.956 | 2.344 | 5.897 | 7.520 | 8.563 | 14.989 | 17.176 | 17.895 |
| Fine mesh | 0.956 | 2.344 | 5.868 | 7.497 | 8.532 | 14.934 | 16.909 | 17.696 |
| % difference | 0.00 | 0.00 | 0.49 | 0.31 | 0.36 | 0.37 | 1.55 | 1.11 |
| Measurement Error | s | ||
|---|---|---|---|
| Very small | |||
| Small | |||
| Moderate | |||
| Large |
| Measurement Error | s | ||
|---|---|---|---|
| Very small | |||
| Small | |||
| Moderate | |||
| Large |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ercan, T.; Papadimitriou, C. Optimal Sensor Placement for Reliable Virtual Sensing Using Modal Expansion and Information Theory. Sensors 2021, 21, 3400. https://doi.org/10.3390/s21103400
Ercan T, Papadimitriou C. Optimal Sensor Placement for Reliable Virtual Sensing Using Modal Expansion and Information Theory. Sensors. 2021; 21(10):3400. https://doi.org/10.3390/s21103400
Chicago/Turabian StyleErcan, Tulay, and Costas Papadimitriou. 2021. "Optimal Sensor Placement for Reliable Virtual Sensing Using Modal Expansion and Information Theory" Sensors 21, no. 10: 3400. https://doi.org/10.3390/s21103400
APA StyleErcan, T., & Papadimitriou, C. (2021). Optimal Sensor Placement for Reliable Virtual Sensing Using Modal Expansion and Information Theory. Sensors, 21(10), 3400. https://doi.org/10.3390/s21103400







