Remote Sensing of Dispersed Oil Pollution in the Ocean—The Role of Chlorophyll Concentration
Abstract
1. Introduction
2. Materials and Methods
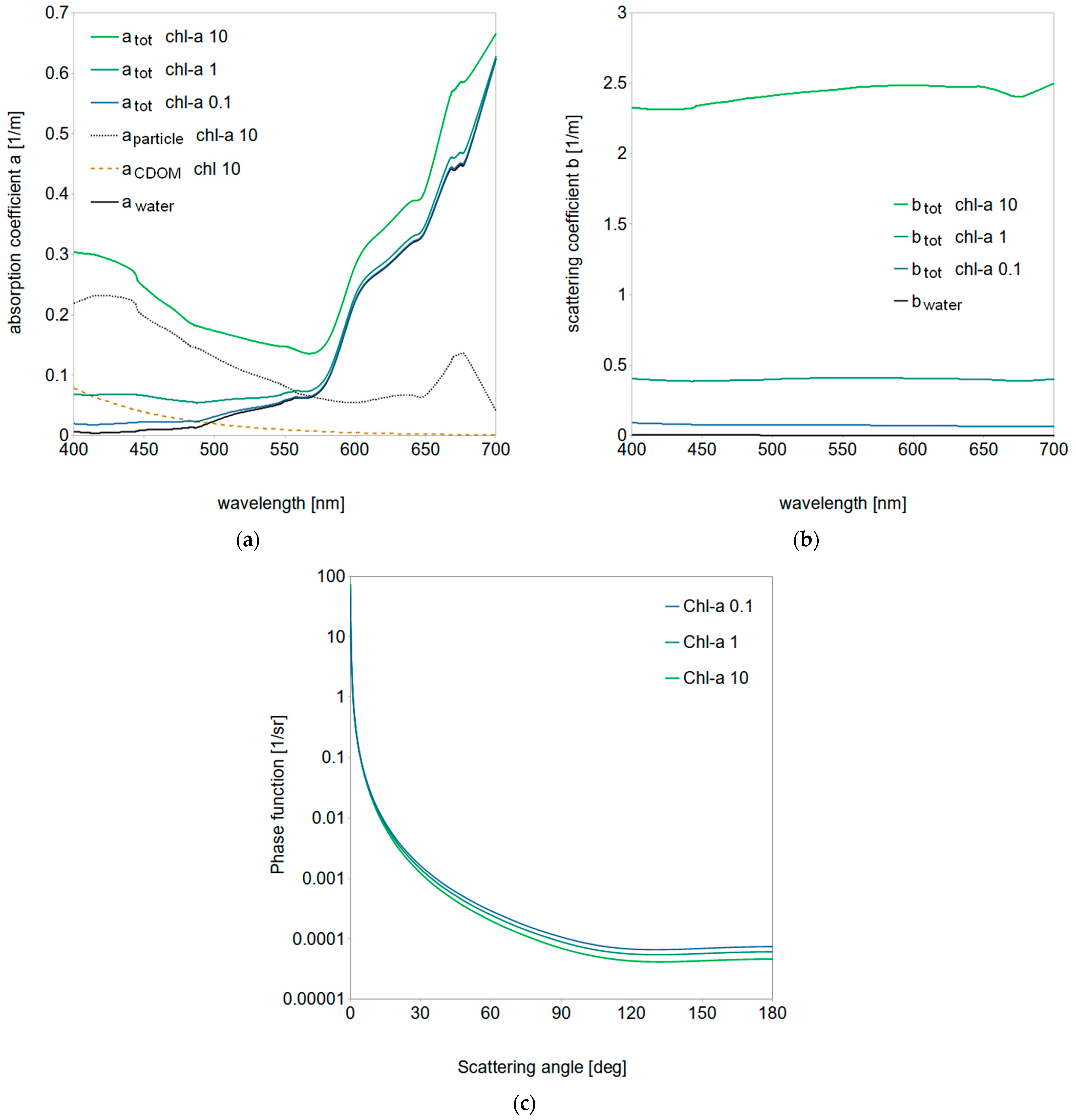
2.1. Optical Model of Oceanic Water
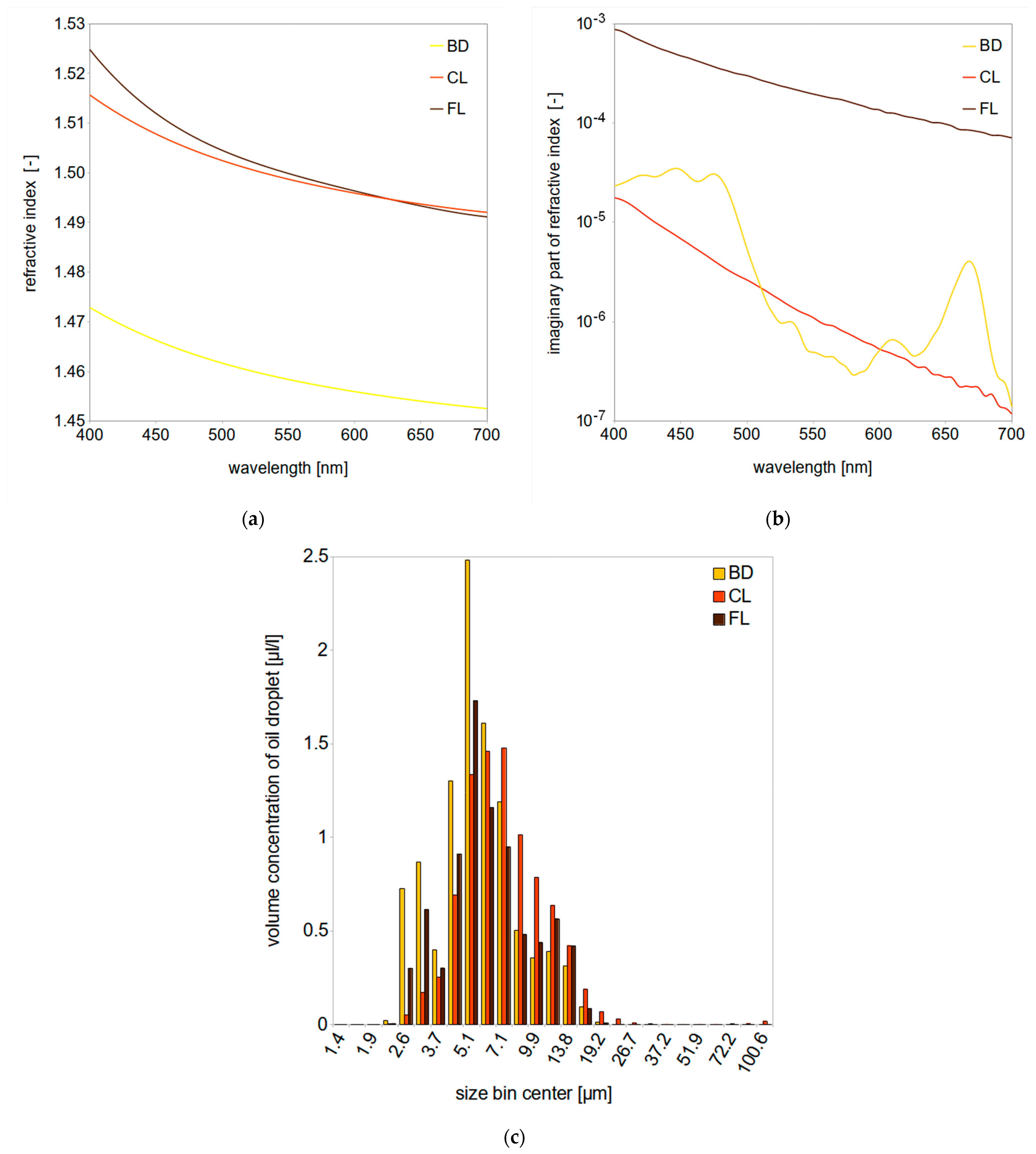
2.2. Optical Model of Dispersed Oil
- Cylinder lubricant oil Cyliten N460 (CL), commercially available at LOTOS S.A., formulated upon deeply refined, dewaxed and hydrorefined mineral oils (>80%) with low susceptibility to coking, and greased with vegetable oil (<20%) to improve lubrication properties [60]. It is designed for lubrication of high-pressure compressors and other special applications as low-speed gears, e.g., in marine ship engine systems.
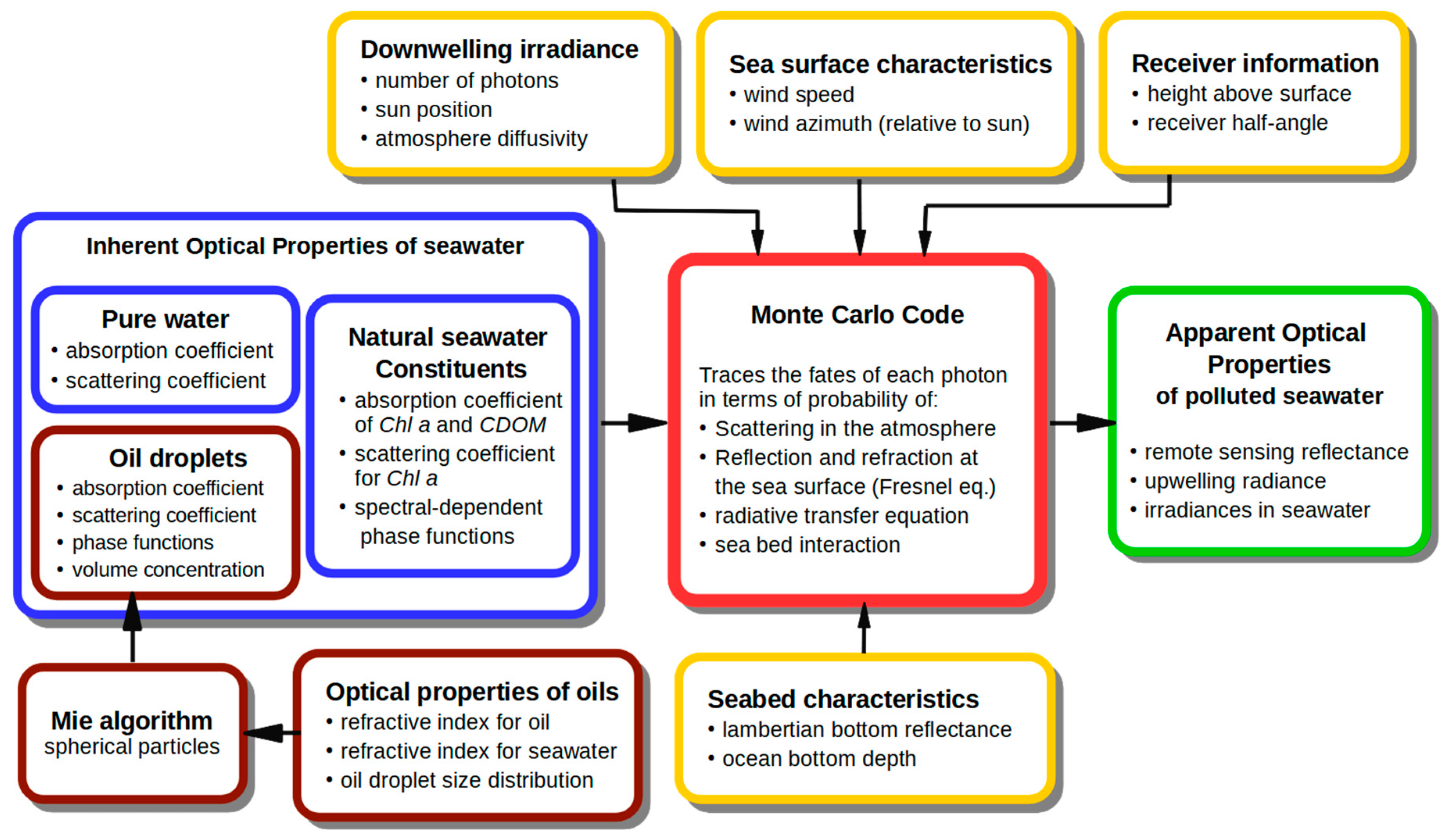
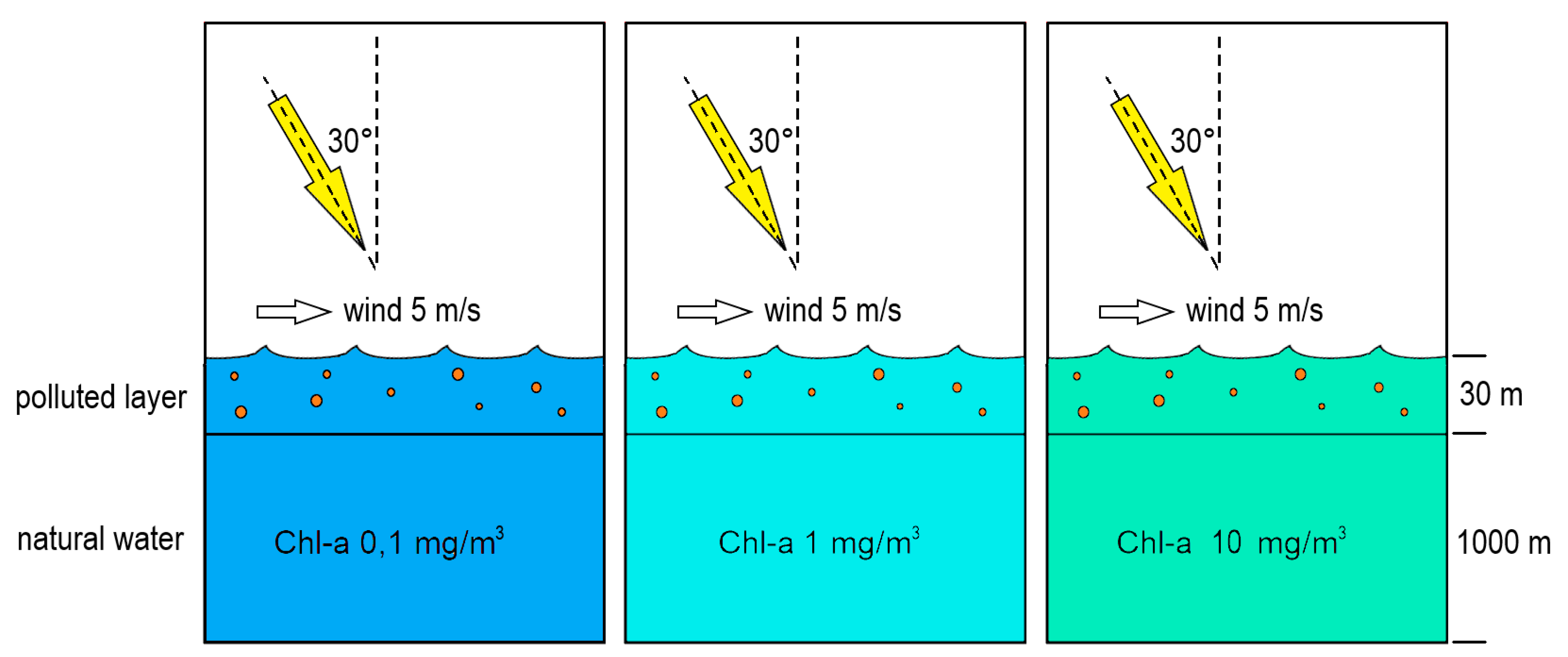
2.3. Radiative Transfer Simulation Setup
3. Results
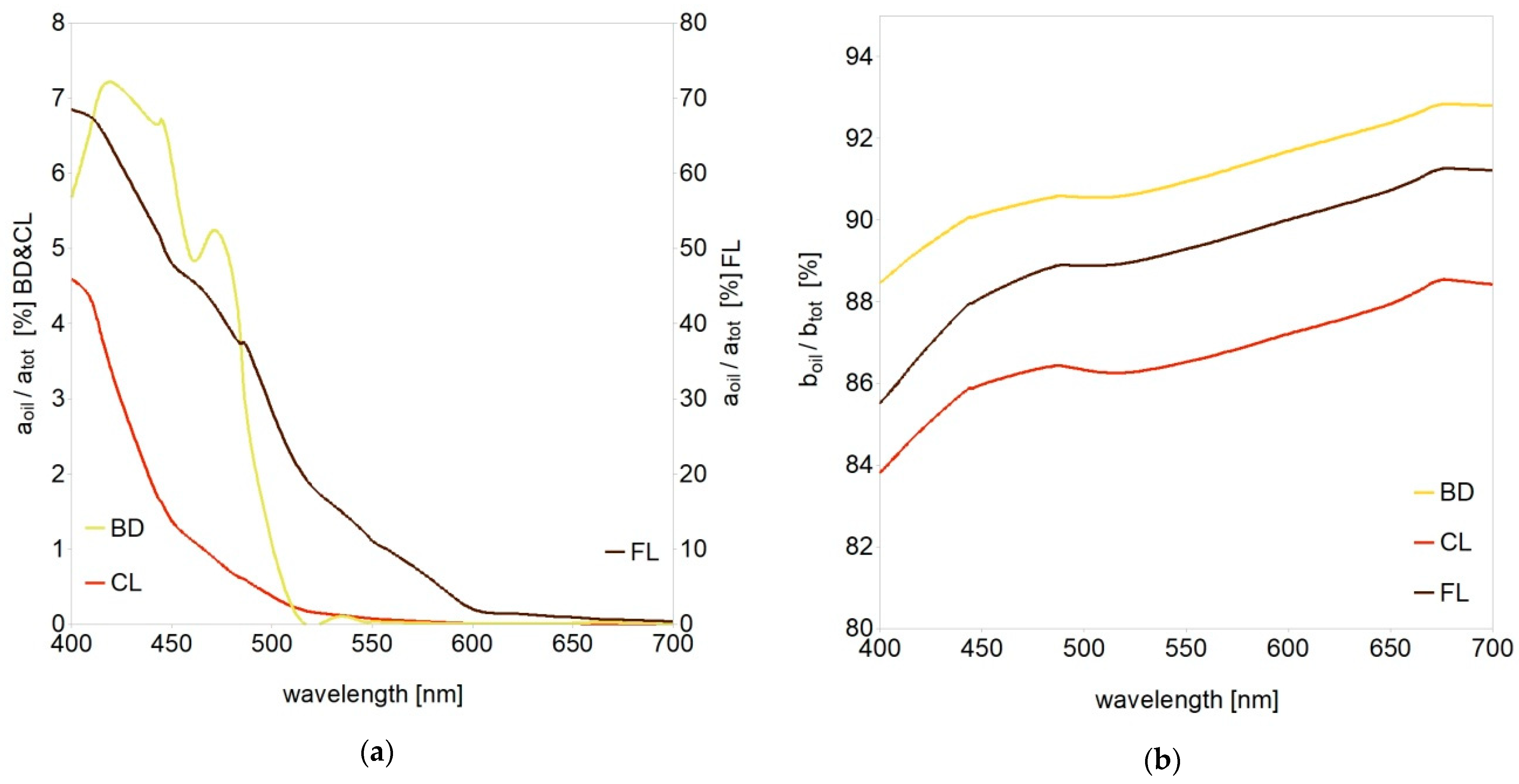
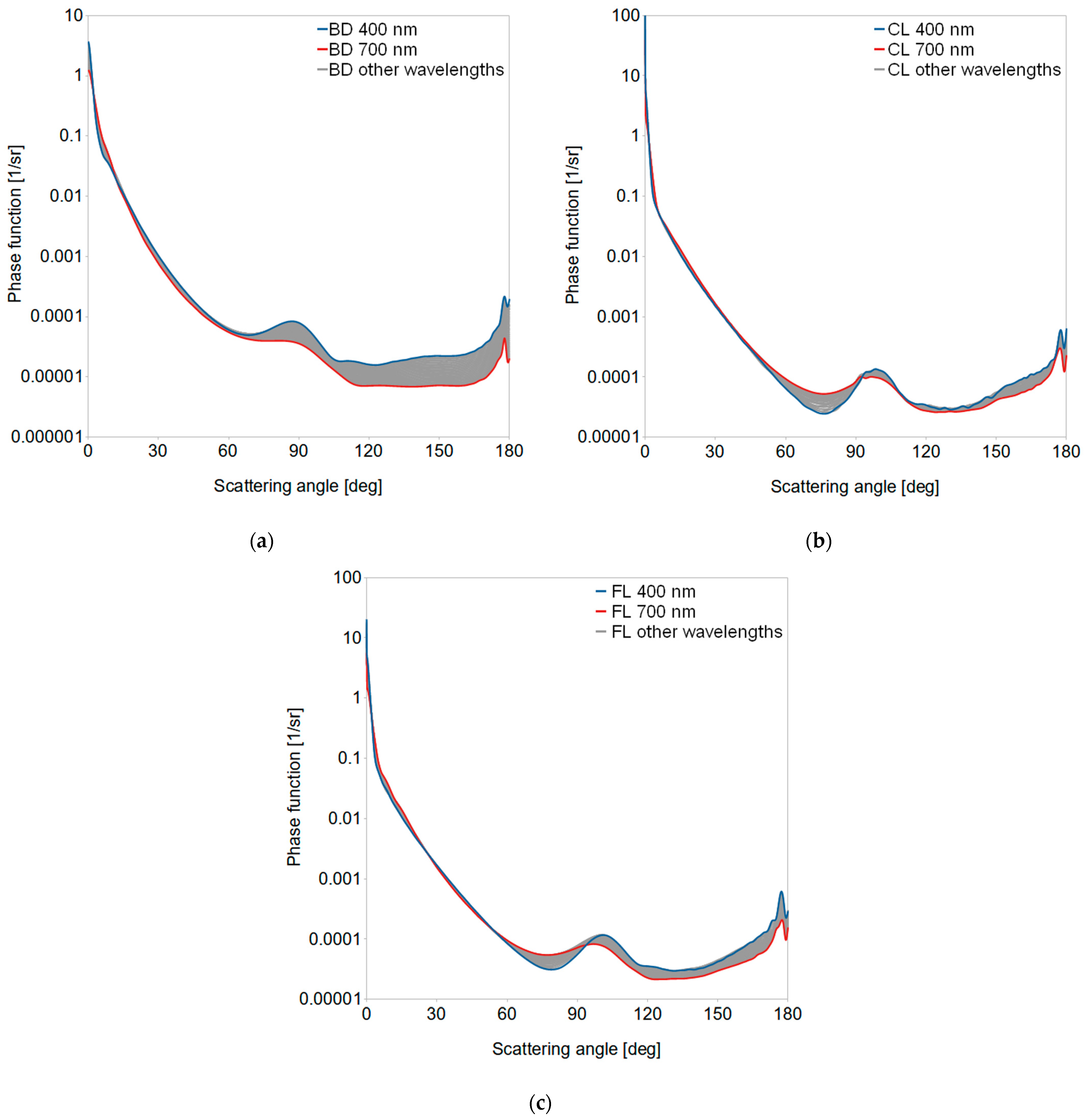
3.1. Dispersed Oil Optical Properties
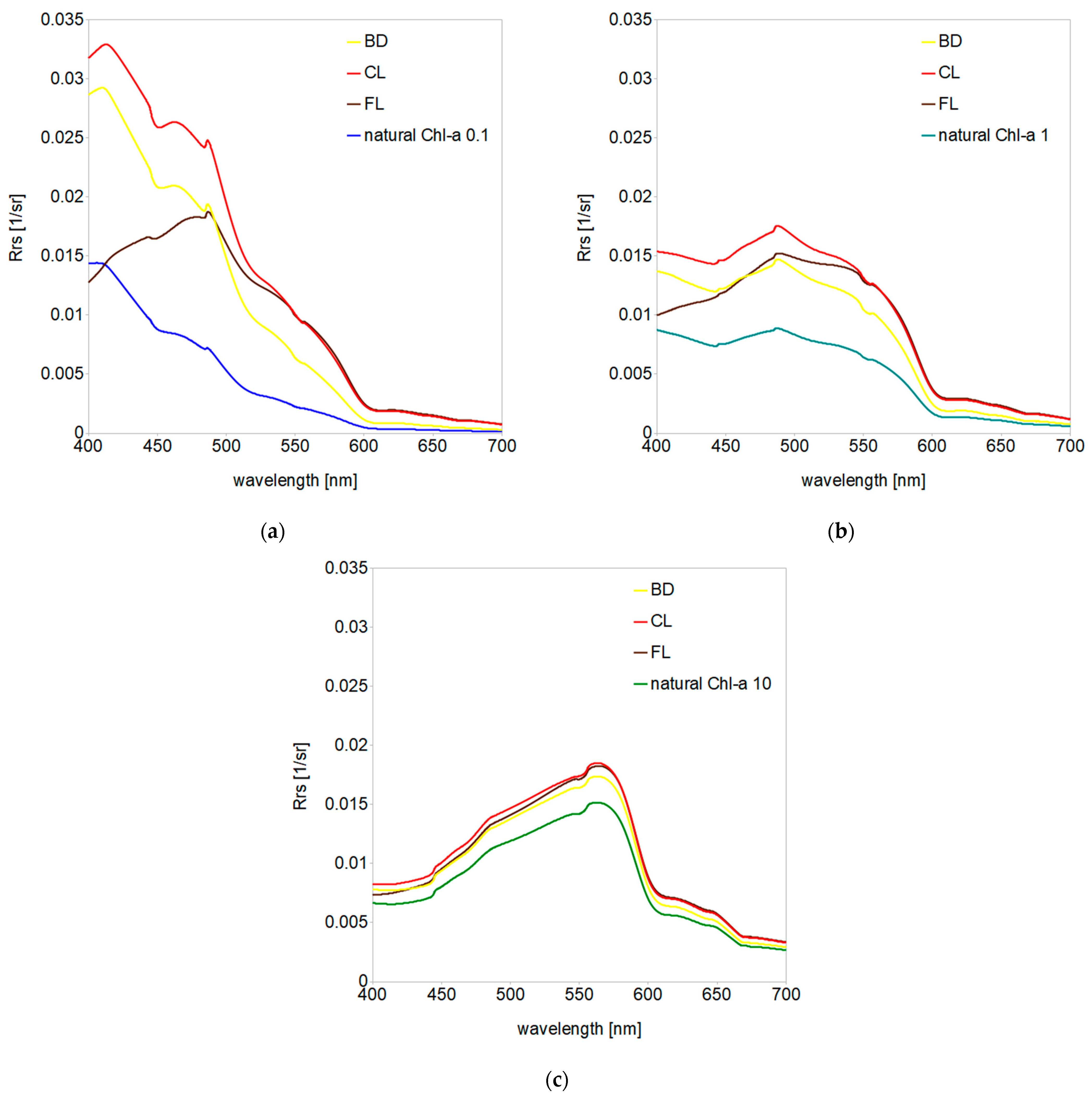
3.2. Remote Sensing Reflectance of Oceanic Water Polluted by Dispersed Oils
4. Discussion
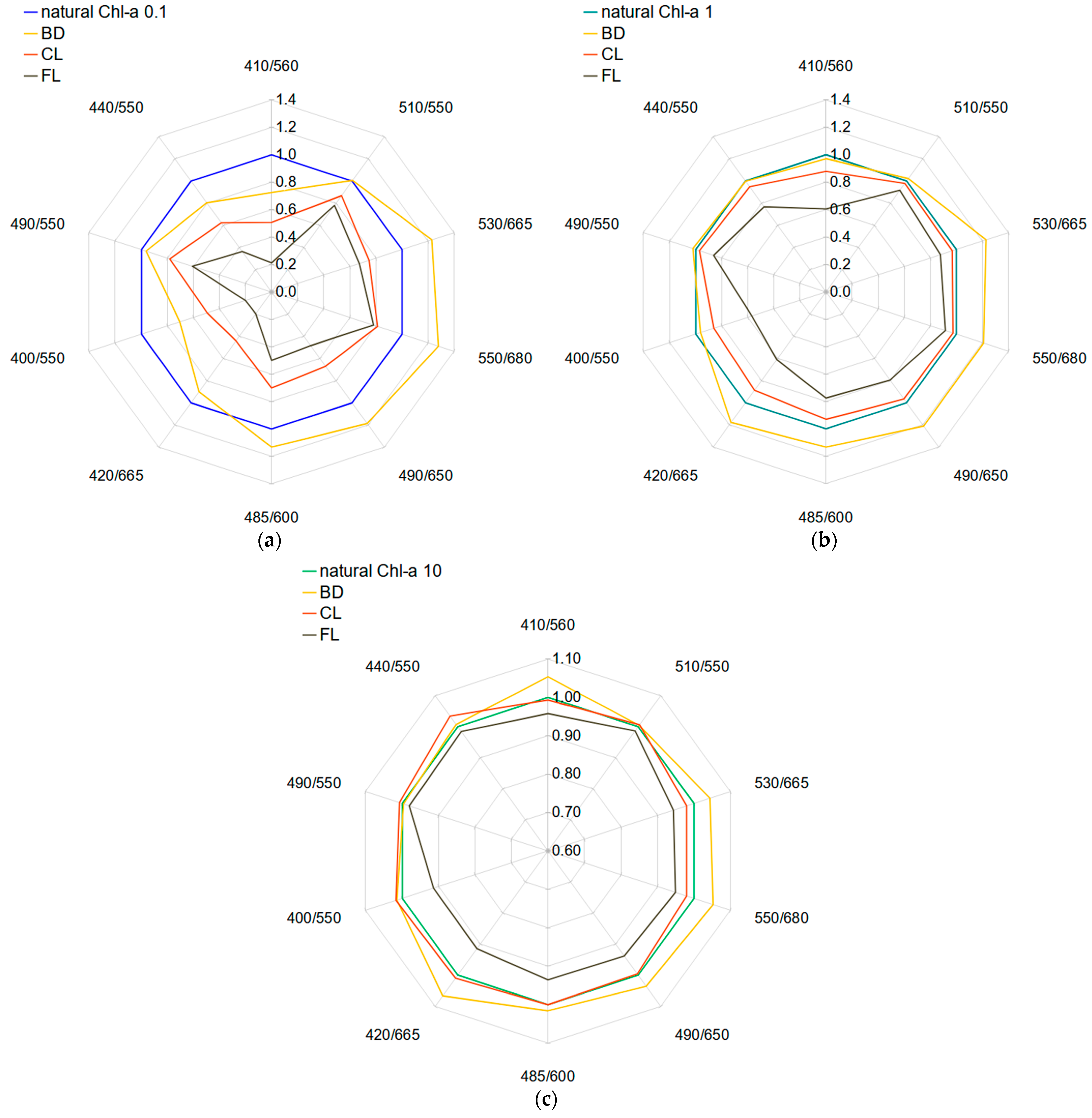
4.1. Influence of Water Type on the Visibility of Dispersed Oil—Analysis of Ocean Color Rrs Band Ratios and Band Differences
4.2. Color Index in Oligotrophic Ocean Waters
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kostianoy, A.G.; Lavrova, O.Y.; Mityagina, M.I.; Solovyov, D.M.; Lebedev, S.A. Satellite Monitoring of Oil Pollution in the Southeastern Baltic Sea. In Oil Pollution in the Baltic Sea; Kostianoy, A.G., Lavrova, O.Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 27, pp. 125–152. [Google Scholar] [CrossRef]
- Transportation Research Board and National Research Council. Oil in the Sea III: Inputs, Fates, and Effects; The National Academies Press: Washington, DC, USA, 2003. [Google Scholar] [CrossRef]
- Muttin, F.; Campbell, R. Oil Spill Containment in Open Areas: Four Atlantic and Mediterranean Experiments. In Oil Spill Studies: Healing the Ocean, Biomarking and the Law; Muttin, F., Ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2018; pp. 19–43. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, X.; Cai, Z.; O’Reilly, S.E.; Hao, X.; Zhao, D. A review of oil, dispersed oil and sediment interactions in the aquatic environment: Influence on the fate, transport and remediation of oil spills. Mar. Pollut. Bull. 2014, 79, 16–33. [Google Scholar] [CrossRef] [PubMed]
- Johansen, Ø.; Reed, M.; Bodsberg, N.R. Natural dispersion revisited. Mar. Pollut. Bull. 2015, 93, 20–26. [Google Scholar] [CrossRef] [PubMed]
- Prince, R.C. Oil Spill Dispersants: Boon or Bane? Environ. Sci. Technol. 2015, 49, 6376–6384. [Google Scholar] [CrossRef]
- Hazen, T.C.; Prince, R.C.; Mahmoudi, N. Marine Oil Biodegradation. Environ. Sci. Technol. 2016, 50, 2121–2129. [Google Scholar] [CrossRef]
- Brakstad, O.G.; Ribicic, D.; Winkler, A.; Netzer, R. Biodegradation of dispersed oil in seawater is not inhibited by a commercial oil spill dispersant. Mar. Pollut. Bull. 2018, 129, 555–561. [Google Scholar] [CrossRef]
- Li, Z.; Lee, K.; King, T.; Boufadel, M.C.; Venosa, A.D. Evaluating crude oil chemical dispersion efficacy in a flow-through wave tank under regular non-breaking wave and breaking wave conditions. Mar. Pollut. Bull. 2009, 58, 735–744. [Google Scholar] [CrossRef] [PubMed]
- Delvigne, G.A. Droplet Size Distribution of Naturally Dispersed Oil. In Fate and Effects of Oil in Marine Ecosystems; Kuiper, J., Van Den Brink, W.J., Eds.; Springer: Dordrecht, The Netherlands, 1987. [Google Scholar] [CrossRef]
- Counihan, K.L. The physiological effects of oil, dispersant and dispersed oil on the bay mussel, Mytilus Trossulus, in Arctic/Subarctic conditions. Aqua. Tox. 2018, 199, 220–231. [Google Scholar] [CrossRef] [PubMed]
- Hansen, B.H.; Altin, D.; Olsen, A.J.; Nordtug, T. Acute toxicity of naturally and chemically dispersed oil on the filter-feeding copepod Calanus finmarchicus. Ecotoxicol. Environ. Saf. 2012, 86, 38–46. [Google Scholar] [CrossRef]
- Agamy, E. Histopathological changes in the livers of rabbit fish (Siganus canaliculatus) following exposure to crude oil and dispersed oil. Toxicol. Pathol. 2012, 40, 1128–1140. [Google Scholar] [CrossRef]
- Anyadiegwu, C.I.C.; Uwaezuoke, N. Benthic Studies and Environmental Assessment in the Oil Producing Area of the Niger Delta. Am. J. Environ. Prot. 2015, 3, 37–43. [Google Scholar] [CrossRef]
- Jorissen, F.J.; Bicchi, E.; Duchemin, G.; Durrieu, J.; Galgani, F.; Cazes, L.; Gaultier, M.; Camps, R. Impact of oil-based drill mud disposal on benthic foraminiferal assemblages on the continental margin off Angola. Deep Sea Res. Part II 2009, 56, 2270–2291. [Google Scholar] [CrossRef]
- Bera, G.; Doyle, S.; Passow, U.; Kamalanathan, M.; Wade, T.L.; Sylvan, J.B.; Sericano, J.L.; Gold, G.; Quigg, A.; Knap, A.H. Biological response to dissolved versus dispersed oil. Mar. Pollut. Bull. 2020, 150, 110713. [Google Scholar] [CrossRef] [PubMed]
- Almeda, R.; Baca, S.; Hyatt, C.; Buskey, E.J. Ingestion and sublethal effects of physically and chemically dispersed crude oil on marine planktonic copepods. Ecotoxicology 2014, 23, 988–1003. [Google Scholar] [CrossRef]
- Zeng, X.; Chen, X.; Zhuang, J. The positive relationship between ocean acidification and pollution. Mar. Pollut. Bull. 2015, 91, 14–21. [Google Scholar] [CrossRef]
- Rahikainen, M.; Hoviniemi, K.-M.; Mäntyniemi, S.; Vanhatalo, J.; Helle, I.; Lehtiniemi, M.; Pönni, J.; Kuikka, S. Impacts of eutrophication and oil spills on the Gulf of Finland herring stock. Can. J. Fish. Aquat. Sci. 2017, 74, 1218–1232. [Google Scholar] [CrossRef]
- Al-Ruzouq, R.; Gibril, M.B.A.; Shanableh, A.; Kais, A.; Hamed, O.; Al-Mansoori, S.; Khalil, M.A. Sensors, features, and machine learning for oil spill detection and monitoring: A review. Remote Sens. 2020, 12, 3338. [Google Scholar] [CrossRef]
- Fingas, M.; Brown, C.E. A review of oil spill remote sensing. Sensors 2018, 18, 91. [Google Scholar] [CrossRef] [PubMed]
- Henry, I.A.; Netzer, R.; Davies, E.; Brakstad, O.G. The influences of phytoplankton species, mineral particles and concentrations of dispersed oil on the formation and fate of marine oil-related aggregates. Sci. Total Environ. 2021, 752. [Google Scholar] [CrossRef] [PubMed]
- Uttieri, M.; Nihongi, A.; Hinow, P.; Motschman, J.; Jiang, H.; Alcaraz, M.; Strickler, J.R. Copepod manipulation of oil droplet size distribution. Sci. Rep. 2019, 9, 547. [Google Scholar] [CrossRef]
- Bacosa, H.P.; Erdner, D.L.; Liu, Z. Differentiating the roles of photooxidation and biodegradation in the weathering of Light Louisiana Sweet crude oil in surface water from the Deepwater Horizon site. Mar. Pollut. Bull. 2015, 95, 265–272. [Google Scholar] [CrossRef]
- Bacosa, H.P.; Liu, Z.; Erdner, D.L. Natural Sunlight Shapes Crude Oil-Degrading Bacterial Communities in Northern Gulf of Mexico Surface Waters. Front. Microbiol. 2015, 6, 1325. [Google Scholar] [CrossRef]
- Bretherton, L.; Hillhouse, J.; Bacosa, H.; Setta, S.; Genzer, J.; Kamalanathan, M.; Finkel, Z.V.; Quigg, A. Growth dynamics and domoic acid production of Pseudo-nitzschia sp. in response to oil and dispersant exposure. Harmful Algae 2019, 86, 55–63. [Google Scholar] [CrossRef]
- Li, J.; An, W.; Gao, H.; Zhao, Y.; Sun, Y. An experimental study on oil droplet size distribution in subsurface oil releases. Acta Oceanolog. Sin. 2018, 37, 88–95. [Google Scholar] [CrossRef]
- Nissanka, I.D.; Yapa, P.D. Calculation of oil droplet size distribution in ocean oil spills: A review. Mar. Pollut. Bull. 2018, 135, 723–734. [Google Scholar] [CrossRef]
- Fingas, M.F.; Yetilmezsoy, K.; Bahramian, M. Development of an Algorithm for Chemically Dispersed Oil Spills. Front. Mar. Sci. 2020, 7, 600614. [Google Scholar] [CrossRef]
- Baszanowska, E.; Otremba, Z. Synchronous fluorescence spectra of water contaminated by dispersed crude oil. Opt. Appl. 2020, 50, 161–169. [Google Scholar] [CrossRef]
- Conmy, R.N.; Coble, P.G.; Farr, J.; Wood, A.M.; Lee, K.; Pegau, W.S.; Walsh, I.D.; Koch, C.R.; Abercrombie, M.I.; Miles, M.S.; et al. Submersible optical sensors exposed to chemically dispersed crude oil: Wave tank simulations for improved oil spill monitoring. Environ. Sci. Technol. 2014, 48, 1803–1810. [Google Scholar] [CrossRef]
- Drozdowska, V.; Freda, W.; Baszanowska, E.; Rudź, K.; Darecki, M.; Heldt, J.R.; Toczek, H. Spectral properties of natural and oil polluted Baltic seawater-results of measurements and modelling. Eur. Phys. J. Spec. Top. 2013, 222, 2157–2170. [Google Scholar] [CrossRef]
- Mendoza, W.G.; Riemer, D.D.; Zika, R.G. Application of fluorescence and PARAFAC to assess vertical distribution of subsurface hydrocarbons and dispersant during the Deepwater Horizon oil spill. Environ. Sci. Proc. Impacts 2013, 15, 1017–1030. [Google Scholar] [CrossRef]
- Hu, C.; Lu, Y.; Sun, S.; Liu, Y. Optical Remote Sensing of Oil Spills in the Ocean: What Is Really Possible? J. Remote Sens. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Jha, M.N.; Levy, J.; Gao, Y. Advances in remote sensing for oil spill disaster management: State-of-the-art sensors technology for oil spill surveillance. Sensors 2008, 8, 236–255. [Google Scholar] [CrossRef]
- Konik, M.; Kowalczuk, P.; Zabłocka, M.; Makarewicz, A.; Meler, J.; Zdun, A.; Darecki, M. Empirical relationships between remote-sensing reflectance and selected inherent optical properties in nordic sea surfacewaters for the MODIS and OLCI ocean colour sensors. Remote Sens. 2020, 12, 2774. [Google Scholar] [CrossRef]
- Otremba, Z. Oil droplets as light absorbents in seawater. Opt. Express 2007, 15, 8592. [Google Scholar] [CrossRef] [PubMed]
- Otremba, Z. Oil droplet clouds suspended in the sea: Can they be remotely detected? Remote Sens. 2016, 8, 857. [Google Scholar] [CrossRef]
- Haule, K.; Freda, W. The effect of dispersed Petrobaltic oil droplet size on photosynthetically active radiation in marine environment. Environ. Sci. Pollut. Res. 2016, 23, 6506–6516. [Google Scholar] [CrossRef]
- Haule, K.; Darecki, M.; Toczek, H. Light penetration in seawater polluted by dispersed oil: Results of radiative transfer modelling. J. Europ. Opt. Soc. Rap. Publ. 2015, 10, 15052. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water, Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994; p. 592. [Google Scholar]
- Freda, W. Comparison of the spectral-angular properties of light scattered in the Baltic Sea and oil emulsions. J. Europ. Opt. Soc. Rap. Publ. 2014, 9, 6. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Xiao, S.; Yang, D. Effect of oil plumes on upper-ocean radiative transfer—A numerical study. Ocean. Modell. 2020, 145, 101522. [Google Scholar] [CrossRef]
- Liu, Q.; Cui, X.; Chen, W.; Liu, C.; Bai, J.; Zhang, Y.; Zhou, Y.; Liu, Z.; Xu, P.; Che, H.; et al. A semianalytic Monte Carlo radiative transfer model for polarized oceanic lidar: Experiment-based comparisons and multiple scattering effects analyses. J. Quant. Spectrosc. Radiat. Transf. 2019, 237, 106638. [Google Scholar] [CrossRef]
- Piskozub, J.; Stramski, D.; Terrill, E.; Melville, W.K. Small-scale effects of underwater bubble clouds on ocean reflectance: 3-D modeling results. Opt. Express 2009, 17, 11747–11752. [Google Scholar] [CrossRef] [PubMed]
- Konik, M.; Kowalewski, M.; Bradtke, K.; Darecki, M. The operational method of filling information gaps in satellite imagery using numerical models. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 68–82. [Google Scholar] [CrossRef]
- Haule, K.; Freda, W.; Darecki, M.; Toczek, H. Possibilities of optical remote sensing of dispersed oil in coastal waters. Estuar. Coast. Shelf Sci. 2017, 195, 76–87. [Google Scholar] [CrossRef]
- Haule, K. Modelling the Influence of Dispersed Oil Droplets on the Upwelling Light Flux in Seawater in Application to Satellite Remote Sensing. Ph.D. Thesis, Institute of Oceanology of Polish Academy of Sciences, Sopot, Poland, 17 June 2019. [Google Scholar]
- Morel, A.; Gentili, B.; Chami, M.; Ras, J. Bio-optical properties of high chlorophyll Case 1 waters and of yellow-substance-dominated Case 2 waters. Deep Sea Res. Part I Oceanogr. Res. Pap. 2006, 53, 1439–1459. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Werdell, J.P. Chlorophyll algorithms for ocean color sensors-OC4, OC5 & OC6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [CrossRef] [PubMed]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water II Integrating cavity measurements. Appl. Opt. 1997, 36, 8710. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Bricaud, A. Inherent optical properties of algal cells including picoplankton theoretical and experimental results. Can. Bull. Fish. Aquat. Sci. 1986, 214, 521–560. [Google Scholar]
- Mobley, C.D.; Sundman, L.K. HydroLight 5.2, EcoLight 5.2 Users’ Guide; Sequoia Scientific, Inc.: Bellevue, WA, USA, 2013; Available online: https://www.sequoiasci.com/wp-content/uploads/2013/07/HE52UsersGuide.pdf (accessed on 11 May 2021).
- Bricaud, A.; Morel, A.; Babin, M.; Allali, K.; Claustre, H. Variation of light absorption by suspended particles with chlorophyll a concentration in oceanic (case 1) waters: Analysis and implications for bio-optical models. J. Geophys. Res. 1998, 103, 31033–31044. [Google Scholar] [CrossRef]
- Loisel, H.; Morel, A. Light scattering and chlorophyll concentration in case 1 waters: A reexamination. Limnol. Oceanogr. 1998, 43, 847–858. [Google Scholar] [CrossRef]
- Morel, A.; Antoine, D.; Gentili, B. Bidirectional reflectance of oceanic waters: Accounting for Raman emission and varying particle scattering phase function. Appl. Opt. 2002, 41, 6289–6306. [Google Scholar] [CrossRef]
- Alleman, T.L.; McCormick, R.L.; Christensen, E.D.; Fioroni, G.; Moriarty, K.; Yanowitz, J. Biodiesel Handling and Use Guide, 4th ed.; DOE/GO-102016-4875; U.S. Department of Energy: Washington, DC, USA, 2016. Available online: https://afdc.energy.gov/fuels/biodiesel_basics.html (accessed on 29 March 2021).
- BIO-100. Available online: https://parkfuels.com.au/page/biodiesel-b100 (accessed on 30 March 2021).
- Cyliten 460N. Available online: https://www.lotos.pl/en/859/p,790,c,567/for_business/industrial_lubes/compressor_oils/cyliten_460n (accessed on 11 May 2021).
- Flotta Terminal. Available online: https://www.repsolsinopecuk.com/operations/infrastructure-code-of-practice/provision-of-information#Flotta (accessed on 29 March 2021).
- Kossert, K. Measurement of wavelength-dependent refractive indices of liquid scintillation cocktails. Appl. Radiat. Isot. 2013, 82, 382–388. [Google Scholar] [CrossRef] [PubMed]
- Quan, X.; Fry, E.S. Empirical equation for the index of refraction of seawater. Appl. Opt. 1995, 34, 3477–3480. [Google Scholar] [CrossRef] [PubMed]
- Wojtasiewicz, B.; Stoń-Egiert, J. Bio-optical characterization of selected cyanobacteria strains present in marine and freshwater ecosystems. J. Appl. Phycol. 2016, 28, 2299–2314. [Google Scholar] [CrossRef]
- Baszanowska, E.; Otremba, Z.; Piskozub, J. Modelling remote sensing reflectance to detect dispersed oil at sea. Sensors 2020, 20, 863. [Google Scholar] [CrossRef]
- Piskozub, J. Effects of surface waves and sea bottom on self-shading of in-water optical instruments. In Proceedings of the Ocean Optics XII, Bergen, Norway, 26 October 1994; Volume 2258. [Google Scholar] [CrossRef]
- Flatau, P.; Piskozub, J.; Zaneveld, J.R.V. Asymptotic light field in the presence of a bubble-layer. Opt. Express 1999, 5, 120–124. [Google Scholar] [CrossRef]
- Bogucki, D.J.; Piskozub, J.; Carr, M.-E.; Spiers, G.D. Monte Carlo simulation of propagation of a short light beam through turbulent oceanic flow. Opt. Express 2007, 15, 13988–13996. [Google Scholar] [CrossRef]
- Piskozub, J.; McKee, D. Effective scattering phase functions for the multiple scattering regime. Opt. Express 2011, 19, 4786. [Google Scholar] [CrossRef]
- Baszanowska, E.; Otremba, Z.; Piskozub, J. Modelling a spectral index to detect dispersed oil in a seawater column depending on the viewing angle: Gulf of Gdańsk case study. Sensors 2020, 20, 5352. [Google Scholar] [CrossRef] [PubMed]
- Dera, J. Marine Physics; Elsevier Oceanography Series 53; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Otremba, Z. The impact on the reflectance in VIS of a type of crude oil film floating on the water surface. Opt. Express 2000, 7, 129. [Google Scholar] [CrossRef] [PubMed]
- Król, T.; Stelmaszewski, A.; Freda, W. Variability In the optical properties of a crude oil–seawater emulsion. Oceanologia 2006, 48, 203–211. [Google Scholar]
- Freda, W. Spectral dependence of the correlation between the backscattering coefficient and the volume scattering function measured in the southern Baltic Sea. Oceanologia 2012, 54, 355–367. [Google Scholar] [CrossRef]
- IOCCG. Earth Observations in Support of Global Water Quality Monitoring. In IOCCG Report Series, No. 17; Greb, S., Dekker, A., Binding, C., Eds.; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2018; p. 125. [Google Scholar]
- IOCCG. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms, and Applications. In IOCCG Report Series, No. 5; Lee, Z.-P., Ed.; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2006; p. 126. [Google Scholar]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. 2012, 117, 25. [Google Scholar] [CrossRef]
- IOCCG. Synergy between Ocean Colour and Biogeochemical/Ecosystem Models. In IOCCG Report Series; Dutkiewicz, S., Ed.; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2020. [Google Scholar] [CrossRef]
| BD | CL | FL | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Blue Bands | Green Bands | Red Bands | Blue Bands | Green Bands | Red Bands | Blue Bands | Green Bands | Red Bands | |
| oligotrophic water (Chl-a 0.1 mg/m3) | ~2-fold | ~3-fold | ~2-fold | ~3-fold | ~4-fold | ~5-fold | ~2-fold | ~4-fold | ~6-fold |
| mesotrophic water (Chl-a 1 mg/m3) | 50–80% | 50–80% | 30–45% | 80–100% | ~2-fold | ~2-fold | <20% | ~2-fold | ~2-fold |
| 30–45% | |||||||||
| 50–80% | |||||||||
| eutrophic water (Chl-a 10 mg/m3) | <20% | <20% | <20% | 20–30% | 20–30% | 20–30% | <20% | 20–30% | 20–30% |
| Oligotrophic | Mesotrophic | Eutrophic | |||||||
|---|---|---|---|---|---|---|---|---|---|
| BD | CL | FL | BD | CL | FL | BD | CL | FL | |
| Rrs band ratios, relative difference, % | |||||||||
| 410/560 | −27 | −49 | −79 | −3 | −12 | −39 | 3 | 3 | −6 |
| 440/550 | −19 | −38 | −64 | 0 | −5 | −23 | 1 | 3 | −2 |
| 490/550 | −4 | −22 | −39 | 2 | −3 | −14 | 0 | 1 | −2 |
| 550/680 | 28 | −19 | −22 | 21 | −3 | −8 | 5 | −2 | −5 |
| 420/665 | −10 | −56 | −80 | 18 | −11 | −39 | 7 | 1 | −9 |
| Rrs band differences, relative difference, % | |||||||||
| 550–440 | 112 | 132 | −18 | 59 | 24 | −250 | 15 | 18 | 22 |
| 665–440 | 128 | 174 | 52 | 66 | 92 | 46 | 22 | 28 | 12 |
| 680–490 | 174 | 244 | 161 | 69 | 97 | 68 | 17 | 23 | 15 |
| Wavelengths, nm | Color Index CI × 103 | Relative Difference, % | |||||||
|---|---|---|---|---|---|---|---|---|---|
| λblue | λgreen | λred | BD | CL | FL | Natural Unpolluted Water | BD | CL | FL |
| 440 | 555 | 670 | −5.95 | −5.46 | 0.67 | −3.11 | −91 | −76 | 121 |
| 440 | 555 | 675 | −6.18 | −5.74 | 0.51 | −3.21 | −92 | −79 | 116 |
| 440 | 550 | 670 | −6.03 | −5.36 | 0.81 | −3.19 | −89 | −68 | 125 |
| 440 | 550 | 675 | −6.25 | −5.63 | 0.66 | −3.29 | −90 | −71 | 120 |
| 445 | 555 | 670 | −5.59 | −5.13 | 0.45 | −2.87 | −95 | −79 | 116 |
| 445 | 555 | 675 | −5.82 | −5.39 | 0.30 | −2.97 | −96 | −82 | 110 |
| 445 | 550 | 670 | −5.66 | −5.02 | 0.59 | −2.94 | −92 | −70 | 120 |
| 445 | 550 | 675 | −5.87 | −5.27 | 0.44 | −3.04 | −93 | −74 | 114 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haule, K.; Freda, W. Remote Sensing of Dispersed Oil Pollution in the Ocean—The Role of Chlorophyll Concentration. Sensors 2021, 21, 3387. https://doi.org/10.3390/s21103387
Haule K, Freda W. Remote Sensing of Dispersed Oil Pollution in the Ocean—The Role of Chlorophyll Concentration. Sensors. 2021; 21(10):3387. https://doi.org/10.3390/s21103387
Chicago/Turabian StyleHaule, Kamila, and Włodzimierz Freda. 2021. "Remote Sensing of Dispersed Oil Pollution in the Ocean—The Role of Chlorophyll Concentration" Sensors 21, no. 10: 3387. https://doi.org/10.3390/s21103387
APA StyleHaule, K., & Freda, W. (2021). Remote Sensing of Dispersed Oil Pollution in the Ocean—The Role of Chlorophyll Concentration. Sensors, 21(10), 3387. https://doi.org/10.3390/s21103387







