An Energy-Efficient and Secure Data Inference Framework for Internet of Health Things: A Pilot Study
Abstract
1. Introduction
- Leveraging model driven prediction, encryption, and data points (DP) with edge computing to propose a two-tier privacy-preserving IoHT framework that does not currently exist.
- Evaluation of the proposed system in terms of efficiency and privacy preservation with up to 98.83% and 95.95% of data savings rate (SR) and accuracy rate (AR), respectively, while maintaining sufficient accuracy that is arbitrarily required by users.
- Presenting potential application scenarios that would benefit from this solution.
2. Related Works
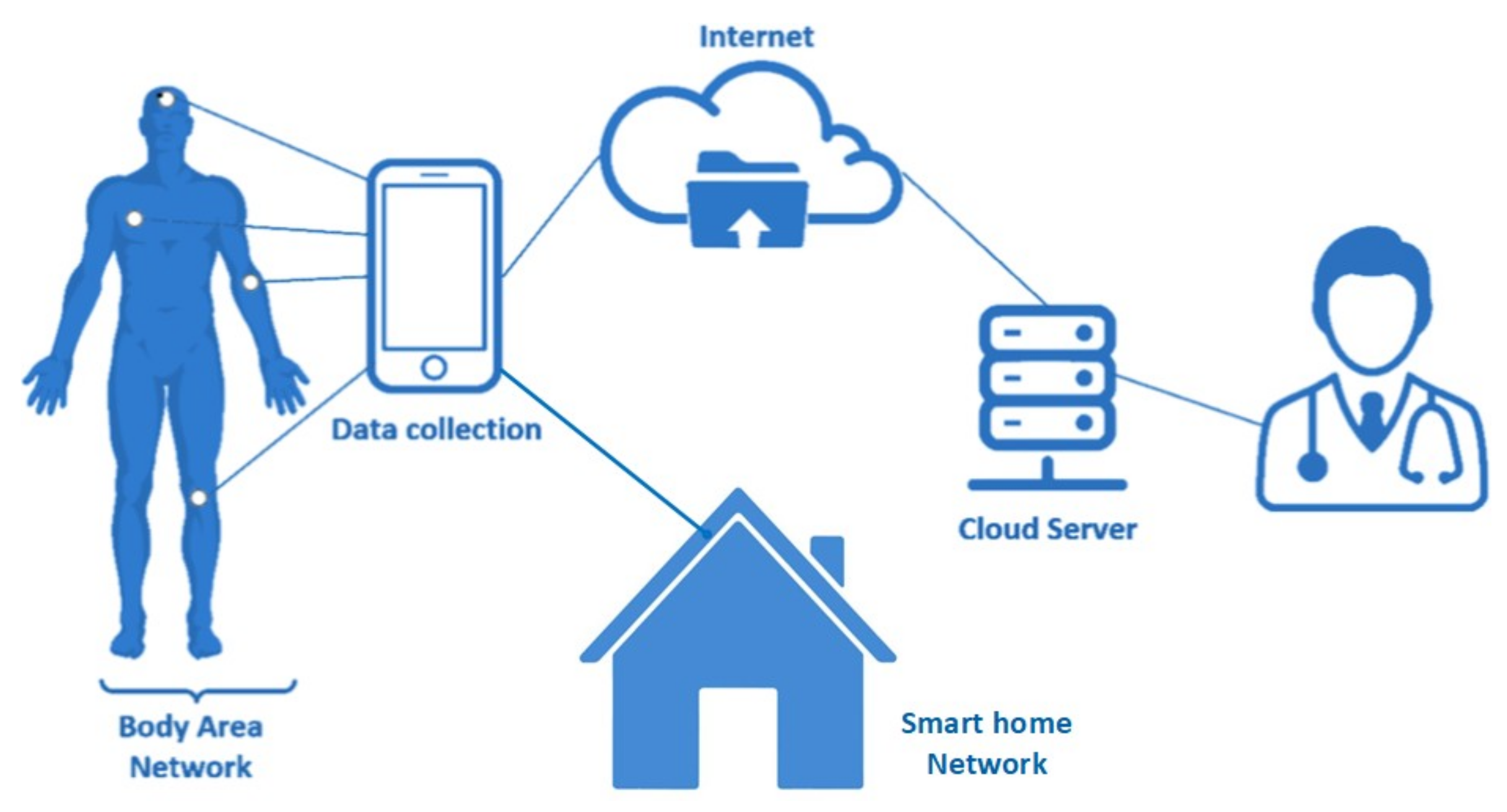
2.1. WBAN and IoT Networks
2.2. Health Inference and Prediction Analysis
2.3. Privacy Preservation
2.3.1. Cryptography-Based Schemes
2.3.2. Differential Privacy-Based Schemes
3. The Proposed Solution
3.1. The First Tier Data Reduction Using a Data Inference Algorithm
| Algorithm 1: Variance rate algorithm initialization; |
|
3.2. The Second Tier Data Protection with Differential Privacy
Definition of Differential Privacy
4. Results and Analysis
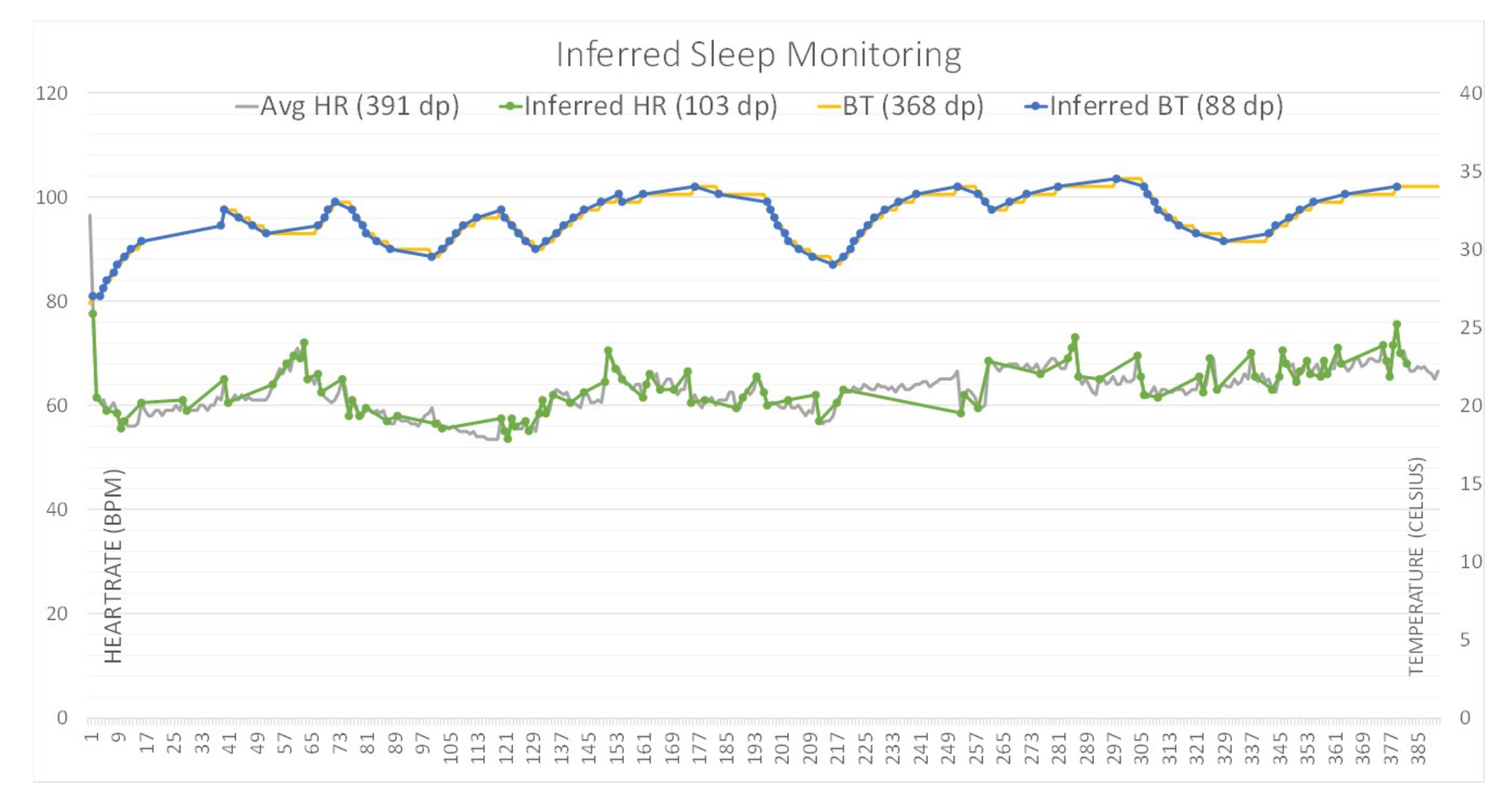
4.1. Efficiency and Accuracy Evaluation
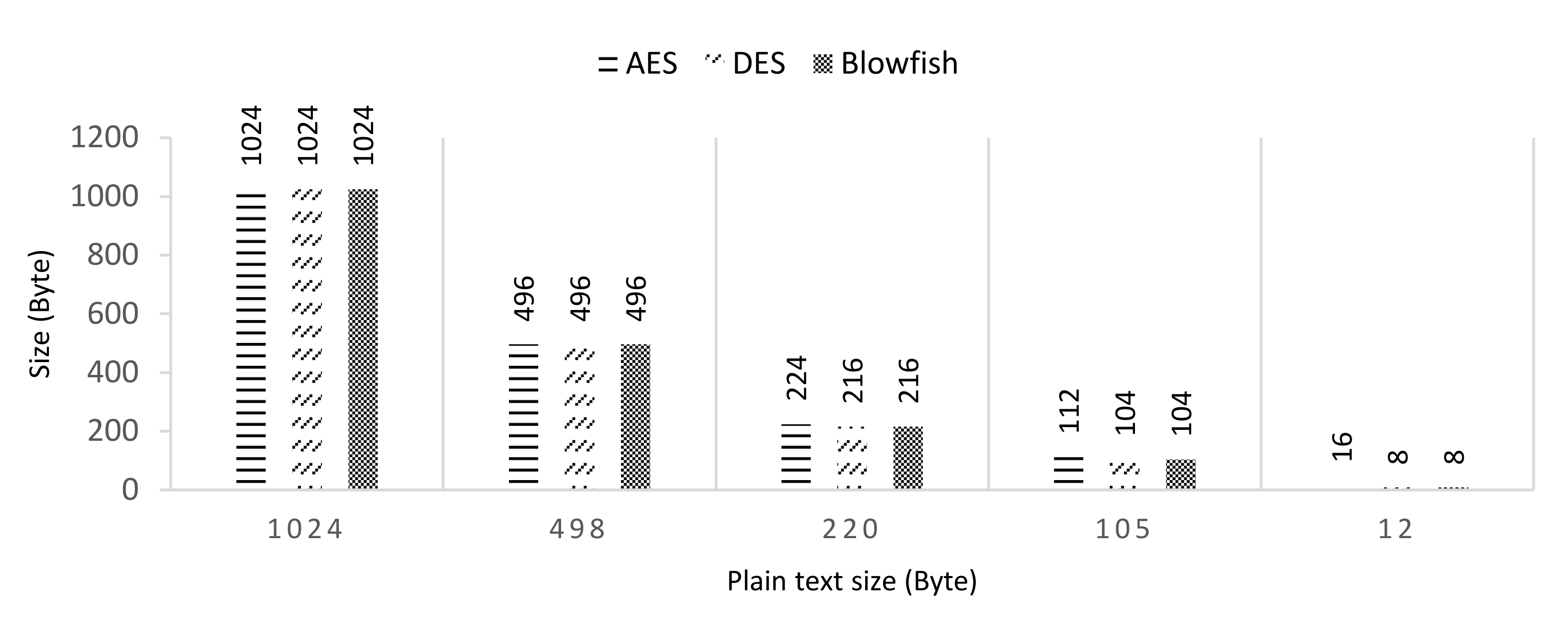
4.2. Privacy Preservation Evaluation
5. Beneficial Applications
5.1. Patient Monitoring of Disease Outbreak
5.2. Battery Conservation of Personal Health Devices
5.3. Health Data for Identificationes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kang, J.J.; Haskell-Dowland, P. How Safe is Covidsafe? What You Should Know about the App’s Issues, and Bluetooth-Related Risks. Available online: https://theconversation.com/how-safe-is-covidsafe-what-you-should-know-about-the-apps-issues-and-bluetooth-related-risks-137894 (accessed on 31 November 2020).
- Liu, S.; Dibaei, M.; Tai, Y.; Chen, C.; Zhang, J.; Xiang, Y. Cyber Vulnerability Intelligence for Internet of Things Binary. IEEE Trans. Ind. Inform. 2020, 16, 2154–2163. [Google Scholar] [CrossRef]
- Omale, G. Gartner Identifies Top 10 Strategic Iot Technologies and Trends. Available online: https://www.gartner.com/en/newsroom/press-releases/2018-11-07-gartner-identifies-top-10-strategic-iot-technologies-and-trends (accessed on 31 November 2020).
- Kang, J.J.; Dibaei, M.; Luo, G.; Yang, W.; Zheng, X. A Privacy-Preserving Data Inference Framework for Internet of Health Things Networks. Available online: https://arxiv.org/abs/2010.09427 (accessed on 31 November 2020).
- Sohrabi, K.; Gao, J.; Ailawadhi, V.; Pottie, G. Protocols for self-organization of a wireless sensor network. IEEE Wirel. Commun. 2000, 7, 16–27. [Google Scholar] [CrossRef]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless mi-crosensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, Hawaii, 4–7 January 2000; p. 10. [Google Scholar]
- Manjeshwar, A.; Agrawal, D. TEEN: A routing protocol for enhanced efficiency in wireless sensor networks. In Proceedings of the 15th International Parallel and Distributed Processing Symposium, Fuzhou, China, 8–10 July 2016; Volume 1, pp. 2009–2015. [Google Scholar]
- Osborne, M.A.; Roberts, S.J.; Rogers, A.; Ramchurn, S.D.; Jennings, N.R. Towards Real-Time Information Processing of Sensor Network Data Using Computationally Efficient Multi-output Gaussian Processes. In Proceedings of the 2008 International Conference on Information Processing in Sensor Networks, St. Louis, MO, USA, 22–24 April 2008; pp. 109–120. [Google Scholar]
- Bragg, D.; Yun, M.; Bragg, H.; Choi, H.-A. Intelligent transmission of patient sensor data in wireless hospital networks. Am. Med. Inform. Assoc. 2012, 2012, 1139. [Google Scholar]
- IEEE Health Informatics–Personal Health Device Communication: Application Profile—Optimized Exchange Protocol; Part 20601; IEEE: Piscataway, NJ, USA, 2019; pp. 1–253.
- Engel, V.J.L.; Supangkat, S.H. Context-aware inference model for cold-chain logistics monitoring. In Proceedings of the 2014 International Conference on ICT For Smart Society (ICISS), Bandung, Indonesia, 24–25 September 2014; pp. 192–196. [Google Scholar]
- Zhu, X.; Kui, F.; Wang, Y. Predictive Analytics by Using Bayesian Model Averaging for Large-Scale Internet of Things. Int. J. Distrib. Sens. Netw. 2013, 9, 723260. [Google Scholar] [CrossRef]
- Ijaz, M.; Li, G.; Wang, H.; El-Sherbeeny, A.; Awelisah, Y.M.; Lin, L.; Koubaa, A.; Noor, A. Intelligent Fog-Enabled Smart Healthcare System for Wearable Physiological Parameter Detection. Electronics 2020, 9, 2015. [Google Scholar] [CrossRef]
- Pazienza, A.; Anglani, R.; Mallardi, G.; Fasciano, C.; Noviello, P.; Tatulli, C.; Vitulano, F. Adaptive Critical Care Intervention in the Internet of Medical Things. In Proceedings of the 2020 IEEE Conference on Evolving and Adaptive Intelligent Systems, Bari, Italy, 27–29 May 2020; pp. 1–8. [Google Scholar]
- Pasupuleti, S.K.; Ramalingam, S.; Buyya, R. An efficient and secure privacy-preserving approach for outsourced data of resource constrained mobile devices in cloud computing. J. Netw. Comput. Appl. 2016, 64, 12–22. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, J.; Liu, J.K.; Yu, J.; Chen, J.; Xie, W. An Efficient File Hierarchy Attribute-Based Encryption Scheme in Cloud Computing. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1265–1277. [Google Scholar] [CrossRef]
- Waters, B. Ciphertext-Policy Attribute-Based Encryption: An Expressive, Efficient, and Provably Secure Realization. In International Workshop on Public Key Cryptography; Springer: Berlin, Germany, 2011; pp. 53–70. [Google Scholar]
- Yin, C.; Xi, J.; Sun, R.; Wang, J. Location privacy protection based on differential privacy strategy for big data in industrial internet of things. IEEE Trans. Ind. Inform. 2017, 14, 3628–3636. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Y.; Jolfaei, A.; Yu, D.; Xu, G.; Zheng, X. Privacy-Preserving Federated Learning Framework Based on Chained Secure Multi-Party Computing. IEEE Internet Things J. 2020, 1. [Google Scholar] [CrossRef]
- Xu, C.; Ren, J.; Zhang, D.; Zhang, Y. Distilling at the Edge: A Local Differential Privacy Obfuscation Framework for IoT Data Analytics. IEEE Commun. Mag. 2018, 56, 20–25. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, C.; Fang, Y. EPIC: A Differential Privacy Framework to Defend Smart Homes against Internet Traffic Analysis. IEEE Internet Things J. 2018, 5, 1206–1217. [Google Scholar] [CrossRef]
- Kang, J.J.W. An Inference System Framework for Personal Sensor Devices in Mobile Health and Internet of Things Networks. Ph.D. Thesis, Deakin University, Melbourne, Australia, 2017. [Google Scholar]
- Kang, J.J.; Luan, T.H.; Larkin, H. Enhancement of Sensor Data Transmission by Inference and Efficient Data Processing. In Proceedings of the International Conference on Applications and Techniques in Information Security, Cairns, Australia, 26–28 October 2016; pp. 81–92. [Google Scholar]
- Abbas, A.; Khan, S.U. A Review on the State-of-the-Art Privacy-Preserving Approaches in the e-Health Clouds. IEEE J. Biomed. Health Inform. 2014, 18, 1431–1441. [Google Scholar] [CrossRef] [PubMed]
- Vadhan, S. The Complexity of Differential Privacy. In Tutorials on the Foundations of Cryptography; Springer: Berlin, Germany, 2017; pp. 347–450. [Google Scholar]
- Dwork, C. Differential Privacy: A Survey of Results. In Proceedings of the International Conference on Theory and Applications of Models of Computation, Xi’an, China, 25–29 April 2008; pp. 1–19. [Google Scholar]
- Heart Rate Time Series. Available online: http://ecg.mit.edu/time-series/ (accessed on 31 November 2020).
- Dibaei, M.; Zheng, X.; Jiang, K.; Abbas, R.; Liu, S.; Zhang, Y.; Xiang, Y.; Yu, S. Attacks and defenses on intelligent connected vehicles: A survey. Digit. Commun. Netw. 2020, 6, 399–421. [Google Scholar] [CrossRef]
- Online Domain Tools. Available online: http://online-domain-tools.com/ (accessed on 31 November 2020).
- Dibaei, M.; Zheng, X.; Xia, Y.; Xu, X.; Jolfaei, A.; Bashir, A.K.; Tariq, U.; Yu, D.; Vasilakos, A.V. Investigating the Prospect of Leveraging Blockchain and Machine Learning to Secure Vehicular Networks: A Survey; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]



| Cases | Evaluation Condition | DP | Savings (%) | Accuracy (%) |
|---|---|---|---|---|
| Case 0 | Original data | 1800 | N/A | N/A |
| Case 1 | Removed duplication | 1716 | 4.67 | 99.74 |
| Case 2 | Beacon Interval = 30 s | 31 | 98.27 | 96.26 |
| Case 3 | Beacon Interval = 60 s | 16 | 99.11 | 95.73 |
| Case 4 | Beacon Interval = 120 s | 9 | 99.50 | 94.18 |
| Case 5 | Beacon Interval = 180 s | 6 | 99.66 | 94.21 |
| Case 6 | Variance Rate (2%) with Beacon Interval = 60 s | 182 | 89.88 | 97.57 |
| Case 7 | Variance Rate (3%) with Beacon Interval = 60 s | 64 | 36.44 | 36.04 |
| Case 8 | Variance Rate (10%) with Beacon Interval = 60 s | 22 | 98.78 | 96.14 |
| Case 9 | Variance Rate (15%) with Beacon Interval = 60 s | 21 | 98.83 | 95.95 |
| Inferred rate | 0 | 1.5% | 2% | 3% | 5% | 10% | 15% |
| Data points | 6720 | 4000 | 3559 | 3002 | 2074 | 1055 | 587 |
| Savings (%) | 0 | 40.7 | 47.0 | 55.3 | 69.1 | 84.3 | 91.2 |
| Accuracy (%) | N/A | 98.3 | 97.0 | 97.2 | 95.6 | 90.5 | 86.6 |
| VR | 0% | 2.5% | 5% | 10% | 20% |
| DP | 1420 | 691 | 306 | 146 | 17 |
| Saving (%) | N/A | 51.3 | 78.5 | 89.7 | 98.8 |
| The value of | 0.01 | 0.05 | 0.1 | 0.2 | 0.5 | 1.0 |
| Average value of raw data | 73.76 | 73.76 | 73.76 | 73.76 | 73.76 | 73.76 |
| Average value of modified data | 73.84 | 73.18 | 73.14 | 73.89 | 73.76 | 73.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.J.; Dibaei, M.; Luo, G.; Yang, W.; Haskell-Dowland, P.; Zheng, X. An Energy-Efficient and Secure Data Inference Framework for Internet of Health Things: A Pilot Study. Sensors 2021, 21, 312. https://doi.org/10.3390/s21010312
Kang JJ, Dibaei M, Luo G, Yang W, Haskell-Dowland P, Zheng X. An Energy-Efficient and Secure Data Inference Framework for Internet of Health Things: A Pilot Study. Sensors. 2021; 21(1):312. https://doi.org/10.3390/s21010312
Chicago/Turabian StyleKang, James Jin, Mahdi Dibaei, Gang Luo, Wencheng Yang, Paul Haskell-Dowland, and Xi Zheng. 2021. "An Energy-Efficient and Secure Data Inference Framework for Internet of Health Things: A Pilot Study" Sensors 21, no. 1: 312. https://doi.org/10.3390/s21010312
APA StyleKang, J. J., Dibaei, M., Luo, G., Yang, W., Haskell-Dowland, P., & Zheng, X. (2021). An Energy-Efficient and Secure Data Inference Framework for Internet of Health Things: A Pilot Study. Sensors, 21(1), 312. https://doi.org/10.3390/s21010312









