Rotation, Strain, and Translation Sensors Performance Tests with Active Seismic Sources
Abstract
1. Introduction
2. The Experiment
2.1. Instruments
2.1.1. 3C Broadband Rotational Seismometers
2.1.2. 1C Broadband Rotation Rate Sensors
2.1.3. 6C Strong Motion Sensors
2.1.4. The Rotaphone Systems
2.1.5. ROMY Ring Laser Gyroscope
2.1.6. The Distributed Acoustic Sensing System
2.1.7. Broadband Seismometers and Geophones
2.2. The Huddle Test
2.3. The Active Experiment
3. Results and Discussion
3.1. Instrument Self-Noise
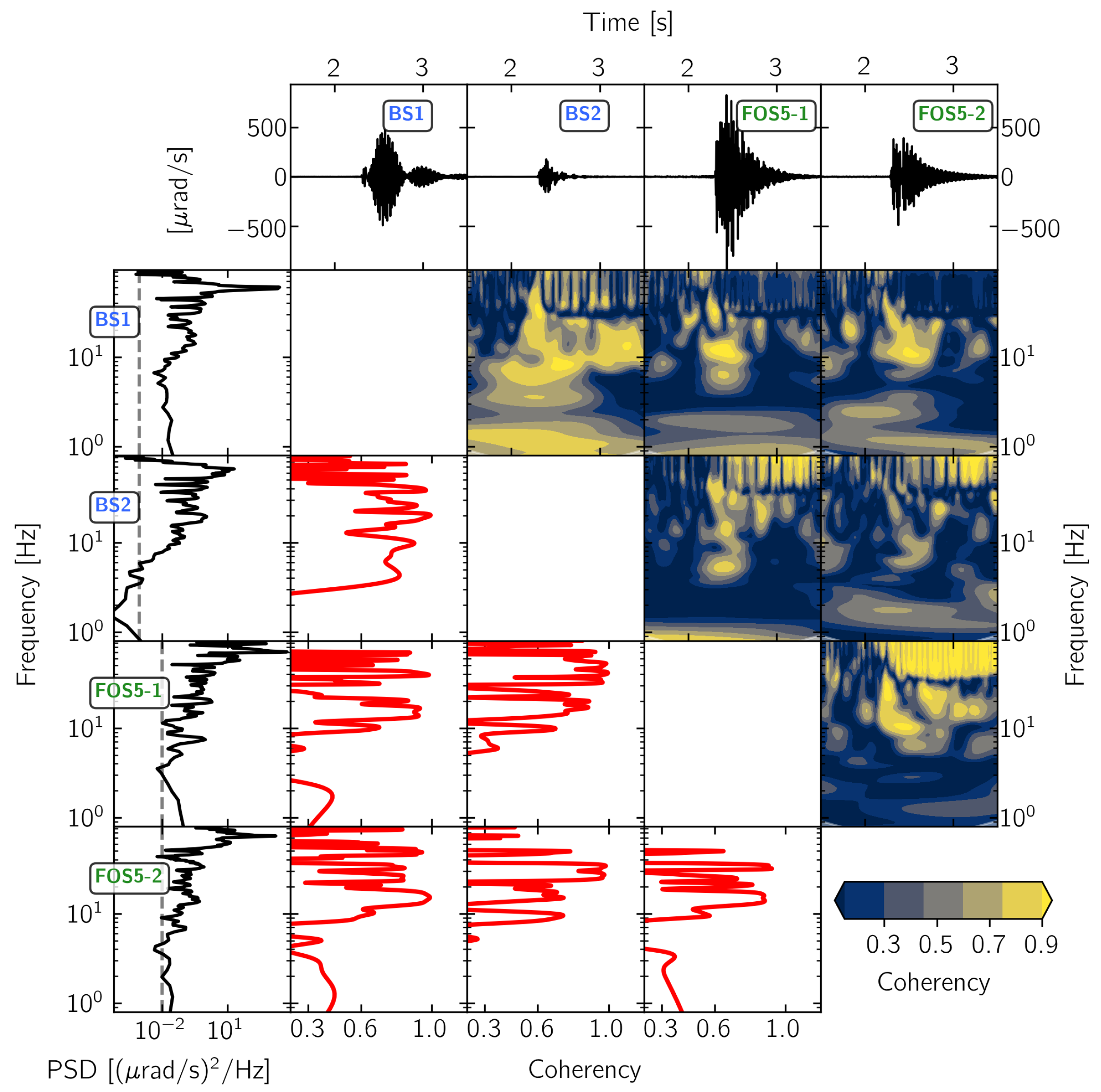
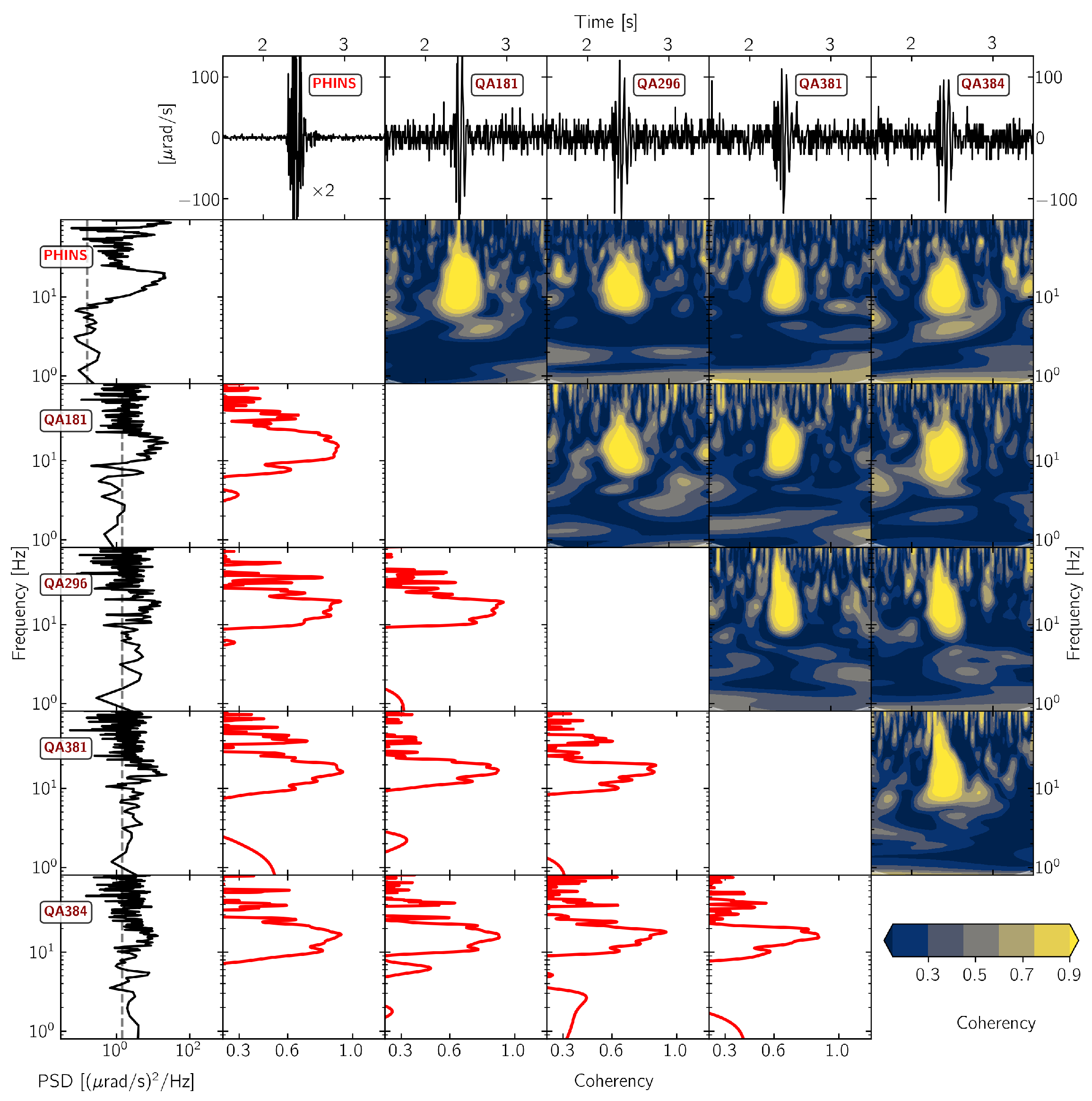
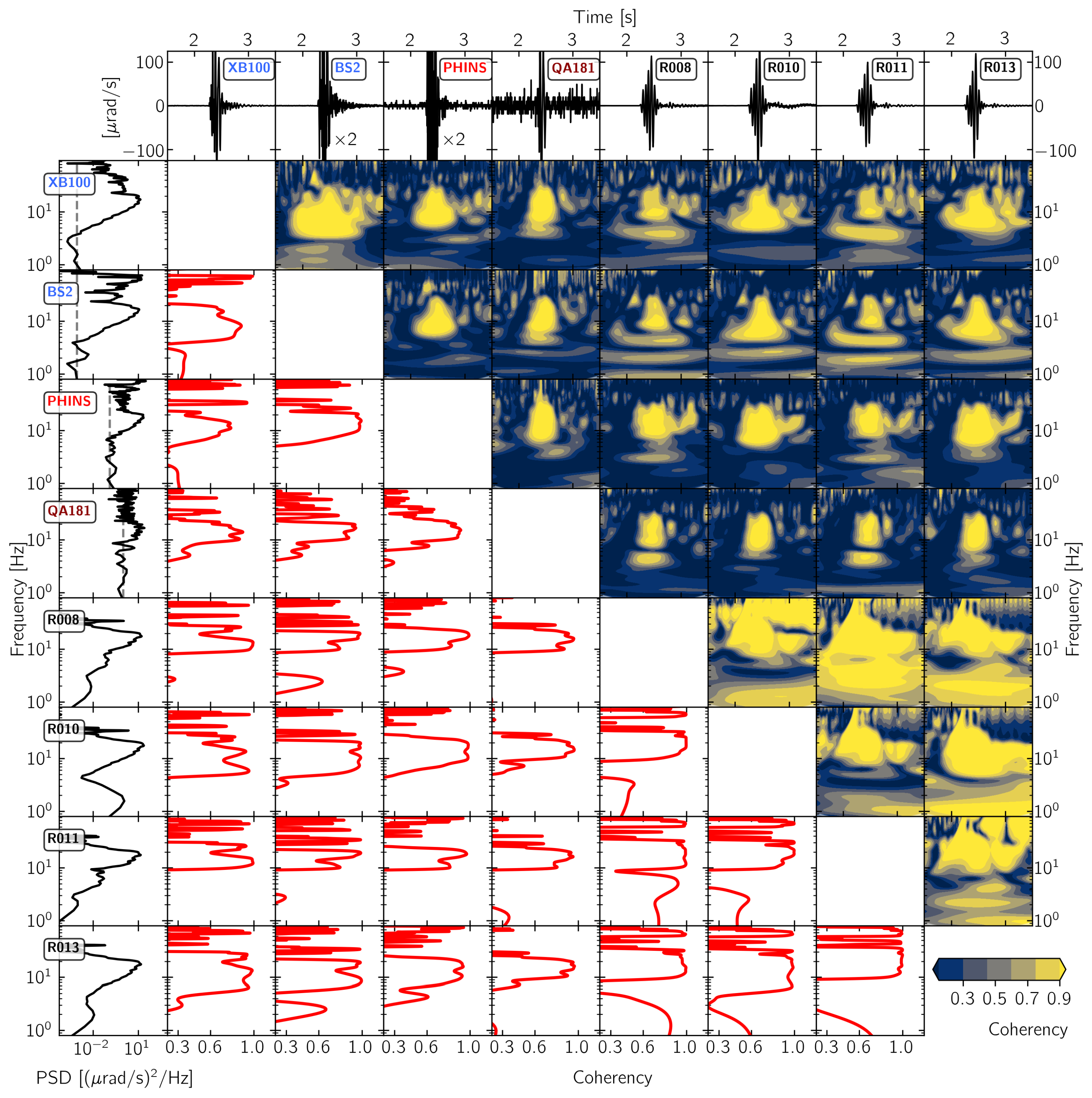
3.2. Waveform Similarity
3.2.1. 3C Broadband Rotational Seismometers
3.2.2. 1C Broadband Rotation Rate Sensors
3.2.3. Strong Motion Sensors
3.2.4. Rotaphone Systems
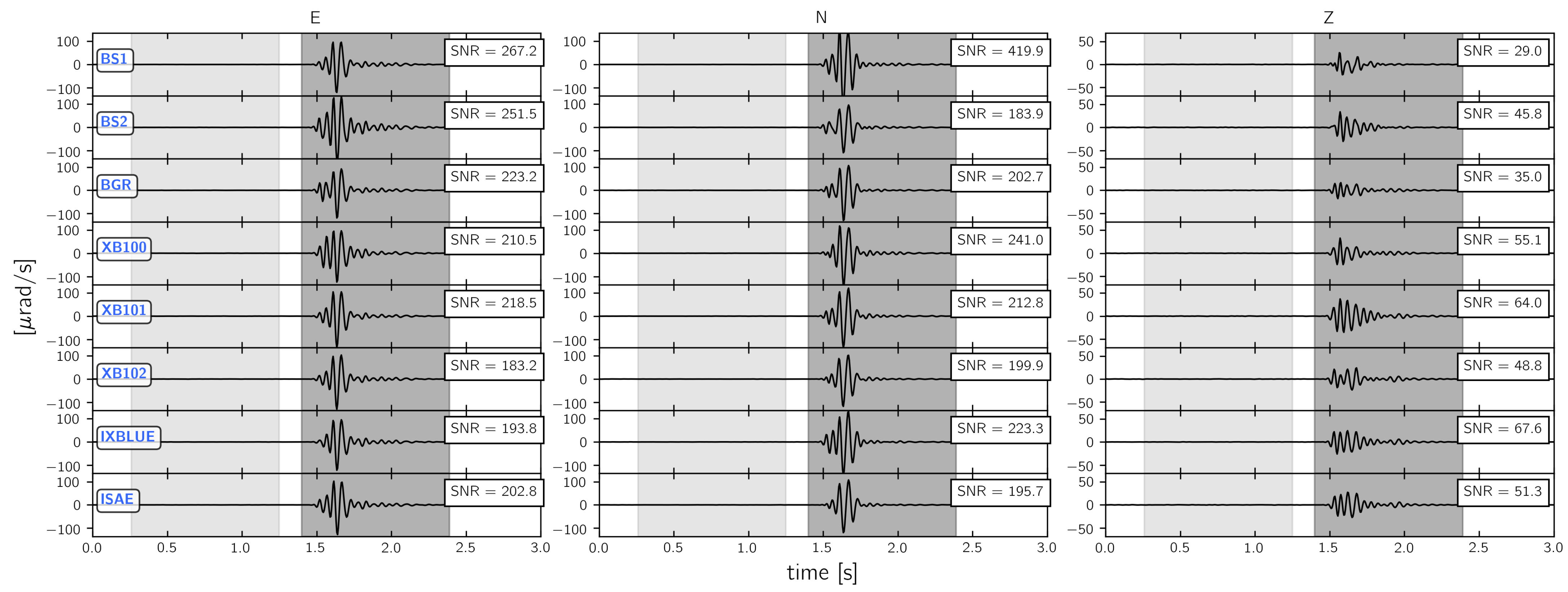
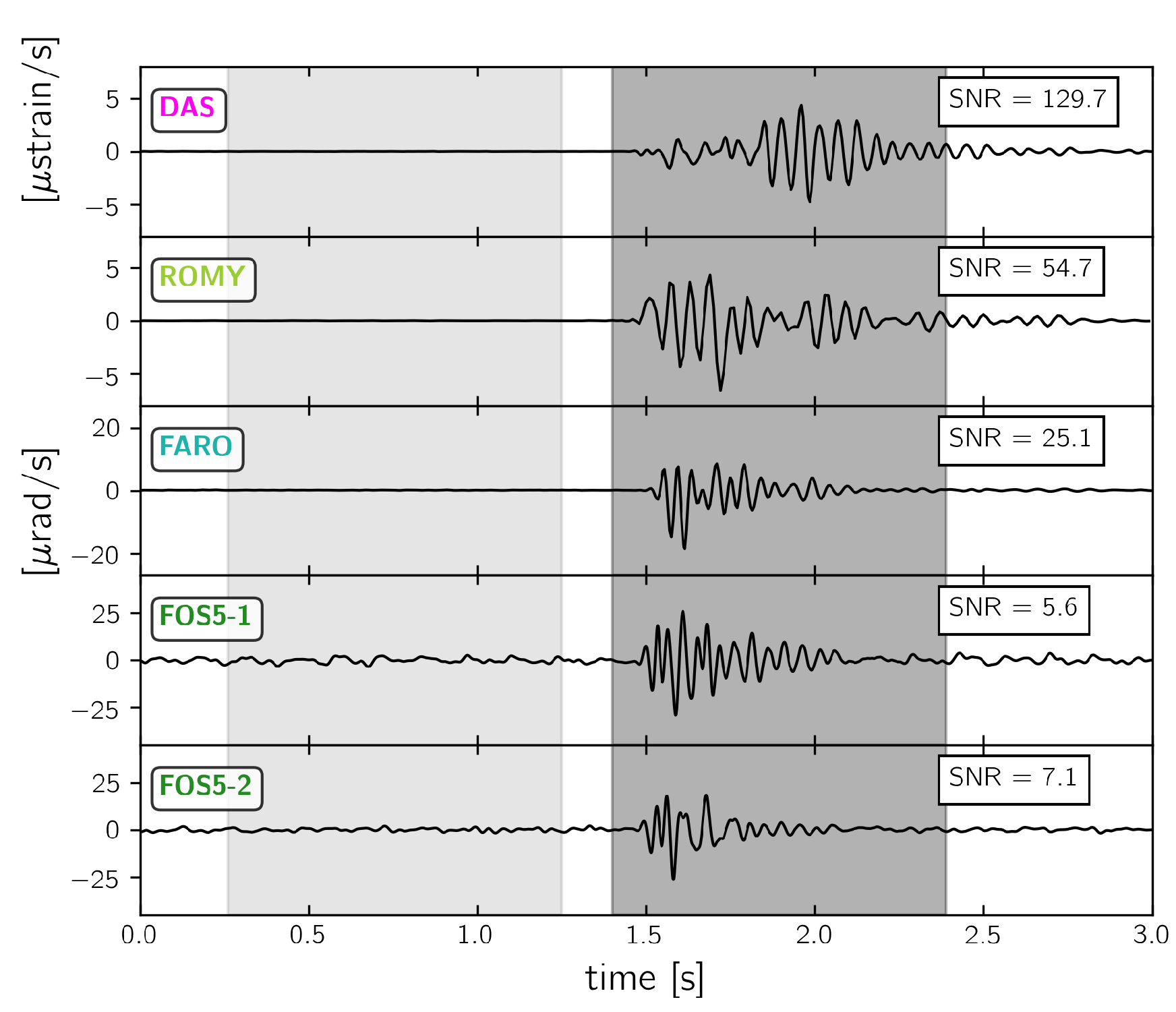
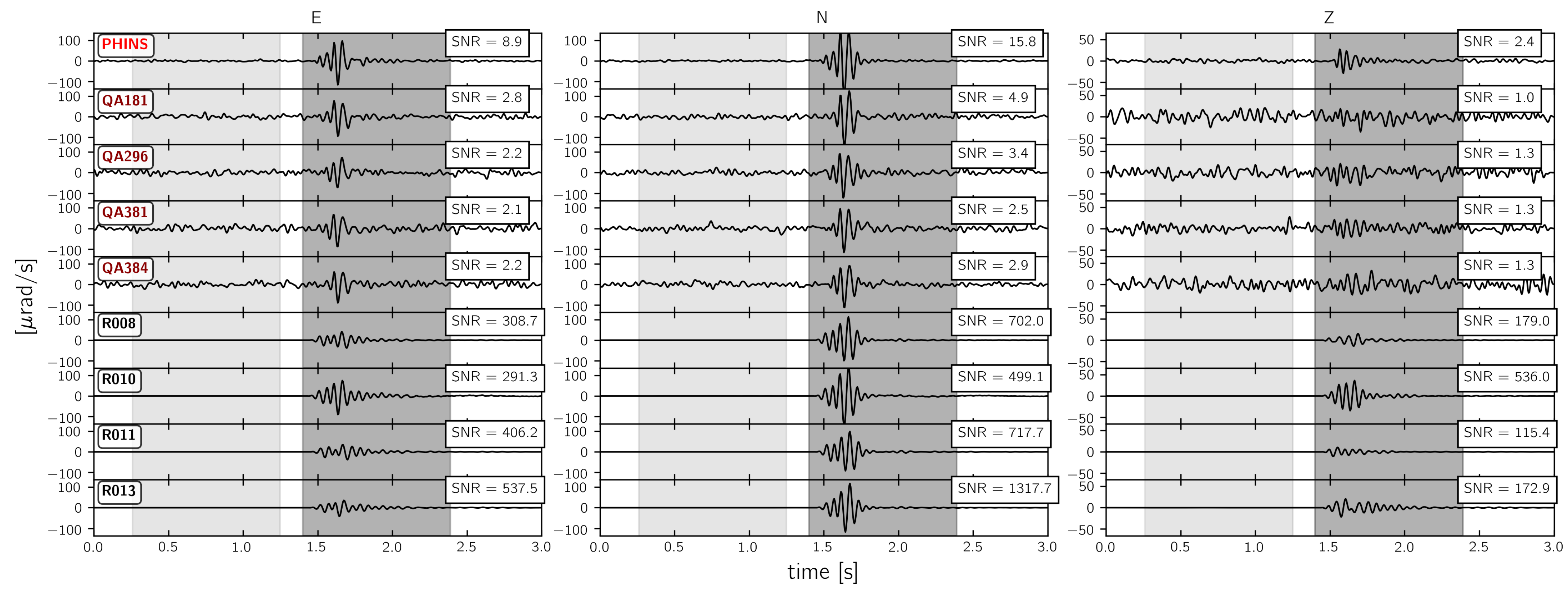
3.3. Signal-To-Noise Ratio
3.3.1. 3C Broadband Rotational Seismometers
3.3.2. 1C Rotation Rate Sensors and DAS
3.3.3. Strong Motion Sensors and Rotaphone Systems
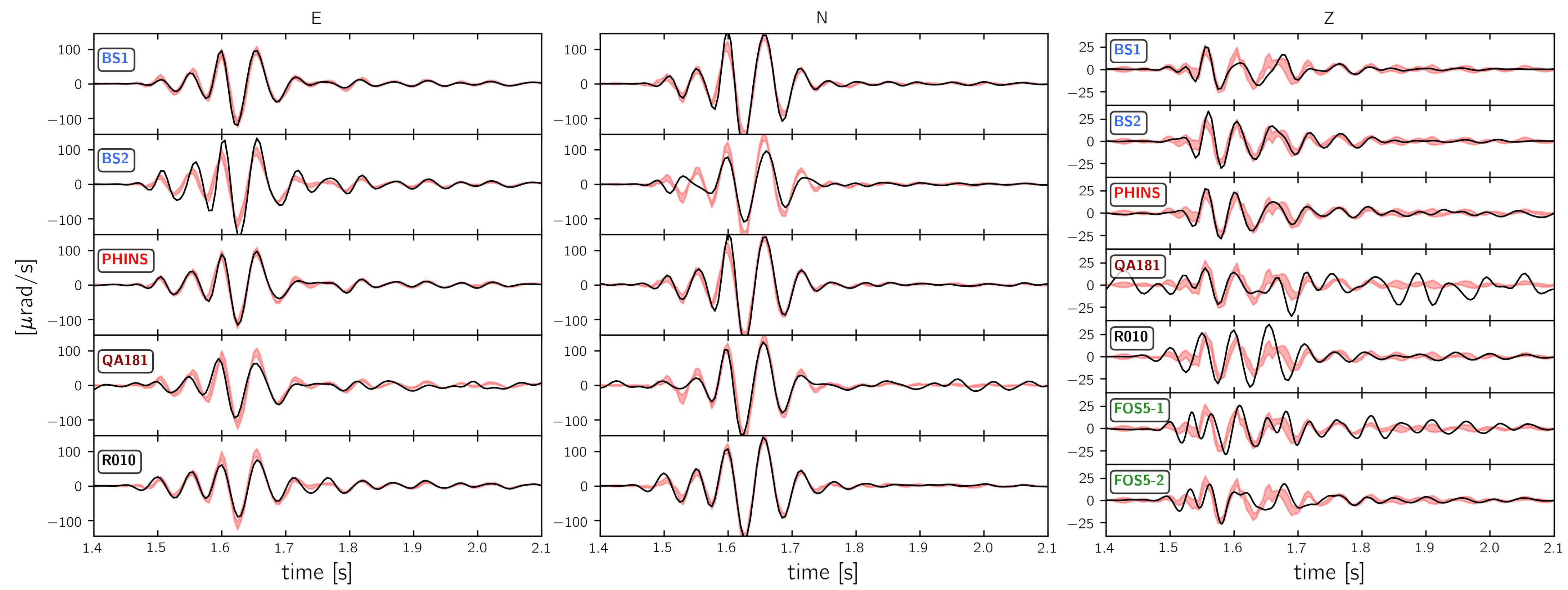
3.4. Comparison to a Reference Waveform
4. Conclusions and Future Work
4.1. Conclusions
4.2. Recommendations for Future Work
- In order to comply with standards for seismic data recording [60,61], the analog output of a sensor should be recorded with standard seismic recording equipment. In the case of closed loop fiber-optic gyroscopes and distributed acoustic sensing systems, where digital signal processing is required before data can be archived, the data recorder is implemented within the instrument. In this case, recording characteristics such as time keeping accuracy must be accessed in dedicated test procedures. In the presented experiment, we found time shifts between the reference recording of vertical translational acceleration from the station FUR and the transverse rotation rate recordings by maximizing the Pearson cross-correlation coefficient with respect to the applied time shift. Another possibility to access time stamp accuracy and time drifts would be to compare parallel recordings of impulse signals, e.g., generated with a tilt table. In this case, the vertical velocity recording from a reference seismometer-recorder combination should be in phase with the rotation rate recording around the transverse horizontal axis. This method has the advantage of the possibility to reproduce a uniform impulse signal with high accuracy over a long time span of e.g., several days and it can reveal estimates of the recorder time drift with respect to standard seismic reference instruments.
- In a comparative sensor test, all of the instruments under test should experience input motion as identical as possible. Therefore, all the instruments should be co-located as close as possible, being mounted onto a monument that is seismically decoupled from any building structure in order to minimize the local influence of building elements.
- In theory, the transfer function of a fiber-optic gyroscope is flat from DC to the Nyquist frequency. However, the implementation of recording units and closed loop electronics, make it necessary to carefully quantify the frequency response of such a system. Therefore it is desired to develop highly reliable calibration facilities and reference sensors, neither of which is available at the moment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schlüter, W. Schwingungsart und Weg der Erdbebenwellen. Beiträge Geophys. 1903, 5, 314–359. [Google Scholar]
- McLeod, D.P.; Stedman, G.E.; Webb, T.H.; Schreiber, U. Comparison of standard and ring laser rotational seismograms. Bull. Seismol. Soc. Am. 1998, 88, 1495–1503. [Google Scholar]
- Pancha, A.; Webb, T.H.; Stedman, G.E.; Mcleod, D.P.; Schreiber, K.U. Ring laser detection of rotations from teleseismic waves. Geophys. Res. Lett. 2000, 27, 3553–3556. [Google Scholar] [CrossRef]
- Wyatt, F.K.; Agnew, D.C.; Gladwin, M. Continuous measurements of crustal deformation for the 1992 Landers earthquake sequence. Bull. Seismol. Soc. Am. 1994, 84, 768–779. [Google Scholar]
- Wassermann, J.; Wietek, A.; Hadziioannou, C.; Igel, H. Toward a Single-Station Approach for Microzonation: Using Vertical Rotation Rate to Estimate Love-Wave Dispersion Curves and Direction Finding. Bull. Seismol. Soc. Am. 2016, 106, 1316–1330. [Google Scholar] [CrossRef]
- Jousset, P.; Reinsch, T.; Ryberg, T.; Blanck, H.; Clarke, A.; Aghayev, R.; Hersir, G.P.; Henninges, J.; Weber, M.; Krawczyk, C.M. Dynamic strain determination using fibre-optic cables allows imaging of seismological and structural features. Nat. Commun. 2018, 9, 2509. [Google Scholar] [CrossRef]
- Wassermann, J.; Bernauer, F.; Shiro, B.; Johanson, I.; Guattari, F.; Igel, H. Six-Axis Ground Motion Measurements of Caldera Collapse at Kīlauea Volcano, Hawaii—More Data, More Puzzles? Geophys. Res. Lett. 2020, e2019GL08599. [Google Scholar] [CrossRef]
- Lindner, F.; Wassermann, J.; Schmidt-Aursch, M.C.; Schreiber, K.U.; Igel, H. Seafloor Ground Rotation Observations: Potential for Improving Signal-to-Noise Ratio on Horizontal OBS Components. Seismol. Res. Lett. 2016, 88, 32–38. [Google Scholar] [CrossRef]
- Lindsey, N.J.; Dawe, T.C.; Ajo-Franklin, J.B. Illuminating seafloor faults and ocean dynamics with dark fiber distributed acoustic sensing. Science 2019, 366, 1103–1107. [Google Scholar] [CrossRef]
- Gutscher, M.A.; Royer, J.Y.; Graindorge, D.; Murphy, S.; Klingelhoefer, F.; Aiken, C.; Cattaneo, A.; Barreca, G.; Quetel, L.; Riccobene, G.; et al. Fiber optic monitoring of active faults at the seafloor: I the FOCUS project. Photoniques 2019, 32–37. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Velikoseltsev, A.; Carr, A.J.; Franco-Anaya, R. The Application of Fiber Optic Gyroscopes for the Measurement of Rotations in Structural Engineering. Bull. Seismol. Soc. Am. 2009, 99, 1207–1214. [Google Scholar] [CrossRef]
- Zembaty, Z.; Kokot, S.; Bobra, P. Application of rotation rate sensors in an experiment of stiffness ‘reconstruction’. Smart Mater. Struct. 2013, 22, 077001. [Google Scholar] [CrossRef]
- Bońkowski, P.A.; Bobra, P.; Zembaty, Z.; Jędraszak, B. Application of Rotation Rate Sensors in Modal and Vibration Analyses of Reinforced Concrete Beams. Sensors 2020, 20, 4711. [Google Scholar] [CrossRef] [PubMed]
- Edme, P.; Muyzert, E. Rotational Data Measurement. In Proceedings of the 75th EAGE Conference & Exhibition Incorporating SPE EUROPEC, London, UK, 10–13 June 2013. [Google Scholar] [CrossRef]
- Schmelzbach, C.; Donner, S.; Igel, H.; Sollberger, D.; Taufiqurrahman, T.; Bernauer, F.; Häusler, M.; van Renterghem, C.; Wassermann, J.; Robertsson, J. Advances in 6C seismology: Applications of combined translational and rotational measurements in global and exploration seimsology. Geophysics 2018, 83, WC53–WC69. [Google Scholar] [CrossRef]
- Sollberger, D.; Greenhalgh, S.A.; Schmelzbach, C.; Van Renterghem, C.; Robertsson, J.O.A. 6-C polarization analysis using point measurements of translational and rotational ground-motion: Theory and applications. Geophys. J. Int. 2018, 213, 77–97. [Google Scholar] [CrossRef]
- Sollberger, D.; Igel, H.; Schmelzbach, C.; Edme, P.; van Manen, D.J.; Bernauer, F.; Yuan, S.; Wassermann, J.; Schreiber, U.; Robertsson, J.O.A. Seismological Processing of Six Degree-of-Freedom Ground-Motion Data. Sensors 2020, 20, 6904. [Google Scholar] [CrossRef]
- Keil, S.; Wassermann, J.; Igel, H. Single-station seismic microzonation using 6C measurements. J. Seismol. 2020. [Google Scholar] [CrossRef]
- Walter, F.; Gräff, D.; Lindner, F.; Paitz, P.; Köpfli, M.; Chmiel, M.; Fichtner, A. Distributed acoustic sensing of microseismic sources and wave propagation in glaciated terrain. Nat. Commun. 2020, 11, 2436. [Google Scholar] [CrossRef]
- Lefèvre, H.C. The Fiber-Optic Gyroscope, 2nd ed.; Artech House: London, UK, 2014. [Google Scholar]
- D’Alessandro, A.; Scudero, S.; Vitale, G. A Review of the Capacitive MEMS for Seismology. Sensors 2019, 19, 3093. [Google Scholar] [CrossRef]
- Brokešová, J.; Málek, J. Rotaphone, a Self-Calibrated Six-Degree-of-Freedom Seismic Sensor and Its Strong-Motion Records. Seismol. Res. Lett. 2013, 84, 737–744. [Google Scholar] [CrossRef]
- Agafonov, V.M.; Neeshpapa, A.V.; Shabalina, A.S. Electrochemical Seismometers of Linear and Angular Motion. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I.A., Patelli, E., Au, I.S.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–19. [Google Scholar] [CrossRef]
- Daley, T.M.; Freifeld, B.M.; Ajo-Franklin, J.; Dou, S.; Pevzner, R.; Shulakova, V.; Kashikar, S.; Miller, D.E.; Goetz, J.; Henninges, J.; et al. Field testing of fiber-optic distributed acoustic sensing (DAS) for subsurface seismic monitoring. Lead. Edge 2013, 32, 699–706. [Google Scholar] [CrossRef]
- Daley, T.; Miller, D.; Dodds, K.; Cook, P.; Freifeld, B. Field testing of modular borehole monitoring with simultaneous distributed acoustic sensing and geophone vertical seismic profiles at Citronelle, Alabama. Geophys. Prospect. 2016, 64, 1318–1334. [Google Scholar] [CrossRef]
- Dou, S.; Lindsey, N.; Wagner, A.M.; Daley, T.M.; Freifeld, B.; Robertson, M.; Peterson, J.; Ulrich, C.; Martin, E.R.; Ajo-Franklin, J.B. Distributed Acoustic Sensing for Seismic Monitoring of The Near Surface: A Traffic-Noise Interferometry Case Study. Sci. Rep. 2017, 7, 11620. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Z. Distributed Acoustic Sensing Turns Fiber-Optic Cables into Sensitive Seismic Antennas. Seismol. Res. Lett. 2019, 91, 1–15. [Google Scholar] [CrossRef]
- Hutt, C.R.; Evans, J.R.; Followill, F.; Nigbor, R.L.; Wielandt, E. Guidelines for Standardized Testing of Broadband Seismometers and Accelerometers; Technical Report; U.S. Geological Survey: Reston, VA, USA, 2010. [CrossRef]
- Wielandt, E. Seismic Sensors and their Calibration. In New Manual of Seismological Observatory Practice 2 (NMSOP-2); Bormann, P., Ed.; Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2012; Volume 2, pp. 1–51. [Google Scholar] [CrossRef]
- Ringler, A.T.; Sleeman, R.; Hutt, C.R.; Gee, L.S. Seismometer Self-Noise and Measuring Methods. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I.A., Patelli, E., Au, I.S.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–13. [Google Scholar] [CrossRef]
- Ringler, A.T.; Evans, J.R.; Hutt, C.R. Self-Noise Models of Five Commercial Strong-Motion Accelerometers. Seismol. Res. Lett. 2015, 86, 1143–1147. [Google Scholar] [CrossRef]
- Ringler, A.T.; Holland, A.A.; Wilson, D.C. Repeatability of Testing a Small Broadband Sensor in the Albuquerque Seismological Laboratory Underground Vault. Bull. Seismol. Soc. Am. 2017, 107, 1557–1563. [Google Scholar] [CrossRef]
- Kearns, A.; Ringler, A.T.; Holland, J.; Storm, T.; Wilson, D.C.; Anthony, R.E. Sensor Suite: The Albuquerque Seismological Laboratory Instrumentation Testing Suite. Seismol. Res. Lett. 2018, 89, 2374–2385. [Google Scholar] [CrossRef]
- Nigbor, R.L.; Evans, J.R.; Hutt, C.R. Laboratory and Field Testing of Commercial Rotational Seismometers. Bull. Seismol. Soc. Am. 2009, 99, 1215–1227. [Google Scholar] [CrossRef]
- Lee, W.H.K.; Evans, J.R.; Huang, B.S.; Hutt, C.R.; Lin, C.J.; Liu, C.C.; Nigbor, R.L. Measuring rotational ground motions in seismological practice. In New Manual of Seismological Observatory Practice 2 (NMSOP-2); Bormann, P., Ed.; Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2012; pp. 1–27. [Google Scholar] [CrossRef]
- Bernauer, F.; Wassermann, J.; Igel, H. Rotational sensors—A comparison of different sensor types. J. Seismol. 2012, 16, 595–602. [Google Scholar] [CrossRef]
- Bernauer, F.; Wassermann, J.; Guattari, F.; Frenois, A.; Bigueur, A.; Gaillot, A.; de Toldi, E.; Ponceau, D.; Schreiber, U.; Igel, H. BlueSeis3A: Full Characterization of a 3C Broadband Rotational Seismometer. Seismol. Res. Lett. 2018, 89, 620–629. [Google Scholar] [CrossRef]
- Sleeman, R. Three-Channel Correlation Analysis: A New Technique to Measure Instrumental Noise of Digitizers and Seismic Sensors. Bull. Seismol. Soc. Am. 2006, 96, 258–271. [Google Scholar] [CrossRef]
- Velikoseltsev, A.; Schreiber, K.U.; Yankovsky, A.; Wells, J.P.R.; Boronachin, A.; Tkachenko, A. On the application of fiber optic gyroscopes for detection of seismic rotations. J. Seismol. 2012, 16, 623–637. [Google Scholar] [CrossRef]
- Jaroszewicz, L.R.; Kurzych, A.; Krajewski, Z.; Dudek, M.; Kowalski, J.K.; Teisseyre, K.P. The Fiber-Optic Rotational Seismograph-Laboratory Tests and Field Application. Sensors 2019, 19, 2699. [Google Scholar] [CrossRef] [PubMed]
- Kurzych, A.T.; Jaroszewicz, L.R.; Krajewski, Z.; Dudek, M.; Teisseyre, K.P.; Kowalski, J.K. Two Correlated Interferometric Optical Fiber Systems Applied to the Mining Activity Recordings. J. Light. Technol. 2019, 37, 4851–4857. [Google Scholar] [CrossRef]
- Allan, D.W. Statistics of atomic frequency standards. Proc. IEEE 1966, 54, 221–230. [Google Scholar] [CrossRef]
- Suryanto, W.; Wassermann, J.; Igel, H.; Cochard, A.; Vollmer, D.; Scherbaum, F.; Velikoseltsev, A.; Schreiber, U. First comparison of seismic array derived rotations with direct ring laser measurements of rotational ground motion. Bull. Seismol. Soc. Am. 2006, 96, 2059–2071. [Google Scholar] [CrossRef]
- Donner, S.; Lin, C.J.; Hadziioannou, C.; Gebauer, A.; Vernon, F.; Agnew, D.C.; Igel, H.; Schreiber, U.; Wassermann, J. Comparing Direct Observation of Strain, Rotation, and Displacement with Array Estimates at Piñon Flat Observatory, California. Seismol. Res. Let. 2017, 88, 1107–1116. [Google Scholar] [CrossRef]
- Yuan, S.; Simonelli, A.; Lin, C.; Bernauer, F.; Donner, S.; Braun, T.; Wassermann, J.; Igel, H. Six Degree-of-Freedom Broadband Ground-Motion Observations with Portable Sensors: Validation, Local Earthquakes, and Signal Processing. Bull. Seismol. Soc. Am. 2020, 110, 953–969. [Google Scholar] [CrossRef]
- Wang, H.F.; Zeng, X.; Miller, D.E.; Fratta, D.; Feigl, K.L.; Thurber, C.H.; Mellors, R.J. Ground motion response to an ML 4.3 earthquake using co-located distributed acoustic sensing and seismometer arrays. Geophys. J. Int. 2018, 213, 2020–2036. [Google Scholar] [CrossRef]
- Lindsey, N.J.; Rademacher, H.; Ajo-Franklin, J.B. On the Broadband Instrument Response of Fiber-Optic DAS Arrays. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018145. [Google Scholar] [CrossRef]
- Paitz, P.; Edme, P.; Gräff, D.; Walter, F.; Doetsch, J.; Chalari, A.; Schmelzbach, C.; Fichtner, A. Empirical Investigations of the Instrument Response for Distributed Acoustic Sensing (DAS) across 17 Octaves. Bull. Seismol. Soc. Am. 2020. [Google Scholar] [CrossRef]
- Brunner, B.; Wiesner, L.; Bernauer, F.; Markendorf, R. Performance and Laboratory Tests with a Prototype of FARO, a One-component, High-resolution Fibre Optic Rotational Seismometer. AGU Fall Meet. Abstr. 2019, 2019, S21G-0595. [Google Scholar]
- Brokešová, J.; Málek, J. Six-degree-of-freedom near-source seismic motions II: Examples of real seismogram analysis and S-wave velocity retrieval. J. Seismol. 2015, 19, 511–539. [Google Scholar] [CrossRef]
- Gebauer, A.; Tercjak, M.; Schreiber, K.U.; Igel, H.; Kodet, J.; Hugentobler, U.; Wassermann, J.; Bernauer, F.; Lin, C.J.; Donner, S.; et al. Reconstruction of the Instantaneous Earth Rotation Vector with Sub-Arcsecond Resolution Using a Large Scale Ring Laser Array. Phys. Rev. Lett. 2020, 125, 033605. [Google Scholar] [CrossRef]
- Igel, H.; Schreiber, K.U.; Gebauer, A.; Bernauer, F.; Egdorf, S.; Simonelli, A.; Lin, C.J.; Wassermann, J.; Donner, S.; Brotzer, A.; et al. ROMY: A Multi-Component Ring Laser for Geodesy and Geophysics. Geophys. J. Int. 2020. accepted. [Google Scholar]
- Hartog, A.H. An Introduction to Distributed Optical Fibre Sensors; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Thomas Constructeurs. Hydrostatic Truck Designed for Moving on and Off-Roads and Complying with European Standards. 2020. Available online: https://www.sercel.com/products/Lists/ProductSpecification/VIB3246_brochure.pdf (accessed on 20 August 2020).
- Pearson, K.; Galton, F., VII. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Lin, C.J.; Huang, H.P.; Pham, N.D.; Liu, C.C.; Chi, W.C.; Lee, W.H.K. Rotational motions for teleseismic surface waves. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Izgi, G.; Donner, S.; Bernauer, F.; Vollmer, D.; Hoffmann, M.; Igel, H.; Stammler, K.; Eibl, E.P.S. BlueSeis Huddle Test in Fürstenfeldbruck. Sensors 2020. submitted. [Google Scholar]
- Asch, G. Seismic Recording Systems. In New Manual of Seismological Observatory Practice (NMSOP); Bormann, P., Ed.; Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2009; pp. 1–20. [Google Scholar] [CrossRef]
- Merchant, B.J.; Slad, G.W. 2018 Nanometrics Centaur Digitizer Evaluation; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2018. [CrossRef]
- Bernauer, F.; Garcia, R.F.; Murdoch, N.; Dehant, V.; Sollberger, D.; Schmelzbach, C.; Stähler, S.; Wassermann, J.; Igel, H.; Cadu, A.; et al. Exploring planets and asteroids with 6DoF sensors: Utopia and realism. Earth Planets Space 2020, 72, 191. [Google Scholar] [CrossRef]
- Ross, M. Precision Mechanical Rotation Sensors for Terrestrial Gravitational Wave Observatories. Ph.D. Thesis, University of Washington, Washington, DC, USA, 2020. [Google Scholar]
- Geiger, R.; Landragin, A.; Merlet, S.; Pereira Dos Santos, F. High-accuracy inertial measurements with cold-atom sensors. AVS Quantum Sci. 2020, 2, 024702. [Google Scholar] [CrossRef]
- Venkateswara, K.; Hagedorn, C.A.; Turner, M.D.; Arp, T.; Gundlach, J.H. A high-precision mechanical absolute-rotation sensor. Rev. Sci. Instrum. 2014, 85, 015005. [Google Scholar] [CrossRef] [PubMed]
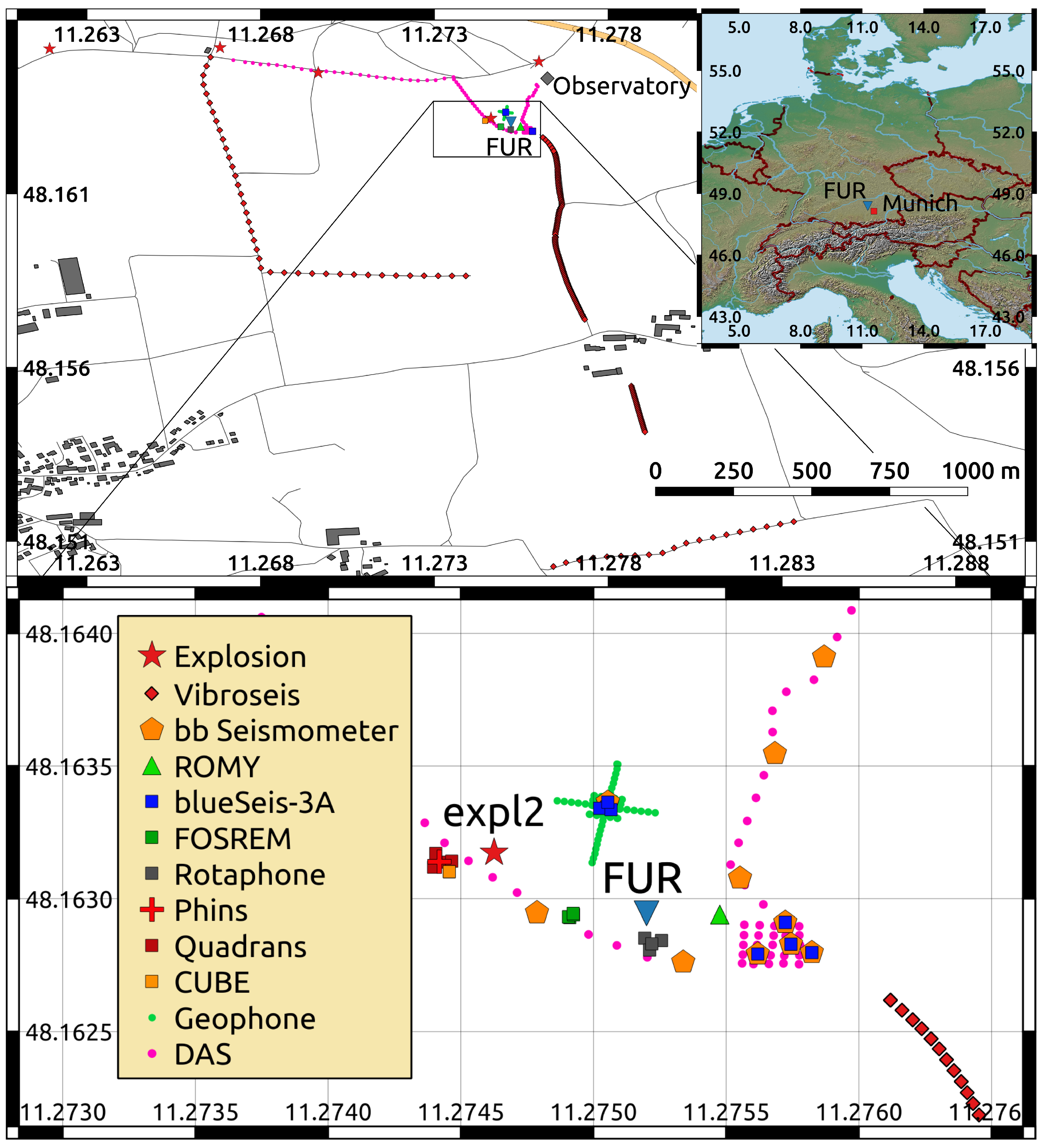
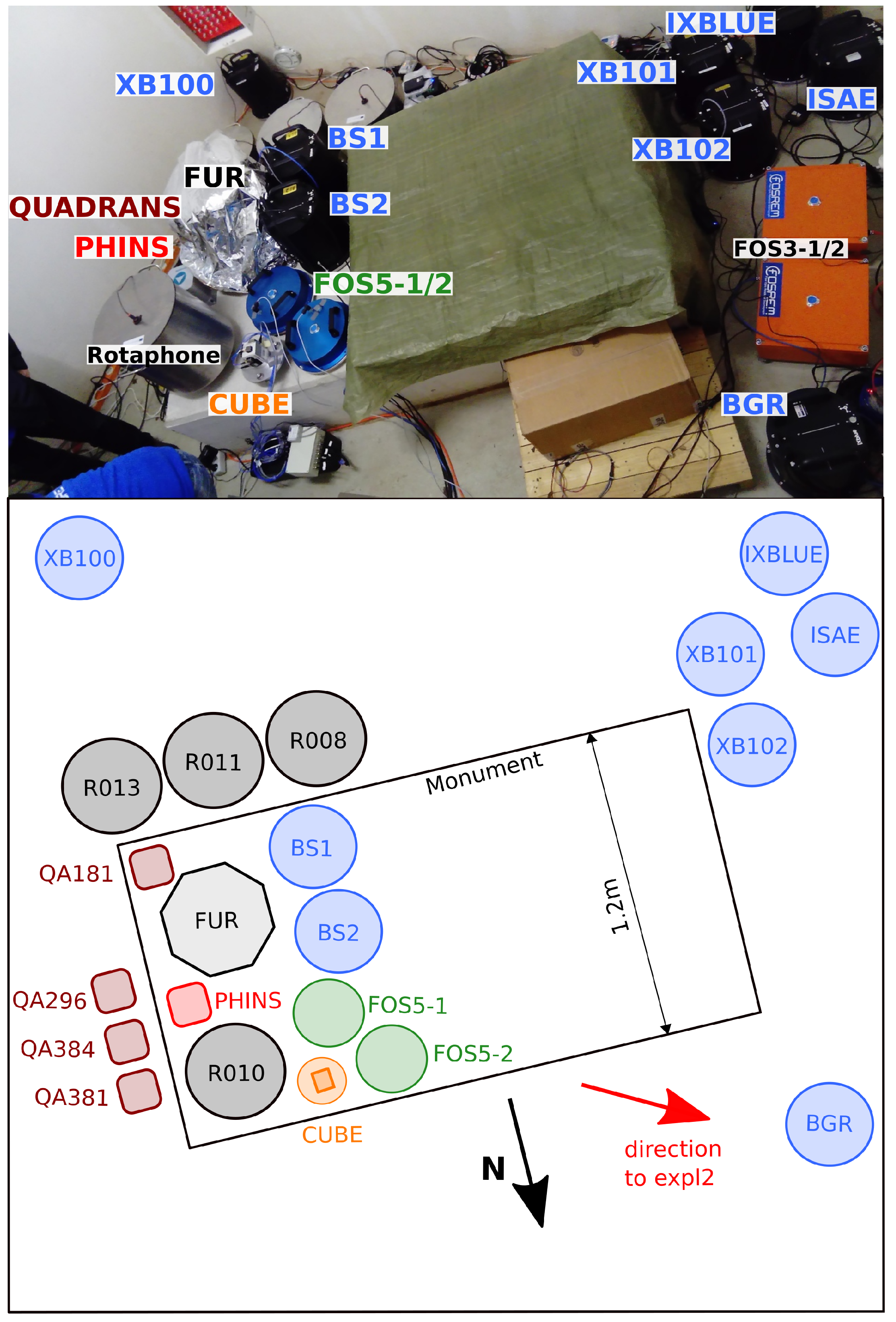

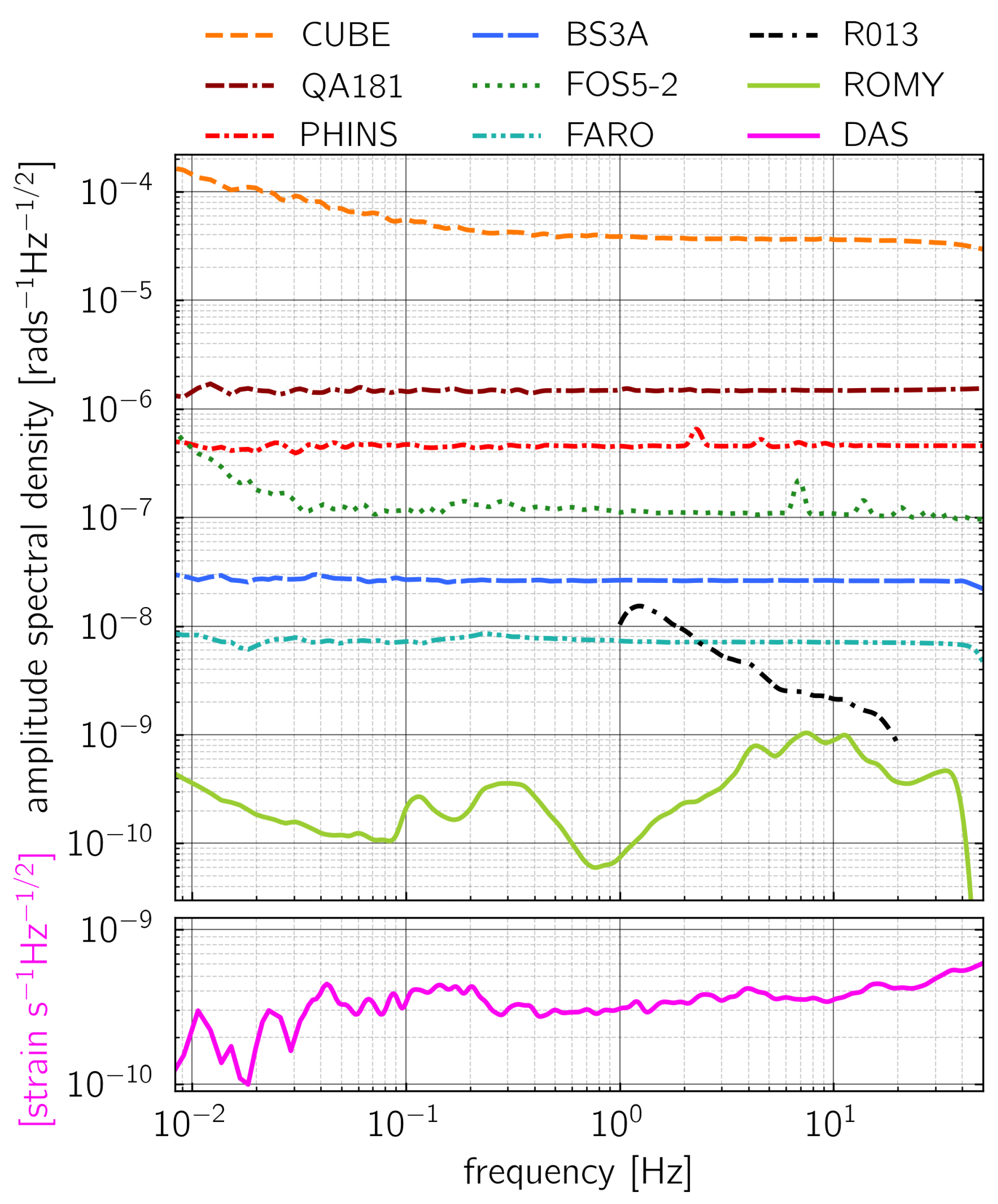
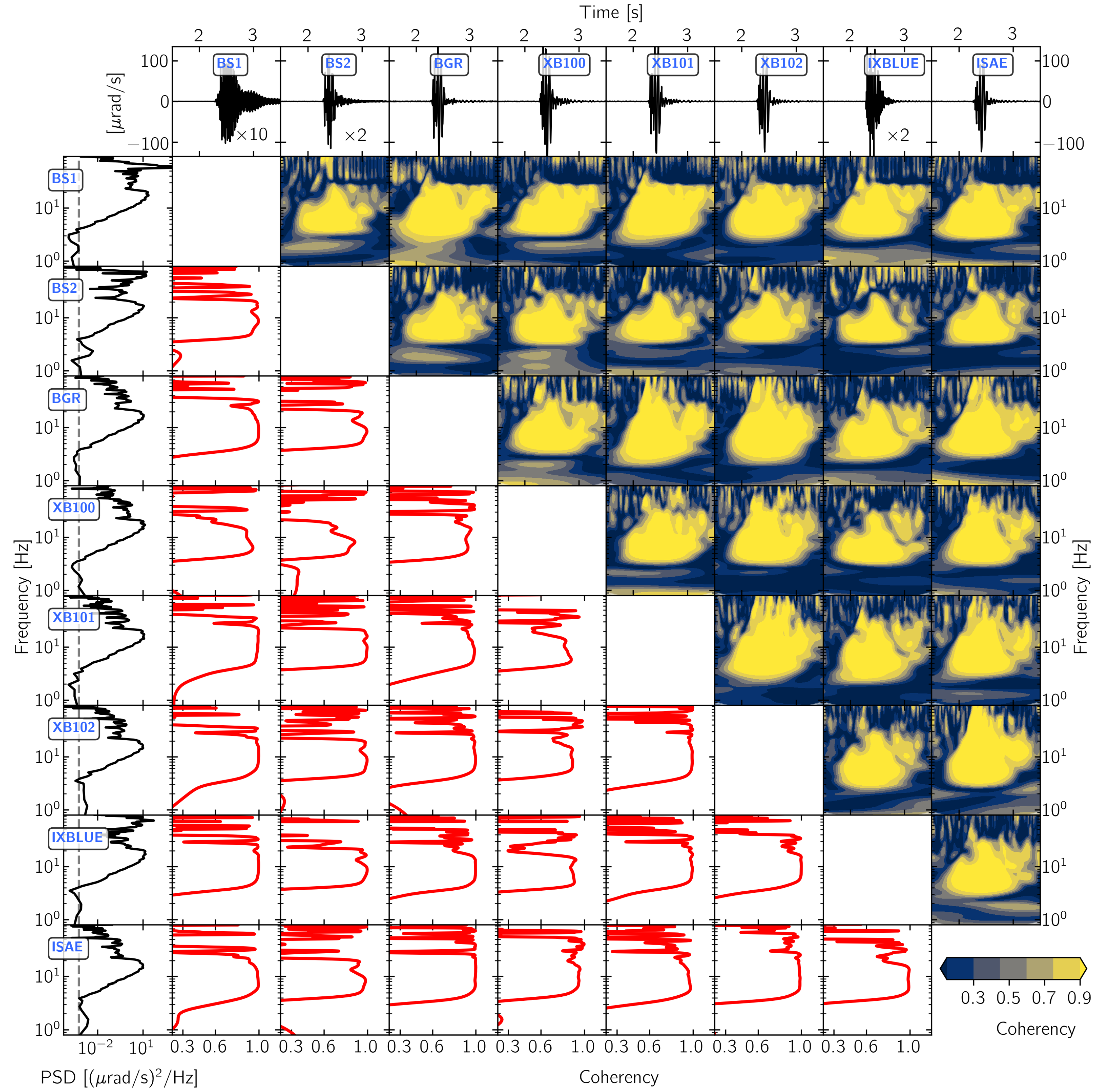
| Location | Sampling Rate [Hz] | Time Source and Synchronisation Method | Time Shift [s] to FUR | Max PCC | |
|---|---|---|---|---|---|
| BS1 | monument | 200 | GNSS/PPS | −0.005 | 0.92 |
| BS2 | monument | 200 | GNSS/PPS | −0.030 | 0.92 |
| BGR | floor | 200 | GNSS/PPS | −0.025 | 0.91 |
| XB100 | floor | 200 | GNSS/PPS | −0.030 | 0.91 |
| XB101 | floor | 200 | GNSS/PPS | −0.025 | 0.93 |
| XB102 | floor | 200 | GNSS/PPS | −0.025 | 0.95 |
| IXBLU | floor | 200 | GNSS/PPS | +0.005 | 0.91 |
| ISAE | floor | 200 | GNSS/PPS | −0.025 | 0.93 |
| FOS5-1 | monument | 1000 | NTP | −0.853 | 0.63 |
| FOS5-2 | monument | 1000 | NTP | −0.896 | 0.81 |
| FARO | aux. monument | 200 | GNSS/PPS | n.a. | n.a. |
| ROMY | own building | 100 | GNSS/PPS | n.a. | n.a. |
| PHINS | monument | 200 | GNSS/PPS | +0.285 | 0.87 |
| QA181 | monument | 200 | GNSS/PPS | +0.230 | 0.92 |
| QA296 | floor | 200 | GNSS/PPS | +0.185 | 0.87 |
| QA381 | floor | 200 | GNSS/PPS | +0.235 | 0.87 |
| QA384 | floor | 200 | GNSS/PPS | +0.195 | 0.91 |
| CUBE | monument | 1000 | NTP | n.a. | n.a. |
| R008 | floor | 250 | GNSS/PPS | −0.200 | 0.75 |
| R010 | monument | 250 | GNSS/PPS | −0.200 | 0.86 |
| R011 | floor | 250 | GNSS/PPS | −0.195 | 0.70 |
| R013 | floor | 250 | GNSS/PPS | −0.200 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernauer, F.; Behnen, K.; Wassermann, J.; Egdorf, S.; Igel, H.; Donner, S.; Stammler, K.; Hoffmann, M.; Edme, P.; Sollberger, D.; et al. Rotation, Strain, and Translation Sensors Performance Tests with Active Seismic Sources. Sensors 2021, 21, 264. https://doi.org/10.3390/s21010264
Bernauer F, Behnen K, Wassermann J, Egdorf S, Igel H, Donner S, Stammler K, Hoffmann M, Edme P, Sollberger D, et al. Rotation, Strain, and Translation Sensors Performance Tests with Active Seismic Sources. Sensors. 2021; 21(1):264. https://doi.org/10.3390/s21010264
Chicago/Turabian StyleBernauer, Felix, Kathrin Behnen, Joachim Wassermann, Sven Egdorf, Heiner Igel, Stefanie Donner, Klaus Stammler, Mathias Hoffmann, Pascal Edme, David Sollberger, and et al. 2021. "Rotation, Strain, and Translation Sensors Performance Tests with Active Seismic Sources" Sensors 21, no. 1: 264. https://doi.org/10.3390/s21010264
APA StyleBernauer, F., Behnen, K., Wassermann, J., Egdorf, S., Igel, H., Donner, S., Stammler, K., Hoffmann, M., Edme, P., Sollberger, D., Schmelzbach, C., Robertsson, J., Paitz, P., Igel, J., Smolinski, K., Fichtner, A., Rossi, Y., Izgi, G., Vollmer, D., ... Brokesova, J. (2021). Rotation, Strain, and Translation Sensors Performance Tests with Active Seismic Sources. Sensors, 21(1), 264. https://doi.org/10.3390/s21010264










