Comparing Direct Observation of Torsion with Array-Derived Rotation in Civil Engineering Structures
Abstract
1. Introduction
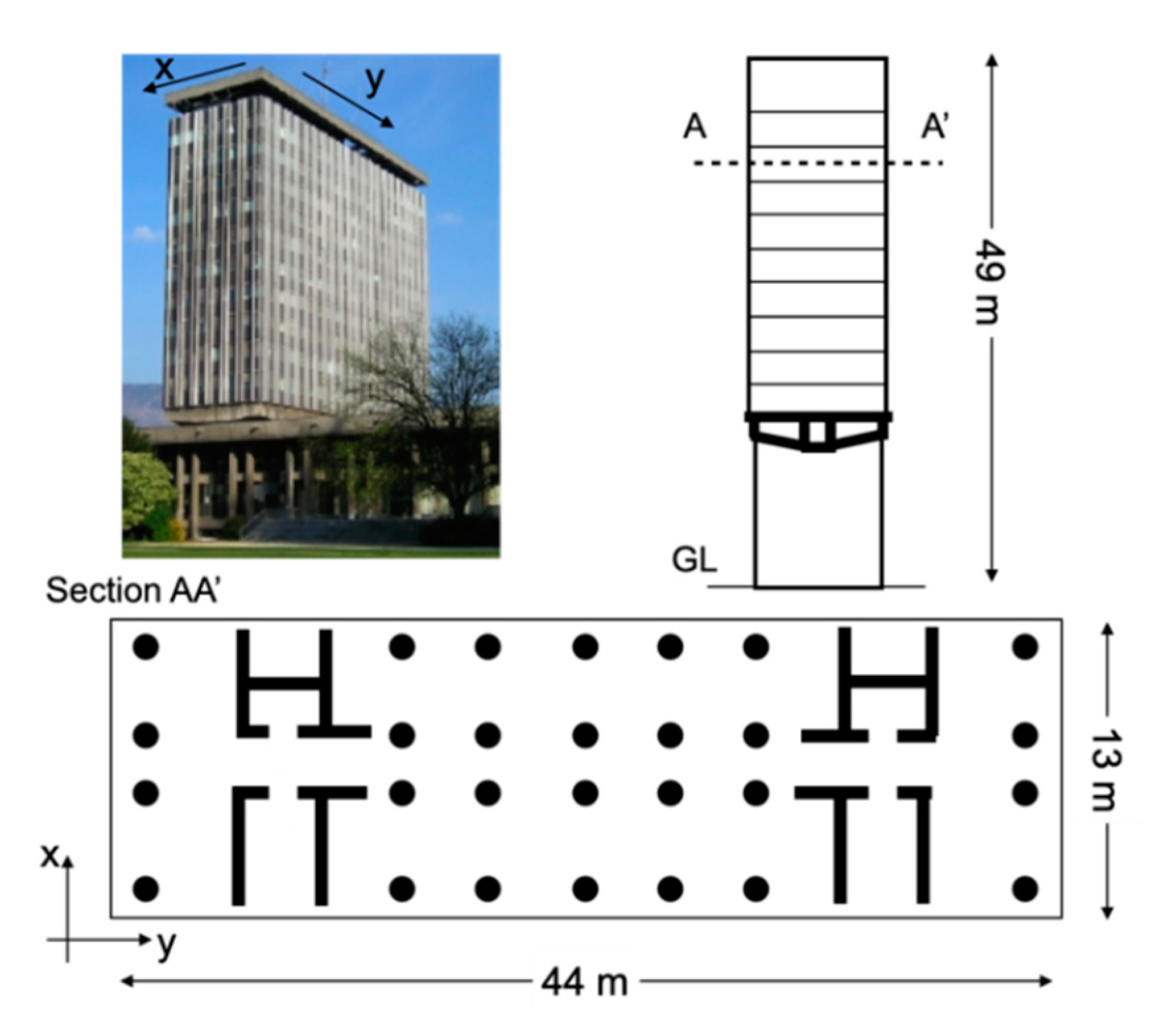
2. Data
3. Data Processing
4. Results and Discussion
4.1. Variation of Translation and Rotation Frequencies
4.2. Comparison of Rotation Values
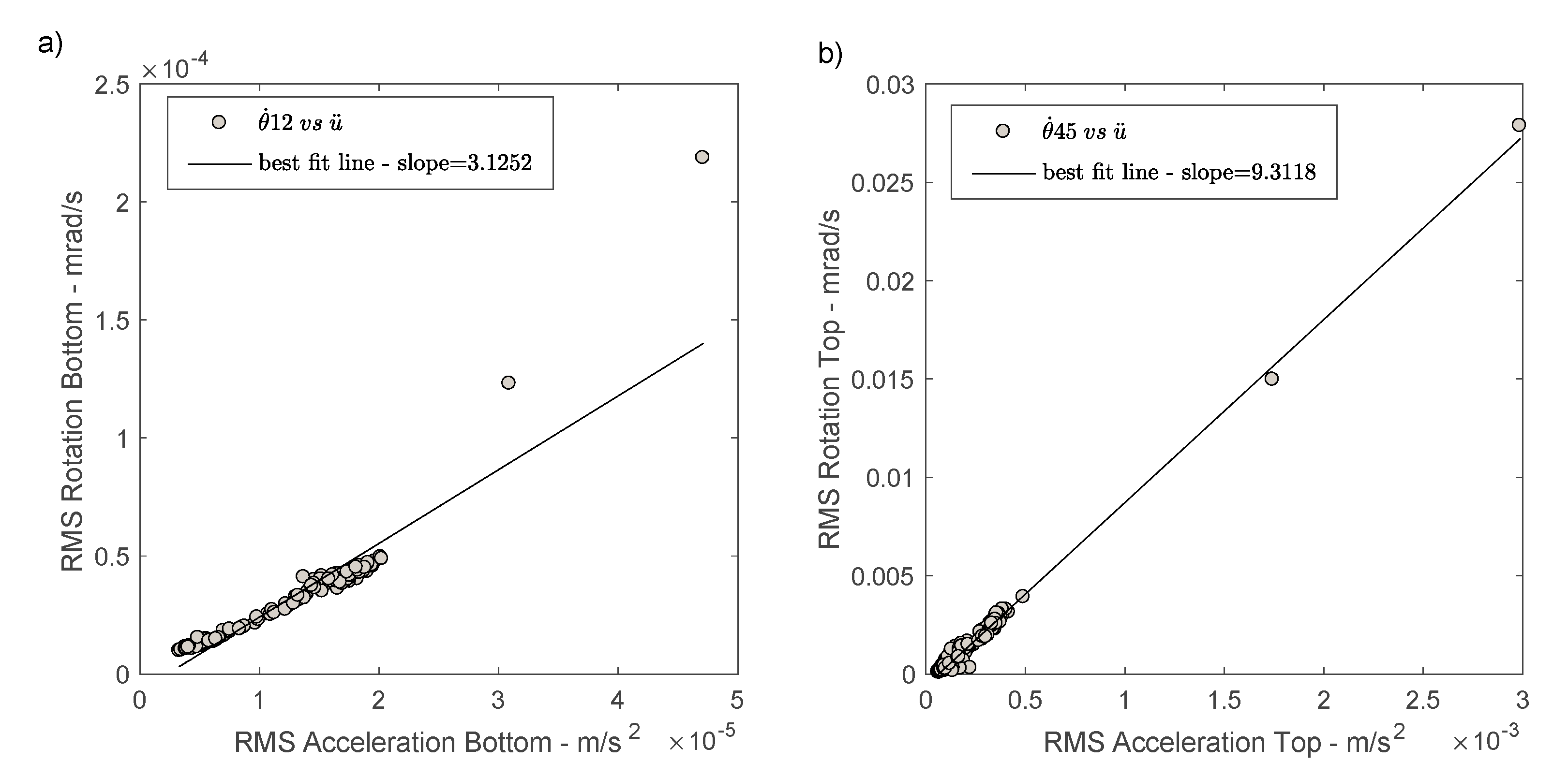
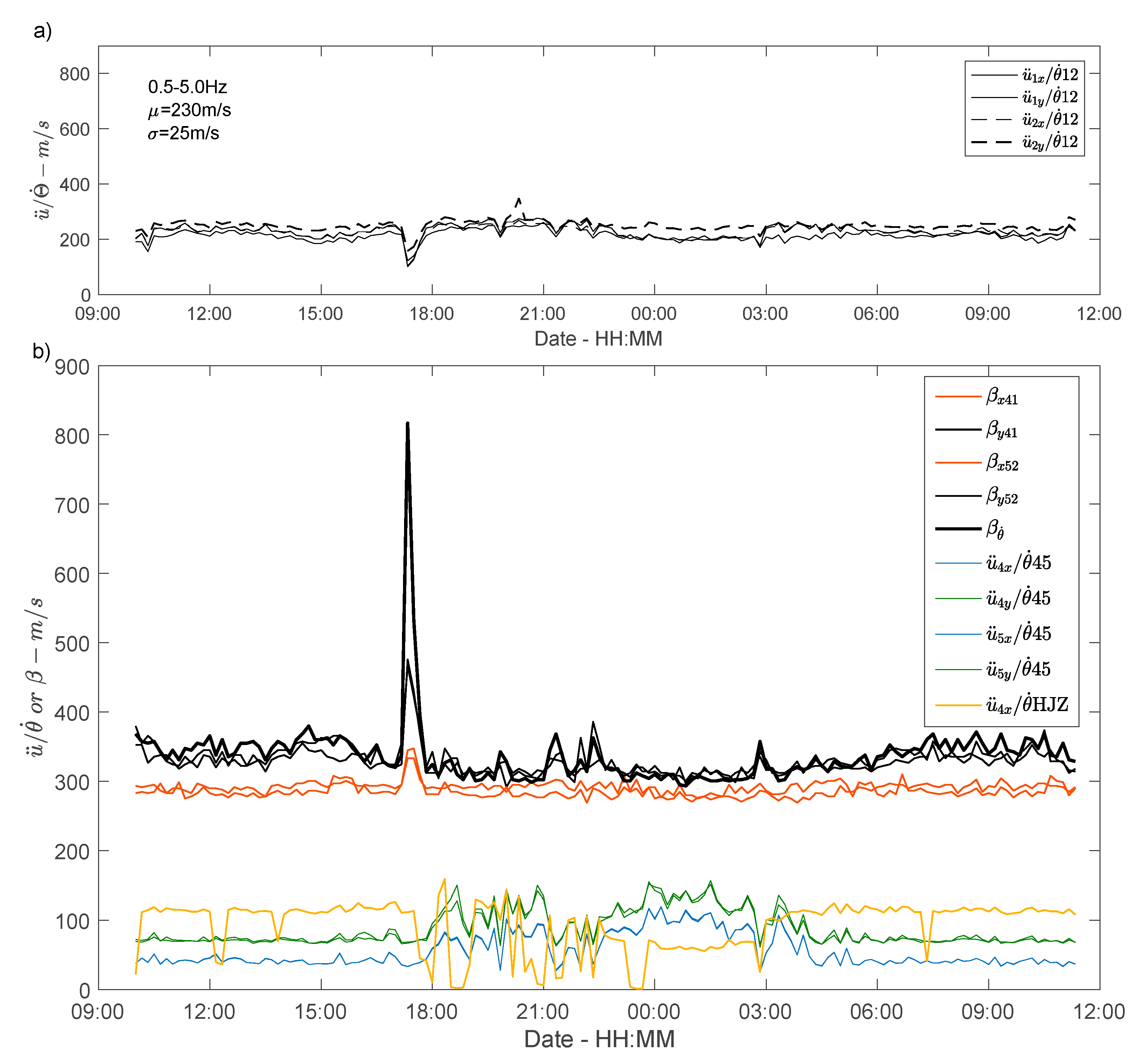
4.3. Acceleration versus Rotation and Phase Velocity
4.4. Phase Velocity Derived from the Rotation Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rutenberg, A. Nonlinear response asymmetric building structures and seismic codes: A state of the art review. In Nonlinear Seismic Analysis and Design of Reinforced Concrete Buildings; Fajfar, P., Krawinkler, H., Eds.; Elsevier Applied Science Eds: London, UK; New York, NY, USA, 1992; pp. 328–356. [Google Scholar]
- Anagnostopoulos, S.A.; Kyrkos, M.T.; Stathopoulos, K.G. Earthquake induced torsion in buildings: Critical review and state of the art. Earthq. Struct. 2015, 8, 305–377. [Google Scholar] [CrossRef]
- Kan, C.L.; Chopra, A.K. Elastic earthquake analysis of torsionally coupled multistorey buildings. Earthq. Eng. Struct. Dyn. 1977, 5, 395–412. [Google Scholar] [CrossRef]
- Chandler, A.M.; Duan, X.N. Inelastic torsional behaviour of asymmetric buildings under severe earthquake shaking. Struct Eng. Rev. 1990, 2, 141–159. [Google Scholar]
- Kan, C.L.; Chopra, A.K. Torsional Coupling and Earthquake Response of Simple Elastic and Inelastic Systems. J. Struct. Div. 1981, 107, 1569–1588. [Google Scholar]
- Chandler, A.M.; Hutchinson, G.L. Torsional coupling effects in the earthquake response of asymmetric buildings. Eng. Struct. 1986, 8, 222–236. [Google Scholar] [CrossRef]
- Newmark, N.M. Torsion in symmetrical buildings. In Proceedings of the 4th World Conference on Earthquake Engineering, Santiago, Chile, 13–18 January 1969; pp. 19–32. [Google Scholar]
- Bolt, B.A.; Tsai, Y.B.; Yeh, K.; Hsu, M.K. Earthquake strong motions recorded by a large near-source array of digital seismographs. Earthq. Eng. Struct. Dyn. 1982, 10, 561–573. [Google Scholar] [CrossRef]
- De la Llera, J.C.; Chopra, A.K. Accidental torsion in buildings due to base rotational excitation. Earthq. Eng. Struct. Dyn. 1994, 23, 1003–1021. [Google Scholar] [CrossRef]
- Hart, G.C.; Lew, M.; DiJulio, R.M. Torsional response of high–rise buildings. J. Struct. Division 1975, 101, 397–416. [Google Scholar]
- Chandler, A.M. Building damage in Mexico City earthquake. Nature 1986, 320, 497–501. [Google Scholar] [CrossRef]
- Ghayamghamian, M.R.; Nouri, G.R.; Igel, H.; Tobita, T. The Effect of Torsional Ground Motion on Structural Response: Code Recommendation for Accidental Eccentricity. Bull. Seismol. Soc. Am. 2009, 99, 1261–1270. [Google Scholar] [CrossRef]
- Şafak, E. Response of a 42–storey steel–frame building to the MS=7.1 Loma Prieta earthquake. Eng. Struct. 1993, 15, 403–421. [Google Scholar] [CrossRef]
- Li, Y.; Mau, S.T. Learning from Recorded Earthquake Motion of Buildings. J. Struct. Eng. 1997, 123, 62–69. [Google Scholar] [CrossRef]
- Todorovska, M.I.; Trifunac, M.D. Earthquake damage detection in the Imperial County Services Building III: Analysis of wave travel times via impulse response functions. Soil Dyn. Earthq. Eng. 2008, 28, 387–404. [Google Scholar] [CrossRef]
- Lemnitzer, A.; Massone, L.M.; Skolnik, D.A.; Martin, J.C.D.L.L.; Wallace, J.W. Aftershock response of RC buildings in Santiago, Chile, succeeding the magnitude 8.8 Maule earthquake. Eng. Struct. 2014, 76, 324–338. [Google Scholar] [CrossRef]
- Çelebi, M. Recorded Earthquake Responses from the Integrated Seismic Monitoring Network of the Atwood Building, Anchorage, Alaska. Earthq. Spectra 2006, 22, 847–864. [Google Scholar] [CrossRef]
- Michel, C.; Guéguen, P.; El Arem, S.; Mazars, J.; Kotronis, P. Full-scale dynamic response of an RC building under weak seismic motions using earthquake recordings, ambient vibrations and modelling. Earthq. Eng. Struct. Dyn. 2010, 39, 419–441. [Google Scholar] [CrossRef]
- Oliveira, C.S.; Bolt, B.A. Rotational components of surface strong ground motion. Earthq. Eng. Struct. Dyn. 1989, 18, 517–526. [Google Scholar] [CrossRef]
- Cochard, A.; Igel, H.; Schuberth, B.; Suryanto, W.; Velikoseltsev, A.; Schreiber, U.; Wassermann, J.; Scherbaum, F.; Vollmer, D. Rotational Motions in Seismology: Theory, Observation, Simulation. In Earthquake Source Asymmetry, Structural Media and Rotation Effects; Springer: Berlin/Heidelberg, Germany, 2006; pp. 391–411. [Google Scholar]
- Castellani, A. Array-derived rotational seismic motions: Revisited. Bull. Earthq. Eng. 2016, 15, 813–825. [Google Scholar] [CrossRef]
- Trifunac, M.D. Differential earthquake motion of building foundations. J. Struct. Eng. 1997, 4, 414–422. [Google Scholar] [CrossRef]
- Guéguen, P.; Bard, P.-Y. Soil-structure and soil-structure-soil interaction: Experimental evidence at the Volvi test site. J. Earthq. Eng. 2005, 9, 657–693. [Google Scholar] [CrossRef]
- Çelebi, M.; Okawa, I.; Kashima, T.; Koyama, S.; Iiba, M. Response of a tall building far from the epicenter of the 11 March 2011 M 9.0 Great East Japan earthquake and aftershocks. Struct. Des. Tall Spec. Build. 2014, 23, 427–441. [Google Scholar] [CrossRef]
- Rahmani, M.; Todorovska, M.I. 1D System identification of a 54-story steel frame building by seismic interferometry. Earthq. Eng. Struct. Dyn. 2014, 43, 627–640. [Google Scholar] [CrossRef]
- Lin, C.-J.; Huang, W.-G.; Huang, H.-P.; Huang, B.S.; Ku, C.-S.; Liu, C.-C. Investigation of array-derived rotation in TAIPEI 101. J. Seismol. 2012, 16, 721–731. [Google Scholar] [CrossRef]
- Hou, S.; Zeng, C.; Zhang, H.; Ou, J. Monitoring interstory drift in buildings under seismic loading using MEMS inclinometers. Constr. Build. Mater. 2018, 185, 453–467. [Google Scholar] [CrossRef]
- Hester, D.; Brownjohn, J.; Huseynov, F.; Obrien, E.; Gonzalez, A.; Casero, M. Identifying damage in a bridge by analysing rotation response to a moving load. Struct. Infrastruct. Eng. 2020, 16, 1050–1065. [Google Scholar] [CrossRef]
- Bas, S.; Apaydın, N.M.; Ilki, A.; Catbas, F.N. Structural health monitoring system of the long-span bridges in Turkey. Struct. Infrastruct. Eng. 2018, 14, 425–444. [Google Scholar] [CrossRef]
- Huseynov, F.; Kim, C.; Obrien, E.J.; Brownjohn, J.M.W.; Hester, D.; Chang, K.C. Bridge damage detection using rotation measurements—Experimental validation. Mech. Syst. Signal Process. 2020, 135, 106380. [Google Scholar] [CrossRef]
- Sousa, H.; Cavadas, F.; Henriques, A.; Bento, J.; Figueiras, J. Bridge deflection evaluation using strain and rotation measurements. Smart Struct. Syst. 2013, 11, 365–386. [Google Scholar] [CrossRef]
- Lee, V.W.; Trifunac, M.D. Empirical Scaling of Rotational Spectra of Strong Earthquake Ground Motion. Bull. Seismol. Soc. Am. 2009, 99, 1378–1390. [Google Scholar] [CrossRef]
- Bernauer, F.; Wassermann, J.; Igel, H. Rotational sensors—a comparison of different sensor types. J. Seismol. 2012, 16, 595–602. [Google Scholar] [CrossRef]
- Igel, H.; Cochard, A.; Wassermann, J.; Flaws, A.; Schreiber, U.; Velikoseltsev, A.; Dinh, N.P. Broad-band observations of earthquake-induced rotational ground motions. Geophys. J. Int. 2007, 168, 182–196. [Google Scholar] [CrossRef]
- Lee, W.H.K.; Huang, B.-S.; Langston, C.A.; Lin, C.-J.; Liu, C.-C.; Shin, T.-C.; Teng, T.-L.; Wu, C.-F. Review: Progress in Rotational Ground-Motion Observations from Explosions and Local Earthquakes in Taiwan. Bull. Seismol. Soc. Am. 2009, 99, 958–967. [Google Scholar] [CrossRef]
- Guéguen, P.; Cornou, C.; Garambois, S.; Banton, J. On the Limitation of the H/V Spectral Ratio Using Seismic Noise as an Exploration Tool: Application to the Grenoble Valley (France), a Small Apex Ratio Basin. Pure Appl. Geophys. 2007, 164, 115–134. [Google Scholar] [CrossRef]
- Cornou, C.; Bard, P.Y.; Dietrich, M. Contribution of dense array analysis to the identification and quantification of basin–edge–induced waves, Part II: Application to Grenoble basin (French Alps). Bull. Seismol. Soc. Am. 2003, 93, 2624–2648. [Google Scholar] [CrossRef]
- Guéguen, P.; Langlais, M.; Garambois, S.; Voisin, C.; Douste-Bacqué, I. How sensitive are site effects and building response to extreme cold temperature? The case of the Grenoble’s (France) City Hall building. Bull. Earthq. Eng. 2017, 15, 889–906. [Google Scholar] [CrossRef]
- Péquegnat, C.; Guéguen, P.; Hatzfeld, D.; Langlais, M. The French Accelerometric Network (RAP) and National Data Centre (RAP-NDC). Seismol. Res. Lett. 2008, 79, 79–89. [Google Scholar] [CrossRef]
- Michel, C. Vulnérabilité Sismique de l’échelle du Bâtiment à Celle de la Ville—Apport des Techniques Expérimentales In Situ—Application à Grenoble. Ph.D. Thesis, Université Joseph–Fourier, Grenoble, France, 2007. [Google Scholar]
- Cao, Y.; Mavroeidis, G.P.; Ashoory, M. Comparison of observed and synthetic near–fault dynamic ground strains and rotations from the 2004 M w 6.0 Parkfield, California, earthquake. Bull. Seismol. Soc. Am. 2018, 108, 1240–1256. [Google Scholar] [CrossRef]
- Spudich, P.; Fletcher, J.B. Observation and Prediction of Dynamic Ground Strains, Tilts, and Torsions Caused by the Mw 6.0 2004 Parkfield, California, Earthquake and Aftershocks, Derived from UPSAR Array Observations. Bull. Seismol. Soc. Am. 2008, 98, 1898–1914. [Google Scholar] [CrossRef]
- Guéguen, P.; Johnson, P.; Roux, P. Nonlinear dynamics induced in a structure by seismic and environmental loading. J. Acoust. Soc. Am. 2016, 140, 582–590. [Google Scholar] [CrossRef]
- Clinton, J.F.; Bradford, S.C.; Heaton, T.H.; Favela, J. The observed wander of the natural frequencies in a structure. Bull. Seismol. Soc. Am. 2006, 96, 237–257. [Google Scholar] [CrossRef]
- Astorga, A.; Guéguen, P.; Kashima, T. Nonlinear Elasticity Observed in Buildings during a Long Sequence of Earthquakes. Bull. Seismol. Soc. Am. 2018, 108, 1185–1198. [Google Scholar] [CrossRef]
- Cole, H. On–Line Failure Detection and Damping Measurement of Aerospace Structures by Random Decrement Signatures; Technical Report NASA CR–2205; NASA: Washington, DC, USA, 1973.
- Takeo, M. Rotational Motions Observed during an Earthquake Swarm in April 1998 Offshore Ito, Japan. Bull. Seismol. Soc. Am. 2009, 99, 1457–1467. [Google Scholar] [CrossRef]
- Liu, C.-C.; Huang, B.-S.; Lee, W.H.K.; Lin, C.-J. Observing Rotational and Translational Ground Motions at the HGSD Station in Taiwan from 2007 to 2008. Bull. Seismol. Soc. Am. 2009, 99, 1228–1236. [Google Scholar] [CrossRef]
- Shakib, H.; Tohidi, R.Z. Evaluation of accidental eccentricity in buildings due to rotational component of earthquake. J. Earthq. Eng. 2002, 6, 431–445. [Google Scholar] [CrossRef]
- Snieder, R.; Şafak, E. Extracting the building response using seismic interferometry: Theory and application to the Millikan Library in Pasadena, California. Bull. Seismol. Soc. Am. 2006, 96, 586–598. [Google Scholar] [CrossRef]
- Mehta, K.; Snieder, R.; Graizer, V. Extraction of near-surface properties for a lossy layered medium using the propagator matrix. Geophys. J. Int. 2007, 169, 271–280. [Google Scholar] [CrossRef]
- Nakata, N.; Snieder, R. Estimating near-surface shear wave velocities in Japan by applying seismic interferometry to KiK-net data. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Chandra, J.; Guéguen, P.; Steidl, J.H.; Bonilla, L.F. In situ assessment of the G–γ curve for characterizing the nonlinear response of soil: Application to the Garner Valley downhole array and the wildlife liquefaction array. Bull. Seismol. Soc. Am. 2015, 105, 993–1010. [Google Scholar] [CrossRef]
- Chandra, J.; Guéguen, P.; Bonilla, L.F. PGA-PGV/Vs considered as a stress–strain proxy for predicting nonlinear soil response. Soil Dyn. Earthq. Eng. 2016, 85, 146–160. [Google Scholar] [CrossRef]
- Nakata, N.; Tanaka, W.; Oda, Y. Damage Detection of a Building Caused by the 2011 Tohoku-Oki Earthquake with Seismic Interferometry. Bull. Seismol. Soc. Am. 2015, 105, 2411–2419. [Google Scholar] [CrossRef][Green Version]
- Ebrahimian, M.; Rahmani, M.; Todorovska, M.I. Nonparametric estimation of wave dispersion in high-rise buildings by seismic interferometry. Earthq. Eng. Struct. Dyn. 2014, 43, 2361–2375. [Google Scholar] [CrossRef]
- Guéguen, P.; Mercerat, E.D.; Alarcon, F. Parametric Study on the Interpretation of Wave Velocity Obtained by Seismic Interferometry in Beam-Like Buildings. Bull. Seismol. Soc. Am. 2019, 109, 1829–1842. [Google Scholar] [CrossRef]
- Michel, C.; Guéguen, P. Interpretation of the velocity measured in buildings by seismic interferometry based on Timoshenko beam theory under weak and moderate motion. Soil Dyn. Earthq. Eng. 2018, 104, 131–142. [Google Scholar] [CrossRef]
- Ferreira, A.M.G.; Igel, H. Rotational Motions of Seismic Surface Waves in a Laterally Heterogeneous Earth. Bull. Seismol. Soc. Am. 2009, 99, 1429–1436. [Google Scholar] [CrossRef]
- Pandey, A.K.; Biswas, M. Damage Detection in Structures Using Changes in Flexibility. J. Sound Vib. 1994, 169, 3–17. [Google Scholar] [CrossRef]
- Roux, P.; Guéguen, P.; Baillet, L.; Hamze, A. Structural-change localization and monitoring through a perturbation-based inverse problem. J. Acoust. Soc. Am. 2014, 136, 2586–2597. [Google Scholar] [CrossRef]








| Parameters | μ | σ | σ/μ | Δ | |
|---|---|---|---|---|---|
| Temperature °C | 18 | 4 | 24% | −30% | |
| Wind speed m/s | 1.6 | 2 | 116 | 78% | |
| Frequency Hz | y-dir | 1.212 | 0.003 | 0.3% | −1.1% |
| x-dir | 1.155 | 0.004 | 0.3% | −1.3% | |
| z-dir () | 1.442 | 0.003 | 0.2% | −0.9% | |
| RMS Ratio | Mean | Std | COV (%) |
|---|---|---|---|
| Top/Bot | 18.3 | 6.3 | 34 |
| / | 40.6 | 26.4 | 65 |
| Top/ | 315.3 | 261.1 | 83 |
| Bot/ | 404.5 | 38.4 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guéguen, P.; Guattari, F.; Aubert, C.; Laudat, T. Comparing Direct Observation of Torsion with Array-Derived Rotation in Civil Engineering Structures. Sensors 2021, 21, 142. https://doi.org/10.3390/s21010142
Guéguen P, Guattari F, Aubert C, Laudat T. Comparing Direct Observation of Torsion with Array-Derived Rotation in Civil Engineering Structures. Sensors. 2021; 21(1):142. https://doi.org/10.3390/s21010142
Chicago/Turabian StyleGuéguen, Philippe, Frédéric Guattari, Coralie Aubert, and Theo Laudat. 2021. "Comparing Direct Observation of Torsion with Array-Derived Rotation in Civil Engineering Structures" Sensors 21, no. 1: 142. https://doi.org/10.3390/s21010142
APA StyleGuéguen, P., Guattari, F., Aubert, C., & Laudat, T. (2021). Comparing Direct Observation of Torsion with Array-Derived Rotation in Civil Engineering Structures. Sensors, 21(1), 142. https://doi.org/10.3390/s21010142






