Single- and Cross-Modality Near Duplicate Image Pairs Detection via Spatial Transformer Comparing CNN
Abstract
1. Introduction
- We propose a CCNN model to the task of near-duplicate image pair detection, which makes more use of rich resolution features to encode the correlations between image pairs.
- We further propose the ST-CCNN model by introducing a spatial transformer module into the comparing CNN architecture, which can improve the robustness to variations, such as cropping, translation, scaling, and non-rigid transformations.
- Comprehensive experiments on both the single-modality and cross-modality (Optical-InfraRed) near-duplicate image pair detection tasks are conducted to verify the effectiveness of the proposed method.
2. Related Work
2.1. Two-Stage Strategies
2.2. End-To-End Strategies
3. Methodology
3.1. Triple-Stream Framework
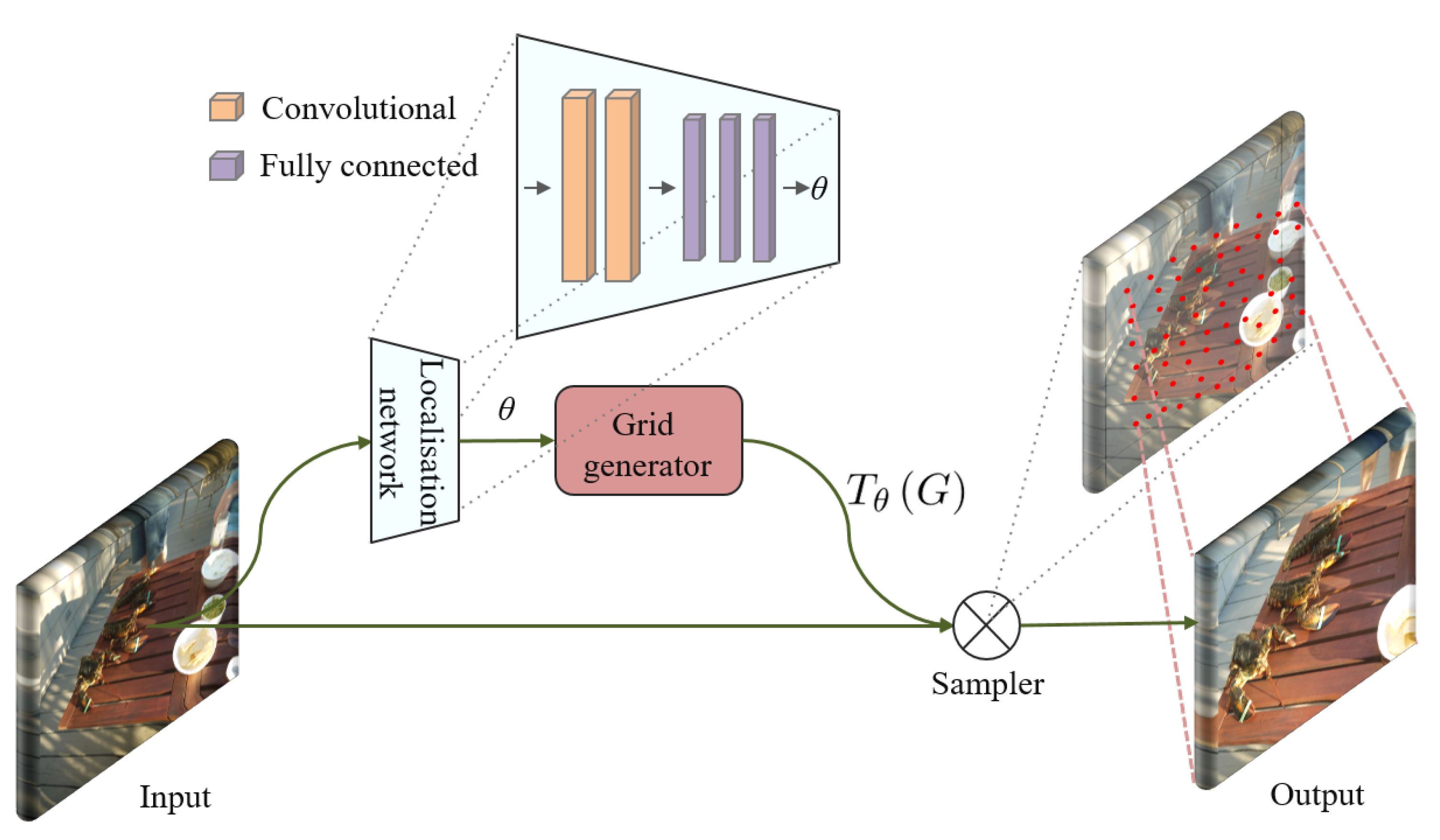
3.2. Spatial Transformer
3.3. Loss Function
4. Experiments
4.1. Datasets and Settings
4.2. Evaluation Metrics
4.3. Result Comparison
4.3.1. Single-Modality Results
4.3.2. Cross-Modality Results
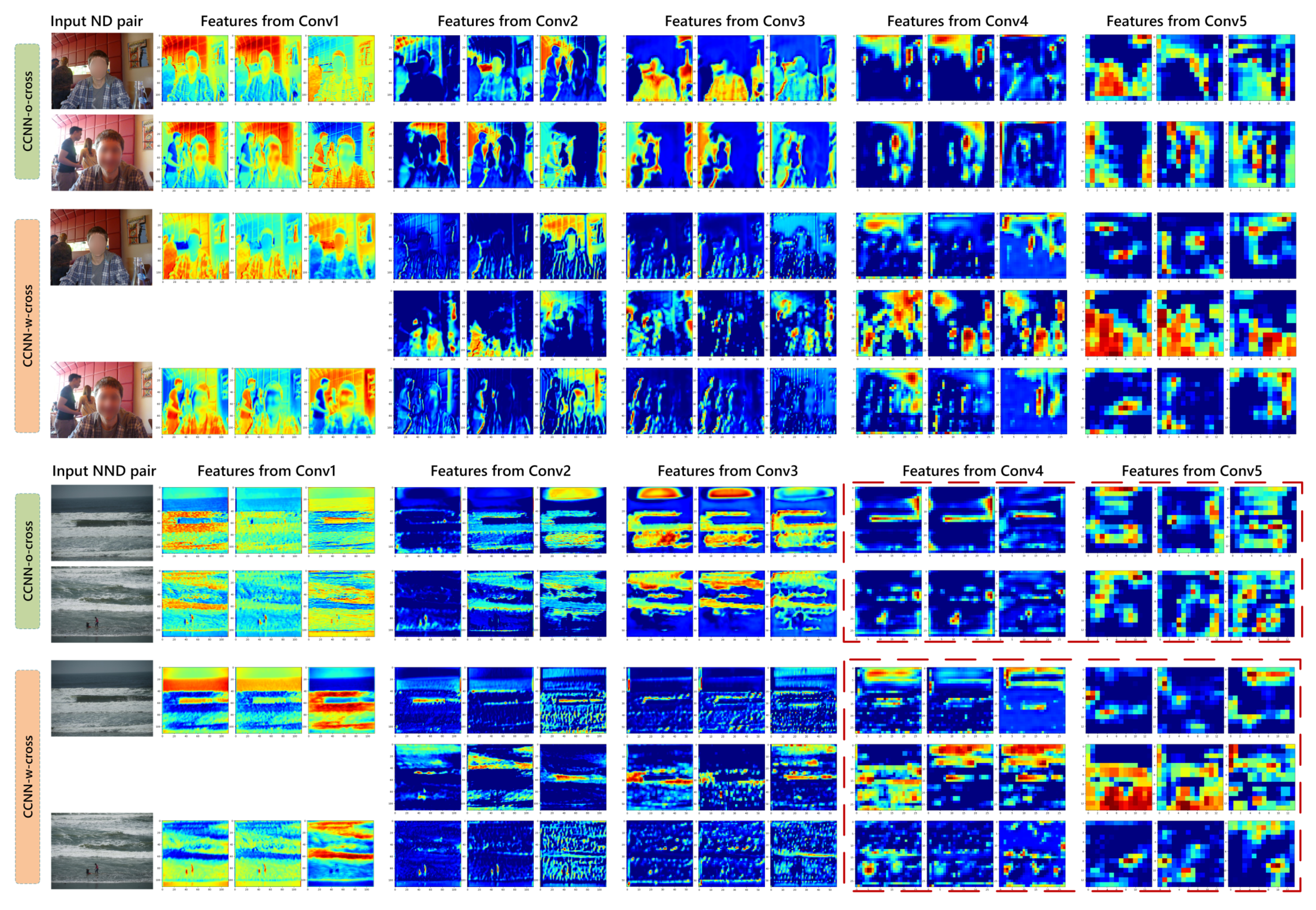
4.4. Ablation Study
4.4.1. Effectiveness of Triple Stream Structures
4.4.2. Effectiveness of Spatial Transformers
4.4.3. Effectiveness of Asymmetric ST Structure
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CNN | convolutional neural networks |
| ST | spatial transformer |
| ST-CCNN | spatial transformer comparing CNN |
| SIFT | scale-invariant feature transform |
| HOG | histograms of oriented gradients |
| VLAD | vector of locally aggregated descriptors |
| PCA-SIFT | principal component analysis scale-invariant feature transform |
| LSH | locality-sensitive hashing |
| BoW | bag-of-word |
| ROI | regions of interest |
| ARG | attributed relational graph |
| GVP | geometry-preserving visual phrases |
| MOP | multi-scale orderless pooling |
| MOF | multi-layer orderless fusion |
| CNNH | convolutional neural network hashing |
| PCA | principle components analysis |
| SPoC | sum-pooled convolutional |
| RPN | region proposal network |
| ND | near duplicate |
| NND | non-near duplicate |
| TP | true positive |
| TN | true negative |
| FP | false positive |
| FN | false negative |
| MFND | mir-Flickr near duplicate |
| ROC | receiver operating characteristic |
| AUC | Area Under Curve |
| AUROC | area under receiver operating characteristic |
References
- Thyagharajan, K.; Kalaiarasi, G. A Review on Near-Duplicate Detection of Images using Computer Vision Techniques. Arch. Comput. Methods Eng. 2020, 1–20. [Google Scholar] [CrossRef]
- Morra, L.; Lamberti, F. Benchmarking unsupervised near-duplicate image detection. Expert Syst. Appl. 2019, 135, 313–326. [Google Scholar] [CrossRef]
- Jinda-Apiraksa, A.; Vonikakis, V.; Winkler, S. California-ND: An annotated dataset for near-duplicate detection in personal photo collections. In Proceedings of the 2013 Fifth International Workshop on Quality of Multimedia Experience (QoMEX), Wörthersee, Austria, 3–5 July 2013; pp. 142–147. [Google Scholar] [CrossRef]
- Connor, R.; MacKenzie-Leigh, S.; Cardillo, F.A.; Moss, R. Identification of MIR-Flickr near-duplicate images: A benchmark collection for near-duplicate detection. In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP 2015), Berlin, Germany, 11–14 March 2015; pp. 565–571. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; Volume 1, pp. 886–893. [Google Scholar] [CrossRef]
- Jégou, H.; Perronnin, F.; Douze, M.; Sánchez, J.; Pérez, P.; Schmid, C. Aggregating Local Image Descriptors into Compact Codes. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1704–1716. [Google Scholar] [CrossRef] [PubMed]
- Perronnin, F.; Dance, C. Fisher Kernels on Visual Vocabularies for Image Categorization. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 18–23 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. Scale & Affine Invariant Interest Point Detectors. Int. J. Comput. Vis. 2004, 60, 63–86. [Google Scholar] [CrossRef]
- Ke, Y.; Sukthankar, R.; Huston, L. Efficient near-duplicate detection and sub-image retrieval. In Proceedings of the ACM International Conference on Multimedia (MM), New York, NY, USA, 10–16 October 2004; Volume 4, p. 5. [Google Scholar]
- Zhang, S.; Tian, Q.; Lu, K.; Huang, Q.; Gao, W. Edge-SIFT: Discriminative Binary Descriptor for Scalable Partial-Duplicate Mobile Search. IEEE Trans. Image Process. 2013, 22, 2889–2902. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.Q.; Chang, S.F. Detecting Image Near-duplicate by Stochastic Attributed Relational Graph Matching with Learning. In Proceedings of the 12th Annual ACM International Conference on Multimedia, MULTIMEDIA ’04, New York, NY, USA, 10–16 October 2004; pp. 877–884. [Google Scholar] [CrossRef]
- Xu, D.; Cham, T.J.; Yan, S.; Duan, L.; Chang, S.F. Near Duplicate Identification With Spatially Aligned Pyramid Matching. IEEE Trans. Circuits Syst. Video Technol. 2010, 20, 1068–1079. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, Z.; Chen, T. Image retrieval with geometry-preserving visual phrases. In Proceedings of the 2011 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 21–23 June 2011; pp. 809–816. [Google Scholar] [CrossRef]
- Chum, O.; Philbin, J.; Zisserman, A. Near Duplicate Image Detection: Min-Hash and tf-idf Weighting. In Proceedings of the British Machine Vision Conference, Leeds, UK, 1–4 September 2008; pp. 50.1–50.10. [Google Scholar] [CrossRef]
- Zhao, W.L.; Ngo, C.W. Scale-Rotation Invariant Pattern Entropy for Keypoint-Based Near-Duplicate Detection. IEEE Trans. Image Process. 2009, 18, 412–423. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Wang, S.; Tian, Q. Coupled Binary Embedding for Large-Scale Image Retrieval. IEEE Trans. Image Process. 2014, 23, 3368–3380. [Google Scholar] [CrossRef] [PubMed]
- Wan, J.; Wang, D.; Hoi, S.C.H.; Wu, P.; Zhu, J.; Zhang, Y.; Li, J. Deep Learning for Content-Based Image Retrieval: A Comprehensive Study. In Proceedings of the 22Nd ACM International Conference on Multimedia, MM ’14, Orlando, FL, USA, 3–7 November 2014; pp. 157–166. [Google Scholar] [CrossRef]
- Babenko, A.; Slesarev, A.; Chigorin, A.; Lempitsky, V. Neural Codes for Image Retrieval. In Computer Vision—ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part I; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 584–599. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, L.; Guo, R.; Lazebnik, S. Multi-scale Orderless Pooling of Deep Convolutional Activation Features. In Computer Vision—ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part VII; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 392–407. [Google Scholar] [CrossRef]
- Mopuri, K.R.; Babu, R.V. Object level deep feature pooling for compact image representation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Boston, MA, USA, 8–10 June 2015; pp. 62–70. [Google Scholar] [CrossRef]
- Xie, L.; Hong, R.; Zhang, B.; Tian, Q. Image Classification and Retrieval Are ONE. In Proceedings of the 5th ACM on International Conference on Multimedia Retrieval, ICMR ’15, Shanghai, China, 23–26 June 2015; pp. 3–10. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, S.; Wang, J.; Tian, Q. Accurate Image Search with Multi-Scale Contextual Evidences. Int. J. Comput. Vis. 2016, 120, 1–13. [Google Scholar] [CrossRef]
- Yan, K.; Wang, Y.; Liang, D.; Huang, T.; Tian, Y. CNN vs. SIFT for Image Retrieval: Alternative or Complementary? In Proceedings of the 2016 ACM on Multimedia Conference, MM ’16, Amsterdam, The Netherlands, 15–19 October 2016; pp. 407–411. [Google Scholar] [CrossRef]
- Babenko, A.; Lempitsky, V. Aggregating local deep features for image retrieval. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1269–1277. [Google Scholar]
- Lai, H.; Pan, Y.; Liu, Y.; Yan, S. Simultaneous feature learning and hash coding with deep neural networks. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 8–10 June 2015; pp. 3270–3278. [Google Scholar] [CrossRef]
- Zhao, F.; Huang, Y.; Wang, L.; Tan, T. Deep Semantic Ranking Based Hashing for Multi-Label Image Retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 8–10 June 2015. [Google Scholar]
- Li, Y.; Kong, X.; Zheng, L.; Tian, Q. Exploiting Hierarchical Activations of Neural Network for Image Retrieval. In Proceedings of the 2016 ACM on Multimedia Conference, Amsterdam, The Netherlands, 15–19 October 2016; pp. 132–136. [Google Scholar]
- Xia, R.; Pan, Y.; Lai, H.; Liu, C.; Yan, S. Supervised Hashing for Image Retrieval via Image Representation Learning. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, AAAI’14, Québec City, QC, Canada, 27–31 July 2014; pp. 2156–2162. [Google Scholar]
- Luo, W.; Schwing, A.G.; Urtasun, R. Efficient Deep Learning for Stereo Matching. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 5695–5703. [Google Scholar] [CrossRef]
- Altwaijry, H.; Trulls, E.; Hays, J.; Fua, P.; Belongie, S. Learning to Match Aerial Images with Deep Attentive Architectures. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3539–3547. [Google Scholar] [CrossRef]
- Žbontar, J.; LeCun, Y. Computing the stereo matching cost with a convolutional neural network. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 8–10 June 2015; pp. 1592–1599. [Google Scholar] [CrossRef]
- Žbontar, J.; LeCun, Y. Stereo Matching by Training a Convolutional Neural Network to Compare Image Patches. J. Mach. Learn. Res. 2016, 17, 2287–2318. [Google Scholar]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial Transformer Networks. In Proceedings of the Advances in Neural Information Processing Systems 28, Palais des Congrès de Montréal, Montréal, QC, Canada, 7–12 December 2015; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; pp. 2017–2025. [Google Scholar]
- Zhang, R.; Lin, L.; Zhang, R.; Zuo, W.; Zhang, L. Bit-Scalable Deep Hashing With Regularized Similarity Learning for Image Retrieval and Person Re-Identification. IEEE Trans. Image Process. 2015, 24, 4766–4779. [Google Scholar] [CrossRef] [PubMed]
- Zagoruyko, S.; Komodakis, N. Learning to compare image patches via convolutional neural networks. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 8–10 June 2015; pp. 4353–4361. [Google Scholar] [CrossRef]
- Gordo, A.; Almazán, J.; Revaud, J.; Larlus, D. Deep image retrieval: Learning global representations for image search. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 10–16 October 2016; pp. 241–257. [Google Scholar]
- Liu, J.; Huang, Z.; Cai, H.; Shen, H.T.; Ngo, C.W.; Wang, W. Near-duplicate Video Retrieval: Current Research and Future Trends. ACM Comput. Surv. 2013, 45, 44:1–44:23. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Sun, J.; Li, H.; Zhu, Y. Learning Near Duplicate Image Pairs using Convolutional Neural Networks. Int. J. Perform. Eng. 2018, 14, 168. [Google Scholar] [CrossRef][Green Version]
- Revaud, J.; Weinzaepfel, P.; Harchaoui, Z.; Schmid, C. DeepMatching: Hierarchical Deformable Dense Matching. Int. J. Comput. Vis. 2016, 120, 300–323. [Google Scholar] [CrossRef]
- Toet, A. The TNO Multiband Image Data Collection. Data Brief 2017, 15, 249–251. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Lapedriza, A.; Xiao, J.; Torralba, A.; Oliva, A. Learning deep features for scene recognition using places database. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 487–495. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Kai, L.; Li, F.-F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef]








| Backbones | ST Layers | ST-1 | ST-2 | ST-3 |
|---|---|---|---|---|
| VGG16 | localization | |||
| FC | ||||
| ResNet34 | localization | |||
| FC |
| Methods | CaliforniaND | MFND | |
|---|---|---|---|
| MFND-IND | MFND-ALL | ||
| 2-channel-VGG16 [39] | 0.792 | 0.906 | 0.850 |
| 2-channel-ResNet34 [39] | 0.852 | 0.959 | 0.896 |
| SP-VGG16-PL [2] | 0.915 | 0.914 | 0.886 |
| SP-VGG16-HY [2] | 0.903 | 0.934 | 0.910 |
| SP-VGG19-IN [2] | 0.887 | 0.940 | 0.908 |
| ResNet101-IN [2] | 0.936 | 0.965 | 0.943 |
| ResNet512-IN [2] | 0.927 | 0.967 | 0.946 |
| DeepRet500 [2] | 0.923 | 0.994 | 0.981 |
| DeepRet800 [2] | 0.934 | 0.996 | 0.984 |
| ST-CCNN-VGG16 | 0.953 | 0.981 | 0.955 |
| ST-CCNN-ResNet34 | 0.990 | 0.994 | 0.992 |
| Methods | AUROC |
|---|---|
| 2-channel-VGG16 [39] | 0.633 |
| 2-channel-ResNet34 [39] | 0.663 |
| SP-VGG16-IN [2] | 0.679 |
| SP-VGG19-IN [2] | 0.667 |
| ResNet101-IN [2] | 0.693 |
| ResNet512-IN [2] | 0.630 |
| DeepRet-IN [2] | 0.745 |
| ST-CCNN-VGG16 | 0.764 |
| ST-CCNN-ResNet34 | 0.782 |
| Models | Backbones | Precision | Recall | F1-Score | AUROC |
|---|---|---|---|---|---|
| CCNN-o-cross | (VGG16) | 0.811 | 0.910 | 0.858 | 0.910 |
| CCNN-w-cross | (VGG16) | 0.826 | 0.921 | 0.871 | 0.938 |
| CCNN-o-cross | (ResNet34) | 0.820 | 0.915 | 0.865 | 0.935 |
| CCNN-w-cross | (ResNet34) | 0.925 | 0.899 | 0.912 | 0.959 |
| Models | Backbones | Precision | Recall | F1-Score | AUROC |
|---|---|---|---|---|---|
| CCNN-o-cross | (VGG16) | 0.730 | 0.748 | 0.739 | 0.703 |
| CCNN-w-cross | (VGG16) | 0.740 | 0.763 | 0.752 | 0.711 |
| CCNN-o-cross | (ResNet34) | 0.715 | 0.772 | 0.742 | 0.710 |
| CCNN-w-cross | (ResNet34) | 0.766 | 0.772 | 0.769 | 0.752 |
| Models | Backbones | Precision | Recall | F1-Score | AUROC |
|---|---|---|---|---|---|
| CCNN | (VGG16) | 0.826 | 0.921 | 0.871 | 0.938 |
| ST-CCNN | (VGG16) | 0.928 | 0.930 | 0.929 | 0.953 |
| CCNN | (ResNet34) | 0.925 | 0.899 | 0.912 | 0.959 |
| ST-CCNN | (ResNet34) | 0.975 | 0.943 | 0.958 | 0.990 |
| Models | Backbones | Precision | Recall | F1-Score | AUROC |
|---|---|---|---|---|---|
| CCNN | (VGG16) | 0.740 | 0.763 | 0.752 | 0.711 |
| ST-CCNN | (VGG16) | 0.805 | 0.716 | 0.758 | 0.764 |
| CCNN | (ResNet34) | 0.766 | 0.772 | 0.769 | 0.752 |
| ST-CCNN | (ResNet34) | 0.786 | 0.780 | 0.783 | 0.782 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, S.; Li, Y.; Zhang, Y. Single- and Cross-Modality Near Duplicate Image Pairs Detection via Spatial Transformer Comparing CNN. Sensors 2021, 21, 255. https://doi.org/10.3390/s21010255
Zhang Y, Zhang S, Li Y, Zhang Y. Single- and Cross-Modality Near Duplicate Image Pairs Detection via Spatial Transformer Comparing CNN. Sensors. 2021; 21(1):255. https://doi.org/10.3390/s21010255
Chicago/Turabian StyleZhang, Yi, Shizhou Zhang, Ying Li, and Yanning Zhang. 2021. "Single- and Cross-Modality Near Duplicate Image Pairs Detection via Spatial Transformer Comparing CNN" Sensors 21, no. 1: 255. https://doi.org/10.3390/s21010255
APA StyleZhang, Y., Zhang, S., Li, Y., & Zhang, Y. (2021). Single- and Cross-Modality Near Duplicate Image Pairs Detection via Spatial Transformer Comparing CNN. Sensors, 21(1), 255. https://doi.org/10.3390/s21010255






