Dynamic Characterisation of Fibre-Optic Temperature Sensors for Physiological Monitoring
Abstract
1. Introduction
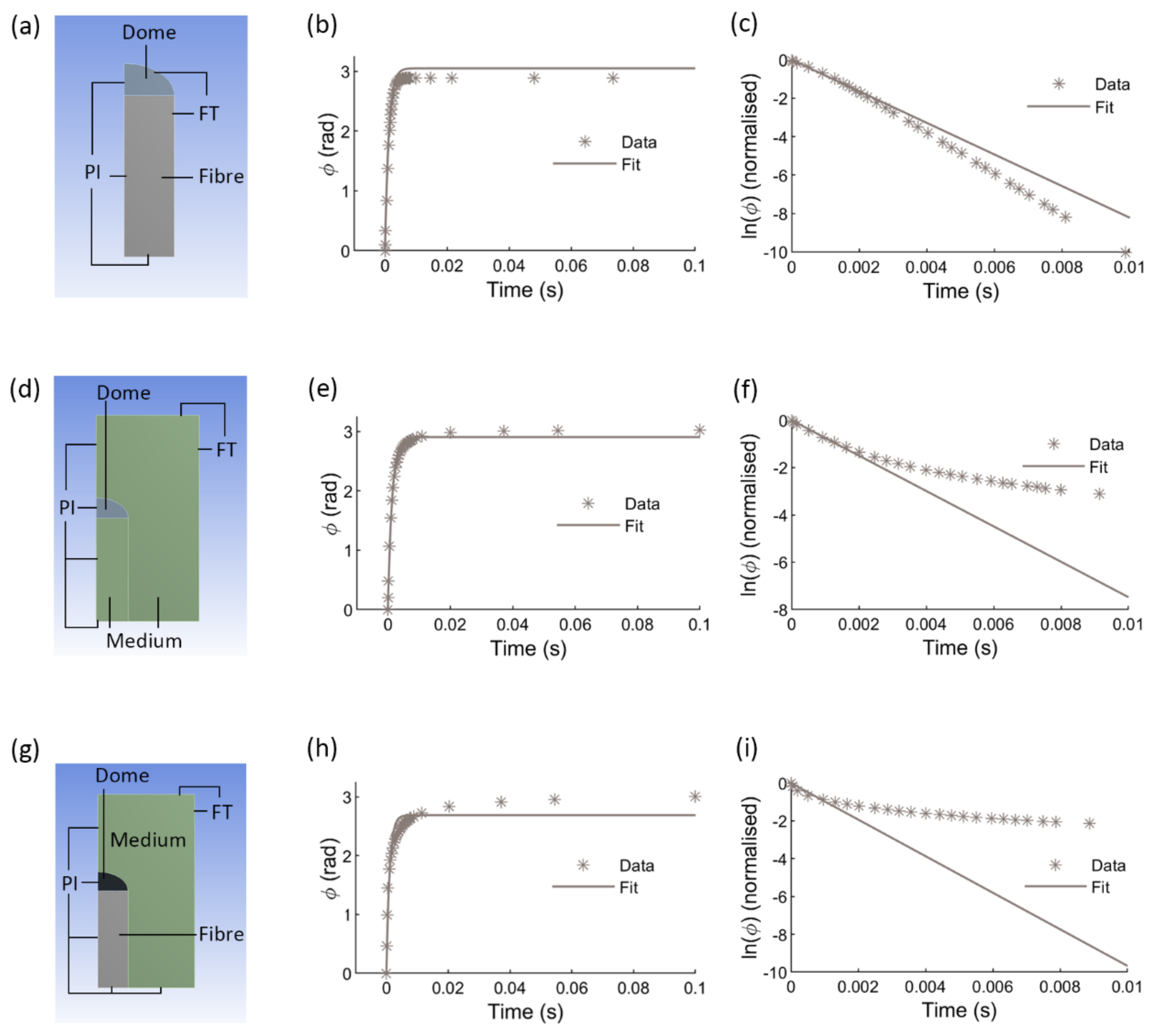
2. Sensor Description
2.1. Theoretical Analysis of the Sensor Response
2.1.1. Static Sensitivity
2.1.2. Dynamic Behaviour
3. Static Characterisation
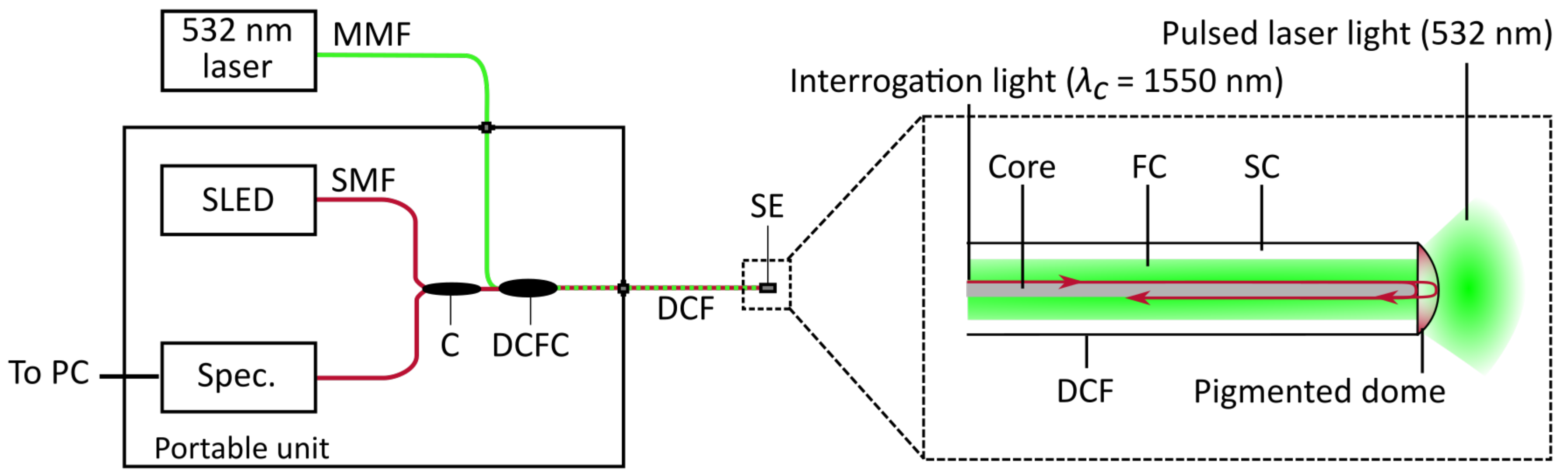
4. Dynamic Characterisation: Experiment
4.1. Experimental Setup
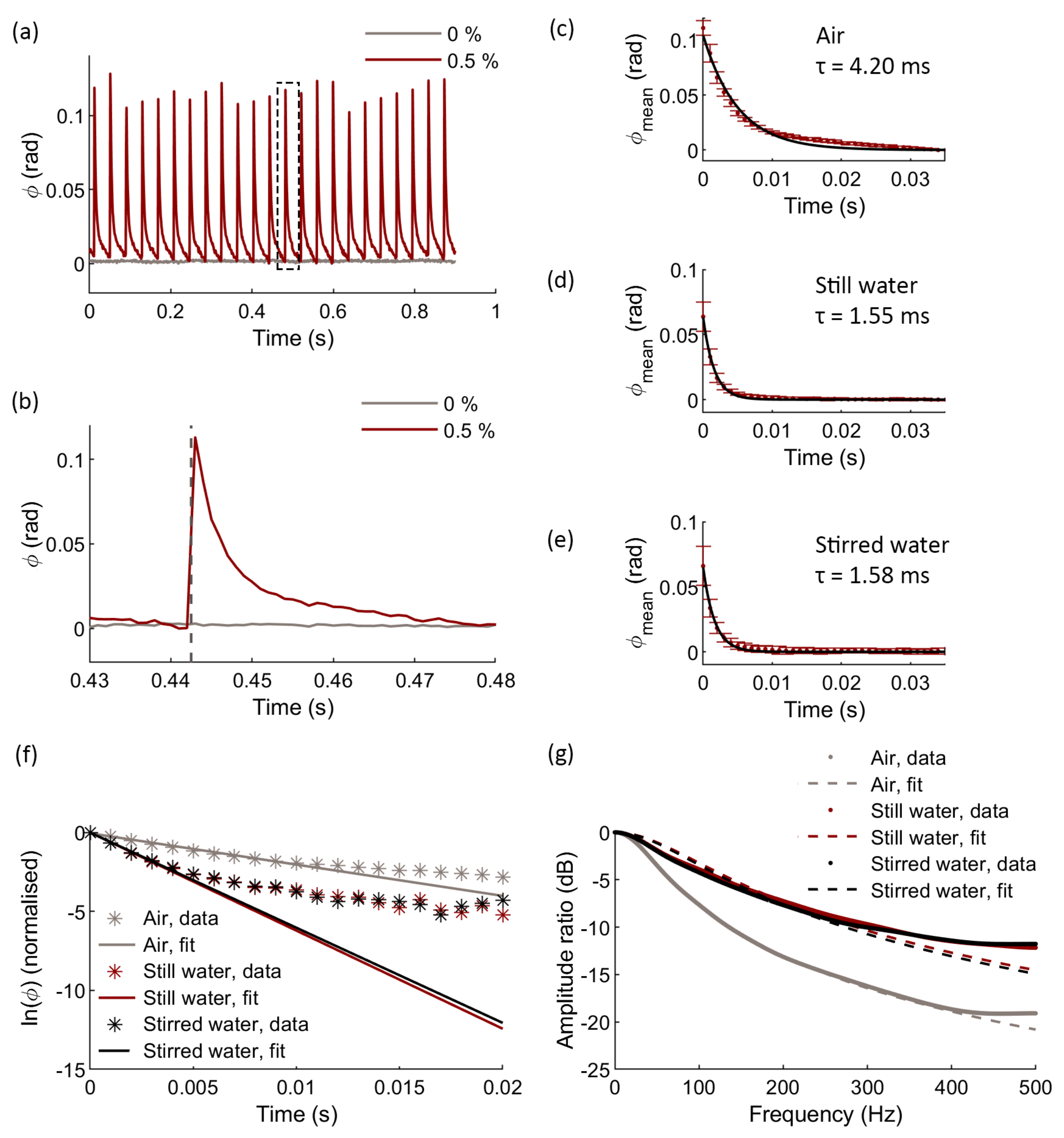
4.2. Experimental Results
5. Dynamic Characterisation: Computational Modelling
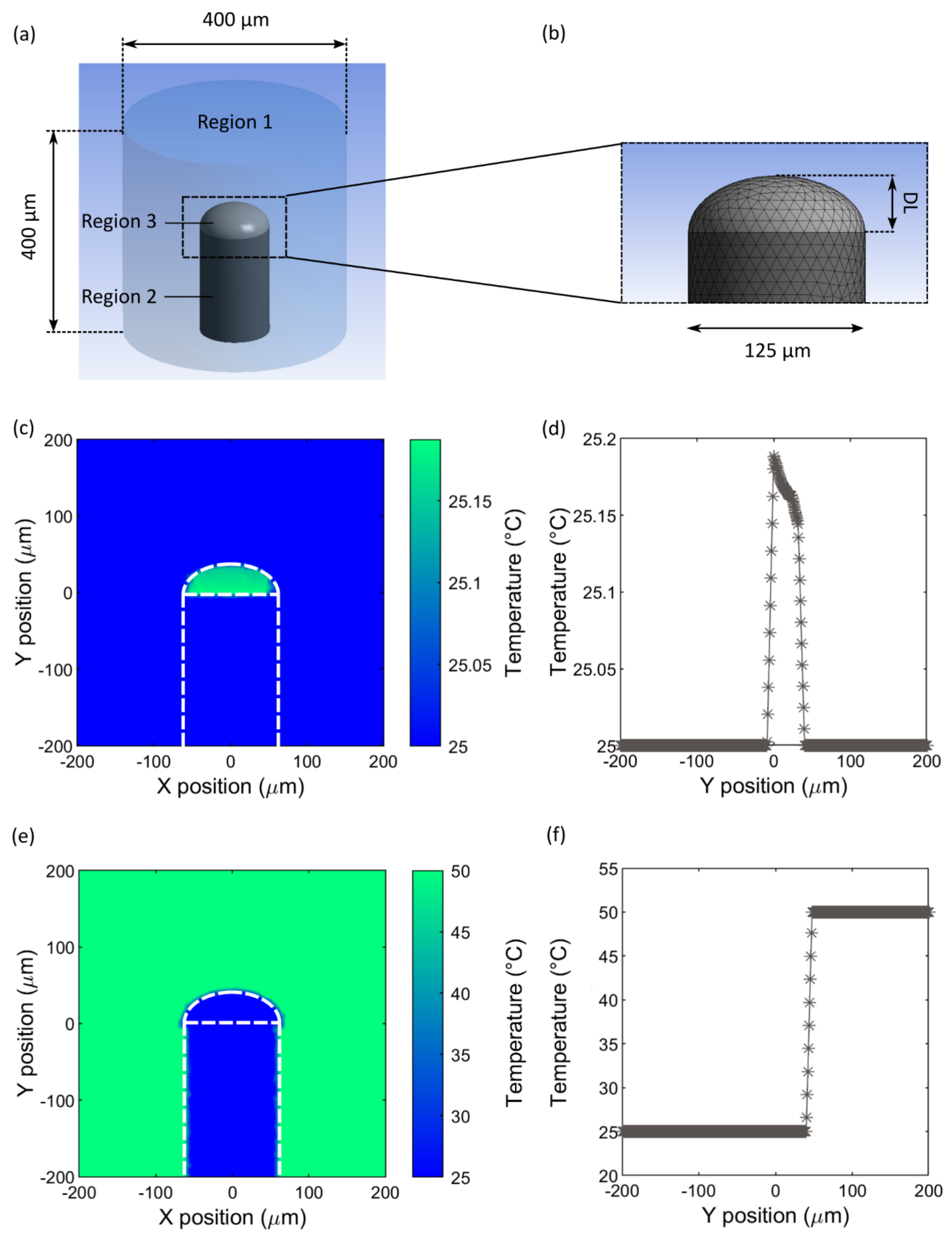
5.1. Simulation Setup
5.1.1. Boundary Conditions
5.1.2. Initial Temperature Distribution: Optical Heating
5.1.3. Initial Temperature Distribution: Step Input
5.1.4. Mesh and Domain Optimisation
5.1.5. Solution
5.2. Simulation Results
5.2.1. Optical Heating Results and Comparison with Experiment
5.2.2. Temperature Step Input Results
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rao, Y.J.; Webb, D.J.; Jackson, D.A.; Zhang, L.; Bennion, I. Optical in-fiber Bragg grating sensor systems for medical applications. J. Biomed. Opt. 1998, 3, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Carr, E.; Mackle, E.C.; Finlay, M.C.; Mosse, C.A.; Coote, J.M.; Papakonstantinou, I.; Desjardins, A.E. Optical interferometric temperature sensors for intravascular blood flow measurements. In Proceedings of the SPIE, Novel Biophotonics Techniques and Applications V, Munich, Germany, 22 July 2019; pp. 1107502:1–1107502:6. [Google Scholar]
- Fearon, W.F.; Balsam, L.B.; Farouque, H.M.O.; Robbins, R.C.; Fitzgerald, P.J.; Yock, P.G.; Yeung, A.C. Novel index for invasively assessing the coronary microcirculation. Circulation 2003, 107, 3129–3132. [Google Scholar] [CrossRef] [PubMed]
- Xaplanteris, P.; Fournier, S.; Keulards, D.C.J.; Adjedj, J.; Ciccarelli, G.; Milkas, A.; Pellicano, M.; van’t Veer, M.; Barbato, E.; Pijls, N.H.J.; et al. Catheter-based measurements of absolute coronary blood flow and microvascular resistance. Circ. Cardiovasc. Interv. 2018, 11, e006194. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Zhang, A.P.; Tam, H.-Y.; Cho, L.H.; Lu, C. All-optical fiber anemometer based on laser heated fiber Bragg gratings. Opt. Express 2011, 19, 10124–10130. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, F.; Duan, Z.; Liu, Z.; Liu, Z.; Wu, Z.; Gu, Y.; Sun, C.; Peng, W. A novel low-power-consumption all-fiber-optic anemometer with simple system design. Sensors 2017, 17, 2107. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, B.; Zhang, X.; Hu, N.; Li, K.; Chiavaioli, F.; Gui, X.; Guo, T. Plasmonic fiber-optic photothermal anemometers with carbon nanotube coatings. J. Lightwave Technol. 2019, 37, 3373–3380. [Google Scholar] [CrossRef]
- Lee, C.-L.; Liu, K.-W.; Luo, S.-H.; Wu, M.-S.; Ma, C.-T. A hot-polymer fiber Fabry–Perot interferometer anemometer for sensing airflow. Sensors 2017, 17, 2015. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H.; Bi, D.; Yang, Y. Research on the optical fiber gas flowmeters based on intermodal interference. Opt. Lasers Eng. 2016, 82, 122–126. [Google Scholar] [CrossRef]
- Bobb, L.C.; Davis, J.P.; Samouris, A.; Larson, D.C. An optical fiber hot-wire anemometer. In Proceedings of the SPIE, Fiber Optic and Laser Sensors VII, Boston, MA, USA, 13 February 1990; Volume 1169, pp. 567–572. [Google Scholar]
- Liu, Z.; Htein, L.; Cheng, L.-K.; Martina, Q.; Jansen, R.; Tam, H.-Y. Highly sensitive miniature fluidic flowmeter based on an FBG heated by Co2+-doped fiber. Opt. Express 2017, 25, 4393–4402. [Google Scholar] [CrossRef]
- Ruiz-Vargas, A.; Morris, S.A.; Hartley, R.H.; Arkwright, J.W. Optical flow sensor for continuous invasive measurement of blood flow velocity. J. Biophotonics 2019, 12, e201900139. [Google Scholar] [CrossRef]
- Zhou, B.; Jiang, H.; Lu, C.; He, S. Hot cavity optical fiber Fabry–Perot interferometer as a flow sensor with temperature self-calibrated. J. Lightwave Technol. 2016, 34, 5044–5048. [Google Scholar] [CrossRef]
- Liu, G.; Sheng, Q.; Hou, W.; Han, M. Optical fiber vector flow sensor based on a silicon Fabry–Perot interferometer array. Opt. Lett. 2016, 41, 4629–4632. [Google Scholar] [CrossRef] [PubMed]
- Pham, N.T.; Lee, S.L.; Park, S.; Lee, Y.W.; Kang, H.W. Real-time temperature monitoring with fiber Bragg grating sensor during diffuser-assisted laser-induced interstitial thermotherapy. J. Biomed. Opt. 2017, 22, 045008. [Google Scholar] [CrossRef]
- Gassino, R.; Vallan, A.; Perrone, G. Evaluation of temperature measurement errors due to FBG sensors during laser ablation of Ex-Vivo porcine liver. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–5. [Google Scholar]
- Chen, W.; Gassino, R.; Liu, Y.; Carullo, A.; Perrone, G.; Vallan, A.; Tosi, D. Performance assessment of FBG temperature sensors for laser ablation of tumors. In Proceedings of the 2015 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Turin, Italy, 7–9 May 2015; pp. 324–328. [Google Scholar]
- Polito, D.; Caponero, M.A.; Polimadei, A.; Saccomandi, P.; Massaroni, C.; Silvestri, S.; Schena, E. A needlelike probe for temperature monitoring during laser ablation based on fiber Bragg grating: Manufacturing and characterization. J. Med. Devices 2015, 9, 041006. [Google Scholar] [CrossRef]
- Schena, E.; Tosi, D.; Saccomandi, P.; Lewis, E.; Kim, T. Fiber optic sensors for temperature monitoring during thermal treatments: An overview. Sensors 2016, 16, 1144. [Google Scholar] [CrossRef] [PubMed]
- Morris, P.; Hurrell, A.; Shaw, A.; Zhang, E.; Beard, P. A Fabry–Pérot fiber-optic ultrasonic hydrophone for the simultaneous measurement of temperature and acoustic pressure. J. Acoust. Soc. Am. 2009, 125, 3611–3622. [Google Scholar] [CrossRef] [PubMed]
- Cepeda Rubio, M.F.J.; Hernánde, A.V.; Salas, L.L.; Ávila-Navarro, E.; Navarro, E.A. Coaxial slot antenna design for microwave hyperthermia using finite-difference time-domain and finite element method. Open Nanomed. J. 2011, 3, 2–9. [Google Scholar] [CrossRef]
- Favazza, C.P.; Gorny, K.R.; King, D.M.; Rossman, P.J.; Felmlee, J.P.; Woodrum, D.A.; Mynderse, L.A. An investigation of the effects from a urethral warming system on temperature distributions during cryoablation treatment of the prostate: A phantom study. Cryobiology 2014, 69, 128–133. [Google Scholar] [CrossRef]
- Petrusca, L.; Salomir, R.; Manasseh, G.; Becker, C.D.; Terraz, S. Spatio-temporal quantitative thermography of pre-focal interactions between high intensity focused ultrasound and the rib cage. Int. J. Hyperth. 2015, 31, 421–432. [Google Scholar] [CrossRef]
- Pennisi, C.P.A.; Leija, L.; Fonseca, W.H.; Vera, A. Fiber optic temperature sensor for use in experimental microwave hyperthermia. In Proceedings of the 2002 IEEE Sensors, Orlando, FL, USA, 12–14 June 2002; Volume 2, pp. 1028–1031. [Google Scholar]
- Kaiplavil, S. Thin photothermal endoscope for biomedical applications. J. Biomed. Opt. 2013, 18, 097008. [Google Scholar] [CrossRef]
- Hartings, M.R.; Castro, N.J.; Gill, K.; Ahmed, Z. A photonic pH sensor based on photothermal spectroscopy. Sens. Actuators B Chem. 2019, 301, 127076. [Google Scholar] [CrossRef] [PubMed]
- Laufer, J.G.; Beard, P.C.; Walker, S.P.; Mills, T.N. Photothermal determination of optical coefficients of tissue phantoms using an optical fibre probe. Phys. Med. Biol. 2001, 46, 2515. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yang, Z.; Yin, G.; Liang, C.; Zhu, T. Photothermal interferometry gas sensor based on the first harmonic signal. IEEE Photonics J. 2018, 10, 1–7. [Google Scholar] [CrossRef]
- Waclawek, J.P.; Kristament, C.; Moser, H.; Lendl, B. Balanced-detection interferometric cavity-assisted photothermal spectroscopy. Opt. Express 2019, 27, 12183–12195. [Google Scholar] [CrossRef]
- Tan, Y.; Jin, W.; Yang, F.; Jiang, Y.; Ho, H.L. Cavity-enhanced photothermal gas detection with a hollow fiber Fabry-Perot absorption cell. J. Lightwave Technol. 2019, 37, 4222–4228. [Google Scholar] [CrossRef]
- Garcia-Ruiz, A.; Pastor-Graells, J.; Martins, H.F.; Tow, K.H.; Thévenaz, L.; Martin-Lopez, S.; Gonzalez-Herraez, M. Distributed photothermal spectroscopy in microstructured optical fibers: Towards high-resolution mapping of gas presence over long distances. Opt. Express 2017, 25, 1789–1805. [Google Scholar] [CrossRef]
- Lee, C.-L.; You, Y.-W.; Dai, J.-H.; Hsu, J.-M.; Horng, J.-S. Hygroscopic polymer microcavity fiber Fizeau interferometer incorporating a fiber Bragg grating for simultaneously sensing humidity and temperature. Sens. Actuators B Chem. 2016, 222, 339–346. [Google Scholar] [CrossRef]
- Zhang, X.; Shao, L.; Zou, X.; Luo, B.; Pan, W.; Yan, L. Chirped fiber tip Fabry-Perot interferometer. Opt. Lett. 2017, 42, 3474–3477. [Google Scholar] [CrossRef]
- Du, C.; Wang, Q.; Zhao, Y. Electrically tunable long period gratings temperature sensor based on liquid crystal infiltrated photonic crystal fibers. Sens. Actuators A Phys. 2018, 278, 78–84. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, J.; Wang, Y.; Dai, X. A fast response temperature sensor based on fiber Bragg grating. Meas. Sci. Technol. 2014, 25, 075105. [Google Scholar] [CrossRef]
- Pan, Y.; Jiang, J.; Liu, K.; Wang, S.; Liu, T. Note: Response time characterization of fiber Bragg grating temperature sensor in water medium. Rev. Sci. Instrum. 2016, 87, 116102. [Google Scholar] [CrossRef] [PubMed]
- Barrera, D.; Finazzi, V.; Villatoro, J.; Sales, S.; Pruneri, V. Packaged optical sensors based on regenerated fiber Bragg gratings for high temperature applications. IEEE Sens. J. 2012, 12, 107–112. [Google Scholar] [CrossRef]
- Rong, Q.; Sun, H.; Qiao, X.; Zhang, J.; Hu, M.; Feng, Z. A miniature fiber-optic temperature sensor based on a Fabry–Perot interferometer. J. Opt. 2012, 14, 045002. [Google Scholar] [CrossRef]
- Bae, H.; Yun, D.; Liu, H.; Olson, D.A.; Yu, M. Hybrid miniature Fabry–Perot sensor with dual optical cavities for simultaneous pressure and temperature measurements. J. Lightwave Technol. 2014, 32, 1585–1593. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yu, Y.S.; Zhu, C.C.; Chen, C.; Yang, R.; Xue, Y.; Chen, Q.D.; Sun, H.B. Miniature end-capped fiber sensor for refractive index and temperature measurement. IEEE Photonics Technol. Lett. 2014, 26, 7–10. [Google Scholar] [CrossRef]
- Sun, B.; Wang, Y.; Qu, J.; Liao, C.; Yin, G.; He, J.; Zhou, J.; Tang, J.; Liu, S.; Li, Z.; et al. Simultaneous measurement of pressure and temperature by employing Fabry-Perot interferometer based on pendant polymer droplet. Opt. Express 2015, 23, 1906–1911. [Google Scholar] [CrossRef] [PubMed]
- Tan, X.; Li, X.; Geng, Y.; Yin, Z.; Wang, L.; Wang, W.; Deng, Y. Polymer microbubble-based Fabry-Perot fiber interferometer and sensing applications. IEEE Photonics Technol. Lett. 2015, 27, 2035–2038. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Gao, R.; Li, Y.; Zhao, X.; Qu, S. Ultracompact fiber sensor tip based on liquid polymer-filled Fabry-Perot cavity with high temperature sensitivity. Sens. Actuators B Chem. 2016, 233, 496–501. [Google Scholar] [CrossRef]
- Arrizabalaga, O.; Durana, G.; Zubia, J.; Villatoro, J. Accurate microthermometer based on off center polymer caps onto optical fiber tips. Sens. Actuators B Chem. 2018, 272, 612–617. [Google Scholar] [CrossRef]
- Coote, J.M.; Alles, E.J.; Noimark, S.; Mosse, C.A.; Little, C.D.; Loder, C.D.; David, A.L.; Rakhit, R.D.; Finlay, M.C.; Desjardins, A.E. Dynamic physiological temperature and pressure sensing with phase-resolved low-coherence interferometry. Opt. Express 2019, 27, 5641–5654. [Google Scholar] [CrossRef]
- Chen, M.; Zhao, Y.; Xia, F.; Peng, Y.; Tong, R. High sensitivity temperature sensor based on fiber air-microbubble Fabry-Perot interferometer with PDMS-filled hollow-core fiber. Sens. Actuators A Phys. 2018, 275, 60–66. [Google Scholar] [CrossRef]
- Hou, L.; Zhao, C.; Xu, B.; Mao, B.; Shen, C.; Wang, D.N. Highly sensitive PDMS-filled Fabry-Perot interferometer temperature sensor based on the Vernier effect. Appl. Opt. 2019, 58, 4858–4865. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.Y.; Park, K.S.; Park, S.J.; Paek, U.-C.; Lee, B.H.; Choi, E.S. Miniature fiber-optic high temperature sensor based on a hybrid structured Fabry–Perot interferometer. Opt. Lett. 2008, 33, 2455–2457. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Tang, M.; Gao, F.; Zhu, B.; Zhao, Z.; Duan, L.; Fu, S.; Ouyang, J.; Wei, H.; Shum, P.P.; et al. Simplified hollow-core fiber-based Fabry–Perot interferometer with modified Vernier effect for highly sensitive high-temperature measurement. IEEE Photonics J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Liu, G.; Han, M.; Hou, W. High-resolution and fast-response fiber-optic temperature sensor using silicon Fabry-Pérot cavity. Opt. Express. 2015, 23, 7237–7247. [Google Scholar] [CrossRef]
- Zhang, C.-L.; Gong, Y.; Zou, W.-L.; Wu, Y.; Rao, Y.-J.; Peng, G.-D.; Fan, X. Microbubble-based fiber optofluidic interferometer for sensing. J. Lightwave Technol. 2017, 35, 2514–2519. [Google Scholar] [CrossRef]
- Liu, D.; Wu, Q.; Mei, C.; Yuan, J.; Xin, X.; Mallik, A.K.; Wei, F.; Han, W.; Kumar, R.; Yu, C.; et al. Hollow core fiber based interferometer for high-temperature (1000 °C) measurement. J. Lightwave Technol. 2018, 36, 1583–1590. [Google Scholar] [CrossRef]
- Cai, L.; Liu, Y.; Hu, S.; Liu, Q. Optical fiber temperature sensor based on modal interference in multimode fiber lengthened by a short segment of polydimethylsiloxane. Microw. Opt. Technol. Lett. 2019, 61, 1656–1660. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Hwang, D.; Moon, S.; Moon, D.S.; Chung, Y. High temperature fiber sensor with high sensitivity based on core diameter mismatch. Opt. Express. 2008, 16, 11369–11375. [Google Scholar] [CrossRef]
- Lopez-Aldaba, A.; Auguste, J.L.; Jamier, R.; Roy, P.; Lopez-Amo, M. Simultaneous strain and temperature multipoint sensor based on microstructured optical fiber. J. Lightwave Technol. 2017, 36, 910–916. [Google Scholar] [CrossRef]
- He, C.; Fang, J.; Zhang, Y.; Yang, Y.; Yu, J.; Zhang, J.; Guan, H.; Qiu, W.; Wu, P.; Dong, J.; et al. High performance all-fiber temperature sensor based on coreless side-polished fiber wrapped with polydimethylsiloxane. Opt. Express 2018, 26, 9686–9699. [Google Scholar] [CrossRef] [PubMed]
- Olivero, M.; Vallan, A.; Orta, R.; Perrone, G. Single-mode–multimode–single-mode optical fiber sensing structure with quasi-two-mode fibers. IEEE Trans. Instrum. Meas. 2018, 67, 1223–1229. [Google Scholar] [CrossRef]
- Zhang, C.; Ning, T.; Zheng, J.; Gao, X.; Lin, H.; Li, J.; Pei, L.; Wen, X. Miniature optical fiber temperature sensor based on FMF-SCF structure. Opt. Fiber Technol. 2018, 41, 217–221. [Google Scholar] [CrossRef]
- Wang, F.; Sun, Z.; Sun, T.; Liu, C.; Chu, P.K.; Bao, L. Highly sensitive PCF-SPR biosensor for hyperthermia temperature monitoring. J. Opt. 2018, 47, 288–294. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Liu, B.; Yao, J. High sensitivity hollow fiber temperature sensor based on surface plasmon resonance and liquid filling. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera-Neto, A.; Marques, C.; Pontes, M.J. A polymer optical fiber temperature sensor based on material features. Sensors 2018, 18, 301. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera-Neto, A.; Marques, C.; Pontes, M.J. Measurement of temperature and relative humidity with polymer optical fiber sensors based on the induced stress-optic effect. Sensors 2018, 18, 916. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Diaz, C.A.R.; Avellar, L.M.; Pontes, M.J.; Marques, C.; Frizera, A. Polymer optical fiber sensors in healthcare applications: A comprehensive review. Sensors 2019, 19, 3156. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Theodosiou, A.; Díaz, C.A.R.; Avellar, L.M.; Kalli, K.; Marques, C.; Frizera, A. FPI-POFBG angular movement sensor inscribed in CYTOP fibers with dynamic angle compensator. IEEE Sens. J. 2020, 20, 5962–5969. [Google Scholar] [CrossRef]
- Technical Data Sheet: Sylgard™ 184 Silicone Elastomer; Dow: Midland, MI, USA, 2017.
- CRC. Handbook of Chemistry and Physics Online. Available online: http://hbcponline.com/faces/contents/ContentsSearch.xhtml (accessed on 12 August 2019).
- Bansal, N.P.; Doremus, R.H. Handbook of Glass Properties; Academic Press Inc.: London, UK, 1986. [Google Scholar]
- Li, Y.; Zhang, Z.; Hao, X.; Yin, W. A Measurement system for time constant of thermocouple sensor based on high temperature furnace. Appl. Sci. 2018, 8, 2585. [Google Scholar] [CrossRef]
- Hill, G.C.; Melamud, R.; Declercq, F.E.; Davenport, A.A.; Chan, I.H.; Hartwell, P.G.; Pruitt, B.L. SU-8 MEMS Fabry-Perot pressure sensor. Sens. Actuators A Phys. 2007, 138, 52–62. [Google Scholar] [CrossRef]
- Ding, M.; Wang, P.; Brambilla, G. Fast-response high-temperature microfiber coupler tip thermometer. IEEE Photonics Technol. Lett. 2012, 24, 1209–1211. [Google Scholar] [CrossRef][Green Version]
- Castellini, P.; Rossi, G.L. Dynamic characterization of temperature sensors by laser excitation. Rev. Sci. Instrum. 1996, 67, 2595–2601. [Google Scholar] [CrossRef]
- Serio, B.; Nika, P.; Prenel, J.P. Static and dynamic calibration of thin-film thermocouples by means of a laser modulation technique. Rev. Sci. Instrum. 2000, 71, 4306–4313. [Google Scholar] [CrossRef]
- Meyer, C.W.; Kimes, W.A.; Ripple, D.C. Determining the thermal response time of temperature sensors embedded in semiconductor wafers. Meas. Sci. Technol. 2008, 19, 055202. [Google Scholar] [CrossRef]
- Garinei, A.; Tagliaferri, E. A laser calibration system for in situ dynamic characterization of temperature sensors. Sens. Actuators A Phys. 2013, 190, 19–24. [Google Scholar] [CrossRef]
- Arwatz, G.; Bahri, C.; Smits, A.J.; Hultmark, M. Dynamic calibration and modeling of a cold wire for temperature measurement. Meas. Sci. Technol. 2013, 24, 125301. [Google Scholar] [CrossRef]
- Choma, M.A.; Ellerbee, A.K.; Yang, C.; Creazzo, T.L.; Izatt, J.A. Spectral-domain phase microscopy. Opt. Lett. 2005, 30, 1162–1164. [Google Scholar] [CrossRef]
- Doebelin, E.O. Measurement Systems: Application and Design, 5th ed.; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Coleman, H.W.; Steele, W.G. Experimentation, Validation, and Uncertainty Analysis for Engineers, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Loock, H.-P.; Wentzell, P.D. Detection limits of chemical sensors: Applications and misapplications. Sens. Actuators B Chem. 2012, 173, 157–163. [Google Scholar] [CrossRef]
- Kuo, A.C.M. Poly(dimethylsiloxane). In Polymer Data Handbook, 2nd ed.; Mark, J.E., Ed.; Oxford University Press Inc.: New York, NY, USA, 2009. [Google Scholar]
- Dong, C.-H.; He, L.; Xiao, Y.-F.; Gaddam, V.R.; Ozdemir, S.K.; Han, Z.-F.; Guo, G.-C.; Yang, L. Fabrication of high-Q polydimethylsiloxane optical microspheres for thermal sensing. Appl. Phys. Lett. 2009, 94, 231119. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, P.; Lin, P.; Sun, F. Thermo-optic coefficients of polymers for optical waveguide applications. Polymer 2006, 47, 4893–4896. [Google Scholar] [CrossRef]
- Kopetz, S.; Cai, D.; Rabe, E.; Neyer, A. PDMS-based optical waveguide layer for integration in electrical–optical circuit boards. Int. J. Electron. Commun. 2007, 61, 163–167. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Díaz, C.R.; Marques, C.; Frizera, A.; Pontes, M.J. Analysis of viscoelastic properties influence on strain and temperature responses of Fabry-Perot cavities based on UV-curable resins. Opt. Laser Technol. 2019, 120, 105743. [Google Scholar] [CrossRef]
- Diamantopoulos, L.; Liu, X.; De Scheerder, I.; Krams, R.; Li, S.; Van Cleemput, J.; Desmet, W.; Serruys, P.W. The effect of reduced blood-flow on the coronary wall temperature: Are significant lesions suitable for intravascular thermography? Eur. Heart. J. 2003, 24, 1788–1795. [Google Scholar] [CrossRef]
- Cuisset, T.; Beauloye, C.; Melikian, N.; Hamilos, M.; Sarma, J.; Sarno, G.; Naslund, M.; Smith, L.; de Vosse, F.V.; Pijls, N.H.; et al. In vitro and in vivo studies on thermistor-based intracoronary temperature measurements: Effect of pressure and flow. Catheter. Cardiovasc. Interv. 2009, 73, 224–230. [Google Scholar] [CrossRef] [PubMed]

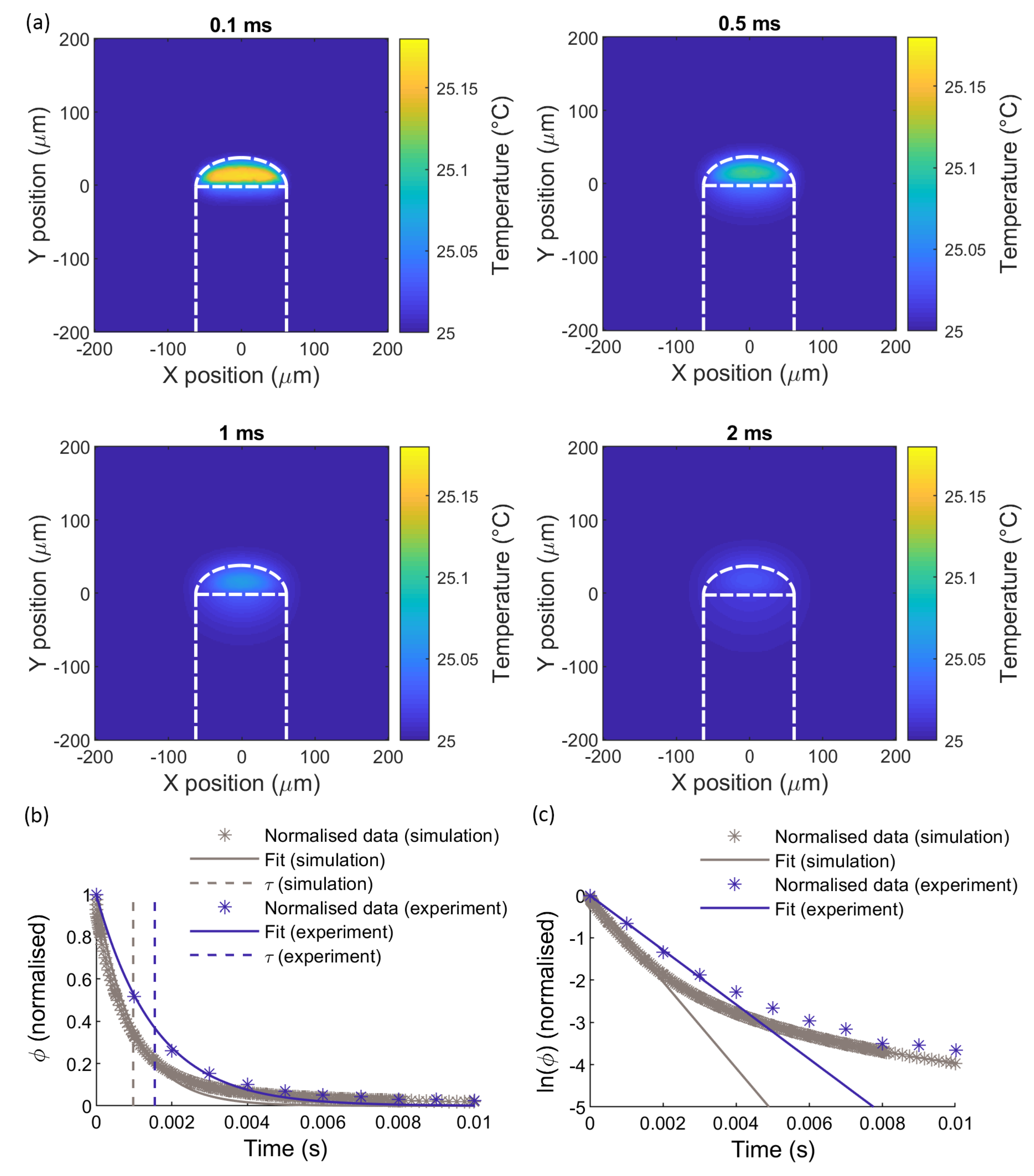
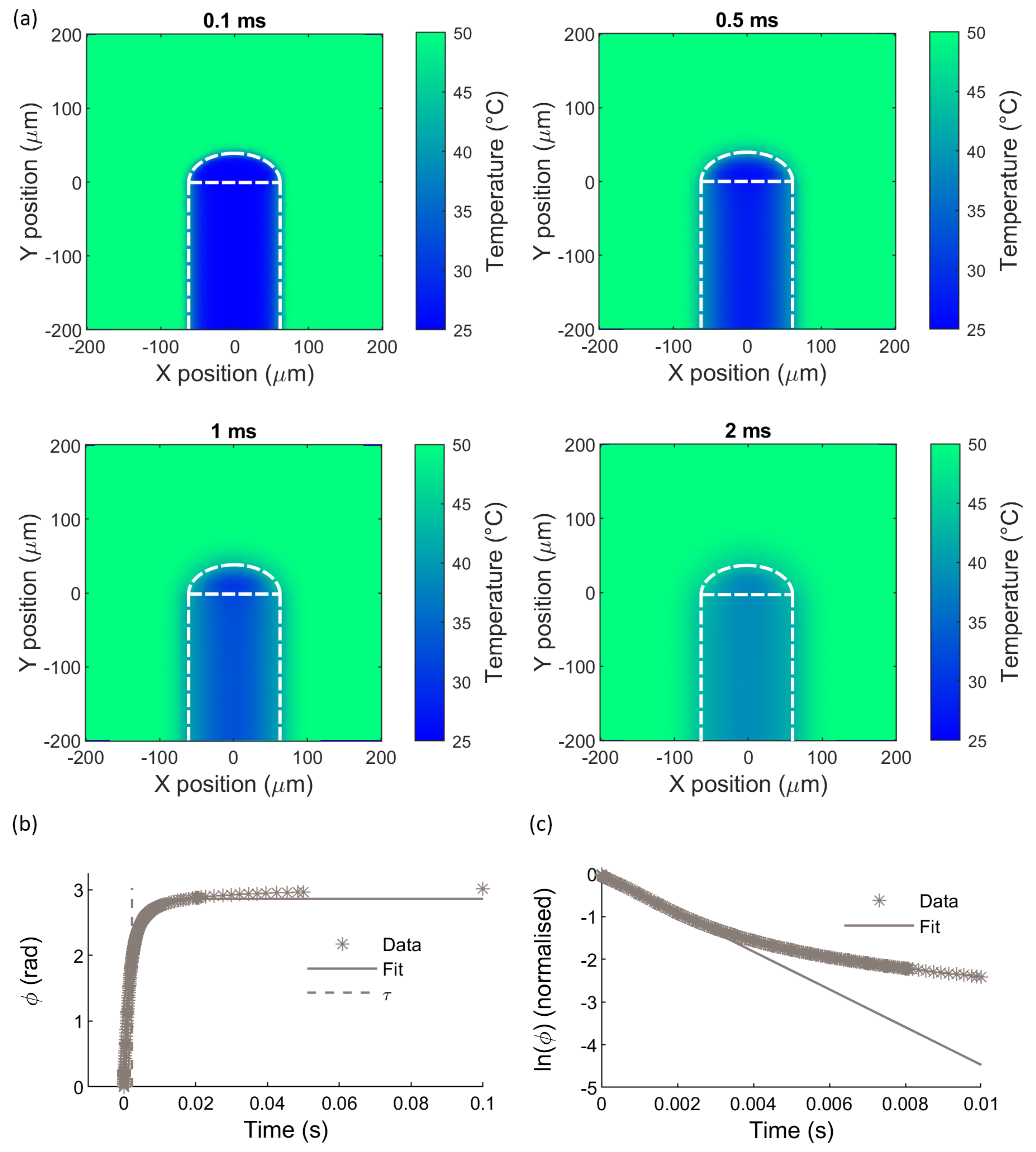
| Property | Region 1: Water | Region 2: Fused Silica | Region 3: PDMS |
|---|---|---|---|
| Thermal conductivity (Wm−1 °C−1) | 0.606523 [66] | 1.37 [67] | 0.27 [65] |
| Density (kgm−3) | 997.05 [66] | 2200 [67] | 970 [80] |
| Specific heat capacity (Jkg−1 °C−1) | 4181.3 [66] | 745.1 [66] | 1460 [80] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coote, J.M.; Torii, R.; Desjardins, A.E. Dynamic Characterisation of Fibre-Optic Temperature Sensors for Physiological Monitoring. Sensors 2021, 21, 221. https://doi.org/10.3390/s21010221
Coote JM, Torii R, Desjardins AE. Dynamic Characterisation of Fibre-Optic Temperature Sensors for Physiological Monitoring. Sensors. 2021; 21(1):221. https://doi.org/10.3390/s21010221
Chicago/Turabian StyleCoote, Joanna M., Ryo Torii, and Adrien E. Desjardins. 2021. "Dynamic Characterisation of Fibre-Optic Temperature Sensors for Physiological Monitoring" Sensors 21, no. 1: 221. https://doi.org/10.3390/s21010221
APA StyleCoote, J. M., Torii, R., & Desjardins, A. E. (2021). Dynamic Characterisation of Fibre-Optic Temperature Sensors for Physiological Monitoring. Sensors, 21(1), 221. https://doi.org/10.3390/s21010221





