Non-Dimensional Star-Identification †
Abstract
1. Introduction
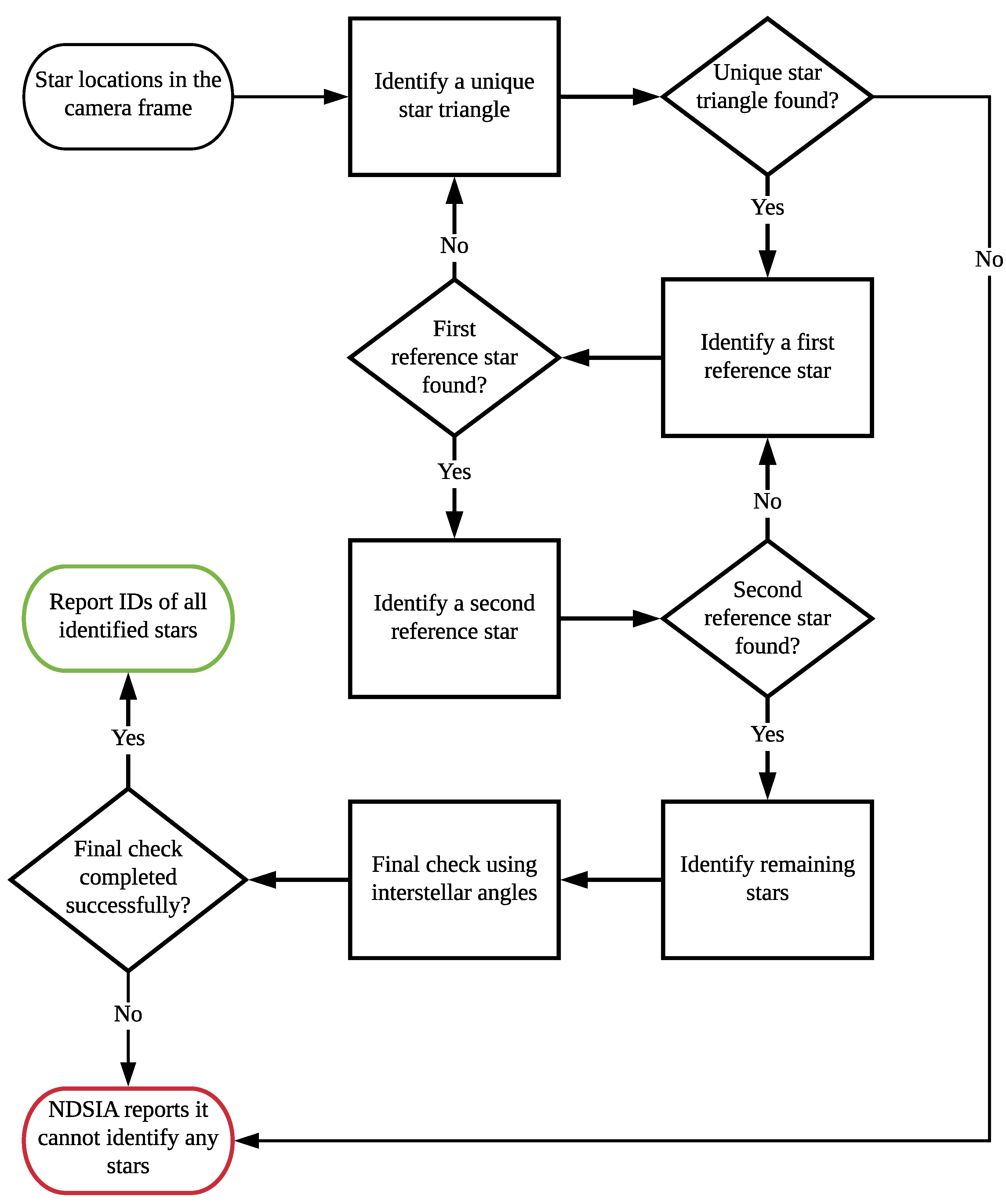
2. The Non-Dimensional Star-ID Algorithm
- The NDSIA uses the n-dimensional k-vector (NDKV) [14] to search among a three-dimensional database. Previous algorithms search among a one- or two-dimensional database [9,10,11,12,13], using searching techniques such as the one-dimensional k-vector [3], or by geometrically hashing asterisms of stars and using a hash-based search algorithm [16].
- The NDSIA performs a final check that uses the identified stars’ interstellar angles to further the confidence in the Star-ID. This check is non-existent in previous algorithms.
2.1. Creating the Non-Dimensional Database
2.2. The Non-Dimensional Star-ID Algorithm
2.2.1. Identify a Unique Star Triangle
2.2.2. Identify a First Reference Star
2.2.3. Identify a Second Reference Star
2.2.4. Identify Remaining Stars
2.2.5. Final Check Using Interstellar Angles
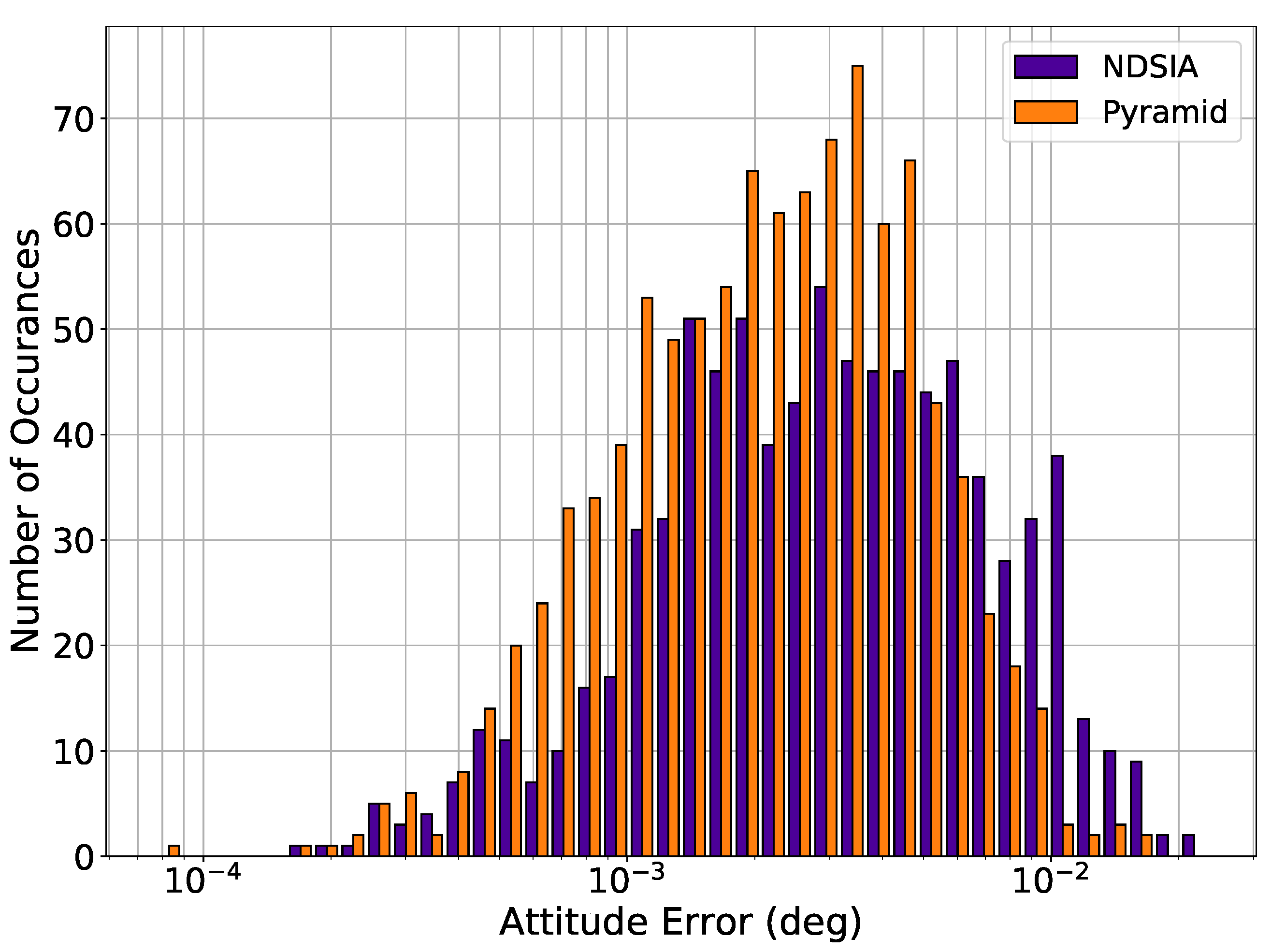
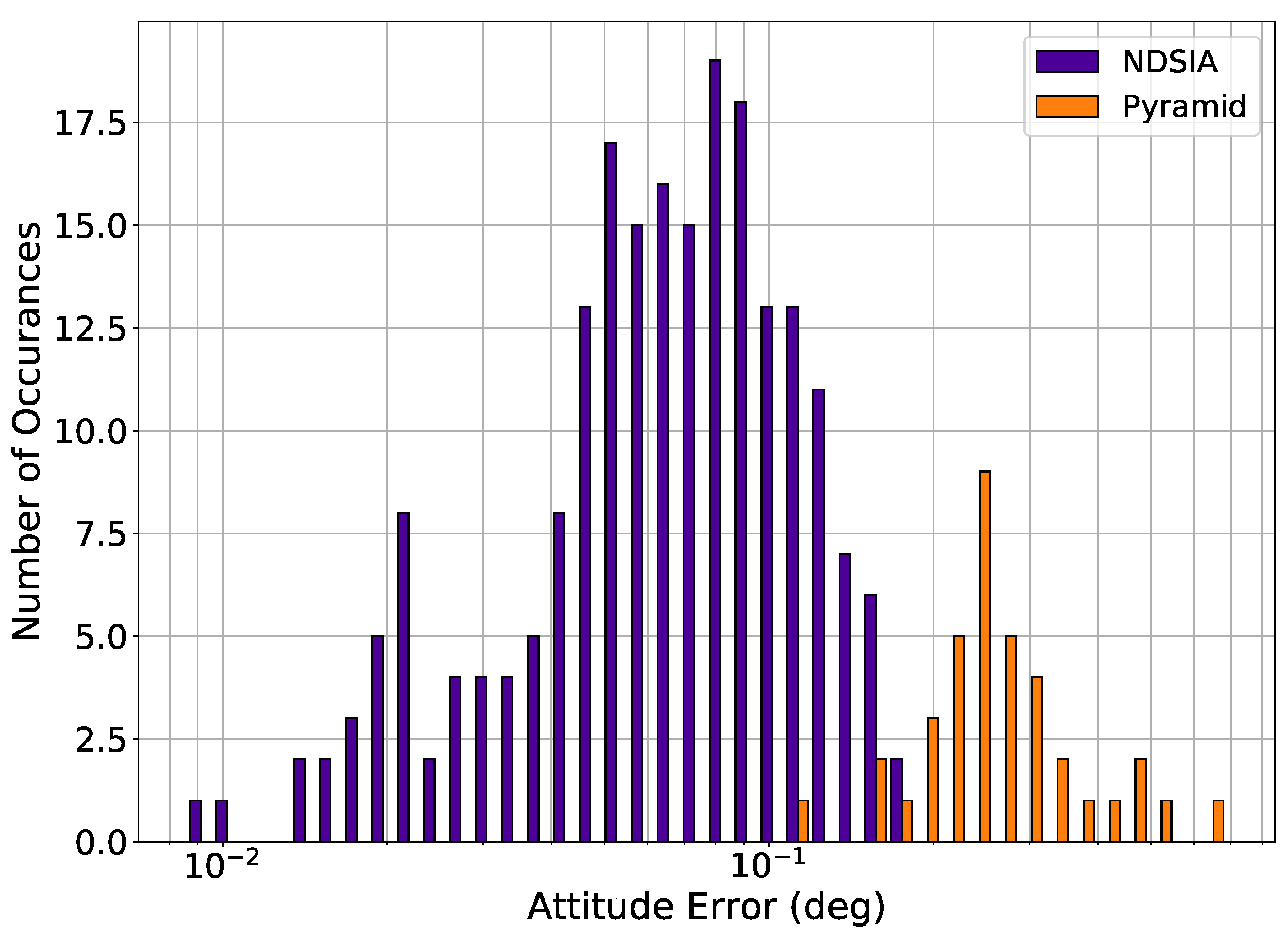
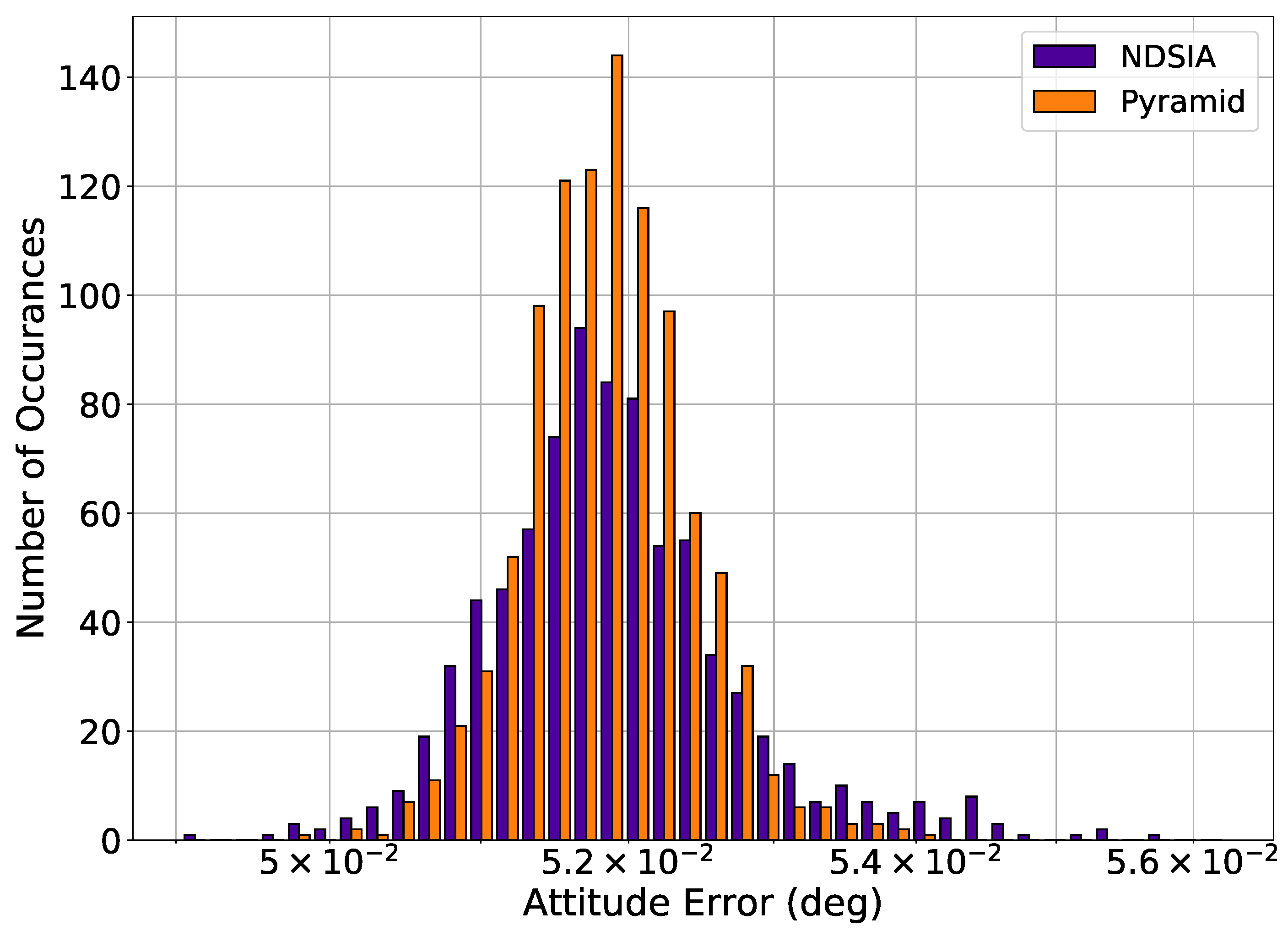
3. The Non-Dimensional Star-ID Algorithm Compared with Pyramid
- Number of scenes wherein the Star-ID was completed. This metric shows whether the algorithm attempted to perform a Star-ID or not. This metric is reported as a percentage of the total number of scenes in the test.
- Number of successful Star-IDs. This metric is calculated as the ratio of the number of times that all stars identified by the algorithm were identified correctly, to the number of times the Star-ID was completed. This ratio is reported as a percentage.
- Average time that it takes to perform one Star-ID. This metric is reported in milliseconds.
- Number of scenes wherein Pyramid did not complete the Star-ID and the NDSIA completed the Star-ID successfully. This metric is reported as a percentage of the number scenes wherein Pyramid did not complete the Star-ID.
- Number of scenes wherein Pyramid completed the Star-ID unsuccessfully (i.e., at least one star was identified incorrectly) and the NDSIA completed the Star-ID successfully. This metric is reported as a percentage of the number of scenes wherein Pyramid completed the Star-ID unsuccessfully.
3.1. Test Conditions
3.2. Results
4. Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FOV | Field-of-View |
| NDKV | n-dimensional k-vector |
| NDSIA | Non-Dimensional Star Identification Algorithm |
| OA | Optical Axis |
| Star-ID | Star Identification |
Appendix A. Interstellar and Dihedral Angles of Spherical Star Triangles

Appendix B. Pyramid Algorithm Summary
- First, the algorithm searches for a unique star triangle. A unique star triangle consists of three stars whose interstellar angles, the angle between a pair of stars, could only form that particular star triangle. In other words, after merging the results of three searches, one for each of the three star pairs, in a database of interstellar angles, only one possible star triangle emerges. The searches in the interstellar angle database are range searches where the range is based on three standard deviations of the star tracker’s centroiding uncertainty. Let the three stars that make up the unique star triangle be denoted as the i, j, and k stars. If no unique star triangle is found, then the algorithm reports that it cannot identify any stars.
- Next, Pyramid searches for a reference star, r. A reference star r is any star in the field-of-view such that the , , and star triangles are unique star triangles. If a reference star is found, then the i, j, k, and r stars are considered identified. They represent the four vertices of a “Pyramid.” If no reference star is found, then the algorithm returns to step one to try to identify a different unique star triangle.
- Finally, Pyramid identifies or discards the remaining stars using the star triangle and the same technique as the reference star. For a given star s, if the , , and star triangles are unique star triangles, then the star s is identified. Otherwise, it is discarded.
References
- Mortari, D.; Bruccoleri, C.; Junkins, J.L. The Pyramid Star Identification Technique. ION Navig. 2004, 51, 171–183. [Google Scholar] [CrossRef]
- Mortari, D. A Fast On-Board Autonomous Attitude Determination System Based on a New Star-ID Technique for a Wide FOV Star Tracker. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Austin, TX, USA, 11–15 February 1996. [Google Scholar]
- Mortari, D.; Neta, B. k-vector Range Searching Techniques. Adv. Astronaut. Sci. 2000, 105, 449–464. [Google Scholar]
- Padgett, C.; Kreutz-Delgado, K. A grid algorithm for autonomous star identification. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 202–213. [Google Scholar] [CrossRef]
- Luo, L.; Xu, L.; Zhang, H. An Autonomous Star Identification Algorithm Based on One-Dimensional Vector Pattern for Star Sensors. Sensors 2015, 15, 16412–16429. [Google Scholar] [CrossRef] [PubMed]
- Samaan, M.; Theil, S. Development of a Low Cost Star Tracker for the SHEFEX Mission. Aerosp. Sci. Technol. 2012, 23, 469–478. [Google Scholar] [CrossRef]
- Liebe, C. Accuracy Performance of Star Trackers: A Tutorial. IEEE Trans. Aerosp. Electron. Syst. 2000, 38, 587–599. [Google Scholar] [CrossRef]
- Schiattarella, V.; Spiller, D.; Curti, F. A novel star identification technique robust to high presence of false objects: The Multi-Poles Algorithm. Adv. Space Res. 2017, 59, 2133–2147. [Google Scholar] [CrossRef]
- Samaan, M.; Mortari, D.; Junkins, J.L. Non-Dimensional Star Identification for Uncalibrated Star Cameras. J. Astronaut. Sci. 2006, 54, 95–111. [Google Scholar] [CrossRef]
- Spratling, B.B.; Mortari, D. The k-vector ND and its Application to Building a Non-Dimensional Star-ID Catalog. J. Astronaut. Sci. 2011, 58, 261–274. [Google Scholar] [CrossRef]
- Rousseau, G.L.A.; Bostel, J.; Mazari, B. Star recognition algorithm for APS star tracker: Oriented triangles. IEEE Aerosp. Electron. Syst. Mag. 2005, 20, 27–31. [Google Scholar] [CrossRef]
- Ajdadi, M.J.; Ghafarzadeh, M.; Taheri, M.; Mosadeq, E.; Ghomi, M.K. Star Identification Algorithm for Uncalibrated, Wide FOV Cameras. Astron. J. 2015, 149, 182. [Google Scholar] [CrossRef]
- Somayehee, F.; Nikkhah, A.A.; Roshanian, J.; Salahshoor, S. Blind Star Identification Algorithm. IEEE Trans. Aerosp. Electron. Syst. 2019. [Google Scholar] [CrossRef]
- Arnas, D.; Leake, C.; Mortari, D. The n-dimensional k-vector and its Application to Orthogonal Range Searching. Appl. Math. Comput. 2020, 372, 125010. [Google Scholar] [CrossRef]
- Shuster, M.D. The TASTE Test. J. Astronaut. Sci. 2009, 57, 61–71. [Google Scholar] [CrossRef]
- Lang, D.; Hogg, D.W.; Mierle, K.; Blanton, M.; Roweis, S. Astrometry.net: Blind astrometric calibration of arbitrary astronomical images. Astron. J. 2010, 139, 1782–1800. [Google Scholar] [CrossRef]
- Arnas, D.; Fialho, M.A.; Mortari, D. Fast and robust kernel generators for star trackers. Acta Astronaut. 2017, 134, 291–302. [Google Scholar] [CrossRef]
- Davenport, P.B. A Vector Approach to the Algebra of Rotations with Applications; Technical Report; Goddard Space Flight Center: Greenbelt, MD, USA, 1965. [Google Scholar]
- Mueller, J.; Sánchez-Sánchez, C.; Simões, L.; Izzo, D. Optimal orderings of k-subsets for star identification. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar] [CrossRef]

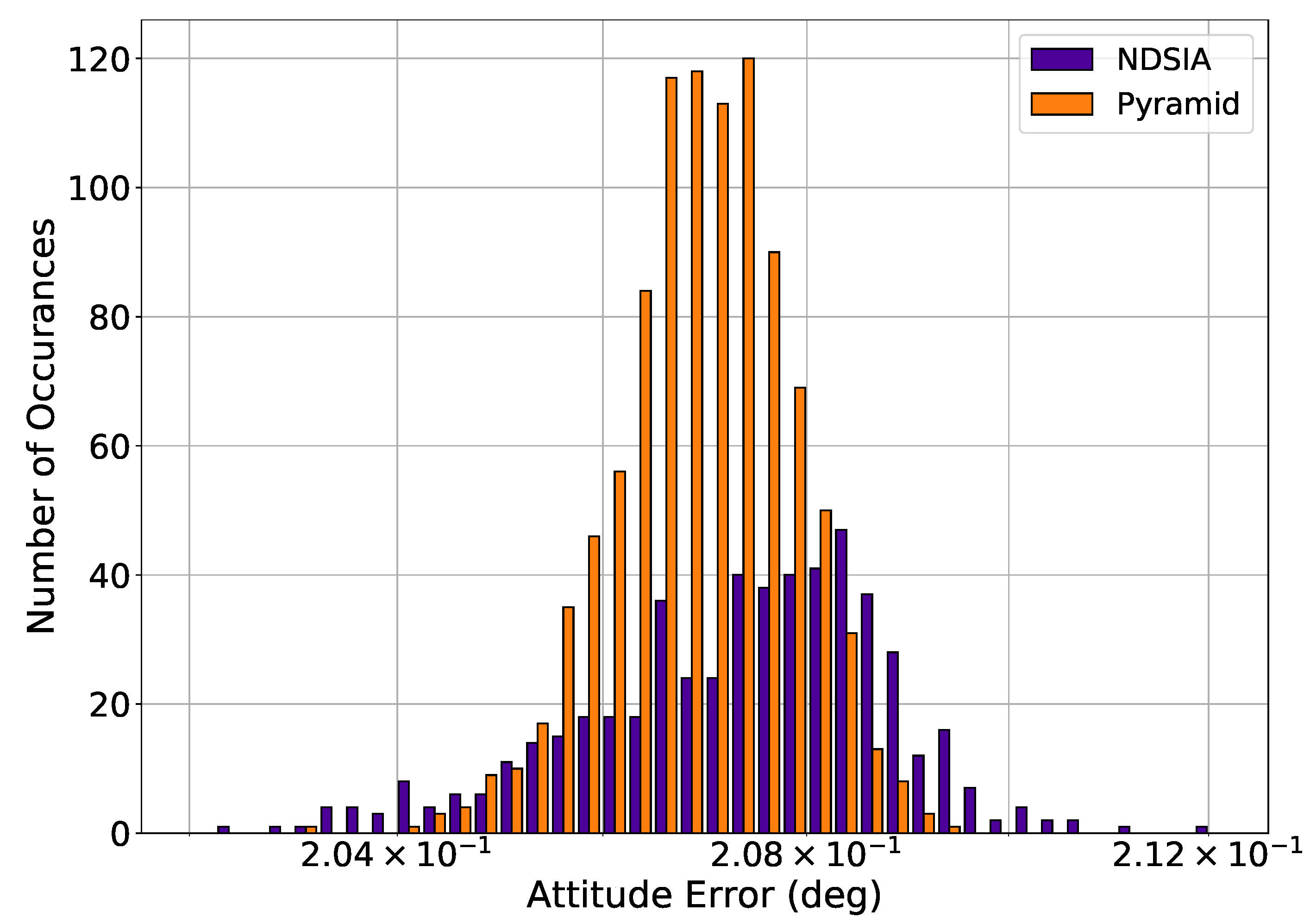
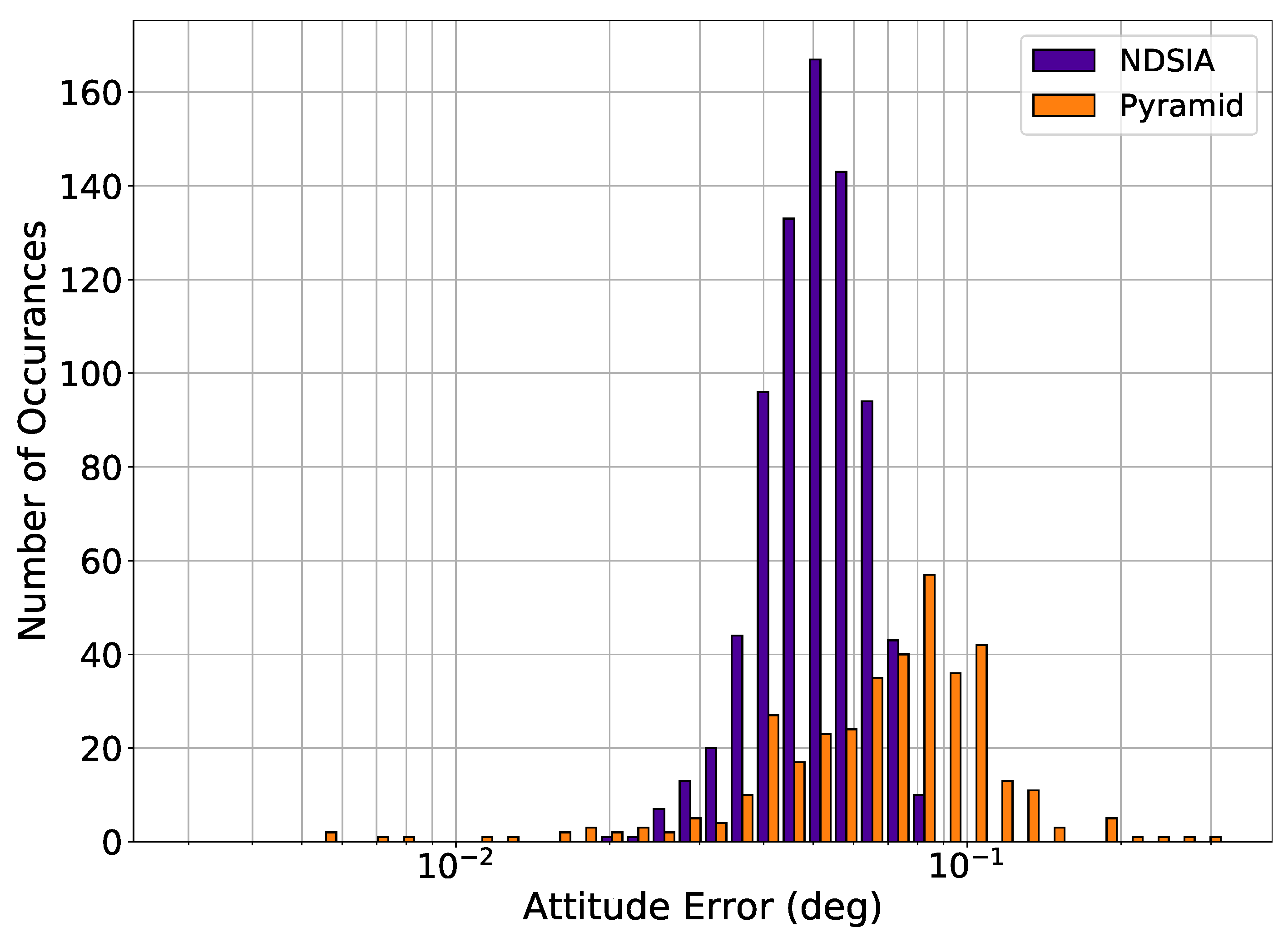
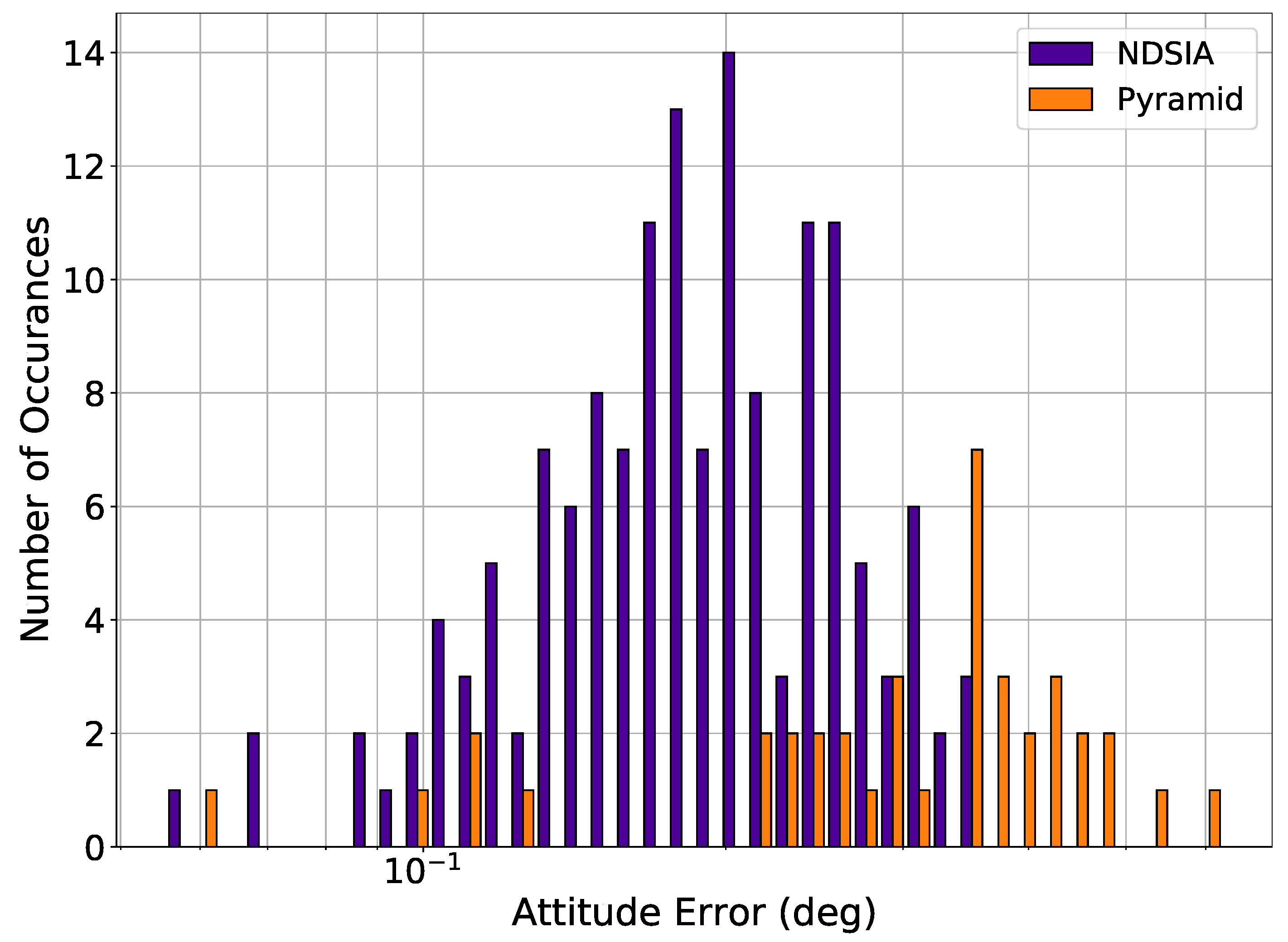
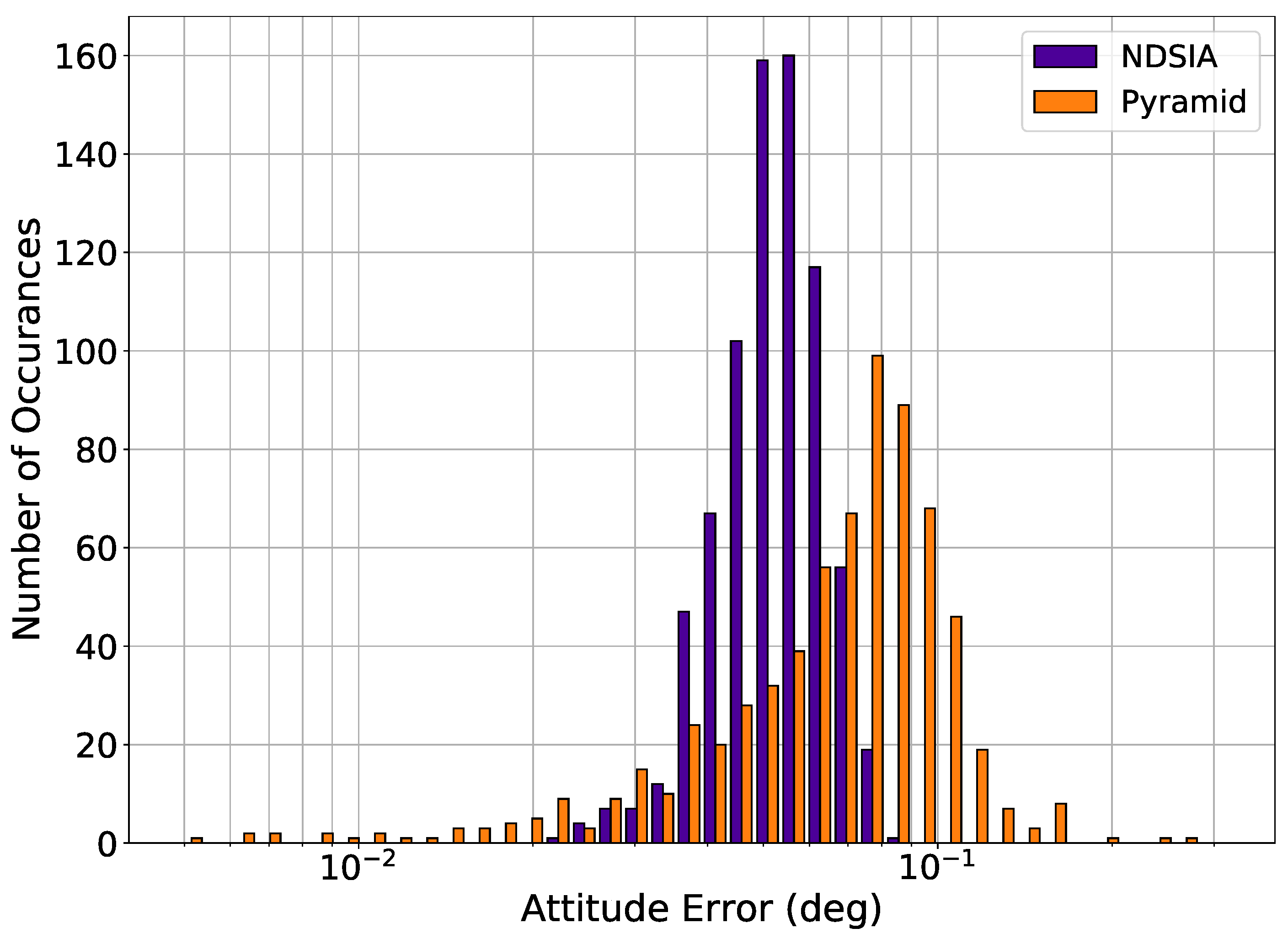
| Test Number | Focal Length Perturbation (% of Nominal Focal Length) | Optical Axis Offset Perturbation (% of Half the Imager Width) | Camera Centroiding Error Standard Deviation (Arcsec) |
|---|---|---|---|
| 1 | 0 | 0 | 10 |
| 2 | 0.5 | 0 | 10 |
| 3 | 2.0 | 0 | 10 |
| 4 | 0 | 0.5 | 10 |
| 5 | 0 | 2.0 | 10 |
| 6 | 0.5 | 0.5 | 10 |
| 7 | 2.0 | 2.0 | 10 |
| 8 | 0.5 | 0.5 | 15 |
| Virtual Star Tracker Parameter | Value |
|---|---|
| centroid error | 10 arcseconds |
| Star magnitude threshold | |
| Number of false stars | |
| Number of pixel rows | 1024 |
| Number of pixel columns | 1024 |
| Pixel pitch | mm |
| Focal length | mm |
| Number of stars in star catalogue | 1673 |
| Number of interstellar angles in Pyramid database | 99,422 |
| Number of star triangles in non-dimensional database | 2,762,895 |
| Test | Pyramid | NDSIA | Joint Statistics | |||||
|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (ms) | (%) | (%) | (ms) | Incomplete Pyramid Star-ID Scenes Completed Successfully by the NDSIA (%) | Unsuccessful Pyramid Star-ID Scenes Completed Successfully by the NDSIA (%) | |
| 1 | 100 | 99.9 | 0.139 | 84.2 | 100 | 2.81 | N/A | 100 |
| 2 | 41.8 | 90.7 | 10.8 | 79.4 | 100 | 3.80 | 68.0 | 92.3 |
| 3 | 9.20 | 41.3 | 27.8 | 21.5 | 100 | 24.3 | 17.8 | 59.3 |
| 4 | 100 | 99.9 | 0.141 | 81.8 | 100 | 3.40 | N/A | 100 |
| 5 | 100 | 99.9 | 0.140 | 53.5 | 100 | 12.6 | N/A | 100 |
| 6 | 41.7 | 89.9 | 10.9 | 77.2 | 100 | 4.32 | 64.5 | 95.2 |
| 7 | 10.2 | 38.2 | 27.6 | 14.7 | 100 | 29.4 | 10.6 | 54.0 |
| 8 | 75.5 | 90.3 | 6.92 | 75.9 | 100 | 7.06 | 46.5 | 91.8 |
| Used for Pyramid Range Search (Arcsec) | (%) | (%) | (ms) |
|---|---|---|---|
| 10 | 41.7 | 89.9 | 10.9 |
| 15 | 74.6 | 90.5 | 7.16 |
| 20 | 93.3 | 90.7 | 3.63 |
| 25 | 98.2 | 88.8 | 2.65 |
| 30 | 99.3 | 90.0 | 2.93 |
| 35 | 99.8 | 89.4 | 4.05 |
| 40 | 99.9 | 89.8 | 7.26 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leake, C.; Arnas, D.; Mortari, D. Non-Dimensional Star-Identification. Sensors 2020, 20, 2697. https://doi.org/10.3390/s20092697
Leake C, Arnas D, Mortari D. Non-Dimensional Star-Identification. Sensors. 2020; 20(9):2697. https://doi.org/10.3390/s20092697
Chicago/Turabian StyleLeake, Carl, David Arnas, and Daniele Mortari. 2020. "Non-Dimensional Star-Identification" Sensors 20, no. 9: 2697. https://doi.org/10.3390/s20092697
APA StyleLeake, C., Arnas, D., & Mortari, D. (2020). Non-Dimensional Star-Identification. Sensors, 20(9), 2697. https://doi.org/10.3390/s20092697






