Compressional-Wave Effects in the Operation of a Quartz Crystal Microbalance in Liquids:Dependence on Overtone Order
Abstract
1. Introduction
- The amplitudes of the compressional waves are weaker than one might think. Even at the fundamental mode (where they are strongest), they amount to less than 5% of the transverse amplitude in air.
- On the overtones (meaning on the higher eigenmodes, which contain more than one nodal plane) the flexural contributions are weaker than on the fundamental mode.
- The presence of a liquid may decrease the flexural contributions.
2. Flexural Contributions are Most Pronounced on the Fundamental Mode
- The quasi-static calculation misses inertial forces, which will reduce the amplitude of normal motion.
- The model treats a bar rather than a cylindrical plate.
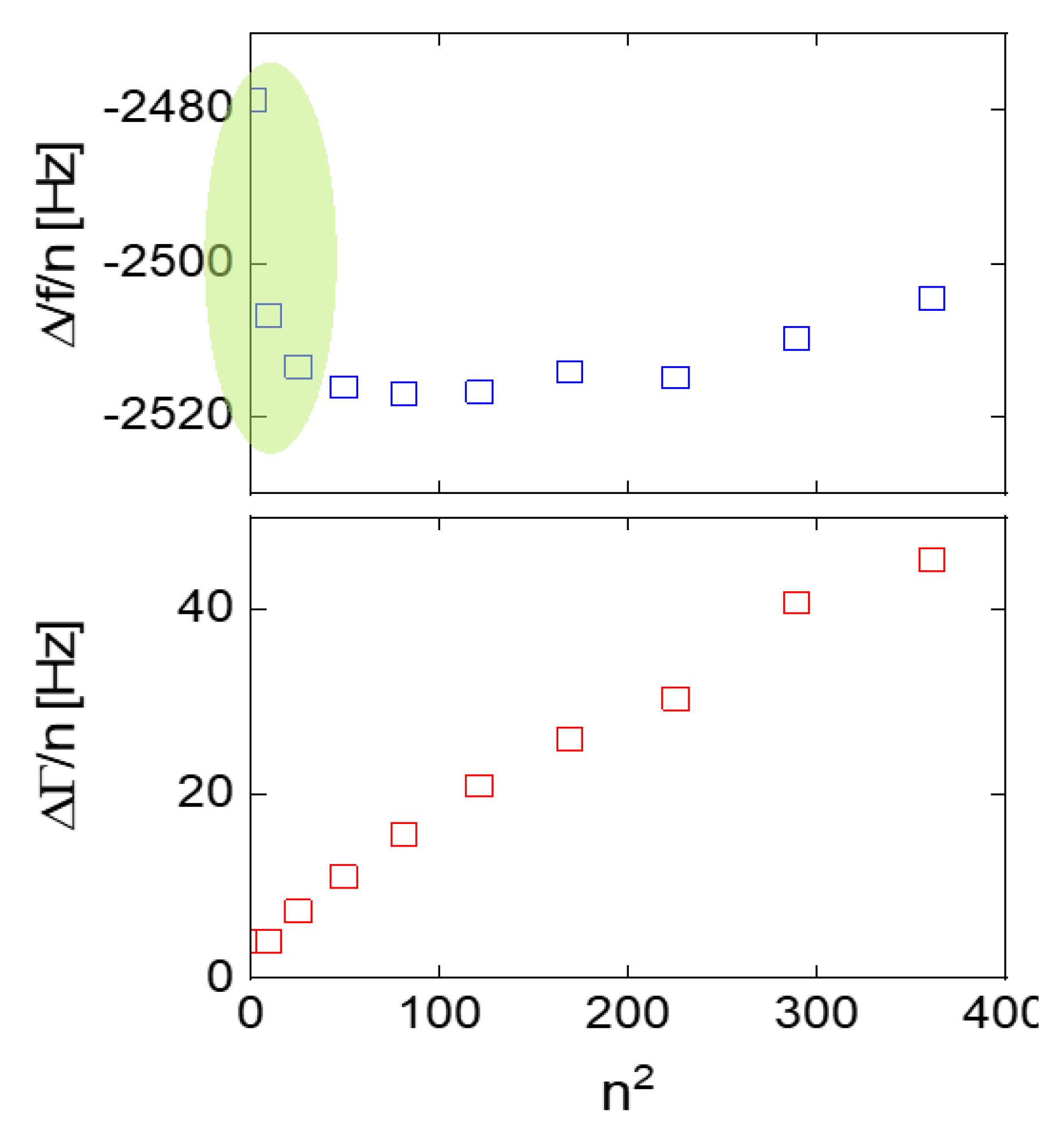
- The characteristic lateral scale L decreases with overtone order because energy trapping becomes more effective [35].
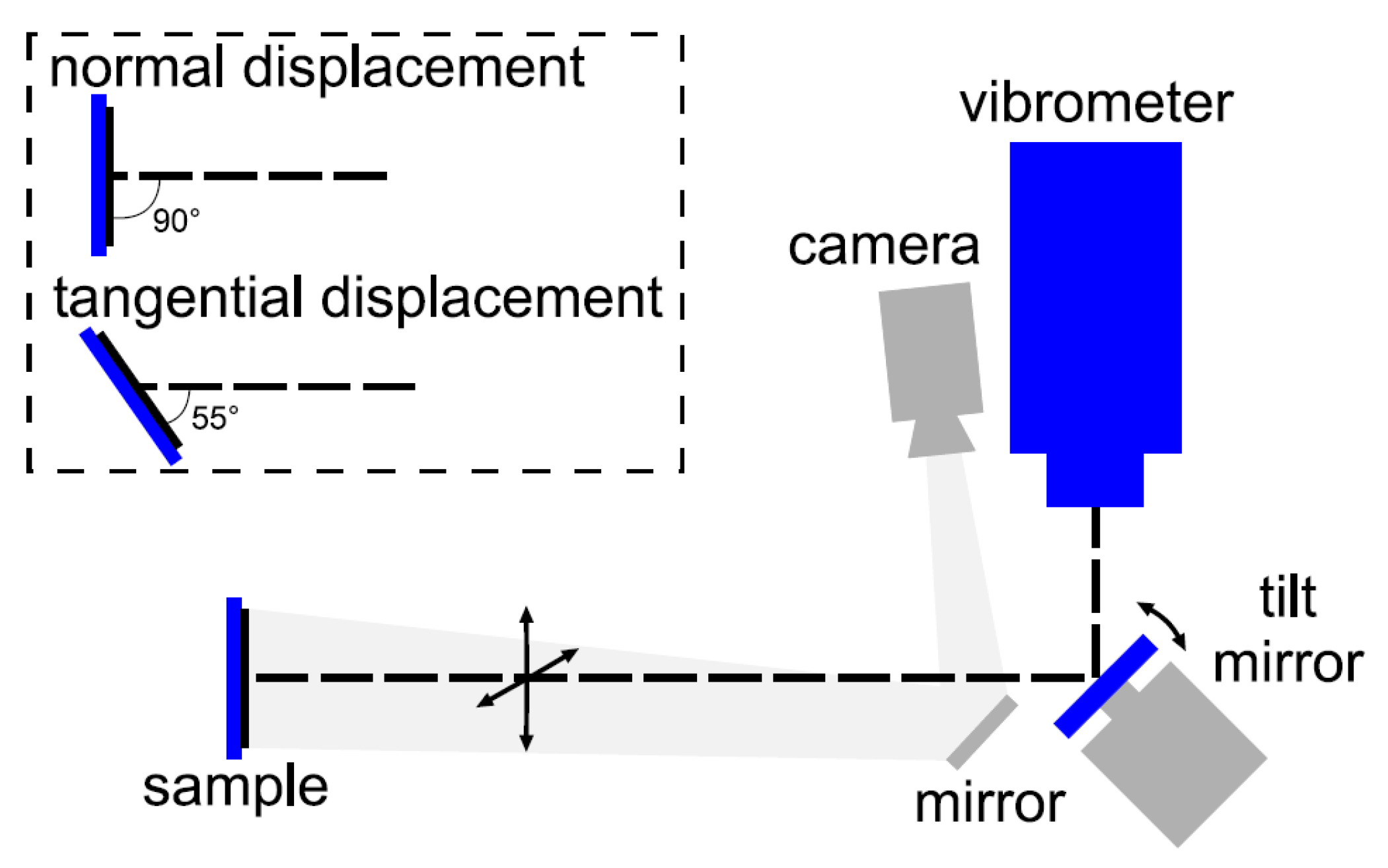
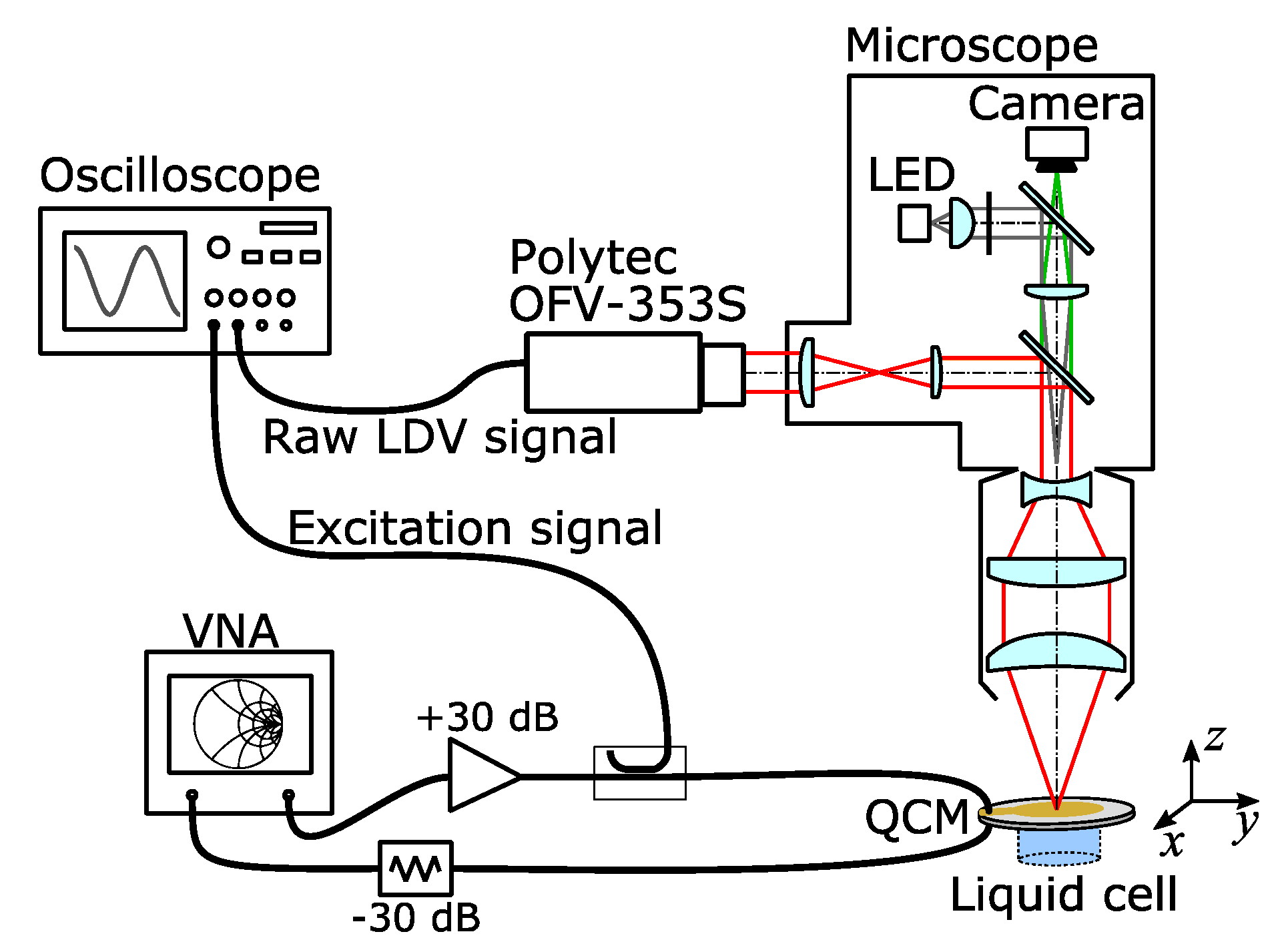
3. Laser-Doppler Vibrometry
4. Results from Laser-Doppler Vibrometry
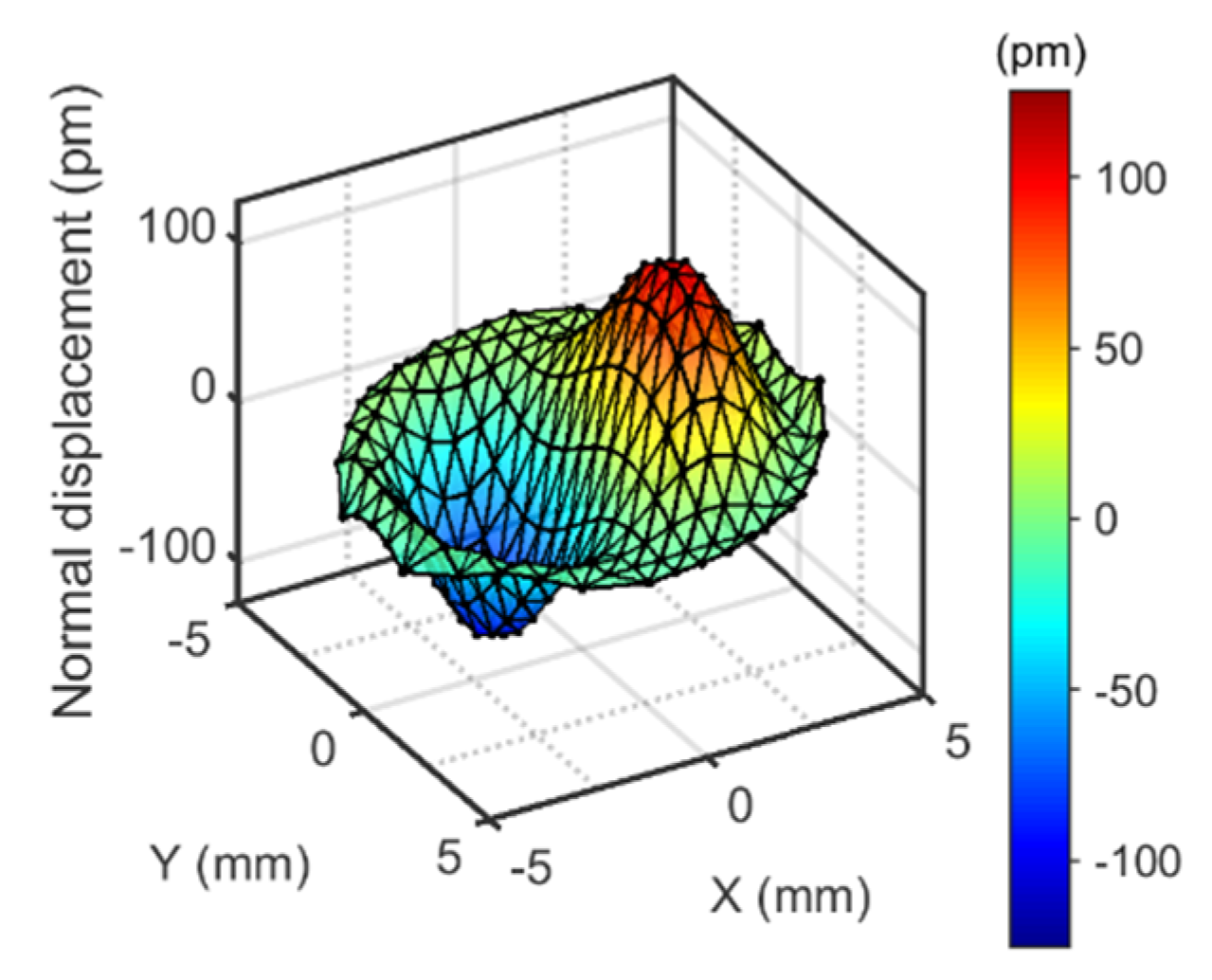
4.1. LDV Under Normal Incidence
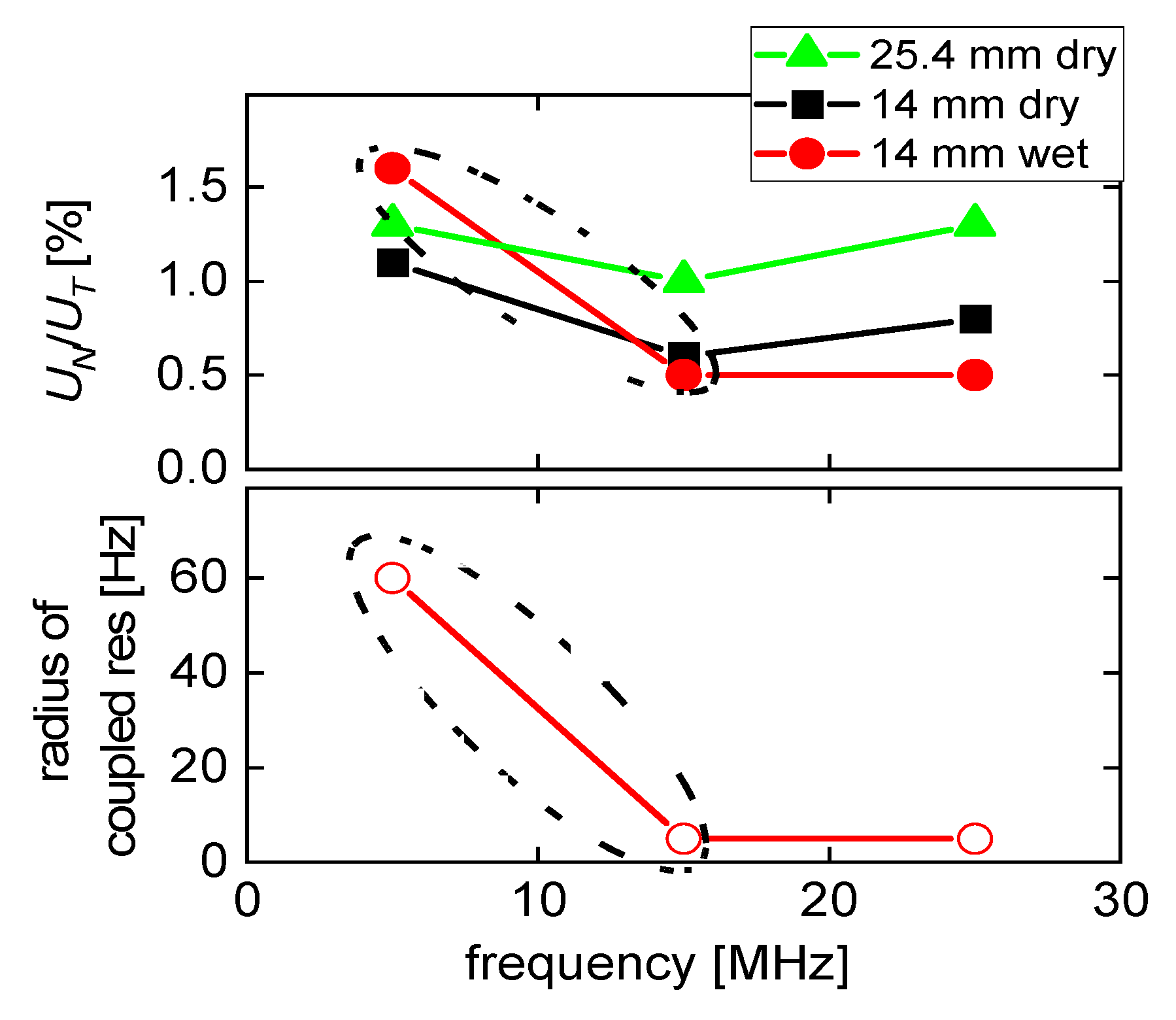
- The UN/UT-ratio is smaller at 15 MHz (n = 3) than at 5 MHz (n = 1). However, the 1/n2-scaling predicted by the model from Section 2 is not quantitatively confirmed. The UN/UT-ratio decreases between n = 1 and n = 3, but it does not decrease by a factor of 9. Comparing n = 3 and n = 5 (15 MHz and 25 MHz), the UN/UT-ratio does not even decrease.
- The UN/UT-ratio is larger for the larger crystal (with a diameter of 25.4 mm). While this is not expected, in principle (in-plane gradients decrease when the diameter of the plate increases), one needs to keep in mind that the thickness and the shape of the back electrode also plays a role in energy trapping.
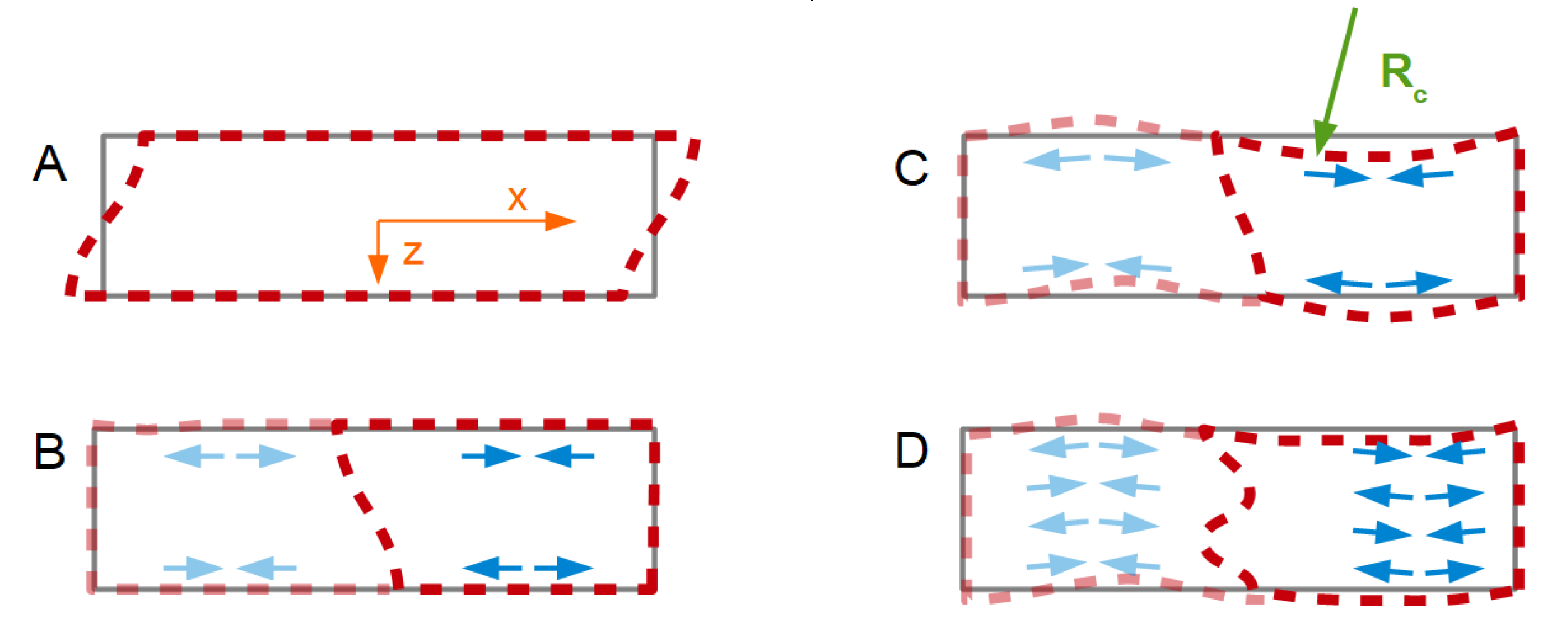
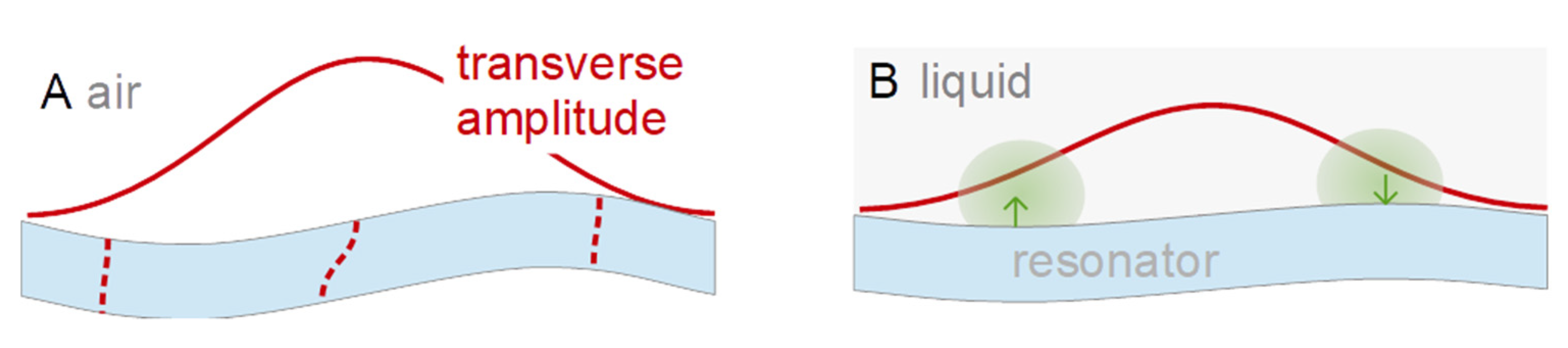
- The UN/UT-ratio decreases when the resonator is immersed in water. This is to be expected based on the argument sketched in Figure 5. Bending reduces the extensional strain inside the crystal, but it also causes a pressure in the adjacent liquid. Given that water is nearly incompressible (compared to air), the pressure is substantial and reduces the bending. This argument invalidates the small-load approximation (Section 6.1.3 in Reference [13]). The small-load approximation implicitly claims the modes shape to be unaffected by the load. A side remark: The UN/UT-ratio might actually change sign when immersing the resonator into the liquid. The pressure exerted by the liquid might outweigh the consequences of the extensional stress inside the plate. The sign is not inverted here. This result contradicts reference [40] (the reasons being unclear).
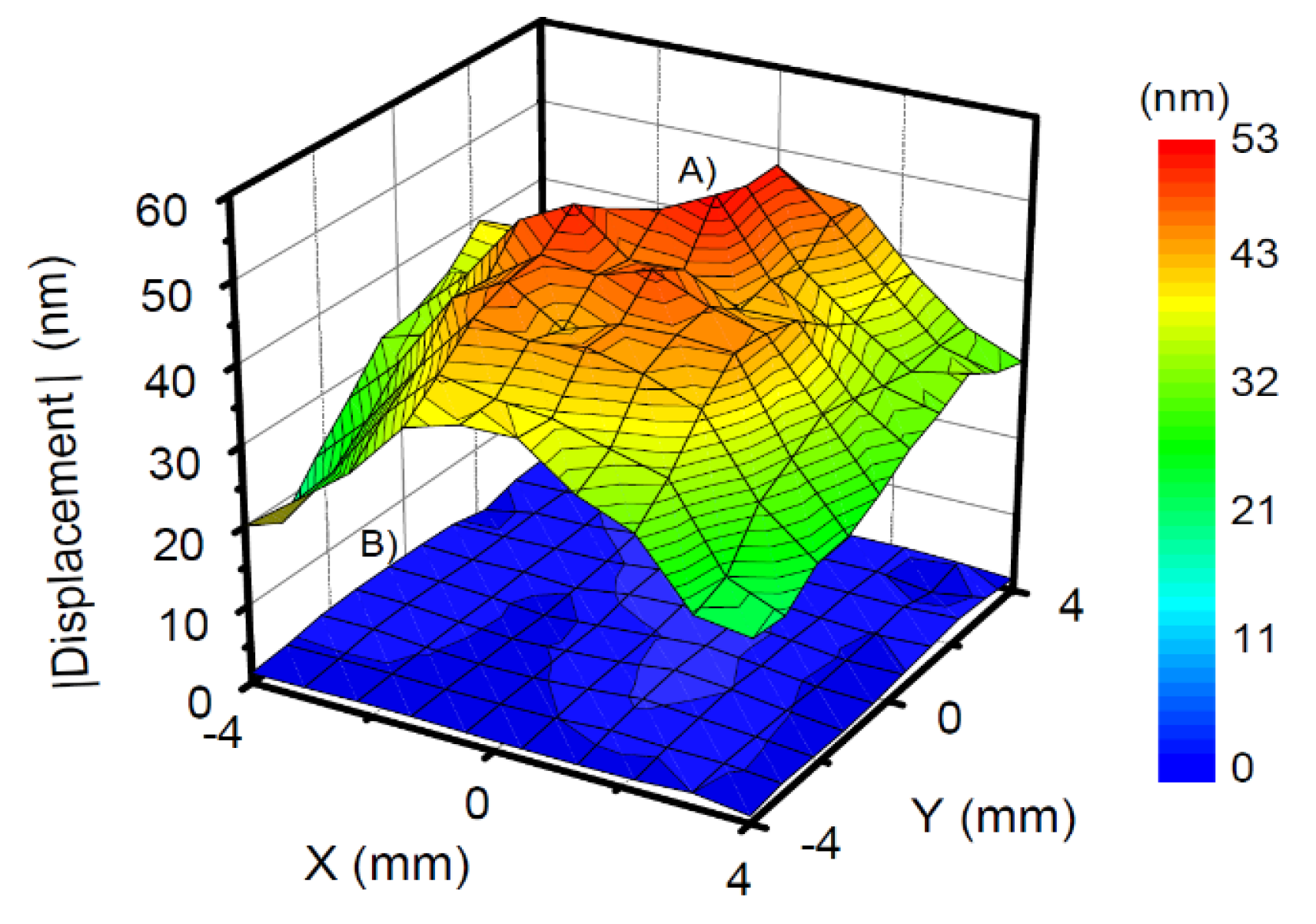
4.2. LDV Under Oblique Incidence
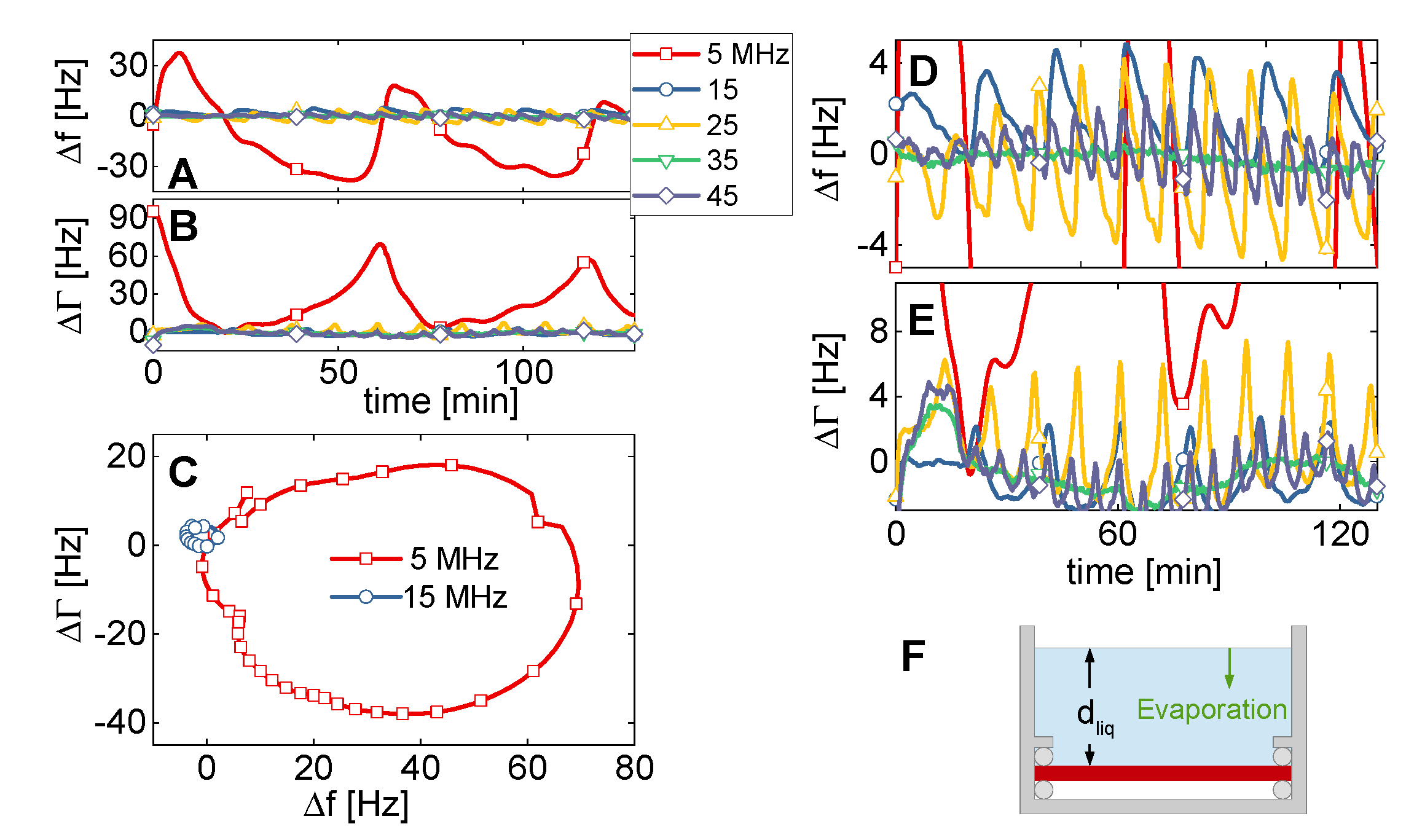
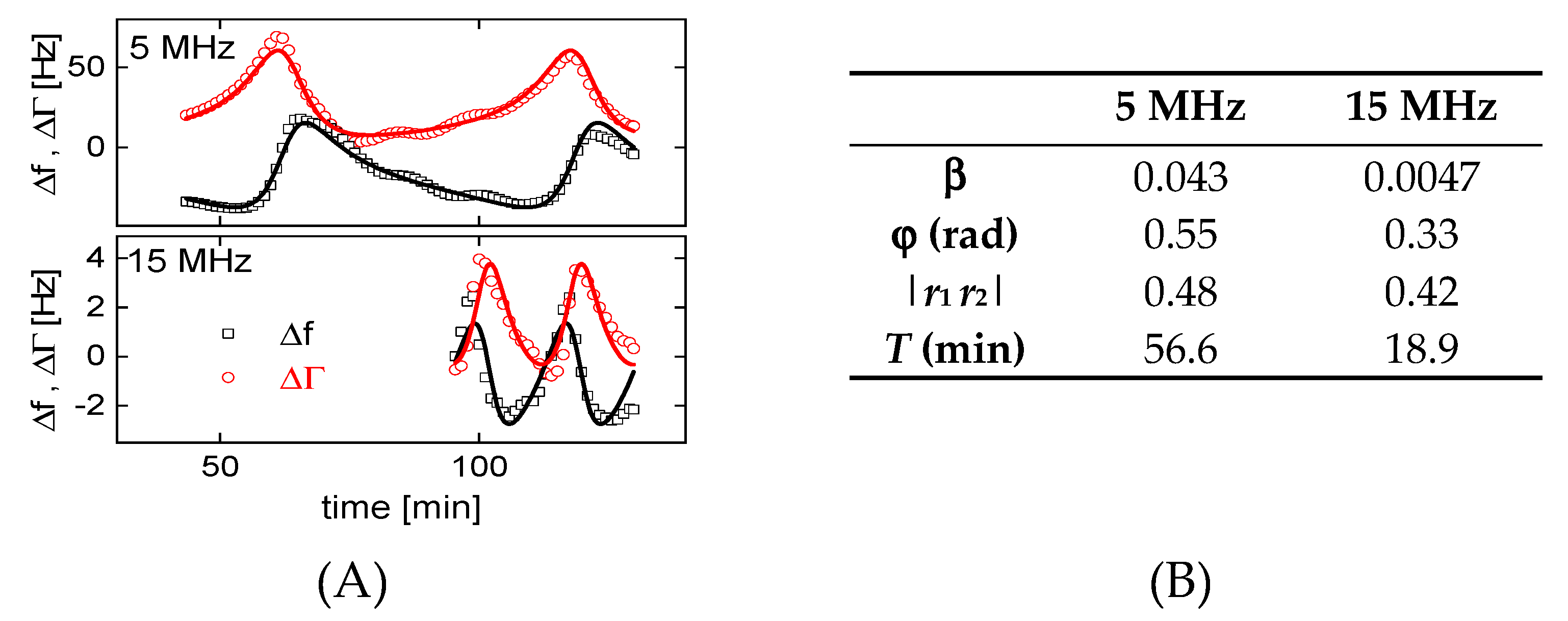
5. Cuvette Resonances
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Treatment of Compressional-Wave Effects in the Frame of the Small-Load Approximation
Appendix B. Estimation of the Transverse Amplitude from the Electrical Power
| 14 mm Diameter (Dry) | 14 mm Diameter (Wet) | 25.4 mm Diameter (Dry) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| f (MHz) | Aeff (mm²) | R1 (Ω) | UT (nm) | Aeff (mm²) | R1 (Ω) | UT (nm) | Aeff (mm²) | R1 (Ω) | UT (nm) |
| 5 | 25 | 19 | 124 | 46 | 280 | 18 | 41 | 16 | 84 |
| 15 | 27 | 24 | 35 | 38 | 590 | 5 | 32 | 42 | 22 |
| 25 | 25 | 52 | 15 | 30 | 980 | 3 | 25 | 52 | 15 |
Appendix C. Zernike Decomposition of the Operating Deflection Shapes
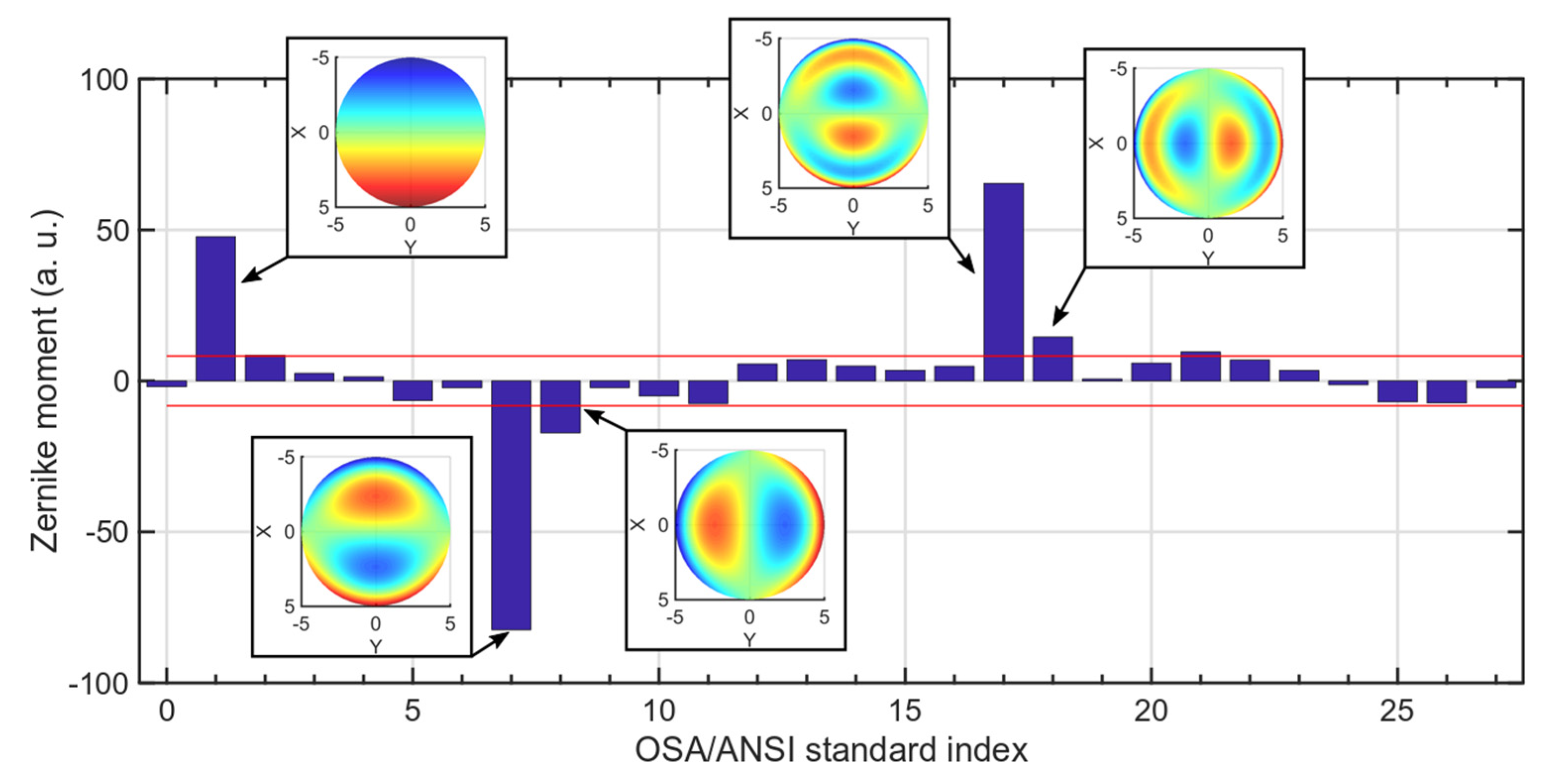
Appendix D. Assessment of the Magnitude of Flexural Admixtures from Experiments in Air
Appendix E. The LDV Instrument Used to Measure Transverse Components of the Displacement
References
- Bruckenstein, S.; Shay, M. Experimental Aspects of Use of the Quartz Crystal Microbalance in Solution. Electrochim. Acta 1985, 30, 1295–1300. [Google Scholar] [CrossRef]
- Nomura, T.; Okuhara, M. Frequency shifts of piezoelectric quartz crystals immersed in organic liquids. Anal. Chim. Acta 1982, 142, 281–284. [Google Scholar] [CrossRef]
- Nomura, T.; Hattori, O. Determination of micromolar concentrations of cyanide in solution with a piezoelectric detector. Anal. Chim. Acta 1980, 115, 323–326. [Google Scholar] [CrossRef]
- Mieure, J.P.; Jones, J.L. Electrogravimetric trace analysis on a piezoelectric detector. Talanta 1969, 16, 149–150. [Google Scholar] [CrossRef]
- Jones, J.L.; Mieure, J.P. Piezoelectric Transducer for Determination of Metals at Micromolar Level. Anal. Chem. 1969, 41, 484–490. [Google Scholar] [CrossRef]
- Janshoff, A.; Galla, H.-J.; Steinem, C. Piezoelectric Mass-Sensing Devices as Biosensors-An Alternative to Optical Biosensors? Angew. Chem. Int. Ed. 2000, 39, 4004–4032. [Google Scholar] [CrossRef]
- Lin, P.-H.; Huang, S.-C.; Chen, K.-P.; Li, B.-R.; Li, Y.-K. Effective Construction of a High-Capacity Boronic Acid Layer on a Quartz Crystal Microbalance Chip for High-Density Antibody Immobilization. Sensors 2018, 19, 28. [Google Scholar] [CrossRef]
- Mason, W.P.; Baker, W.O.; McSkimin, H.J.; Heiss, J.H. Measurement of Shear Elasticity and Viscosity of Liquids at Ultrasonic Frequencies. Phys. Rev. 1949, 75, 936–946. [Google Scholar] [CrossRef]
- Mason, W.P.; Baerwald, H. Piezoelectric Crystals and Their Applications to Ultrasonics. Phys. Today 1951, 4, 23. [Google Scholar] [CrossRef]
- Spencer, W.J. Coupled Thickness Shear and Flexure Displacements in Rectangular AT Quartz Plates. J. Acoust. Soc. Am. 1966, 39, 929. [Google Scholar] [CrossRef]
- Lin, Z.; Ward, M.D. The Role of Longitudinal Waves in Quartz Crystal Microbalance Applications in Liquids. Anal. Chem. 1995, 67, 685–693. [Google Scholar] [CrossRef]
- Schneider, T.W.; Martin, S.J. Influence of compressional wave generation on thickness-shear mode resonator response in a fluid. Anal. Chem. 1995, 67, 3324–3335. [Google Scholar] [CrossRef]
- Johannsmann, D. The Quartz Crystal Microbalance in Soft Matter Research; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Mindlin, R.D.; Deresiewicz, H. Thickness-Shear Vibrations of Piezoelectric Crystal Plates with Incomplete Electrodes. J. Appl. Phys. 1954, 25, 21. [Google Scholar] [CrossRef]
- Bottom, V.E. Introduction to Quartz Crystal Unit Design; Van Nostrand Reinhold: New York, NY, USA, 1982. [Google Scholar]
- Martin, B.A.; Hager, H.E. Velocity profile on quartz crystals oscillating in liquids. J. Appl. Phys. 1989, 65, 2630–2635. [Google Scholar] [CrossRef]
- Lucklum, R.; Schranz, S.; Behling, C.; Eichelbaum, F.; Hauptmann, P. Analysis of compressional-wave influence on thickness-shear-mode resonators in liquids. Sens. Actuators A Phys. 1997, 60, 40–48. [Google Scholar] [CrossRef]
- Friedt, J.M.; Choi, K.-H.; Frederix, F.; Campitelli, A.P. Simultaneous AFM and QCM Measurements - Methodology Validation Using Electrodeposition. J. Electrochem. Soc. 2003, 150, H229–H234. [Google Scholar] [CrossRef]
- Sauerbrey, G. Proceedings of the Annual Symposium on Frequency Control; Army Research and Development Laboratory: Fort Monmouth, NJ, USA, 1967; Volume 17, p. 63. [Google Scholar]
- Spencer, W.J. Physical Acoustics, Principles and Methods; Mason, W.P., Ed.; Academic Press: Cambridge, MA, USA, 1968; Volume 5, pp. 111–161. [Google Scholar]
- Williamson, R.J. Non-destructive means for determining mode shape in thickness-shear resonators. In Proceedings of the 44th Annual Symposium on Frequency Control, Baltimore, MD, USA, 23–25 May 1990; pp. 424–436. [Google Scholar] [CrossRef]
- Mecea, V.M.; Carlsson, J.-O.; Alm, O.; Boman, M. Out-of-plane vibrations of quartz resonators used in quartz crystal microbalance measurements in gas phase. Sens. Actuators A Phys. 2006, 125, 143–147. [Google Scholar] [CrossRef]
- Edvardsson, M.; Zhdanov, V.P.; Höök, F. Controlled Radial Distribution of Nanoscale Vesicles During Binding to an Oscillating QCM Surface. Small 2007, 3, 585–589. [Google Scholar] [CrossRef]
- Hess, C.; Borgwarth, K.; Heinze, J. Integration of an electrochemical quartz crystal microbalance into a scanning electrochemical microscope for mechanistic studies of surface patterning reactions. Electrochim. Acta 2000, 45, 3725–3736. [Google Scholar] [CrossRef]
- Castellini, P.; Martarelli, M.; Tomasini, E.P. Laser Doppler Vibrometry: Development of advanced solutions answering to technology’s needs. Mech. Syst. Sig. Process. 2006, 20, 1265–1285. [Google Scholar] [CrossRef]
- Rembe, C.; Dräbenstedt, A. Laser-scanning confocal vibrometer microscope: Theory and experiments. Rev. Sci. Instrum. 2006, 77, 083702. [Google Scholar] [CrossRef]
- Watanabe, Y.; Shikama, Y.; Goka, S.; Sato, T.; Sekimoto, H. Mode Shape Measurement of Piezoelectric Resonators Using Image Processing Technique. Jpn. J. Appl. Phys. 2001, 40, 3572–3574. [Google Scholar] [CrossRef]
- Brown, G.C.; Pryputniewicz, R.J. Holographic microscope for measuring displacements of vibrating microbeams using time-averaged, electro-optic holography. Opt. Eng. 1998, 37, 1398. [Google Scholar] [CrossRef]
- Stevens, D.S. An analysis of doubly rotated quartz resonators utilizing essentially thickness modes with transverse variation. J. Acoust. Soc. Am. 1986, 79, 1811. [Google Scholar] [CrossRef]
- Eernisse, E. Analysis of thickness modes of contoured doubly rotated, quartz resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2001, 48, 1351–1361. [Google Scholar] [CrossRef]
- Eernisse, E.; Benes, E.; Schmid, M. The role of localized rotational imbalance in drive level dependence phenomena. In Proceedings of the 2002 IEEE International Frequency Control Symposium and PDA Exhibition (Cat. No.02CH37234), New Orleans, LA, USA, 31–31 May 2002. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Ma, C.-C. Finite element and experimental results of transverse vibration for GT-cut and SC-cut quartz plates with fixed and free boundary conditions and multiple methods of excitation. Smart Mater. Struct. 2009, 18, 85017. [Google Scholar] [CrossRef]
- Kowarsch, R.; Rembe, C. Heterodyne interferometry at ultra-high frequencies with frequency-offset-locked semiconductor lasers. Meas. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, C.; Jiang, X.; Feng, G.-P. Thickness shear mode quartz crystal resonators with optimized elliptical electrodes. Chin. Phys. B 2011, 20, 47701. [Google Scholar] [CrossRef]
- Mindlin, R.D. Optimum Sizes and Shapes of Electrodes for Quartz Resonators. J. Acoust. Soc. Am. 1968, 43, 1329. [Google Scholar] [CrossRef]
- Steger, H.; Wörtge, M.; Rtge, M.; Siegmund, G.; Rembe, C. Measuring MEMS in Motion by Laser Doppler Vibrometry. Opt. Sci. Eng. 2006, 109, 245–292. [Google Scholar]
- Rembe, C.; Kowarsch, R.; Ochs, W.; Dräbenstedt, A.; Giesen, M.; Winter, M. Optical three-dimensional vibrometer microscope with picometer-resolution in x, y, and z. Opt. Eng. 2014, 53, 34108. [Google Scholar] [CrossRef]
- Kowarsch, R.; Janzen, J.; Rembe, C.; Cho, H.; Choo, H. Scanning confocal vibrometer microscope for vibration analysis of energy-harvesting MEMS in wearables. TM–Tech. Mess. 2017, 84, 131–137. [Google Scholar] [CrossRef]
- Schmidtchen, S. Ph.D. Thesis, Clausthal University of Technology, Clausthal-Zellerfeld, Germany, 2013.
- König, R.; Langhoff, A.; Johannsmann, D. Steady flows above a quartz crystal resonator driven at elevated amplitude. Phys. Rev. E 2014, 89, 043016. [Google Scholar] [CrossRef]
- Olsson, A.L.J.; Van Der Mei, H.C.; Johannsmann, D.; Busscher, H.J.; Sharma, P.K. Probing Colloid–Substratum Contact Stiffness by Acoustic Sensing in a Liquid Phase. Anal. Chem. 2012, 84, 4504–4512. [Google Scholar] [CrossRef]
- Kanazawa, K.K.; Gordon, J.G. Frequency of a quartz microbalance in contact with liquid. Anal. Chem. 1985, 57, 1770–1771. [Google Scholar] [CrossRef]
- Rodahl, M.; Kasemo, B. Frequency and dissipation-factor responses to localized liquid deposits on a QCM electrode. Sens. Actuators B Chem. 1996, 37, 111–116. [Google Scholar] [CrossRef]
- Hecht, E. Optics, 5th ed.; Pearson: Boston, MA, USA; Columbus, OH, USA; Indianapolis, IN, USA, 2017; ISBN 9780133977226. [Google Scholar]
- Patel, M.S.; Yong, Y.-K.; Tanaka, M. Drive level dependency in quartz resonators. Int. J. Solids Struct. 2009, 46, 1856–1871. [Google Scholar] [CrossRef]
- Sauerbrey, G. Verwendung von Schwingquarzen zur Wägung Dünner Schichten und zur Mikrowägung. Z. Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Petri, J.; Johannsmann, D. Determination of the Shear Modulus of Thin Polymer Films with a Quartz Crystal Microbalance: Application to UV-Curing. Anal. Chem. 2018, 91, 1595–1602. [Google Scholar] [CrossRef]

| 14 mm Diameter (Dry) | 14 mm Diameter (Wet) | 25.4 mm diameter (Dry) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| f (MHz) | UN (nm) | UT (nm) | UN/UT (%) | UN (nm) | UT (nm) | UN/UT (%) | UN (nm) | UT (nm) | UN/UT (%) |
| 5 | 1.38 | 124 | 1.1 | 0.29 | 18 | 1.6 | 1.10 | 84 | 1.3 |
| 15 | 0.20 | 35 | 0.6 | 0.027 | 5 | 0.5 | 0.22 | 22 | 1.0 |
| 25 | 0.12 | 15 | 0.8 | 0.016 | 3 | 0.5 | 0.20 | 15 | 1.3 |
| 14 mm Diameter (Dry) | 14 mm Diameter (Wet) | 25.4 mm Diameter (Dry) | |
|---|---|---|---|
| f (MHz) | D (mm) | D (mm) | D (mm) |
| 5 | 5.3 | 5.8 | 5.7 |
| 15 | 4.5 | 4.4 | 4.0 |
| 25 | 4.1 | 4.1 | 3.4 |
| f (MHz) | Diameter of Circle (Hz) |
|---|---|
| 5 | 60 |
| 15 | 5 |
| 25 | 5 |
| 35 | 1 |
| 45 | 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowarsch, R.; Suhak, Y.; Eduarte, L.C.; Mansour, M.; Meyer, F.; Peschel, A.; Fritze, H.; Rembe, C.; Johannsmann, D. Compressional-Wave Effects in the Operation of a Quartz Crystal Microbalance in Liquids:Dependence on Overtone Order. Sensors 2020, 20, 2535. https://doi.org/10.3390/s20092535
Kowarsch R, Suhak Y, Eduarte LC, Mansour M, Meyer F, Peschel A, Fritze H, Rembe C, Johannsmann D. Compressional-Wave Effects in the Operation of a Quartz Crystal Microbalance in Liquids:Dependence on Overtone Order. Sensors. 2020; 20(9):2535. https://doi.org/10.3390/s20092535
Chicago/Turabian StyleKowarsch, Robert, Yuriy Suhak, Lucia Cortina Eduarte, Mohammad Mansour, Frederick Meyer, Astrid Peschel, Holger Fritze, Christian Rembe, and Diethelm Johannsmann. 2020. "Compressional-Wave Effects in the Operation of a Quartz Crystal Microbalance in Liquids:Dependence on Overtone Order" Sensors 20, no. 9: 2535. https://doi.org/10.3390/s20092535
APA StyleKowarsch, R., Suhak, Y., Eduarte, L. C., Mansour, M., Meyer, F., Peschel, A., Fritze, H., Rembe, C., & Johannsmann, D. (2020). Compressional-Wave Effects in the Operation of a Quartz Crystal Microbalance in Liquids:Dependence on Overtone Order. Sensors, 20(9), 2535. https://doi.org/10.3390/s20092535





