A Distributed Clustering Algorithm Guided by the Base Station to Extend the Lifetime of Wireless Sensor Networks
Abstract
1. Introduction
- Centralized Clustering. The BS has full control about how the clustering is performed. The BS always decides which nodes are converted into CHs. For this operation, the BS needs information about all the nodes in order to choose the most appropriate ones as CHs. The most common properties used for this decision are the location of the node within the sensing area and the residual energy of each node. The first one is not always available in all the applications because nodes usually cannot afford GPS equipment or similar hardware.
- Distributed Clustering. The nodes are completely autonomous and decide by themselves if they become CH or not. This decision is supported by the properties that the node can know/estimate by itself. Then, that information is weighted by some methods that indicate whether to become CH or not. Finally, those nodes that selected themselves as CH send a message to the network so that the other nodes can join them to their clusters.
- It is a distributed clustering algorithm guided by the BS in a simple way, with just three transmissions during the network lifetime. The transmissions help the nodes know about the status of the network.
- It uses a dynamic value to keep the same CH structure in the network during a number of rounds. In this way, the configuration of the value is adapted to the dynamic inertia of the network during its operative time. As a consequence, the network can reduce the energy consumption for the CH configuration more efficiently.
- The present paper constitutes a novelty concerning the type of fuzzy system used in the nodes. The nodes implement a new Type-2 Tagaki–Sugeno–Kang (TSK) model for the fuzzy system [24]. Previous fuzzy-logic based clustering algorithms rely on a Mandami model. However, the TSK has revealed itself more appropriate in real-time applications. Moreover, the input variables in the fuzzy system are carefully selected to extend the network lifetime as it is described in Section 2.1.1.
2. Proposed Algorithm
2.1. Interval Type-2 Fuzzy System
- The crisp values of the inputs are fuzzified with interval Type-2 fuzzy sets that are stored in the Knowledge Base (KB).
- Fuzzified inputs are bound together through the rules found in the KB.
- The inference process binds the inputs, the rules, and the outputs.
- The interval Type-2 fuzzy is reduced to a Type-1 set by the type-reducer block.
- The last step is to obtain the output. In our case, the highest and lowest values of the interval are used, each one in a different stage of the process.
2.1.1. Variables of the Type-2 Fuzzy System
- . Remaining energy. This variable measures the percentage of energy that a node has with respect to its initial one. Thus, it ranges from 1 (full battery) to 0 (empty battery). If this value is low, the probability of the node of being chosen as CH should be smaller.
- . This input evaluates the number of times a node has become a CH compared with the total of advice messages of surrounding CHs that it has previously received. follows Equation (1). If the node has not been selected as a CH for a long time, this value will be high hence. As a consequence of this, the probability of becoming CH will increase:where is the number of times that the node has been selected as CH and is the total number of advice messages received from other CH since the network started to operate.
- . It is the energy that the node has when compared with the average energy of all the nodes that were selected as CHs in the previous round. Consequently, each time a node becomes a CH, it includes its remaining energy in the advice message and then each node computes the average of all the values received from the CHs in the previous iteration to obtain this value. The value is normalized according to Equation (2):where E is the energy of the node and is the average of the energy values received in the advice messages in the preceding iteration. This message is sent to the entire sensing area, so it reaches all nodes. The election of the value 1.5 for the normalization parameter of the threshold in the equation is due to the need for limiting the range of the variability of . We have empirically determined that setting to a value greater than does not affect the results significantly. We also observed that the proposed setting also reduces the fluctuation of the system. Alternatively, a node that has been chosen as a CH in a previous round is very likely to have lower energy than those nodes which have only been sensors. In this case, this value will be small, and it would not be chosen again as CH.
- . It is a function of the number of rounds past since a node became CH. It is calculated as indicated in Equation (3):where R is the number of rounds since a node has not been CH and is the total number of sensors in the network. If a node has not acted as CH for a long time, this variable will have a high value, which will try to increase the output of the IT2FS. This input prevents a node from remaining as a contributing sensor for a long time.
2.1.2. Knowledge Base of the Type-2 Fuzzy System
2.2. Skip Value Setup
- At network startup. The BS sends a message for the nodes to start working. In that message, it will include the initial value of or . This message allows each node to estimate the distance to the BS based on the RSSI of the received signal.
- After the first death of a node. To detect that instant, each time a CH sends information to the BS, it includes the number of its contributing nodes. Consequently, the BS, after receiving all the CH data messages, can detect if the total number of nodes that sent information is lower than the initial one. If this happens, the BS will assume that there is one dead node at least. Thus, when it detects the first death of a sensor, it will send a new configuration message with a new value of the parameter or .
- After half of the nodes are dead. When the BS detects this event, it configures the nodes with . This value will be kept constant until the network stops operating.
2.3. Algorithm for the Cluster Head Election
| Algorithm 1: Election of Cluster Head |
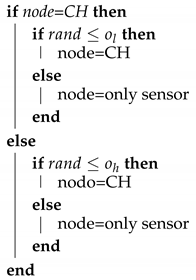 |
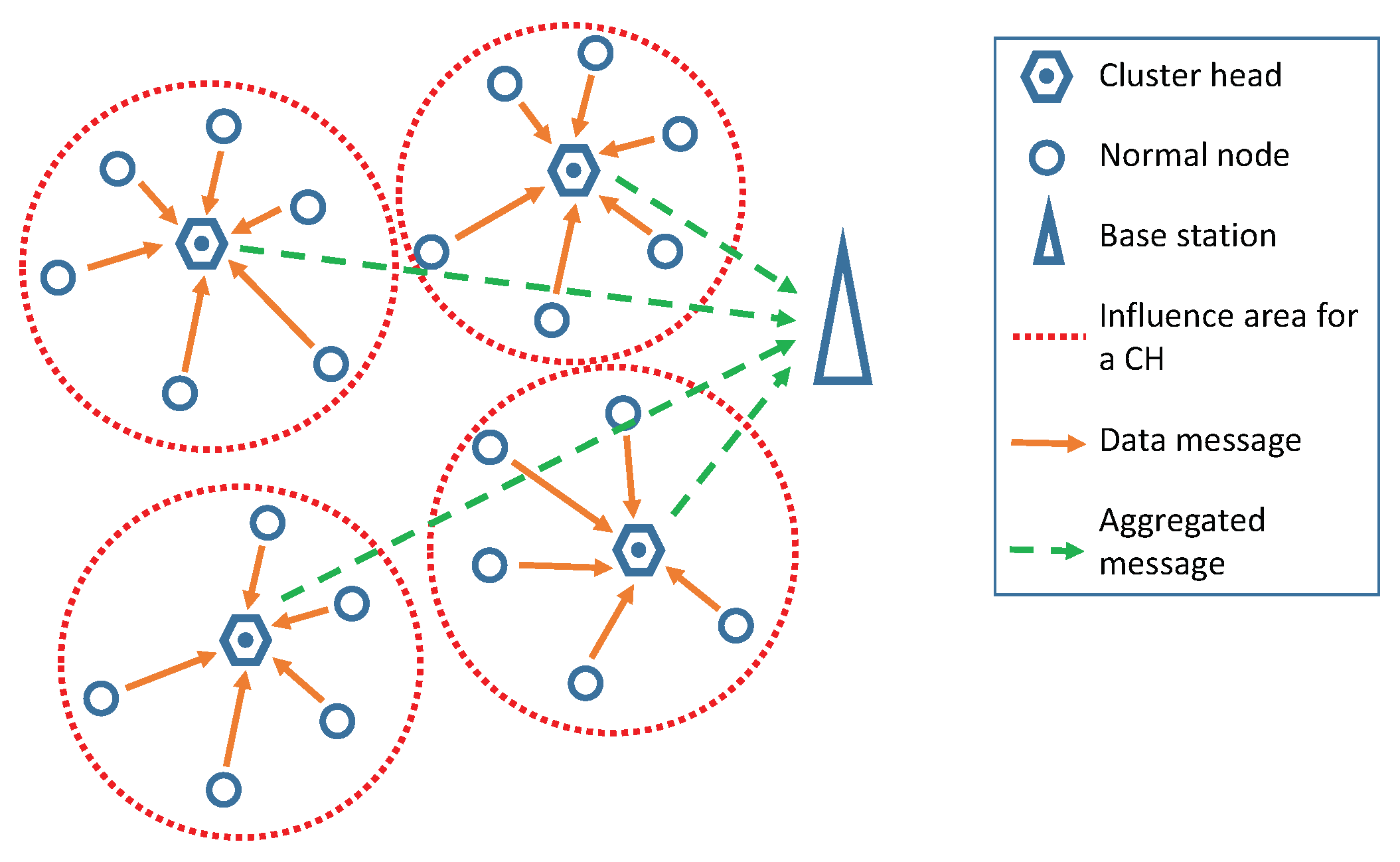
3. Evaluation
3.1. Energy Model
- l is the number of bits of the message.
- is the energy that consumes the transmitter or the receiver circuitry for each bit.
- d stands for the distance between the sender and the receiver of the message.
- is the energy consumed by the amplifier according to the free space model to get an acceptable bit error rate (in Figure 4, it appears as for both cases).
- is the energy consumed by the amplifier in the multi-path (mp) model to obtain an acceptable bit error rate (in Figure 4 appears as for both cases).
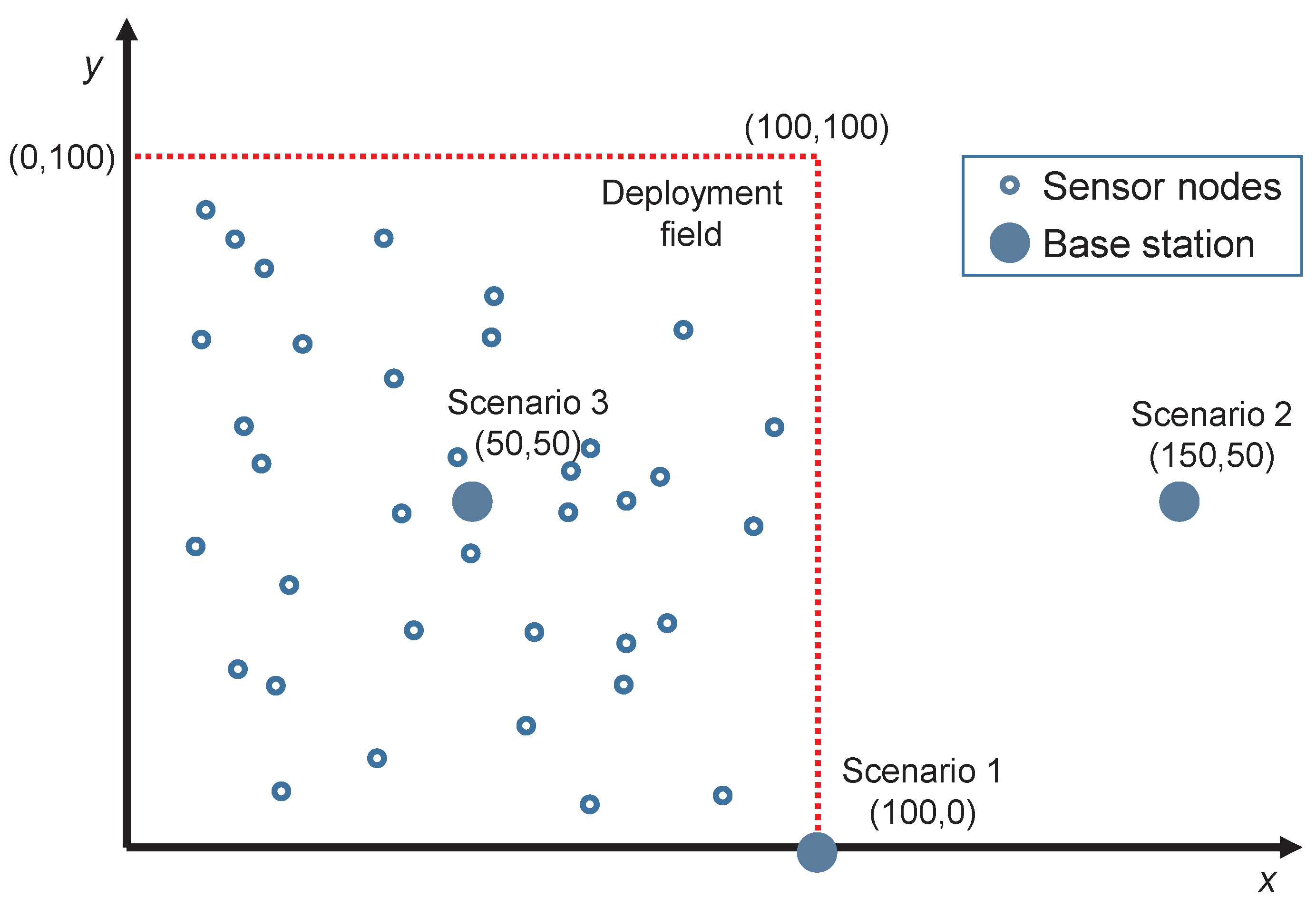
3.2. Experiment Design
- Scenario 1. The BS is at one corner of the square field at coordinates (100,0) meters.
- Scenario 2. The BS is far and outside the sensing area at coordinates (150,50) meters.
- Scenario 3. The BS is at the center of the deployment field at coordinates (50,50) meters.
- Low-Energy Adaptive Clustering Hierarchy (LEACH) [5]. It is a distributed algorithm based on a pure stochastic CH selection method which is used like a reference in most clustering proposals. The parameter p of this algorithm is set to 0.05 in our simulations.
- Cluster-Head Election using Fuzzy logic for wireless sensor networks (CHEF) [17]. CHEF is a centralized method that decides the best CH based on an expert system. The fuzzy system has three input variables: energy, concentration, and centrality of nodes.
- Energy-Efficient Distributed Clustering algorithm based on a Fuzzy approach with non-uniform distribution (EEDCF) [34]. EEDCF is a distributed algorithm based on fuzzy logic. The inputs are energy, the number of neighbor nodes, and the energy of those nodes. This method has a phase in which different nodes compete to be CH. The node with the best fuzzy output becomes the CH eventually.
- Enhanced Unequal Distributed Type-2 Fuzzy Clustering algorithm (EUDFC) [23]. EUDFC is an interval Type-2 fuzzy distributed system. The system variables are energy, distance to the BS, the average of the distances of the nodes that join a CH, and the number of rounds that a node is only a sensor. EUDFC has a competition phase in which only CHs is chosen, where n is the number of nodes in the system.
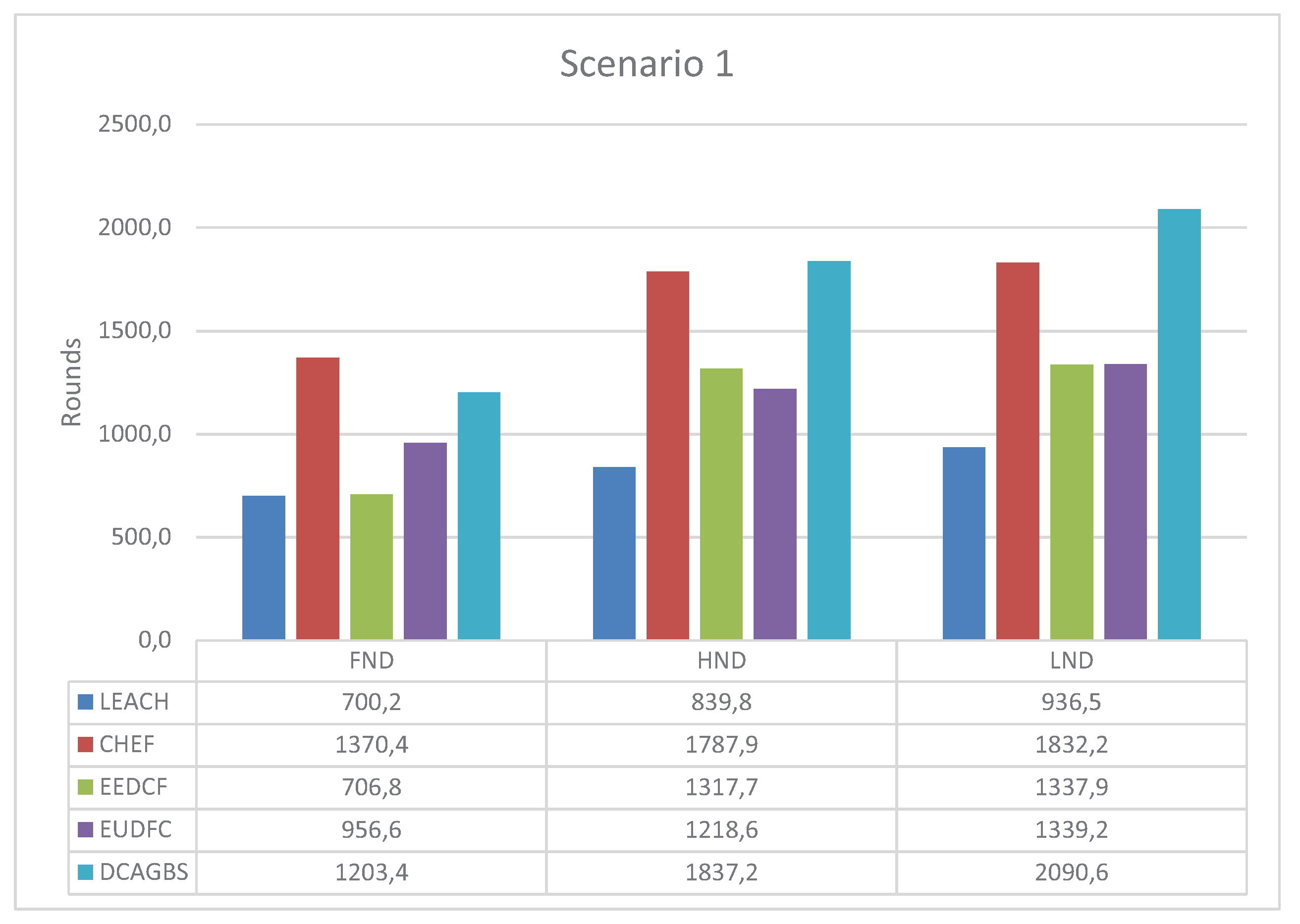
3.3. Scenario 1
3.4. Scenario 2
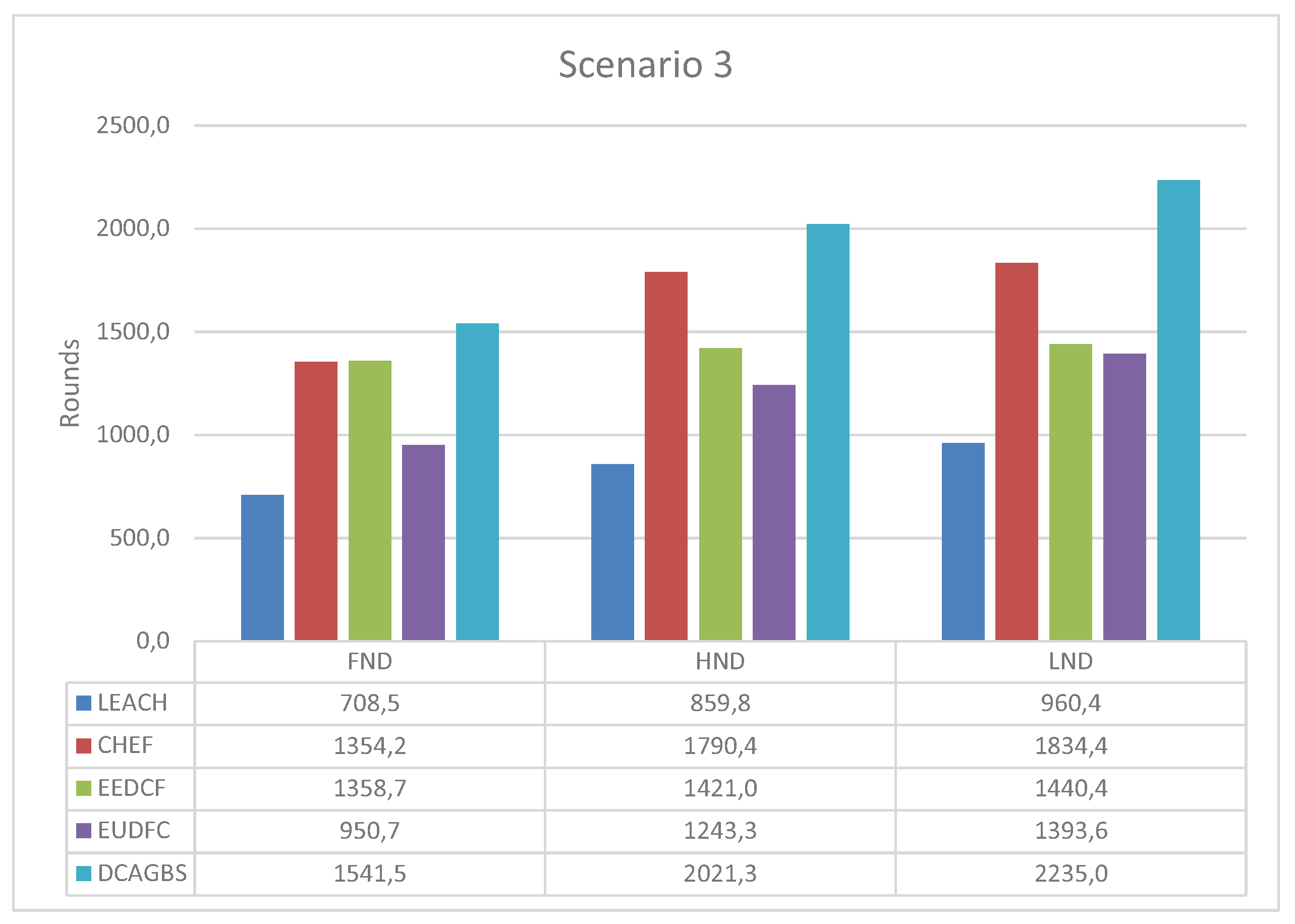
3.5. Scenario 3
3.6. Analysis of the Results
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mohamed, R.E.; Saleh, A.I.; Abdelrazzak, M.; Samra, A.S. Survey on wireless sensor network applications and energy efficient routing protocols. Wirel. Pers. Commun. 2018, 101, 1019–1055. [Google Scholar] [CrossRef]
- Pike, M.; Mustafa, N.M.; Towey, D.; Brusic, V. Sensor Networks and Data Management in Healthcare: Emerging Technologies and New Challenges. In Proceedings of the 2019 IEEE 43rd Annual Computer Software and Applications Conference (COMPSAC), Milwaukee, WI, USA, 15–19 July 2019; Volume 1, pp. 834–839. [Google Scholar] [CrossRef]
- Abujubbeh, M.; Al-Turjman, F.; Fahrioglu, M. Software-defined wireless sensor networks in smart grids: An overview. Sustain. Cities Soc. 2019, 51, 101754. [Google Scholar] [CrossRef]
- Liu, X. A Survey on Clustering Routing Protocols in Wireless Sensor Networks. Sensors 2012, 12, 11113–11153. [Google Scholar] [CrossRef] [PubMed]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2000; Volume 2, p. 10. [Google Scholar] [CrossRef]
- Kia, G.; Hassanzadeh, A. A multi-threshold long life time protocol with consistent performance for wireless sensor networks. AEU-Int. J. Electron. Commun. 2019, 101, 114–127. [Google Scholar] [CrossRef]
- Younis, O.; Fahmy, S. HEED: A hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks. IEEE Trans. Mob. Comput. 2004, 3, 366–379. [Google Scholar] [CrossRef]
- Ye, M.; Li, C.; Chen, G.; Wu, J. EECS: An energy efficient clustering scheme in wireless sensor networks. In Proceedings of the 24th IEEE International Performance, Computing, and Communications Conference, Phoenix, AZ, USA, 7–9 April 2005; pp. 535–540. [Google Scholar]
- Pietrabissa, A.; Liberati, F. Dynamic distributed clustering in wireless sensor networks via Voronoi tessellation control. Int. J. Control 2019, 92, 1001–1014. [Google Scholar] [CrossRef]
- Huo, H.; Guo, J.; Li, Z.L. Hyperspectral Image Classification for Land Cover Based on an Improved Interval Type-II Fuzzy C-Means Approach. Sensors 2018, 18, 363. [Google Scholar] [CrossRef]
- Gencer, A. Analysis and Control of Fault Ride-Through Capability Improvement for Wind Turbine Based on a Permanent Magnet Synchronous Generator Using an Interval Type-2 Fuzzy Logic System. Energies 2019, 12, 2289. [Google Scholar] [CrossRef]
- Jiang, Q.; Jin, X.; Hou, J.; Lee, S.; Yao, S. Multi-Sensor Image Fusion Based on Interval Type-2 Fuzzy Sets and Regional Features in Nonsubsampled Shearlet Transform Domain. IEEE Sens. J. 2018, 18, 2494–2505. [Google Scholar] [CrossRef]
- Pandey, M.; Litoriya, R.; Pandey, P. Identifying causal relationships in mobile app issues: An interval type-2 fuzzy DEMATEL approach. Wirel. Pers. Commun. 2019, 108, 683–710. [Google Scholar] [CrossRef]
- Cuevas-Martinez, J.C.; Yuste-Delgado, A.J.; Triviño-Cabrera, A. Cluster Head Enhanced Election Type-2 Fuzzy Algorithm for Wireless Sensor Networks. IEEE Commun. Lett. 2017, 21, 2069–2072. [Google Scholar] [CrossRef]
- Moorthi; Thiagarajan, R. Energy consumption and network connectivity based on Novel-LEACH-POS protocol networks. Comput. Commun. 2020, 149, 90–98. [Google Scholar] [CrossRef]
- Agrawal, D.; Pandey, S. FUCA: Fuzzy-based unequal clustering algorithm to prolong the lifetime of wireless sensor networks. Int. J. Commun. Syst. 2018, 31, e3448. [Google Scholar] [CrossRef]
- Gupta, I.; Riordan, D.; Sampalli, S. Cluster-head election using fuzzy logic for wireless sensor networks. In Proceedings of the 3rd Annual Communication Networks and Services Research Conference (CNSR’05), Halifax, NS, Canada, 16–18 May 2005; pp. 255–260. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, Q.; Sun, Z. ICT2TSK: An improved clustering algorithm for WSN using a type-2 Takagi-Sugeno-Kang Fuzzy Logic System. In Proceedings of the 2013 IEEE Symposium on Wireless Technology Applications (ISWTA), Kuching, Malaysia, 22–25 September 2013; pp. 153–158. [Google Scholar] [CrossRef]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Thangaramya, K.; Kulothungan, K.; Logambigai, R.; Selvi, M.; Ganapathy, S.; Kannan, A. Energy aware cluster and neuro-fuzzy based routing algorithm for wireless sensor networks in IoT. Comput. Netw. 2019, 151, 211–223. [Google Scholar] [CrossRef]
- Shivappa, N.; Manvi, S.S. Fuzzy-based cluster head selection and cluster formation in wireless sensor networks. IET Netw. 2019, 8, 390–397. [Google Scholar] [CrossRef]
- Merabtine, N.; Djenouri, D.; Zegour, D.E.; Boumessaidia, B.; Boutahraoui, A. Balanced clustering approach with energy prediction and round-time adaptation in wireless sensor networks. Int. J. Commun. Netw. Distrib. Syst. 2019, 22, 245–274. [Google Scholar] [CrossRef]
- Yuste-Delgado, A.J.; Cuevas-Martinez, J.C.; Triviño-Cabrera, A. EUDFC-Enhanced Unequal Distributed Type-2 Fuzzy Clustering Algorithm. IEEE Sens. J. 2019, 19, 4705–4716. [Google Scholar] [CrossRef]
- Sugeno, M. Industrial Applications of Fuzzy Control; Elsevier Science Inc.: New York, NY, USA, 1985. [Google Scholar]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers; World Scientific: Singapore, 1996; Volume 6. [Google Scholar]
- Castillo, O.; Melin, P. A review on interval type-2 fuzzy logic applications in intelligent control. Inf. Sci. 2014, 279, 615–631. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of fuzzy algorithms for control of simple dynamic plant. Proc. Inst. Electr. Eng. 1974, 121, 1585–1588. [Google Scholar] [CrossRef]
- Jassbi, J.J.; Serra, P.J.A.; Ribeiro, R.A.; Donati, A. A Comparison of Mandani and Sugeno Inference Systems for a Space Fault Detection Application. In Proceedings of the 2006 World Automation Congress, Budapest, Hungary, 24–26 July 2006; pp. 1–8. [Google Scholar]
- Tikk, D.; Kóczy, L.T.; Gedeon, T.D. A survey on universal approximation and its limits in soft computing techniques. Int. J. Approx. Reason. 2003, 33, 185–202. [Google Scholar] [CrossRef]
- Subhedar, M.; Birajdar, G. Comparison of mamdani and sugeno inference systems for dynamic spectrum allocation in cognitive radio networks. Wirel. Pers. Commun. 2013, 71, 805–819. [Google Scholar] [CrossRef]
- Cuevas-Martinez, J.C.; Yuste-Delgado, A.J.; Leon-Sanchez, A.J.; Saez-Castillo, A.J.; Triviño-Cabrera, A. A New Centralized Clustering Algorithm for Wireless Sensor Networks. Sensors 2019, 19, 4391. [Google Scholar] [CrossRef] [PubMed]
- Trakadas, P.; Zahariadis, T.; Leligou, H.C.; Voliotis, S.; Papadopoulos, K. Analyzing energy and time overhead of security mechanisms in Wireless Sensor Networks. In Proceedings of the 2008 15th International Conference on Systems, Signals and Image Processing, Bratislava, Slovak Republic, 25–28 June 2008; pp. 137–140. [Google Scholar]
- Dhand, G.; Tyagi, S. Data aggregation techniques in WSN: Survey. Procedia Comput. Sci. 2016, 92, 378–384. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Han, D.; Wu, H.; Zhou, R. Fuzzy-logic based distributed energy-efficient clustering algorithm for wireless sensor networks. Sensors 2017, 17, 1554. [Google Scholar] [CrossRef]

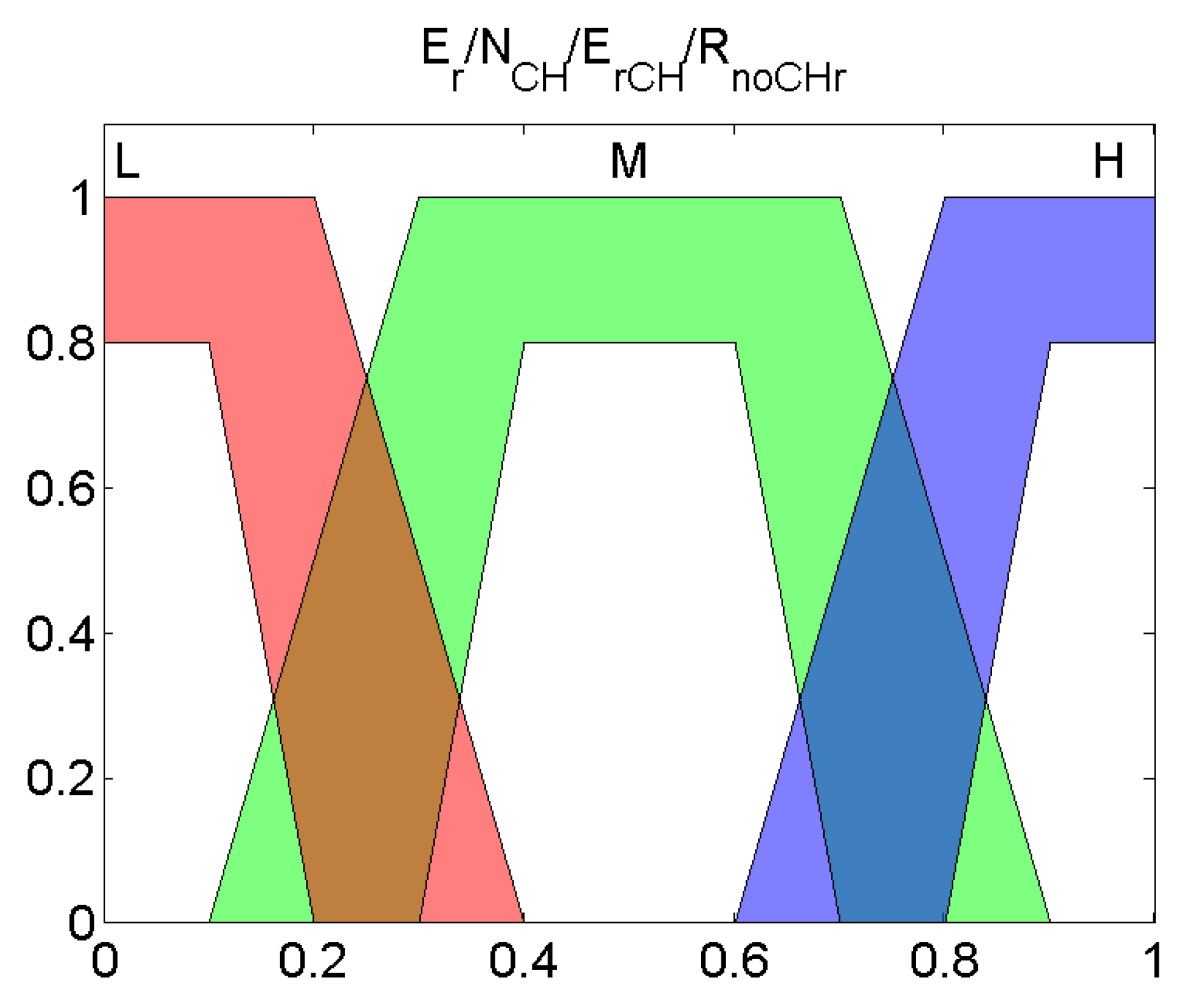


| Name | Lower Interval Limit | Upper Interval Limit |
|---|---|---|
| Very Low | 0 | 0.3 |
| Low | 0.2 | 0.4 |
| Medium | 0.3 | 0.6 |
| High | 0.6 | 0.8 |
| Very High | 0.75 | 1 |
| Rule | Score | Rule | Score | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | L | L | L | L | VL | 42 | M | M | M | H | H | |
| 2 | L | L | L | M | VL | 43 | M | M | H | L | M | |
| 3 | L | L | L | H | L | 44 | M | M | H | M | H | |
| 4 | L | L | M | L | L | 45 | M | M | H | H | H | |
| 5 | L | L | M | M | L | 46 | M | H | L | L | L | |
| 6 | L | L | M | H | VL | 47 | M | H | L | M | L | |
| 7 | L | L | H | L | VL | 48 | M | H | L | H | L | |
| 8 | L | L | H | M | L | 49 | M | H | M | L | VL | |
| 9 | L | L | H | H | L | 50 | M | H | M | M | L | |
| 10 | L | M | L | L | VL | 51 | M | H | M | H | M | |
| 11 | L | M | L | M | VL | 52 | M | H | H | L | M | |
| 12 | L | M | L | H | L | 53 | M | H | H | M | H | |
| 13 | L | M | M | L | VL | 54 | M | H | H | H | VH | |
| 14 | L | M | M | M | L | 55 | H | L | L | L | VL | |
| 15 | L | M | M | H | L | 56 | H | L | L | M | VL | |
| 16 | L | M | H | L | VL | 57 | H | L | L | H | L | |
| 17 | L | M | H | M | L | 58 | H | L | M | L | VL | |
| 18 | L | M | H | H | L | 59 | H | L | M | M | VL | |
| 19 | L | H | L | L | VL | 60 | H | L | M | H | L | |
| 20 | L | H | L | M | VL | 61 | H | L | H | L | VL | |
| 21 | L | H | L | H | L | 62 | H | L | H | M | VL | |
| 22 | L | H | M | L | L | 63 | H | L | H | H | L | |
| 23 | L | H | M | M | L | 64 | H | M | L | L | L | |
| 24 | L | H | M | H | VL | 65 | H | M | L | M | L | |
| 25 | L | H | H | L | VL | 66 | H | M | L | H | M | |
| 26 | L | H | H | M | VL | 67 | H | M | M | L | L | |
| 27 | L | H | H | H | L | 68 | H | M | M | M | L | |
| 28 | M | L | L | L | L | 69 | H | M | M | H | M | |
| 29 | M | L | L | M | M | 70 | H | M | H | L | L | |
| 30 | M | L | L | H | H | 71 | H | M | H | M | M | |
| 31 | M | L | M | L | M | 72 | H | M | H | H | H | |
| 32 | M | L | M | M | M | 73 | H | H | L | L | L | |
| 33 | M | L | M | H | H | 74 | H | H | L | M | L | |
| 34 | M | L | H | L | M | 75 | H | H | L | H | L | |
| 35 | M | L | H | M | H | 76 | H | H | M | L | M | |
| 36 | M | L | H | H | VH | 77 | H | H | M | M | M | |
| 37 | M | M | L | L | L | 78 | H | H | M | H | M | |
| 38 | M | M | L | M | M | 79 | H | H | H | L | M | |
| 39 | M | M | L | H | M | 80 | H | H | H | M | H | |
| 40 | M | M | M | L | M | 81 | H | H | H | H | VH | |
| 41 | M | M | M | M | M |
| Skip | Value |
|---|---|
| 5% | |
| 2.5% | |
| 2 |
| Parameter | Value |
|---|---|
| Deployment field | 100 × 100 m |
| Nodes deployed | 250 |
| Initial energy of nodes | 0.5 J |
| Length of control message | 200 bits |
| Length of data message | 2000 bits |
| Parameter | Value |
|---|---|
| 50 nJ/bit | |
| 5 nJ/bit | |
| 10 pJ/bit/m | |
| 0.0013 pJ/bit/m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuste-Delgado, A.-J.; Cuevas-Martinez, J.-C.; Triviño-Cabrera, A. A Distributed Clustering Algorithm Guided by the Base Station to Extend the Lifetime of Wireless Sensor Networks. Sensors 2020, 20, 2312. https://doi.org/10.3390/s20082312
Yuste-Delgado A-J, Cuevas-Martinez J-C, Triviño-Cabrera A. A Distributed Clustering Algorithm Guided by the Base Station to Extend the Lifetime of Wireless Sensor Networks. Sensors. 2020; 20(8):2312. https://doi.org/10.3390/s20082312
Chicago/Turabian StyleYuste-Delgado, Antonio-Jesus, Juan-Carlos Cuevas-Martinez, and Alicia Triviño-Cabrera. 2020. "A Distributed Clustering Algorithm Guided by the Base Station to Extend the Lifetime of Wireless Sensor Networks" Sensors 20, no. 8: 2312. https://doi.org/10.3390/s20082312
APA StyleYuste-Delgado, A.-J., Cuevas-Martinez, J.-C., & Triviño-Cabrera, A. (2020). A Distributed Clustering Algorithm Guided by the Base Station to Extend the Lifetime of Wireless Sensor Networks. Sensors, 20(8), 2312. https://doi.org/10.3390/s20082312







