Self-Calibration for the Time Difference of Arrival Positioning
Abstract
1. Introduction
2. Related Work
2.1. Localization Systems
2.2. Mathematical Formulation
3. TDOA Localization
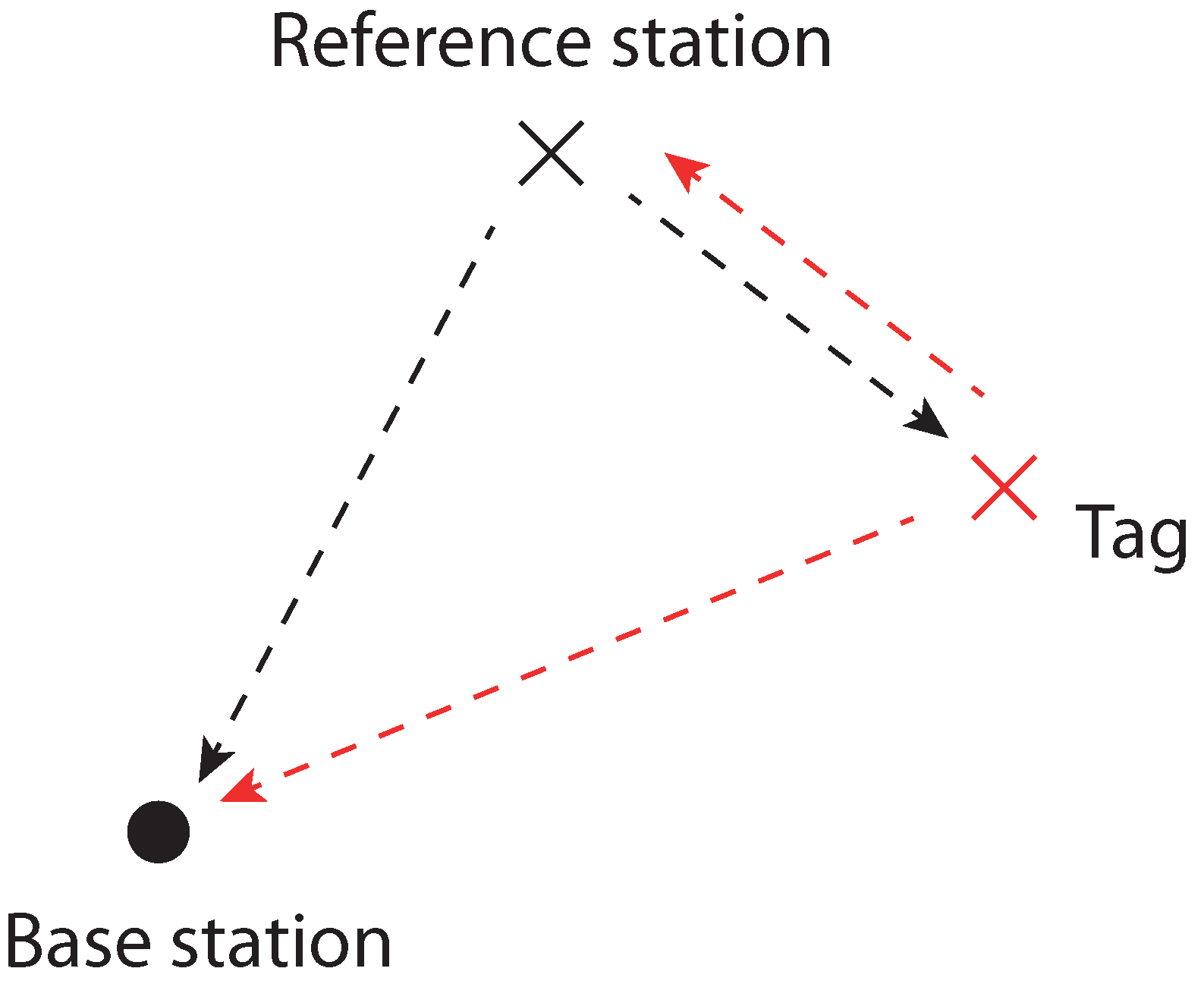
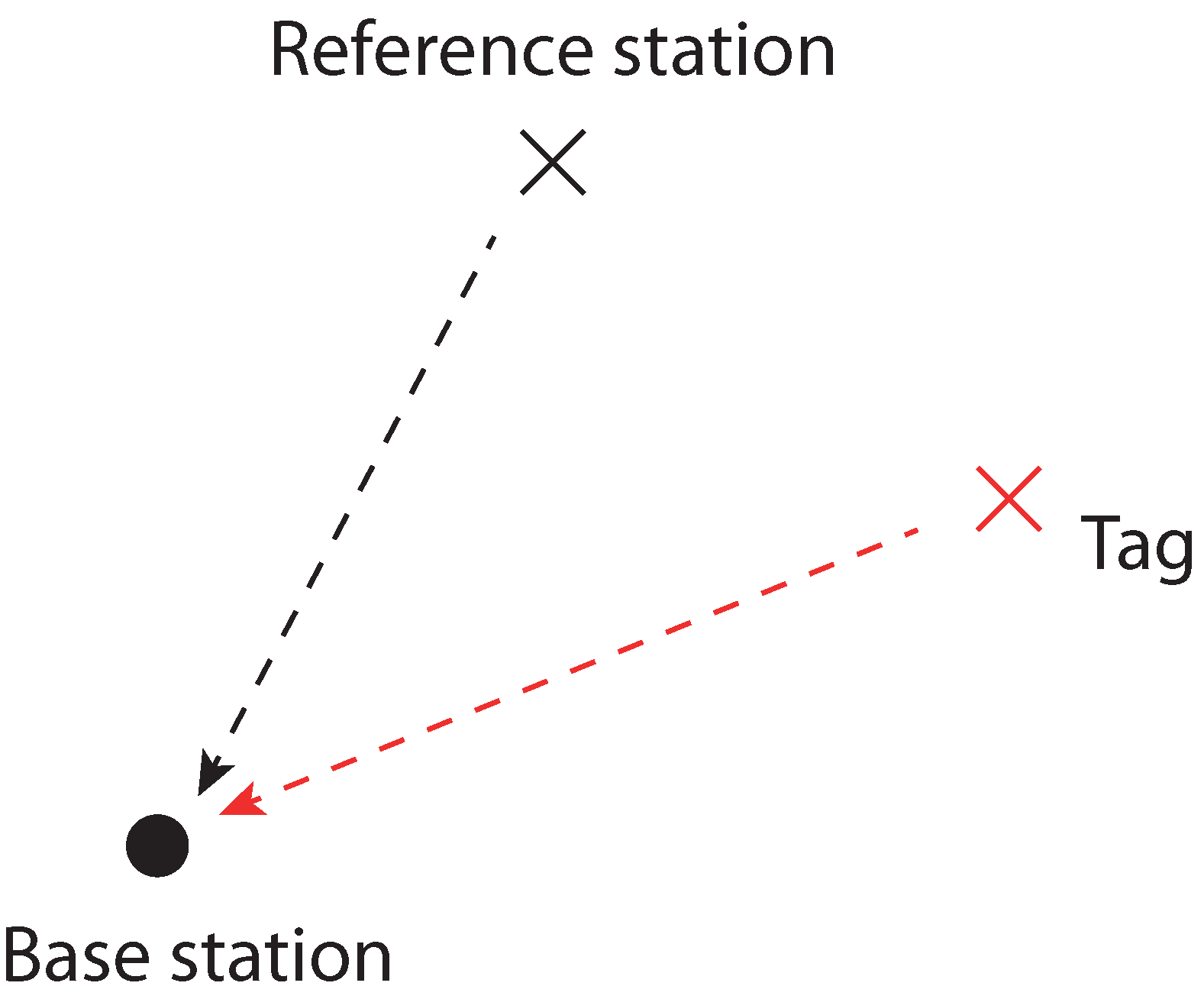
4. TDOA Self-Calibration
4.1. Objective Functions
4.2. Fully-Numerical Method
4.3. Partially-Analytical Method
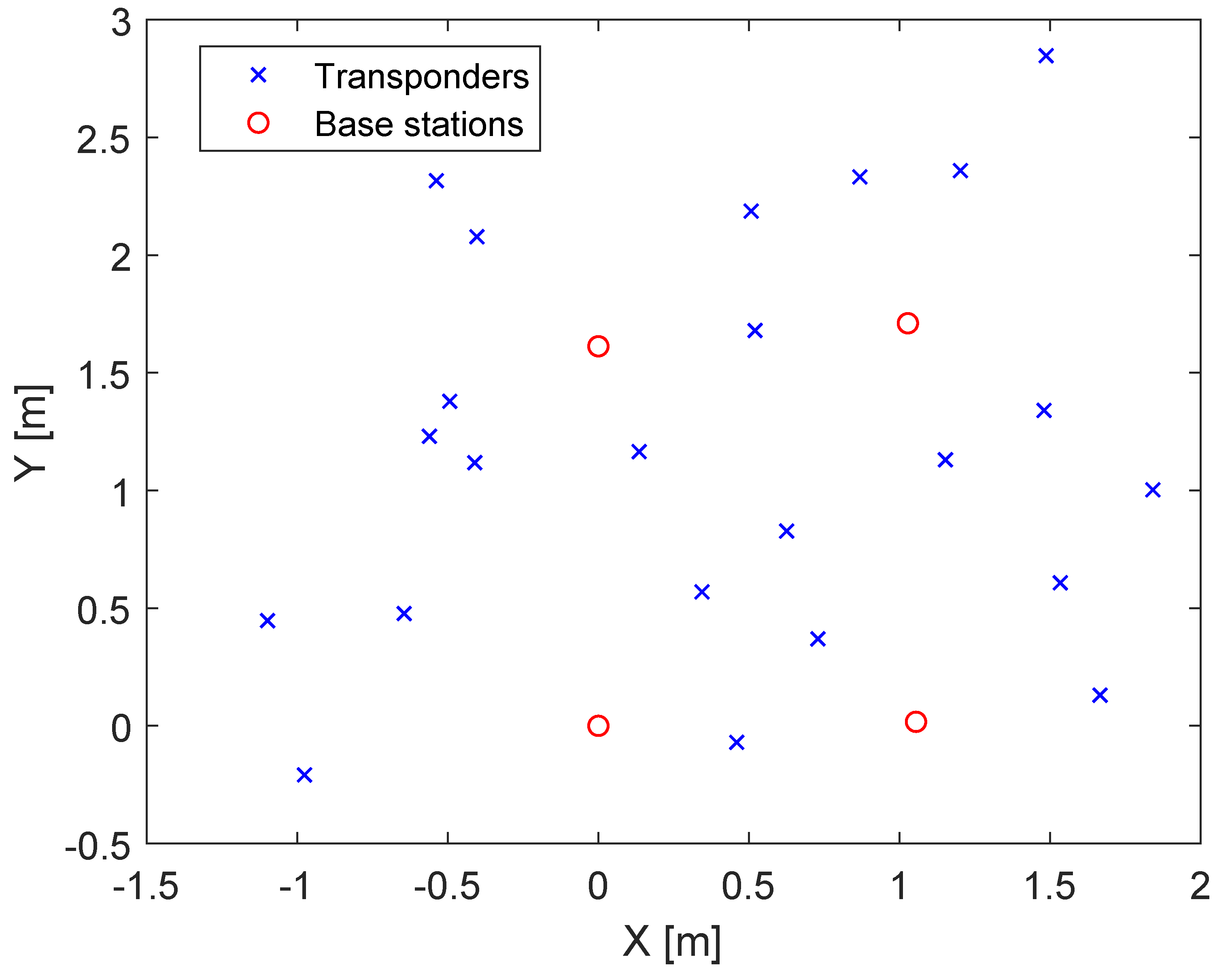
5. TDOA with the Decawave UWB System
5.1. Synthetic Data
5.1.1. Random Geometry
5.1.2. Selected Geometry
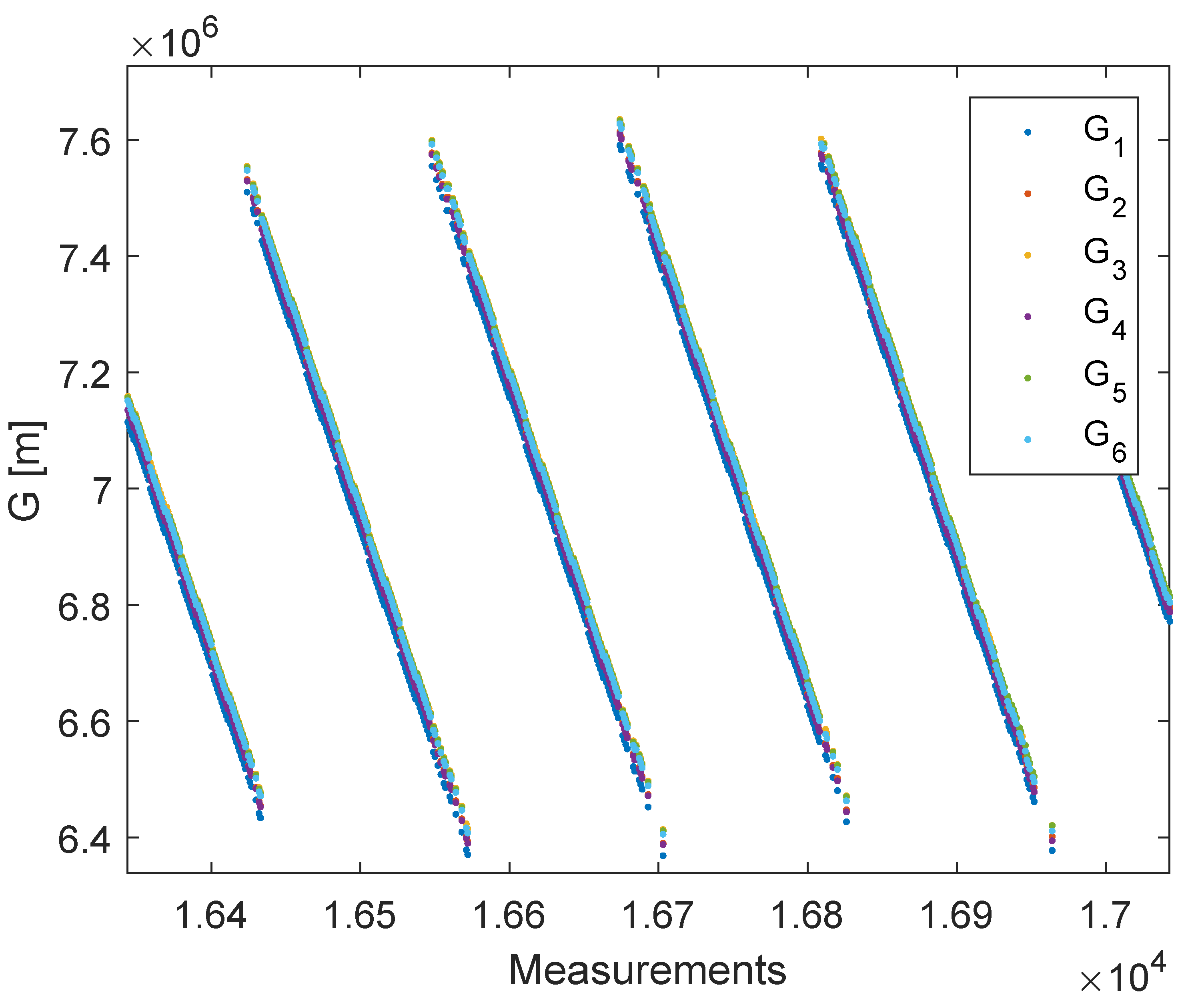
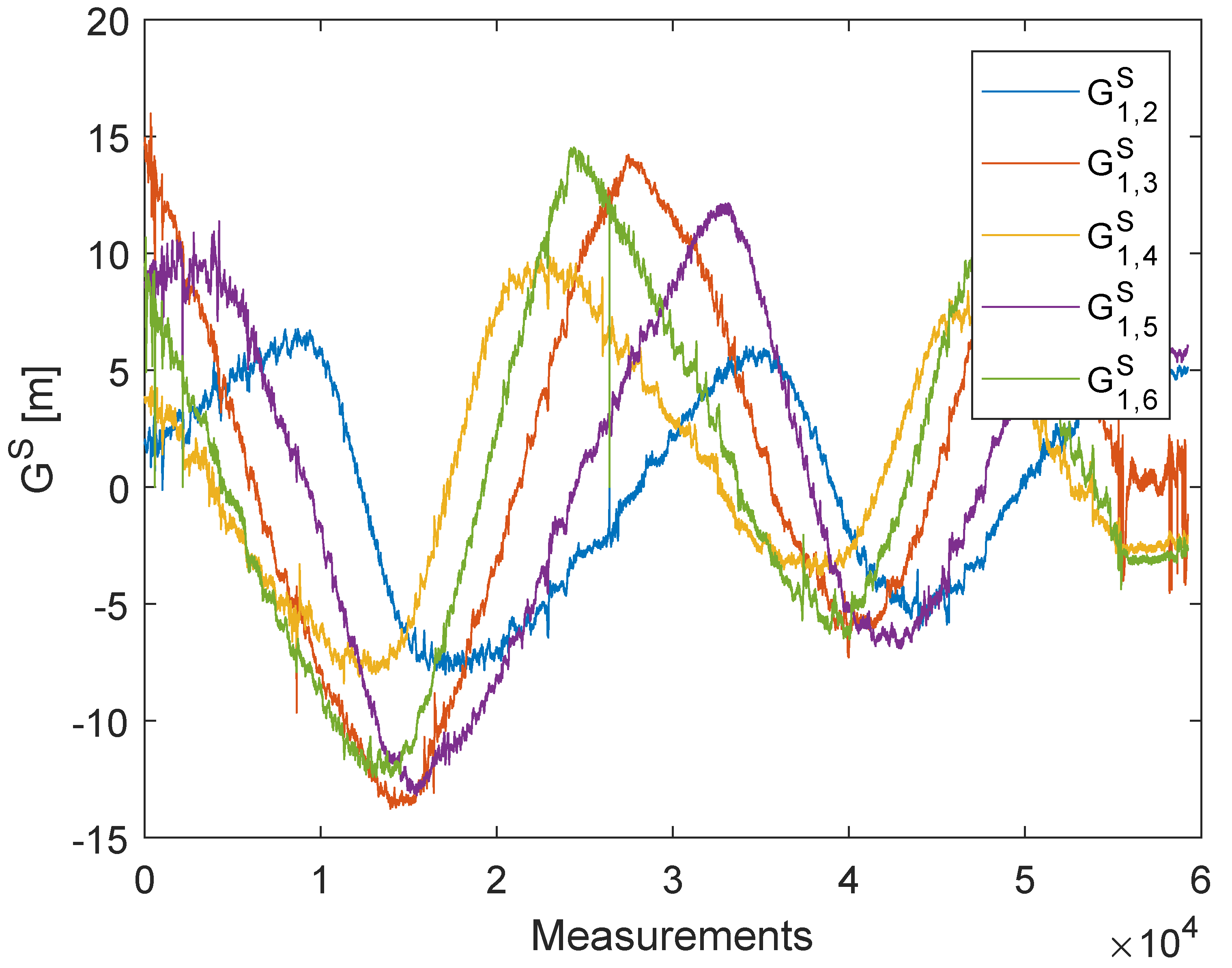
5.2. Real Measurements
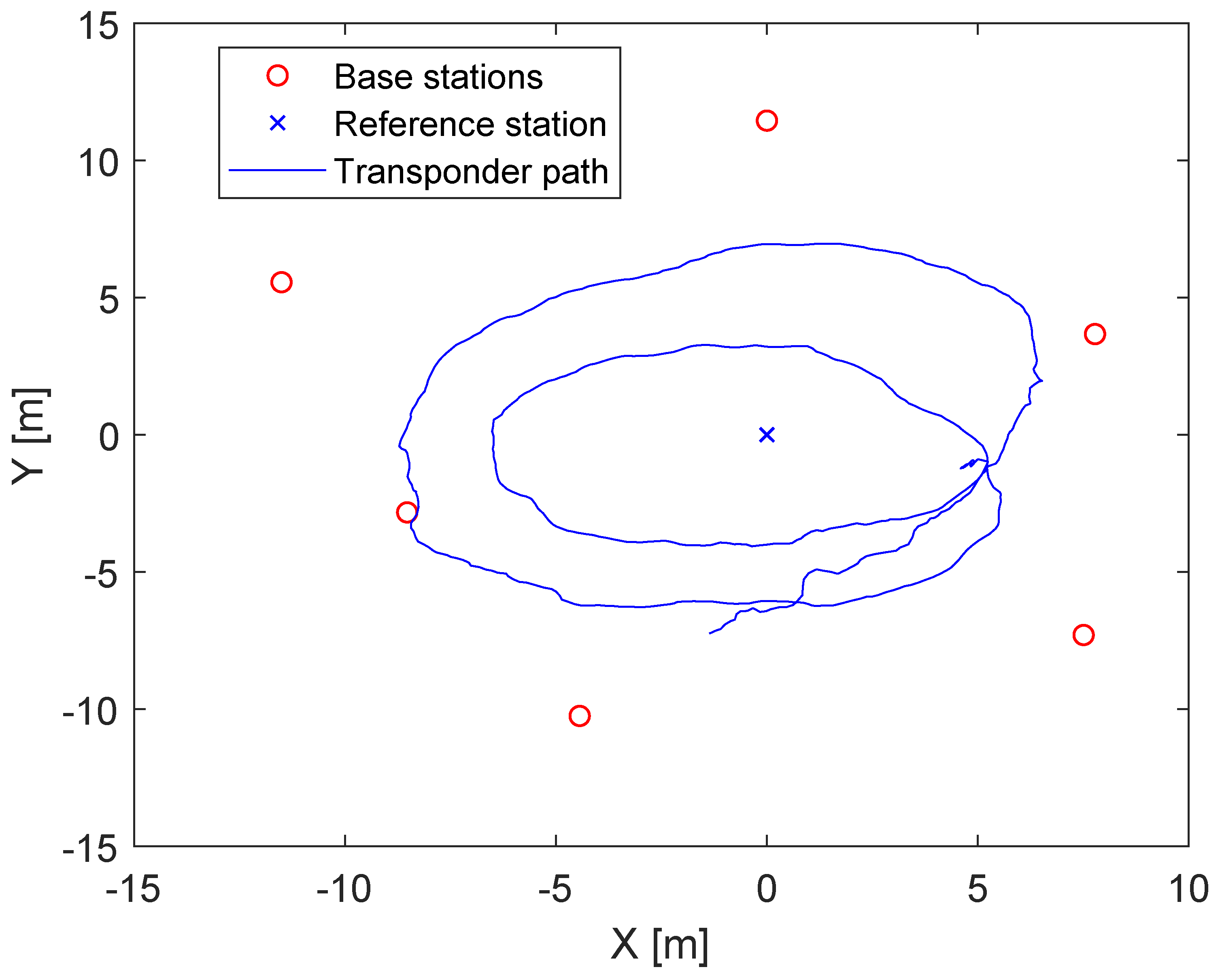
6. TDOA with the Abatec LPM System
6.1. Synthetic Data
6.2. Real Measurements
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kheradpisheh, S.R.; Ghodrati, M.; Ganjtabesh, M.; Masquelier, T. Deep Networks Can Resemble Human Feed-Forward Vision in Invariant Object Recognition. Sci. Rep. 2016, 6, 32672. [Google Scholar] [CrossRef] [PubMed]
- Stewénius, H. Gröbner Basis Methods for Minimal Problems in Computer Vision. Ph.D. Thesis, Centre for Mathematical Sciences, Lund University, Lund, Sweden, 2005. [Google Scholar]
- Batstone, K.; Oskarsson, M.; Åström, K. Robust time-of-arrival selfcalibration with missing data and outliers. In Proceedings of the 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; pp. 2370–2374. [Google Scholar]
- Ono, N.; Kohno, H.; Ito, N.; Sagayama, S. Blind alignment of asynchronously recorded signals for distributed microphone array. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 18–21 October 2009; pp. 161–164. [Google Scholar]
- Wendeberg, J.; Höflinger, F.; Schindelhauer, C.; Reindl, L. Anchor-free TDOA self-localization. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Guimarães, Portugal, 21–23 September 2011; pp. 1–10. [Google Scholar]
- Wendeberg, J.; Höflinger, F.; Schindelhauer, C.; Reindl, L. Calibration-free tdoa self-localisation. J. Locat. Based Serv. 2013, 7, 121–144. [Google Scholar] [CrossRef]
- Jiang, F.; Kuang, Y.; Åström, K. Time delay estimation for TDOA selfcalibration using truncated nuclear norm regularization. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3885–3889. [Google Scholar]
- Kuang, Y.; Åström, K. Stratified sensor network self-calibration from TDOA measurements. In Proceedings of the 21st European Signal Processing Conference (EU-SIPCO 2013), Marrakech, Morocco, 9–13 September 2013; pp. 1–5. [Google Scholar]
- Zou, Y.; Wan, Q.; Liu, H. Semidefinite Programming for Tdoa Localization with Locally Synchronized Anchor Nodes. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 3524–3528. [Google Scholar]
- Mekonnen, Z.W.; Wittneben, A. Self-calibration method for TOA based localization systems with generic synchronization requirement. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 4618–4623. [Google Scholar]
- Biswas, P.; Lian, T.; Wang, T.; Ye, Y. Semidefinite programming based algorithms for sensor network localization. ACM Trans. Sens. Netw. 2006, 2, 188–220. [Google Scholar] [CrossRef]
- Le, T.; Ono, N. Closed-form solution for TDOA-based joint source and sensor localization in two-dimensional space. In Proceedings of the 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 28 August–2 September 2016; pp. 1373–1377. [Google Scholar]
- Kuang, Y.; Burgess, S.; Torstensson, A.; Åström, K. A complete characterization and solution to the microphone position self-calibration problem. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3875–3879. [Google Scholar]
- Le, T.; Ono, N. Closed-Form and Near Closed-Form Solutions for TOA-Based Joint Source and Sensor Localization. IEEE Trans. Signal Process. 2016, 64, 4751–4766. [Google Scholar] [CrossRef]
- Crocco, M.; Del Bue, A.; Bustreo, M.; Murino, V. A closed form solution to the microphone position self-calibration problem. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2597–2600. [Google Scholar]
- Wang, L.; Hon, T.-K.; Reiss, J.D.; Cavallaro, A. Self-localization of ad-hoc arrays using time difference of arrivals. IEEE Trans. Signal Process. 2015, 64, 1018–1033. [Google Scholar] [CrossRef]
- Sidorenko, J.; Schatz, V.; Doktorski, L.; Scherer-Negenborn, N.; Arens, M.; Hugentobler, U. Improved time of arrival measurement model for non-convex optimization. Navigation 2019, 66, 117–128. [Google Scholar] [CrossRef]
- Sidorenko, J.; Scherer-Negenborn, N.; Arens, M.; Michaelsen, E. Improved Linear Direct Solution for Asynchronous Radio Network Localization (RNL). In Proceedings of the ION 2017 Pacific PNT Meeting, Honolulu, HI, USA, 1–4 May 2017; pp. 376–382. [Google Scholar]
- Haluza, M.; Vesely, J. Analysis of signals from the decawave trek1000 wideband positioning system using akrs system. In Proceedings of the International Conference on Military Technologies (ICMT), Brno, Czech Republic, 31 May–2 June 2017; pp. 424–429. [Google Scholar]
- Zwick, T.; Wiesbeck, W.; Timmermann, J.; Adamiuk, G. Ultra-Wideband RF System Engineering (EuMA High Frequency Technologies Series; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Sidorenko, J.; Schatz, V.; Scherer-Negenborn, N.; Arens, M.; Hugentobler, U. Improved time of arrival measurement model for non-convex optimization with noisy data. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 Sepember 2018; pp. 206–212. [Google Scholar]
- Resch, A.; Pfeil, R.; Wegener, M.; Stelzer, A. Review of the LPM local positioning measurement system. In Proceedings of the International Conference on Localization and GNSS (ICL-GNSS), Starnberg, Germany, 25–27 June 2012; pp. 1–5. [Google Scholar]
- Pourvoyeur, K.; Stelzer, A.; Fischer, A.; Gassenbauer, G. Adaptation of a 3-D local position measurement system for 1-D applications. In Proceedings of the Radar Conference EURAD, Paris, France, 3–4 October 2005; pp. 343–346. [Google Scholar]
- Pfeil, R.; Pourvoyeur, K.; Stelzer, A.; Stelzhammer, G. Distributed fault detection for precise and robust local positioning. In Proceedings of the 13th IAIN World Congress and Exhibition, Stockholm, Sweden, 27–30 October 2009. [Google Scholar]
- Pourvoyeur, K.; Stelzer, A.; Gahleitner, T.; Schuster, S.; Gassenbauer, G. Effects of motion models and sensor data on the accuracy of the LPM positioning system. In Proceedings of the 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–7. [Google Scholar]
- Pourvoyeur, K.; Stelzer, A.; Gassenbauer, G. Position estimation techniques for the local position measurement system LPM. In Proceedings of the Microwave Conference APMC, Yokohama, Japan, 12–15 December 2006; pp. 1509–1514. [Google Scholar]
- Stelzer, A.; Pourvoyeur, K.; Fischer, A. Concept and application of lpm- a novel 3-d local position measurement system. IEEE Trans. Microw. Theory Tech. 2004, 52, 2664–2669. [Google Scholar] [CrossRef]
- Pfeil, R.; Schuster, S.; Scherz, P.; Stelzer, A.; Stelzhammer, G. A robust position estimation algorithm for a local positioning measurement system. In Proceedings of the IEEE MTT-S International Microwave Workshop in Local Positioning and RFID, IMWS2009, Cavtat, Croatia, 24–25 September 2009; pp. 1–4. [Google Scholar]
- Güvenc, I.; Sahinoglu, Z.; Gezici, S. Ultra-Wideband Positioning Systems Theoretical Limits, Ranging Algorithms, and Protocols; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Zhu, W.; Sun, W.; Wang, Y.; Liu, S.; Xu, K. An improved ransac algorithm based on similar structure constraints. In Proceedings of the International Conference on Robots Intelligent System (ICRIS), Zhangjiajie, China, 27–28 August 2016; pp. 94–98. [Google Scholar]

| Notations | Definition |
|---|---|
| Base stations, | |
| D | Number of dimensions |
| N | Number of base stations |
| M | Number of independent measurements |
| Number of equations/number of unknowns | |
| Tags, |
| Notations | Definition | Status |
|---|---|---|
| b | Position of base station | Unknown |
| t | Position of transponder | Unknown |
| Distance measurements between and | Known | |
| Local Position Measurement (LPM) time offset | Unknown | |
| Additional dimension of | Unknown | |
| Additional dimension of | Unknown | |
| r | Distance between the base and reference station | Unknown |
| False Result Rate (%) | UWB | LPM with Offset | LPM (Subtracted) |
|---|---|---|---|
| General TDOA | 13.19 | 6.99 | 9.88 |
| Lifted TDOA | 0 | 0.10 | 0.08 |
| UWB | LPM | |
|---|---|---|
| Fully-Numerical | ||
| Partially-Analytical |
| , | , | , | , | |
|---|---|---|---|---|
| Ratio : fully-numerical | 1.14 | 1.07 | 1.30 | 1.41 |
| Ratio : partially-analytical | 7.6 | 3 | 6 | 9 |
| False results: fully-numerical (%) | 70.91 | 51.09 | 57.61 | 61.44 |
| False results: partially-analytical (%) | 48.75 | 55.97 | 55.41 | 55.76 |
| False results: lifted fully-numerical (%) | 7.71 | 5.46 | 2.73 | 2.03 |
| False results: lifted partially-analytical (%) | 8.13 | 11.68 | 10.28 | 10.64 |
| Station ID | X (m) | Y (m) | Z (m) |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1.613 | 0 |
| 3 | 1.028 | 1.710 | 0 |
| 4 | 1.055 | 0.017 | 0 |
| , | |
|---|---|
| Ratio : fully-numerical | 1.14 |
| Ratio : partially-analytical | 7.6 |
| False results: fully-numerical (%) | 51.28 |
| False results: partially-analytical (%) | 55.41 |
| False results: lifted fully-numerical (%) | 20.90 |
| False results: lifted partially-analytical (%) | 99.92 |
| , | |
|---|---|
| Ratio : fully-numerical | 1.14 |
| Ratio : partially-analytical | 7.6 |
| False results: fully-numerical (%) | 33.37 |
| False results: partially-analytical (%) | 54.47 |
| False results: lifted fully-numerical (%) | 6.91 |
| False results: lifted partially-analytical (%) | 0.45 |
| , | , | , | , | , | |
|---|---|---|---|---|---|
| Ratio : fully-numerical | 1.08 | 1.14 | 1.1 | 1.28 | 1.34 |
| Ratio : partially-analytical | 8.3 | 12.5 | 12.86 | 8.57 | 12.86 |
| False results: fully-numerical (%) | 83.30 | 88.06 | 63.51 | 74.34 | 81.32 |
| False results: partially-analytical (%) | 88.70 | 89.82 | 74.35 | 77.61 | 79.59 |
| False results: lifted fully-numerical (%) | 57.43 | 60.89 | 32.06 | 33.22 | 39.43 |
| False results: lifted partially-analytical (%) | 85.62 | 86.63 | 43.28 | 38.10 | 38.72 |
| , | , | , | , | , | |
|---|---|---|---|---|---|
| Ratio : fully-numerical | 1.08 | 1.14 | 1.1 | 1.28 | 1.34 |
| Ratio : partially-analytical | 8.3 | 12.5 | 12.86 | 8.57 | 12.86 |
| False results: fully-numerical (%) | 78.81 | 84.61 | 58.43 | 66.83 | 74.92 |
| False results: partially-analytical (%) | 84.57 | 86.08 | 68.85 | 71.80 | 74.95 |
| False results: lifted fully-numerical (%) | 55.84 | 60.31 | 31.99 | 33.14 | 40.55 |
| False results: lifted partially-analytical (%) | 82.78 | 83.30 | 37.78 | 31.01 | 30.11 |
| , | , | , | |
|---|---|---|---|
| Ratio : fully-numerical | 1.1 | 1.28 | 1.34 |
| Ratio : partially-analytical | 4.29 | 8.57 | 12.86 |
| False results: fully-numerical (%) | 79.49 | 92.21 | 96.41 |
| False results: partially-analytical (%) | 93.17 | 96.47 | 98.73 |
| False results: lifted fully-numerical (%) | 89.30 | 87.12 | 91.13 |
| False results: lifted partially-analytical (%) | 99.81 | 99.98 | 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidorenko, J.; Schatz, V.; Bulatov, D.; Scherer-Negenborn, N.; Arens, M.; Hugentobler, U. Self-Calibration for the Time Difference of Arrival Positioning. Sensors 2020, 20, 2079. https://doi.org/10.3390/s20072079
Sidorenko J, Schatz V, Bulatov D, Scherer-Negenborn N, Arens M, Hugentobler U. Self-Calibration for the Time Difference of Arrival Positioning. Sensors. 2020; 20(7):2079. https://doi.org/10.3390/s20072079
Chicago/Turabian StyleSidorenko, Juri, Volker Schatz, Dimitri Bulatov, Norbert Scherer-Negenborn, Michael Arens, and Urs Hugentobler. 2020. "Self-Calibration for the Time Difference of Arrival Positioning" Sensors 20, no. 7: 2079. https://doi.org/10.3390/s20072079
APA StyleSidorenko, J., Schatz, V., Bulatov, D., Scherer-Negenborn, N., Arens, M., & Hugentobler, U. (2020). Self-Calibration for the Time Difference of Arrival Positioning. Sensors, 20(7), 2079. https://doi.org/10.3390/s20072079






