An Effective Simulation Analysis of Transient Electromagnetic Multiple Faults
Abstract
1. Introduction
- (1)
- We propose an analysis model on lightweight Midori that can be used to analyze most of the random multiple fault attacks. We increase the number of analysis faults from one to six. The random multiple fault attack model can effectively analyze complex fault attacks.
- (2)
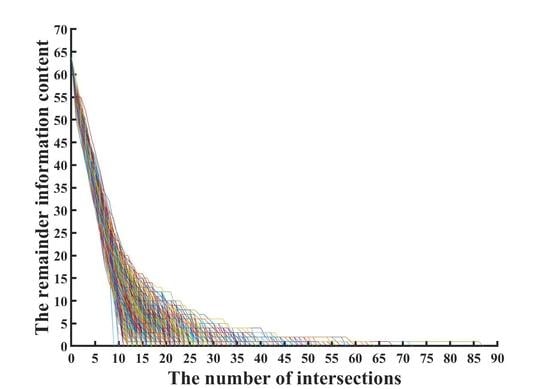
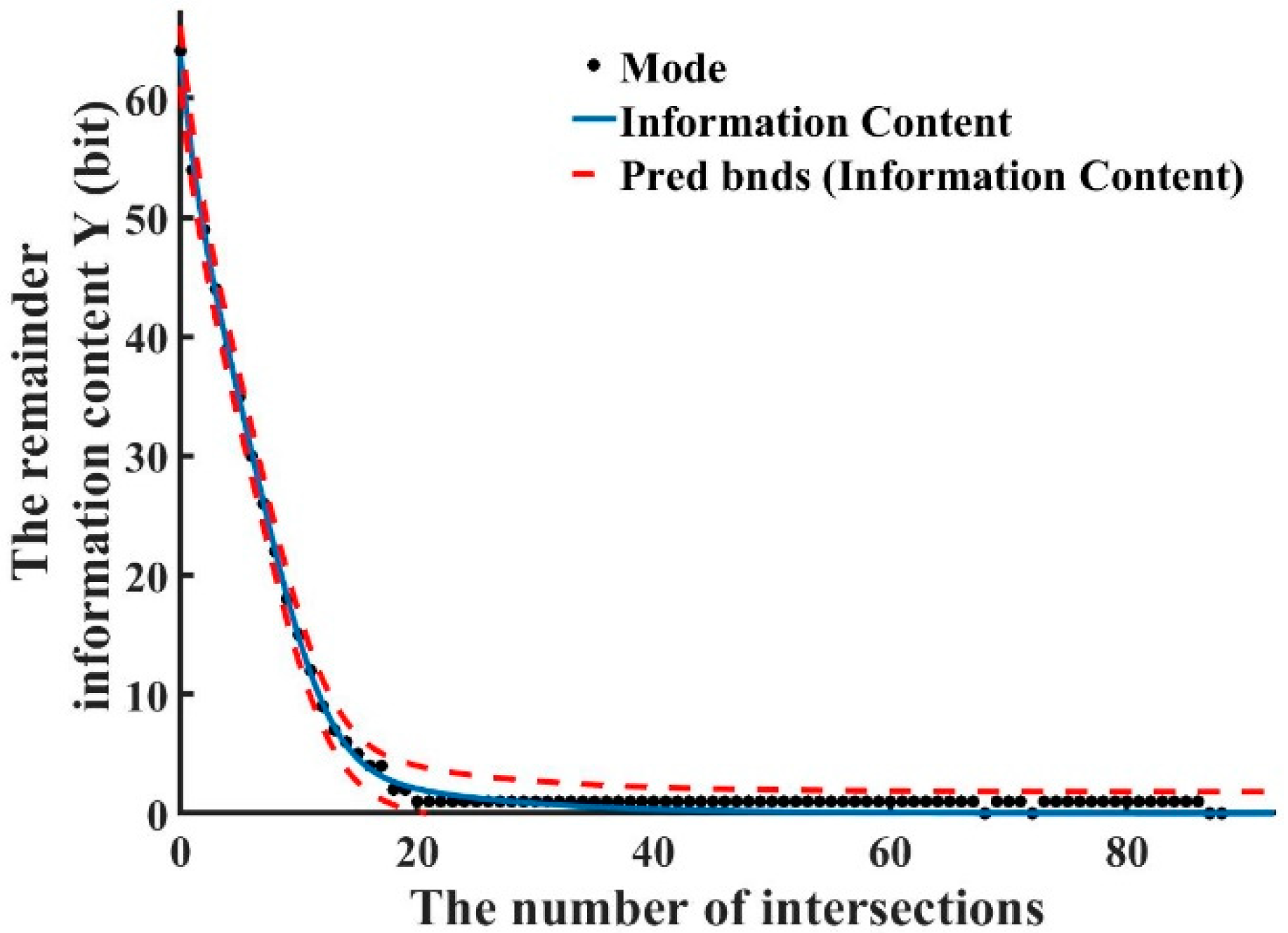
- Through experimental simulation analysis, a linear function relationship between the number of fault attacks and the remaining key information content is obtained.
- (3)
- The ciphertext-only fault attack is the attack method with the least known information. In this paper, the secret key is obtained by combining the impossible attack and the differential fault attack. Using the secret key invariant subspace, the secret key can be obtained by intersection of the subspace.
2. Specifications of Midori and Symbol Description
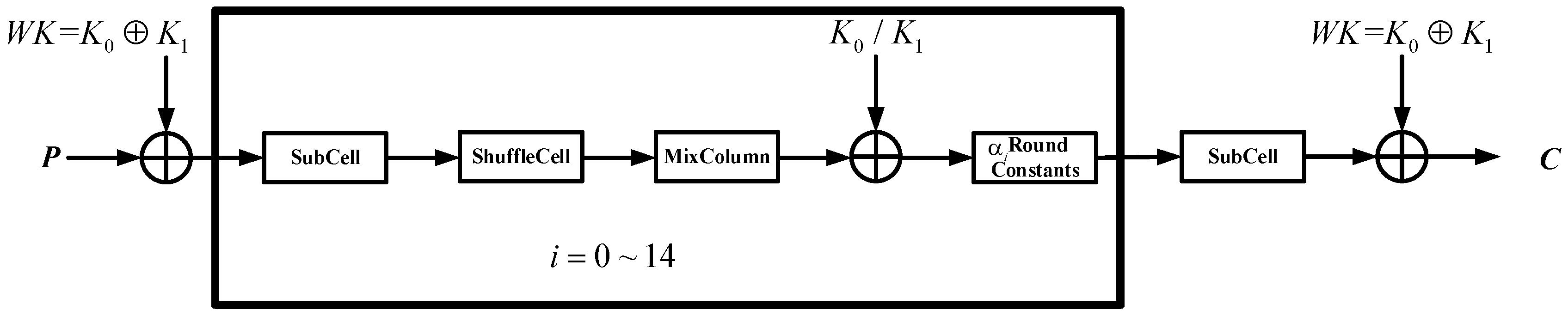
2.1. Midori
- (1)
- The KeyAdd operation uses the XOR operator with the key. The key of the first round and the last round is the key whitening operation. From the 2nd to the 15th round, and alternately XORed with the round function in the cryptosystem.
- (2)
- SubCell transform is the only non-linear operation. SubCell operation minimizes the bit flip between input and output. Forward and inverse S-boxes are the same mathematical form.
- (3)
- ShuffleCell rearranges the cell position in a fixed order.
- (4)
- The MixColumn and inverse MixColumn operations are multiplied by the following matrix:
- (5)
- Round Constants operation is XORed by the form of 4 × 4 binary matrices.
2.2. Symbol Description
3. Random Multi-Fault Attack Model
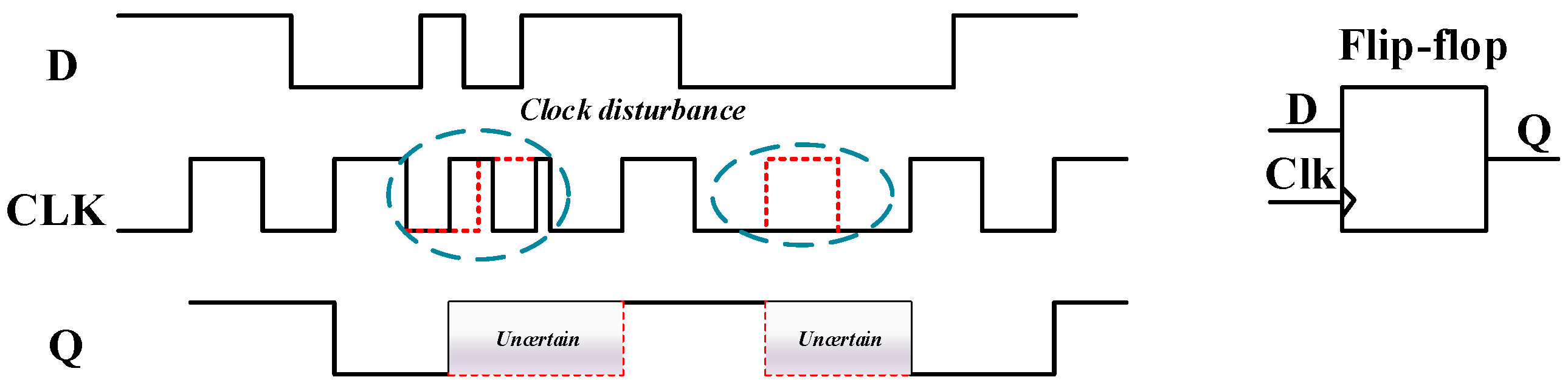
3.1. Fault Attacks Hypothesis
3.2. Analysis of Random Multiple Fault Attack Models
- Problem 1: The location of no faults in each column of , and is unknown. There are four positions in a column. We estimate all four fault positions as fault-free, and then take the union of the estimated invariant space in the column.
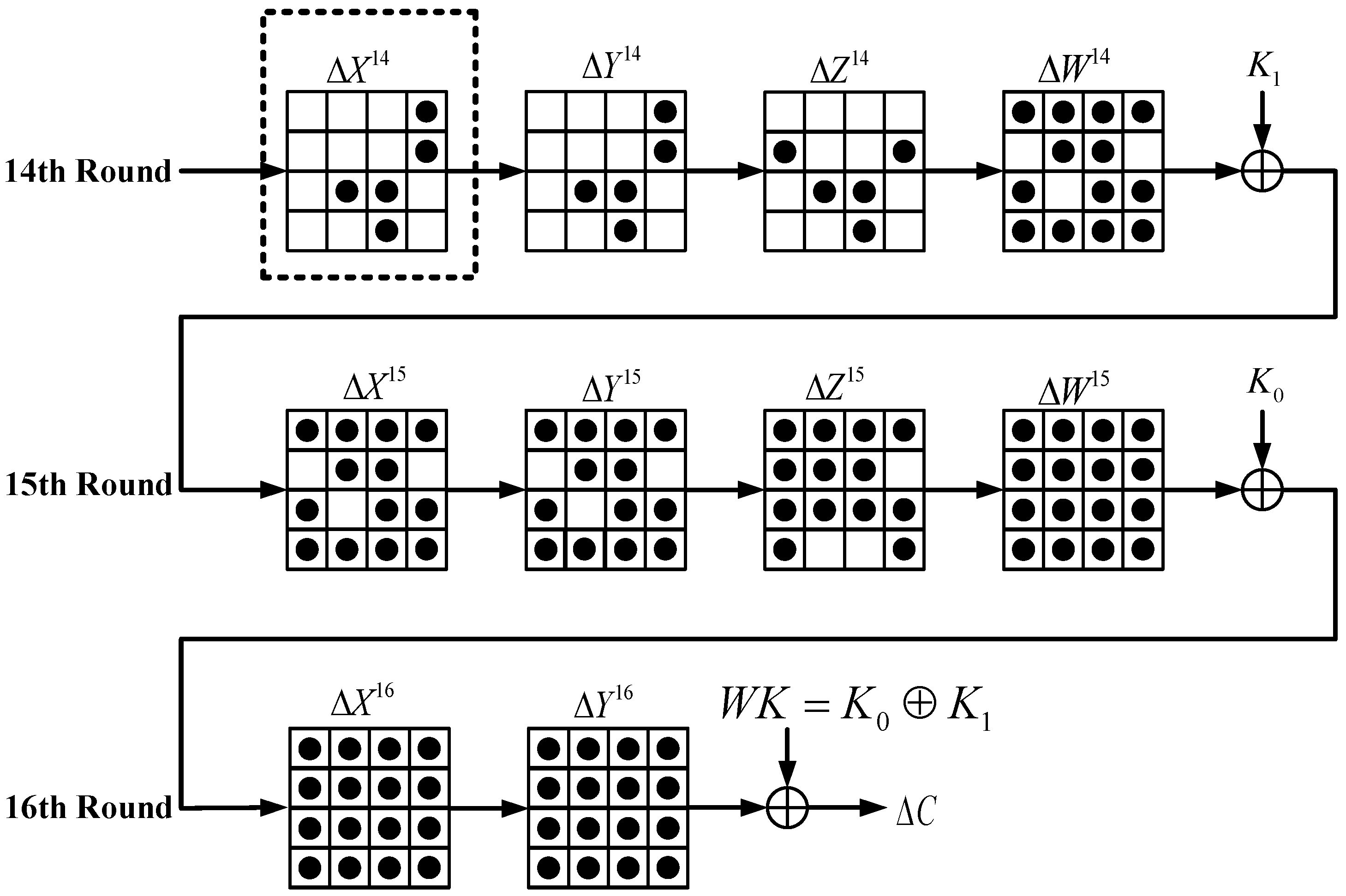
- Problem 2: As the location and number of each fault injection are unknown, there may be 0–4 faults in a certain column of . After injecting random multiple faults two or three times into the cryptosystem, an adversary takes a fault-free union at each position of . It is possible that the number of faults in a column is four. If the adversary predicts this column as fault-free, an error will occur. To avoid mistakes, the adversary can inject faults two or three times into the cryptosystem. In other words, the adversary avoids mistakes by taking the unions multiple times. We provide a detailed explanation using the following differential fault attack equations.
4. Analysis of Fault Difference Equations
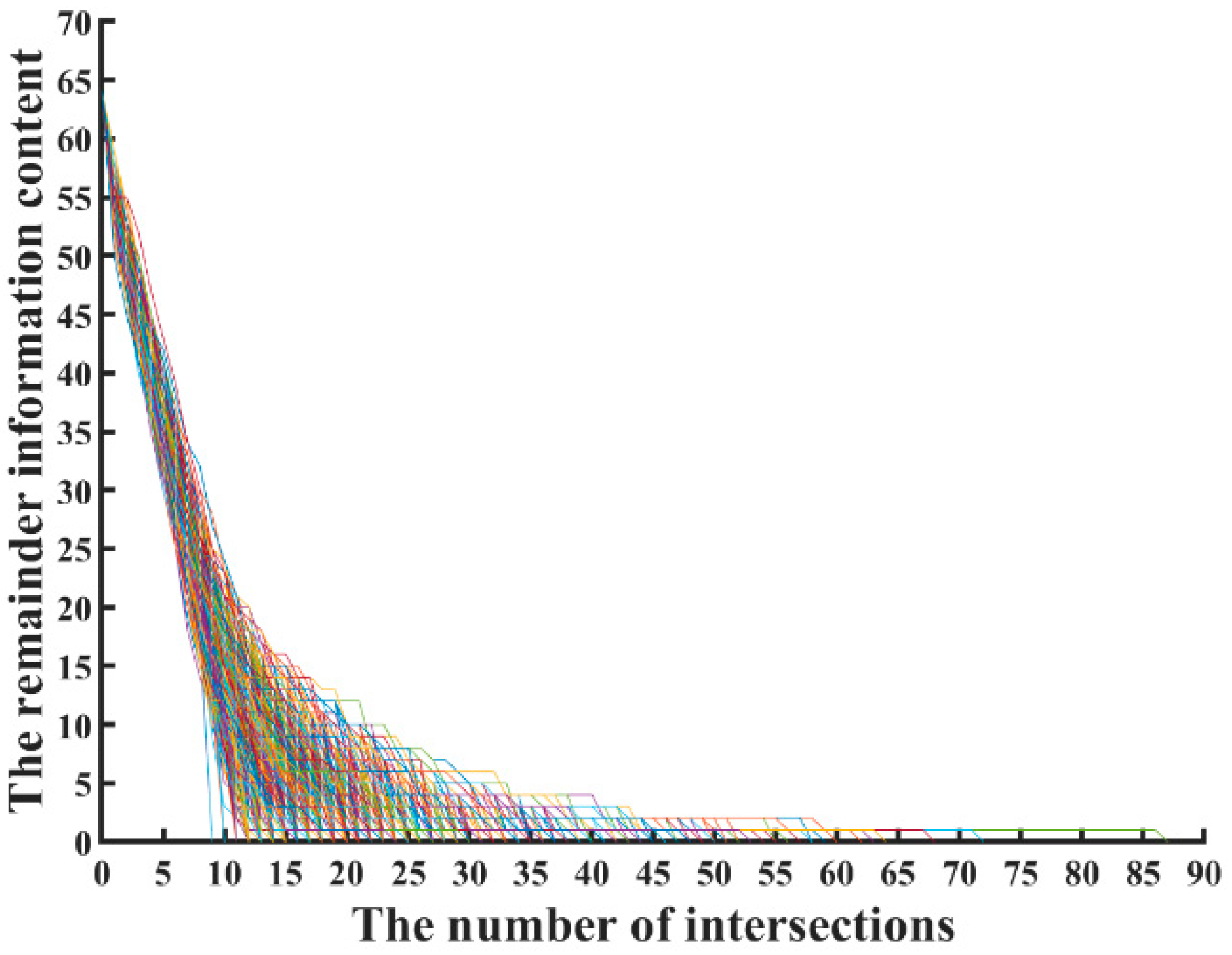
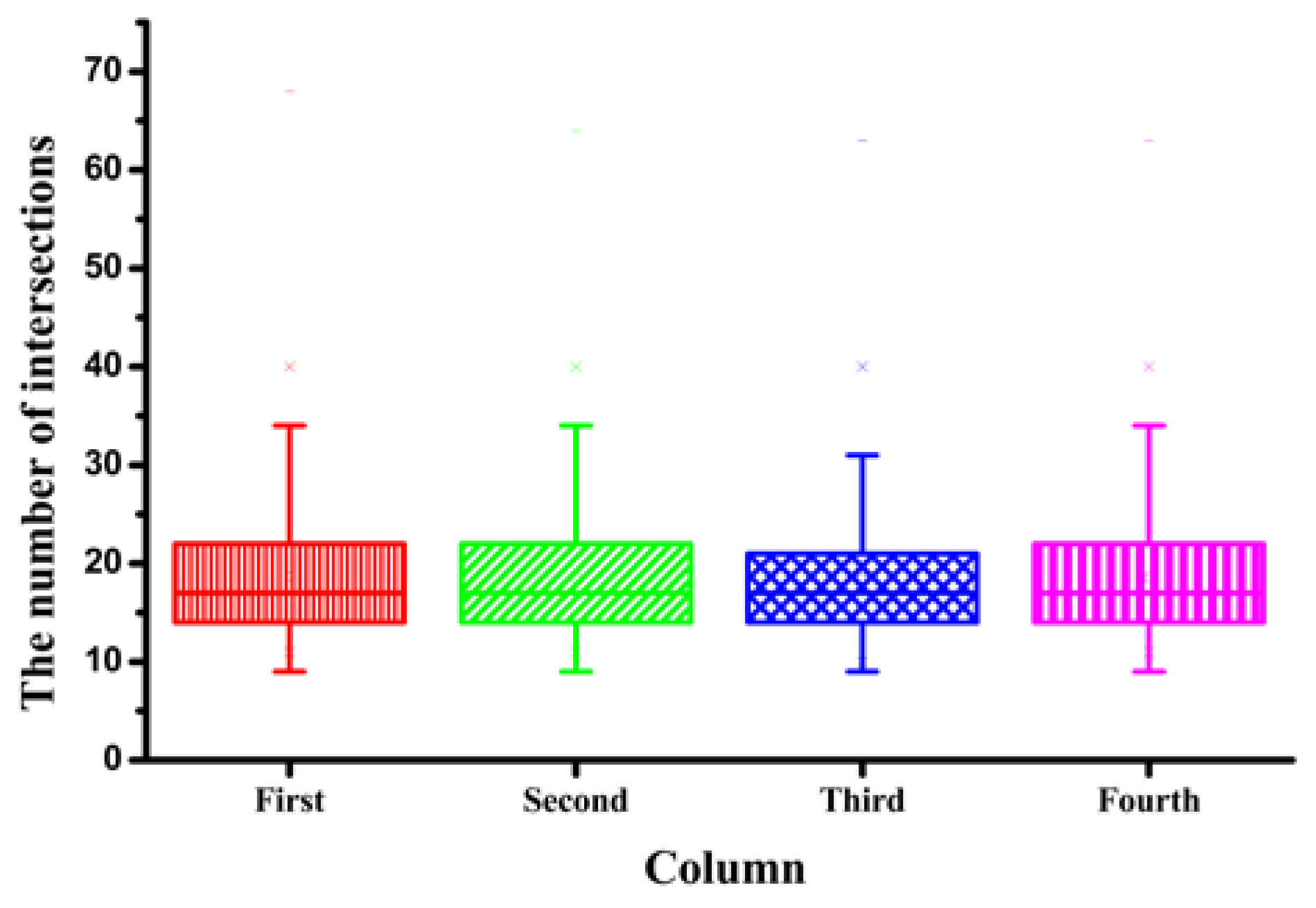
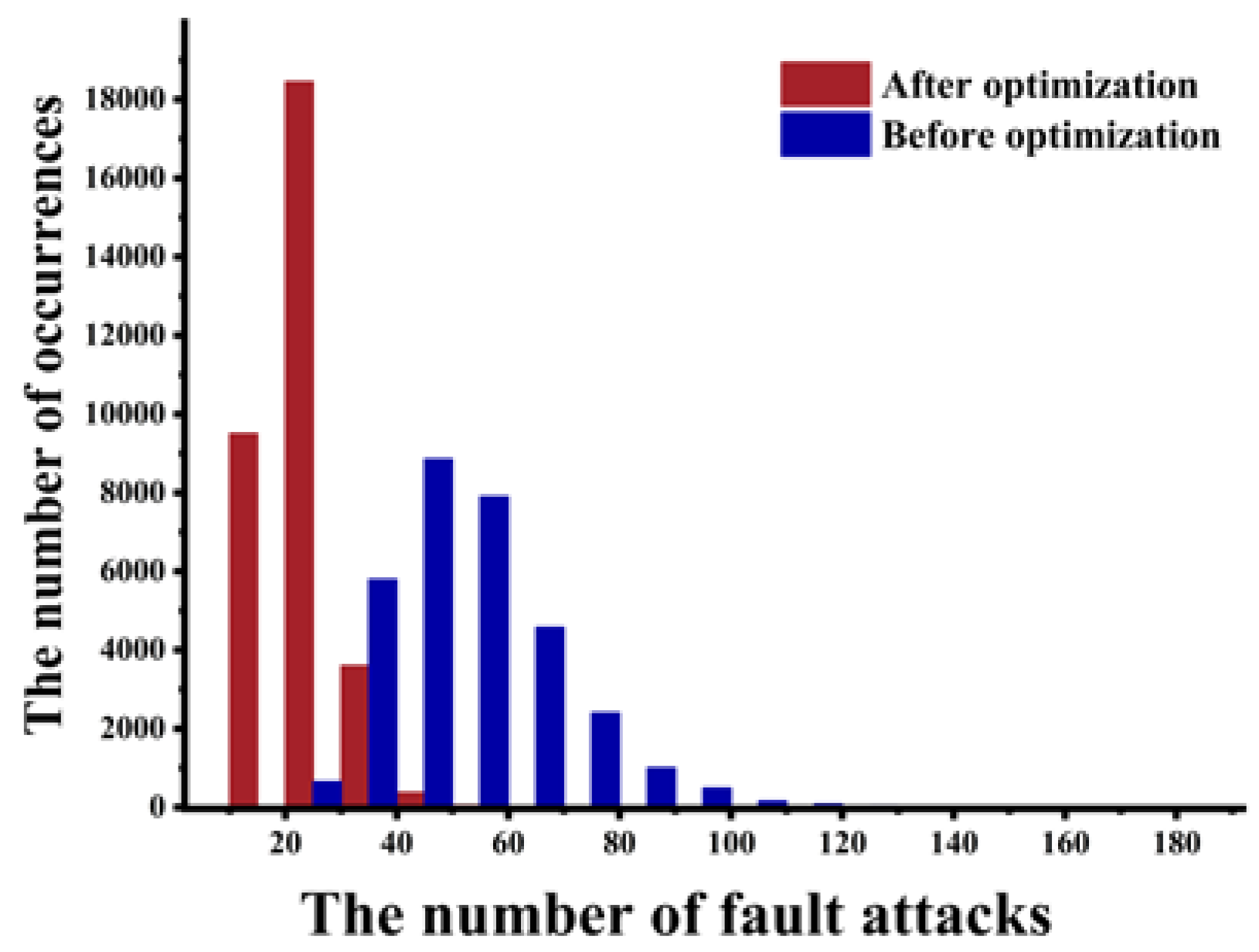
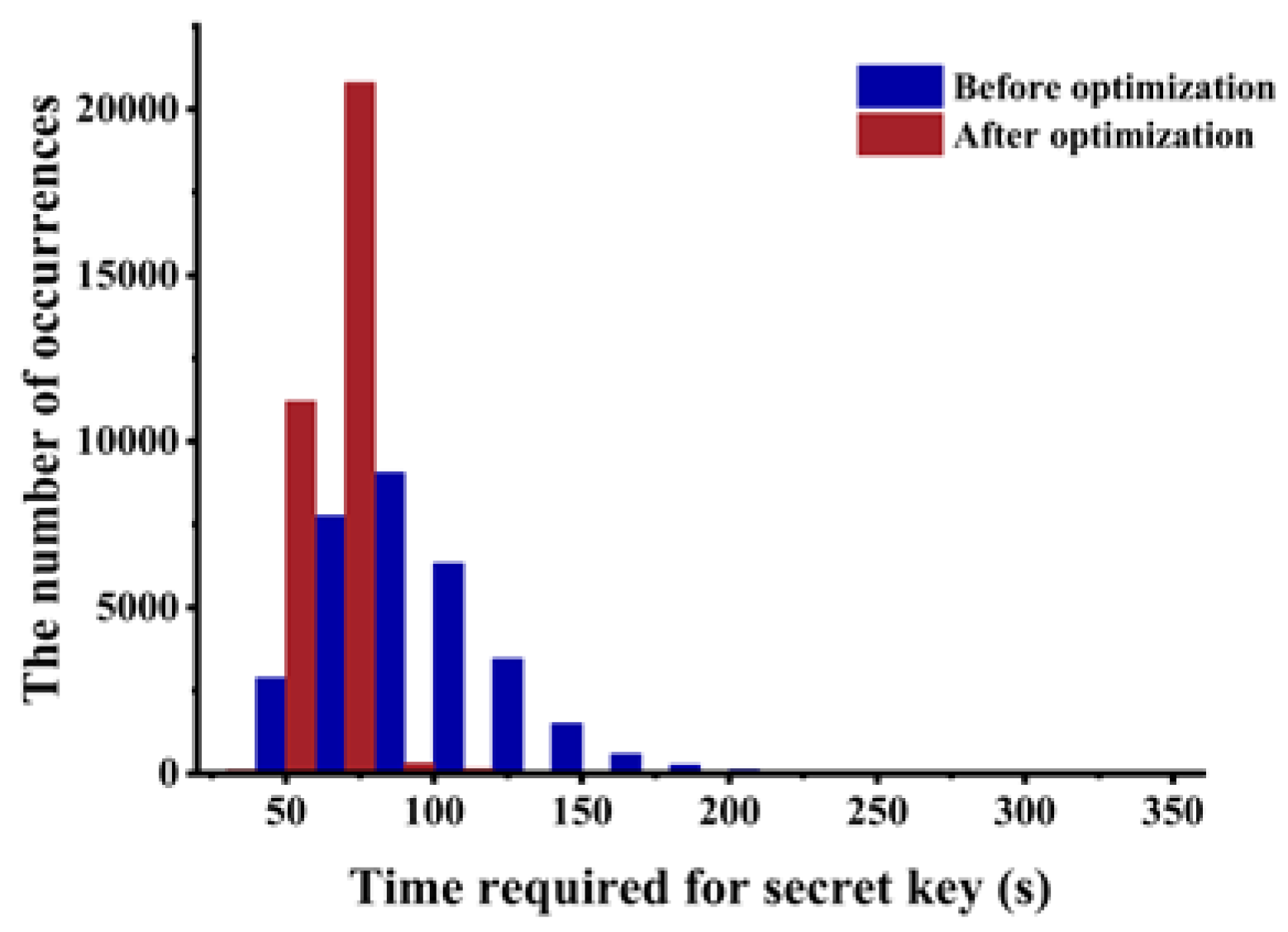
5. Experimental Analysis and Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jean-Jacques, Q.; David, S. Simple electromagnetic analysis for smart cards: New results. In Proceedings of the Crypto 2000, Santa Barbara, CA, USA, 20–24 August 2000. [Google Scholar]
- Ding, G.L.; Chu, J.; Yuan, L.; Zhao, Q. Correlation Electromagnetic Analysis for Cryptographic Device. In Proceedings of the Pacific-Asia Conference on Circuits, Communications and Systems, Chengdu, China, 16–17 May 2009. [Google Scholar]
- De Mulder, E.; Ors, S.B.; Preneel, B.; Verbauwhede, I. Differential Electromagnetic Attack on an FPGA Implementation of Elliptic Curve Cryptosystems. In Proceedings of the World Automation Congress, Budapest, Hungary, 24–26 July 2006. [Google Scholar]
- Selmke, B.; Brummer, S.; Heyszl, J.; Sigl, G. Precise Laser Fault Injections into 90 nm and 45 nm SRAM-cells. In Proceedings of the Smart Card Research and Advanced Application (CARDIS 2015), Bochum, Germany, 4–6 November 2015. [Google Scholar]
- Van Woudenberg, J.G.J.; Witteman, M.F.; Menarini, F. Practical Optical Fault Injection on Secure Microcontrollers. In Proceedings of the Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC 2011), Nara, Japan, 28 September 2011. [Google Scholar]
- Dutertre, J.M.; Beroulle, V.; Candelier, P.; De Castro, S.; Faber, L.B.; Flottes, M.L.; Philippe, G.; David, H.; Regis, L.; Paolo, M.; et al. Laser Fault Injection at the CMOS 28 nm Technology Node: An Analysis of the Fault Model. In Proceedings of the Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC 2018), Amsterdam, The Netherlands, 13 September 2018. [Google Scholar]
- Dehbaoui, A.; Dutertre, J.M.; Robisson, B.; Orsatelli, P.; Maurine, P.; Tria, A. Injection of Transient Faults Using Electromagnetic Pulses Practical Results on a Cryptographic System. Available online: https://eprint.iacr.org/2012/123.pdf (accessed on 5 March 2012).
- Ordas, S.; Guillaume-Sage, L.; Maurine, P. EM Injection: Fault Model and Locality. In Proceedings of the Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC 2015), St. Malo, France, 13 September 2015. [Google Scholar]
- Boneh, D.; DeMillo, R.A.; Lipton, R.J. On the Importance of Checking Cryptographic Protocols for Faults. In Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques, Konstanz, Germany, 11–15 May 1997. [Google Scholar]
- Li, W.; Zhang, W.; Gu, D.; Cao, Q.; Tao, Z.; Zhou, Z.; Liu, Y.; Liu, Z. Impossible differential fault analysis on the LED lightweight cryptosystem in the vehicular ad–hoc networks. IEEE Trans. Dependable Secur. Comput. 2016, 13, 84–92. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, H.; Wang, X. Cryptanalysis of Midori128 Using Impossible Differential Techniques. In Proceedings of the 12th International Conference, ISPEC 2016, Zhangjiajie, China, 16–18 November 2016. [Google Scholar]
- Shahmirzadi, A.R.; Azimi, S.A.; Salmasizadeh, M.; Mohajeri, J.; Aref, M.R. Impossible differential cryptanalysis of reduced-round midori64 block cipher. ISC Int. J. Inf. Secur. 2018, 10, 3–13. [Google Scholar]
- Zhao, X.; Guo, S.; Zhang, F.; Shi, Z.; Ma, C.; Wang, T. Improving and Evaluating Differential Fault Analysis on LED with Algebraic Techniques. In Proceedings of the Workshop on Fault Diagnosis Tolerance Cryptography (FDTC 2013), Santa Barbara, CA, USA, 20 August 2013. [Google Scholar]
- Li, W.; Rijmen, V.; Tao, Z.; Wang, Q.; Chen, H.; Liu, Y. Impossible meet-in-the-middle fault analysis on the LED lightweight cipher in VANETs. Sci. China Inf. Sci. 2018, 61, 32110. [Google Scholar] [CrossRef]
- Cheng, W.; Zhou, Y.; Sauvage, L. Differential Fault Analysis on Midori. In Proceedings of the Information and Communications Security (ICICS 2016), Singapore, 29 November–2 December 2016. [Google Scholar]
- Korkikian, R.; Pelissier, S.; Naccache, D. Blind Fault Attack Against SPN Ciphers. In Proceedings of the 2014 Workshop on Fault Diagnosis and Tolerance in Cryptography, Busan, South Korea, 23 September 2014. [Google Scholar]
- Li, W.; Gu, D.W.; Xia, X.L.; Zhao, C.; Liu, Z.Q.; Liu, Y.; Wang, Q.J. Single byte differential fault analysis on the LED lightweight cipher in the wireless sensor network. Int. J. Comput. Intell. Syst. 2012, 5, 896–904. [Google Scholar] [CrossRef]
- Vasquez, J.D.C.G.; Borges, F.; Portugal, R.; Lara, P. An Efficient One-Bit Model for Differential Fault Analysis on SIMON Family. In Proceedings of the Workshop on Fault Diagnosis Tolerance Cryptography (FDTC), St. Malo, France, 13 September 2015. [Google Scholar]
- Saha, D.; Mukhopadhyay, D.; Chowdhury, D.R. A Diagonal Fault Attack on the Advanced Encryption Standard. Available online: https://eprint.iacr.org/2009/581.pdf (accessed on 30 November 2009).
- Zhang, F.; Lou, X.; Zhao, X.; Bhasin, S.; He, W.; Ding, R.; Qureshi, S.; Ren, K. Persistent fault analysis on block ciphers. IACR Trans. Cryptol. Hardw. Embed. Syst. 2018, 3, 150–172. [Google Scholar]
- Mendel, F.; Rechberger, C.; Schläffer, M.; Thomsen, S.S. The Rebound Attack: Cryptanalysis of Reduced Whirlpool and Grøstl. In Proceedings of the Fast Software Encryption (FSE), Leuven, Belgium, 22–25 February 2009. [Google Scholar]
- Moro, N.; Dehbaoui, A.; Heydemann, K.; Robisson, B.; Encrenaz, E. Electromagnetic Fault Injection: Towards a Fault Model on a 32-bit Microcontroller. In Proceedings of the Workshop on Fault Diagnosis Tolerance Cryptography (FDTC 2013), Santa Barbara, CA, USA, 20 August 2013. [Google Scholar]
- Gandolfi, K.; Mourtel, C.; Olivier, F. Electromagnetic analysis: Concrete results. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Paris, France, 14–16 May 2001. [Google Scholar]
- Agoyan, M.; Dutertre, J.M.; Mirbaha, A.P.; Naccache, D.; Ribotta, A.L.; Tria, A. Single-Bit DFA Using Multiple-Byte Laser Fault Injection. In Proceedings of the 2010 IEEE International Conference on Technologies for Homeland Security (HST), Waltham, MA, USA, 8–10 November 2010. [Google Scholar]
- Banik, S.; Bogdanov, A.; Isobe, T.; Shibutani, K.; Hiwatari, H.; Akishita, T.; Regazzoni, F. Midori: A Block Cipher for Low Energy. In Proceedings of the Advances in Cryptology—ASIACRYPT 2015, Auckland, New Zealand, 29 November–3 December 2015. [Google Scholar]
- Nozaki, Y.; Yoshikawa, M. Statistical Fault Analysis for a Lightweight Cipher Midori. In Proceedings of the International Conference on Information and Automation (ICIA 2017), Macau, China, 18–20 July 2017. [Google Scholar]
- Todo, Y.; Leander, G.; Sasaki, Y. Nonlinear invariant attack: Practical attack on full scream, iscream, and midori64. J. Crypt. 2019, 32, 1383–1422. [Google Scholar] [CrossRef]
- Knudsen, L. DEAL-A 128-bit cipher. Complexity 1998, 258, 216. [Google Scholar]
- Biham, E.; Shamir, A. Differential Fault Analysis of Secret Key Cryptosystems. In Proceedings of the 17th Annual International Cryptology Conference Advances in Cryptology (CRYPTO 1997), Santa Barbara, CA, USA, 17–21 August 1997. [Google Scholar]
- Jovanovic, P.; Kreuzer, M.; Polian, I. An Algebraic Fault Attack on the LED Block Cipher. Available online: https://eprint.iacr.org/2012/400.pdf (accessed on 17 July 2012).
- Li, W.; Liao, L.; Gu, D.; Cao, S.; Wu, Y.; Li, J.; Zhou, Z.; Guo, Z.; Liu, Y. Ciphertext-only fault analysis on the Midori lightweight cryptosystem. Sci. China Inf. Sci. 2020, 63, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Liao, N.; Cui, X.; Liao, K.; Wang, T.; Yu, D.; Cui, X. Improving DFA attacks on AES with unknown and random faults. Sci. China Inf. Sci. 2017, 60, 210–215. [Google Scholar] [CrossRef]
- Sakiyama, K.; Li, Y.; Iwamoto, M.; Ohta, K. Information-theoretic approach to optimal differential fault analysis. IEEE Trans. Inf. Forensics Secur. 2012, 7, 109–120. [Google Scholar] [CrossRef]


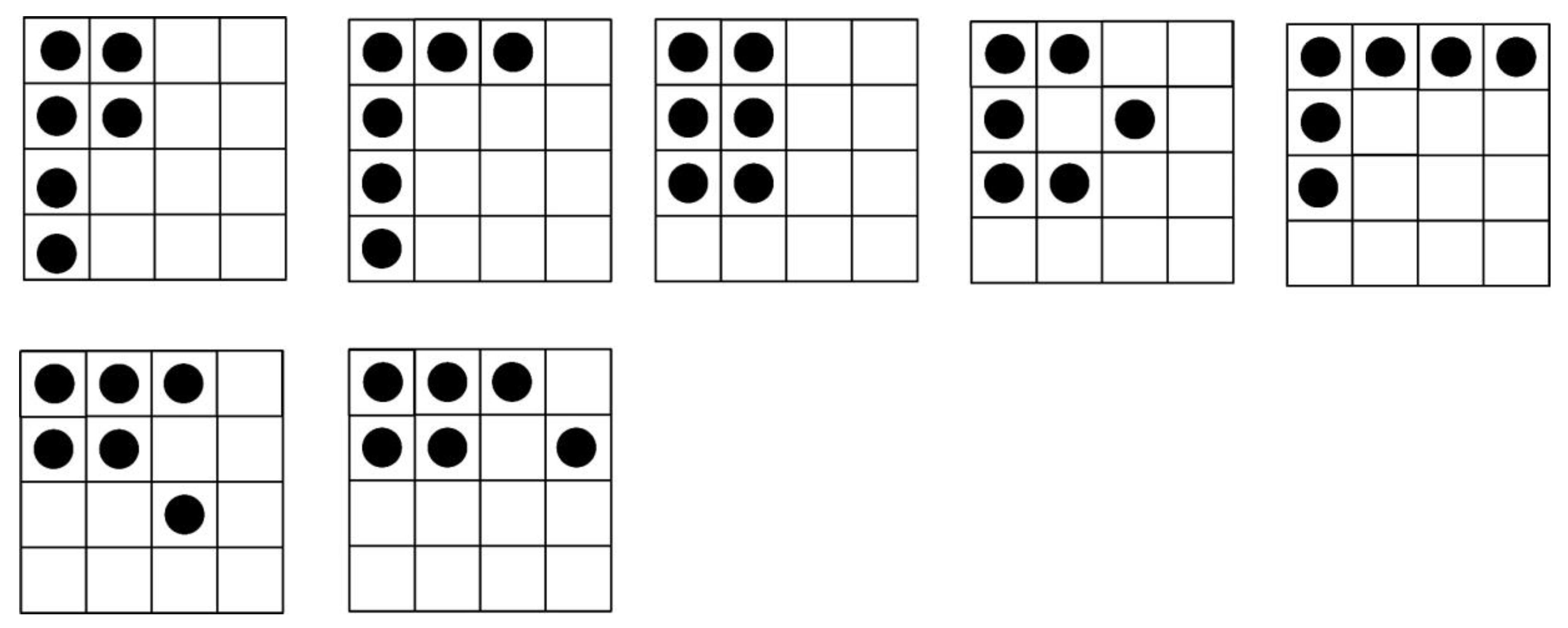
| Reference | Fault Model | Number of Faults | ||||
|---|---|---|---|---|---|---|
| Method | Probability | Round | Value | Distinguish multiple- nibble fault | ||
| [31] | HW | 100% | R = 15 | 1 Nibble | No | 280 |
| [15] | DFA | 80% | R = 14 | 1 Nibble | No | 2 |
| this paper | IDFA | 100% | R = 14 | 1–6 Nibble(s) | Yes | 11 |
| 1 | 1 2 4 5 6 8 14 |
| 2 | 1 4 9 12 |
| 3 | 4 6 7 8 9 13 15 |
| 4 | 1 2 3 4 5 8 11 |
| 5 | 1 4 7 9 10 12 |
| 6 | 1 3 7 8 12 13 15 |
| 7 | 3 5 6 11 13 14 |
| 8 | 1 3 4 6 9 11 12 14 |
| 9 | 2 3 5 8 9 11 12 |
| 10 | 5 10 13 15 |
| 11 | 4 7 8 9 11 13 15 |
| 12 | 5 6 8 9 12 14 |
| 13 | 3 6 7 10 11 14 |
| 14 | 1 7 8 12 13 14 15 |
| 15 | 3 6 10 11 14 15 |
| 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Zhang, H.; Sun, S.; Zhu, L.; Cui, X.; Ghosh, B.K. An Effective Simulation Analysis of Transient Electromagnetic Multiple Faults. Sensors 2020, 20, 1976. https://doi.org/10.3390/s20071976
Dong L, Zhang H, Sun S, Zhu L, Cui X, Ghosh BK. An Effective Simulation Analysis of Transient Electromagnetic Multiple Faults. Sensors. 2020; 20(7):1976. https://doi.org/10.3390/s20071976
Chicago/Turabian StyleDong, Liang, Hongxin Zhang, Shaofei Sun, Lei Zhu, Xiaotong Cui, and Bablu K. Ghosh. 2020. "An Effective Simulation Analysis of Transient Electromagnetic Multiple Faults" Sensors 20, no. 7: 1976. https://doi.org/10.3390/s20071976
APA StyleDong, L., Zhang, H., Sun, S., Zhu, L., Cui, X., & Ghosh, B. K. (2020). An Effective Simulation Analysis of Transient Electromagnetic Multiple Faults. Sensors, 20(7), 1976. https://doi.org/10.3390/s20071976