Temperature Sensor Denoising Algorithm Based on Curve Fitting and Compound Kalman Filtering
Abstract
1. Introduction
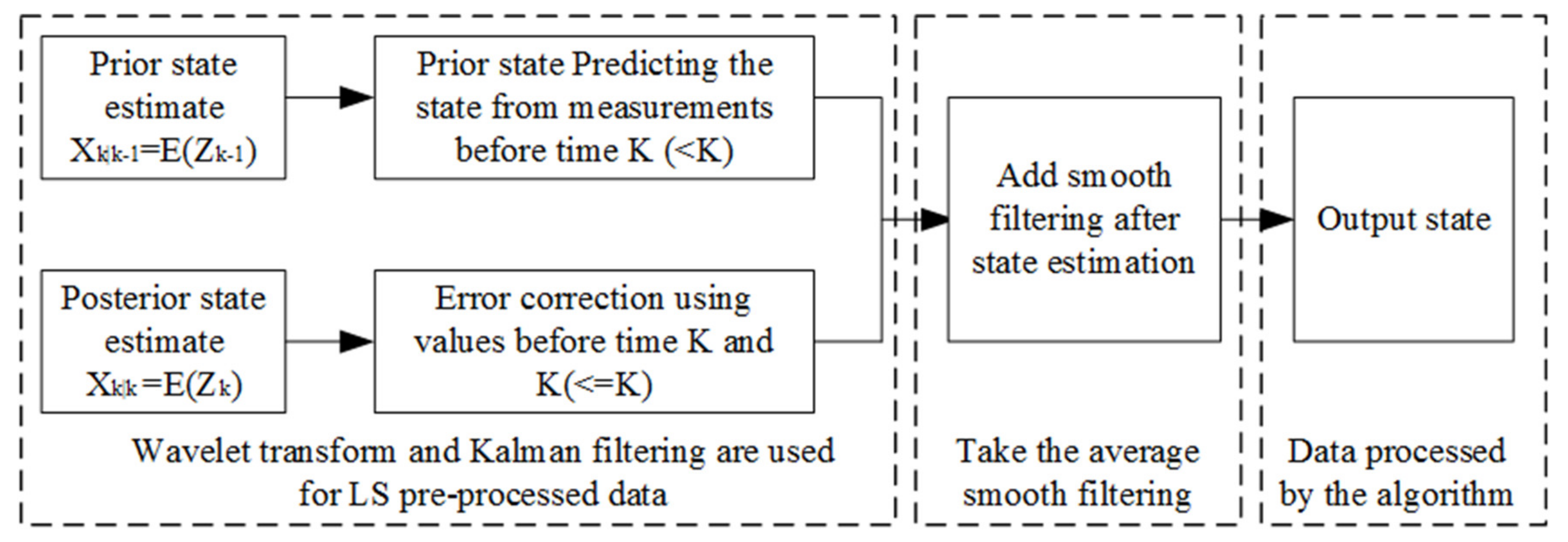
2. CKSF Denoising Algorithm Analysis
2.1. Kalman Filter Model of Temperature Sensor
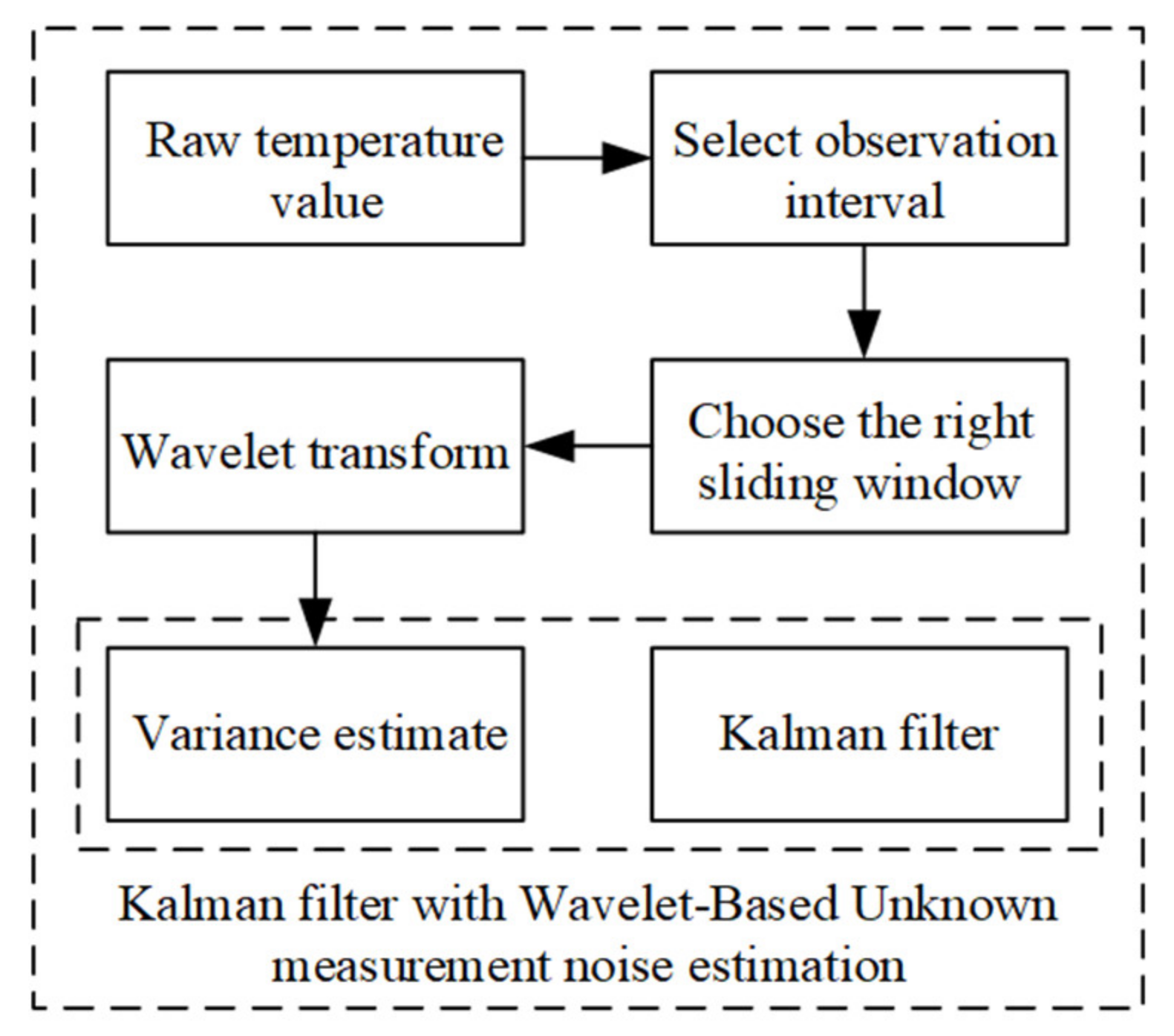
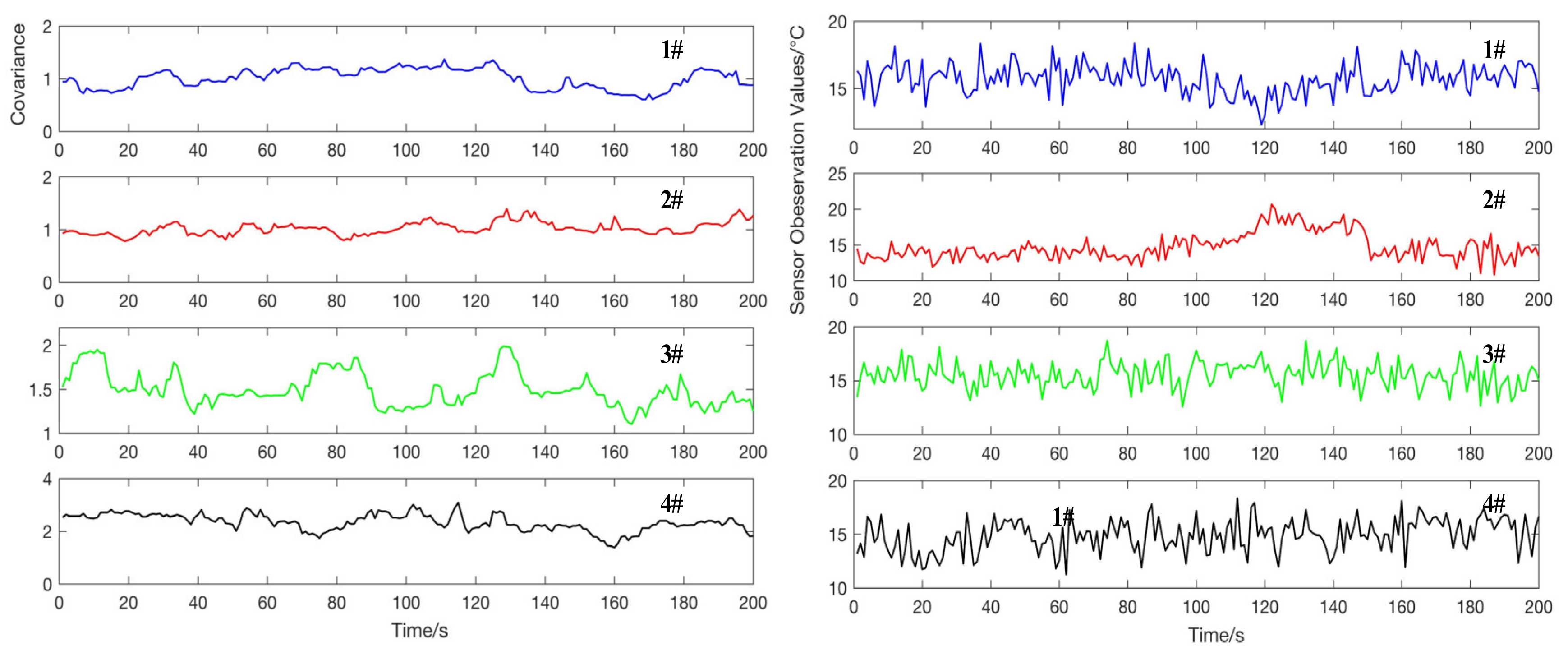
2.2. Estimation of Noise Variance During Temperature Observation
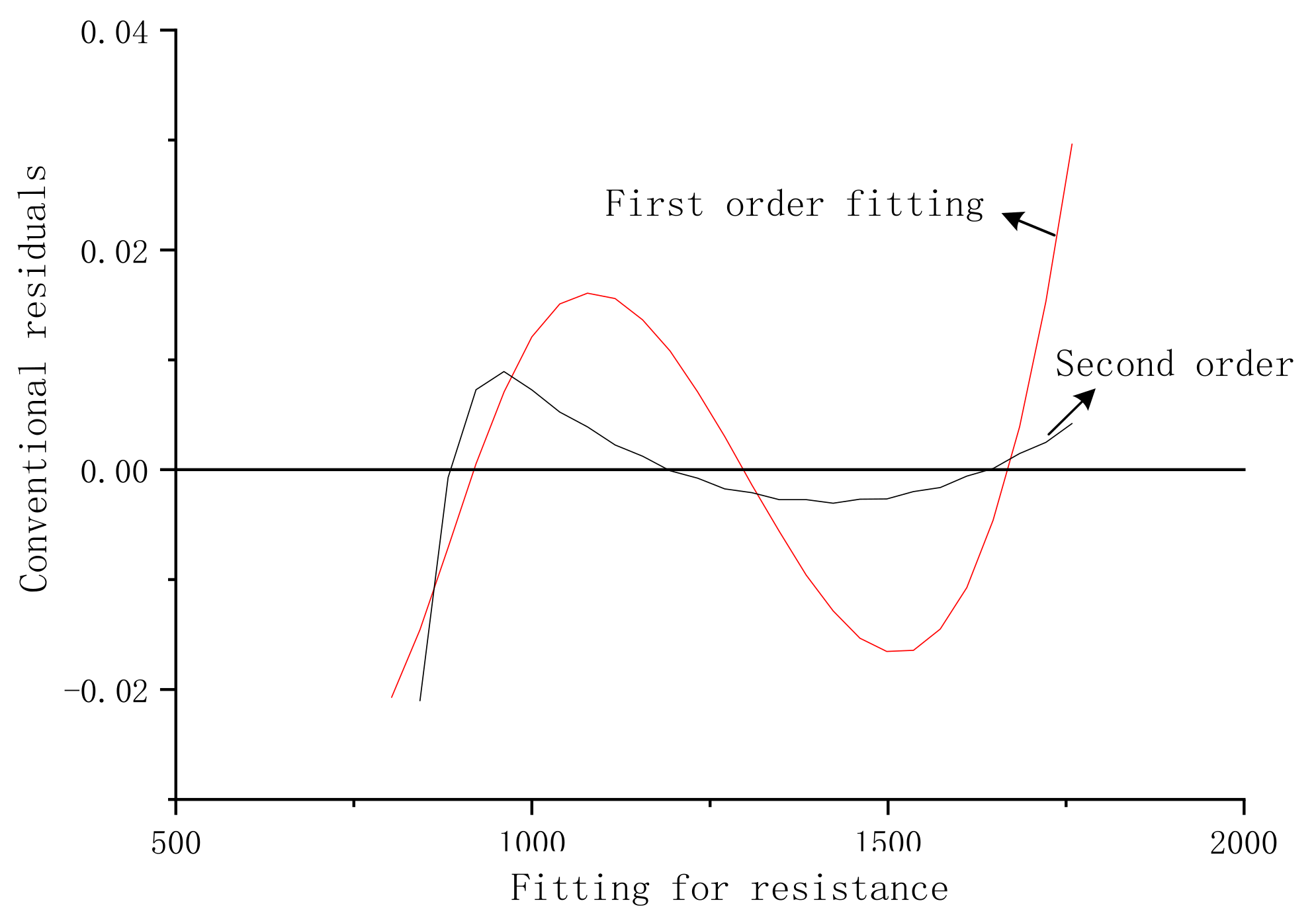
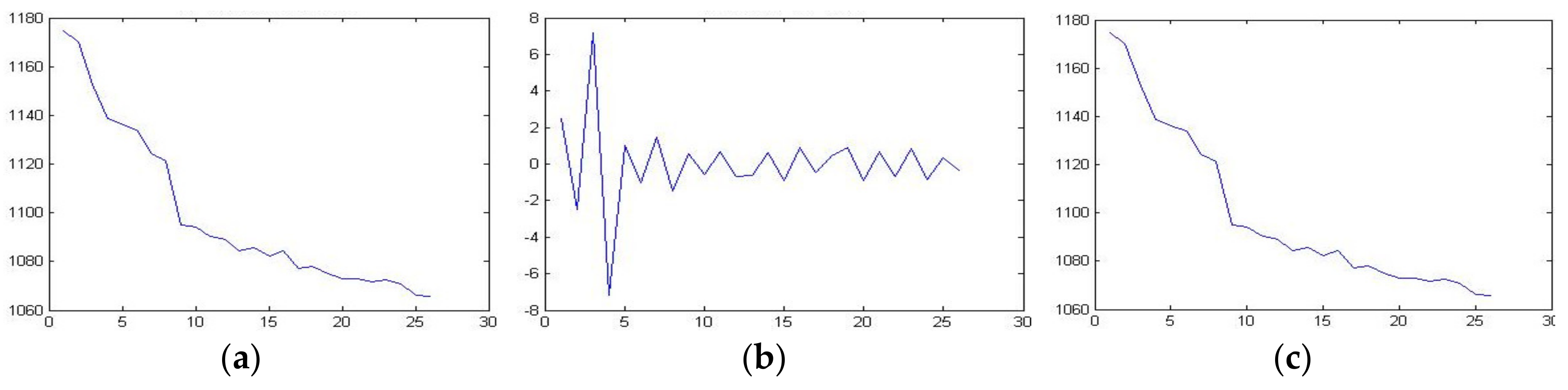
2.3. Sensor Resistance and Temperature (R_T) Fitting Model
3. Experimental Data Analysis and Discussion
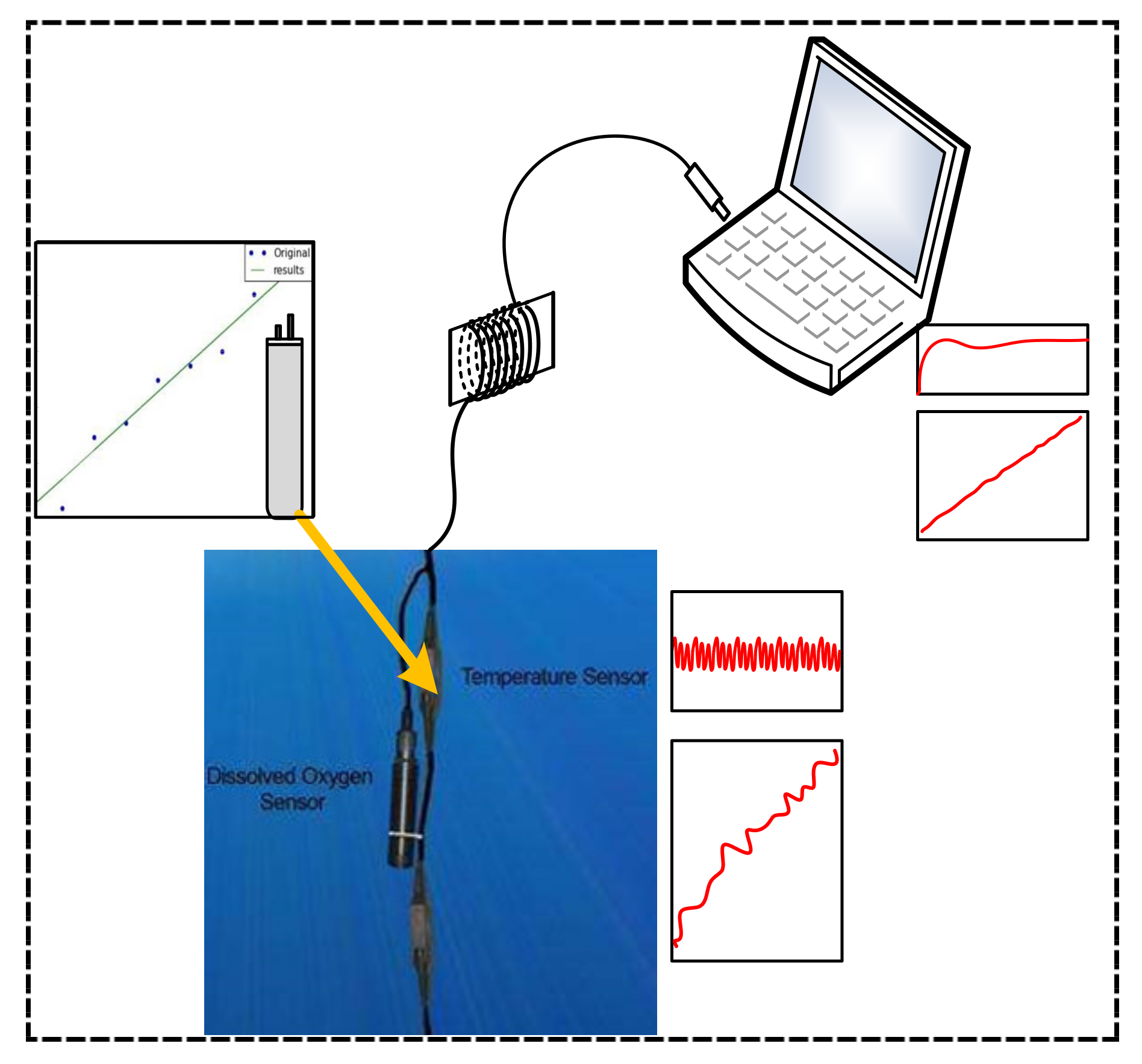
3.1. Temperature Sensor Selection and Application
3.2. The Analysis of Least Squares Method Results
3.3. The Analysis of Wavelet Transforms Results
3.4. Comparative Analysis with Other Algorithms
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kang, A.; Zhang, C.; Luo, Z. SAW RFID Enabled Multi-Functional Sensors for Food Safety Applications. In Proceedings of the IEEE International Conference on RFID-Technology and Applications, Guangzhou, China, 17–19 June 2010. [Google Scholar]
- Stroganov, K.; Kornilov, T.; Onidov, T.; Luylin, B. SAW Temperature Sensors for Electric Power Transmission Lines. In Proceedings of the European Frequency and Time Forum, Denver, CO, USA, 13–15 April 2015. [Google Scholar]
- Munday, P.L.; Crawley, N.E.; Nilsson, G.E. Interacting effects of elevated temperature and ocean acidification on the aerobic performance of coral reef fishes. Mar. Ecol. Prog. 2009, 388, 235–242. [Google Scholar] [CrossRef]
- Izadi, D.; Abawajy, J.H.; Ghanavati, S.; Herawan, T. A data fusion method in wireless sensor networks. Sensors 2015, 15, 2964–2979. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y. Theory and Application of Self-Confirmation Sensor; Fudan University: Shanghai, China, 2008. [Google Scholar]
- Cradoso, J.F. Infomax and maximum likelihood for blind source separation. IEEE Signal Process. Lett. 1997, 4, 112–114. [Google Scholar] [CrossRef]
- Liu, X.; Peng, K.; Chen, Z.; Pu, H.; Yu, Z. A new capacitive displacement sensor with nanometer accuracy and long range. IEEE Sens. J. 2016, 16, 2306–2316. [Google Scholar] [CrossRef]
- Liu, Z.C. Research on On-Line Sensor Performance Evaluation and Fault Diagnosis Method; National Defense Industry Press: Beijing, China, 2013. [Google Scholar]
- Wang, S.Y.; Huang, J.W.; Xie, Z.G. Principle and Application of Nonlinear Kalman Filter; Electronic Industry Press: Beijing, China, 2015. [Google Scholar]
- Fan, X.; Dong, C.; Miao, H. A wavelet adaptive cancellation algorithm based on multi-inertial sensors for the reduction of motion artifacts in ambulatory ECGs. Sensors 2020, 20, 970. [Google Scholar]
- Li, X.; Wang, Y.; Khoshelham, K. Comparative analysis of robust extended Kalman filter and incremental smoothing for UWB/PDR fusion positioning in NLOS environments. Acta Geod. Geophys. 2019, 54, 157–179. [Google Scholar] [CrossRef]
- Musoff, H.; Zarchan, P. Fundamentals of Kalman filtering: A practical approach, second edition. Prog. Astronaut. Aeronaut. 2015, 190, 83. [Google Scholar]
- Abbas, S.; Tsui, C.Y. Approximate Matrix Inversion for Linear Pre-coders in Massive MIMO. IFIP/IEEE International Conference on Very Large-Scale Integration System on a Chip, Tallinn, Estonia, 26–28 September 2016. [Google Scholar]
- Zeng, C.; Yang, Q.; Wang, J. Chaos and mixed synchronization of a new fractional-order system with one saddle and two stable node-foci. Nonlinear Dyn. 2011, 65, 457–466. [Google Scholar] [CrossRef]
- Zuo, J.; Liang, Y.; Zhang, Y. Particle filter with multimode sampling strategy. Signal Process. 2013, 93, 3192–3201. [Google Scholar] [CrossRef]
- Paek, J.; Ko, J.G. K-means clustering-based data compression scheme for wireless imaging sensor networks. IEEE Syst. J. 2017, 11, 2652–2662. [Google Scholar] [CrossRef]
- Timothy, P.; Idris, A.E.; Hernando, C.O. Dynamic classification using multivariate locally stationary wavelet processes. Signal Process. 2018, 152, 118–129. [Google Scholar]
- Feng, W.; Ke, Y.; Mingming, Y. Self-Adaptive Wavelet Denoising for Feature Extraction of Mechanical Fault Diagnosis Based on a Modified Sparse Coding Shrinkage. In Proceedings of the 2012 international conference on Intelligent Control, Automatic Detection and High-End, Beijing, China, 27–29 July 2012. [Google Scholar]
- Xu, L.; Zhang, J.Q.; Yan, Y.A. Wavelet-Based Multi-sensor Data Fusion Algorithm. IEEE Trans. Instrum. Meas. 2004, 53, 1539–1545. [Google Scholar] [CrossRef]
- Parida, A.K.; Maity, K. Effect of nose radius on forces, and process parameters in hot machining of Inconel 718 using finite element analysis. Eng. Sci. Technol. Int. J. 2017, 20, 687–693. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, S.; Zhou, L. Single channel blind source separation for wind turbine aeroacoustics signals based on variational mode decomposition. IEEE Access 2018, 6, 73952–73964. [Google Scholar] [CrossRef]
- Sun, X.; Dong, X.; Cai, L. Visible-NIR spectroscopy and least square support vector machines regression for determination of vitamin C of mandarin fruit. Sens. Lett. 2012, 10, 506–510. [Google Scholar] [CrossRef]
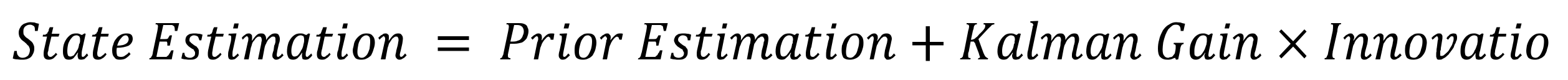



| Temperature/°C 1 | Fitting Para | Manual |
|---|---|---|
| 20 | 19.6 | 19.3 |
| 30 | 29.7 | 29.1 |
| 40 | 39.9 | 39.0 |
| 50 | 49.5 | 49.1 |
| 60 | 59.9 | 59.4 |
| 70 | 69.8 | 69.8 |
| Temp1 1 | Error1 2 | Temp2 3 | Error2 4 |
|---|---|---|---|
| 25.776 | −2.734 | 28.542 | 0.032 |
| 28.485 | −0.025 | 28.323 | −0.187 |
| 28.416 | −0.094 | 28.254 | −0.256 |
| 28.505 | −0.005 | 28.233 | −0.277 |
| 28.495 | −0.015 | 28.167 | −0.343 |
| 28.498 | −0.012 | 28.075 | −0.435 |
| 28.483 | −0.027 | 28.054 | −0.456 |
| 28.221 | −0.289 | 28.337 | −0.173 |
| 28.36 | −0.150 | 28.433 | −0.077 |
| 28.457 | −0.053 | 28.248 | −0.262 |
| 28.199 | −0.311 | 28.005 | −0.505 |
| 28.499 | −0.0011 | 28.016 | −0.494 |
| 28.491 | −0.019 | 28.334 | −0.176 |
| 28.51 | 0.000 | 28.280 | −0.23 |
| 28.445 | −0.065 | 28.117 | −0.393 |
| 28.265 | −0.245 | 28.371 | −0.139 |
| 28.322 | −0.188 | 28.556 | 0.046 |
| 28.423 | −0.087 | 28.386 | −0.124 |
| 28.424 | −0.086 | 28.365 | −0.145 |
| 28.356 | −0.154 | 28.696 | 0.186 |
| 28.500 | −0.010 | 28.708 | 0.198 |
| 28.534 | 0.024 | 28.905 | 0.395 |
| 28.543 | 0.033 | 28.579 | 0.069 |
| 28.571 | 0.061 | 28.694 | 0.184 |
| 28.554 | 0.044 | 28.476 | −0.034 |
| 28.566 | 0.056 | 28.610 | 0.100 |
| 28.57 | 0.060 | 28.685 | 0.175 |
| 28.589 | 0.079 | 28.664 | 0.154 |
| 28.597 | 0.087 | 28.629 | 0.119 |
| 28.562 | 0.052 | 28.429 | −0.081 |
| 28.52 | 0.010 | 28.353 | −0.157 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, R.; Li, S.; Qi, S. Temperature Sensor Denoising Algorithm Based on Curve Fitting and Compound Kalman Filtering. Sensors 2020, 20, 1959. https://doi.org/10.3390/s20071959
Zhang Y, Wang R, Li S, Qi S. Temperature Sensor Denoising Algorithm Based on Curve Fitting and Compound Kalman Filtering. Sensors. 2020; 20(7):1959. https://doi.org/10.3390/s20071959
Chicago/Turabian StyleZhang, Yang, Rong Wang, Shouzhe Li, and Shengbo Qi. 2020. "Temperature Sensor Denoising Algorithm Based on Curve Fitting and Compound Kalman Filtering" Sensors 20, no. 7: 1959. https://doi.org/10.3390/s20071959
APA StyleZhang, Y., Wang, R., Li, S., & Qi, S. (2020). Temperature Sensor Denoising Algorithm Based on Curve Fitting and Compound Kalman Filtering. Sensors, 20(7), 1959. https://doi.org/10.3390/s20071959





