Operational Global Actual Evapotranspiration: Development, Evaluation, and Dissemination
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
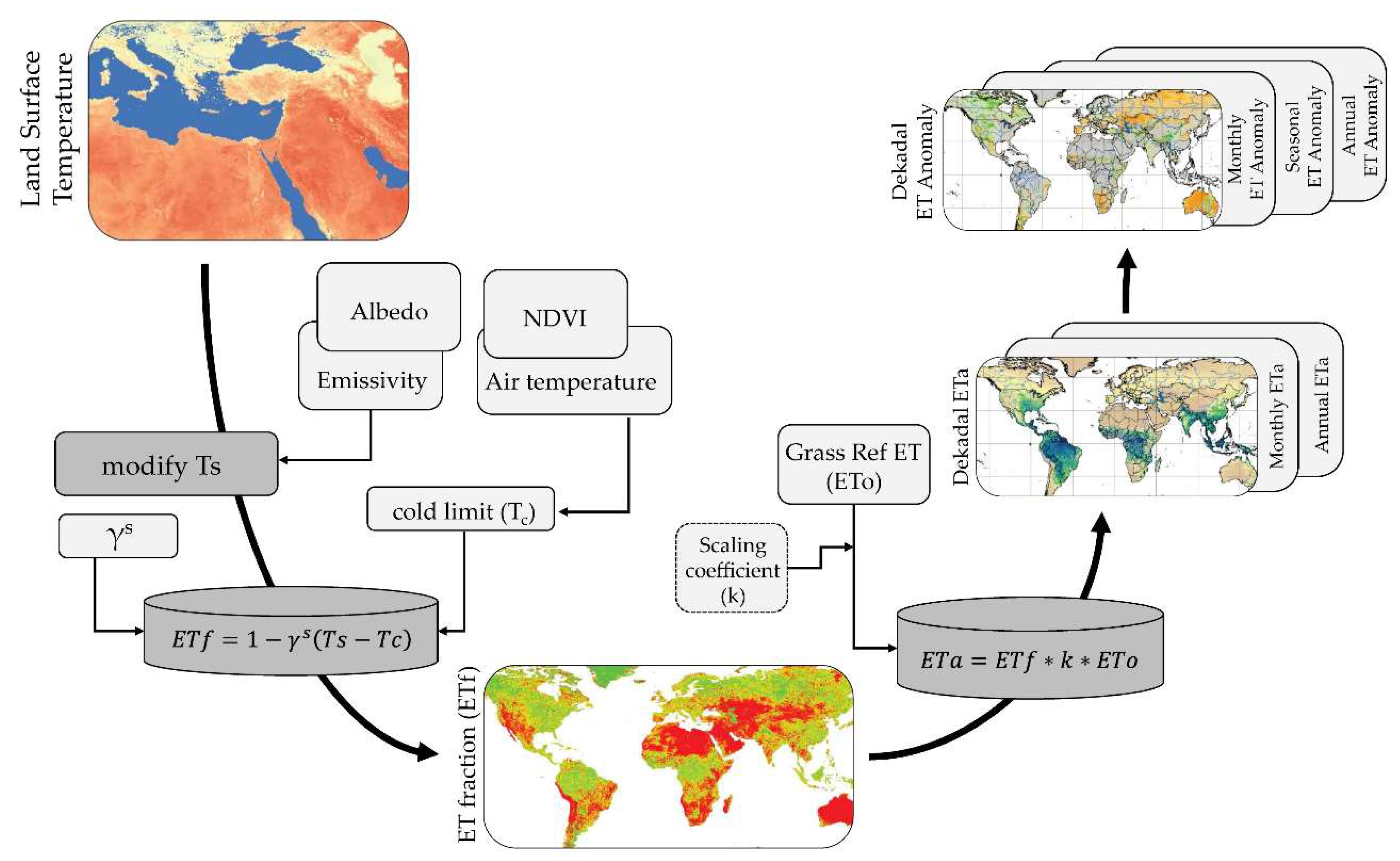
2.2. SSEBop Model Approach
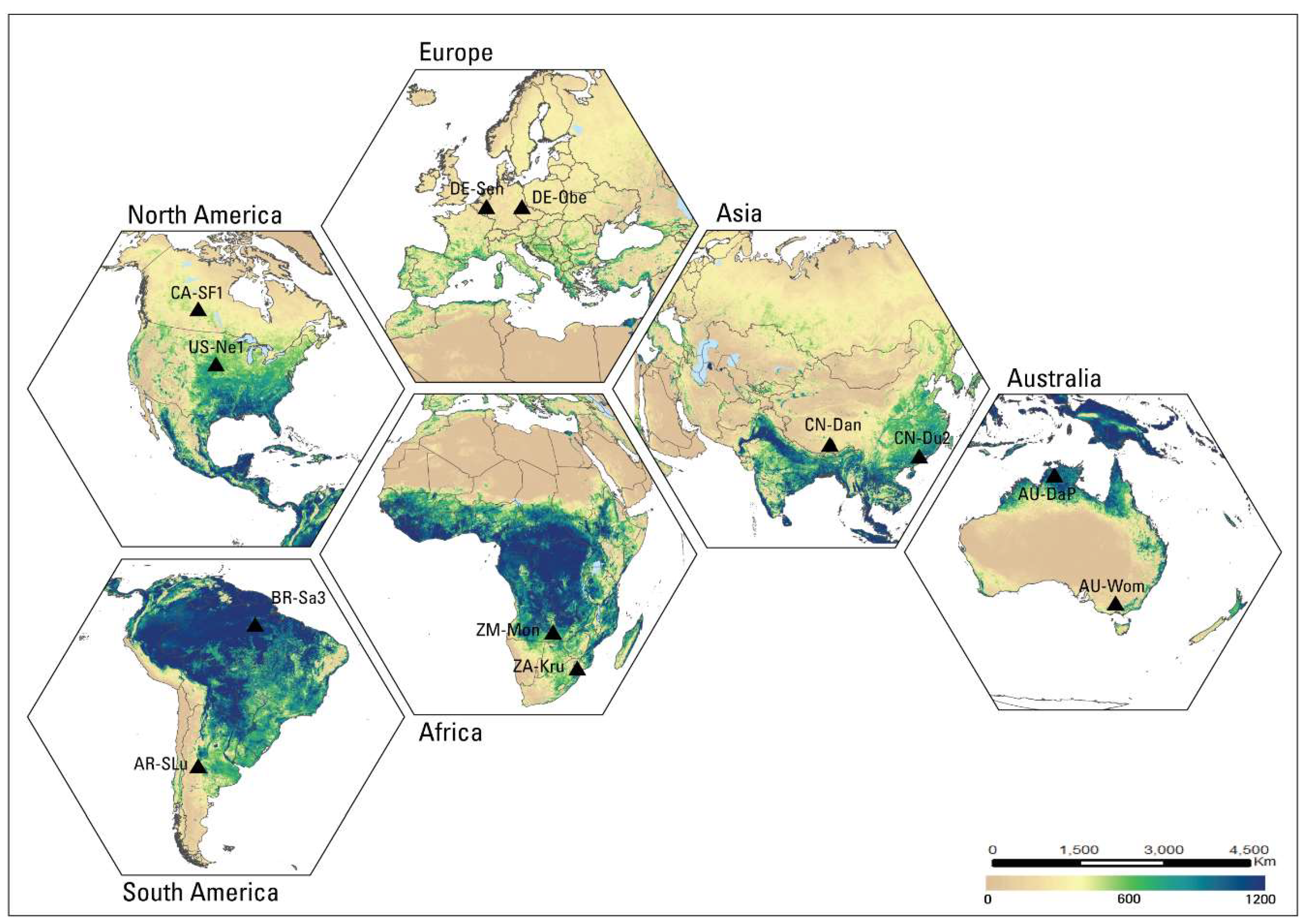
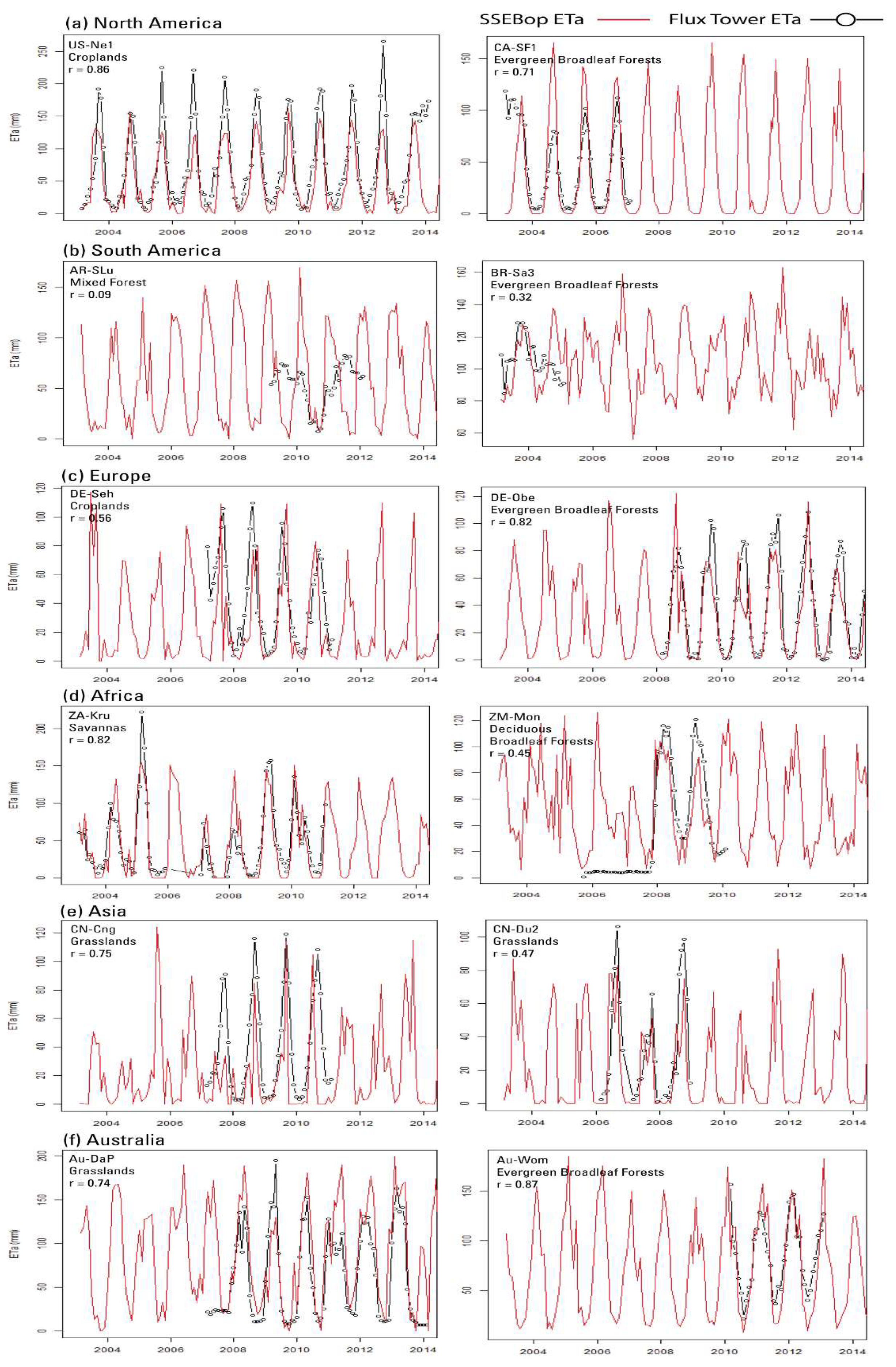
2.3. Evaluation of SSEBop ETa Estimates Using Eddy Covariance Flux Towers
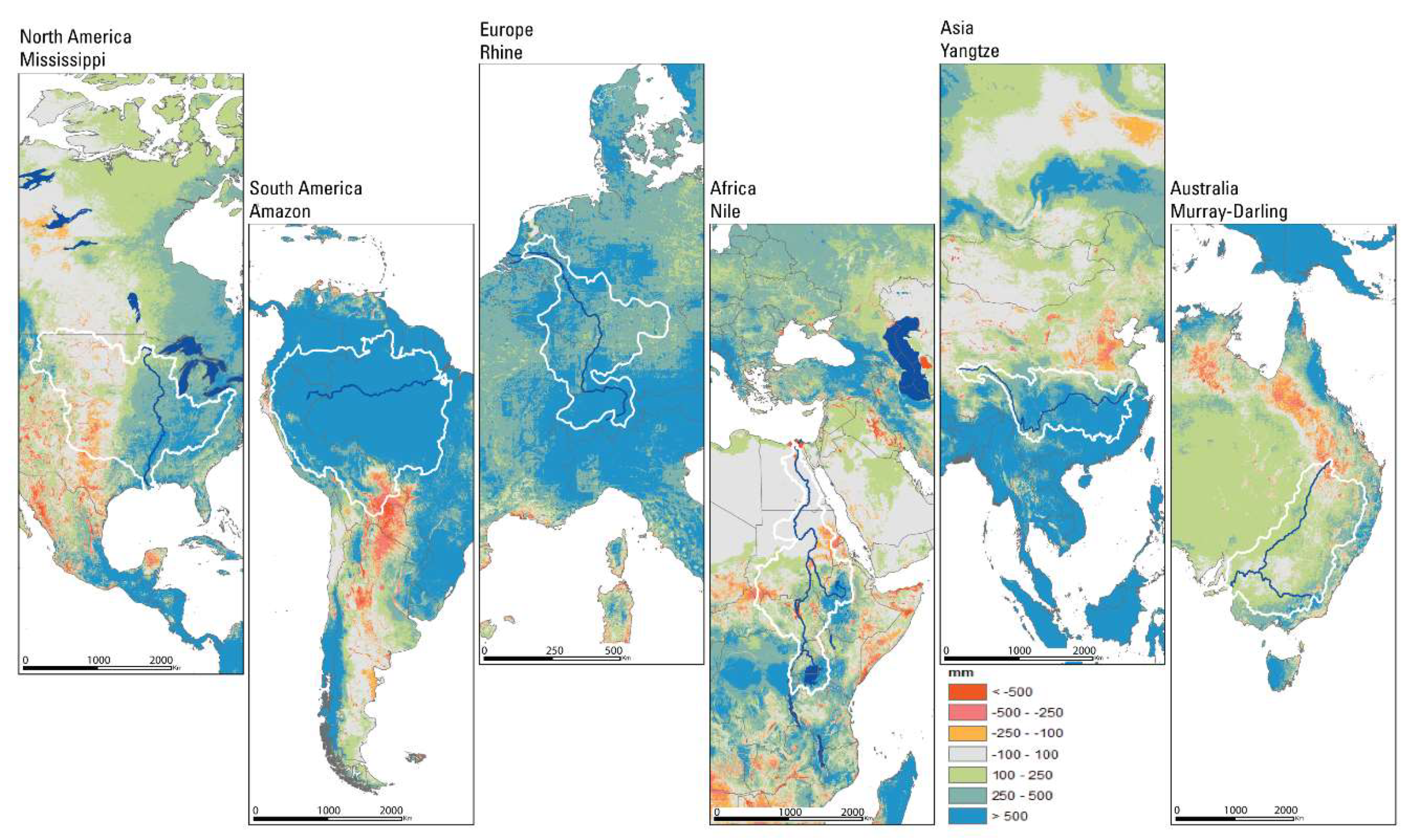
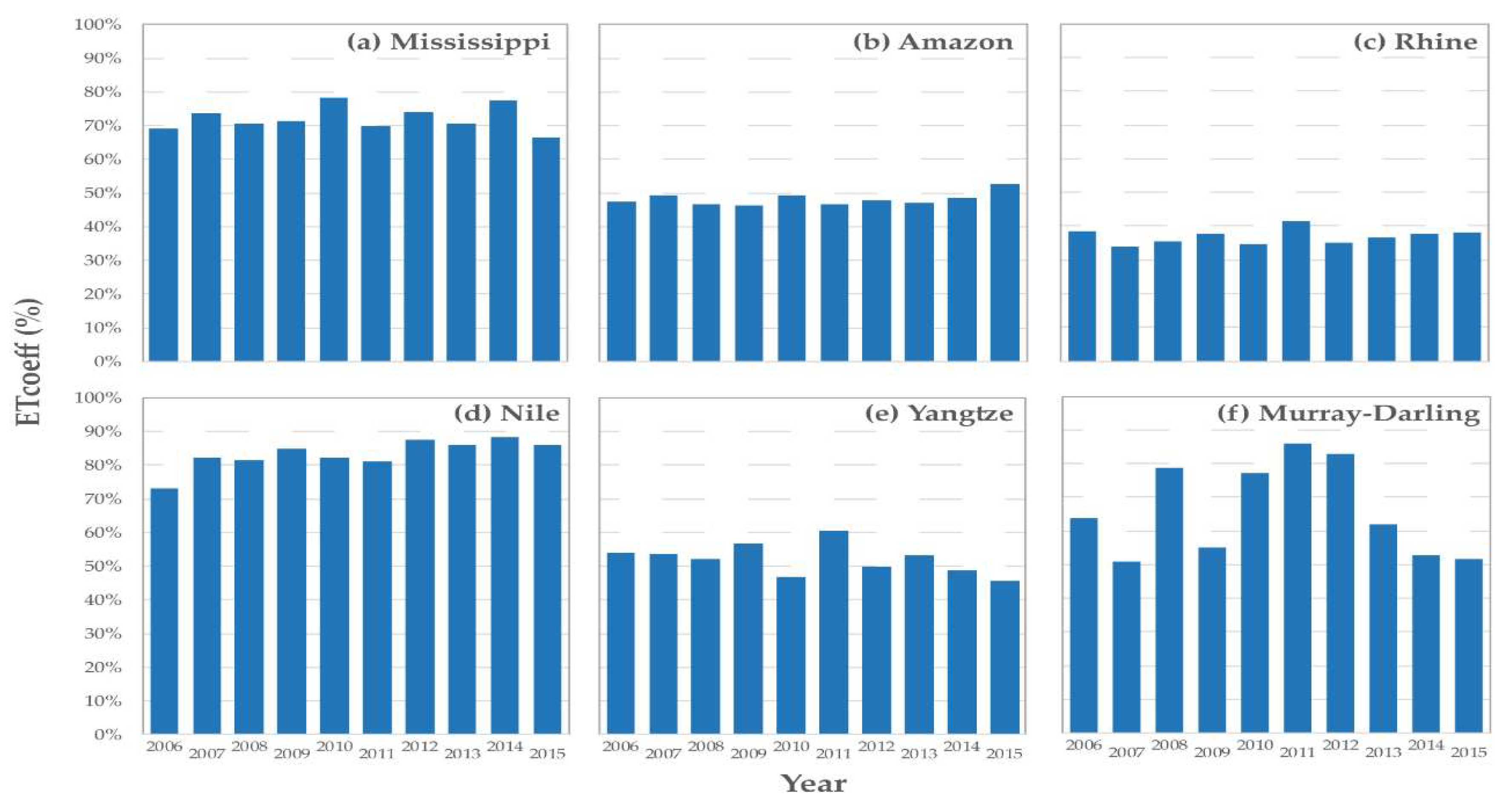
2.4. Evaluation of SSEBop ETa Using Annual Water Budget at Pixel and Basin Scales
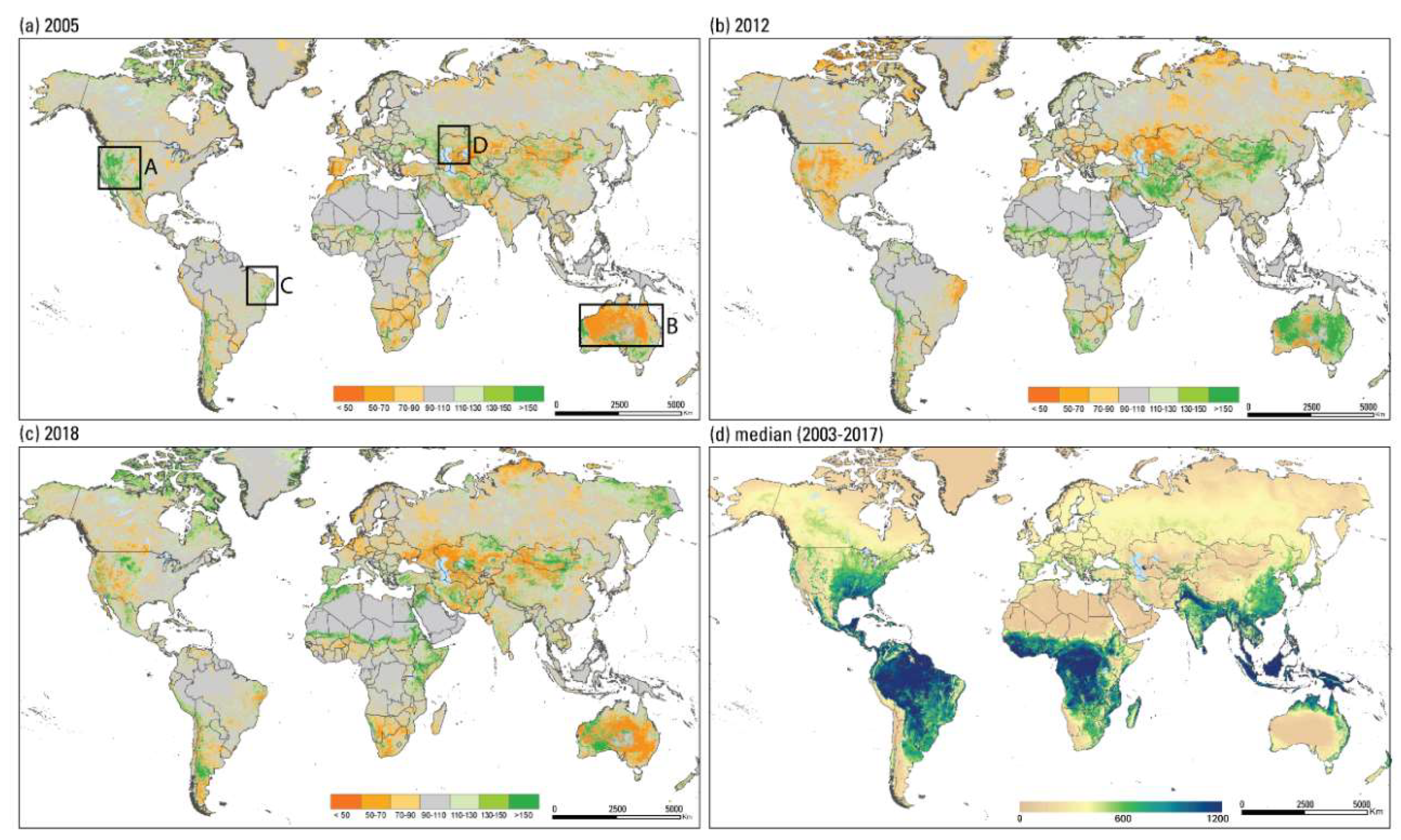
2.5. ETa Anomalies for Drought Monitoring
3. Results and Discussion
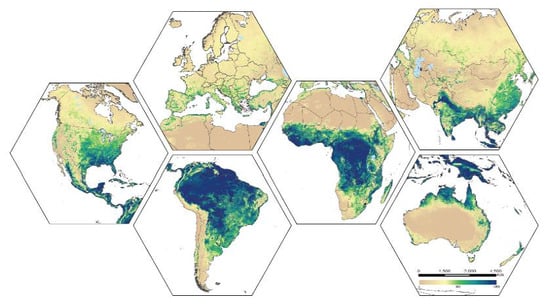
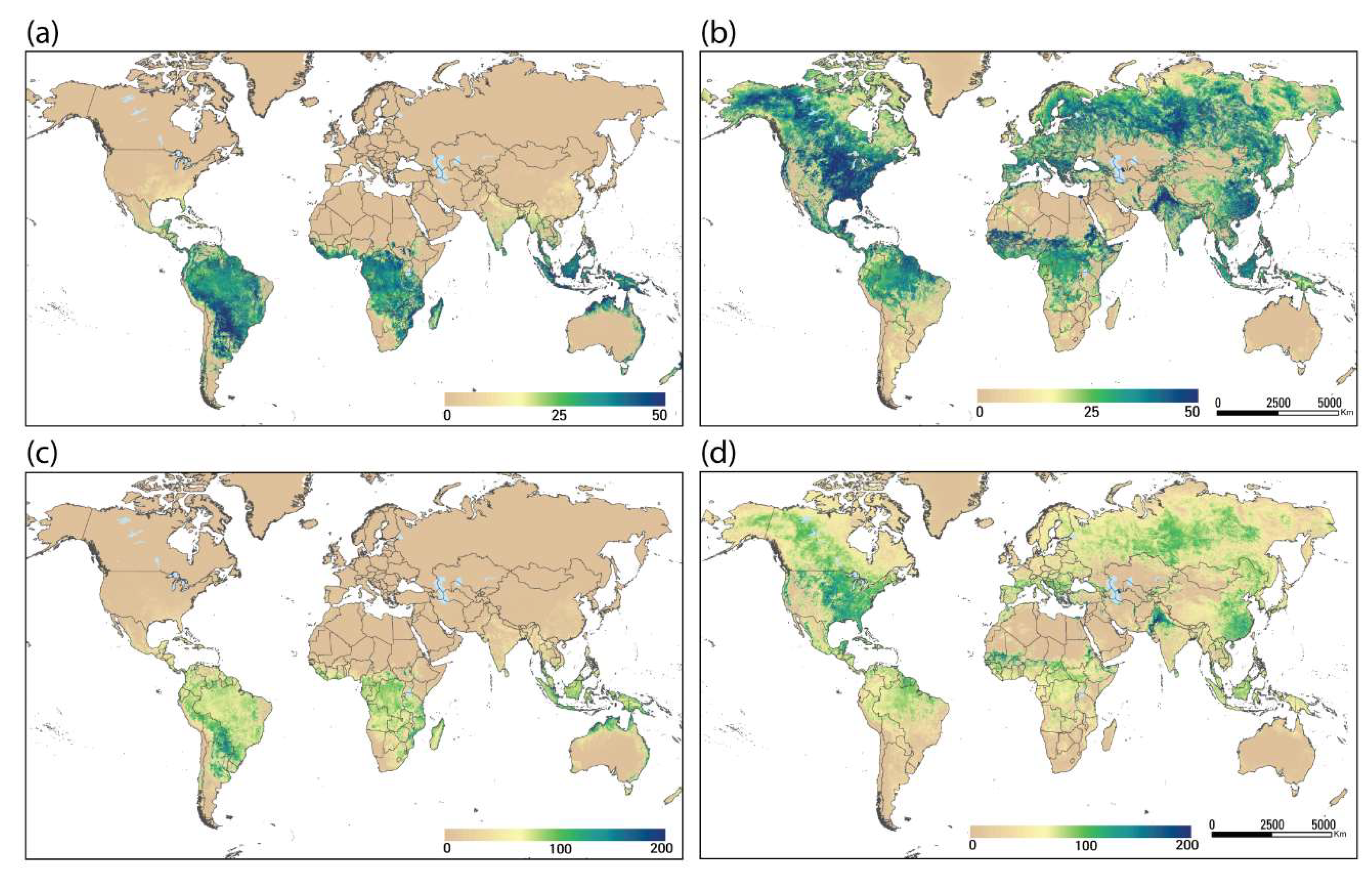
3.1. SSEBop ETa Estimates
3.2. Evaluation of ETa Estimates Using Eddy Covariance (EC) Data
3.3. Evaluation of ETa with Annual Water Budget
3.4. Drought Monitoring Using ET Anomalies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vörösmarty, C.J.; Federer, C.A.; Schloss, A.L. Potential evaporation functions compared on US watersheds: Possible implications for global-scale water balance and terrestrial ecosystem modeling. J. Hydrol. 1998, 207, 147–169. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, G. Measurement and modelling of evapotranspiration over a reed (Phragmites australis) marsh in Northeast China. J. Hydrol. 2009, 372, 41–47. [Google Scholar] [CrossRef]
- Senay, G.B.; Leake, S.; Nagler, P.L.; Artan, G.; Dickinson, J.; Cordova, J.T.; Glenn, E.P. Estimating basin scale evapotranspiration (ET) by water balance and remote sensing methods. Hydrol. Process. 2011, 25, 4037–4049. [Google Scholar] [CrossRef]
- Martens, B.; Gonzalez Miralles, D.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.; Verhoest, N. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Van Dijk, A.I.; Mattersdorf, G.; Beringer, J.; Hutley, L.B.; Leuning, R.; Pipunic, R.C.; Sherman, B.S. Scaling of potential evapotranspiration with MODIS data reproduces flux observations and catchment water balance observations across Australia. J. Hydrol. 2009, 369, 107–119. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Nagler, P.L.; Scott, R.L.; Westenburg, C.; Cleverly, J.R.; Glenn, E.P.; Huete, A.R. Evapotranspiration on western US rivers estimated using the Enhanced Vegetation Index from MODIS and data from eddy covariance and Bowen ratio flux towers. Remote Sens. Environ. 2005, 97, 337–351. [Google Scholar] [CrossRef]
- Zheng, C.; Jia, L.; Hu, G.; Lu, J.; Wang, K.; Li, Z. Global evapotranspiration derived by ETMonitor model based on earth observations. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 222–225. [Google Scholar]
- Fisher, J.B.; DeBiase, T.A.; Qi, Y.; Xu, M.; Goldstein, A.H. Evapotranspiration models compared on a Sierra Nevada forest ecosystem. Environ. Model. Softw. 2005, 20, 783–796. [Google Scholar] [CrossRef]
- Senay, G.B. Modeling landscape evapotranspiration by integrating land surface phenology and a water balance algorithm. Algorithms 2008, 1, 52–68. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.; Sheffield, J.; Goulden, M.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R. Recent deceleration of global land evapotranspiration due to moisture supply limitation. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Mueller, B.; Seneviratne, S.I.; Jimenez, C.; Corti, T.; Hirschi, M.; Balsamo, G.; Ciais, P.; Dirmeyer, P.; Fisher, J.; Guo, Z. Evaluation of global observations-based evapotranspiration datasets and IPCC AR4 simulations. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Thornton, P.; Thornton, M.; Mayer, B.; Wei, Y.; Devarakonda, R.; Vose, R.; Cook, R. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 3; ORNL DAAC Oak Ridge Tenn.: Oak Ridge, TN, USA, 2017. [Google Scholar]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Senay, G.; Budde, M.; Verdin, J.; Melesse, A. A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef]
- Senay, G.B.; Friedrichs, M.; Singh, R.K.; Velpuri, N.M. Evaluating Landsat 8 evapotranspiration for water use mapping in the Colorado River Basin. Remote Sens. Environ. 2016, 185, 171–185. [Google Scholar] [CrossRef]
- Senay, G.B. Satellite Psychrometric Formulation of the Operational Simplified Surface Energy Balance (SSEBop) Model for Quantifying and Mapping Evapotranspiration. Appl. Eng. Agric. 2018, 34, 555–566. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A quasi-global precipitation time series for drought monitoring. US Geol. Surv. Data Ser. 2014, 832, 1–12. [Google Scholar]
- Franssen, H.H.; Stöckli, R.; Lehner, I.; Rotenberg, E.; Seneviratne, S.I. Energy balance closure of eddy-covariance data: A multisite analysis for European FLUXNET stations. Agric. For. Meteorol. 2010, 150, 1553–1567. [Google Scholar] [CrossRef]
- Stoy, P.C.; Mauder, M.; Foken, T.; Marcolla, B.; Boegh, E.; Ibrom, A.; Arain, M.A.; Arneth, A.; Aurela, M.; Bernhofer, C. A data-driven analysis of energy balance closure across FLUXNET research sites: The role of landscape scale heterogeneity. Agric. For. Meteorol. 2013, 171, 137–152. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; Van Dijk, A.I.; McVicar, T.R.; Adler, R.F. MSWEP V2 global 3-hourly 0.1 precipitation: Methodology and quantitative assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef]
- Senay, G.B.; Kagone, S. Operational Global Actual Evapotranspiration Using the SSEBop Model: US Geological Survey Data Release. 2020. Available online: https://www.sciencebase.gov/catalog/item/5e39c336e4b0a79317e15d7a (accessed on 24 March 2020).
- Sanford, W.E.; Selnick, D.L. Estimation of evapotranspiration across the conterminous United States using a regression with climate and land-cover data 1. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 217–230. [Google Scholar] [CrossRef]
- Wittwer, G.; Griffith, M. Modelling drought and recovery in the southern Murray-Darling basin. Aust. J. Agric. Resour. Econ. 2011, 55, 342–359. [Google Scholar] [CrossRef]
- Long, D.; Scanlon, B.R.; Longuevergne, L.; Sun, A.Y.; Fernando, D.N.; Save, H. GRACE satellite monitoring of large depletion in water storage in response to the 2011 drought in Texas. Geophys. Res. Lett. 2013, 40, 3395–3401. [Google Scholar] [CrossRef]
- Nielsen-Gammon, J.W. The 2011 texas drought. Tex. Water J. 2012, 3, 59–95. [Google Scholar]
- Cai, W.; Purich, A.; Cowan, T.; van Rensch, P.; Weller, E. Did climate change–induced rainfall trends contribute to the Australian Millennium Drought? J. Clim. 2014, 27, 3145–3168. [Google Scholar] [CrossRef]
- Loch, A.; Adamson, D. Drought and the rebound effect: A Murray–Darling Basin example. Nat. Hazards 2015, 79, 1429–1449. [Google Scholar] [CrossRef]
- Cunha, A.P.; Zeri, M.; Deusdará Leal, K.; Costa, L.; Cuartas, L.A.; Marengo, J.A.; Tomasella, J.; Vieira, R.M.; Barbosa, A.A.; Cunningha, C. Extreme Drought Events over Brazil from 2011 to 2019. Atmosphere 2019, 10, 642. [Google Scholar] [CrossRef]
| Dataset | Abbreviation | Source | Version | Purpose | |
|---|---|---|---|---|---|
| 1 | Land Surface Temperature | LST(or Ts) | MODIS (Aqua) | V6 | ETf |
| 2 | Maximum Air Temperature | Ta | Daymet/WorldClim | V3/V2 | Tc |
| 3 | Reference evapotranspiration | ETo | GDAS/IWMI | - | ETa |
| 4 | Emissivity | e | MODIS (Aqua) | V6 | Ts |
| 5 | Normalized Difference Vegetation Index | NDVI | MODIS (Aqua) | V6 | Ts, c factor |
| 6 | Albedo | a | MODIS | V6 | Ts |
| Parameter | Constraints |
|---|---|
| c factor | NDVI >= 0.7 |
| Ts > 270 K | |
| −10 K <= (Ta–Ts) <= 5 K C factor is established under the above 3 conditions | |
| Ts | albedo correction |
| If a >= 250 & NDVI >= 0 & desert pixel mask | |
| Then, Ts,a = Ts + 0.1(a -50) | |
| Emissivity correction | |
| If e > 0.965 & (0.001 < NDVI < 0.25) | |
| Then, Ts,e = Ts, a(e/0.965) |
| Site | Continent | Land Cover | SSEBop ETa (mm) | Flux Tower ETa (mm) | Range (mm) | Bias (mm) | Bias (%) | RMSE (mm) | RMSEm | RMSEr | r |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AU-DaP | Australia | Grasslands | 89.7 | 63.2 | 188.2 | 26.5 | 42% | 35.7 | 56% | 19% | 0.74 |
| AU-Wom | Australia | Evergreen Broadleaf Forests | 77.8 | 85.4 | 134.1 | −7.6 | −9% | 13.6 | 16% | 10% | 0.87 |
| CA-SF1 | North America | Evergreen Needleleaf Forests | 53.0 | 54.7 | 107.4 | −1.7 | −3% | 17.8 | 33% | 17% | 0.71 |
| US-Ne1 | North America | Croplands | 51.3 | 76.9 | 258.1 | −25.6 | −33% | 38.7 | 50% | 15% | 0.86 |
| CN-Cng | Asia | Grasslands | 22.9 | 38.0 | 116.2 | −15.1 | −40% | 13.6 | 36% | 12% | 0.75 |
| CN-Du2 | Asia | Grasslands | 38.4 | 49.1 | 102.4 | −10.8 | −22% | 11.3 | 23% | 11% | 0.47 |
| DE-Obe | Europe | Evergreen Needleleaf Forests | 32.6 | 40.4 | 109.2 | −7.8 | −19% | 15.8 | 39% | 14% | 0.82 |
| DE-Seh | Europe | Croplands | 27.8 | 41.7 | 106.3 | −13.8 | −33% | 18.3 | 44% | 17% | 0.56 |
| ZA-Kru | Africa | Savannas | 44.6 | 37.7 | 221.4 | 7.0 | 18% | 18.3 | 49% | 8% | 0.82 |
| ZM-Mon | Africa | Deciduous Broadleaf Forests | 52.6 | 35.1 | 120.2 | 17.5 | 50% | 24.7 | 70% | 21% | 0.45 |
| AR-SLu | South America | Mixed Forest | 59.1 | 54.6 | 75.2 | 4.5 | 8% | 43.7 | 80% | 58% | 0.09 |
| BR-Sa3 | South America | Evergreen Broadleaf Forests | 104.8 | 106.0 | 43.8 | −1.2 | −1% | 7.5 | 7% | 17% | 0.32 |
| Site | Continent | #Days | #Days_low | %low | #Days_high | %high |
|---|---|---|---|---|---|---|
| AU-DaP | Australia | 2063 | 12 | 0.58 | 1034 | 50.1 |
| AU-Wom | Australia | 992 | 246 | 24.8 | 396 | 39.9 |
| CA-SF1 | North America | 1220 | 316 | 25.9 | 479 | 39.3 |
| US-Ne1 | North America | 4360 | 632 | 14.5 | 2001 | 45.9 |
| CN-Cng | Asia | 1131 | 198 | 17.5 | 509 | 45 |
| CN-Du2 | Asia | 238 | 11 | 4.6 | 120 | 50.4 |
| DE-Obe | Europe | 2451 | 837 | 34.2 | 938 | 38.3 |
| DE-Seh | Europe | 1198 | 363 | 30.3 | 444 | 37.1 |
| ZA-Kru | Africa | 1939 | 290 | 14.9 | 843 | 43.5 |
| ZM-Mon | Africa | 685 | 17 | 2.5 | 322 | 47 |
| AR-SLu | South America | 448 | 29 | 6.5 | 230 | 51.3 |
| BR-Sa3 | South America | 1058 | 18 | 1.7 | 523 | 49.4 |
| Basin Name | Area (km2) | PPT (mm) | ETa (mm) | ETcoeff (%) | |
|---|---|---|---|---|---|
| 1 | Mississippi | 2,981,076 | 812 | 582 | 72% |
| 2 | Amazon | 7,049,948 | 2339 | 1120 | 48% |
| 3 | Rhine | 185,000 | 916 | 328 | 36% |
| 4 | Nile | 3,254,555 | 625 | 511 | 82% |
| 5 | Yangtze | 1,808,589 | 1119 | 576 | 51% |
| 6 | Murray-Darling | 1,061,469 | 463 | 303 | 65% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senay, G.B.; Kagone, S.; Velpuri, N.M. Operational Global Actual Evapotranspiration: Development, Evaluation, and Dissemination. Sensors 2020, 20, 1915. https://doi.org/10.3390/s20071915
Senay GB, Kagone S, Velpuri NM. Operational Global Actual Evapotranspiration: Development, Evaluation, and Dissemination. Sensors. 2020; 20(7):1915. https://doi.org/10.3390/s20071915
Chicago/Turabian StyleSenay, Gabriel B., Stefanie Kagone, and Naga M. Velpuri. 2020. "Operational Global Actual Evapotranspiration: Development, Evaluation, and Dissemination" Sensors 20, no. 7: 1915. https://doi.org/10.3390/s20071915
APA StyleSenay, G. B., Kagone, S., & Velpuri, N. M. (2020). Operational Global Actual Evapotranspiration: Development, Evaluation, and Dissemination. Sensors, 20(7), 1915. https://doi.org/10.3390/s20071915