Effects of Air Cavity in Dynamic Pressure Sensors: Experimental Validation
Abstract
1. Introduction
2. Methods
3. Results
3.1. Finite Element Simulation
3.2. Experimental Results
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Ried, R.P.; Hong, D.M.; Muller, R.S.; Kim, E.S. Piezoelectric microphone with on-chip CMOS circuits. J. Microelectromech. Syst. 1993, 2, 111–120. [Google Scholar] [CrossRef]
- Ko, S.C.; Kim, Y.C.; Lee, S.S.; Choi, S.H.; Kim, S.R. Micromachined piezoelectric membrane acoustic device. Sens. Actuators A Phys. 2003, 103, 130–134. [Google Scholar] [CrossRef]
- Schellin, R.; Hess, G. A silicon subminiature microphone based on piezoresistive polysilicon strain gauges. Sens. Actuators A. Phys. 1992, 32, 555–559. [Google Scholar] [CrossRef]
- Hall, N.A.; Okandan, M.; Littrell, R.; Bicen, B.; Degertekin, F.L. Micromachined optical microphone structures with low thermal-mechanical noise levels. J. Acoust. Soc. Am. 2007, 122, 2031–2037. [Google Scholar] [CrossRef]
- Yu, M.; Balachandran, B. Acoustic measurements using a fiber optic sensor system. J. Intell. Mater. Syst. Struct. 2003, 14, 409–414. [Google Scholar] [CrossRef]
- Scheeper, P.R.; Nordstrand, B.; Gulløv, J.O.; Liu, B.; Clausen, T.; Midjord, L.; Storgaard-Larsen, T. A new measurement microphone based on MEMS technology. J. Microelectromech. Syst. 2003, 12, 880–891. [Google Scholar] [CrossRef]
- Scheeper, P.R.; Olthuis, W.; Bergveld, P. A silicon condenser microphone with a silicon nitride diaphragm and backplate. J. Micromech. Microeng. 1992, 2, 187–189. [Google Scholar] [CrossRef]
- Pedersen, M.; Olthuis, W.; Bergveld, P. A silicon condenser microphone with polyimide diaphragm and backplate. Sens. Actuators A Phys. 1997, 63, 97–104. [Google Scholar] [CrossRef]
- Dahlin, A.B. Size matters: Problems and advantages associated with highly miniaturized sensors. Sensors 2012, 12, 3018–3036. [Google Scholar] [CrossRef]
- Hierold, C. From micro- to nanosystems: Mechanical sensors go nano. J. Micromech. Microeng. 2004, 14, S1–S11. [Google Scholar] [CrossRef]
- Beranek, L.L. Acoustics; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- Bao, M.; Yang, H. Squeeze film air damping in MEMS. Sens. Actuators A Phys. 2007, 136, 3–27. [Google Scholar] [CrossRef]
- Lee, S.M.; Cha, B.S.; Okuyama, M. The influence of acoustic damping on the transformation efficiency of capacitive micromachined ultrasonic transducer in air. J. Appl. Phys. 2010, 108, 074512. [Google Scholar] [CrossRef]
- Andrews, M.; Harris, I.; Turner, G. A comparison of squeeze-film theory with measurements on a microstructure. Sens. Actuators A. Phys. 1993, 36, 79–87. [Google Scholar] [CrossRef]
- Le Van Suu, T.; Durand, S.; Bruneau, M. On the modelling of clamped plates loaded by a squeeze fluid film: Application to miniaturised sensors. Acta Acust. United Acust. 2010, 96, 923–935. [Google Scholar] [CrossRef]
- Škvor, Z. On the acoustical resistance due to viscous losses in the air gap of electrostatic transducers. Acustica 1967, 19, 295–299. [Google Scholar]
- Dowell, E.H.; Gorman, G.F.; Smith, D.A. Acoustoelasticity: General theory, acoustic natural modes and forced response to sinusoidal excitation, including comparisons with experiment. J. Sound Vib. 1977, 52, 519–542. [Google Scholar] [CrossRef]
- Gorman, D.G.; Reese, J.M.; Horácek, J.; Dedouch, K. Vibration analysis of a circular disc backed by a cylindrical cavity. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2001, 215, 1303–1312. [Google Scholar] [CrossRef]
- Pan, J. The forced response of an acoustic-structural coupled system. J. Acoust. Soc. Am. 1992, 91, 949. [Google Scholar] [CrossRef]
- Guy, R.W. The response of a cavity backed panel to external airborne excitation: A general analysis. J. Acoust. Soc. Am. 1979, 65, 719–731. [Google Scholar] [CrossRef]
- Pretlove, A.J. Free vibrations of a rectangular panel backed by a closed rectangular cavity. J. Sound Vib. 1965, 2, 197–209. [Google Scholar] [CrossRef]
- Pretlove, A.J.; Craggs, A. A simple approach to coupled panel-cavity vibrations. J. Sound Vib. 1970, 11, 207-IN1. [Google Scholar] [CrossRef]
- Qaisi, M.I. Free vibrations of a rectangular plate-cavity system. Appl. Acoust. 1988, 24, 49–61. [Google Scholar] [CrossRef]
- Rajalingham, C.; Bhat, R.B.; Xistris, G.D. Natural vibration of a cavity backed rectangular plate using a receptor-rejector system model. J. Vib. Acoust. 1995, 117, 416. [Google Scholar] [CrossRef]
- Rajalingham, C.; Bhat, R.B.; Xistris, G.D. Vibration of circular membrane backed by cylindrical cavity. Int. J. Mech. Sci. 1998, 40, 723–734. [Google Scholar] [CrossRef]
- Gladwell, G.M.L.; Zimmermann, G. On energy and complementary energy formulations of acoustic and structural vibration problems. J. Sound Vib. 1966, 3, 233–241. [Google Scholar] [CrossRef]
- Liu, H.; Olson, D.A.; Yu, M. Modeling of an air-backed diaphragm in dynamic pressure sensors: Effects of the air cavity. J. Sound Vib. 2014, 333, 7051–7075. [Google Scholar] [CrossRef]
- Dong, Q.; Bae, H.; Zhang, Z.; Chen, Y.; Wen, Z.; Olson, D.A.; Yu, M.; Liu, H. Miniature fiber optic acoustic pressure sensors with air-backed graphene diaphragms. J. Vib. Acoust. 2019, 141, 041003. [Google Scholar] [CrossRef]
- Blackstock, D.T. Fundamentals of Physical Acoustics; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Homentcovschi, D.; Miles, R.N. Viscous damping of perforated planar micromechanical structures. Sens. Actuators A Phys. 2005, 119, 544–552. [Google Scholar] [CrossRef]
- Bao, M.; Yang, H.; Sun, Y.; French, P.J. Modified Reynolds’ equation and analytical analysis of squeeze-film air damping of perforated structures. J. Micromech. Microeng. 2003, 13, 795–800. [Google Scholar] [CrossRef]
- Senturia, S.D. Microsystem Design; Springer: New York, NY, USA, 2000. [Google Scholar]


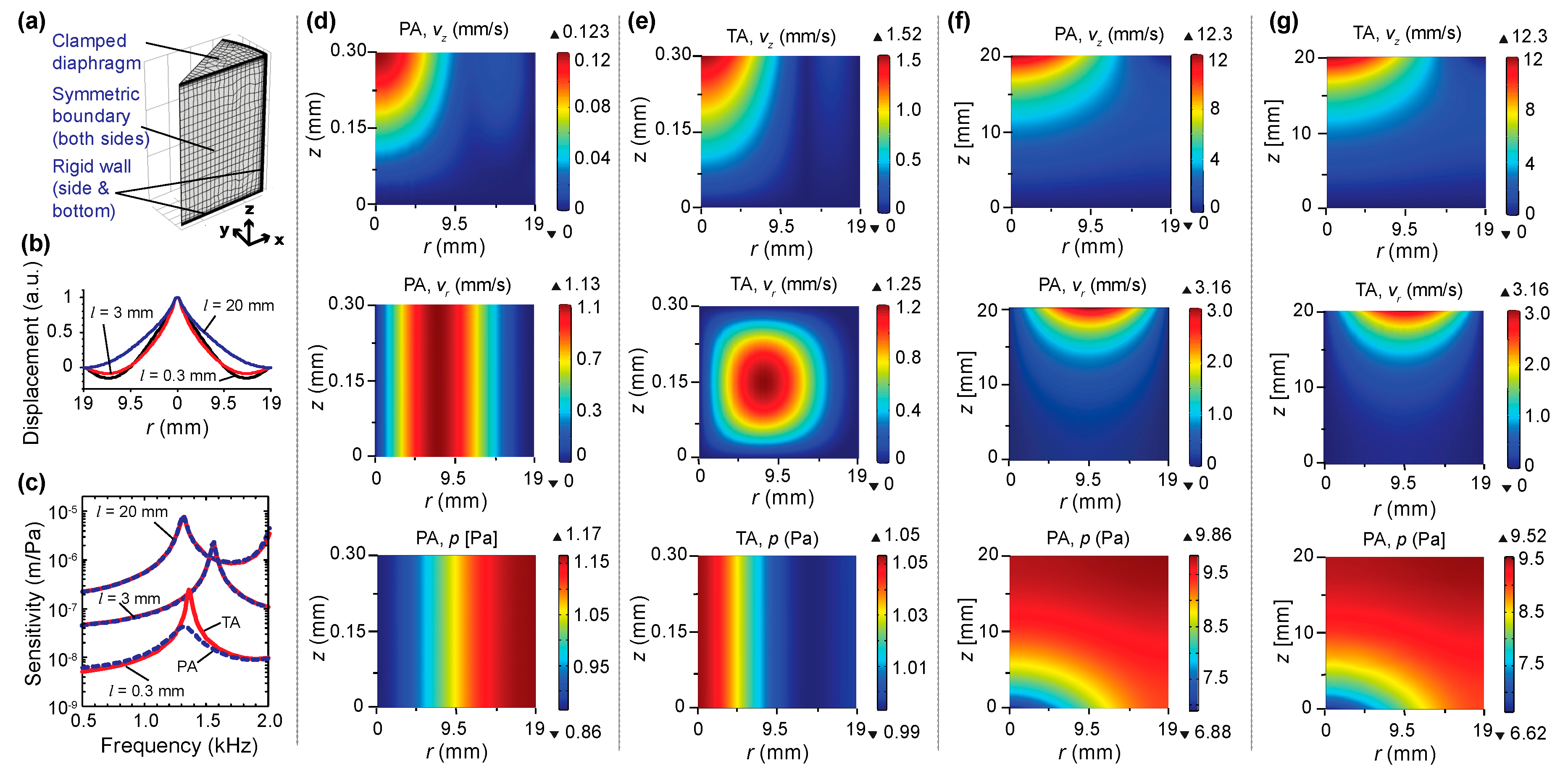
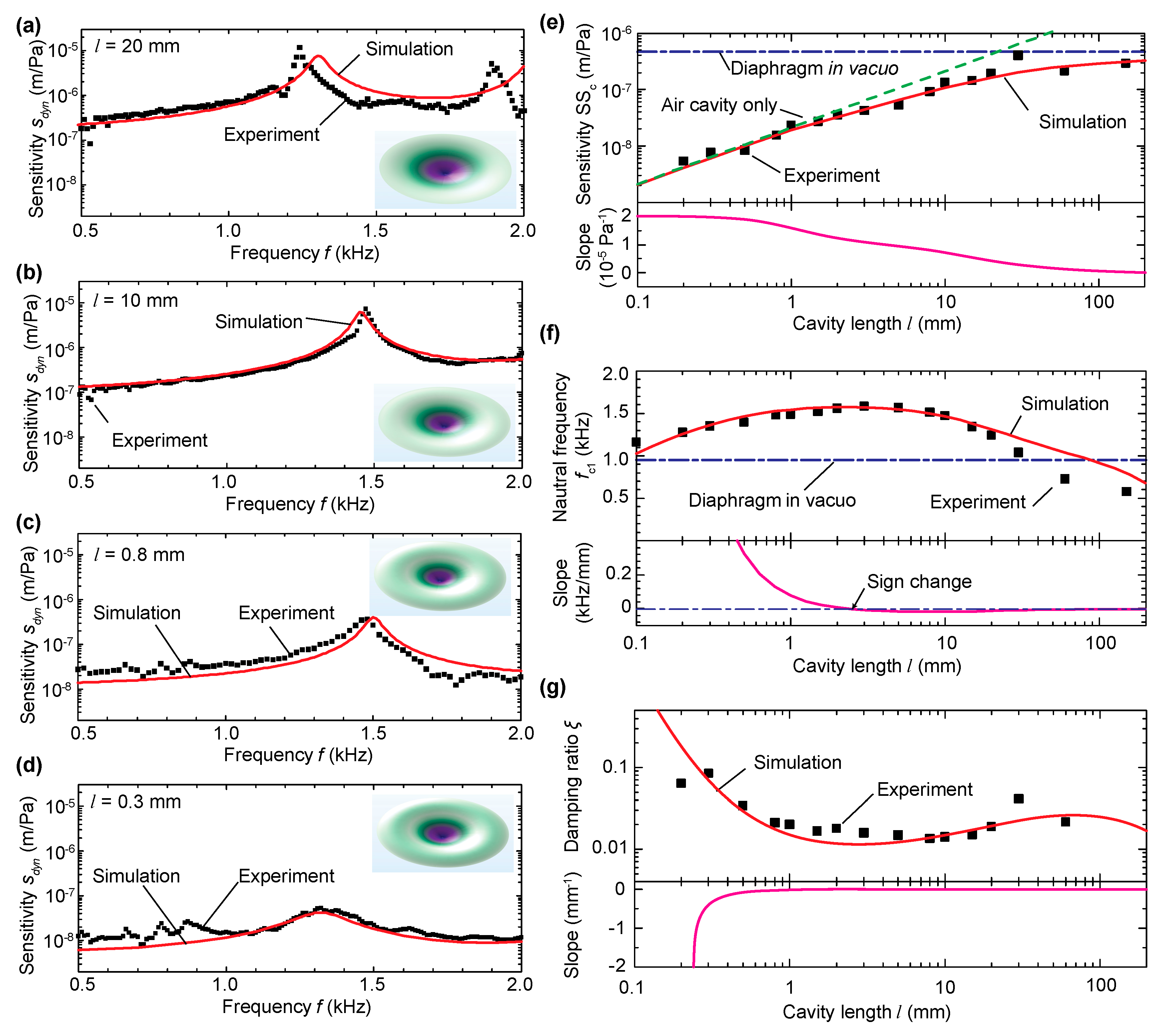
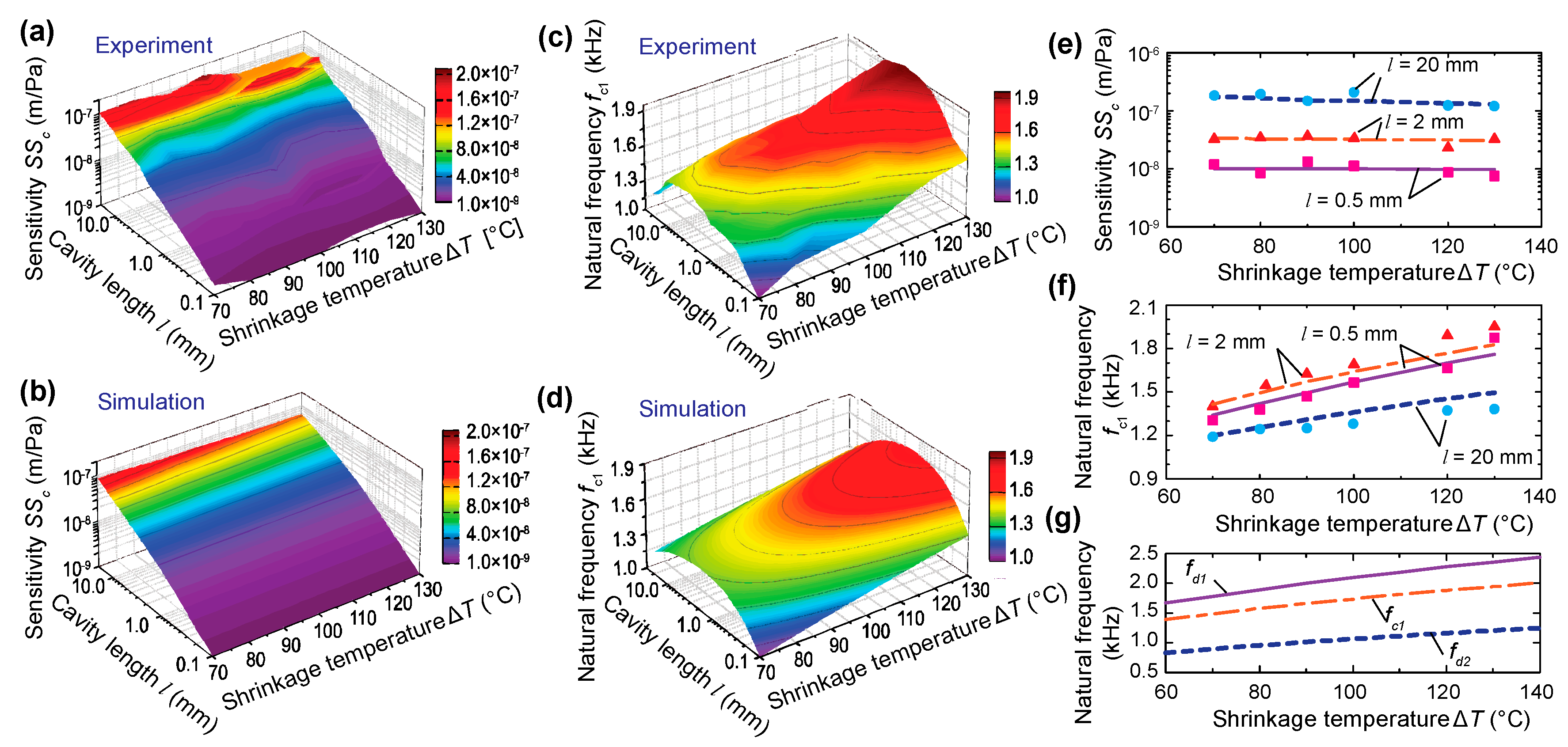
| Young’s modulus Ed | 2.2 GPa |
| Poisson’s ratio v | 0.3 |
| Density ρd | 1290 kg/m3 |
| Radius a | 19 mm |
| Thickness hd | 50.8 μm |
| Expansion temperature ΔT | 80 °C |
| Coefficient of thermal expansion μ | 12.8 × 10−6 K−1 |
| Rayleigh damping α (β = 0) | 500 s−1 |
| Point mass at the center | 3 mg |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Q.; Song, X.; Liu, H. Effects of Air Cavity in Dynamic Pressure Sensors: Experimental Validation. Sensors 2020, 20, 1759. https://doi.org/10.3390/s20061759
Dong Q, Song X, Liu H. Effects of Air Cavity in Dynamic Pressure Sensors: Experimental Validation. Sensors. 2020; 20(6):1759. https://doi.org/10.3390/s20061759
Chicago/Turabian StyleDong, Qian, Xiaolei Song, and Haijun Liu. 2020. "Effects of Air Cavity in Dynamic Pressure Sensors: Experimental Validation" Sensors 20, no. 6: 1759. https://doi.org/10.3390/s20061759
APA StyleDong, Q., Song, X., & Liu, H. (2020). Effects of Air Cavity in Dynamic Pressure Sensors: Experimental Validation. Sensors, 20(6), 1759. https://doi.org/10.3390/s20061759




