Validation of a Device to Measure Knee Joint Angles for a Dynamic Movement
Abstract
1. Introduction
2. Materials and Methods
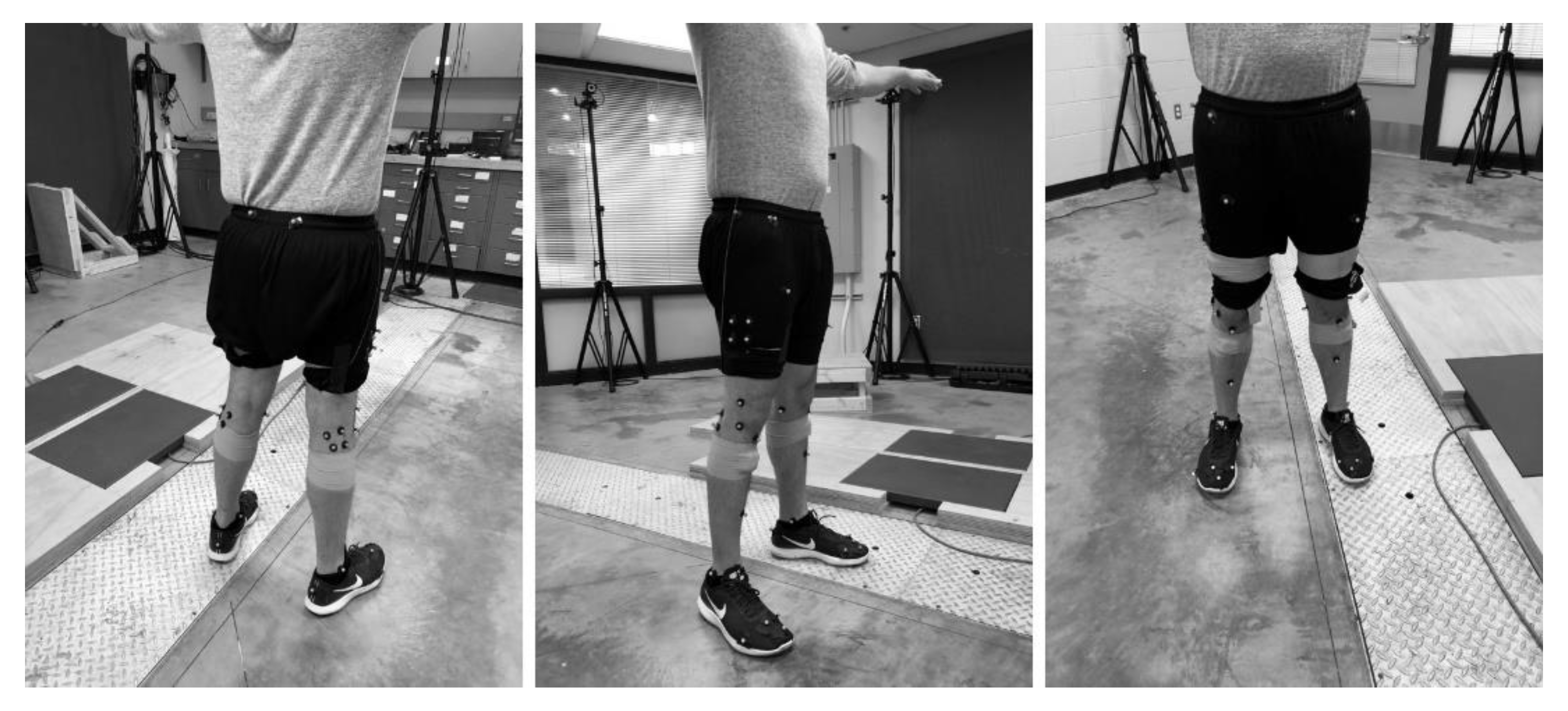
2.1. Subjects and Instrumentation
2.2. Testing Procedure
2.3. Statistical Analysis
3. Results
3.1. Root Mean Square Error (RMSE) and Linear Regression Model
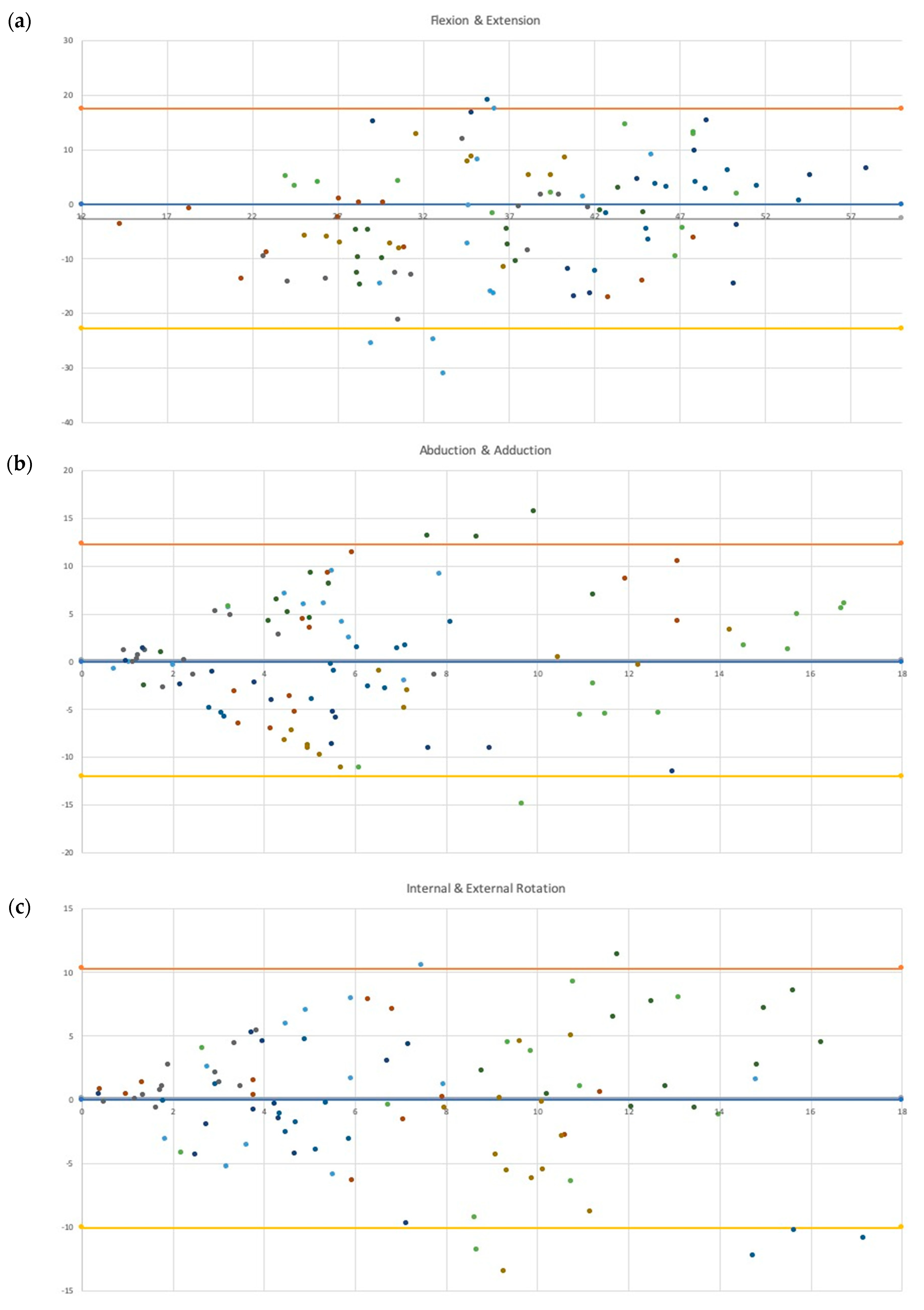
3.2. Bland–Altman Plots
3.3. Comparison of Means
4. Discussion
4.1. IMU Comparison
4.2. Potential IMU Performance
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Woods, R.A. Sports and Exercise Labor; U.S. Bureau of Labor Statistics: Washington, DC, USA, 2017; pp. 1–27.
- Saeed, I.O. MRI evaluation for post-traumatic knee joint injuries. J. Nurs. Health Sci. 2018, 7, 48–51. [Google Scholar]
- Alghamdi, W.; Alzahrani, A.; Alsuwaydi, A.; Alzahrani, A.; Albaqqar, O.; Fatani, M.; Alaidarous, H. Prevalence of cruciate logaments injury among physical education students of umm al-qura university and the relation betwen the dominant body side and ligament injury side in non-contact injury type. Am. J. Med. Med. Sci. 2017, 7, 14–19. [Google Scholar]
- Zebis, M.K.; Bencke, J.; Andersen, L.L.; Alkjaer, T.; Suetta, C.; Mortensen, P.; Kjaer, M.; Aagaard, P. Acute fatigue impairs neuromuscular activity of anterior cruciate ligament-agonist muscles in female team handball players. Scand. J. Med. Sci. Sports 2011, 21, 833–840. [Google Scholar] [CrossRef] [PubMed]
- Renstrom, P.; Ljungqvist, A.; Arendt, E.; Beynnon, B.; Fukubayashi, T.; Garrett, W.; Georgoulis, T.; Hewett, T.E.; Johnson, R.; Krosshaug, T.; et al. Non-contact ACL injuries in female athletes: An International Olympic Committee current concepts statement. Br. J. Sports Med. 2008, 42, 394–412. [Google Scholar] [CrossRef] [PubMed]
- Boden, B.P.; Dean, G.S.; Feagin, J.A., Jr.; Garrett, W.E., Jr. Mechanisms of anterior cruciate ligament injury. Orthopedics 2000, 23, 573–578. [Google Scholar] [CrossRef]
- Malinzak, R.A.; Colby, S.M.; Kirkendall, D.T.; Yu, B.; Garrett, W.E. A comparison of knee joint motion patterns between men and women in selected athletic tasks. Clin. Biomech. 2001, 16, 438–445. [Google Scholar] [CrossRef]
- Arendt, E.; Dick, R. Knee injury patterns among men and women in collegiate basketball and soccer. NCAA data and review of literature. Am. J. Sports Med. 1995, 23, 694–701. [Google Scholar] [CrossRef]
- Anderson, A.F.; Dome, D.C.; Gautam, S.; Awh, M.H.; Rennirt, G.W. Correlation of anthropometric measurements, strength, anterior cruciate ligament size, and intercondylar notch characteristics to sex differences in anterior cruciate ligament tear rates. Am. J. Sports Med. 2001, 29, 58–66. [Google Scholar] [CrossRef]
- Arendt, E.A.; Bershadsky, B.; Agel, J. Periodicity of noncontact anterior cruciate ligament injuries during the menstrual cycle. J. Gend. Specif. Med. 2002, 5, 19–26. [Google Scholar]
- Arif, M.; Kattan, A. Physical activities monitoring using wearable acceleration sensors attached to the body. PLoS ONE 2015, 10, e0130851. [Google Scholar] [CrossRef]
- Ananthanarayan, S.; Sheh, M.; Chien, A.; Profita, H.; Siek, K.A. Designing wearable interfaces for knee rehabilitation. In Proceedings of the 8th International Conference on Pervasive Computing Technologies for Healthcare, Oldenburg, Germany, 20–23 May 2014; pp. 101–108. [Google Scholar] [CrossRef]
- Griffin, L.Y.; Agel, J.; Albohm, M.J.; Arendt, E.A.; Dick, R.W.; Garrett, W.E.; Garrick, J.G.; Hewett, T.E.; Huston, L.; Ireland, M.L.; et al. Noncontact anterior cruciate ligament injuries: Risk factors and prevention strategies. J. Am. Acad. Orthop. Surg. 2000, 8, 141–150. [Google Scholar] [CrossRef] [PubMed]
- Olsen, O.E.; Myklebust, G.; Engebretsen, L.; Bahr, R. Injury mechanisms for anterior cruciate ligament injuries in team handball: A systematic video analysis. Am. J. Sports Med. 2004, 32, 1002–1012. [Google Scholar] [CrossRef] [PubMed]
- Koga, H.; Nakamae, A.; Shima, Y.; Iwasa, J.; Myklebust, G.; Engebretsen, L.; Bahr, R.; Krosshaug, T. Mechanisms for noncontact anterior cruciate ligament injuries: Knee joint kinematics in 10 injury situations from female team handball and basketball. Am. J. Sports Med. 2010, 38, 2218–2225. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.T.; Novak, A.C.; Brouwer, B.; Li, Q. Concurrent validation of Xsens MVN measurement of lower limb joint angular kinematics. Physiol. Meas. 2013, 34, N63–N69. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Jeon, K. Comparisons of knee and ankle joint angles and ground reaction force according to functional differences during single-leg drop landing. J. Phys. Ther. Sci. 2016, 28, 1150–1154. [Google Scholar] [CrossRef] [PubMed]
- Hewett, T.E.; Torg, J.S.; Boden, B.P. Video analysis of trunk and knee motion during non-contact anterior cruciate ligament injury in female athletes: Lateral trunk and knee abduction motion are combined components of the injury mechanism. Br. J. Sports Med. 2009, 43, 417–422. [Google Scholar] [CrossRef]
- Ageberg, E.; Forssblad, M.; Herbertsson, P.; Roos, E.M. Sex differences in patient-reported outcomes after anterior cruciate ligament reconstruction: Data from the Swedish knee ligament register. Am. J. Sports Med. 2010, 38, 1334–1342. [Google Scholar] [CrossRef]
- Agel, J.; Olson, D.E.; Dick, R.; Arendt, E.A.; Marshall, S.W.; Sikka, R.S. Descriptive epidemiology of collegiate women’s basketball injuries: National collegiate athletic association injury surveillance system, 1988–1989 through 2003–2004. J. Athl. Train. 2007, 42, 202–210. [Google Scholar]
- Cutti, A.G.; Ferrari, A.; Garofalo, P.; Raggi, M.; Cappello, A.; Ferrari, A. ‘Outwalk’: A protocol for clinical gait analysis based on inertial and magnetic sensors. Med. Biol. Eng. Comput. 2010, 48, 17–25. [Google Scholar] [CrossRef]
- Favre, J.; Aissaoui, R.; Jolles, B.M.; de Guise, J.A.; Aminian, K. Functional calibration procedure for 3D knee joint angle description using inertial sensors. J. Biomech. 2009, 42, 2330–2335. [Google Scholar] [CrossRef]
- Favre, J.; Crevoisier, X.; Jolles, B.M.; Aminian, K. Evaluation of a mixed approach combining stationary and wearable systems to monitor gait over long distance. J. Biomech. 2010, 43, 2196–2202. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.; Cutti, A.G.; Garofalo, P.; Raggi, M.; Heijboer, M.; Cappello, A.; Davalli, A. First in vivo assessment of “Outwalk”: A novel protocol for clinical gait analysis based on inertial and magnetic sensors. Med. Biol. Eng. Comput. 2010, 48, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.F.; Kulic, D. Human pose recovery using wireless inertial measurement units. Physiol. Meas. 2012, 33, 2099–2115. [Google Scholar] [CrossRef] [PubMed]
- Picerno, P.; Cereatti, A.; Cappozzo, A. Joint kinematics estimate using wearable inertial and magnetic sensing modules. Gait Posture 2008, 28, 588–595. [Google Scholar] [CrossRef]
- Bakhshi, S.; Mahoor, M.H.; Davidson, B.S. Development of a body joint angle measurement system using IMU sensors. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 6923–6926. [Google Scholar] [CrossRef]
- Takeda, R.; Tadano, S.; Natorigawa, A.; Todoh, M.; Yoshinari, S. Gait posture estimation using wearable acceleration and gyro sensors. J. Biomech. 2009, 42, 2486–2494. [Google Scholar] [CrossRef]
- Tong, K.; Granat, M.H. A practical gait analysis system using gyroscopes. Med. Eng. Phys. 1999, 21, 87–94. [Google Scholar] [CrossRef]
- Watanabe, T.; Saito, H. Tests of wireless wearable sensor system in joint angle measurement of lower limbs. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 5469–5472. [Google Scholar] [CrossRef]
- Teufl, W.; Miezal, M.; Taetz, B.; Frohlich, M.; Bleser, G. Validity of inertial sensor based 3D joint kinematics of static and dynamic sport and physiotherapy specific movements. PLoS ONE 2019, 14, e0213064. [Google Scholar] [CrossRef]
- Elvin, N.G.; Elvin, A.A.; Arnoczky, S.P. Correlation between ground reaction force and tibial acceleration in vertical jumping. J. Appl. Biomech. 2007, 23, 180–189. [Google Scholar] [CrossRef]
- Mukaka, M.M. Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Bell, K.M.; Onyeukwu, C.; McClincy, M.P.; Allen, M.; Bechard, L.; Mukherjee, A.; Hartman, R.A.; Smith, C.; Lynch, A.D.; Irrgang, J.J. Verification of a portable motion tracking system for remote management of physical rehabilitation of the knee. Sensors 2019, 19, 1021. [Google Scholar] [CrossRef] [PubMed]
- Zugner, R.; Tranberg, R.; Timperley, J.; Hodgins, D.; Mohaddes, M.; Karrholm, J. Validation of inertial measurement units with optical tracking system in patients operated with Total hip arthroplasty. BMC Musculoskelet. Disord. 2019, 20, 52. [Google Scholar] [CrossRef] [PubMed]
- Krosshaug, T.; Bahr, R. A model-based image-matching technique for three-dimensional reconstruction of human motion from uncalibrated video sequences. J. Biomech. 2005, 38, 919–929. [Google Scholar] [CrossRef] [PubMed]
- Allseits, E.; Kim, K.J.; Bennett, C.; Gailey, R.; Gaunaurd, I.; Agrawal, V. A novel method for estimating knee angle using two leg-mounted gyroscopes for continuous monitoring with mobile health devices. Sensors 2018, 18, 2759. [Google Scholar] [CrossRef] [PubMed]
- Taylor, L.; Miller, E.; Kaufman, K.R. Static and dynamic validation of inertial measurement units. Gait Posture 2017, 57, 80–84. [Google Scholar] [CrossRef]
- Fasel, B.; Sporri, J.; Chardonnens, J.; Kroll, J.; Muller, E.; Aminian, K. Joint inertial sensor orientation drift reduction for highly dynamic movements. IEEE J. Biomed. Health Inform. 2018, 22, 77–86. [Google Scholar] [CrossRef]
| Statistical Analysis | |||||
|---|---|---|---|---|---|
| Pearson’s R | RMSE | R-sq | Mean (SD) | 95% CI | |
| Flexion/Extension | 0.58 | 8.11 | 0.34 (p < 0.01) | 8.43 (6.33) | (7.16, 9.71) |
| Abduction/Adduction | 0.25 | 4.61 | 0.06 (p = 0.02) | 4.91 (3.70) | (4.17, 5.66) |
| Internal/External Rotation | 0.49 | 4.60 | 0.24 (p < 0.01) | 3.86 (3.40) | (3.18, 4.55) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajdaroski, M.; Tadakala, R.; Nichols, L.; Esquivel, A. Validation of a Device to Measure Knee Joint Angles for a Dynamic Movement. Sensors 2020, 20, 1747. https://doi.org/10.3390/s20061747
Ajdaroski M, Tadakala R, Nichols L, Esquivel A. Validation of a Device to Measure Knee Joint Angles for a Dynamic Movement. Sensors. 2020; 20(6):1747. https://doi.org/10.3390/s20061747
Chicago/Turabian StyleAjdaroski, Mirel, Ruchika Tadakala, Lorraine Nichols, and Amanda Esquivel. 2020. "Validation of a Device to Measure Knee Joint Angles for a Dynamic Movement" Sensors 20, no. 6: 1747. https://doi.org/10.3390/s20061747
APA StyleAjdaroski, M., Tadakala, R., Nichols, L., & Esquivel, A. (2020). Validation of a Device to Measure Knee Joint Angles for a Dynamic Movement. Sensors, 20(6), 1747. https://doi.org/10.3390/s20061747




