Experimental Study on Vibration Characteristics of Unit-Plate Ballastless Track Systems Laid on Long-Span Bridges Using Full-Scale Test Rigs
Abstract
1. Introduction
2. Test Program
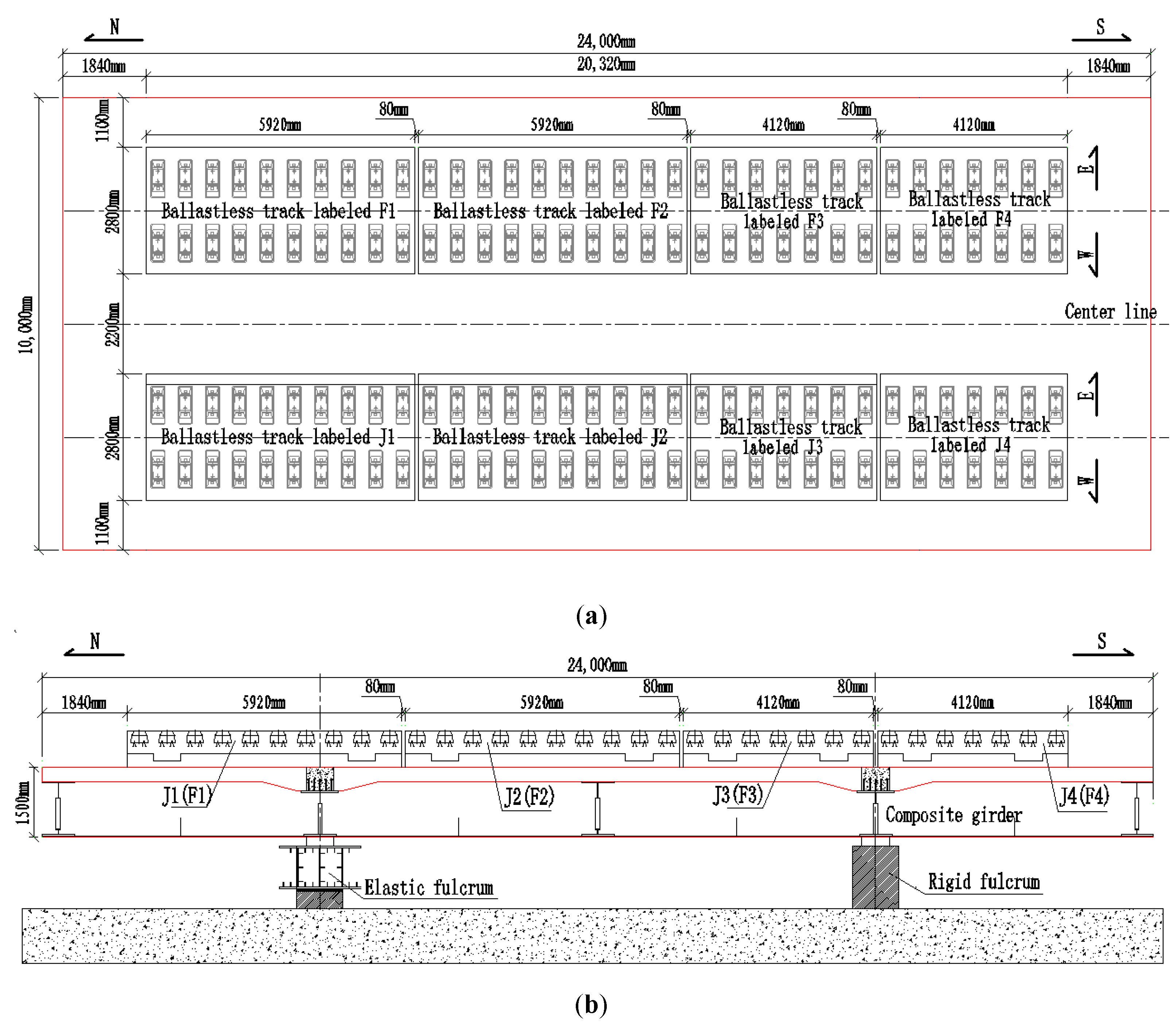
2.1. Description of the Test Rig
2.2. Sensors and Test Procedure
2.3. Modal Measurement
2.4. Vibration Characteristics Measurement
3. Modal Characteristics
4. Vibration Characteristics
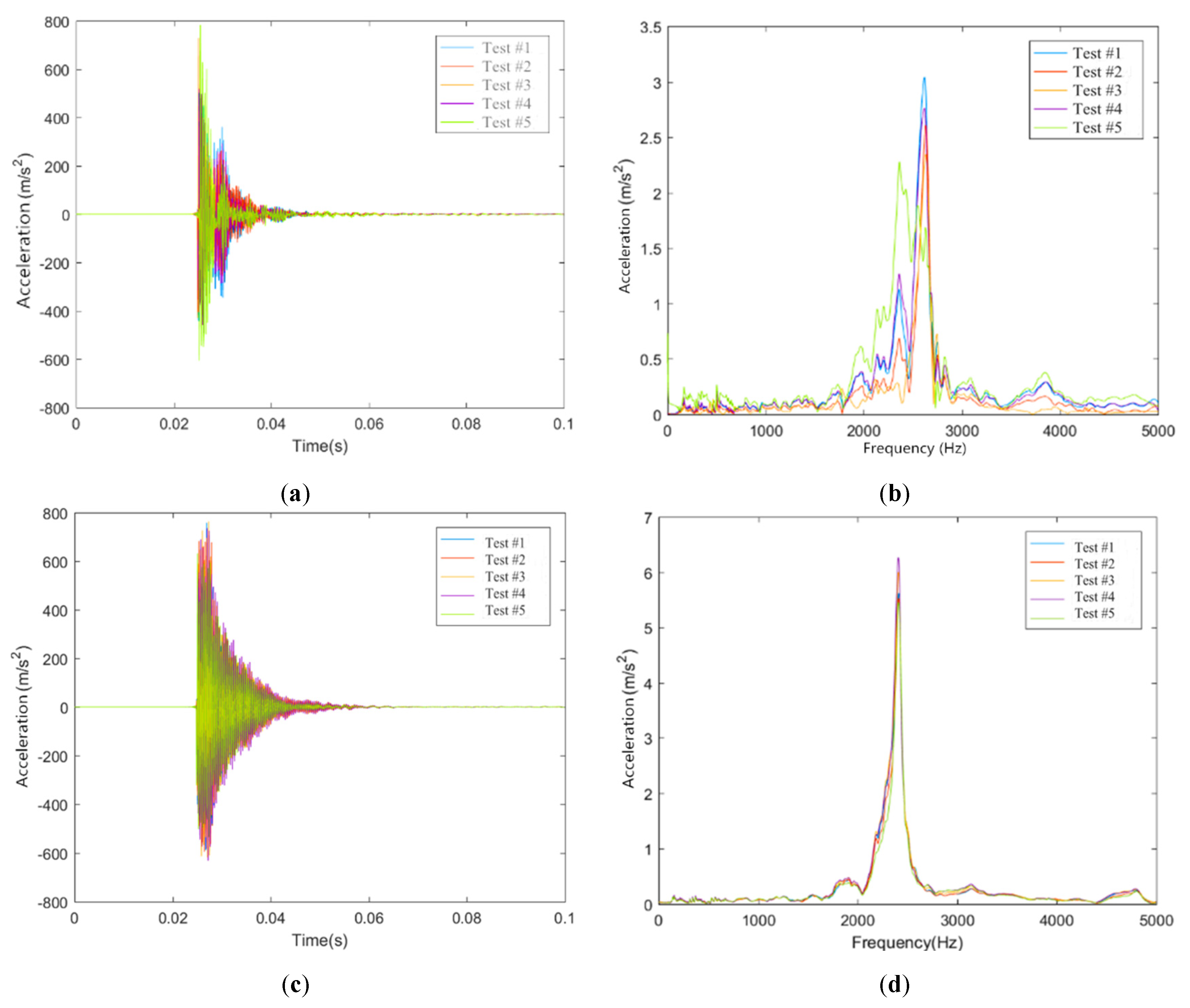
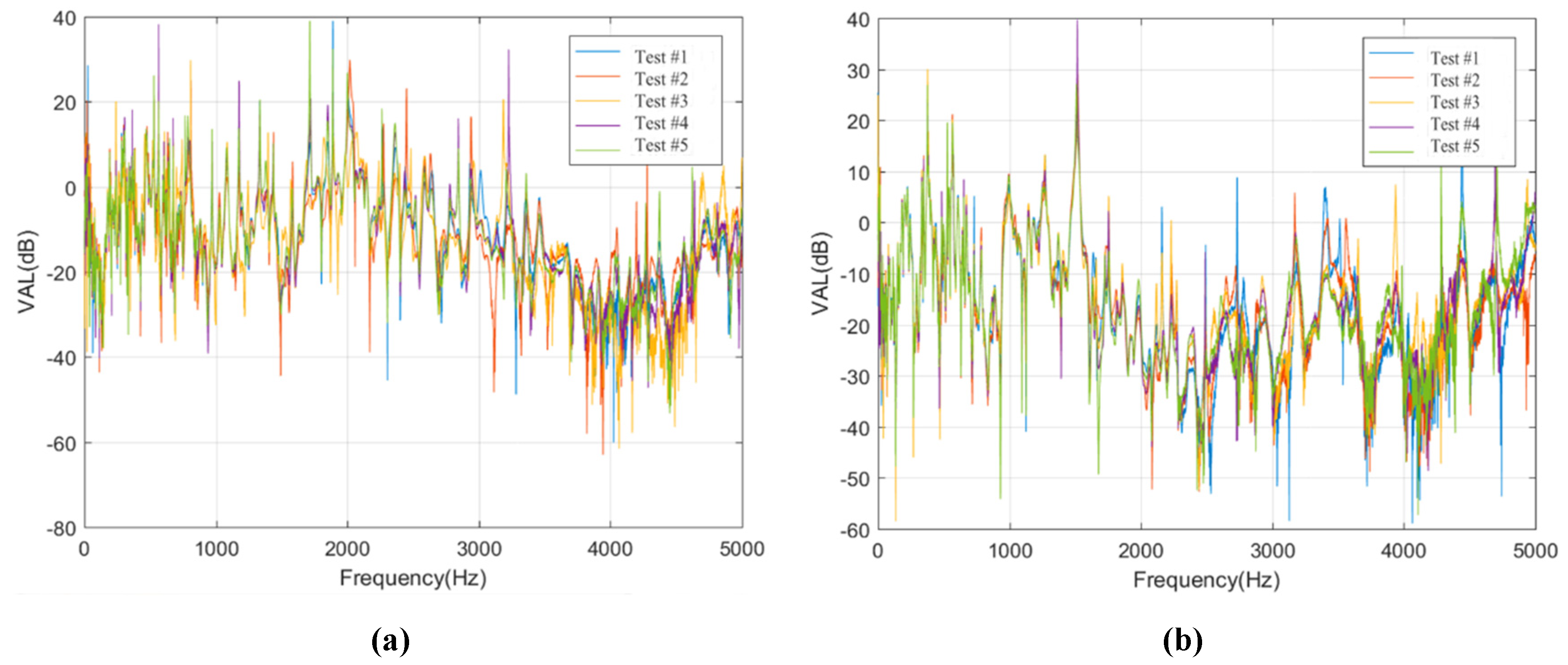
4.1. Vibration Characteristics of Rails
4.2. Vibration Characteristics of Track Slabs
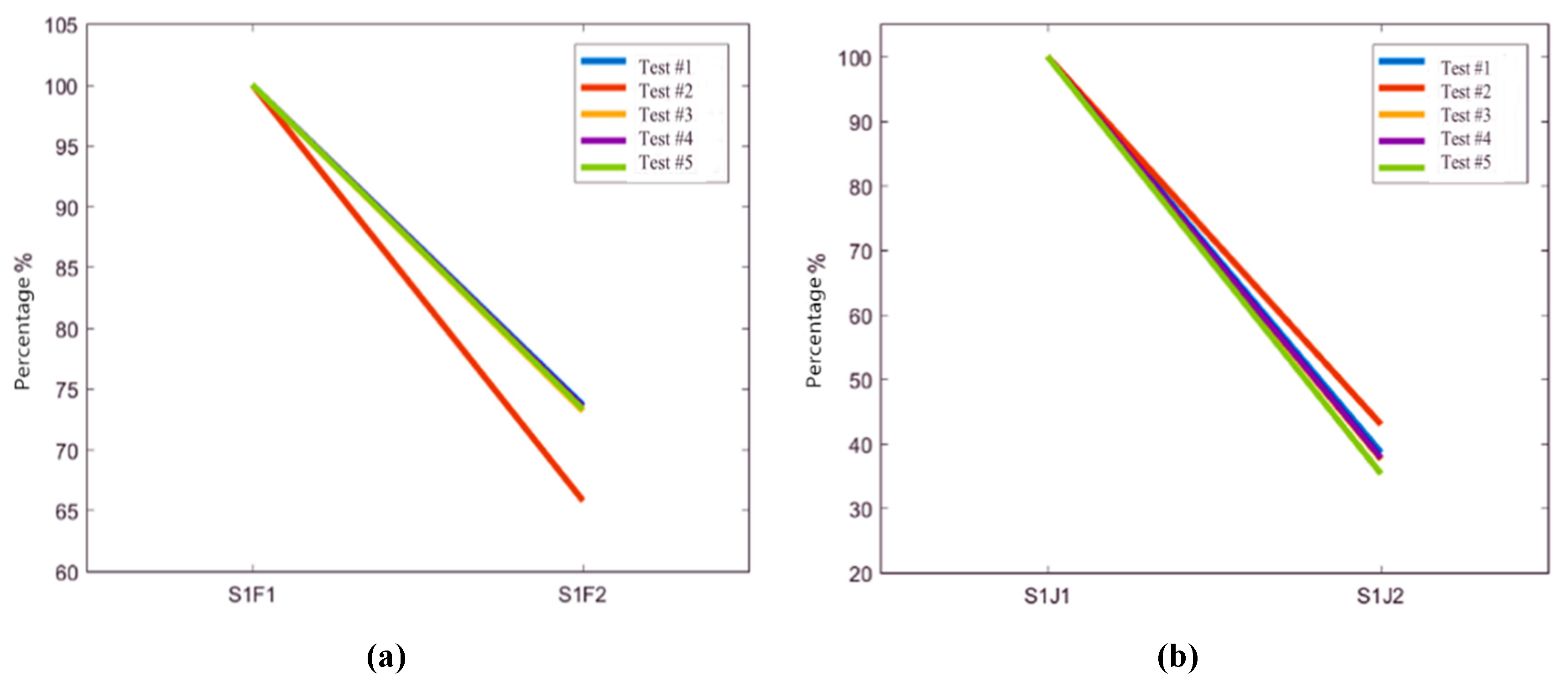
5. Vibration Transmission Characteristics
5.1. Evaluation Method of Vibration Transmission
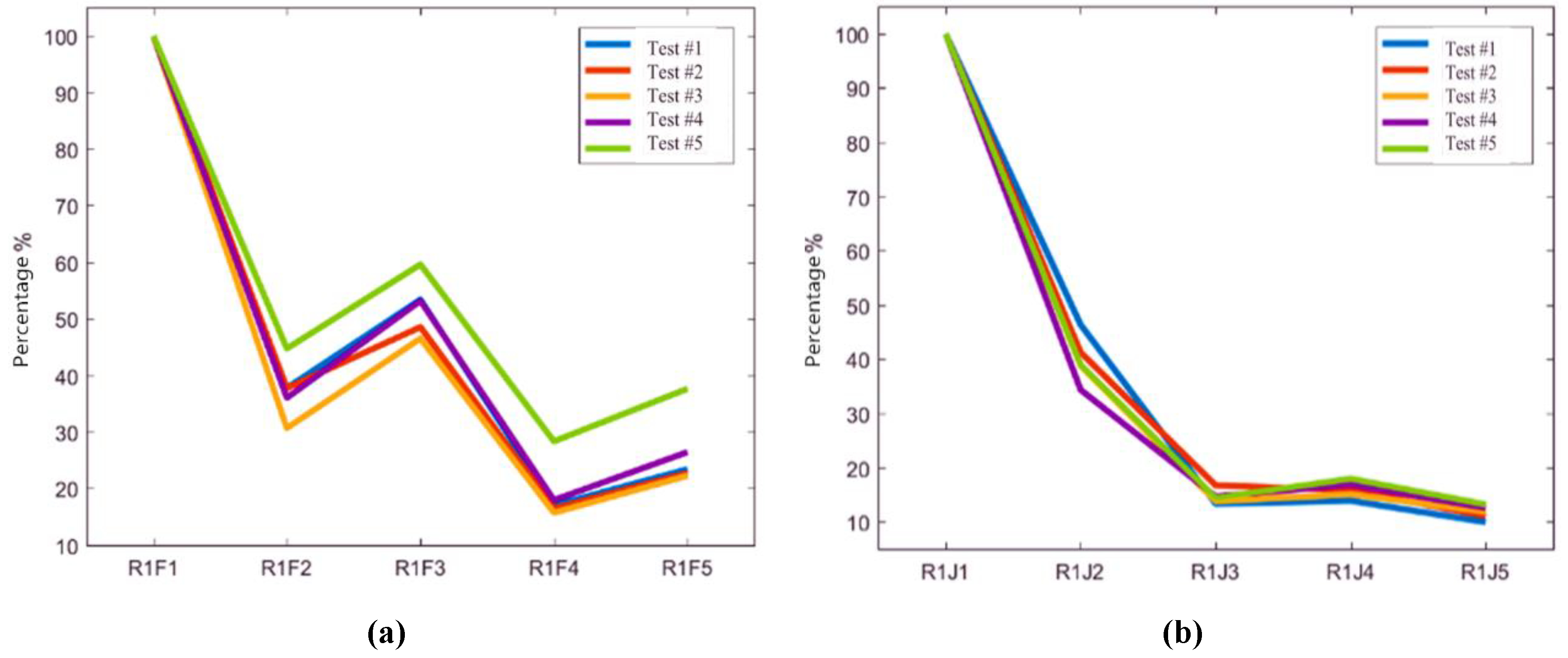
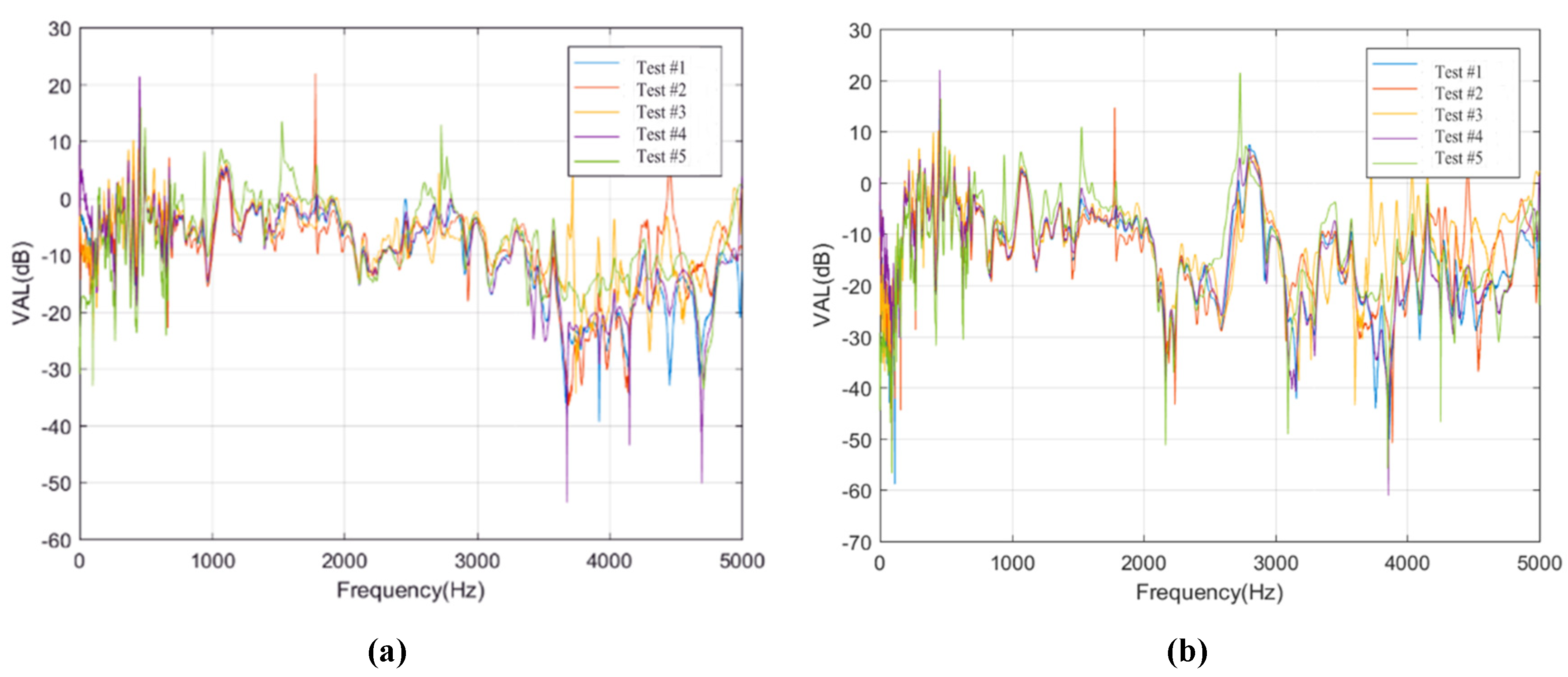
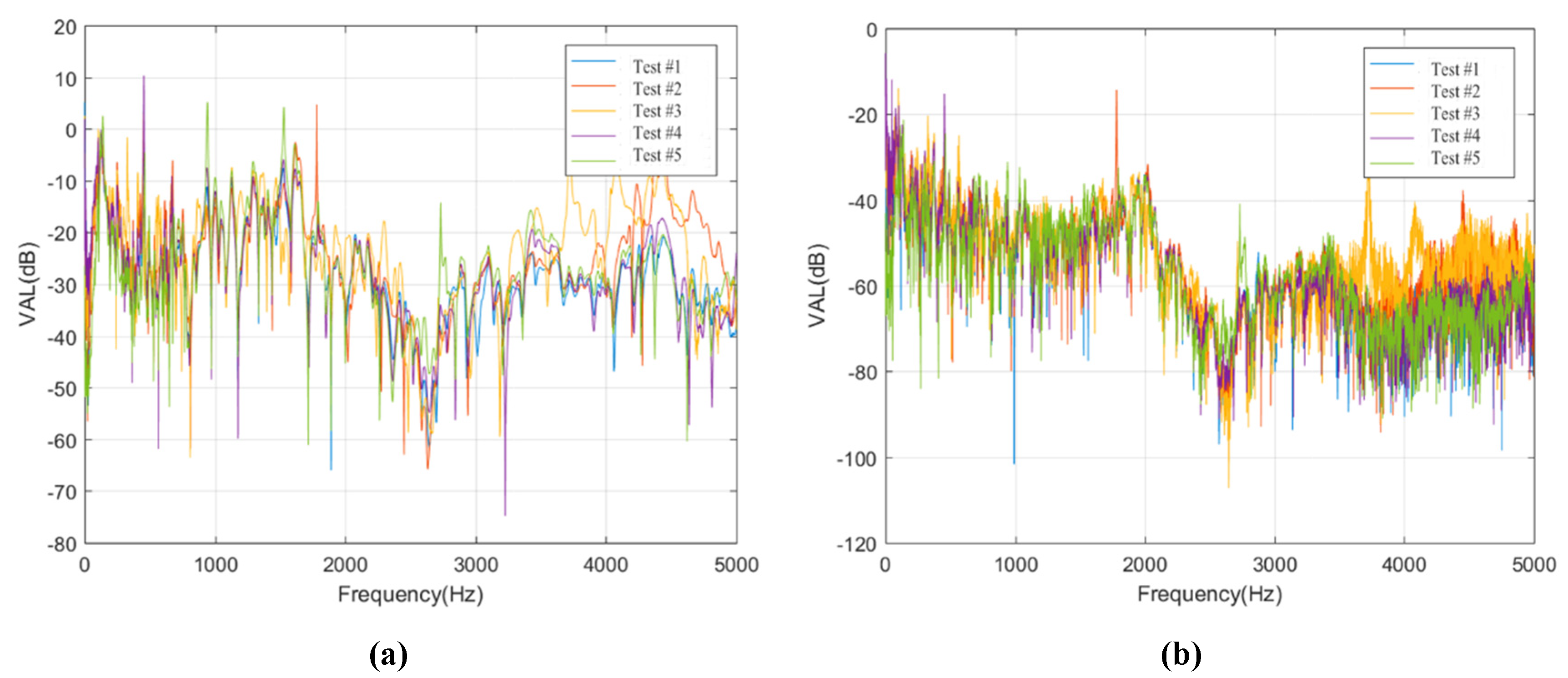
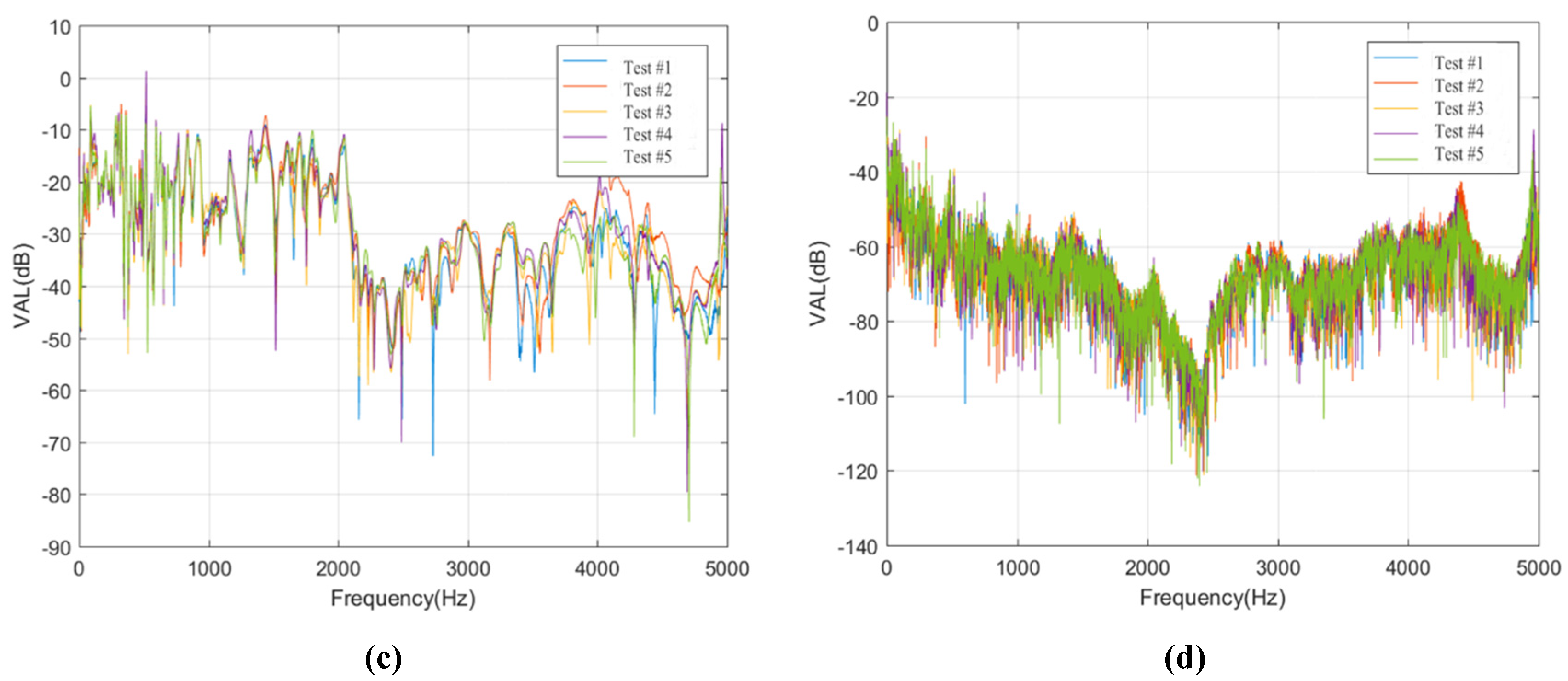
5.2. Vibration Transmission Characteristics of Rails
5.3. Vibration Transmission Characteristics of Track Slabs
5.4. Vibration Isolation Performances
6. Conclusions
- (1)
- The isolation layers change the vibration characteristics of track slab. The introduction of the rubber isolation layer in the ballastless track greatly reduces the vibration of track slab, and it also changes the vibration characteristics of track slab.
- (2)
- The isolation layers effect the vibration transmission characteristics in ballastless tracks. For the ballastless track with geotextile isolation layers or rubber isolation layers, the main difference of rail vibration is in frequency range of 2000 to 3000 Hz, and the reduction effects on rail vibration transmission caused by the rubber isolation layers are apparent. Moreover, the vibrations of the track slabs in ballastless tracks with geotextile or rubber isolation layers are reduced by 30% or 60%, which means that the vibration reduction effect of the rubber isolation layer is significant.
- (3)
- The application of rubber isolation layer makes the excited vibration frequency ranges of the ballastless tracks concentrated. Furthermore, the vibration attenuations of the ballastless tracks with rubber isolation layers are stable.
- (4)
- In the vertical vibration transmission process of the ballastless tracks with different types of isolation layers, the attenuation laws are slightly different in frequency domain. The vibration attenuation rate of the ballastless track with rubber isolation layers is about ten times larger than that of ballastless track with geotextile isolation layers, and the vibration reduction on vertical transmission in ballastless track with rubber isolation layers is apparent.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, M.Z.; Cai, C.B.; Zhu, S.Y.; Zhai, W.M. Experimental study on dynamic performance of typical ballastless track systems using a full-scale test rig. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 231, 1–12. [Google Scholar]
- Costa, P.A.; Calcada, R.; Cardoso, A.S. Track-ground vibrations induced by railway traffic: In-situ measurements and validation of a 2.5D FEM-BEM model. Soil Dyn. Earthq. Eng. 2012, 32, 111–128. [Google Scholar] [CrossRef]
- Ferreira, P.A.; Lopze-Pita, A. Numerical modelling of high speed train/track system for the reduction of vibration levels and maintenance needs of railway tracks. Constr. Build. Mater. 2015, 79, 14–21. [Google Scholar] [CrossRef]
- Zhai, W.M.; Wei, K.; Song, X.; Shao, M. Experimental investigation into ground vibrations induced by very high speed trains on a non-ballasted track. Soil Dyn. Earthq. Eng. 2015, 72, 24–36. [Google Scholar] [CrossRef]
- Galvin, P.; Dominguez, J. Experimental and numerical analyses of vibrations induced by high-speed trains on the Cordoba–Malaga line. Soil Dyn. Earthq. Eng. 2009, 29, 641–657. [Google Scholar]
- Zhu, S.Y.; Yang, J.Z.; Cai, C.B.; Pan, Z.L.; Zhai, W.M. Application of dynamic vibration absorbers in designing a vibration isolation track at low-ferquency domain. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 546–557. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Wang, L.D.; Costa, P.A.; Bai, Y.; Yu, Z.W. An efficient approach for predicting subway train-induced ground vibrations considering random track unevenness. J. Sound Vib. 2019, 455, 359–379. [Google Scholar] [CrossRef]
- Cox, S.J.; Wang, A.; Morison, C.; Carels, P.; Kelly, R.; Bewes, O.G. A test rig to investigate slab track structures for controlling ground vibration. J. Sound Vib. 2006, 293, 901–909. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Wang, P. Experimental study on dynamic characteristic of rail-fastener coupled system. J. Vib. Meas. Diagn. 2014, 34, 680–685. [Google Scholar]
- Zhao, C.Y.; Wang, P. Experimental study on the vibration damping performance of rubber absorbs for ballastless tracks on viaduct. China Railw. Sci. 2013, 34, 8–13. [Google Scholar]
- Lee, Y.Y.; Ngai, K.W.; Ng, C.F. The local vibration modes due to impact on the edge of a viaduct. Appl. Acoust. 2004, 11, 1077–1093. [Google Scholar] [CrossRef]
- Kraśkiewicz, C.; Lipko, C.; Płudowska, M. Static and Dynamic Characteristics of Resilient Mats for Vibration Isolation of Railway Tracks. Procedia Eng. 2016, 153, 317–324. [Google Scholar] [CrossRef]
- Li, X.Z.; Song, L.Z.; Zhang, X. Study on vibration transmission characteristics of high-speed railway simply-supported box-girders based on in-situ hammer excitation test. China Civ. Eng. J. 2016, 49, 120–128. [Google Scholar]
- Sheng, X.W.; Zheng, W.Q.; Zhu, Z.H.; Yan, A.G.; Qin, Y.P. Ganjiang Bridge: A high-speed railway long-span cable-stayed bridge laying ballastless tracks. Struct. Eng. Int. 2019, 10, 1671157. [Google Scholar] [CrossRef]
- Cui, R.X.; Gao, L.; Cai, X.P.; Hou, B.W. Vibration and noise reduction properties of different damped rails in high-speed railway. Noise Control Eng. J. 2014, 62, 176–185. [Google Scholar] [CrossRef]
- Liu, L.Y.; Song, R.; Zhou, Y.L.; Qin, J.L. Noise and vibration mitigation performance of damping pad under CRTS-Ⅲ ballastless track in high speed rail viaduct. KSCE J. Civ. Eng. 2019, 23, 3525–3534. [Google Scholar] [CrossRef]
- Huang, J.J.; Su, Q.; Wang, W.; Phong, P.D.; Liu, K.W. Field investigation and full-scale model testing of mud pumping and its effect on the dynamic properties of the slab track-subgrade interface. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 802–816. [Google Scholar] [CrossRef]
- Sheng, X.W.; Zheng, W.Q.; Zhu, Z.H. Mechanical behaviors and fatigue performance of the ballastless tracks laid on the long-span cable-stayed bridge with different arrangements. Sensors 2019, 19, 4195. [Google Scholar] [CrossRef]
- Bian, X.C.; Jiang, H.G.; Cheng, C.; Chen, Y.M.; Chen, R.P.; Jiang, J.Q. Full-scale model testing on a ballastless high-speed railway under simulated train moving loads. Soil Dyn. Earthq. Eng. 2014, 66, 368–384. [Google Scholar] [CrossRef]
- Jiang, H.W.; Gao, L. Study of the vibration-energy properties of the CRTS-Ⅲ track based on the power flow method. Symmetry 2019, 12, 69. [Google Scholar] [CrossRef]
- Dai, G.L.; Ge, H.; Liu, W.S.; Chen, Y.F. Interaction analysis of continuous slab track (CST) on large-span continuous high-speed rail bridges. Struct. Eng. Mech. 2017, 63, 713–723. [Google Scholar]
- Yu, Z.W.; Xie, Y.; Tian, X.Q. Research on Mechanical Performance of CRTS III Plate-Type Ballastless Track Structure under Temperature Load Based on Probability Statistics. Adv. Civ. Eng. 2019, 8, 2975274. [Google Scholar] [CrossRef]
- Ministry of Railways of the People’s Republic of China (MRPRC). TB 10621-2014: Code for Design of High Speed Railway; China Railway Publishing House: Beijing, China, 2015. [Google Scholar]
- Ministry of Railways of the People’s Republic of China (MRPRC). TJ/GW 114-2013: Temporary Technical Conditions of EPDM Elastic Buffer Cushion for CRTS III Plate Ballastless Track of High Speed Railway; China Railway Publishing House: Beijing, China, 2013. [Google Scholar]
- Sheng, X.W.; Zheng, W.Q.; Zhu, Z.H.; Luo, T.J.; Zheng, Y.H. Properties of rubber under-ballast mat used as ballastless track isolation layer in high-speed railway. Constr. Build. Mater. 2020, 240, 117822. [Google Scholar] [CrossRef]
- Kouroussis, G.; Verlinden, O.; Conti, C. Free field vibrations caused by high-speed lines: Measurement and time domain simulation. Soil Dyn. Earthq. Eng. 2011, 31, 692–707. [Google Scholar] [CrossRef]
- Huang, C.F.; Wang, P.; He, M.C.; Xiao, J.Y.; Ju, S.; Jiang, D. Analysis of natural vibration characteristics of large composite truss structure based on hammering method. J. Natl. Univ. Def. Technol. 2018, 40, 37–41. [Google Scholar]
- General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. GB/T 13441.1-2007 Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-Body Vibration-Part 1: General Requirements; Standards Press of China: Beijing, China, 2007. [Google Scholar]








| Ballastless Track with Geotextile Isolation Layers | Ballastless Track with Rubber Isolation Layers | ||
|---|---|---|---|
| First-order mode | Frequency (Hz) | First-order mode | Frequency (Hz) |
 | 97.8 | 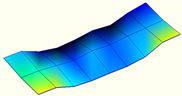 | 34.4 |
| Second-order mode | Frequency (Hz) | Second-order mode | Frequency (Hz) |
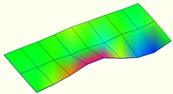 | 112.1 |  | 54.6 |
| Third-order mode | Frequency (Hz) | Third-order mode | Frequency (Hz) |
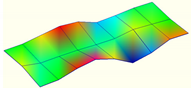 | 140.4 | 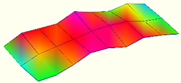 | 63.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, W.; Sheng, X.; Zhu, Z.; Luo, T.; Liu, Z. Experimental Study on Vibration Characteristics of Unit-Plate Ballastless Track Systems Laid on Long-Span Bridges Using Full-Scale Test Rigs. Sensors 2020, 20, 1744. https://doi.org/10.3390/s20061744
Zheng W, Sheng X, Zhu Z, Luo T, Liu Z. Experimental Study on Vibration Characteristics of Unit-Plate Ballastless Track Systems Laid on Long-Span Bridges Using Full-Scale Test Rigs. Sensors. 2020; 20(6):1744. https://doi.org/10.3390/s20061744
Chicago/Turabian StyleZheng, Weiqi, Xingwang Sheng, Zhihui Zhu, Tianjing Luo, and Zecheng Liu. 2020. "Experimental Study on Vibration Characteristics of Unit-Plate Ballastless Track Systems Laid on Long-Span Bridges Using Full-Scale Test Rigs" Sensors 20, no. 6: 1744. https://doi.org/10.3390/s20061744
APA StyleZheng, W., Sheng, X., Zhu, Z., Luo, T., & Liu, Z. (2020). Experimental Study on Vibration Characteristics of Unit-Plate Ballastless Track Systems Laid on Long-Span Bridges Using Full-Scale Test Rigs. Sensors, 20(6), 1744. https://doi.org/10.3390/s20061744





