Non-Destructive Evaluation Device for Monitoring Fluid Viscosity
Abstract
1. Introduction
2. Design and Fabrication
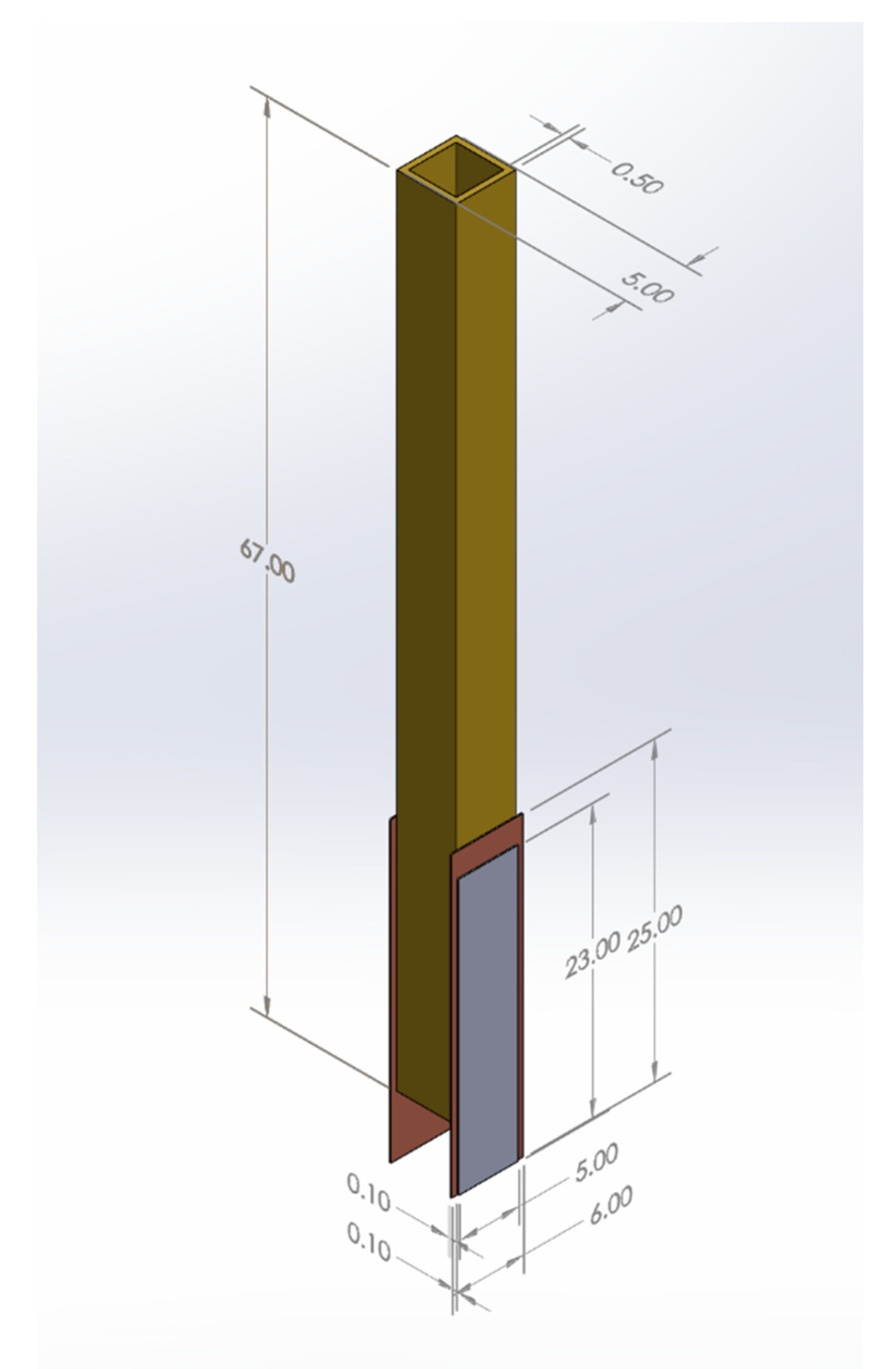
2.1. Design
2.2. Fabrication
2.2.1. Materials
2.2.2. Assembly
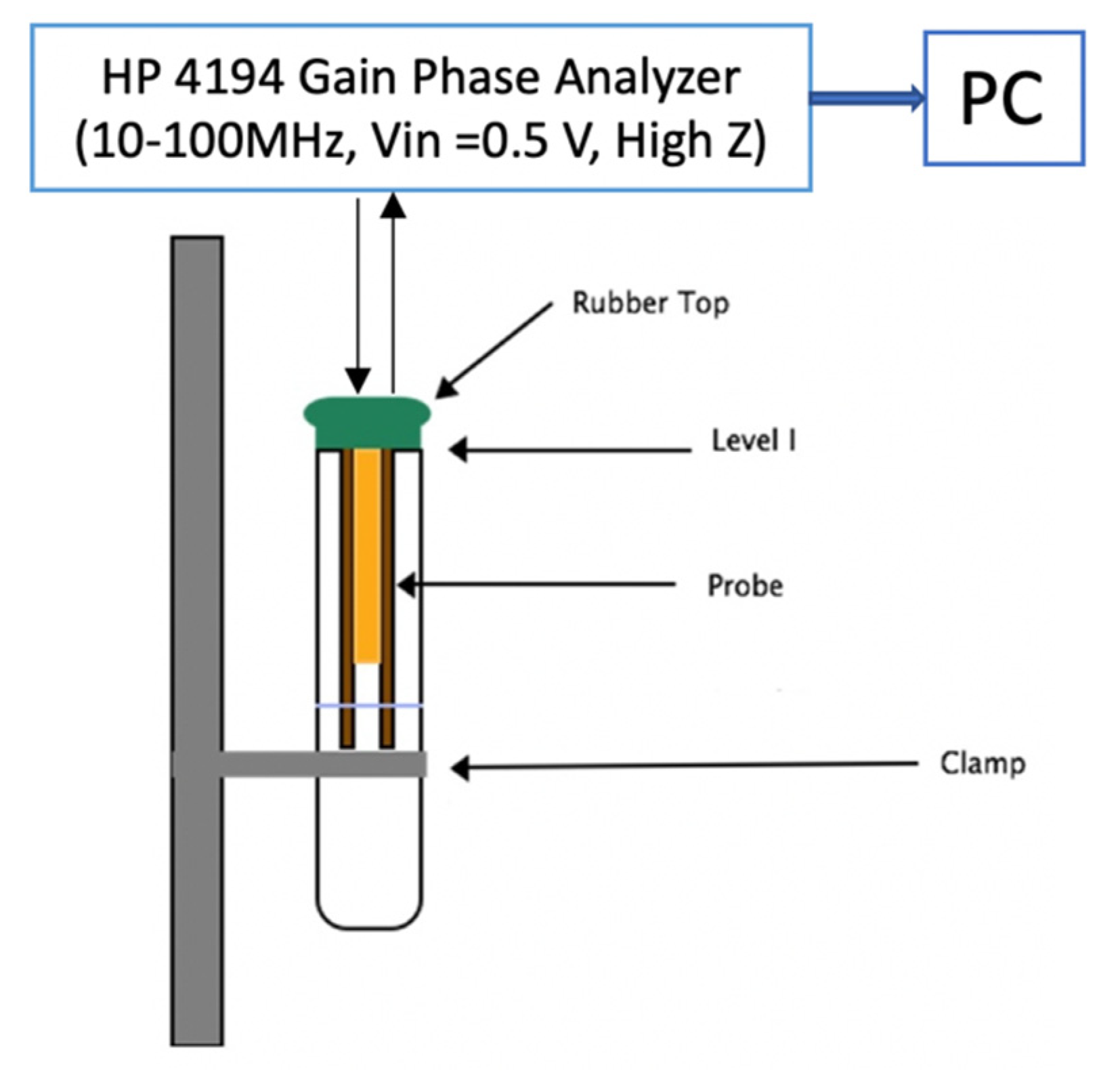
3. Experimental Setup
4. Modeling
5. Results
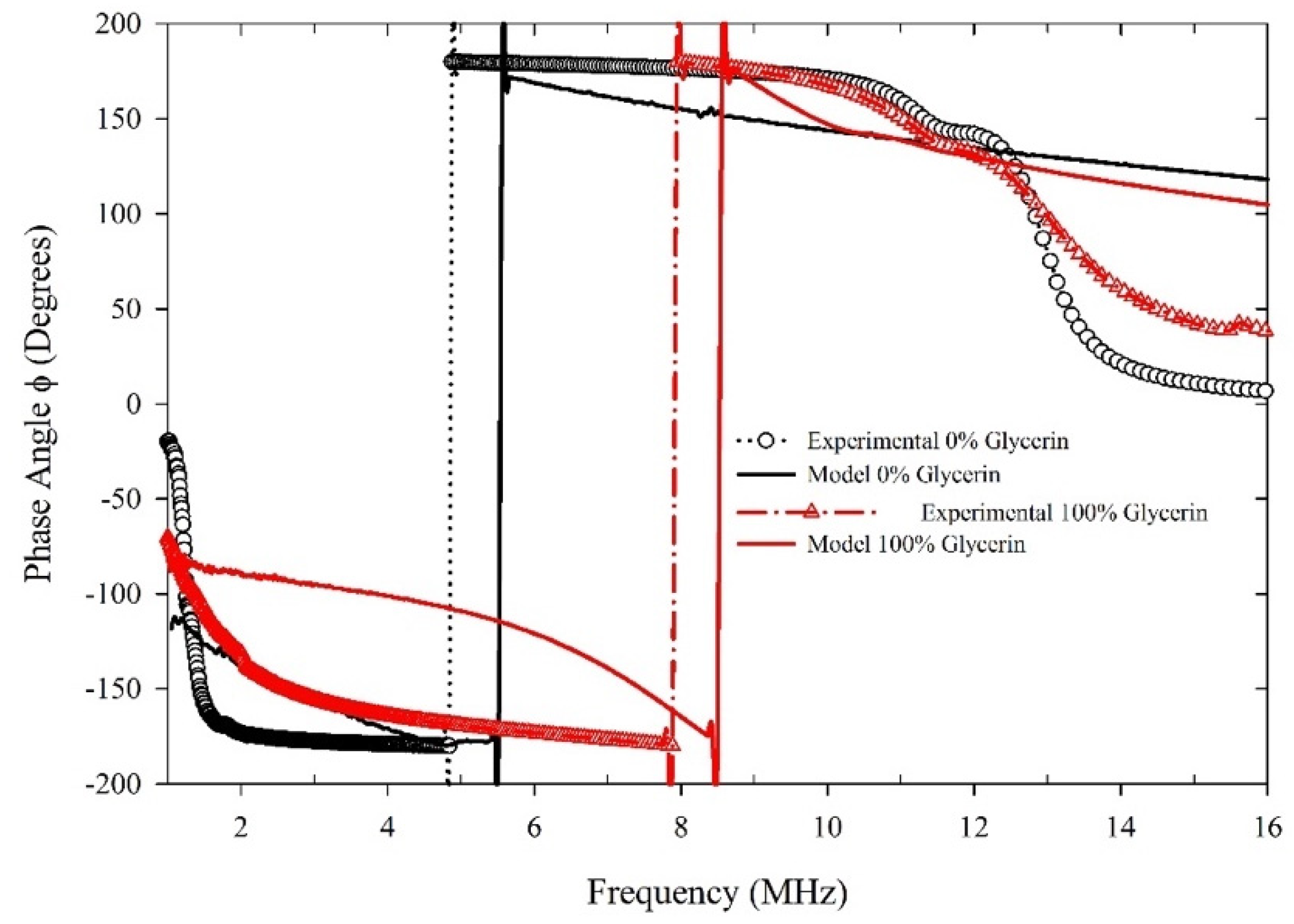
5.1. Experimental Phase Shift Measurements
5.2. Numerical Simulation Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Antlinger, H.; Clara, S.; Beigelbeck, R.; Cerimovic, S.; Keplinger, F.; Jakoby, B. Sensing the characteristic acoustic impedance of a fluid utilizing acoustic pressure waves. Sens. Actuators Phys. 2012, 186, 94–99. [Google Scholar] [CrossRef] [PubMed]
- Jakoby, B.; Vellekoop, M.J. Physical sensors for liquid properties. IEEE Sens. J. 2011, 11, 3076–3085. [Google Scholar] [CrossRef]
- Youssry, M.; Belmiloud, N.; Caillard, B.; Ayela, C.; Pellet, C.; Dufour, I. A straightforward determination of fluid viscosity and density using microcantilevers: From experimental data to analytical expressions. Sens. Actuators Phys. 2011, 172, 40–46. [Google Scholar] [CrossRef]
- Zhu, X.; Zhong, C.; Zhe, J. Lubricating oil conditioning sensors for online machine health monitoring–A review. Tribol. Int. 2017, 109, 473–484. [Google Scholar] [CrossRef]
- Toledo, J.; Jiménez-Márquez, F.; Úbeda, J.; Ruiz-Díez, V.; Pfusterschmied, G.; Schmid, U.; Sánchez-Rojas, J.L. Piezoelectric MEMS resonators for monitoring grape must fermentation. J. Phys. Conf. Ser. 2016, 757, 012020. [Google Scholar] [CrossRef]
- Muñoz, J.A.; Ancheyta, J.; Castañeda, L.C. Required viscosity values to ensure proper transportation of crude oil by pipeline. Energy Fuels 2016, 30, 8850–8854. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.; Zu, H.; Wang, J.H.-C.; Wang, Q.-M. Real-time monitoring of platelet activation using quartz thickness-shear mode resonator sensors. Biophys. J. 2016, 110, 669–679. [Google Scholar] [CrossRef]
- Anderson, A.M.; Bruno, B.A.; Smith, L.S. Viscosity measurement. Mech. Eng. Handb. 2014, 1, 1–28. [Google Scholar]
- Antlinger, H.; Clara, S.; Beigelbeck, R.; Cerimovic, S.; Keplinger, F.; Jakoby, B. Utilizing acoustic pressure waves for sensing fluid properties. Procedia Eng. 2011, 25, 775–778. [Google Scholar] [CrossRef][Green Version]
- Zhao, L.; Hu, Y.; Wang, T.; Ding, J.; Liu, X.; Zhao, Y.; Jiang, Z. A MEMS resonant sensor to measure fluid density and viscosity under flexural and torsional vibrating modes. Sensors 2016, 16, 830. [Google Scholar] [CrossRef]
- Ma, J.; Huang, X.; Bae, H.; Zheng, Y.; Liu, C.; Zhao, M.; Yu, M. Liquid viscosity measurement using a vibrating flexure hinged structure and a fiber-optic sensor. IEEE Sens. J. 2016, 16, 5249–5258. [Google Scholar] [CrossRef]
- Hongbin, Y.; Liang, L.; Yuandong, A.G. Capacitive micromachined ultrasonic transducer (CMUT) based micro viscosity sensor. Sens. Actuators B Chem. 2016, 227, 346–351. [Google Scholar] [CrossRef]
- Nwankwo, E.; Durning, C.J. Fluid property investigation by impedance characterization of quartz crystal resonators: Part I: Methodology, crystal screening, and Newtonian fluids. Sens. Actuators Phys. 1999, 72, 99–109. [Google Scholar] [CrossRef]
- Shah, V.V.; Balasubramaniam, K. Measuring Newtonian viscosity from the phase of reflected ultrasonic shear wave. Ultrasonics 2000, 38, 921–927. [Google Scholar] [CrossRef]
- Markova, L.V.; Makarenko, V.M.; Semenyuk, M.S.; Zozulya, A.P. On-line monitoring of the viscosity of lubricating oils. J. Frict. Wear 2010, 31, 433–442. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Kaluvan, S. PZN-PT based smart probe for high temperature fluid viscosity measurements. Measurement 2016, 94, 753–758. [Google Scholar] [CrossRef]
- Aguilar Sandoval, F.; Sepúlveda, M.; Bellon, L.; Melo, F. High resolution viscosity measurement by thermal noise detection. Sensors 2015, 15, 27905–27916. [Google Scholar] [CrossRef]
- Yan, F.; Chan, H.L. Analytical model of piezoelectric cantilever as rheological sensor. Phys. B Condens. Matter 2011, 406, 3605–3608. [Google Scholar] [CrossRef]
- Ju, F.; Ling, S.-F. Sensing fluid viscosity and density through mechanical impedance measurement using a whisker transducer. Meas. Sci. Technol. 2013, 24, 055105. [Google Scholar] [CrossRef]
- Goodwin, A.R.H.; Fitt, A.D.; Ronaldson, K.A.; Wakeham, W.A. A vibrating plate fabricated by the methods of microelectromechanical systems (MEMS) for the simultaneous measurement of density and viscosity: Results for argon at temperatures between 323 and 423K at pressures up to 68 MPa. Int. J. Thermophys. 2006, 27, 1650–1676. [Google Scholar] [CrossRef]
- Etchart, I.; Chen, H.; Dryden, P.; Jundt, J.; Harrison, C.; Hsu, K.; Marty, F.; Mercier, B. MEMS sensors for density–viscosity sensing in a low-flow microfluidic environment. Sens. Actuators Phys. 2008, 141, 266–275. [Google Scholar] [CrossRef]
- Lu, X.; Hou, L.; Zhang, L.; Tong, Y.; Zhao, G.; Cheng, Z.-Y. Piezoelectric-excited membrane for liquids viscosity and mass density measurement. Sens. Actuators Phys. 2017, 261, 196–201. [Google Scholar] [CrossRef]
- Abdallah, A.; Reichel, E.K.; Voglhuber-Brunnmaier, T.; Jakoby, B. Characterization of viscous and viscoelastic fluids using parallel plate shear-wave transducers. IEEE Sens. J. 2016, 16, 2950–2957. [Google Scholar] [CrossRef]
- Purohit, P.; Yadav, Y.K.; Jain, S.K. A study of determination of dynamic viscosity in liquids using radial mode piezo-resonator. Ferroelectrics 2017, 519, 236–240. [Google Scholar] [CrossRef]
- Yan, J.; Wright, W.M.; O’Mahony, J.A.; Roos, Y.; Cuijpers, E.; van Ruth, S.M. A sound approach: Exploring a rapid and non-destructive ultrasonic pulse echo system for vegetable oils characterization. Food Res. Int. 2019, 125, 108552. [Google Scholar] [CrossRef]
- Pfusterschmied, G.; Kucera, M.; Weinmann, C.; Schneider, M.; Bittner, A.; Sánchez-Rojas, J.L.; Schmid, U. Two-step procedure for multi-mode MEMS resonator-based sensing of fluid properties. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017. [Google Scholar]
- Toledo, J.; Ruiz-Díez, V.; Pfusterschmied, G.; Schmid, U.; Sánchez-Rojas, J.L. Characterization of oscillator circuits for monitoring the density-viscosity of liquids by means of piezoelectric MEMS microresonators. In Proceedings of the Smart Sensors, Actuators, and MEMS VIII.; International Society for Optics and Photonics, Barcelona, Spain, 8–10 May 2017. [Google Scholar]
- Toledo, J.; Ruiz-Díez, V.; Pfusterschmied, G.; Schmid, U.; Sánchez-Rojas, J.L. Flow-through sensor based on piezoelectric MEMS resonator for the in-line monitoring of wine fermentation. Sens. Actuators B Chem. 2018, 254, 291–298. [Google Scholar] [CrossRef]
- Nguyen, T.-V.; Nguyen, M.-D.; Takahashi, H.; Matsumoto, K.; Shimoyama, I. Viscosity measurement based on the tapping-induced free vibration of sessile droplets using MEMS-based piezoresistive cantilevers. Lab Chip 2015, 15, 3670–3676. [Google Scholar] [CrossRef]
- Abdolvand, R.; Bahreyni, B.; Lee, J.E.-Y.; Nabki, F. Micromachined resonators: A review. Micromachines 2016, 7, 160. [Google Scholar] [CrossRef]
- Prek, M. Analysis of wave propagation in fluid-filled viscoelastic pipes. Mech. Syst. Signal Process. 2007, 21, 1907–1916. [Google Scholar] [CrossRef]
- Song, F.; Huang, G.L.; Hudson, K. Guided wave propagation in honeycomb sandwich structures using a piezoelectric actuator/sensor system. Smart Mater. Struct. 2009, 18, 125007. [Google Scholar] [CrossRef]
- Park, S.; Yun, C.-B.; Roh, Y.; Lee, J.-J. PZT-based active damage detection techniques for steel bridge components. Smart Mater. Struct. 2006, 15, 957. [Google Scholar] [CrossRef]
- Martowicz, A.; Rosiek, M. Electromechanical impedance method. Adv. Struct. Damage Detect. Theory Eng. Appl. 2013, 1, 141–176. [Google Scholar]
- Gere, J.M. Mechanics of Materials; Thomson Learning Inc.: Belmont, CA, USA, 2004. [Google Scholar]
- Moosrainer, M. Analyzing vibration with acoustic–Structural coupling. ANSYS Advant. 2009, 3, 40–42. [Google Scholar]
- Liang, Q.W.; Rodríguez, C.G.; Egusquiza, E.; Escaler, X.; Farhat, M.; Avellan, F. Numerical simulation of fluid added mass effect on a francis turbine runner. Comput. Fluids 2007, 36, 1106–1118. [Google Scholar] [CrossRef]
- Nechibvute, A.; Chawanda, A.; Luhanga, P. Finite element modeling of a piezoelectric composite beam and comparative performance study of piezoelectric materials for voltage generation. ISRN Mater. Sci. 2012, 2012, 921361. [Google Scholar] [CrossRef]
- Association, S.D. Glycerine: An overview. Terms Tech. Data Prop. Perform. 1990, 1, 1–27. [Google Scholar]






| Method | Viscometer Type | Typical Measurable Range (cP) | Price | Disposable |
|---|---|---|---|---|
| Displacement (1st type) | Capillary * | 0.2–200 | $$$ | No |
| Rotating * | 0.3–320 M | $$$$$ | No | |
| Vibration/mass (2nd type) | Vibration * | 0.3–100 k | $$$$ | No |
| MEMS ** | variable | variable | No | |
| Acoustic (3rd type) | Wave reflection *** | 1.005–1400 | variable | No |
| Non-destructive | 1.005–1600 | $ | Yes |
| Material | Piece # | Dimensions (mm) | Density (kg/m3) | Modulus of Elasticity (N/m2) |
|---|---|---|---|---|
| Hollow brass | 1 | 5 × 5 × 70 | 8500 | 96 × 109 |
| Copper | 2 | 6 × 0.1 × 25 | 8900 | 110 × 109 |
| PZT 5A | 2 | 5 × 0.1 × 23 | 7550 |
| R | R2 | Adjusted R2 | Standard Error of Estimate | |
|---|---|---|---|---|
| 0.9987 | 0.9975 | 0.9969 | 22.19 | |
| Coefficient | Std. Error | t | P | |
| a | 1341.292 | 342,891,640 | 3.91 × 10−6 | 1.00 |
| b | 0.115 | 118,380 | 9.73 × 10−7 | 1.00 |
| f0 | 7.365 | 213,305 | 3.687 × 10−5 | 1.00 |
| Analysis of Variance | ||||
| DF | SS | MS | ||
| Regression | 3 | 1,812,696 | 604,232 | |
| Residual | 8 | 3940 | 492 | |
| Fluid | Density (kg/m3) | Speed of Sound (m/s) | Mode 1 | Mode 2 | Mode 3 |
|---|---|---|---|---|---|
| Air | 1.2 | 343 | 683.86 | 684.24 | 2358 |
| Water | 1000 | 1484 | 499.88 | 533.88 | 1080.2 |
| Glycerin | 1260 | 1920 | 468.53 | 501.72 | 625.45 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulkareem, A.; Erturun, U.; Mossi, K. Non-Destructive Evaluation Device for Monitoring Fluid Viscosity. Sensors 2020, 20, 1657. https://doi.org/10.3390/s20061657
Abdulkareem A, Erturun U, Mossi K. Non-Destructive Evaluation Device for Monitoring Fluid Viscosity. Sensors. 2020; 20(6):1657. https://doi.org/10.3390/s20061657
Chicago/Turabian StyleAbdulkareem, Ahmed, Ugur Erturun, and Karla Mossi. 2020. "Non-Destructive Evaluation Device for Monitoring Fluid Viscosity" Sensors 20, no. 6: 1657. https://doi.org/10.3390/s20061657
APA StyleAbdulkareem, A., Erturun, U., & Mossi, K. (2020). Non-Destructive Evaluation Device for Monitoring Fluid Viscosity. Sensors, 20(6), 1657. https://doi.org/10.3390/s20061657





