Non-Local SVD Denoising of MRI Based on Sparse Representations
Abstract
1. Introduction
2. Sparse Representation
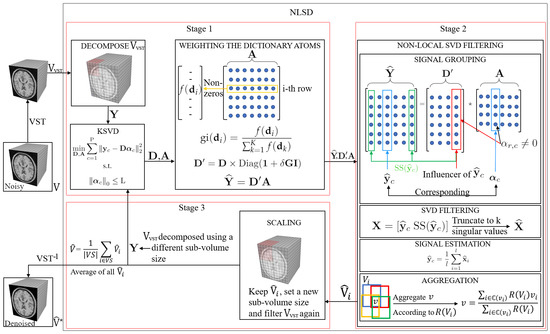
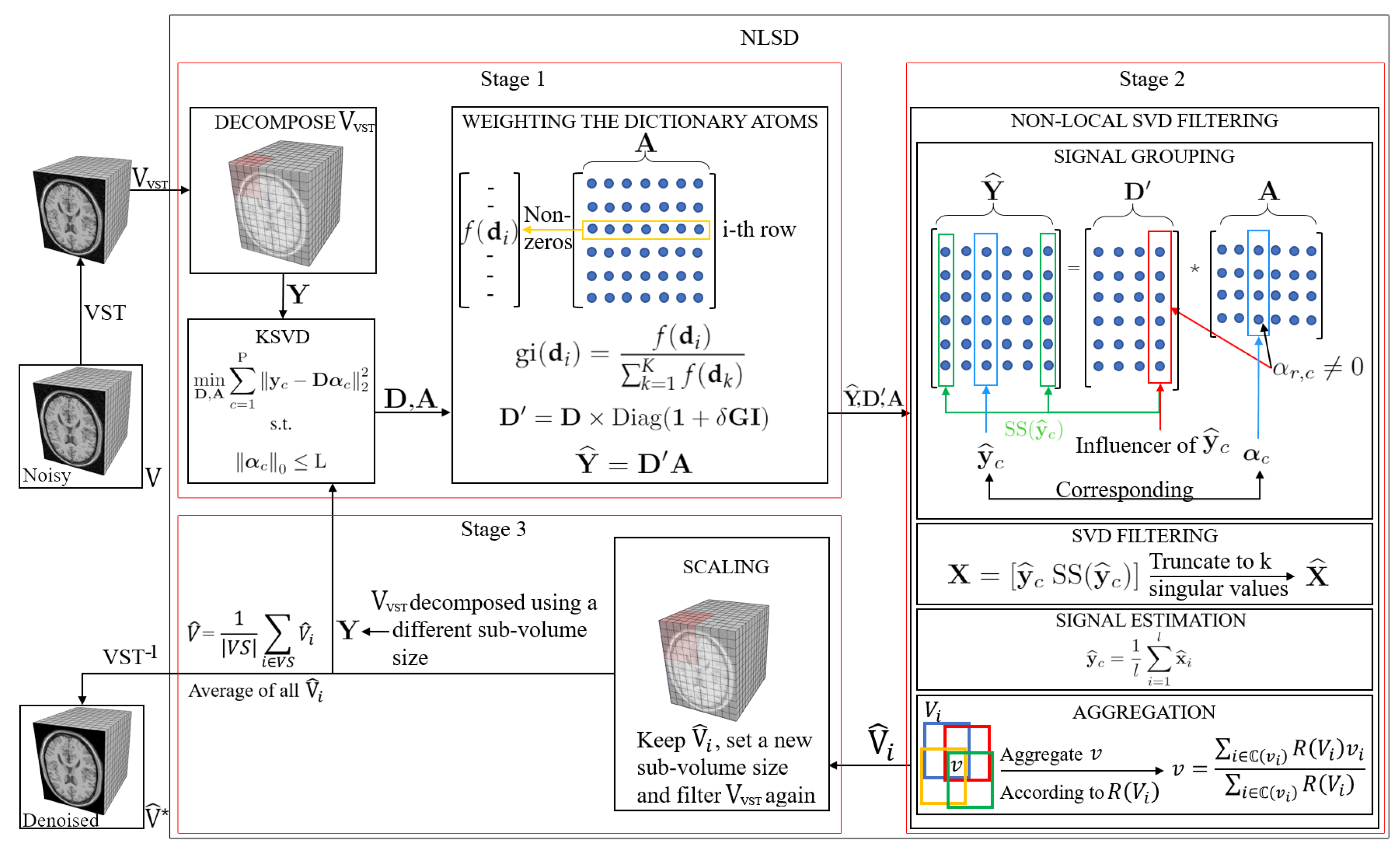
3. Proposed Method for MRI Denoising
3.1. Weighting the Dictionary Atoms
3.2. Non-Local SVD Filtering
3.2.1. Signal Grouping
3.2.2. Efficient SVD Filtering
3.2.3. Signal Estimation
3.2.4. Aggregation
3.3. Scaling
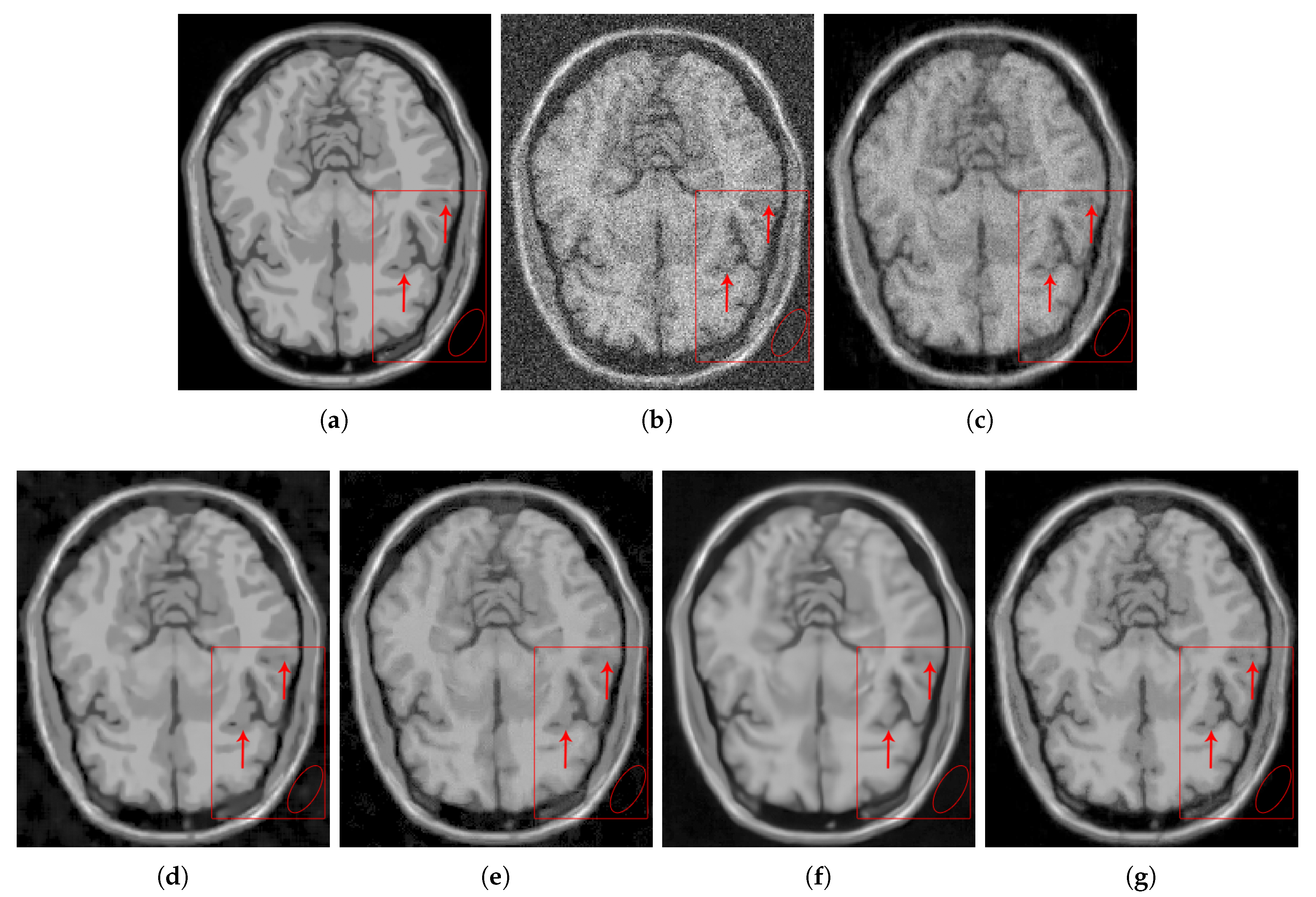
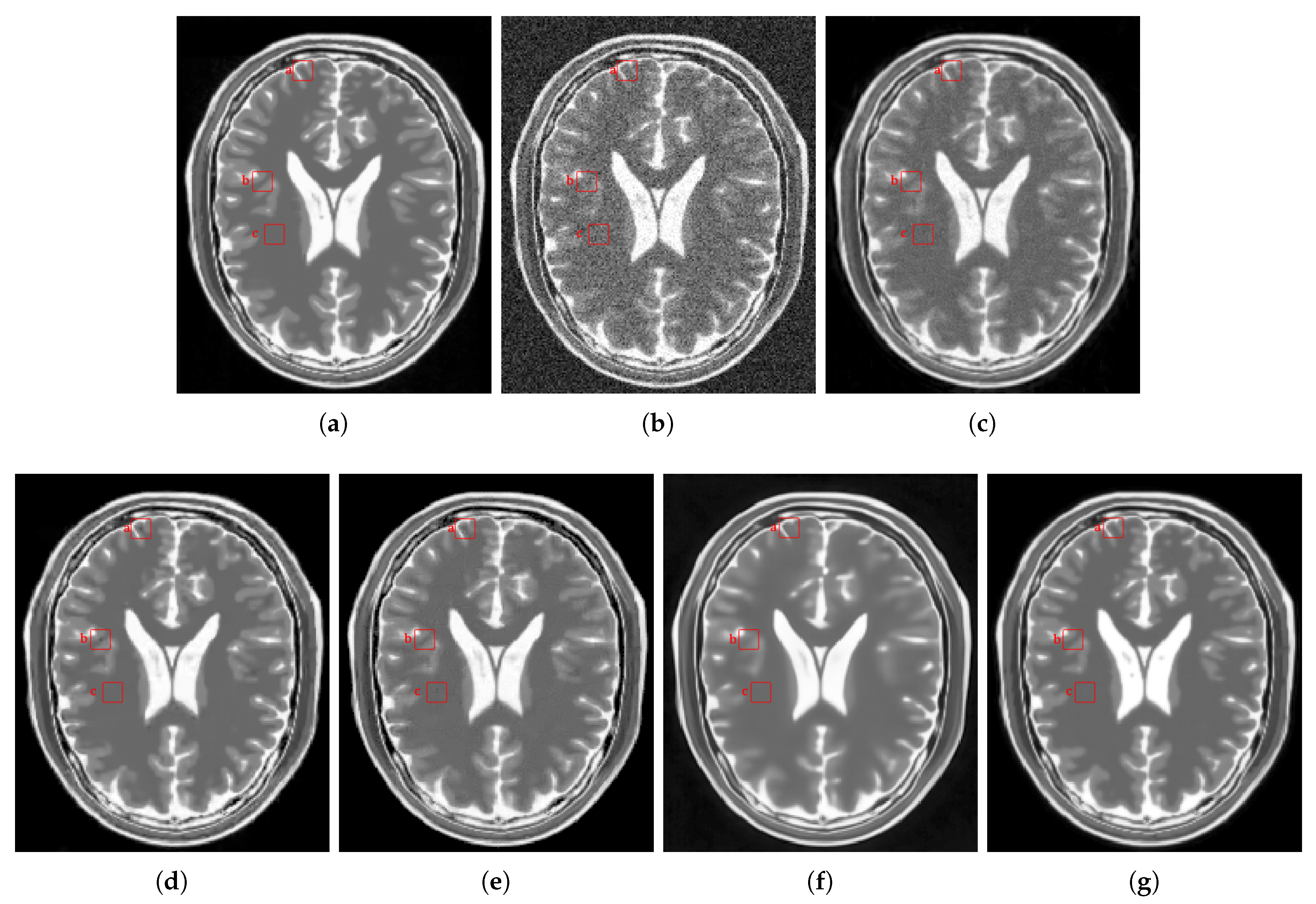
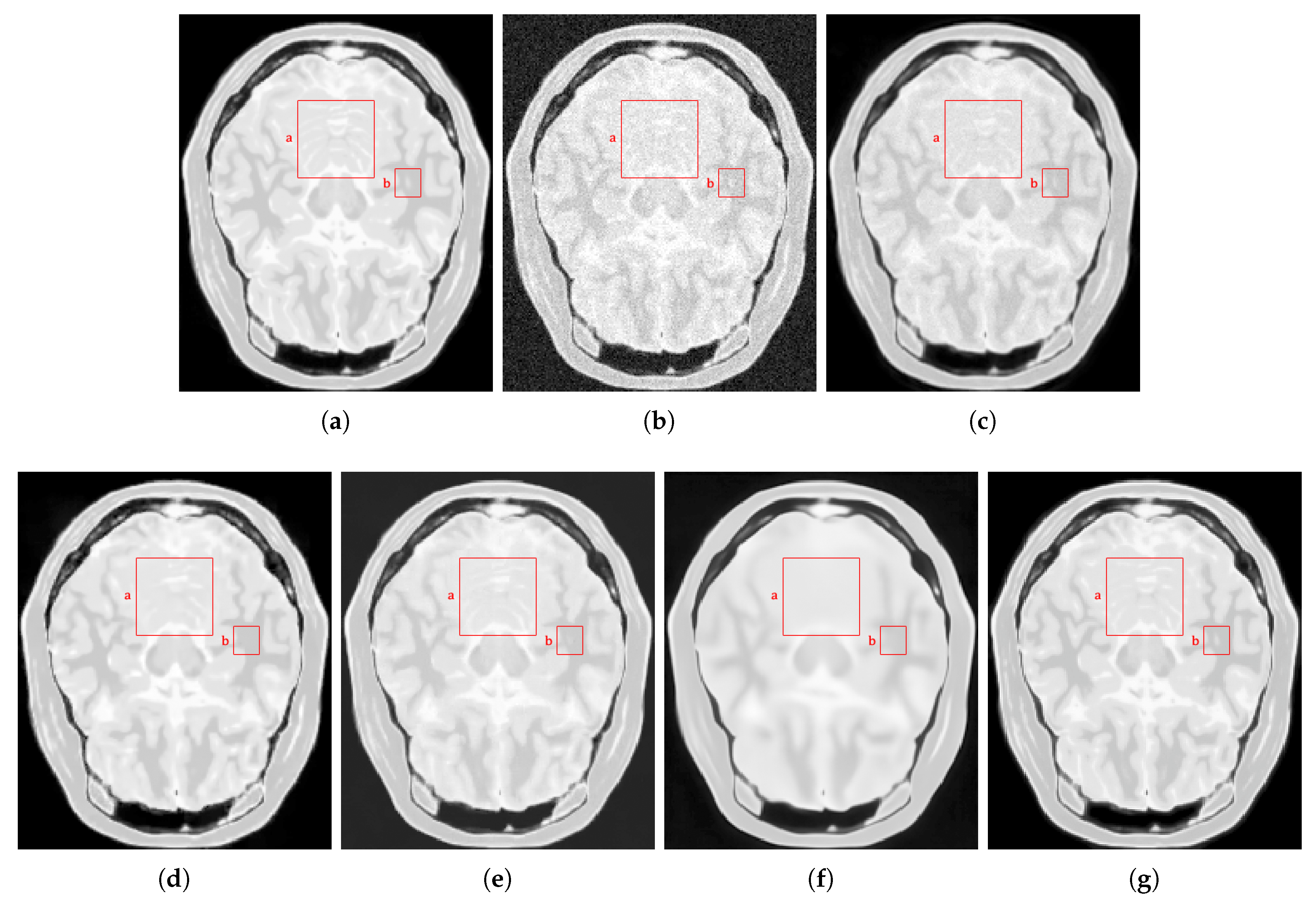
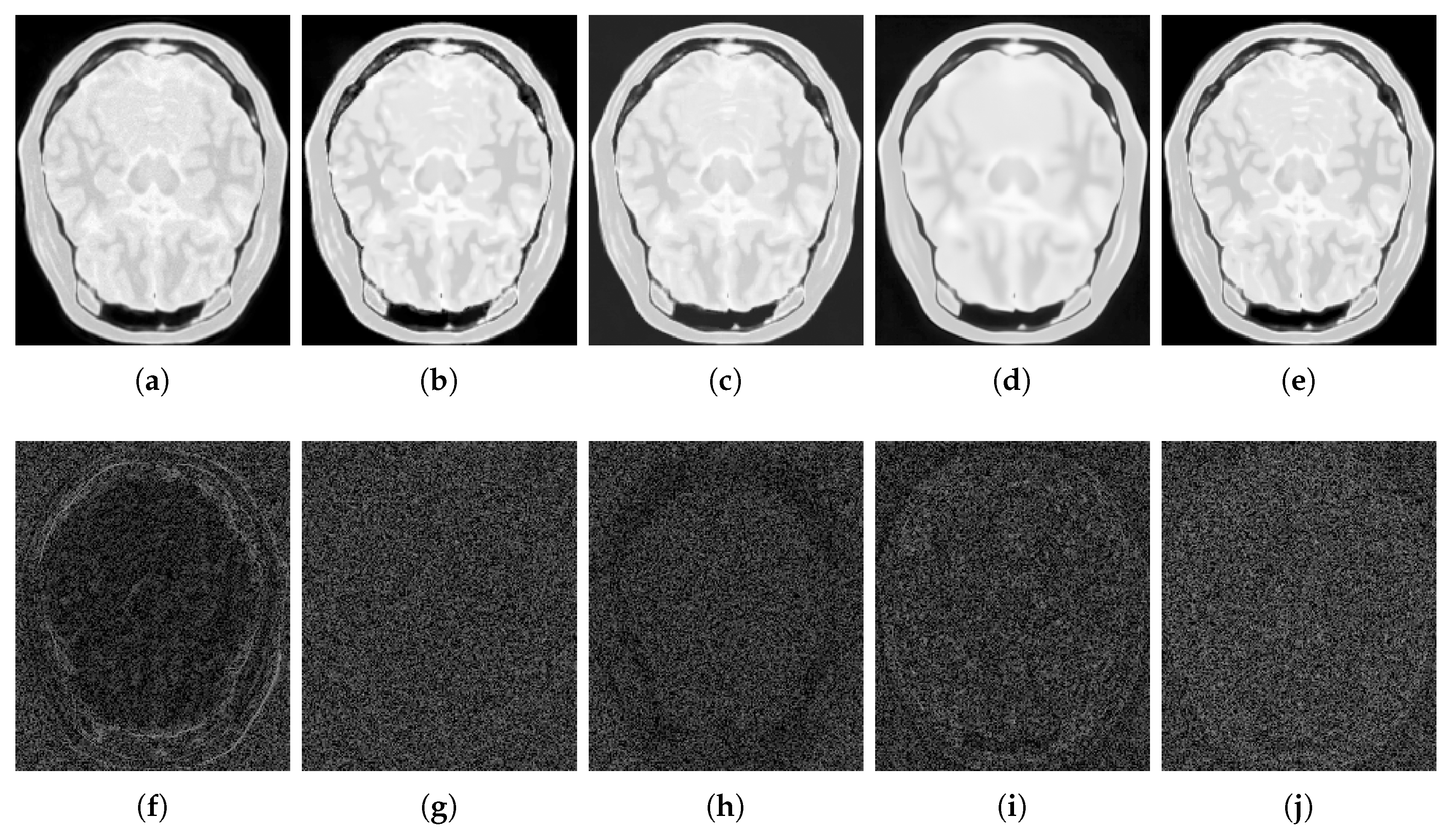
4. Results and Discussion
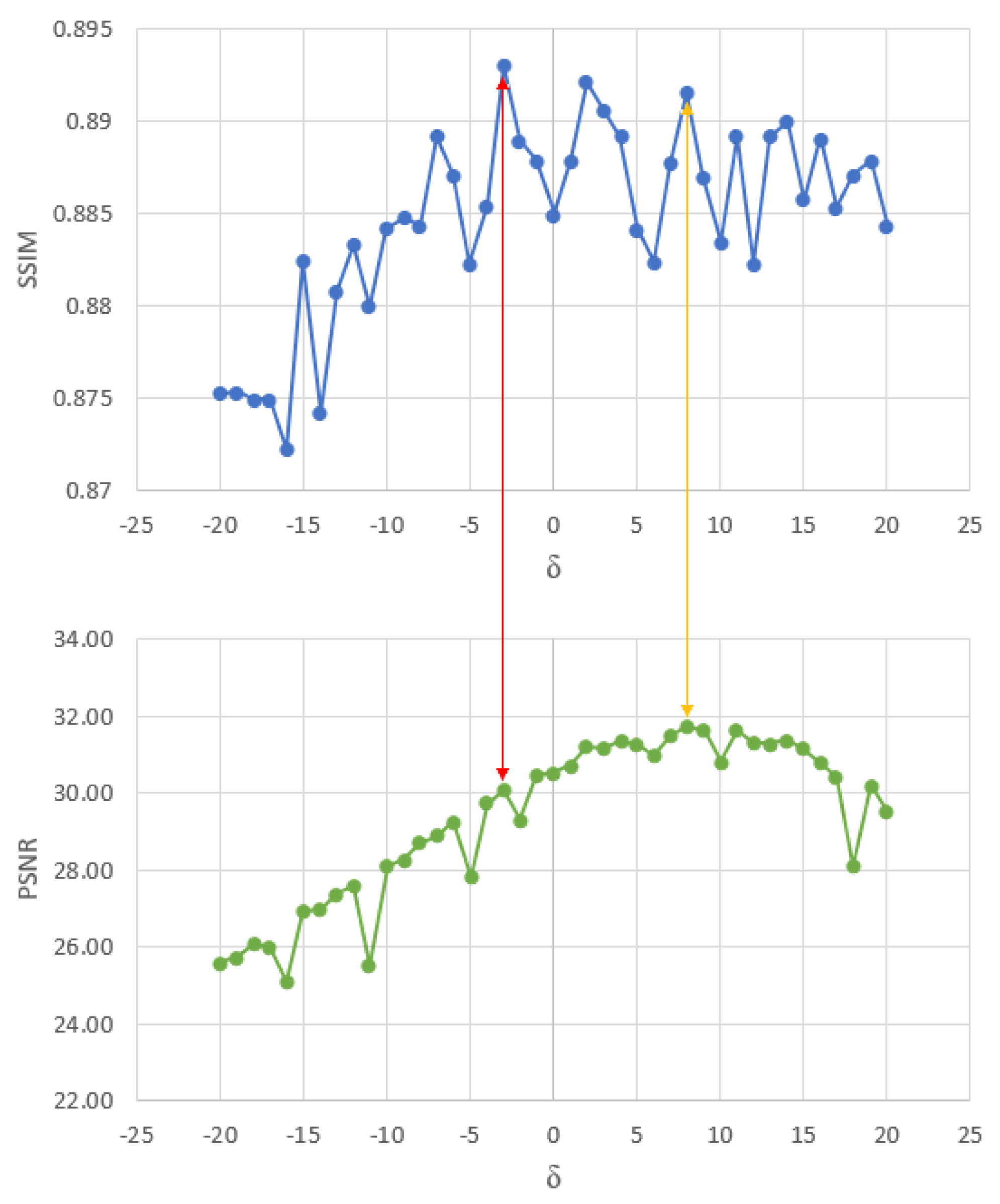
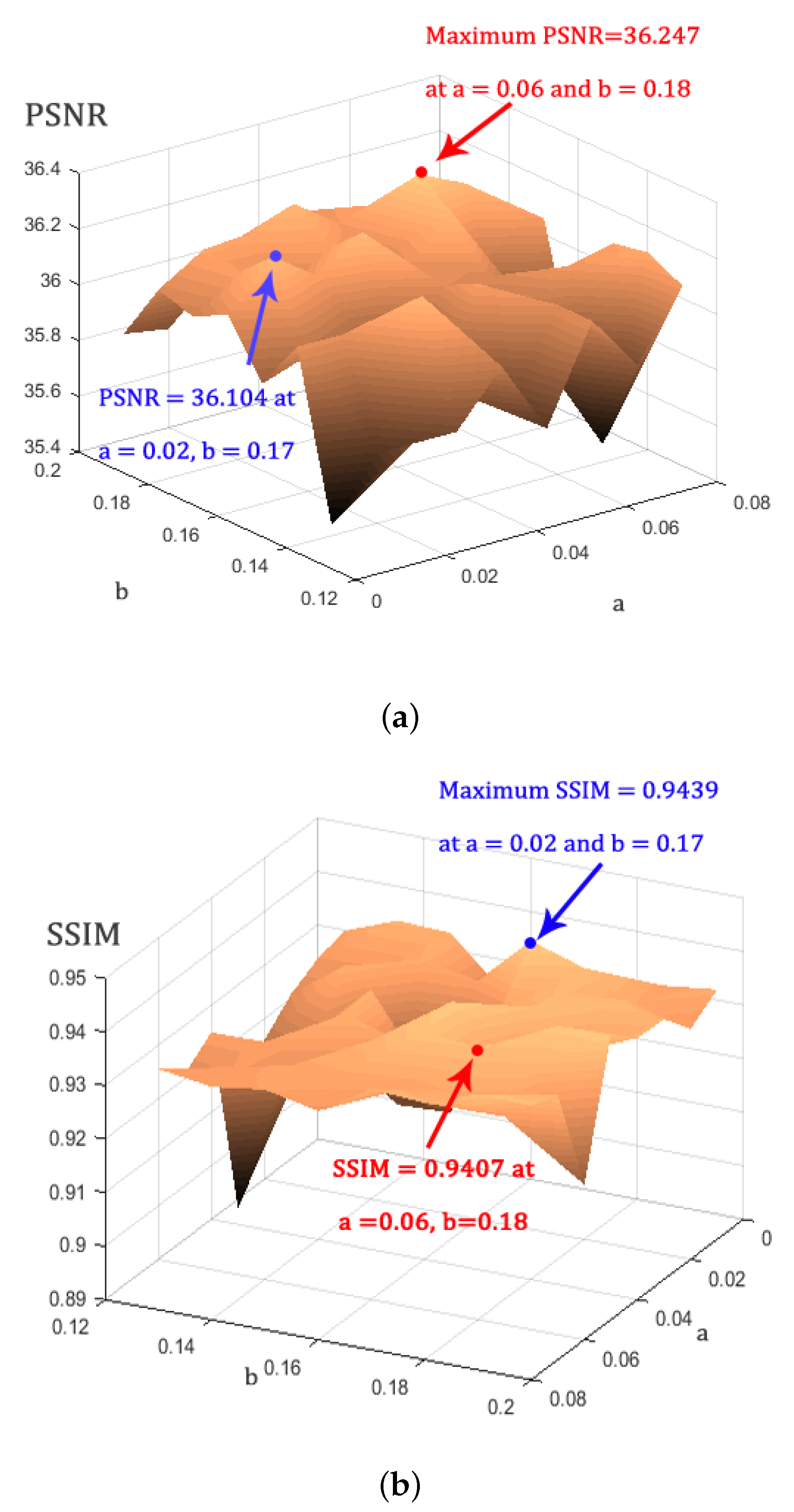
4.1. Parameter Estimation
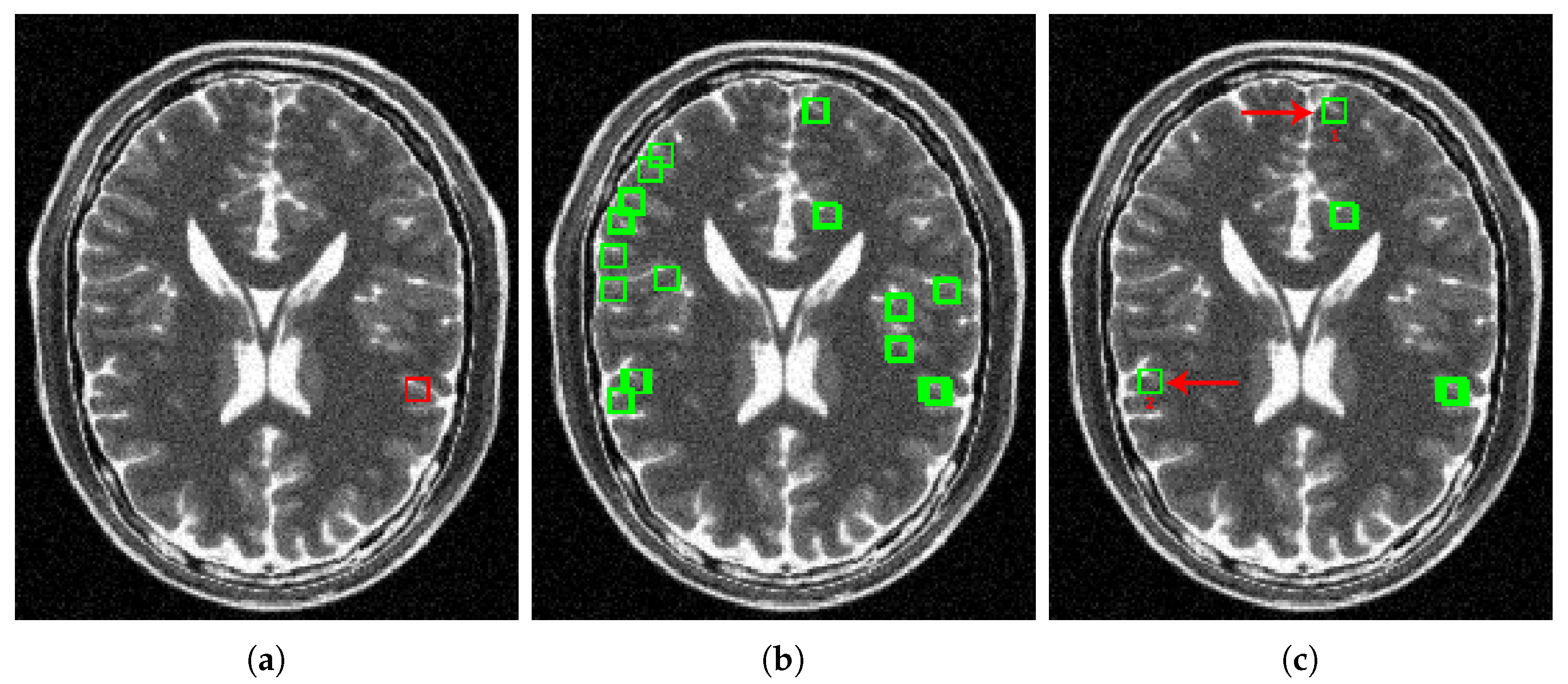
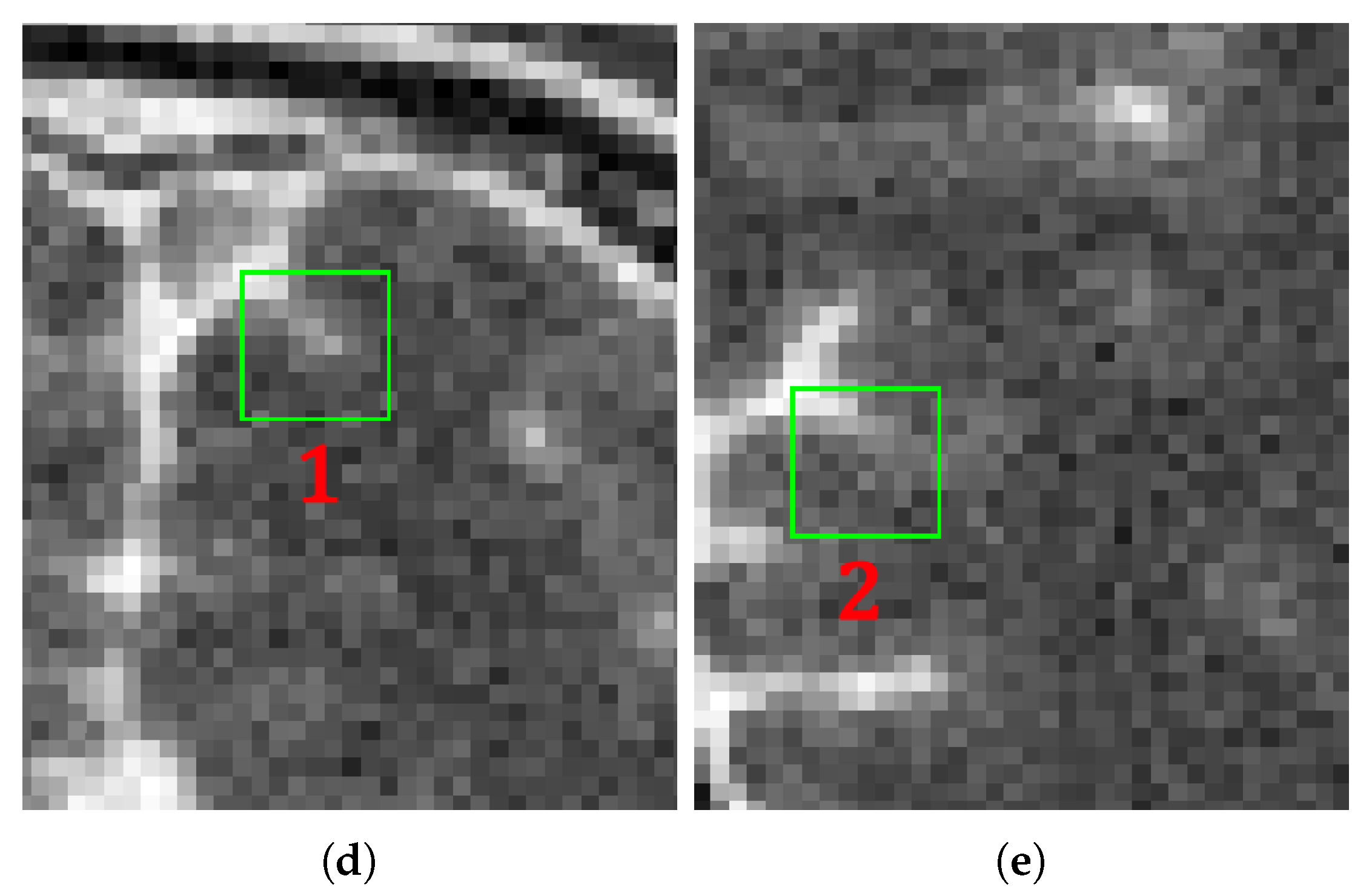
4.2. Methods Comparison
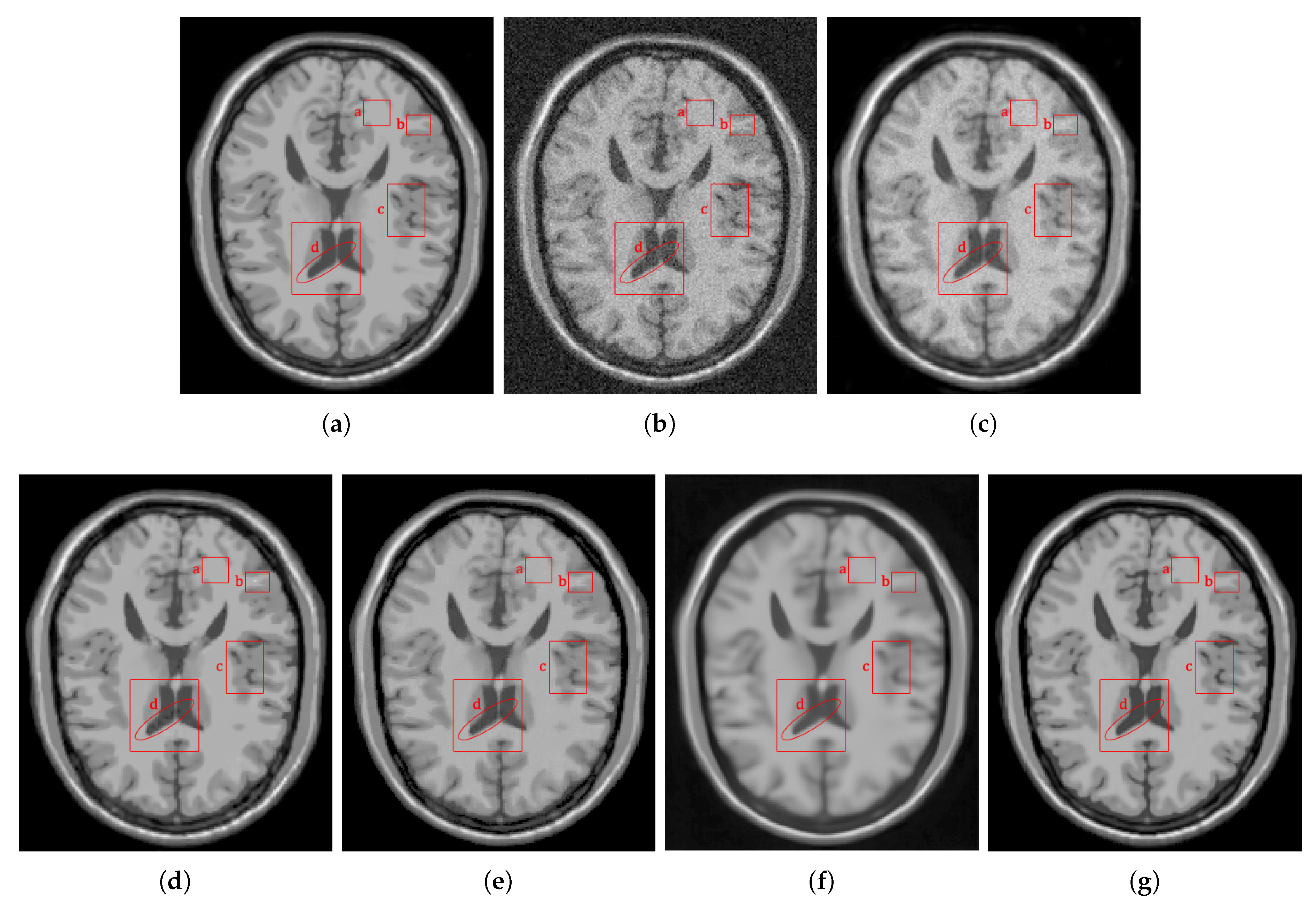
4.2.1. Synthetic Data
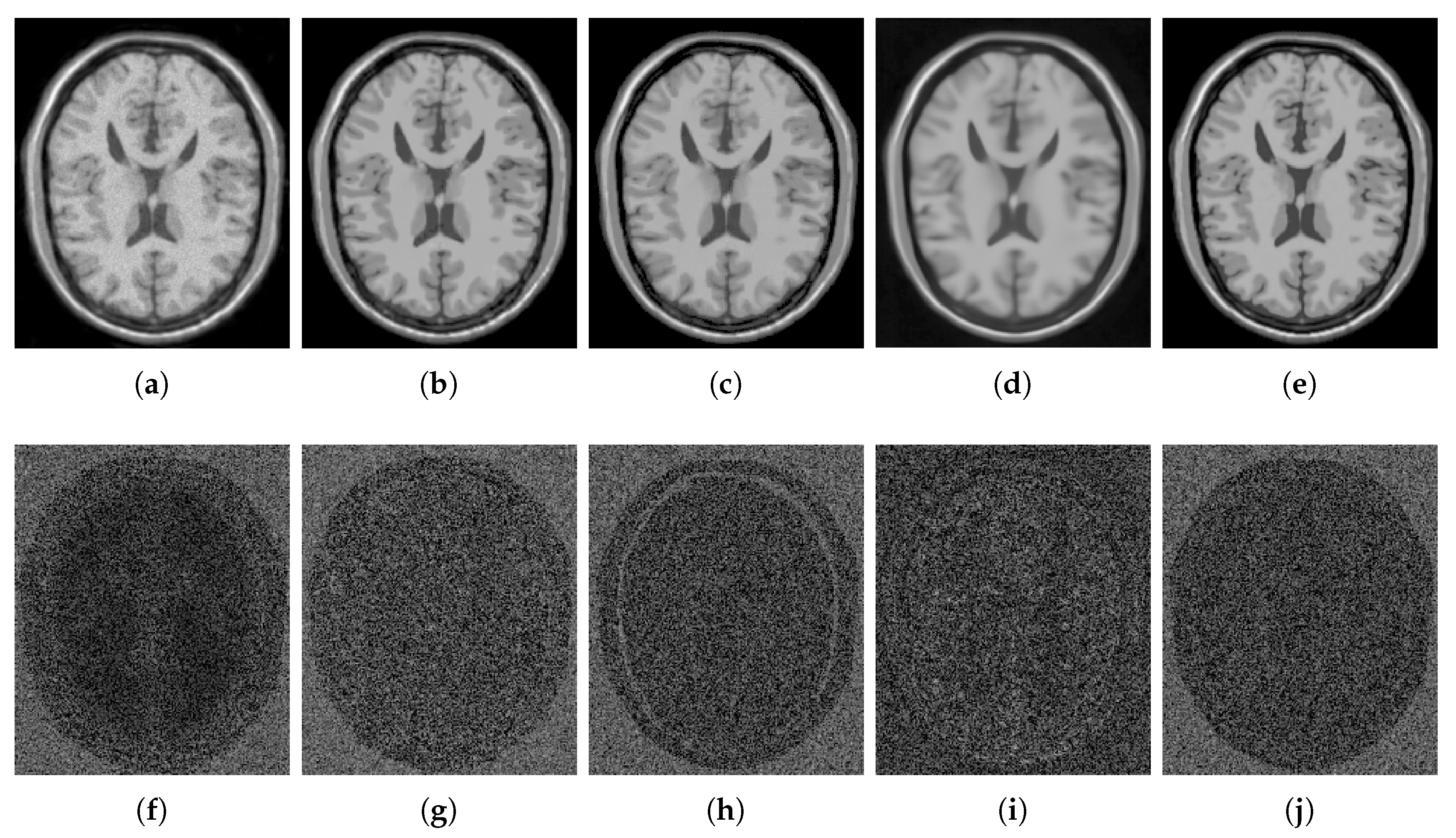
4.2.2. Real Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aja-Fernandez, S.; Tristan-Vega, A. A Review on Statistical Noise Models for Magnetic Resonance Imaging; Technical Report LPI, TECH-LPI2013-01; Universidad de Valladolid: Valladolid, Spain, 2013. [Google Scholar]
- Renfrew, D.L.; Franken, E.A.; Berbaum, K.S.; Weigelt, F.H.; Abu-Yousef, M.M. Error in radiology: Classification and lessons in 182 cases presented at a problem case conference. Radiology 1992, 183, 145–150. [Google Scholar] [CrossRef] [PubMed]
- Fitzgerald, R. Error in radiology. Clin. Radiol. 2001, 56, 938–946. [Google Scholar] [CrossRef] [PubMed]
- Mohan, J.; Krishnaveni, V.; Guo, Y. A survey on the magnetic resonance image denoising methods. Biomed. Signal Process. Control. 2014, 9, 56–69. [Google Scholar] [CrossRef]
- Ran, M.; Hu, J.; Chen, Y.; Chen, H.; Sun, H.; Zhou, J.; Zhang, Y. Denoising of 3D magnetic resonance images using a residual encoder decoder Wasserstein generative adversarial network. Med Image Anal. 2019, 55, 165–180. [Google Scholar] [CrossRef]
- Chang, H.H.; Li, C.Y.; Gallogly, A.H. Brain MR image restoration using an automatic trilateral filter with GPU-based acceleration. IEEE Trans. Biomed. Eng. 2018, 65, 400–413. [Google Scholar] [CrossRef]
- Kang, M.; Jung, M.; Kang, M. Rician denoising and deblurring using sparse representation prior and nonconvex total variation. J. Vis. Commun. Image Represent. 2018, 54, 80–99. [Google Scholar] [CrossRef]
- Benou, A.; Veksler, R.; Friedman, A.; Riklin, R.T. Ensemble of expert deep neural networks for spatio-temporal denoising of contrast-enhanced MRI sequences. Med Image Anal. 2017, 42, 145–159. [Google Scholar] [CrossRef]
- Veraart, J.; Novikov, D.S.; Christiaens, D.; Ades-aron, B.; Sijbers, J.; Fieremans, E. Denoising of diffusion MRI using random matrix theory. NeuroImage 2016, 142, 394–406. [Google Scholar] [CrossRef]
- Manjón, J.V.; Coupé, P.; Buades, A. MRI noise estimation and denoising using non-local PCA. Med Image Anal. 2015, 22, 35–47. [Google Scholar] [CrossRef]
- Gudbjartsson, H.; Patz, S. The Rician distribution of noisy MRI data. Magn. Reson. Med. 1995, 34, 910–914. [Google Scholar] [CrossRef]
- Foi, A. Noise estimation and removal in MR imaging: The variance-stabilization approach. In Proceedings of the IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Chicago, IL, USA, 30 March–2 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1809–1814. [Google Scholar] [CrossRef]
- Zhou, Z.; Tian, R.; Wang, Z.; Yang, Z.; Liu, Y.; Liu, G.; Wang, R.; Gao, J.; Song, J.; Nie, L.; et al. Artificial local magnetic field inhomogeneity enhances T2 relaxivity. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Hong, H.; Zhang, L.; Xie, F.; Zhuang, R.; Jiang, D.; Liu, H.; Li, J.; Yang, H.; Zhang, X.; Nie, L.; et al. Rapid one-step 18F-radiolabeling of biomolecules in aqueous media by organophosphine fluoride acceptors. Nat. Commun. 2019, 10, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Buades, A.; Coll, B.; Morel, J.M. A non-Local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 60–65. [Google Scholar]
- Wang, G.; Liu, Y.; Xiong, W.; Li, Y. An improved non-local means filter for color image denoising. Optik 2018, 173, 157–173. [Google Scholar] [CrossRef]
- Coupé, P.; Yger, P.; Prima, S.; Hellier, P.; Kervrann, C.; Barillot, C. An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images. IEEE Trans. Med Imaging 2008, 27, 425–441. [Google Scholar] [CrossRef] [PubMed]
- Manjón, J.V.; Carbonell, J.; Lull, J.; García, G.; Martí, L.; Robles, M. MRI denoising using Non-Local Means. Med. Image Anal. 2008, 12, 514–523. [Google Scholar] [CrossRef]
- Hu, J.; Zhou, J.; Wu, X. Non-local MRI denoising using random sampling. Magn. Reson. Imaging 2016, 34, 990–999. [Google Scholar] [CrossRef]
- Klosowski, J.; Frahm, J. Image denoising for real-Time MRI. Magn. Reson. Med. 2017, 77, 1340–1352. [Google Scholar] [CrossRef]
- Manjón, J.V.; Coupé, P.; Buades, A.; Collins, L.; Robles, M. New methods for MRI denoising based on sparseness and self-similarity. Med. Image Anal. 2012, 16, 18–27. [Google Scholar] [CrossRef]
- Wang, M.; Yan, W.; Zhou1, S. Image denoising using singular value difference in the wavelet domain. Math. Probl. Eng. 2018, 2018, 1–19. [Google Scholar] [CrossRef]
- Malini, S.; Moni, R.S. Image denoising using multiresolution singular value decomposition transform. Procedia Comput. Sci. 2015, 46, 1708–1715. [Google Scholar] [CrossRef]
- Hou, Z. Adaptive singular value decomposition in wavelet domain for image denoising. Pattern Recognit. 2003, 36, 1747–1763. [Google Scholar] [CrossRef]
- Rajwade, A.; Rangarajan, A.; Banerjee, A. Image denoising using the higher order singular value decomposition. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 849–862. [Google Scholar] [CrossRef] [PubMed]
- Zhanga, X.; Peng, J.; Xu, M.; Yang, W.; Zhang, Z.; Guo, H.; Chen, W.; Feng, Q.; Wu, E.X.; Feng, Y. Denoise diffusion-weighted images using higher-order singular value decomposition. NeuroImage 2017, 156, 128–145. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xu, Z.; Jia, N.; Yang, W.; Feng, Q.; Chen, W.; Feng, Y. Denoising of 3D magnetic resonance images by using higher-order singular value decomposition. Med. Image Anal. 2015, 19, 75–86. [Google Scholar] [CrossRef] [PubMed]
- Kong, Z.; Han, L.; Liu, X.; Yang, X. A New 4-D nonlocal transform-domain filter for 3-D magnetic resonance images denoising. IEEE Trans. Med. Imaging 2018, 37, 941–954. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Shi, G.; Li, X. Nonlocal image restoration with bilateral variance estimation: A low-rank approach. IEEE Trans. Image Process. 2013, 22, 700–711. [Google Scholar] [CrossRef]
- Dong, W.; Shi, G.; Li, X. Efficient nonlocal-means denoising using the SVD. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1732–1735. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising with block-matching and 3D filtering. In Image Processing: Algorithms and Systems, Neural Networks, and Machine Learning; International Society for Optics and Photonics, SPIE: Philadelphia, PA, USA, 2006; Volume 6064, pp. 354–365. [Google Scholar] [CrossRef]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. A nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 2013, 22, 119–133. [Google Scholar] [CrossRef]
- Xu, P.; Chen, B.; Xue, L.; Zhang, J.; Zhu, L.; Duan, H. A new MNF BM4D denoising algorithm based on guided filtering for hyperspectral images. ISA Trans. 2019, 92, 315–324. [Google Scholar] [CrossRef]
- Tao, D.; Cheng, J.; Gao, X.; Li, X.; Deng, C. Robust sparse coding for mobile image labeling on the cloud. IEEE Trans. Circuits Syst. Video Technol. 2016, 27, 62–72. [Google Scholar] [CrossRef]
- Moradi, N.; Mahdavi-Amiri, N. Kernel sparse representation based model for skin lesions segmentation and classification. Comput. Methods Programs Biomed. 2019, 182. [Google Scholar] [CrossRef]
- Li, Z.; He, H.; Yin, Z.; Chen, F. A color-gradient patch sparsity based image inpainting algorithm with structure coherence and neighborhood consistency. Signal Process. 2014, 99, 116–128. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Khedr, W.; Ali, R.; Ismail, F. Image denoising using K-SVD algorithm based on Gabor wavelet dictionary. Int. J. Comput. Appl. 2012, 59, 30–33. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, X.; Peng, X.; Liu, Y.; Zhao, W. Improved image denoising algorithm dased on superpixel clustering and sparse representation. Appl. Sci. 2017, 7, 436. [Google Scholar] [CrossRef]
- Yuan, J. MRI denoising via sparse tensors with reweighted regularization. Appl. Math. Model. 2019, 69, 552–562. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z.; Hu, J.; Zou, S.; Fu, Y. MRI denoising using low rank prior and sparse gradient prior. IEEE Access 2019, 7, 45858–45865. [Google Scholar] [CrossRef]
- Li, H.; He, X.; Tao, D.; Tang, Y.; Wang, R. Joint medical image fusion, denoising and enhancement via discriminative low-rank sparse dictionaries learning. Pattern Recognit. 2018, 79, 130–146. [Google Scholar] [CrossRef]
- Phophalia, A.; Mitra, S.K. 3D MR image denoising using rough set and kernel PCA method. Magn. Reson. Imaging 2017, 36, 135–145. [Google Scholar] [CrossRef]
- Baselice, F.; Ferraioli, G.; Pascazio, V.; Sorriso, A. Bayesian MRI denoising in complex domain. Magn. Reson. Imaging 2017, 38, 112–122. [Google Scholar] [CrossRef]
- Aja-Fernández, S.; Pieciak, T.; Vegas-Sánchez-Ferrero, G. Spatially variant noise estimation in MRI: A homomorphic approach. Med Image Anal. 2015, 20, 184–197. [Google Scholar] [CrossRef]
- Pieciak, T.; Rabanillo-Viloria, I.; Aja-Fernández, S. Bias correction for non-stationary noise filtering in MRI. In Proceedings of the IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 307–310. [Google Scholar]
- Liu, L.; Yang, H.; Fan, J.; Wen, R.; Duan, Y. Rician noise and intensity nonuniformity correction (NNC) model for MRI data. Biomed. Signal Process. Control. 2019, 49, 506–519. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Dou, W.; Vosters, L.; Xu, X.; Sun, Y.; Tan, T. Denoising of 3D magnetic resonance images with multi-channel residual learning of convolutional neural network. Jpn. J. Radiol. 2018, 36, 566–574. [Google Scholar] [CrossRef] [PubMed]
- Kidoh, M.; Shinoda, K.; Kitajima, M.; Isogawa, K.; Nambu, M.; Uetani, H.; Morita, K.; Nakaura, T.; Tateishi, M.; Yamashita, Y.; et al. Deep Learning Based Noise Reduction for Brain MR Imaging: Tests on Phantoms and Healthy Volunteers. Magn. Reson. Med. Sci. 2019, 1–12. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Yang, J.; Li, X.; Zhang, D. A Survey of sparse representation: Algorithms and applications. IEEE Access 2015, 3, 490–530. [Google Scholar] [CrossRef]
- Bao, C.; Ji, H. Dictionary learning for sparse coding: Algorithms and convergence analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1356–1369. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A.M. The K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A.M. On the uniqueness of overcomplete dictionaries, and a practical way to retrieve them. J. Linear Algebra Appl. 2006, 416, 48–67. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2017; p. 175. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A review of image denoising algorithms, with a new one. Multiscale Model. Simul. Siam Interdiscip. J. Soc. Ind. Appl. Math. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Raghuvanshi, D.; Hasan, S.; Agrawal, M. Analysing image denoising using non local means algorithm. Int. J. Comput. Appl. 2012, 56, 7–11. [Google Scholar] [CrossRef][Green Version]
- Ramirez, I.; Sprechmann, P.; Sapiro, G. Classification and clustering via dictionary learning with structured incoherence and shared features. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 3501–3508. [Google Scholar] [CrossRef]
- Sprechmann, P.; Sapiro, G. Dictionary learning and sparse coding for unsupervised clustering. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 15–19 March 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2042–2045. [Google Scholar] [CrossRef]
- Kimpe, T.; Tuytschaever, T. Increasing the number of gray shades in medical display systems how much is enough? J. Digit. Imaging 2007, 20, 422–432. [Google Scholar] [CrossRef] [PubMed]
- Sadek, R. SVD based image processing applications: State of the art, contributions and research challenges. Int. J. Adv. Comput. Sci. Appl. IJACSA 2012, 3, 26–34. [Google Scholar]
- Eckart, C.; Young, G. The approximation of one matrix by another of lower rank. Psychometrika 1936, 1, 211–218. [Google Scholar] [CrossRef]
- Leal, N.; Moreno, S.; Zurek, E. Simple method for detecting visual saliencies based on dictionary learning and sparse coding. In Proceedings of the 14th Iberian Conference on Information Systems and Technologies (CISTI), Coimbra, Portugal, 19–22 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Cocosco, C.A.; Kollokian, V.; Kwan, R.K.S.; Evans, A.C. BrainWeb: Simulated Brain Database. 1997. Available online: https://brainweb.bic.mni.mcgill.ca (accessed on 6 July 2019).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Coupé, P. Personal Home Page. 2019. Available online: https://sites.google.com/site/pierrickcoupe/softwares (accessed on 6 July 2019).
- Foi, A. Image and Video Denoising by Sparse 3D Transform-Domain Collaborative Filtering. 2019. Available online: http://http://www.cs.tut.fi/~foi/GCF-BM3D (accessed on 6 July 2019).
- Zhang, K. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising (TIP, 2017). Available online: https://github.com/cszn/DnCNN/tree/4a4b5b8bcac5a5ac23433874d4362329b25522ba (accessed on 2 February 2019).








| 1% | 3% | 5% | 7% | 9% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM |
| Noisy | 39.980 | 0.9658 | 30.451 | 0.8084 | 25.982 | 0.6644 | 23.045 | 0.5536 | 20.888 | 0.4693 |
| KSVD | 40.421 | 0.9773 | 32.637 | 0.9225 | 29.509 | 0.8605 | 27.588 | 0.8014 | 26.423 | 0.7368 |
| PRINLM | 44.299 | 0.9930 | 38.589 | 0.9655 | 35.512 | 0.9281 | 33.642 | 0.8654 | 33.177 | 0.8332 |
| BM4D | 44.688 | 0.9911 | 38.129 | 0.9799 | 35.618 | 0.9643 | 32.799 | 0.9404 | 30.412 | 0.9115 |
| DnCNN | 43.109 | 0.9756 | 37.843 | 0.9602 | 34.790 | 0.9581 | 33.744 | 0.9478 | 31.501 | 0.9163 |
| NLSD | 44.901 | 0.9970 | 38.723 | 0.9895 | 35.801 | 0.9776 | 33.982 | 0.9630 | 33.130 | 0.9296 |
| 1% | 3% | 5% | 7% | 9% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM |
| Noisy | 39.992 | 0.9709 | 30.418 | 0.8330 | 26.016 | 0.7151 | 23.073 | 0.6242 | 20.928 | 0.5606 |
| KSVD | 40.104 | 0.9706 | 32.098 | 0.9166 | 29.342 | 0.8669 | 26.530 | 0.8134 | 24.664 | 0.7633 |
| PRINLM | 43.985 | 0.9943 | 37.786 | 0.9703 | 34.738 | 0.9262 | 32.918 | 0.8852 | 31.347 | 0.8286 |
| BM4D | 43.655 | 0.9614 | 37.166 | 0.9473 | 34.140 | 0.9373 | 31.887 | 0.9273 | 30.030 | 0.9100 |
| DnCNN | 42.897 | 0.9569 | 37.003 | 0.9354 | 34.362 | 0.9210 | 32.544 | 0.9162 | 31.045 | 0.9139 |
| NLSD | 44.099 | 0.9978 | 37.973 | 0.9885 | 34.910 | 0.9522 | 33.546 | 0.9327 | 31.601 | 0.9233 |
| 1% | 3% | 5% | 7% | 9% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM |
| Noisy | 39.971 | 0.9636 | 30.441 | 0.7901 | 25.984 | 0.6341 | 23.088 | 0.5250 | 20.898 | 0.4408 |
| KSVD | 39.980 | 0.9639 | 29.633 | 0.8956 | 27.626 | 0.8128 | 26.224 | 0.7357 | 24.952 | 0.6589 |
| PRINLM | 44.699 | 0.9940 | 38.079 | 0.9752 | 35.111 | 0.9228 | 33.101 | 0.8638 | 32.562 | 0.8211 |
| BM4D | 44.603 | 0.9626 | 38.621 | 0.9399 | 35.683 | 0.9280 | 33.653 | 0.9147 | 31.887 | 0.8990 |
| DnCNN | 43.245 | 0.9567 | 37.991 | 0.9268 | 35.700 | 0.9372 | 33.419 | 0.9075 | 30.643 | 0.8986 |
| NLSD | 44.980 | 0.9987 | 38.906 | 0.9894 | 35.973 | 0.9532 | 33.625 | 0.9387 | 32.656 | 0.9102 |
| PRINLM | BM4D | DnCNN | KSVD | NLSD | |
|---|---|---|---|---|---|
| Language | MATLAB - C++ | MATLAB - C++ | MATLAB | MATLAB | MATLAB |
| Average running time | 45.32 s | 46.83 s | 65.64 min | 70.13 min | 120.84 min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leal, N.; Zurek, E.; Leal, E. Non-Local SVD Denoising of MRI Based on Sparse Representations. Sensors 2020, 20, 1536. https://doi.org/10.3390/s20051536
Leal N, Zurek E, Leal E. Non-Local SVD Denoising of MRI Based on Sparse Representations. Sensors. 2020; 20(5):1536. https://doi.org/10.3390/s20051536
Chicago/Turabian StyleLeal, Nallig, Eduardo Zurek, and Esmeide Leal. 2020. "Non-Local SVD Denoising of MRI Based on Sparse Representations" Sensors 20, no. 5: 1536. https://doi.org/10.3390/s20051536
APA StyleLeal, N., Zurek, E., & Leal, E. (2020). Non-Local SVD Denoising of MRI Based on Sparse Representations. Sensors, 20(5), 1536. https://doi.org/10.3390/s20051536