Optimal Design of Water Quality Monitoring Networks in Semi-Enclosed Estuaries
Abstract
1. Introduction
2. Materials and Methods
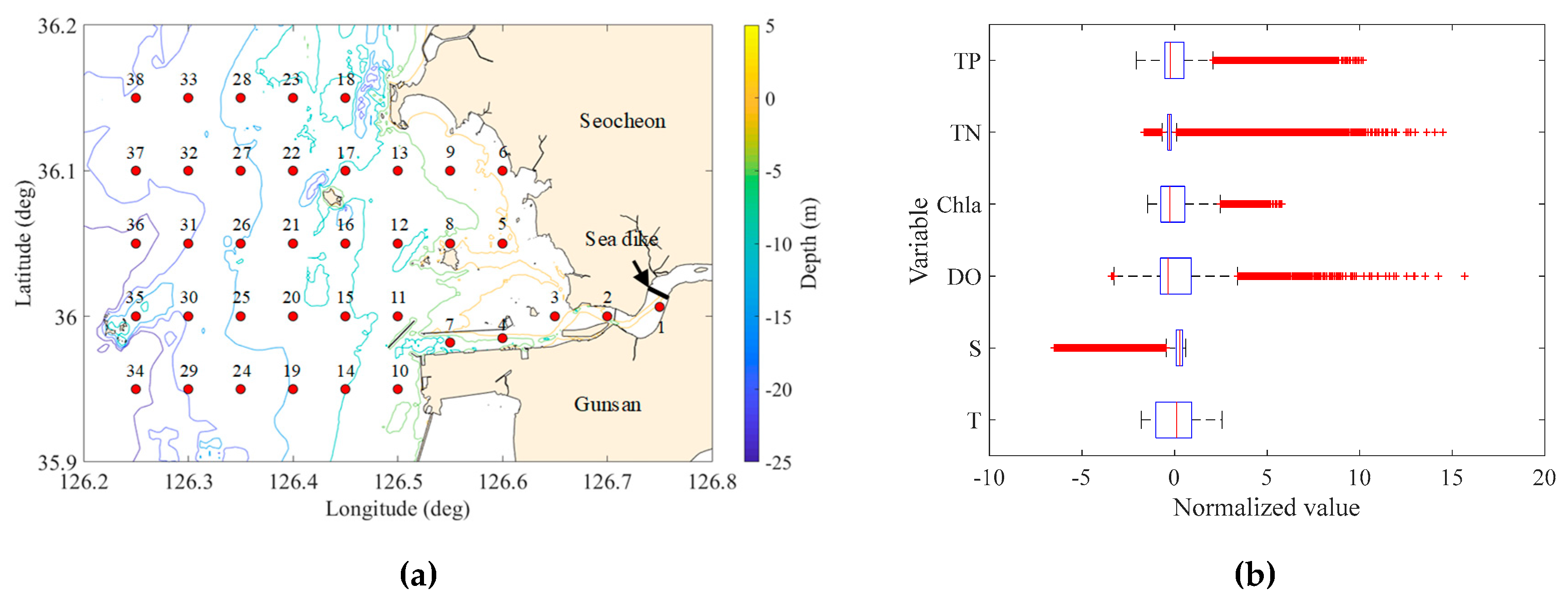
2.1. Characteristics of the Study Area
2.2. Numerical Model (Input Data)
2.3. Design Variables
2.4. Finding the Optimal Solutions
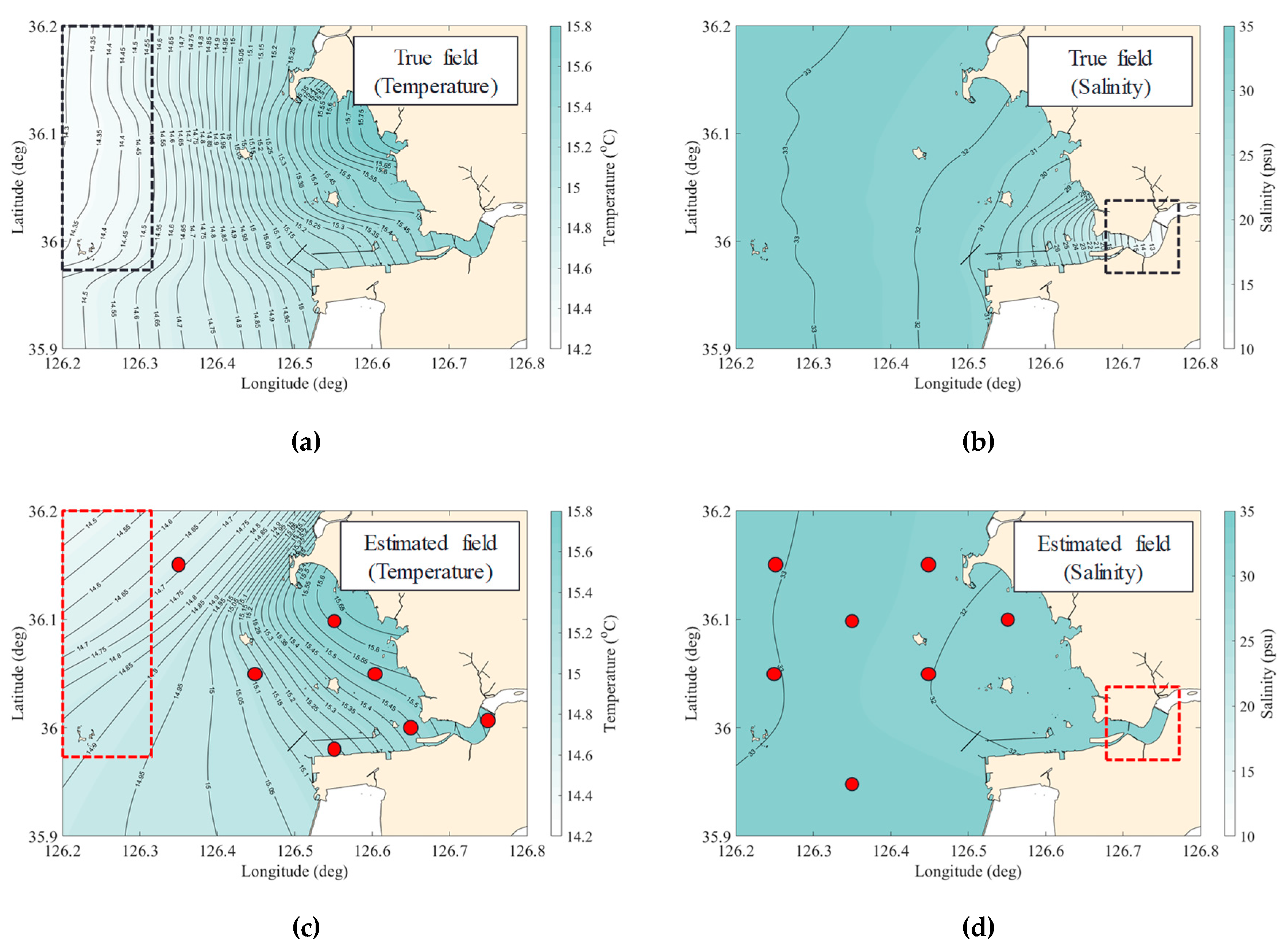
2.5. Methods of Performance Evaluation
3. Results and Discussion
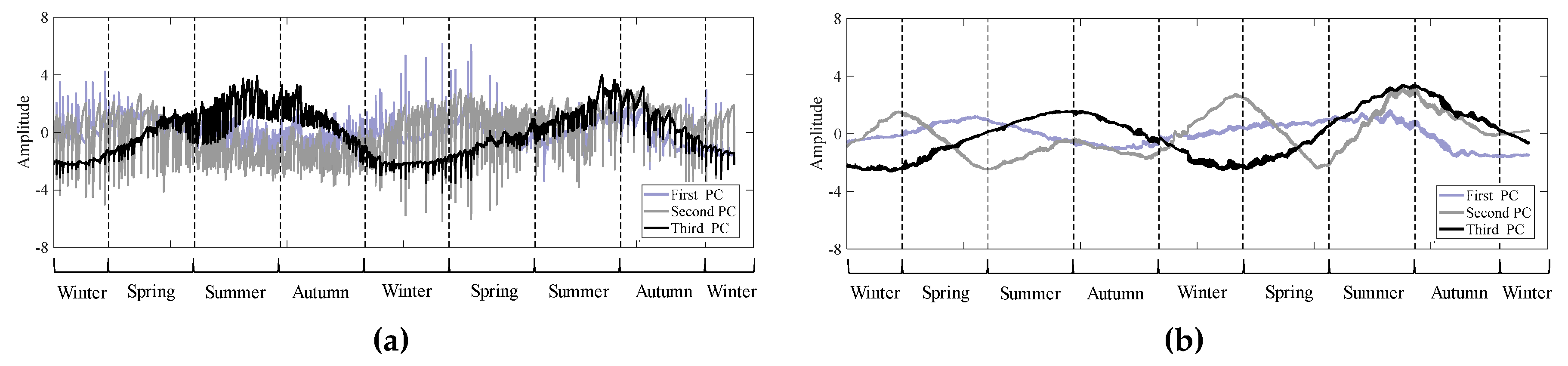
3.1. Decomposition of the Spatiotemporally Dependent Variable
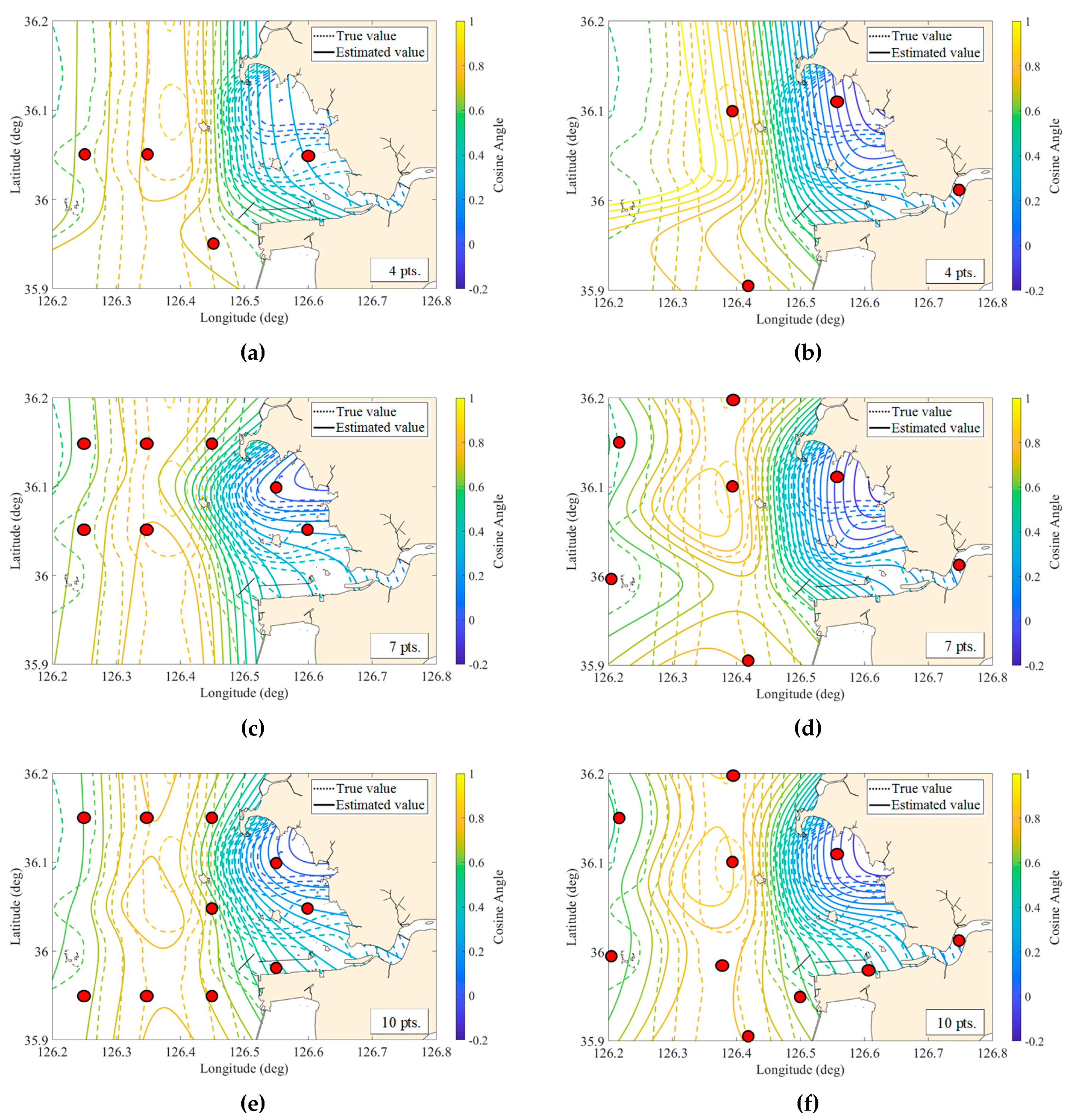
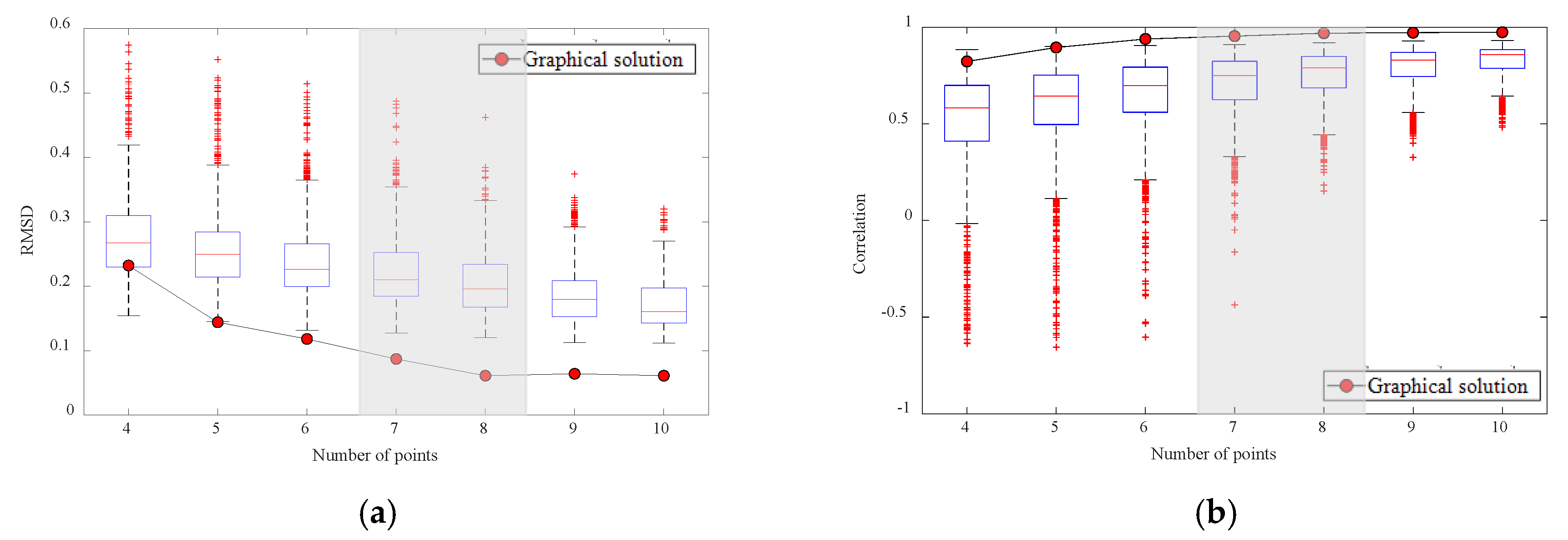
3.2. Solutions for the Monitoring Array
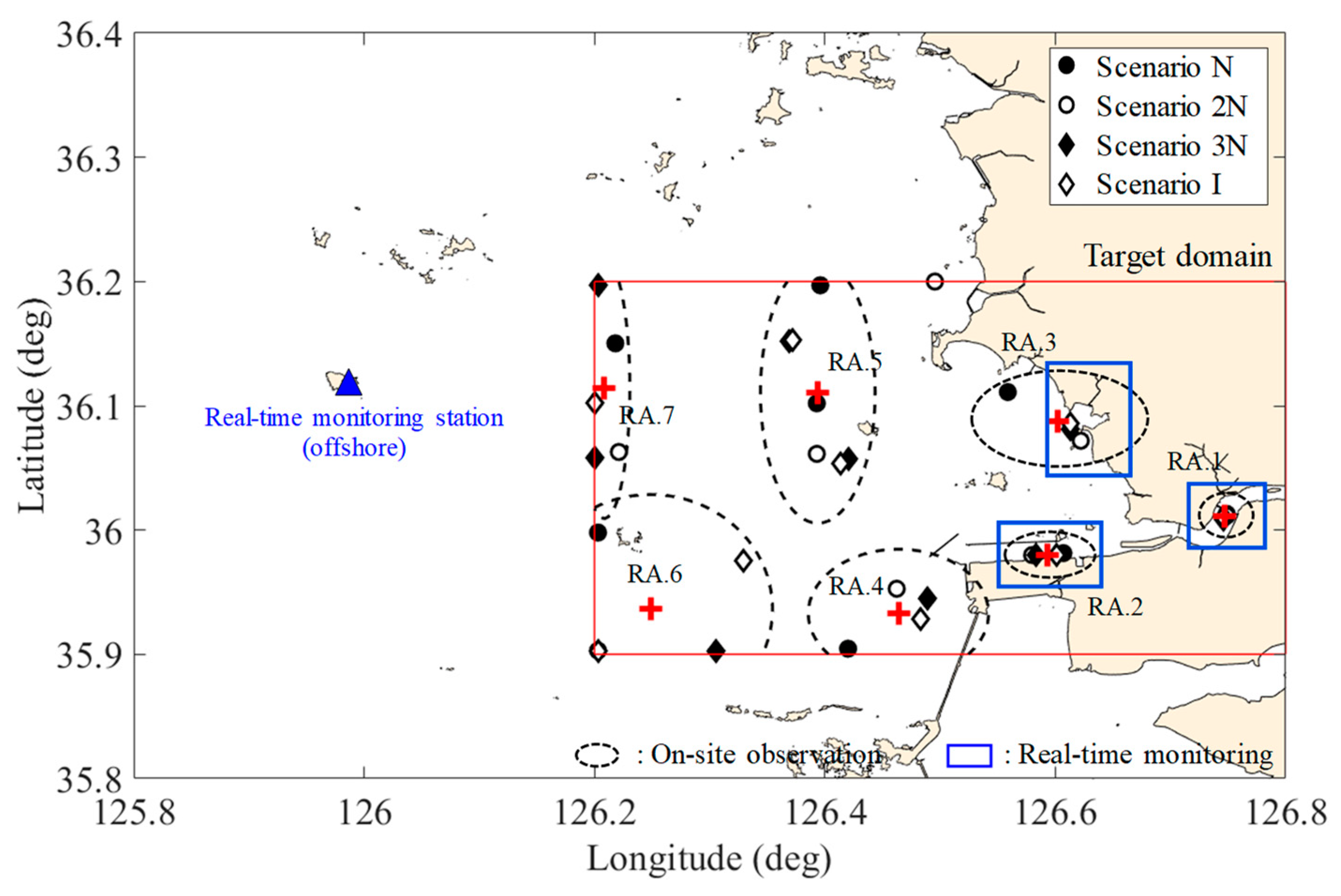
3.3. Optimal Design of the Water Quality Monitoring Network
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BOA | Barnes Objective Analysis |
| Chl-a | Chlorophyll-a |
| COR | Correlation |
| CRMSD | Centered Root Mean Square Difference |
| DO | Dissolved Oxygen |
| EOF | Empirical Orthogonal Function |
| G | Graphical optimization |
| GE | Geumgang Estuary |
| IOA | Index Of Agreement |
| OI | Optimal Interpolation |
| PC | Principal Component |
| Q | Quantitative optimization |
| RA | Representative Area |
| RE | Relative Error |
| RMSE | Root-Mean-Square Error |
| S | Salinity |
| SD | Standard Deviation |
| T | Water Temperature |
| TN | Total Nitrogen |
| TP | Total Phosphorus |
Appendix A
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Annual | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Season | Winter | Spring | Summer | Autumn | Winter | |||||||||
| Discharge (106 ton) | 159 | 160 | 179 | 228 | 263 | 468 | 1202 | 1111 | 795 | 284 | 200 | 201 | 5250 | |
| Frequency | 9 | 9 | 11 | 13 | 16 | 19 | 33 | 33 | 25 | 15 | 12 | 11 | 206 | |
| Total Time | 22 | 23 | 28 | 35 | 42 | 59 | 131 | 127 | 93 | 38 | 28 | 28 | 654 | |
| Time/count | 2.4 | 2.6 | 2.5 | 2.7 | 2.6 | 3.1 | 4.0 | 3.8 | 3.7 | 2.5 | 2.3 | 2.5 | 3.2 | |
| Variable | Parameter | Skill Score | Skill Index | |
|---|---|---|---|---|
| Calibration | Validation | |||
| Wave | Hs | 0.95 | 0.96 | IOA |
| Tide | Semi-range | 0.98 | 0.98 | RE |
| Phase-lag | 1.00 | 0.99 | ||
| Tidal current | Amp. | 0.82 | 0.87 | RE |
| Phase-lag | 0.89 | 0.97 | ||
| SSC | - | 0.65 | 0.64 | RE |
| Water quality | Water temperature | 0.99 | 0.99 | IOA |
| Salinity | 0.57 | 0.85 | ||
| Chl-a | 0.67 | 0.67 | ||
| TN | 0.95 | 0.95 | ||
| TP | 0.71 | 0.71 | ||
| DO | 0.85 | 0.65 | ||
References
- Jang, D.; Hwang, J.H. Estuary classification method for considering climate change effects in South Korea. J. Coast. Res. 2013, SI65, 962–967. [Google Scholar] [CrossRef]
- Newton, A.; Icely, J.; Cristina, S.; Brito, A.; Cardoso, A.C.; Colijn, F.; Riva, S.D.; Gertz, F.; Hansen, J.W.; Holmer, M.; et al. An overview of ecological status, vulnerability and future perspectives of European large shallow, semi-enclosed coastal systems, lagoons and transitional waters. Estuar. Coast. Shelf Sci. 2014, 140, 95–122. [Google Scholar] [CrossRef]
- Yoon, S.J.; Hong, S.; Kwon, B.O.; Ryu, J.; Lee, C.H.; Nam, J.; Khim, J.S. Distributions of persistent organic contaminants in sediments and their potential impact on macrobenthic faunal community of the Geum River Estuary and Saemangeum Coast, Korea. Chemosphere 2017, 173, 216–226. [Google Scholar] [CrossRef] [PubMed]
- Kim, N.H.; Hwang, J.H.; Hyeon, K.D. Evaluation of Mixing and Stratification in an Estuary of Korea. J. Coast. Res. 2018, 96–100. [Google Scholar] [CrossRef]
- Kim, N.H.; Hwang, J.H.; Ku, H. Stratification of tidal influenced navigation channel. J. Coast. Res. 2016, 63–67. [Google Scholar] [CrossRef]
- Masunaga, E.; Yamazaki, H. A new tow-yo instrument to observe high-resolution coastal phenomena. J. Mar. Syst. 2014, 129, 425–436. [Google Scholar] [CrossRef]
- Hwang, J.H.; Van, S.P.; Choi, B.J.; Chang, Y.S.; Kim, Y.H. The physical processes in the Yellow Sea. Ocean Coast. Manag. 2014, 102, 449–457. [Google Scholar] [CrossRef]
- Kim, H.C.; Son, S.; Kim, Y.H.; Khim, J.S.; Nam, J.; Chang, W.K.; Lee, J.H.; Lee, C.H.; Ryu, J. Remote sensing and water quality indicators in the Korean West coast: Spatio-temporal structures of MODIS-derived chlorophyll-a and total suspended solids. Mar. Pollut. Bull. 2017, 121, 425–434. [Google Scholar] [CrossRef]
- Ostrander, C.E.; McManus, M.A.; DeCarlo, E.H.; Mackenzie, F.T. Temporal and spatial variability of freshwater plumes in a semienclosed estuarine-bay system. Estuaries Coasts 2008, 31, 192–203. [Google Scholar] [CrossRef]
- Figueroa, S.M.; Lee, G.H.; Shin, H.J. The effect of periodic stratification on floc size distribution and its tidal and vertical variability: Geum Estuary, South Korea. Mar. Geol. 2019, 412, 187–198. [Google Scholar] [CrossRef]
- Koh, C.H.; Khim, J.S. The Korean tidal flat of the Yellow Sea: Physical setting, ecosystem and management. Ocean Coast. Manag. 2014, 102, 398–414. [Google Scholar] [CrossRef]
- Lie, H.J.; Cho, C.H.; Lee, S.; Kim, E.S.; Koo, B.J.; Noh, J.H. Changes in marine environment by a large coastal development of the Saemangeum Reclamation Project in Korea. Ocean Polar Res. 2008, 30, 475–784. [Google Scholar] [CrossRef]
- Yih, W.; Kim, H.S.; Myung, G.; Park, J.W.; Yoo, Y.D.; Jeong, H.J. The red-tide ciliate Mesodinium rubrum in Korean coastal waters. Harmful Algae 2013, 30, S53–S61. [Google Scholar] [CrossRef]
- Bellinger, E.G.; Sigee, D.C. Freshwater Algae: Identification and use as bioindicators; Wiley-Blackwell: Chichester, West Sussex, UK, 2015. [Google Scholar]
- Kim, H.C.; Song, Y.S.; Kim, Y.H.; Son, S.; Cho, J.G.; Chang, W.K.; Lee, C.H.; Nam, J.; Ryu, J. Implications of Estuarine and Coastal Management in the Growth of Porphyra sp in the Geum River Estuary, South Korea: A Modeling Study. J. Coast. Res. 2018, 396–400. [Google Scholar] [CrossRef]
- Nishikawa, T.; Tarutani, K.; Yamamoto, T. Nitrate and phosphate uptake kinetics of the harmful diatom Eucampia zodiacus Ehrenberg, a causative organism in the bleaching of aquacultured Porphyra thalli. Harmful Algae 2009, 8, 513–517. [Google Scholar] [CrossRef]
- Karydis, M.; Kitsiou, D. Marine water quality monitoring: A review. Mar. Pollut. Bull. 2013, 77, 23–36. [Google Scholar] [CrossRef]
- National Coastal Condition Assessment: Site Evaluation Guidelines; EPA 843-10-004; United States Environmental Protection Agency: Washington, DC, USA, 2015.
- Kim, N.H.; Hwang, J.H.; Cho, J.; Kim, J.S. A framework to determine the locations of the environmental monitoring in an estuary of the Yellow Sea. Environ. Pollut. 2018, 241, 576–585. [Google Scholar] [CrossRef]
- Kitsiou, D.; Tsirtsis, G.; Karydis, M. Developing an optimal sampling design. A case study in a coastal marine ecosystem. Environ. Monit. Assess. 2001, 71, 1–12. [Google Scholar] [CrossRef]
- Bretherton, F.P.; Davis, R.E.; Fandry, C.B. A technique for objective analysis and design of oceanographic experiments applied to MODE-73. Deep Sea Res. Oceanogr. Abstr. 1976, 23, 559–582. [Google Scholar] [CrossRef]
- Barth, N.; Wunsch, C. Oceanographic experiment design by simulated annealing. J. Phys. Oceanogr. 1990, 20, 1249–1263. [Google Scholar] [CrossRef]
- Barth, N.H. Oceanographic experiment design II: Genetic algorithms. J. Atmos. Ocean. Technol. 1992, 9, 434–443. [Google Scholar] [CrossRef]
- Hernandez, F.; Letraon, P.Y.; Barth, N.H. Optimizing a drifter cast strategy with a genetic algorithm. J. Atmos. Ocean. Technol. 1995, 12, 330–345. [Google Scholar] [CrossRef]
- Hackert, E.C.; Miller, R.N.; Busalacchi, A.J. An optimized design for a moored instrument array in the tropical Atlantic Ocean. J. Geophys. Res. Ocean. 1998, 103, 7491–7509. [Google Scholar] [CrossRef]
- Baehr, J.; McInerney, D.; Keller, K.; Marotzke, J. Optimization of an observing system design for the North Atlantic meridional overturning circulation. J. Atmos. Ocean. Technol. 2008, 25, 625–634. [Google Scholar] [CrossRef][Green Version]
- Bennett, A.F. Array design by inverse methods. Prog. Oceanogr. 1985, 15, 129–156. [Google Scholar] [CrossRef]
- McIntosh, P.C. Systematic design of observational arrays. J. Phys. Oceanogr. 1987, 17, 885–902. [Google Scholar] [CrossRef]
- Gao, B.-B.; Wang, J.-F.; Fan, H.-M.; Xu, K.; Hu, M.-G.; Chen, Z.-Y. A stratified optimization method for a multivariate marine environmental monitoring network in the Yangtze River estuary and its adjacent sea. Int. J. Geogr. Inf. Sci. 2015, 29, 1332–1349. [Google Scholar] [CrossRef]
- Fan, H.M.; Gao, B.B.; Xu, R.; Wang, J.F. Optimization of Shanghai marine environment monitoring sites by integrating spatial correlation and stratified heterogeneity. Acta Oceanol. Sin. 2017, 36, 111–121. [Google Scholar] [CrossRef]
- Bian, X.L.; Li, X.M.; Qi, P.; Chi, Z.H.; Ye, R.; Lu, S.W.; Cai, Y.H. Quantitative design and analysis of marine environmental monitoring networks in coastal waters of China. Mar. Pollut. Bull. 2019, 143, 144–151. [Google Scholar] [CrossRef]
- Rogowski, P. A technique for optimizing the placement of oceanographic sensors with example case studies for the New York Harbor region. In Proceedings of the OCEANS 2007, Vancouver, BC, Canada, 29 September–4 October 2007. [Google Scholar]
- Kim, N.H.; Hwang, J.H. Reconstruction of TS spatial distribution using minimum points in Geumgang Estuary. J. Korean Soc. Mar. Environ. Energy 2018, 21, 351–360. [Google Scholar] [CrossRef]
- De Jonge, V.N.; Elliott, M.; Brauer, V.S. Marine monitoring: Its shortcomings and mismatch with the EU water framework directive’s objectives. Mar. Pollut. Bull. 2006, 53, 5–19. [Google Scholar] [CrossRef] [PubMed]
- Karydis, M.; Kitsiou, D. Eutrophication and environmental policy in the Mediterranean Sea: A review. Environ. Monit. Assess. 2012, 184, 4931–4984. [Google Scholar] [CrossRef] [PubMed]
- Pham, V.S.; Hwang, J.H.; Ku, H. Optimizing dynamic downscaling in one-way nesting using a regional ocean model. Ocean Model. 2016, 106, 104–120. [Google Scholar] [CrossRef]
- Jeong, S.; Yeon, K.; Hur, Y.; Oh, K. Salinity intrusion characteristics analysis using EFDC model in the downstream of Geum River. J. Environ. Sci. 2010, 22, 934–939. [Google Scholar] [CrossRef]
- Deltares. Delft3D-FLOW user manual. 2014, p. 684. Available online: https://oss.deltares.nl/documents/183920/185723/Delft3D-FLOW_User_Manual.pdf (accessed on 26 February 2020).
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 10th ed.; Dover Publications: Mineola, NY, USA, 1972. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev.: Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Thomson, R.E.; Emery, W.J. Data Analysis Methods in Physical Oceanography, 3rd ed.; Elsevier: Miami, FL, USA, 2014. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. A globally convergent augmented Lagrangian algorithm for optimization with general constraints and simple bounds. Siam J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.; Toint, P.L. A globally convergent Lagrangian barrier algorithm for optimization with general inequality constraints and simple bounds. Math. Comput. 1997, 66, 26. [Google Scholar] [CrossRef]
- Deb, K. Optimization for Engineering Design: Algorithms and Examples, 2nd ed.; PHI Learning Private Limited: New Delhi, India, 2012. [Google Scholar]
- Venkataraman, P. Applied Optimization with MATLAB Programming, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Gandin, L.S. The Objective Analysis of Meteorological Field, Israel Program for Scientific Translations; Quarterly Journal of the Royal Meteorological Society: Jerusalem, Israel, 1965; p. 240. [Google Scholar]
- Barnes, S.L. A technique for maximizing details in numerical weather map analysis. J. Appl. Meteorol. 1964, 3, 396–409. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M. Improved global sea-surface temperature analyses using optimum interpolation. J. Clim. 1994, 7, 929–948. [Google Scholar] [CrossRef]
- Zhang, M.H.; Lin, J.L.; Cederwall, R.T.; Yio, J.J.; Xie, S.C. Objective analysis of ARM IOP data: Method and sensitivity. Mon. Weather Rev. 2001, 129, 295–311. [Google Scholar] [CrossRef]
- Guinehut, S.; Larnicol, G.; Le Traon, P.Y. Design of an array of profiling floats in the North Atlantic from model simulations. J. Mar. Syst. 2002, 35, 1–9. [Google Scholar] [CrossRef]
- Hoyer, J.L.; She, J. Optimal interpolation of sea surface temperature for the North Sea and Baltic Sea. J. Mar. Syst. 2007, 65, 176–189. [Google Scholar] [CrossRef]
- Cressman, C.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Koch, S.E.; Desjardins, M.; Kocin, P.J. An interactive Barnes objective map analysis scheme for use with satellite and conventional data. J. Clim. Appl. Meteorol. 1983, 22, 1487–1503. [Google Scholar] [CrossRef]
- Spencer, P.L.; Janish, P.R.; Doswell, C.A. A four-dimensional objective analysis scheme and multitriangle technique for wind profiler data. Mon. Weather Rev. 1999, 127, 279–291. [Google Scholar] [CrossRef][Green Version]
- Sinha, S.K.; Narkhedakar, S.G.; Mitra, A.K. Barnes objective analysis scheme of daily rainfall over Maharashtra (India) on a mesoscale grid. Atmosfera 2006, 19, 109–126. [Google Scholar]
- Carr, F.H.; Spencer, P.L.; Doswell, C.A.; Powell, J.D. A comparison of 2 objective analysis techniques for profiler time-height data. Mon. Weather Rev. 1995, 123, 2165–2180. [Google Scholar] [CrossRef][Green Version]
- Marquardt, D.W. An algorithm for the least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Barnes, S.L. Applications of the Barnes objective analysis scheme 3: Tuning for minimum error. J. Atmos. Ocean. Technol. 1994, 11, 1459–1479. [Google Scholar] [CrossRef][Green Version]
- Zhang, A.; Hess, K.W.; Aikman, F. User-based skill assessment techniques for operational hydrodynamic forecast systems. J. Oper. Oceanogr. 2010, 3, 11–24. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Jolliff, J.K.; Kindle, J.C.; Shulman, I.; Penta, B.; Friedrichs, M.A.M.; Helber, R.; Arnone, R.A. Summary diagrams for coupled hydrodynamic-ecosystem model skill assessment. J. Mar. Syst. 2009, 76, 64–82. [Google Scholar] [CrossRef]
- Bengraine, K.; Marhaba, T.F. Using principal component analysis to monitor spatial and temporal changes in water quality. J. Hazard. Mater. 2003, 100, 179–195. [Google Scholar] [CrossRef]
- Kim, N.H.; Pham, V.S.; Hwang, J.H.; Won, N.I.; Ha, H.K.; Im, J.; Kim, Y. Effects of seasonal variations on sediment-plume streaks from dredging operations. Mar. Pollut. Bull. 2018, 129, 26–34. [Google Scholar] [CrossRef]




| Category | Principal Component | Eigenvalue | Eigenvector | |||||
|---|---|---|---|---|---|---|---|---|
| T | S | DO | Chl-a | TN | TP | |||
| Spatial (Entire domain) | 1st PC (43%) | 2.56 | 0.26 | −0.50 | −0.21 | 0.11 | 0.57 | 0.55 |
| 2nd PC (32%) | 1.91 | −0.64 | −0.36 | 0.64 | −0.10 | 0.23 | 0.01 | |
| 3rd PC (18%) | 1.06 | 0.02 | 0.15 | 0.27 | 0.94 | −0.07 | 0.12 | |
| Category | Principal Component | Eigenvalue | Eigenvector | |||||
|---|---|---|---|---|---|---|---|---|
| T | S | DO | Chl-a | TN | TP | |||
| Temporal (Pt.1 – near the sea-dike) | 1st PC (43%) | 2.59 | 0.58 | 0.10 | −0.53 | 0.18 | 0.22 | 0.54 |
| 2nd PC (32%) | 2.20 | −0.03 | 0.62 | −0.20 | 0.51 | −0.50 | −0.25 | |
| 3rd PC (18%) | 0.67 | −0.14 | 0.10 | 0.39 | 0.66 | 0.62 | 0.05 | |
| Temporal (Pt.38 – ocean side) | 1st PC (47%) | 2.85 | 0.58 | 0.50 | −0.52 | 0.31 | 0.04 | 0.23 |
| 2nd PC (35%) | 2.11 | −0.10 | −0.20 | 0.23 | 0.41 | 0.65 | 0.55 | |
| 3rd PC (11%) | 0.67 | −0.18 | 0.38 | 0.37 | 0.69 | −0.09 | −0.46 | |
| Statistics | Water Temperature | Salinity | Dissolved Oxygen | Chlorophyll-a | Total Nitrogen | Total Phosphorus |
|---|---|---|---|---|---|---|
| COR | 0.99 | 0.99 | 0.80 | 0.93 | 0.98 | 0.96 |
| RMSD | 0.07 | 0.46 | 0.06 | 0.24 | 0.06 | 0.00 |
| MEAN | 15.48 | 31.64 | 8.43 | 4.39 | 0.52 | 0.05 |
| STD | 0.45 | 2.68 | 0.10 | 0.60 | 0.25 | 0.01 |
| Statistics | Water temperature | ||||||
|---|---|---|---|---|---|---|---|
| RA1 | RA2 | RA3 | RA4 | RA5 | RA6 | RA7 | |
| COR | 1.00 | 0.99 | 1.00 | 0.96 | 0.95 | 0.88 | 0.90 |
| RMSD | 0.00 | 1.65 | 0.85 | 2.80 | 3.20 | 4.79 | 4.26 |
| BIAS | 0.00 | 0.50 | −0.02 | 0.94 | 1.00 | 1.53 | 1.32 |
| MEAN | 16.38 | 15.88 | 16.40 | 15.44 | 15.38 | 14.85 | 15.06 |
| STD | 9.35 | 9.17 | 9.52 | 8.83 | 8.47 | 7.72 | 8.15 |
| Salinity | |||||||
| COR | 1.00 | 0.38 | 0.45 | 0.35 | 0.37 | 0.22 | 0.26 |
| RMSD | 0.00 | 14.36 | 16.87 | 17.53 | 18.15 | 18.71 | 18.75 |
| BIAS | 0.00 | −13.02 | −15.73 | −16.37 | −17.01 | −17.56 | −17.61 |
| MEAN | 15.47 | 28.48 | 31.20 | 31.84 | 32.48 | 33.03 | 33.08 |
| STD | 6.55 | 2.50 | 1.28 | 1.01 | 0.67 | 0.51 | 0.53 |
| Dissolved Oxygen | |||||||
| COR | 1.00 | 0.75 | 0.72 | 0.72 | 0.72 | 0.72 | 0.72 |
| RMSD | 0.00 | 1.94 | 2.01 | 2.05 | 2.10 | 2.12 | 2.11 |
| BIAS | 0.00 | 0.52 | 0.17 | 0.45 | 0.40 | 0.44 | 0.49 |
| MEAN | 8.82 | 8.31 | 8.65 | 8.38 | 8.43 | 8.38 | 8.33 |
| STD | 2.73 | 1.53 | 1.28 | 1.29 | 1.16 | 1.11 | 1.17 |
| Chlorophyll-a | |||||||
| COR | 1.00 | 0.82 | 0.80 | 0.77 | 0.73 | 0.66 | 0.69 |
| RMSD | 0.00 | 1.57 | 2.81 | 1.79 | 1.90 | 2.32 | 2.03 |
| BIAS | 0.00 | −0.20 | −2.02 | 0.37 | −0.13 | −0.35 | 0.20 |
| MEAN | 4.07 | 4.27 | 6.08 | 3.70 | 4.20 | 4.41 | 3.87 |
| STD | 2.71 | 2.22 | 3.30 | 1.91 | 2.31 | 2.86 | 2.32 |
| Total Nitrogen | |||||||
| COR | 1.00 | 0.54 | 0.30 | 0.27 | 0.16 | 0.20 | 0.15 |
| RMSD | 0.00 | 1.26 | 1.68 | 1.67 | 1.72 | 1.72 | 1.72 |
| BIAS | 0.00 | 1.10 | 1.51 | 1.50 | 1.56 | 1.56 | 1.56 |
| MEAN | 1.99 | 0.89 | 0.47 | 0.48 | 0.43 | 0.43 | 0.43 |
| STD | 0.74 | 0.27 | 0.05 | 0.05 | 0.04 | 0.04 | 0.04 |
| Total Phosphorus | |||||||
| COR | 1.00 | 0.84 | 0.59 | 0.62 | 0.62 | 0.66 | 0.64 |
| RMSD | 0.00 | 0.03 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 |
| BIAS | 0.00 | 0.02 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 |
| MEAN | 0.07 | 0.06 | 0.04 | 0.05 | 0.04 | 0.05 | 0.05 |
| STD | 0.03 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| Statistics | Water temperature | |||||||
|---|---|---|---|---|---|---|---|---|
| RA1 | RA2 | RA3 | RA4 | RA5 | RA6 | RA7 | Offshore | |
| COR | 0.76 | 0.84 | 0.79 | 0.90 | 0.92 | 0.97 | 0.96 | 1.00 |
| RMSD | 6.58 | 5.51 | 6.49 | 4.52 | 3.98 | 2.49 | 3.09 | 0.00 |
| BIAS | −2.28 | −1.78 | −2.30 | −1.34 | −1.27 | −0.75 | −0.96 | 0.00 |
| MEAN | 16.38 | 15.88 | 16.40 | 15.44 | 15.38 | 14.85 | 15.06 | 14.10 |
| STD | 9.35 | 9.17 | 9.52 | 8.83 | 8.47 | 7.72 | 8.15 | 5.99 |
| Salinity | ||||||||
| COR | 0.16 | 0.29 | 0.10 | 0.65 | 0.56 | 0.89 | 0.85 | 1.00 |
| RMSD | 18.79 | 5.21 | 2.30 | 1.50 | 0.83 | 0.26 | 0.29 | 0.00 |
| BIAS | 17.63 | 4.61 | 1.89 | 1.26 | 0.62 | 0.06 | 0.02 | 0.00 |
| MEAN | 15.47 | 28.48 | 31.20 | 31.84 | 32.48 | 33.03 | 33.08 | 33.10 |
| STD | 6.55 | 2.50 | 1.28 | 1.01 | 0.67 | 0.51 | 0.53 | 0.38 |
| Dissolved Oxygen | ||||||||
| COR | 0.72 | 0.97 | 0.97 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 |
| RMSD | 2.13 | 0.59 | 0.41 | 0.31 | 0.17 | 0.13 | 0.21 | 0.00 |
| BIAS | −0.35 | 0.17 | −0.17 | 0.10 | 0.05 | 0.10 | 0.15 | 0.00 |
| MEAN | 8.82 | 8.31 | 8.65 | 8.38 | 8.43 | 8.38 | 8.33 | 8.48 |
| STD | 2.73 | 1.53 | 1.28 | 1.29 | 1.16 | 1.11 | 1.17 | 1.04 |
| Chlorophyll-a | ||||||||
| COR | 0.62 | 0.76 | 0.80 | 0.82 | 0.94 | 0.99 | 0.96 | 1.00 |
| RMSD | 3.37 | 2.90 | 2.45 | 3.11 | 2.27 | 1.53 | 2.39 | 0.00 |
| BIAS | 1.32 | 1.13 | −0.69 | 1.69 | 1.19 | 0.98 | 1.53 | 0.00 |
| MEAN | 4.07 | 4.27 | 6.08 | 3.70 | 4.20 | 4.41 | 3.87 | 5.39 |
| STD | 2.71 | 2.22 | 3.30 | 1.91 | 2.31 | 2.86 | 2.32 | 3.93 |
| Total Nitrogen | ||||||||
| COR | 0.28 | 0.40 | 0.75 | 0.80 | 0.94 | 0.98 | 0.95 | 1.00 |
| RMSD | 1.71 | 0.52 | 0.05 | 0.06 | 0.02 | 0.01 | 0.02 | 0.00 |
| BIAS | −1.55 | −0.46 | −0.04 | −0.05 | 0.00 | 0.01 | 0.01 | 0.00 |
| MEAN | 1.99 | 0.89 | 0.47 | 0.48 | 0.43 | 0.43 | 0.43 | 0.43 |
| STD | 0.74 | 0.27 | 0.05 | 0.05 | 0.04 | 0.04 | 0.04 | 0.05 |
| Total Phosphorus | ||||||||
| COR | 0.69 | 0.90 | 0.94 | 0.96 | 0.98 | 0.99 | 0.99 | 1.00 |
| RMSD | 0.03 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| BIAS | −0.03 | −0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| MEAN | 0.07 | 0.06 | 0.04 | 0.05 | 0.04 | 0.05 | 0.05 | 0.05 |
| STD | 0.03 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, N.-H.; Hwang, J.H. Optimal Design of Water Quality Monitoring Networks in Semi-Enclosed Estuaries. Sensors 2020, 20, 1498. https://doi.org/10.3390/s20051498
Kim N-H, Hwang JH. Optimal Design of Water Quality Monitoring Networks in Semi-Enclosed Estuaries. Sensors. 2020; 20(5):1498. https://doi.org/10.3390/s20051498
Chicago/Turabian StyleKim, Nam-Hoon, and Jin Hwan Hwang. 2020. "Optimal Design of Water Quality Monitoring Networks in Semi-Enclosed Estuaries" Sensors 20, no. 5: 1498. https://doi.org/10.3390/s20051498
APA StyleKim, N.-H., & Hwang, J. H. (2020). Optimal Design of Water Quality Monitoring Networks in Semi-Enclosed Estuaries. Sensors, 20(5), 1498. https://doi.org/10.3390/s20051498





