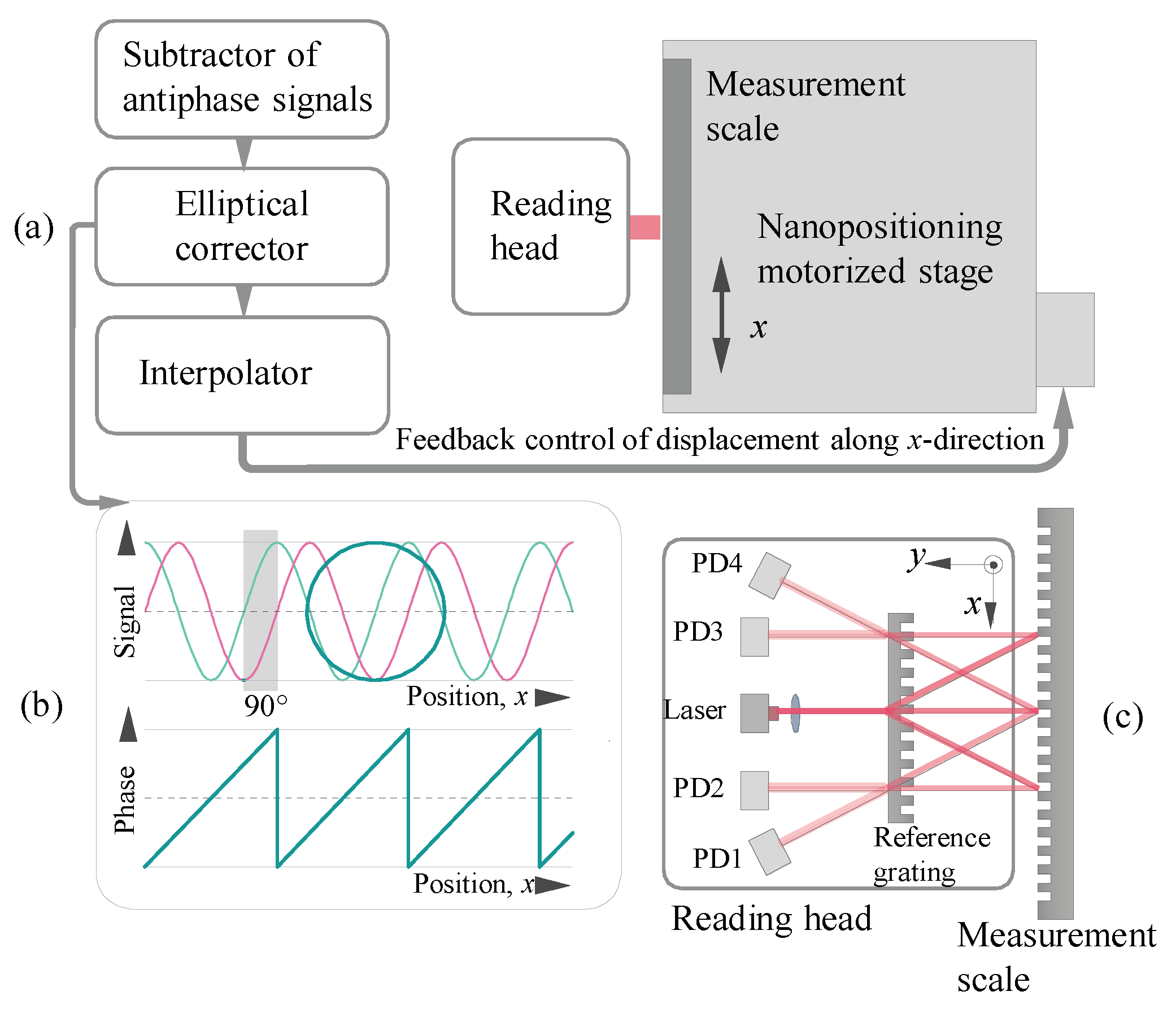
1. Introduction
Linear displacement sensors with fixed reading head determine the current coordinate and displacement direction of an object connected with the measurement scale [
1,
2,
3]. Optical interferential sensors show the highest resolution and accuracy for linear displacement measurements. There are many optical schemes that form two sinusoidal signals shifted in phase by π/2 and implement a quadrature detector with the help of optical interference. The arctangent of the ratio of these signals amplitudes is a linear function within one period, wherefrom the current location of the measurement scale is calculated. Subnanometer resolution levels can be achieved by subsequent interpolation of this function. In order for the interpolation to achieve high resolution, it is necessary to generate the pair of quadrature signals as perfectly as possible. The main problems of quadrature modulation are associated with signal distortions such as the inequality of amplitudes, shift of zero levels (offset), and the deviation of the phase shift from the π/2, i.e., phase imbalance. Last error is measured in electrical degrees. The amplitude imbalance can be eliminated by application of differential scheme. In this paper, we investigate phase retardations occurring in optical branch and achievable phase balance levels. We present the rationale of correct quadrature modulation in linear displacement sensor with two holographic gratings. In this regard, it is necessary to control the phase of the optical components not excluding the gain monitoring of the detectors.
Although quadrature modulation is widely used in grating interferometers, only a few publications discuss the corresponding problems for creating quadrature phase shift [
3,
4,
5]. At present, the problem of eliminating the phase imbalance of quadrature signals in the optical branch remains unsolved. Correction of this type of distortion is carried out electronically in the presence of an acceptable value, but can be minimized optically, which simplifies signal processing in real time.
The proposed method may be useful in other areas of interferometric measurements, specifically for biological applications [
6,
7] and coherence tomography [
8,
9]. In shearing interferometry, optimization of the reference element parameters can help to perform quantitative linear phase retardance [
10,
11,
12]. The presented analysis of laser radiation conversion in the interferometer may improve phase unwrapping of interferometric fringes [
13] or multistep phase-shift extraction [
14,
15]. The method can be applied to uncertainty precalculation before experimental implementation of digital methods as digital holographic interferometry [
16,
17] or digital speckle interferometry [
11]. Thereby, the studied method is not limited to displacement measurements, and can be applied to optimize phase relationships in any interferometric schemes with diffractive or holographic elements.
The article is organized as follows.
Section 2 presents an optical concept and quadrature signals generation in the optical branch.
Section 3 gives the optimization condition for the formation of quadrature signals. To simulate the conversions of optical radiation by diffraction gratings, a rigorous coupled waves analysis (RCWA) was used. Phase imbalance and amplification coefficients are deduced using Heydemann elliptic correction [
18,
19].
Section 4 describes the application of the proposed method to identify an instrumental uncertainty of double grating linear displacement sensor by estimating phase imbalance in the presence of various uncertainty contributions in the optical scheme.
3. Results
Tracing the path of each of the interfering beams considers the process of amplitude dividing and phase transformation in detail. At each diffraction, in addition to the amplitude conversion of light in accordance with diffraction efficiency, the wavefront undergoes a certain phase shift [
26,
27].
Table 1 presents the structure of the successive transformations in each of the beams and the parameters of each diffraction are introduced: diffraction efficiencies η and phase shifts Φ.
To consider the interference of a pair of signals, it is convenient to introduce the complex wave amplitude in an exponential form. The initial complex wave amplitude after the collimator is expressed as Einc = E0 × exp(I × Φ0). Then, after the first diffraction three operating waves are formed on the reference grating with amplitudes E11 = η11 × E0 × exp(I × [Φ0 + Φ11]), E12 = η12 × E0·exp(i × [Φ0 + Φ12]) and E13 = η13 E0 × exp(I × [Φ0 + Φ13]). During the second diffraction on the measurement scale, the dependence on the displacement and the phase shift during diffraction are introduced into the signal; forming four signals with complex amplitudes E21(x) = η21 × η11 × E0 × exp(i × [Φ0 + Φ11 + Φ21 − Ω(x)]), E22(x) = η22 × η12 × E0 ×exp(I × [Φ0 + Φ12 + Φ22 + Ω(x)]), E23(x) = η23 × η12 × E0 × exp(i × [Φ0 + Φ12 + Φ23 − Ω(x)]), E24(x) = η24 × η13 E0 × exp(I × [Φ0 + Φ13 + Φ24 + Ω(x)]). These signals have become dependent on displacement value. After the third diffraction, each of these waves is subdivided into two, forming four pairs of signals E31(x) and E34(x), E32(x) and E33(x), E35(x) and E38(x), and E36(x) and E37(x), which are superimposed due to the interference.
The complex amplitude of the wave arriving at the first detector PD1 is
Then, an intensity signal that is also equivalent to a voltage signal is
where A
PD1 = η
32 × η
21 × η
11 × E
0, B
PD1 = η
33 × η
22 × η
12 × E
0, V
PD1 = 2 A
PD1 × B
PD1 /(A
PD12 + B
PD12) = 2η
32 × η
21 × η
11 × η
33 × η
22 × η
12/[(η
32 η
21 η
11)
2 + (η
33 η
22 η
12)
2], and Ψ
PD1 = Φ
32 + Φ
21 + Φ
11 − Φ
33 − Φ
22 − Φ
12 − 2Ω(
x).
Similarly, we determine the optical signals
IPD2,
IPD3, and
IPD4 arriving to the remaining detectors A
PD2 = η
31 η
21 η
11 E
0, B
PD2 = η
34 η
22 η
12 E
0, Ψ
PD2 = Φ
31 + Φ
21 + Φ
11 − Φ
34 − Φ
22 − Φ
12 − 2Ω(
x); A
PD3 = η
35 η
23 η
12 E
0, B
PD3 = η
38 η
24 η
13 E
0, Ψ
PD3 = Φ
38 + Φ
24 + Φ
13 − Φ
35 − Φ
23 − Φ
12 + 2Ω(
x); A
PD4 = η
36 η
23 η
12 E
0, B
PD4 = η
37 η
24 η
13 E
0, Ψ
PD4 = Φ
13 + Φ
24 + Φ
37 − Φ
12 − Φ
23 − Φ
36 + 2Ω(
x). The received four signals
IPD1–
IPD4 are shown schematically in
Figure 2c. Due to the symmetry condition of a sinusoidal or rectangular profile of the grating, the diffraction efficiencies and optical phase shifts will be equal under symmetric diffraction conditions
It should be noted that the interference contrast
V is determined by six values of diffraction efficiency. The current phase is determined by six values of the phases introduced during diffractions, and the doubled phase, depending on the displacement. The presence of 2Ω(
x) indicates that, in the studied optical scheme, the signals period is half the period of the measurement scale. Currently, scientists can achieve eight-fold optical division of the period of the measurement scale that provides a corresponding increase in resolution [
28]. For any interferential implementation, the laser beam arriving at the reflective measurement scale, within the entire contact surface, must cover the area of the desired period to be sure of the correct phase shifting within the displacement period; therefore, the diffraction grating should be represented as a qualitatively uniform structure of a constant period without frames. It is possible to make a measurement scale with large frames with help of a two-probe scheme [
29], when the reading head is designed in such a way to generate and receive two sets of beams separated in space. Each signal set is responsible for own control zone on the measurement scale. Then, when passing the frame border, one of the beams always falls into the region with a uniform period within one frame.
To ensure quadrature modulation, it is necessary for the phase difference between I
PD1 and I
PD2 to be 90°
It turned out that the final phase difference, and therefore quadrature modulation, is determined by the third diffraction inside of the double grating optical system. By generating and controlling the phase shifts introduced during this third diffraction, we set the requirements for the reference grating. In this regard, we are able to control the quadrature modulation in the optical branch without introducing additional optical phase components. The combined energy and phase calculation of the diffracted waves helps to create the quadrature modulation. The two remaining signals from the photodiodes PD3 and PD4 must be out of phase in order to effectively reset the offset: ΔΨ1-4 = ΨPD1–ΨPD4 = Φ11 + Φ21 + Φ32 − Φ12 − Φ22 − Φ33 − 2Ω(x) − [Φ13 + Φ24 + Φ37 − Φ12 − Φ23 − Φ36+2Ω(x)] = −4Ω(x). Therefore, ΨPD4 = ΨPD1 + 4Ω(x). ΔΨ2-3 = ΨPD2 − ΨPD3 = Φ11 + Φ21 + Φ31 − Φ12 − Φ22 − Φ34 − 2Ω(x) − [Φ13 + Φ24 + Φ38 − Φ12 − Φ23 − Φ35 + 2Ω(x)] = −4Ω(x). Therefore, ΨPD3 = ΨPD2 + 4Ω(x). The antiphase signals are determined by various signs in front of the phase term containing the cosine function.
Distorted signals after the subtraction are
where
p = (η
32 η
21 η
11 E
0)
2 + (η
33 η
22 η
12 E
0)
2 − (η
36 η
23 η
12 E
0)
2 − (η
37 η
24 η
13 E
0)
2→0;
Rcos = 2E
02(η
32 η
21 η
11 η
33 η
22 η
12 + η
36 η
23 η
12 η
37 η
24 η
13) → 4η
32 η
21 η
11 η
33 η
22 η
12 E
02;
q = (η
31 η
21 η
11 E
0)
2 + (η
34 η
22 η
12 E
0)
2 − (η
35 η
23 η
12 E
0)
2 − (η
38 η
24 η
13)
2→0;
Rsin = 2E
02(η
31 η
21 η
11 η
34 η
22 η
12 + η
35 η
23 η
12 η
38 η
24 η
13) → 4 η
31 η
21 η
11 η
34 η
22 η
12 E
02; and α = |Φ
32 + Φ
34 − Φ
33 − Φ
31 − 90°|→0°.
Rcos and
Rsin are the amplitudes of the signals, which relation defines the needed amplification in the channels;
p and
q are the offset levels of the sine and cosine channels, respectively; and α is the quadrature error or phase imbalance. When the condition in Equation (5) is fulfilled, the signal amplitude doubles, and the offset level is zeroed (
p →0
, q →0). The advantage of this procedure, in addition to zeroing and equalizing the basic signal levels, is that it also consists in an increase in the signal-to-noise ratio. The period of the signals decreases by half relative to the period of the measurement scale;
p and
q are different if the diffraction efficiencies are different for different diffraction conditions. α expresses the residual ellipticity (imperfect quadrature alignment) that is zeroed out in the practical implementation of the condition in Equation (5)—successful adjustment of the phase imbalance due to proper manufacturing of the static reference scale. In electronic processing, we no longer work with the optical signals
Icos and
Isin, but with the proportional voltage signals
Ucos and
Usin, which are schematically shown in
Figure 2d.
3.1. Elliptical Correction Phase Analysis
When the signals are presented in the form of Equation (6), we can apply the Heydemann correction [
19] of quadrature measurement errors in interferometers. For the interferential scheme in
Figure 2, the perfect quadrature detection would be
Ucosperf =
R cos(Ψ),
Usinperf =
R sin(Ψ), where = 2Ω(
x)
= 4π
x/
d,
R =
Rcos = G Rsin is the radius of the Lissajous figure in the form of a circle, and
G = Rcos/
Rsin is the—the amplification coefficient. Measurements of the instantaneous coordinate values based on instantaneous signals
Ucosperf и
Ucosperf are possible by the interpolation between the calculated points of zero intersections
x in the Lissajous figure. These intersections correspond to a quarter of the period of the quadrature signal. Fractional distance values in phase representation Ψ are obtained from the arctangent function of the ratio of signal amplitudes. The main difficulty in digital adjustment of phase imbalance is to determine the coefficients
r,
p,
q, and α from the experimental signal (Equation (6)), assuming that these are the only significant demodulation errors. To provide it, a sufficiently large distance
x is covered, accumulating experimental data to determine these four components. This operation is carried out by selecting the least square method.
In a real system, the end of the vector (
Ucos,
Usin) is not located on a circle, but on a distorted ellipse, which leads to significant errors in determining the fractional part Ψ of a quarter of the period. The circle (
Ucosperf)
2 + (
Ucosperf)
2 =
R2 turns into an ellipse (
Ucos)
2 + (
Usin)
2 =
R2. The trajectory of the end of the vector (
Ucos,
Usin) representing a distorted ellipse can be described according to
Then, the signals
Ucos and
Usin (
Figure 2d) can be corrected and reduced to the form
U’cos and
U’sin (
Figure 2e), respectively
where G = η
32 η
33/η
31 η
34→1; α = |Φ
32 + Φ
34 − Φ
33 − Φ
31 − 90°|→0°.
To avoid problems caused by the multi-valued nature of this arctangent function, the current phase Ψ and displacement value ∆
x is led to the following form
where indices 1 and 0 correspond to samples of zero intersections of
x before and after the distance has changed. Encoder resolution and accuracy depend directly on how accurately
x and Ψ are determined.
To formulate the requirements for the reference diffraction scale and determine whether it is possible to correct the ellipticity in the optical branch, it is necessary to simulate the diffraction problem. The optimization of the parameters of the reference scale is carried out in accordance with the condition
These conditions can be implemented when choosing the parameters of the reference scale—grating period and groove depth. At the same time, during the simulation and analysis, the polarization, wavelength, and shape of the grating relief are varied. The numerical solution of the diffraction problem and the corresponding calculation of the parameters of the reference scale η
31, η
32, η
33, η
34, Φ
31, Φ
32, Φ
33, and Φ
34 were carried out using MATLAB environment (ETMC Exponenta Ltd., Moscow, Russian Federation). To simulate the diffraction in sinusoidal grating, the RCWA method with the built-in method of curvilinear coordinates was used [
30,
31].
3.2. Phase Imbalance and Amplification in Quadrature Signals
Simulation for a sinusoidal diffraction scale is considered. The modulation zone of the diffraction grating is made of polymethyl methacrylate. The absolute value of the phase accumulated in the substrate of the diffraction grating does not affect the result of phase contribution calculation due to the symmetry of the optical scheme. The period of quadrature signals and, consequently, the period of the scales are selected from the division condition during interpolation with the powers of “2”, or based on the geometry of the optical scheme.
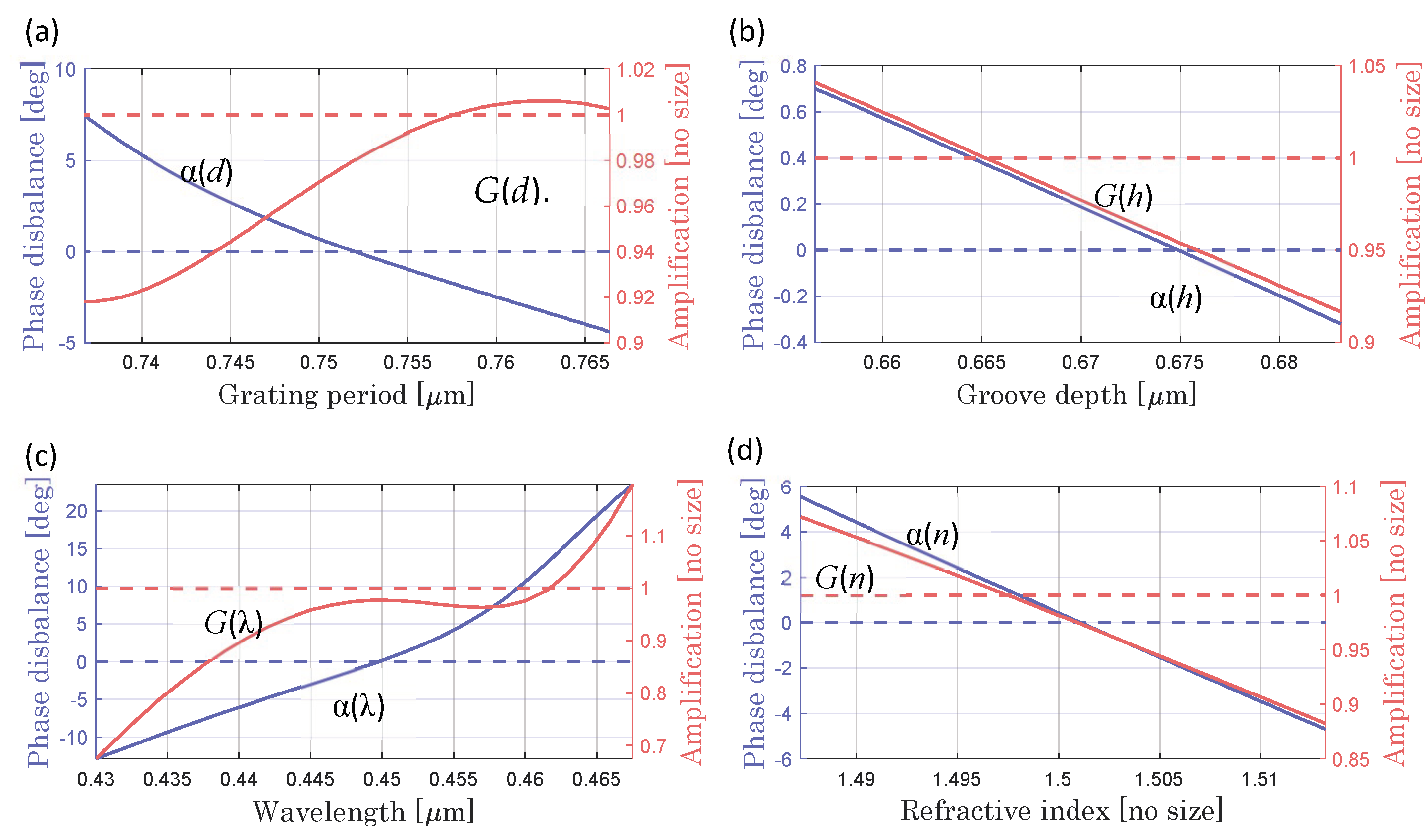
Figure 3 shows the simulation results for the phase imbalance and amplification depending on the period and height of the reference diffraction scale. To analyze the phase imbalance and amplification in this work, simulation for a wide range of periods is carried out. Convenient propagation geometry corresponds to diffraction angles θ
1 from 25° to 45° (
Figure 2), which determines the periods for a laser wavelength using Equation (1). Different polarization conditions are considered; TE polarization is recommended. The groove depth in the analysis is limited by the maximum value of the period.
The value of the phase difference is restricted to the range from −180° to 180°; the contours at
Figure 3 show the lines of the uniform phase imbalance in increments of 45°. It is important to note that the value of the phase imbalance, in contrast to the value of the amplification, keeps itself for different wavelengths while maintaining the diffraction angle. This suggests that it is possible to work with different sets of scales with different periods and corresponding coherent radiation sources in the same beam path geometry in the optical scheme.
For different laser wavelength the calculated reference scale parameters are: dB = 0.751 μm, hB = 0.67 μm for λB = 450 nm; dG = 0.875 μm, hG = 0.785 μm for λG = 0.52 μm; and dR = 1.123 μm, hR = 1.125 μm for λR = 0.66 μm. Furthermore, to analyze the contribution of the instrumental uncertainty in linear displacement encoder under study, the influence of manufacturing errors of reference scale and the stability of operating conditions are considered. It should be noted that, if these parameters do not match the calculated ones, it will be necessary to use an ellipticity correction in the interface electronics.
4. Discussion
The calculation of the diffraction gratings for double grating linear interference sensor includes: a light-energy calculation defining the conditions for the maximum interference contrast in photodetectors plane; calculation of phase relations according to the propagation of laser radiation inside the optical system; calculation of tolerance for the grating period and groove depth of the scales; and calculations of tolerances for refractive index changes and wavelength changes during operation. The input data of the optimization model are all the parameters necessary to solve the rigorous diffraction problem: parameters of the relief profile, spectral functions of the dielectric permittivity of the media used, and parameters of the incident radiation (wavelength, incidence vector, and polarization condition). Within the model framework, it is assumed that the optical system is aligned for observing the interference band of infinite width at photodetectors. It should be noted that consideration of conical diffraction allows analyzing the tolerances for angular displacements in the scheme, such as the rotation of the reference scale relative to the incident beam; accuracy of the laser adjustment is expressed in the illuminating angle deviation.
The proposed model allows calculating the uncertainty budget in the optical system related to the instrumental uncertainty. The contributions from the influencing parameters to the output signal are estimated by two key quadrature modulation characteristics: phase imbalance and amplification in the pair of channels. Usually, it is preferred to eliminate systematic uncertainty in possible ways. The proposed analysis allows evaluating the boundaries of permissible uncertainty values, knowing the manufacturing errors of the reference scale.
Figure 4 shows the dependencies of the phase imbalance and amplification, independent for each of the parameters affecting to the condition of uncertainty contributions. Four parameters were considered: period
d and groove depth
h of the reference scale, refractive index
n, and wavelength λ. Uncertainties of the period Δ
d and groove depth Δ
h of the reference scale arise due to manufacturing inaccuracies. The wavelength uncertainty Δλ is associated with the heating of the radiation source and the corresponding change in the generation wavelength. The uncertainty of the refractive index Δ
n is associated with the heating of the read head during the work. Functions α(
d), α(
h), α(λ), and α(
n) allow us to estimate the contribution of the uncertainty to the phase imbalance, while the functions
G(
d),
G(
h),
G(λ), and G(
n) the contribution to the amplification.
In the presence of 2% uncertainties of each of the considered parameters: Δα (Δ
d) = ± 2.5738°; Δ
G (Δ
d) = ± 0.0353 for Δ
d = ± 0.01
d; Δα (Δ
h) = ± 0.2581°; ΔG (Δ
h) = ± 0.0315 for Δ
h = ± 0.01
h; Δα (Δλ) = ± 2.4489°; Δ
G(Δλ) = ± 0.038 for Δλ = ± 0.01λ; Δα(Δ
n) = ± 0.0597°; and Δ
G(Δ
n) = ± 0.0011 for Δ
n = ± 0.01
n. In accordance with the above analysis, an assessment of the instrumental uncertainty is performed. Period and wavelength errors make the greatest contribution. The phase imbalance value is most sensitive to the period of the reference scale, whereas the amplification value is most sensitive to wavelength. In the considered double grating linear displacement sensor, exactly the groove parameters of the reference scale determine the ability to create the quadrature modulation. Operating conditions (temperature, humidity, and pressure) have a significant impact on the interferometer and must be normalized. Fluctuations of these parameters influence the system parameters as wavelength and refractive index of the scales, which was analyzed (
Figure 4). This problem is also solved by manufacturing components from materials with a zero linear expansion coefficient (Sitall and Zerodur). The generalized uncertainties Δα of the phase imbalance function α(
d, h, λ
, n) and Δ
G of the gain function in the channels
G(
d, h, λ
, n) can be estimated in accordance with the equations
The generalized uncertainties in the presence of 2% deviations of the considered parameters, as visualized in
Figure 4, are Δα(Δ
d, Δ
h, Δλ
, Δ
n) = 3.5626° and Δ
G(Δ
d, Δ
h, Δλ
, Δ
n) = 0.0475. The proposed method of analysis and optimization justifies the errors associated with the phase imbalance, allowing to predict the value for subsequent compensation. The correction of ellipticity becomes more effective as the optimization conditions are more accurately fulfilled in practice. The accuracy of the method under study is determined by the iteration step chosen for the calculation. In the current simulation (
Figure 3 and
Figure 4), this step was 1 nm. The chosen iterative step for each influential parameter should be several times smaller than the errors of the real diffraction scale. The limitations of the optimization method in practical implementation are related to manufacturing capabilities. Optical structures, manufactured according to calculation, provide good usability and performance for quadrature modulation. The resulting value of the phase imbalance provided by the fabricated reference grating with deviated parameters defines the practical limit of double-grating optical quadrature homodyne interferometry.
5. Conclusions
For reliable bi-directional motion detection, many interferometers generate two sinusoidal electrical outputs, which ideally should be equal in amplitude, have no relative offset, and have a phase difference of 90°. In practice, these criteria are not realized, and, therefore, it is necessary to apply corrections to quadrature phase signals to obtain nanometric resolution. This paper discusses a method to minimize these amendments. Deficiencies in the optical system of the sensor and, therefore, in quadrature signals are the main cause of the interpolation error. Even in high quality encoders, the interpolation error can range 1–2% of the signal period. Therefore, the interface electronics must include amplification, level adjustment, and phase balance of the signal to withstand interpolation errors. Application of the described method for analyzing the phase relations in the linear displacement sensor allows one to optimize the parameters of diffraction gratings in the optical scheme, as well as evaluate and eliminate the contribution of the instrumental uncertainty. Direct drive systems can operate with high gain control loop, which allows responding quickly to correct errors in position. However, with a high interpolation error, the frequency of the error increases, and the controller cannot cope with it. Then, the engine consumes more current, trying to react, which leads to noise and excessive heating of the engine. Understanding the instrumental error inside the sensor can simplify the requirements for interface electronics. The proposed analysis justifies errors associated with phase imbalance, thereby allowing us to predict the need for subsequent compensation. Elliptical correction becomes the more effective as the optimization conditions are more accurately fulfilled in the system. Using this approach, any of the schemes of homodyne or heterodyne displacement interferometers can be analyzed.