Estimation Methods for Viscosity, Flow Rate and Pressure from Pump-Motor Assembly Parameters
Abstract
1. Introduction
2. Materials and Methods
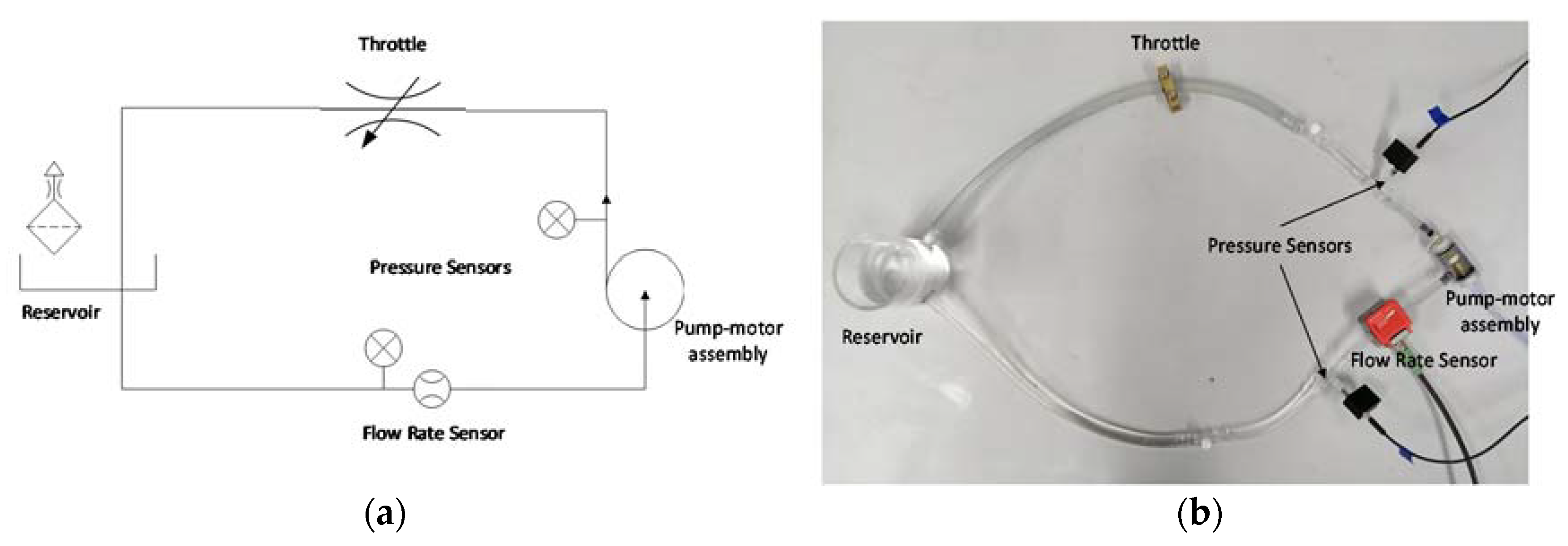
2.1. Data Collection and Data Processing
2.2. Viscosity and Blood Modeling
2.3. Measurement Protocol
2.4. Gaussian Process Models
2.5. Gaussian Process Models Optimization
- Mean Function: {none, constant, linear, quadratic}
- Covariance Function: {automatic relevance determination (ARD) exponential, ARD Matern kernel 3/2, ARD Matern kernel 5/2, ARD rational quadratic, ARD squared exponential, exponential, Matern kernel 3/2, Matern kernel 5/2, rational quadratic, squared exponential}
2.6. Viscosity Estimation GP
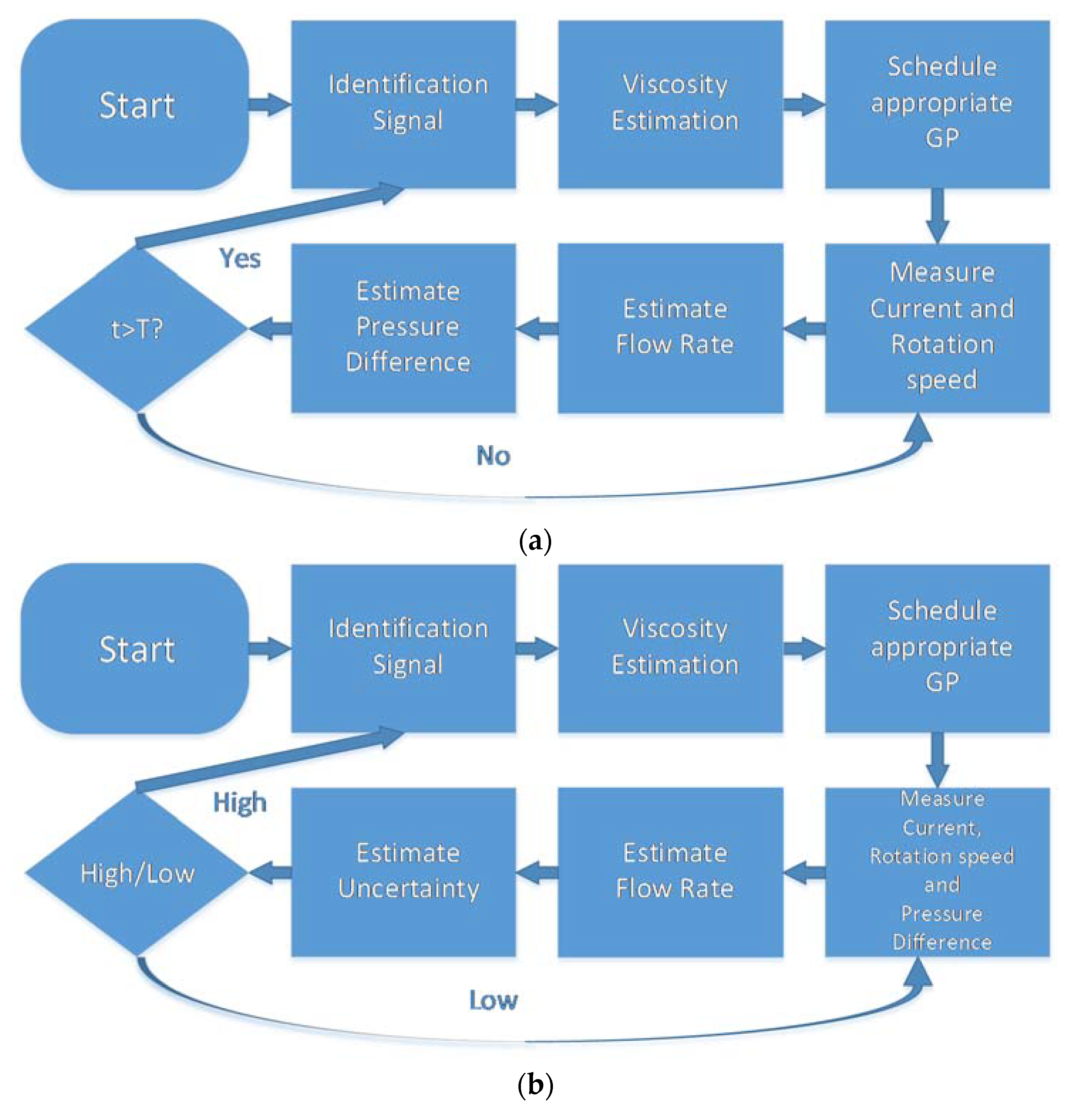
2.7. Estimation Algorithm
3. Results
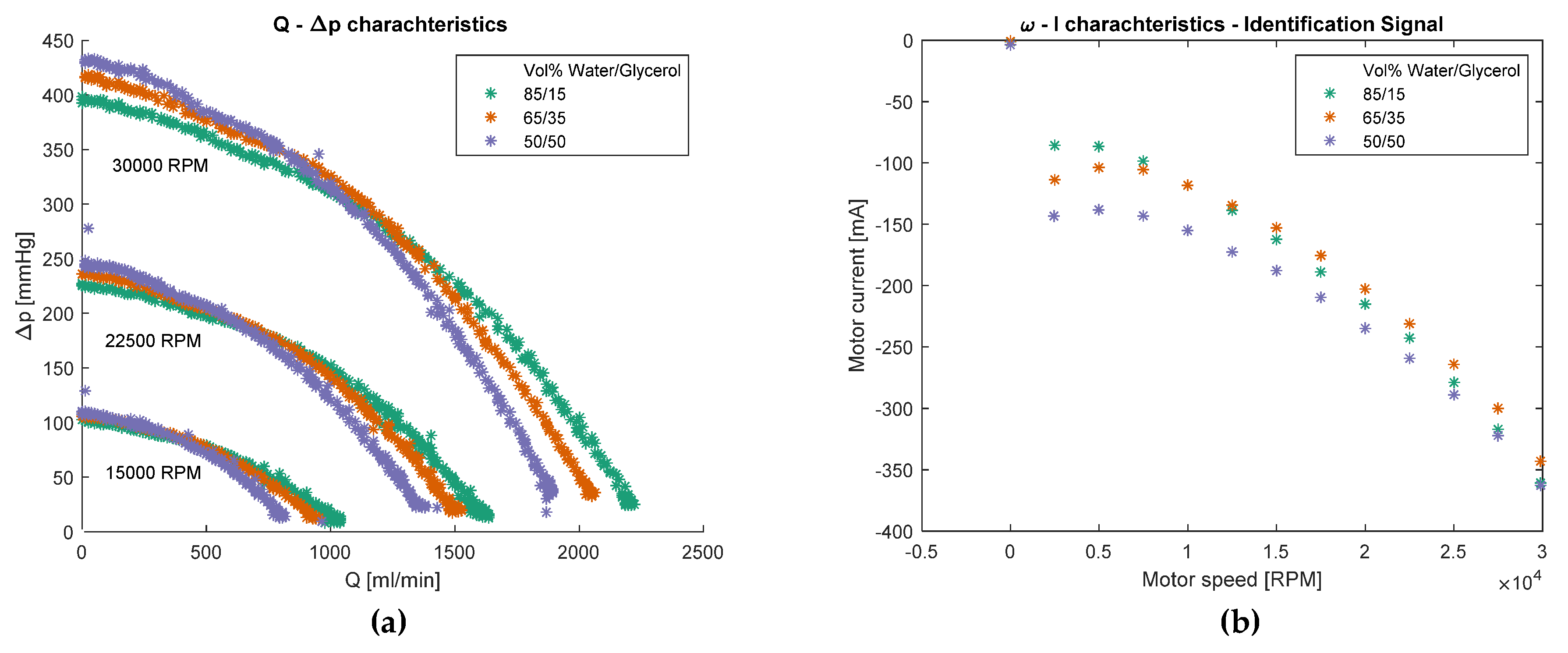
3.1. System Characterization
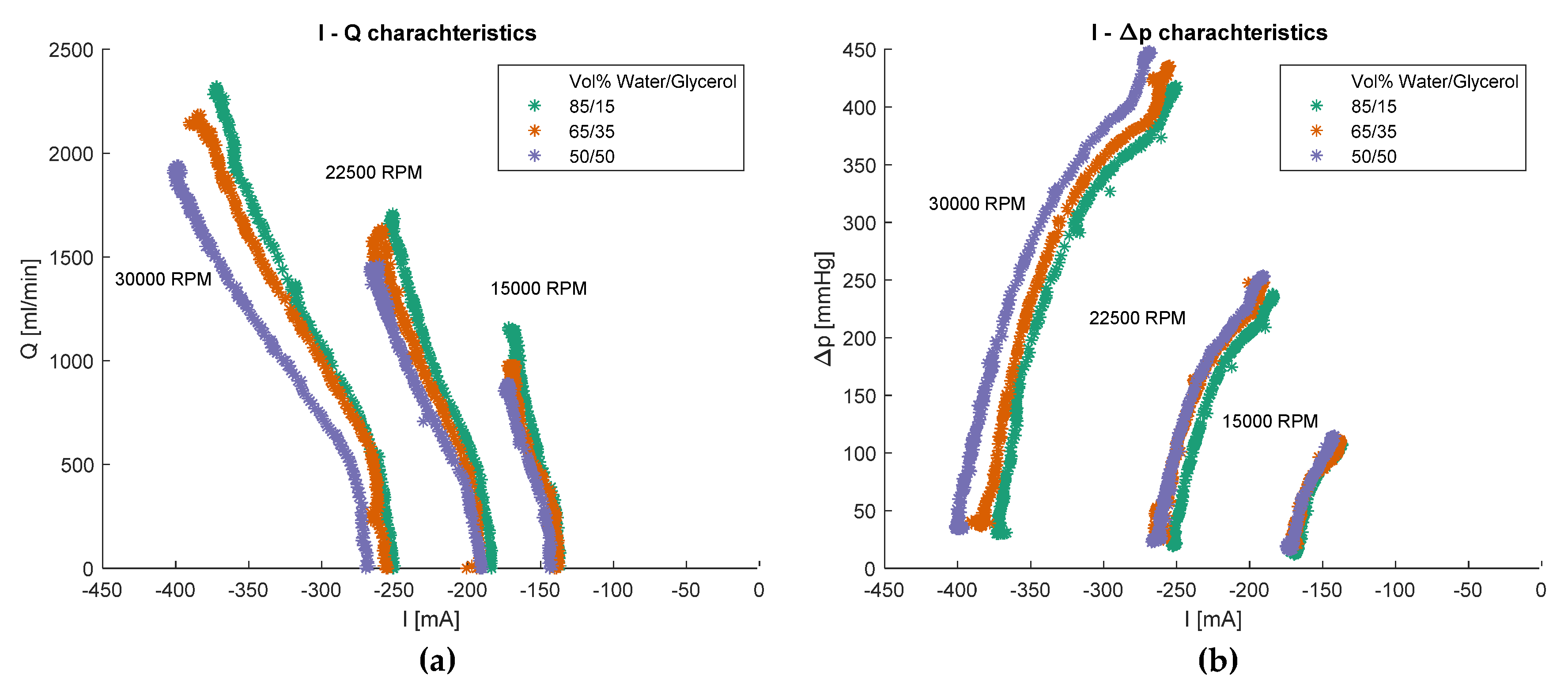
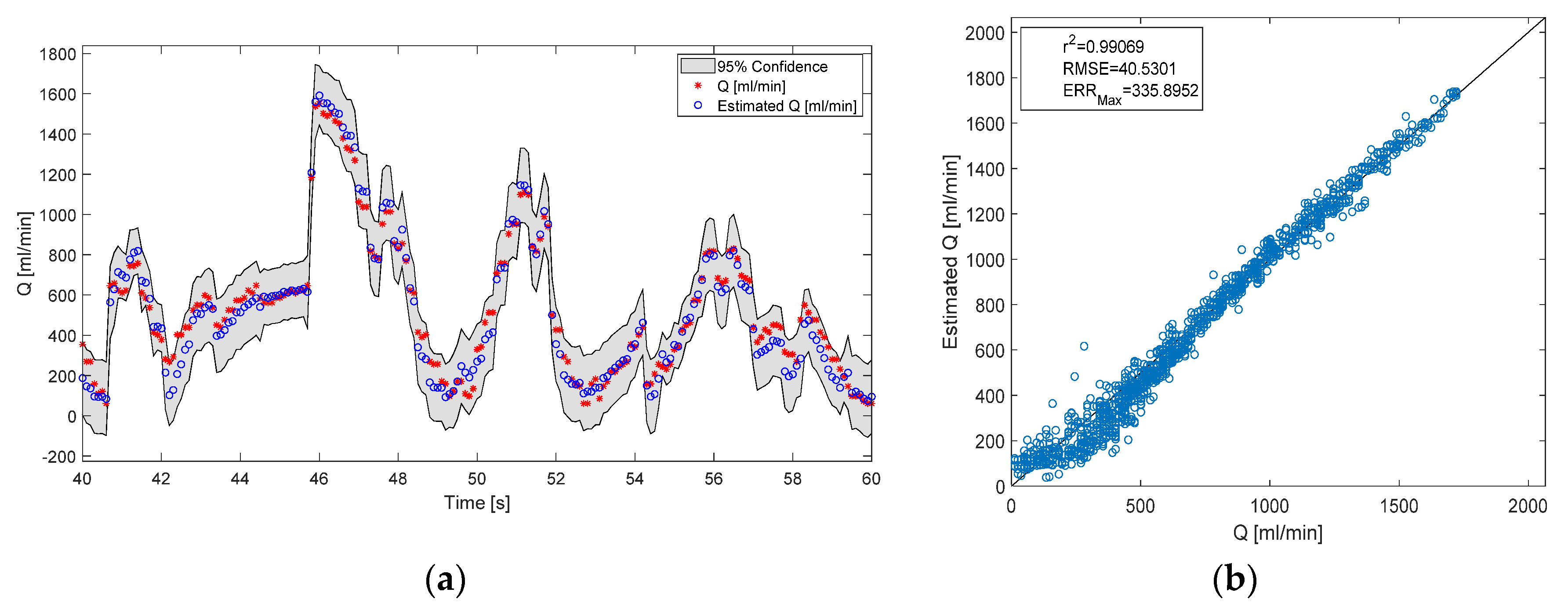
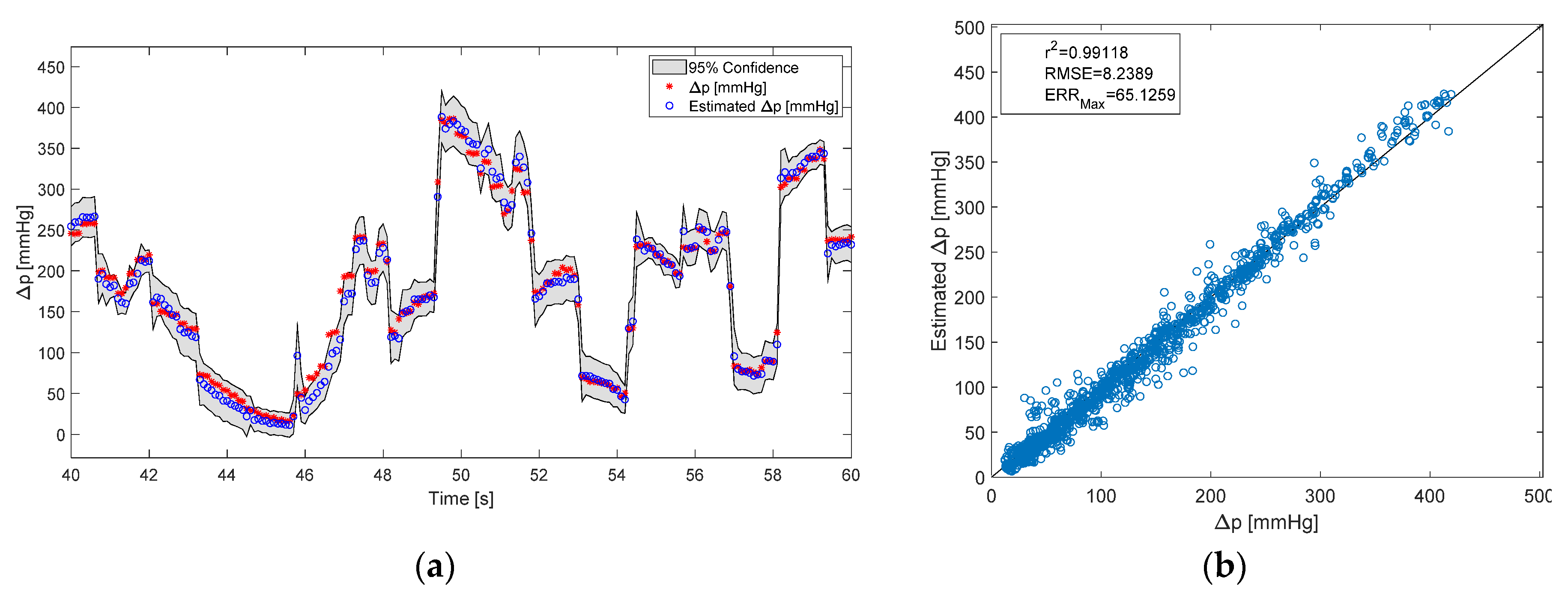
3.2. Estimating the Flow Rate and Pressure Difference
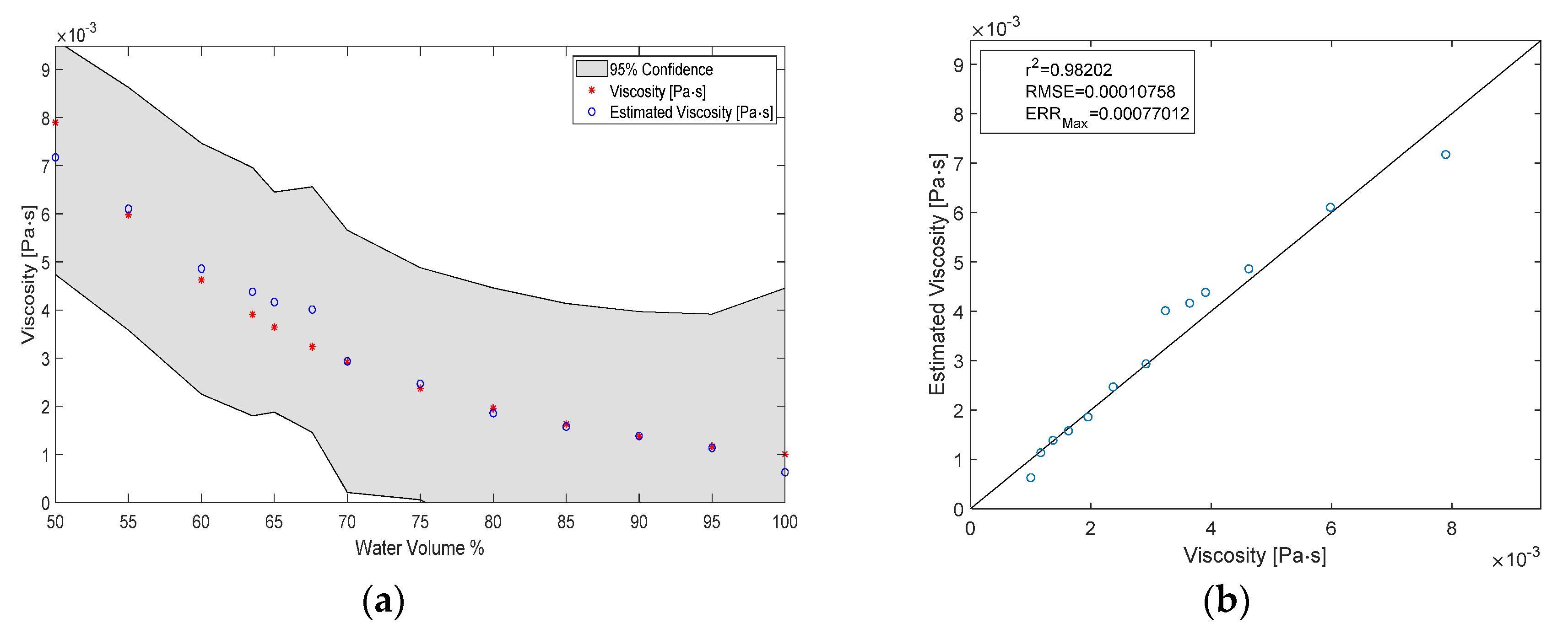
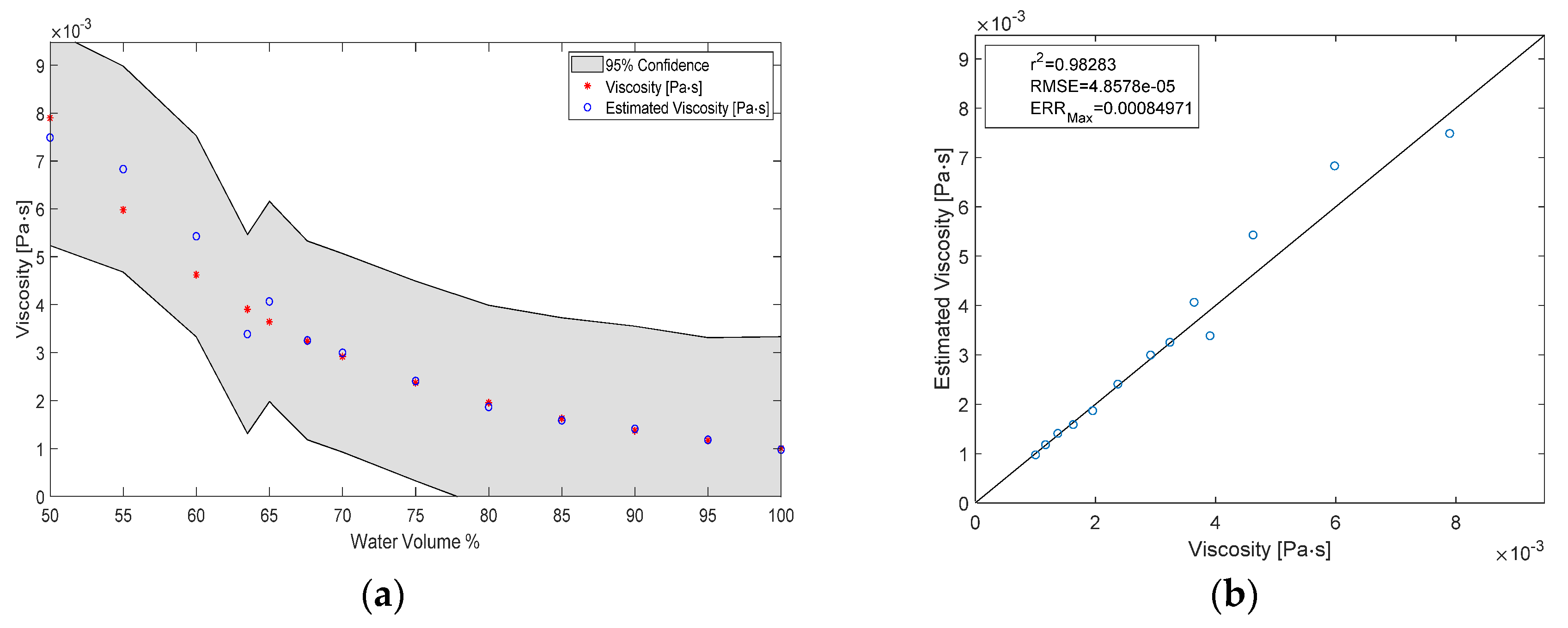
3.3. Estimating the Viscosity of the Test Liquid
3.4. Estimation of Uncertainty
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
Measures of Fitness
References
- Beitler, J.R.; Malhotra, A.; Thompson, B.T. Ventilator-Induced Lung Injury. Clin. Chest Med. 2017, 37, 633–646. [Google Scholar] [CrossRef] [PubMed]
- Jeffries, R.G.; Lund, L.; Frankowski, B.; Federspiel, W.J. An Extracorporeal Carbon Dioxide Removal (ECCO 2 R) Device Operating at Hemodialysis Blood Flow Rates. ICMx 5 2017, 41, 1–12. [Google Scholar]
- Makdisi, G.; Wang, I.W. Extra Corporeal Membrane Oxygenation (ECMO) Review of a Lifesaving Technology. J. Thorac. Dis. 2015, 7, E166–E176. [Google Scholar]
- Matsuda, H. Rotary Blood Pumps: New Developments and Current Applications, 1st ed.; Springer: Tokio, Japan, 2000. [Google Scholar] [CrossRef]
- Cattaneo, G.; Strauß, A.; Reul, H. Compact Intra- and Extracorporeal Oxygenator Developments. Perfusion 2004, 19, 251–255. [Google Scholar] [CrossRef]
- Cattaneo, G.F.M.; Reul, H.; Schmitz-Rode, T.; Steinseifer, U. Intravascular Blood Oxygenation Using Hollow Fibers in a Disk-Shaped Configuration: Experimental Evaluation of the Relationship Between Porosity and Performance. ASIAO J. 2006, 52, 180–185. [Google Scholar] [CrossRef]
- Thomson, I.R. Cardiovascular Physiology: VENOUS RETURN. Can. Anaesth. Soc. J. 1984, 31 (Suppl. 3), 31–37. [Google Scholar] [CrossRef]
- Giridharan, G.A.; Skliar, M. Control Strategy for Maintaining Physiological Perfusion with Rotary Blood Pumps. Artif. Organs 2003, 27, 639–648. [Google Scholar] [CrossRef]
- Bertram, C.D. Measurement for Implantable Rotary Blood Pumps. Physiol. Meas. 2005, 26, 99–117. [Google Scholar] [CrossRef]
- Lim, E.; Karantonis, D.M.; Reizes, J.A.; Cloherty, S.L.; Mason, D.G.; Lovell, N.H. Noninvasive Average Flow and Differential Pressure Estimation for an Implantable Rotary Blood Pump Using Dimensional Analysis. IEEE Trans. Biomed. Eng. 2008, 55, 2094–2101. [Google Scholar] [CrossRef]
- Malagutti, N.; Karantonis, D.M.; Cloherty, S.L.; Ayre, P.L.; Mason, D.G.; Salamonsen, R.F.; Lovell, N.H. Noninvasive Average Flow Estimation for an Implantable Rotary Blood Pump: A New Algorithm Incorporating the Role of Blood Viscosity. Artif. Organs 2007, 31, 45–52. [Google Scholar] [CrossRef]
- Hijikata, W.; Rao, J.; Abe, S.; Takatani, S.; Shinshi, T. Estimating Flow Rate Using the Motor Torque in a Rotary Blood Pump. Sens. Mater. 2015, 27, 297–308. [Google Scholar] [CrossRef]
- Funakubo, A.; Ahmed, S.; Sakuma, I.; Fukui, Y. Flow Rate and Pressure Head Estimation in a Centrifugal Blood Pump. Artif. Organs 2002, 26, 985–990. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.T.; Alomari, A.H.; Savkin, A.V.; Ayre, P.J.; Lim, E.; Salamonsen, R.F.; Rosenfeldt, F.L.; Lovell, N.H. In Vivo Validation of Pulsatile Flow and Differential Pressure Estimation Models in a Left Ventricular Assist Device. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 2517–2520. [Google Scholar]
- Granegger, M.; Moscato, F.; Casas, F.; Wieselthaler, G.; Schima, H. Development of a Pump Flow Estimator for Rotary Blood Pumps to Enhance Monitoring of Ventricular Function. Artif. Organs 2012, 36, 691–699. [Google Scholar] [CrossRef] [PubMed]
- Moscato, F.; Danieli, G.A.; Schima, H. Dynamic Modeling and Identification of an Axial Flow Ventricular Assist Device. Int. J. Artif. Organs 2009, 32, 336–343. [Google Scholar] [CrossRef]
- Tsukiya, T.; Akamatsu, T. Use of Motor Current in Flow Rate Measurement for the Magnetically Suspended Centrifugal Blood Pump. Artif. Organs 1997, 21, 396–401. [Google Scholar] [CrossRef]
- Kitamura, T.; Matsushima, Y.; Tokuyama, T.; Kono, S.; Nishimura, K.; Komeda, M.; Yanai, M.; Kijima, T.; Nojiri, C. Physical Model-Based Indirect Measurements of Blood Pressure and Flow Using a Centrifugal Pump. Artif. Organs 2000, 24, 589–593. [Google Scholar] [CrossRef]
- Shida, S.; Masuzawa, T.; Osa, M. Flow Rate Estimation of a Centrifugal Blood Pump Using the Passively Stabilized Eccentric Position of a Magnetically Levitated Impeller. Int. J. Artif. Organs 2019, 42, 291–298. [Google Scholar] [CrossRef]
- Hijikata, W.; Maruyama, T.; Suzumori, Y. Measuring Real-Time Blood Viscosity with a Ventricular Assist Device. J. Eng. Med. 2019, 233, 562–569. [Google Scholar] [CrossRef]
- Hijikata, W.; Rao, J.; Abe, S.; Takatani, S.; Shinshi, T. Sensorless Viscosity Measurement in a Magnetically-Levitated Rotary Blood Pump. Artif. Organs 2015, 39, 559–568. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning, 2006, 1st ed.; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Galdi, G.P.; Robertson, A.M.; Rannacher, R.; Turek, S. Hemodynamical Flows; Oberwolfach Seminars; Birkhäuser: Basel, Schweiz, 2008; Volume 37. [Google Scholar] [CrossRef]
- Fraser, K.H.; Taskin, M.E.; Griffith, B.P.; Wu, Z.J. The Use of Computational Fluid Dynamics in the Development of Ventricular Assist Devices. Med. Eng. Phys. 2011, 33, 263–280. [Google Scholar] [CrossRef]
- Gonzalez, J.A.T.; Longinotti, M.P.; Corti, H.R. The Viscosity of Glycerol-Water Mixtures Including the Supercooled Region. J. Chem. Eng. Data 2011, 56, 1397–1406. [Google Scholar] [CrossRef]
- Cheng, N.S. Formula for the Viscosity of a Glycerol-Water Mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. 2012, 4, 2951–2959. [Google Scholar]
- Lightbody, G.; Gregorc, G. Gaussian Process Approach for Modelling of Nonlinear Systems. Eng. Appli. Artif. Int. 2009, 22, 522–533. [Google Scholar]
- Park, J.; Sandberg, I.W. Universal Approximation Using Radial-Basis-Function Networks. Neural Comput. 1991, 3, 246–257. [Google Scholar] [CrossRef]
- Takens, F.; Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical systems and turbulence, Warwick 1980; Rand, D., Young, L.-S., Eds.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar] [CrossRef]
- Campo-Deaño, L.; Dullens, R.P.A.; Aarts, D.G.A.L.; Pinho, F.T.; Oliveira, M.S.N. Viscoelasticity of Blood and Viscoelastic Blood Analogues for Use in Polydymethylsiloxane In Iitro Models of the Circulatory System. Biomicrofluidics 2013, 7, 1–11. [Google Scholar] [CrossRef]
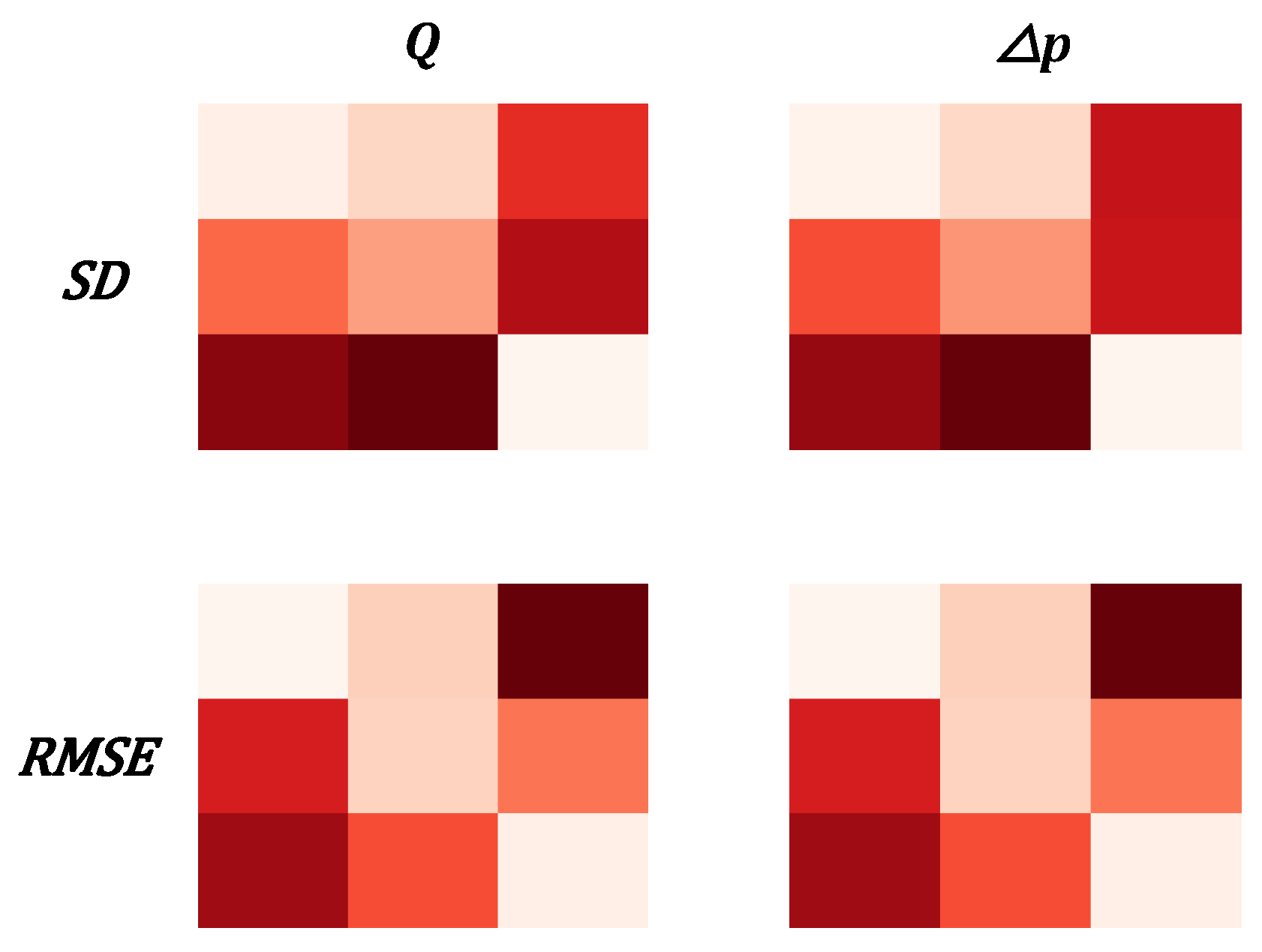
| Water/Glycerol Vol% | 100/0 | 95/5 | 90/10 | 85/15 | 80/20 | 75/25 | 70/30 | 65/35 | 60/40 | 55/45 | 50/50 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Kinematic Viscosity [µm2.s−1] @23 °C | 0.934 | 1.08 | 1.26 | 1.49 | 1.78 | 2.15 | 2.64 | 3.28 | 4.16 | 5.38 | 7.11 |
| Dynamic Viscosity [µPa.s−1] @23 °C | 1006 | 1156 | 1341 | 1571 | 1861 | 2231 | 2711 | 3344 | 4194 | 5359 | 6995 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elenkov, M.; Ecker, P.; Lukitsch, B.; Janeczek, C.; Harasek, M.; Gföhler, M. Estimation Methods for Viscosity, Flow Rate and Pressure from Pump-Motor Assembly Parameters. Sensors 2020, 20, 1451. https://doi.org/10.3390/s20051451
Elenkov M, Ecker P, Lukitsch B, Janeczek C, Harasek M, Gföhler M. Estimation Methods for Viscosity, Flow Rate and Pressure from Pump-Motor Assembly Parameters. Sensors. 2020; 20(5):1451. https://doi.org/10.3390/s20051451
Chicago/Turabian StyleElenkov, Martin, Paul Ecker, Benjamin Lukitsch, Christoph Janeczek, Michael Harasek, and Margit Gföhler. 2020. "Estimation Methods for Viscosity, Flow Rate and Pressure from Pump-Motor Assembly Parameters" Sensors 20, no. 5: 1451. https://doi.org/10.3390/s20051451
APA StyleElenkov, M., Ecker, P., Lukitsch, B., Janeczek, C., Harasek, M., & Gföhler, M. (2020). Estimation Methods for Viscosity, Flow Rate and Pressure from Pump-Motor Assembly Parameters. Sensors, 20(5), 1451. https://doi.org/10.3390/s20051451






