Experimental Research on Shear Failure Monitoring of Composite Rocks Using Piezoelectric Active Sensing Approach
Abstract
1. Introduction
2. Aims of Research and Principle of Detection
2.1. Aims of Research
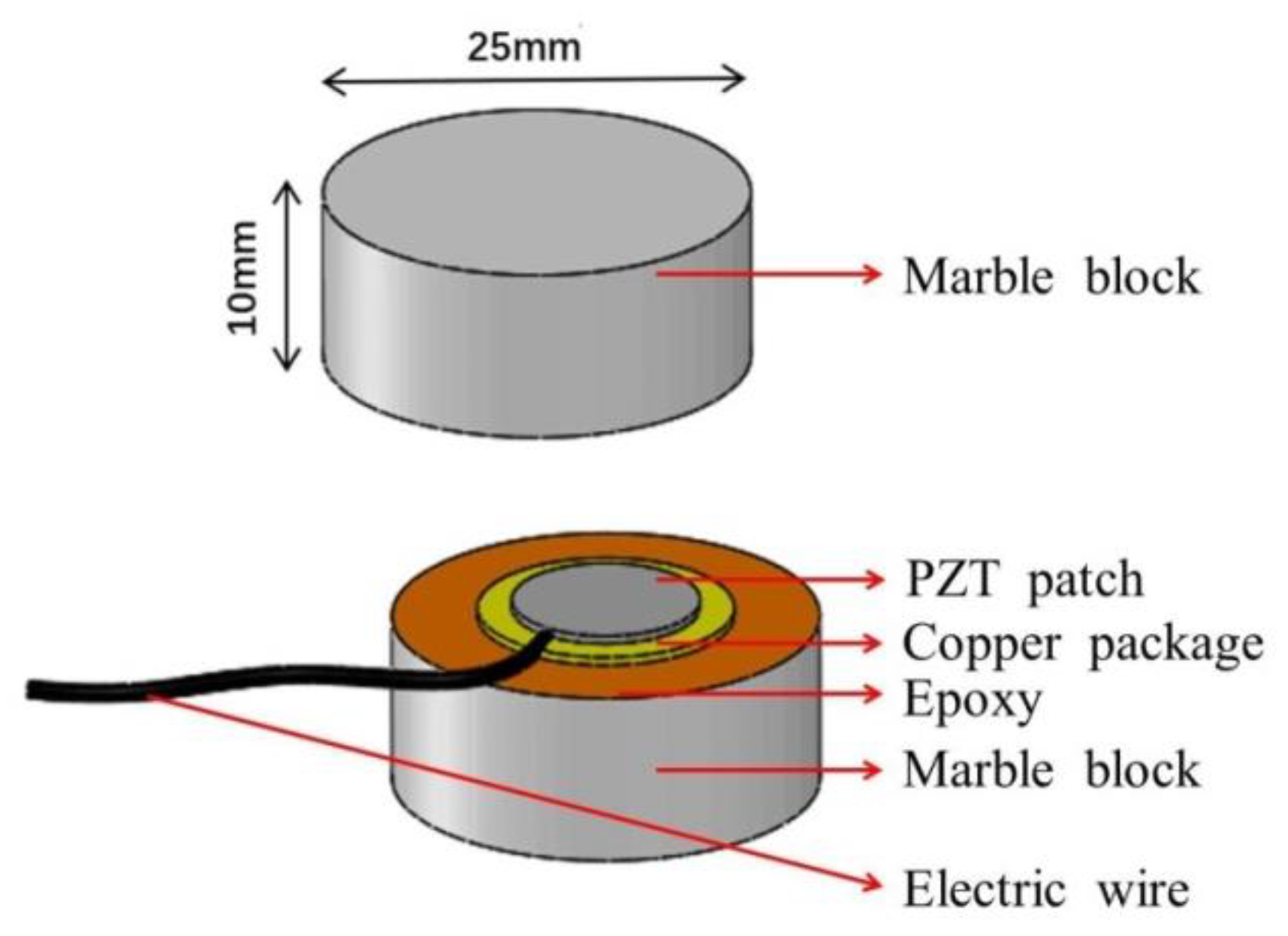
2.2. The Piezoceramic Transducers
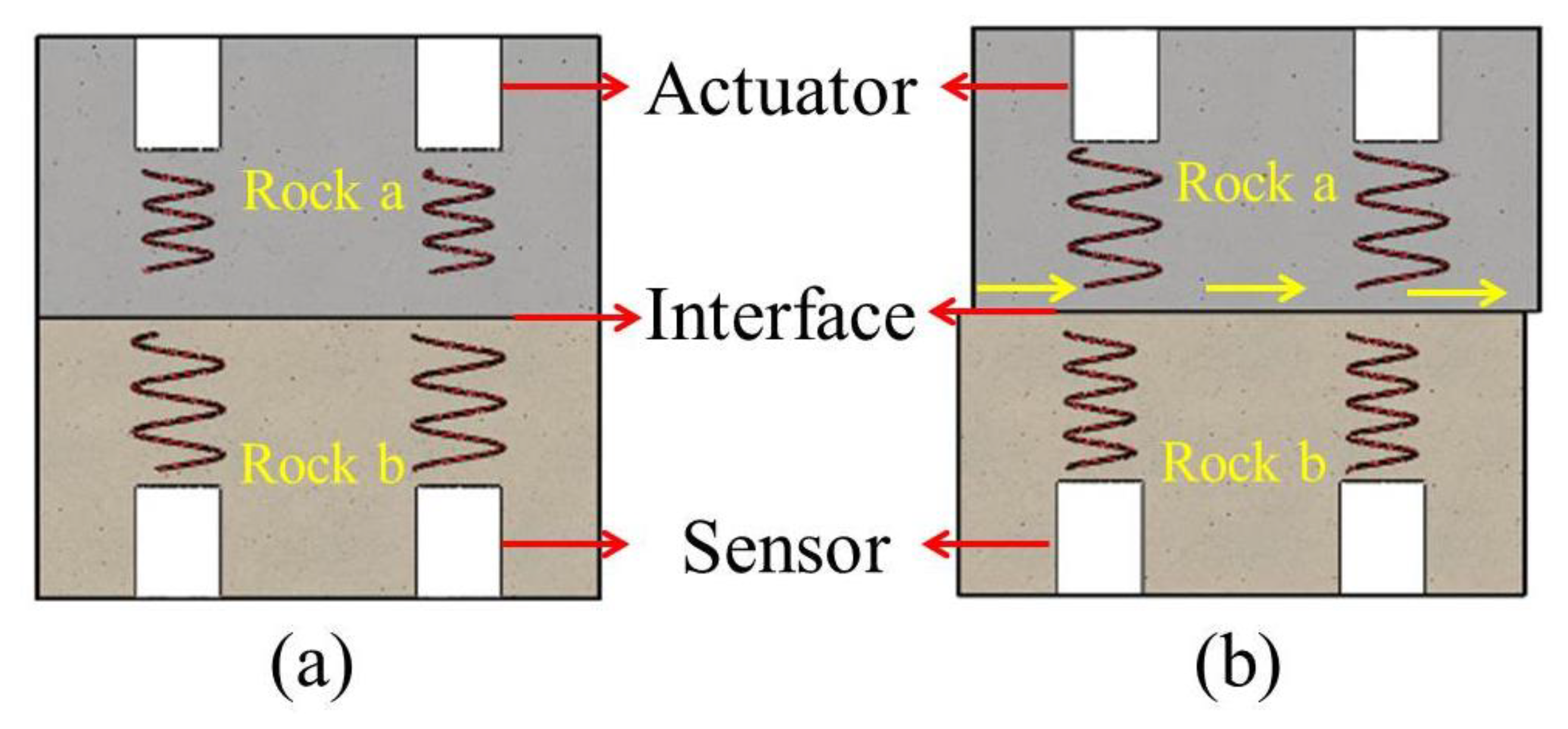
2.3. Principle of Piezoelectric Active Sensing Method
2.4. The Shear Failure Damage Index of Rock
3. Experimental Setup and Methodology
3.1. Specimen Preparation and SA Installation
3.2. Test Device and Parameter Setting
3.3. Test Steps
4. Experimental Results and Discussions
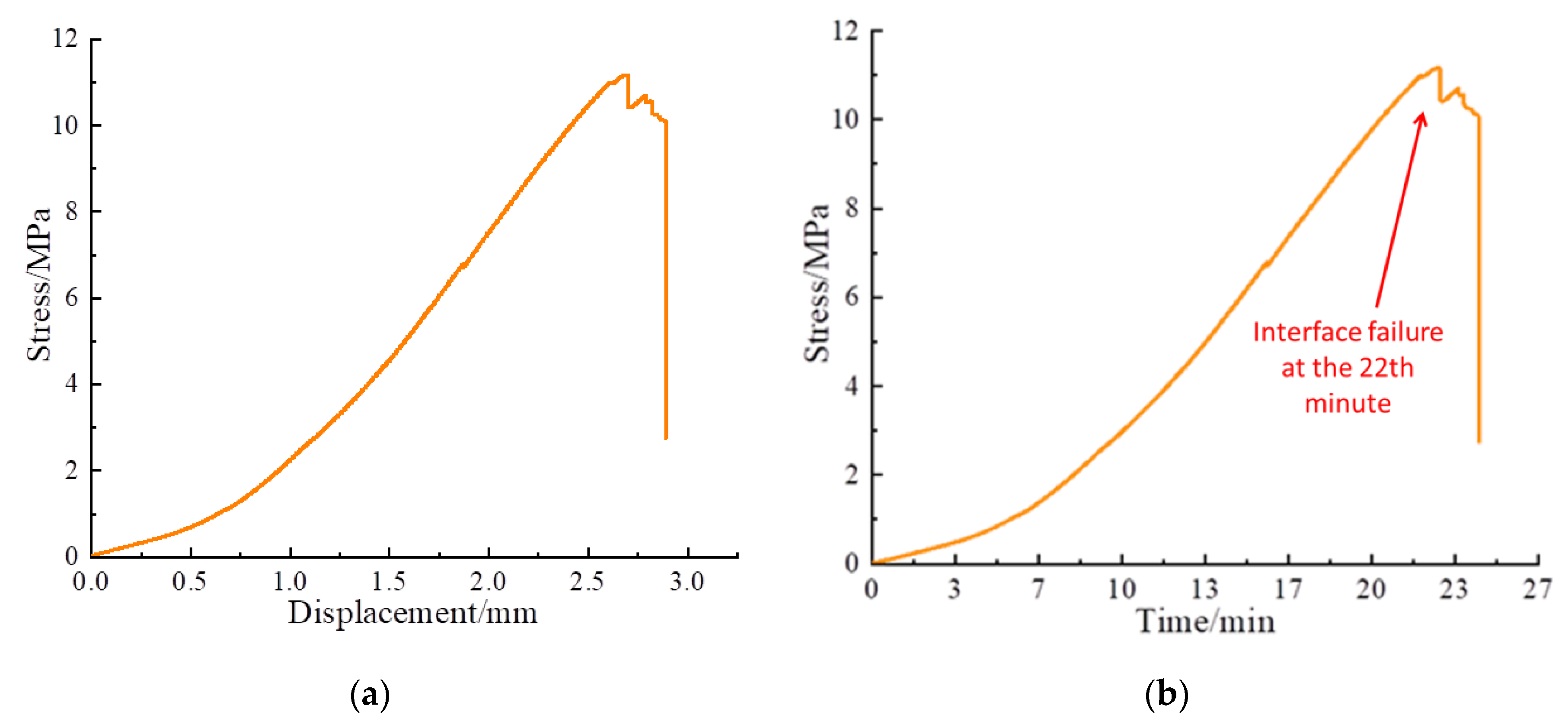
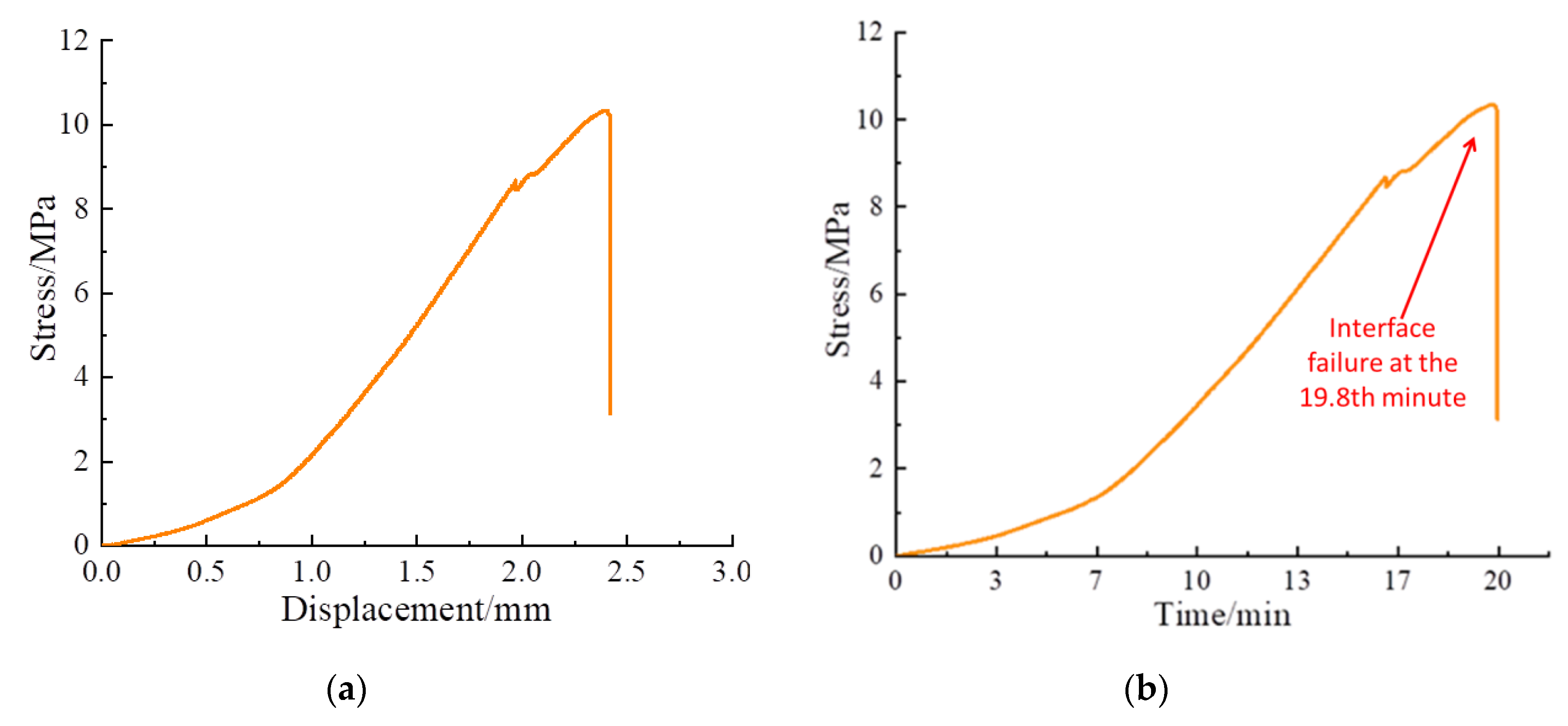
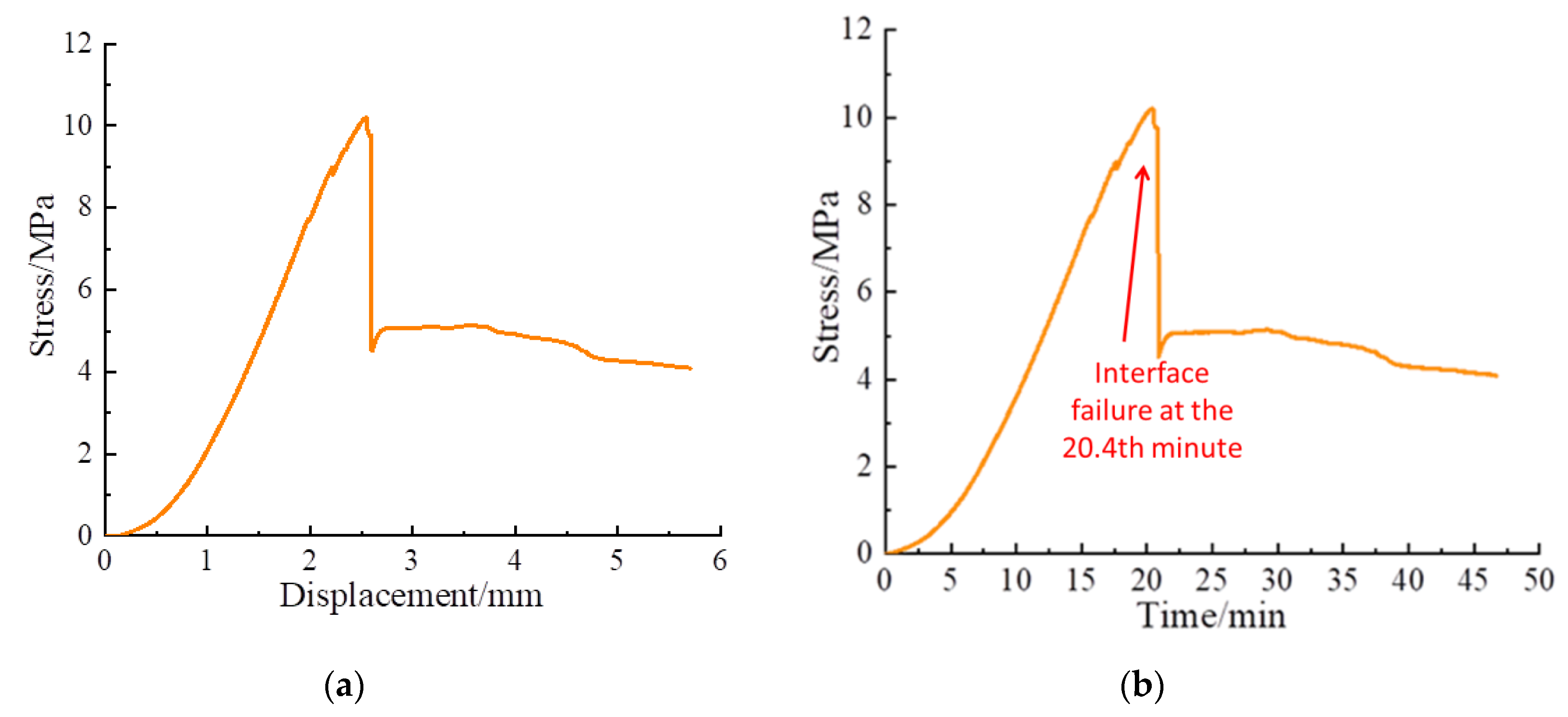
4.1. Analysis of the Shear Test Results of Composite Specimens
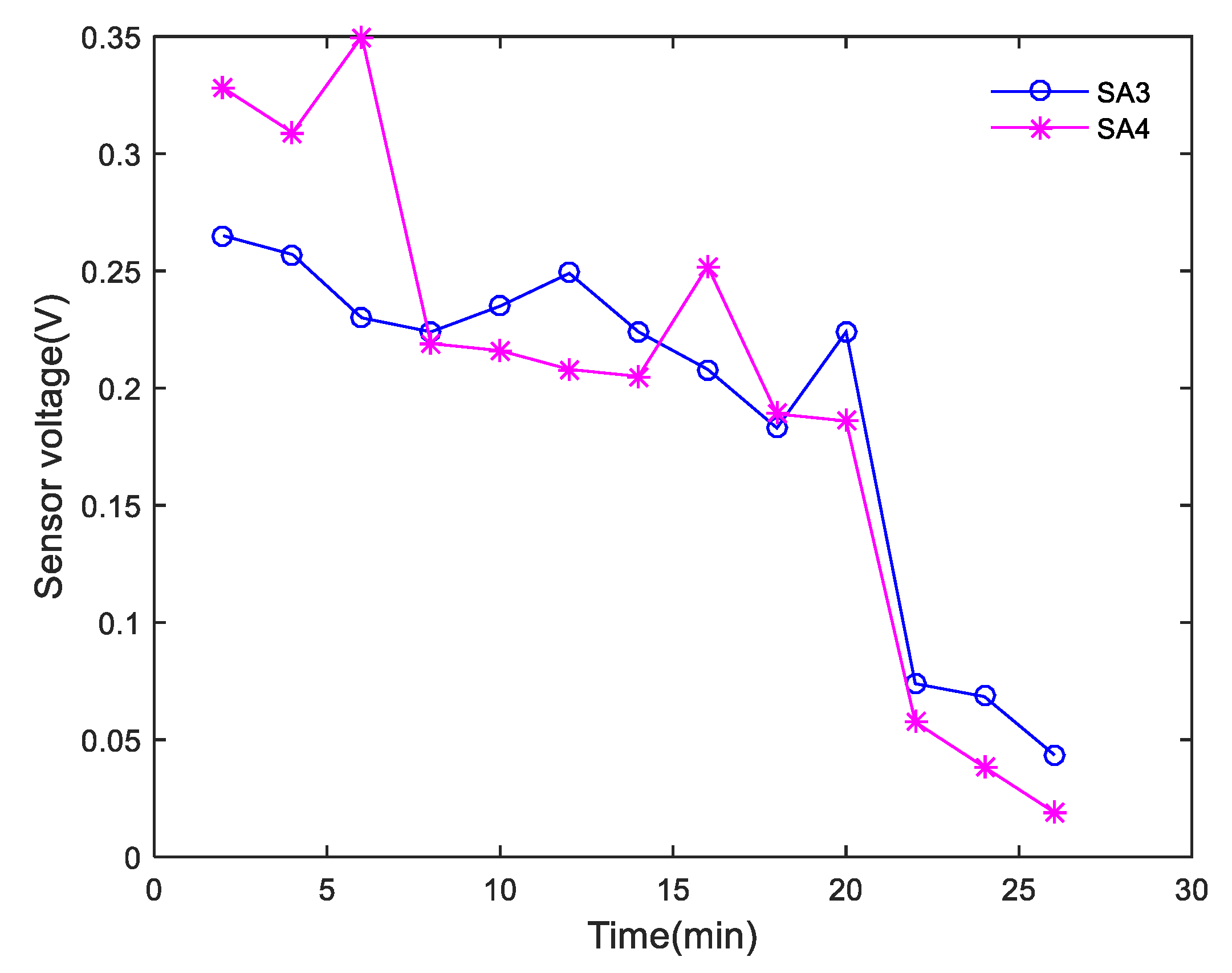
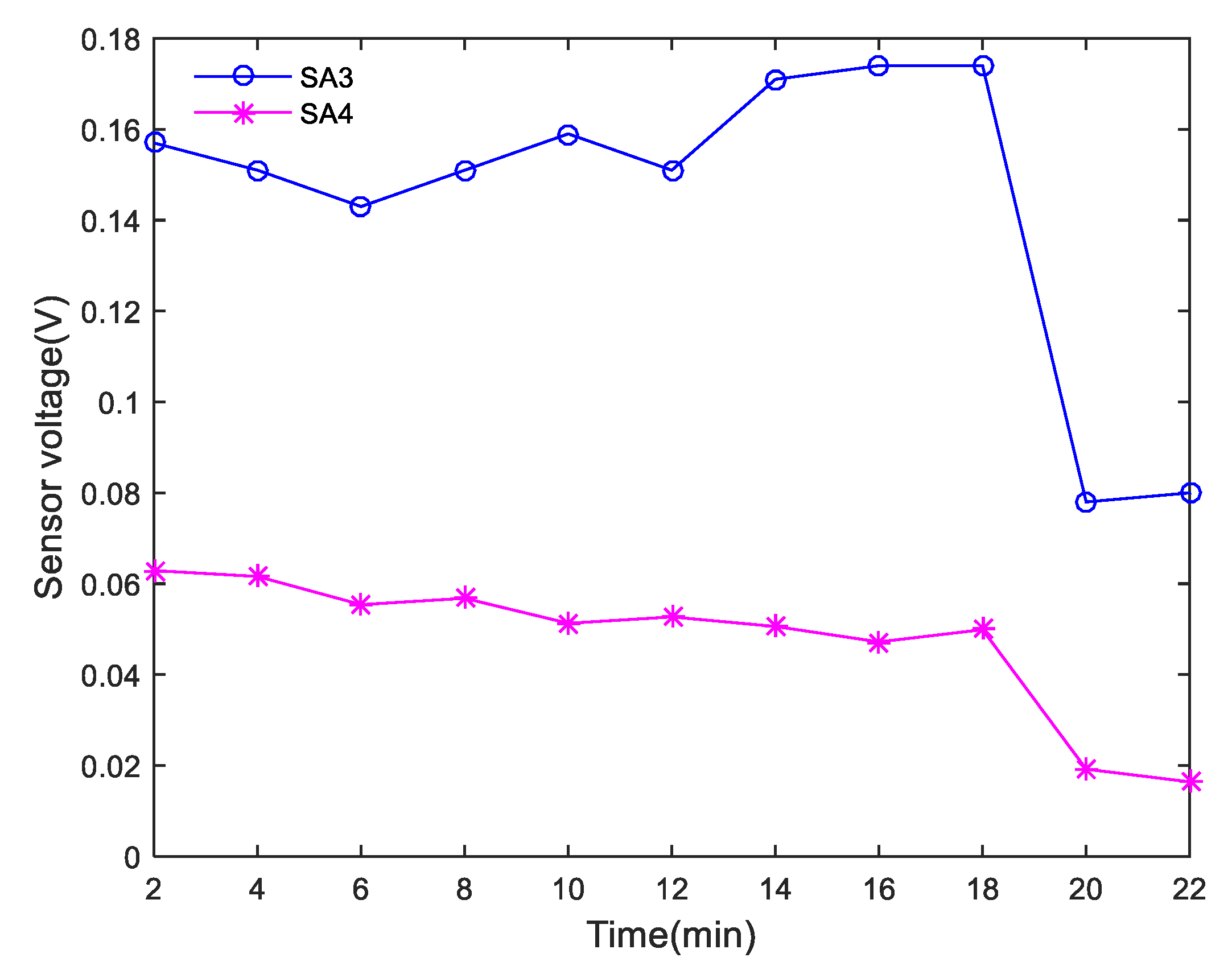
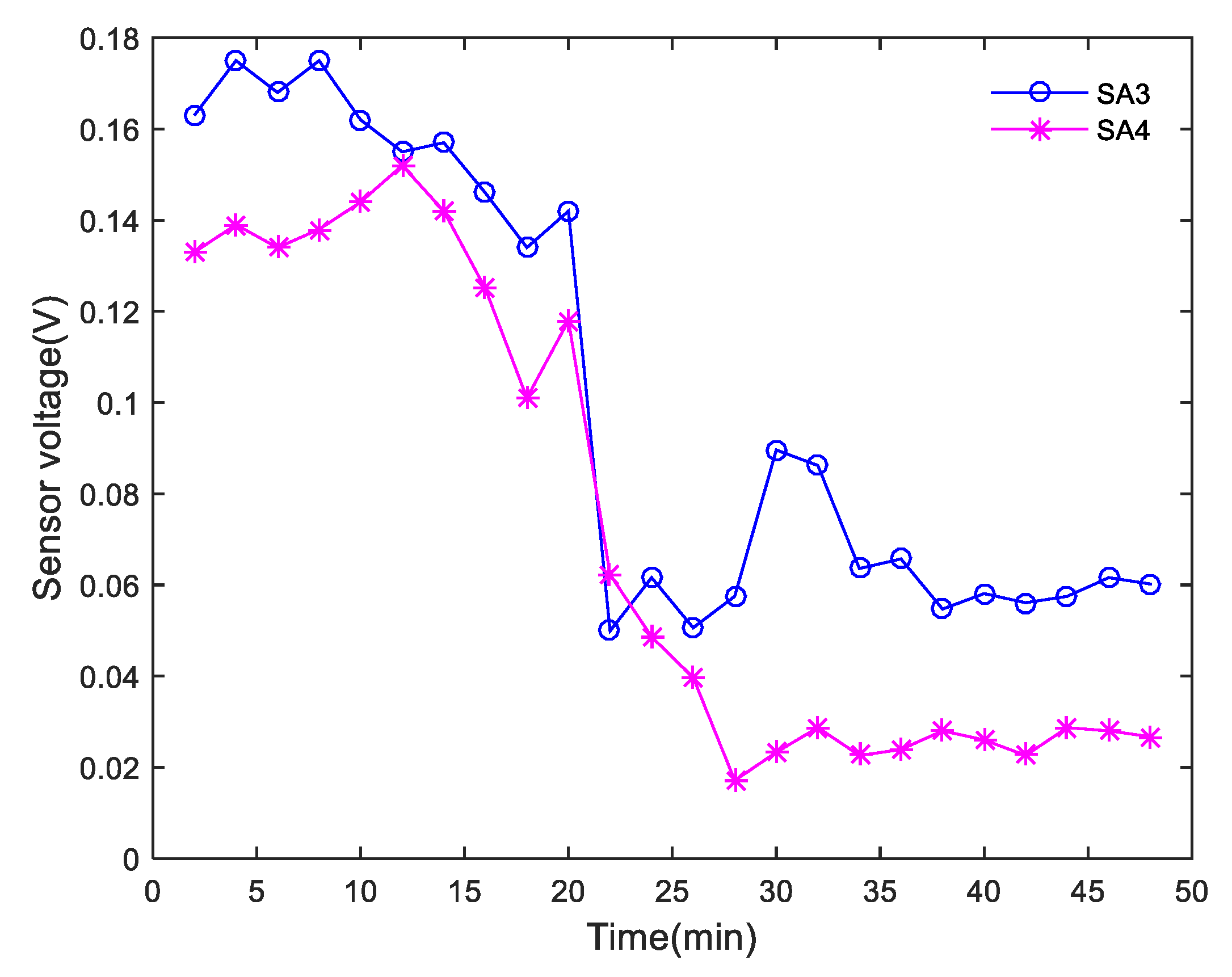
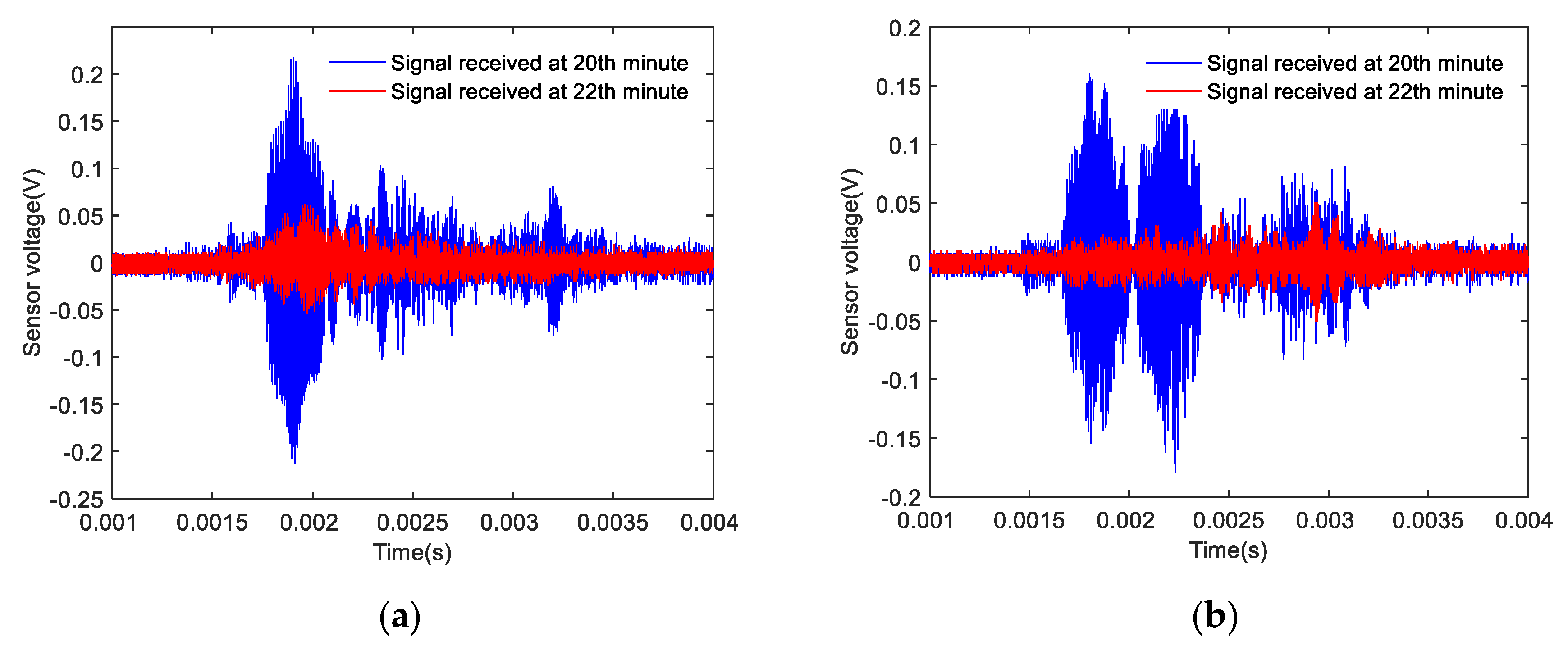
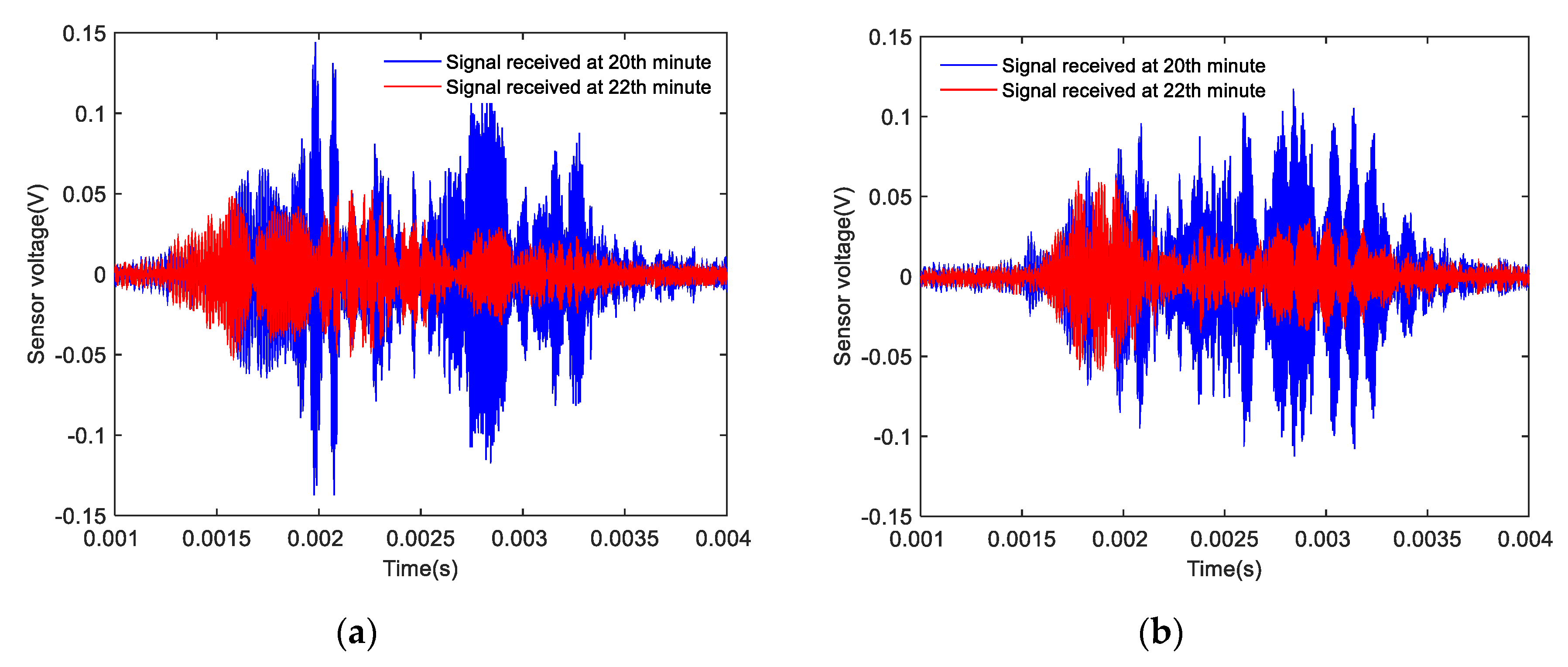
4.2. Time-Domain Analysis of Monitoring Signals
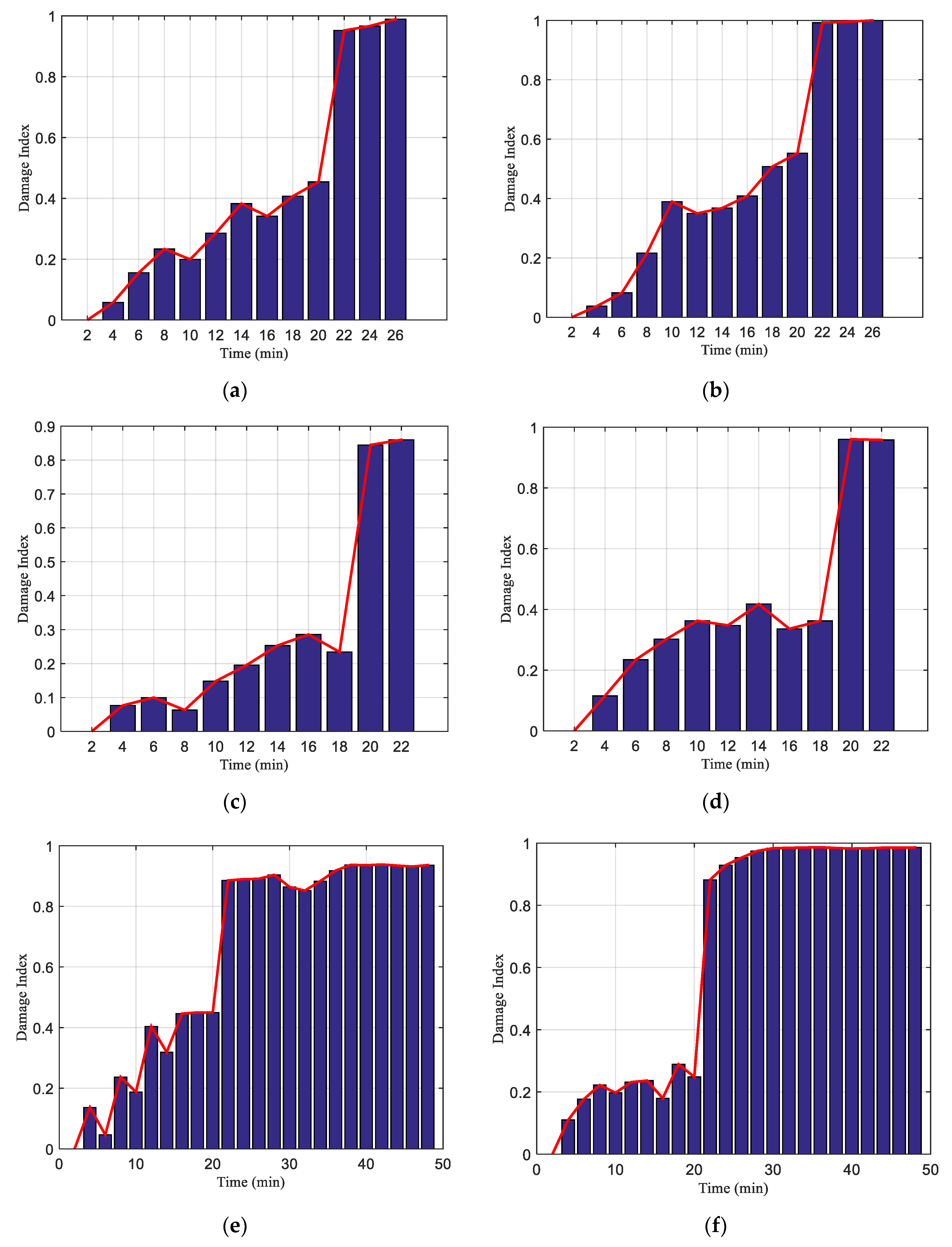
4.3. Rock Shear Damage Index Based on Wavelet Packet
4.4. Further Discussions
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Wen, S.; Zhang, C.S.; Chang, Y.L.; Hu, P. Dynamic compression characteristics of layered rock mass of significant strength changes in adjacent layers. J. Rock Mech. Geotech. Eng. 2019, 9, 1–13. [Google Scholar] [CrossRef]
- Wang, W.Q.; Ye, Y.C.; Wang, Q.H.; Liu, X.Y.; Yuan, Z.H.; Li, P.C. Effects of Differences in Mechanical Parameters of Media on Mechanical Properties and Failure Form of Composite Specimens. KSCE J. Civ. Eng. 2020, 24, 424–434. [Google Scholar] [CrossRef]
- Yang, S.Q.; Yin, P.F.; Huang, Y.H.; Cheng, J.L. Strength, deformability and X-ray micro-CT observations of transversely isotropic composite rock under different confining pressures. Eng. Fract. Mech. 2019, 214, 1–20. [Google Scholar] [CrossRef]
- He, J.M.; Afolagboye, L.O. Influence of layer orientation and interlayer bonding force on the mechanical behavior of shale under Brazilian test conditions. Acta Mech. Sin. 2018, 34, 349–358. [Google Scholar] [CrossRef]
- Feng, W.K.; Huang, R.Q.; Li, T.B. Deformation analysis of a soft–hard rock contact zone surrounding a tunnel. Tunn. Undergr. Space Technol. 2012, 32, 190–197. [Google Scholar] [CrossRef]
- Zhou, H.; Qu, C.K.; Hu, D.W.; Zhang, C.Q.; Azhar, M.U.; Shen, Z.; Chen, J. In situmonitoring of tunnel deformation evolutions fromauxiliary tunnel in deep mine. Eng. Geol. 2017, 221, 10–15. [Google Scholar] [CrossRef]
- Bryn, M.Y.; Afonina, D.A.; Bogomolova, N.N.; Nikitchin, A.A. Monitoring of transport tunnel deformation at the construction stage. Procedia Eng. 2017, 189, 417–420. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, Y.C.; Wang, Q.H.; Liu, X.Y. Stability Prediction Model of Roadway Surrounding Rock Based on Concept Lattice Reduction and a Symmetric Alpha Stable Distribution Probability Neural Network. Appl. Sci. 2018, 8, 2164. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, Y.C.; Wang, Q.H.; Liu, X.Y.; Wang, W.Q. Predicting the Loose Zone of Roadway Surrounding Rock Using Wavelet Relevance Vector Machine. Appl. Sci. 2019, 9, 2064. [Google Scholar] [CrossRef]
- Bayer, B.; Simoni, A.; Schmidt, D.; Bertello, L. Using advanced InSAR techniques to monitor landslide deformations induced by tunneling in the Northern Apennines, Italy. Eng. Geol. 2017, 226, 20–32. [Google Scholar] [CrossRef]
- Gage, J.R.; Fratta, D.; Turner, A.L.; MacLaughlin, M.M.; Wang, H.F. Validation and implementation of a new method for monitoring in situ strain and temperature in rock masses using fiber-optically instrumented rock strain and temperature strips. Int. J. Rock Mech. Min. Sci. 2013, 61, 244–255. [Google Scholar] [CrossRef]
- Gage, J.R.; Wang, H.F.; Fratta, D.; Turner, A.L. In situ measurements of rock mass deformability using fiber Bragg grating strain gauges. Int. J. Rock Mech. Min. Sci. 2014, 71, 350–361. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, T.H.; Zhang, P.H.; Zhou, J.G.; Yu, Q.L.; Deng, W.X. The analysis of rock damage process based on the microseismic monitoring and numerical simulations. Tunn. Undergr. Space Technol. 2017, 69, 1–17. [Google Scholar] [CrossRef]
- Zhao, J.S.; Feng, X.T.; Jiang, Q.; Zhou, Y.Y. Microseismicity monitoring and failure mechanism analysis of rock masses with weak interlayer zone in underground intersecting chambers: A case study from the Baihetan Hydropower Station. Eng. Geol. 2018, 245, 44–60. [Google Scholar] [CrossRef]
- Meng, F.Z.; Wong, L.N.Y.; Zhou, H.; Wang, Z.Q.; Zhang, L.M. Asperity degradation characteristics of soft rock-like fractures under shearing based on acoustic emission monitoring. Eng. Geol. 2020, 266, 105392. [Google Scholar] [CrossRef]
- Yang, J.H.; Dai, J.H.; Yao, C.; Jiang, S.H.; Zhou, C.B.; Jiang, Q.H. Estimation of rock mass properties in excavation damage zones of rock slopes based on the Hoek-Brown criterion and acoustic testing. Int. J. Rock Mech. Min. Sci. 2020, 126, 104192. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.P.; Cai, W.B.; Li, S.C.; Zhang, Q.Y. Stability monitoring of surrounding rock mass on a forked tunnel using both strain gauges and FBG sensors. Measurement 2020, 153, 107449. [Google Scholar] [CrossRef]
- Peng, J.; Hu, S.; Zhang, J.; Cai, C.S.; Li, L.Y. Influence of cracks on chloride diffusivity in concrete: A five-phase mesoscale model approach. Constr. Build. Mater. 2019, 197, 587–596. [Google Scholar] [CrossRef]
- Li, W.; Xu, C.; Ho, S.C.M.; Wang, B.; Song, G. Monitoring concrete deterioration due to reinforcement corrosion by integrating acoustic emission and FBG strain measurements. Sensors 2017, 17, 657. [Google Scholar] [CrossRef]
- Peng, J.; Xiao, L.; Zhang, J.; Cai, C.S.; Wang, L. Flexural behavior of corroded HPS beams. Eng. Struct. 2019, 195, 274–287. [Google Scholar] [CrossRef]
- Wang, W.; Hua, X.; Wang, X.; Wu, J.; Sun, H.; Song, G. Mechanical behavior of magnetorheological dampers after long-term operation in a cable vibration control system. Struct. Control Health Monit. 2019, 26, 2280. [Google Scholar] [CrossRef]
- Yin, X.; Song, G.; Liu, Y. Vibration suppression of wind/traffic/bridge coupled system using multiple pounding tuned mass dampers (MPTMD). Sensors 2019, 19, 1133. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Zheng, Y.; Song, G.; Chen, D.; Ye, Y. Identification of the structural damage mechanism of BFRP bars reinforced concrete beams using smart transducers based on time reversal method. Constr. Build. Mater. 2019, 220, 615–627. [Google Scholar] [CrossRef]
- Di, B.; Wang, J.; Li, H.; Zheng, J. Investigation of bonding behavior of FRP and steel bars in self-compacting concrete structures using acoustic emission method. Sensors 2019, 19, 159. [Google Scholar] [CrossRef]
- Zhao, S.; Al-Qadi, I.L.; Wang, S. Prediction of thin asphalt concrete overlay thickness and density using nonlinear optimization of GPR data. NDT E Int. 2018, 100, 20–30. [Google Scholar] [CrossRef]
- Zhao, S.; Imad, L.; Al-Qadi, I.L. Algorithm development for real-time thin asphalt concrete overlay compaction monitoring using ground-penetrating radar. NDT E Int. 2019, 104, 114–123. [Google Scholar] [CrossRef]
- Ciampoli, L.B.; Tosti, F.; Brancadoro, M.G.; D’Amico, F.; Alani, A.M.; Benedetto, A. A spectral analysis of ground-penetrating radar data for the assessment of the railway ballast geometric properties. NDT E Int. 2017, 90, 39–47. [Google Scholar] [CrossRef]
- Benedetto, A.; Tosti, F.; Ciampoli, L.B.; Calvi, A.; Brancadoro, M.G.; Alani, A.M. Railway ballast condition assessment using ground-penetrating radar –An experimental, numerical simulation and modelling development. Constr. Build. Mater. 2017, 140, 508–520. [Google Scholar] [CrossRef]
- Kong, Q.; Robert, R.H.; Silva, P.; Mo, Y.L. Cyclic crack monitoring of a reinforced concrete column under simulated pseudo-dynamic loading using piezoceramic-based smart aggregates. Appl. Sci. 2016, 6, 341. [Google Scholar] [CrossRef]
- Luo, M.; Li, W.; Hei, C.; Song, G. Concrete infill monitoring in concrete-filled FRP tubes using a PZT-based ultrasonic time-of-flight method. Sensors 2016, 16, 2083. [Google Scholar] [CrossRef]
- Xu, K.; Ren, C.; Deng, Q.; Jin, Q.; Chen, X. Real-time monitoring of bond slip between GFRP bar and concrete structure using piezoceramic transducer-enabled active sensing. Sensors 2018, 18, 2653. [Google Scholar] [CrossRef] [PubMed]
- Huynh, T.C.; Ho, D.D.; Dang, N.L.; Kim, J.T. Sensitivity of Piezoelectric-Based Smart Interfaces to Structural Damage in Bolted Connections. Sensors 2019, 19, 3670. [Google Scholar] [CrossRef] [PubMed]
- Wu, A.; He, S.; Ren, Y.; Wang, N. Design of a new stress wave-based pulse position modulation (PPM) communication system with piezoceramic transducers. Sensors 2019, 19, 558. [Google Scholar] [CrossRef] [PubMed]
- Ji, Q.; Ho, M.; Zheng, R.; Ding, Z. An exploratory study of stress wave communication in concrete structures. Smart Struct. Syst. 2015, 15, 135–150. [Google Scholar] [CrossRef]
- Raaja, B.P.; Daniel, R.J.; Sumangala, K. A simple analytical model for mems cantilever beam piezoelectric accelerometer and high sensitivity design for shm (structural health monitoring) applications. Trans. Electr. Electron. Mater. 2017, 18, 78–88. [Google Scholar] [CrossRef]
- Annamdas, V.G.M.; Soh, C.K. Load monitoring using a calibrated piezo diaphragm based impedance strain sensor and wireless sensor network in real time. Smart Mater. Struct. 2017, 26, 045036. [Google Scholar] [CrossRef]
- Peddigari, M.; Kim, G.Y.; Park, C.H.; Min, Y.; Kim, J.W.; Ahn, C.W.; Choi, J.J.; Hahn, B.D.; Choi, J.H.; Park, D.S.; et al. A comparison study of fatigue behavior of hard and soft piezoelectric single crystal macro-fiber composites for vibration energy harvesting. Sensors 2019, 19, 2196. [Google Scholar] [CrossRef]
- Ma, Y.; Ji, Q.; Chen, S.; Song, G. An experimental study of ultra-low power wireless sensor-based autonomous energy harvesting system. J. Renew. Sustain. Energy 2017, 9, 054702. [Google Scholar] [CrossRef]
- Ji, Q.; Parvasi, S.M.; Ho, S.C.M.; Franchek, M.; Song, G. Wireless energy harvesting using time reversal technique: An experimental study with numerical verification. J. Intell. Mater. Syst. Struct. 2017, 28, 2705–2716. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, T. Bending analysis of a piezoelectric curved actuator with a generally graded property for the piezoelectric parameter. Smart Mater. Struct. 2008, 17, 045018. [Google Scholar] [CrossRef]
- Dziendzikowski, M.; Kurnyta, A.; Dragan, K.; Klysz, S.; Leski, A. In situ Barely Visible Impact Damage detection and localization for composite structures using surface mounted and embedded PZT transducers: A comparative study. Mech. Syst. Signal Process. 2016, 78, 91–106. [Google Scholar] [CrossRef]
- Sethi, V.; Song, G. Optimal vibration control of a model frame structure using piezoceramic sensors and actuators. J. Vib. Control 2005, 11, 671–684. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.; Hsu, T.; Dhonde, H. Concrete structural health monitoring using embedded piezoceramic transducers. Smart Mater. Struct. 2007, 16, 959. [Google Scholar] [CrossRef]
- Song, G.; Mo, Y.; Otero, K.; Gu, H. Health monitoring and rehabilitation of a concrete structure using intelligent materials. Smart Mater. Struct. 2006, 15, 309. [Google Scholar] [CrossRef]
- Huo, L.; Cheng, H.; Kong, Q.; Chen, X. Bond-slip monitoring of concrete structures using smart sensors—A review. Sensors 2019, 19, 1231. [Google Scholar] [CrossRef]
- Liao, W.I.; Chiu, C.K. Seismic health monitoring of a space reinforced concrete frame structure using piezoceramic-based sensors. J. Aerosp. Eng. 2019, 32, 04019015. [Google Scholar] [CrossRef]
- Chiu, C.K.; Sugianto, S.; Liao, W.I.; Ho, C.E. Crack-based damage quantification for shear-critical HSRC column members using piezoceramic transducers. Eng. Struct. 2019, 201, 109777. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L. SAs: Multi-functional sensors for concrete structures—A tutorial and a review. Smart Mater. Struct. 2008, 17, 033001. [Google Scholar] [CrossRef]
- Moslehy, Y.; Gu, H.; Belarbi, A.; Mo, Y.; Song, G. SA based damage detection of circular RC columns under cyclic combined loading. Smart Mater. Struct. 2010, 19, 065021. [Google Scholar] [CrossRef]
- Gu, H.; Moslehy, Y.; Sanders, D.; Song, G.; Mo, Y.L. Multi-functional SA-based structural health monitoring of circular reinforced concrete columns subjected to seismic excitations. Smart Mater. Struct. 2010, 19, 065026. [Google Scholar] [CrossRef]
- Na, W.S.; Baek, J. A review of the piezoelectric electromechanical impedance based structural health monitoring technique for engineering structures. Sensors 2018, 18, 1307. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Song, G. Bolt early looseness monitoring using modified vibro-acoustic modulation by time-reversal. Mech. Syst. Signal Process. 2019, 130, 349–360. [Google Scholar] [CrossRef]
- Li, N.; Wang, F.; Song, G. New entropy-based vibro-acoustic modulation method for metal fatigue crack detection: An exploratory study. Measurement 2020, 150, 107075. [Google Scholar] [CrossRef]
- Huynh, T.C.; Lee, S.Y.; Dang, N.L.; Kim, J.T. Sensing region characteristics of smart piezoelectric interface for damage monitoring in plate-like structures. Sensors 2019, 19, 1377. [Google Scholar] [CrossRef]
- Wu, J.C.; Kong, Q.Z.; Lim, I.; Song, G. Feasibility Study of Interlayer Slide Monitoring Using Postembedded Piezoceramic SAs. J. Sens. 2018, 2018, 1953528. [Google Scholar] [CrossRef]
- Wu, J.C.; Li, W.J.; Feng, Q. Electro-Mechanical Impedance (EMI) Based Interlayer Slide Detection Using Piezoceramic SAs—A Feasibility Study. Sensors 2018, 18, 3524. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Zhang, T.; Song, G.; Gu, H.C. Active interface debonding detection of a concrete-filled steel tube with piezoelectric technologies using wavelet packet analysis. Mech. Syst. Signal Process. 2013, 36, 7–17. [Google Scholar] [CrossRef]
- Wu, J.; Kong, Q.; Li, W.; Lim, I.; Song, G. Interlayer slide detection using piezoceramic SAs based on active sensing approach. IEEE Sens. J. 2017, 17, 6160–6166. [Google Scholar] [CrossRef]
- Usol’tseva, O.; Tsoi, P.; Semenov, V. The Influence of Anisotropy Angle on the Strength and Deformation Properties of Artificial Geomaterials and Rock. Procedia Eng. 2017, 191, 512–519. [Google Scholar] [CrossRef]
- Hu, B.; Yang, S.Q.; Xu, P.; Cheng, J.L. Cyclic loading–unloading creep behavior of composite layered specimens. Acta Geophys. 2019, 67. [Google Scholar] [CrossRef]
- Wang, F.; Huo, L.; Song, G. A piezoelectric active sensing method for quantitative monitoring of bolt loosening using energy dissipation caused by tangential damping based on the fractal contact theory. Smart Mater. Struct. 2017, 27, 015023. [Google Scholar] [CrossRef]
- Wang, F.; Ho, S.C.M.; Huo, L.; Song, G. A novel fractal contact-electromechanical impedance model for quantitative monitoring of bolted joint looseness. IEEE Access 2018, 6, 40212–40220. [Google Scholar] [CrossRef]








| No. | Elastic Modulus | Cohesive Forces/MPa | The Angle of Internal Friction/θ | Tensile Strength /MPa | Plaster-Gray Ratio | Sand-Rubber Ratio | Water-Cement Ratio |
|---|---|---|---|---|---|---|---|
| a | 3.62 | 4.36 | 45.65 | 1.80 | 0.30 | 0.65 | 0.39 |
| b | 4.58 | 5.40 | 49.85 | 2.79 | 0.15 | 0.50 | 0.36 |
| The Number of Composite Specimen | Ⅰ | Ⅱ | Ⅲ |
|---|---|---|---|
| The time of Monitoring (min) | 22 | 20 | 22 |
| Damage index of SA 3 | 0.9520 | 0.8445 | 0.8857 |
| Damage index of SA 4 | 0.9922 | 0.9605 | 0.8818 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ye, Y.; Wang, Q.; Wang, W. Experimental Research on Shear Failure Monitoring of Composite Rocks Using Piezoelectric Active Sensing Approach. Sensors 2020, 20, 1376. https://doi.org/10.3390/s20051376
Liu Y, Ye Y, Wang Q, Wang W. Experimental Research on Shear Failure Monitoring of Composite Rocks Using Piezoelectric Active Sensing Approach. Sensors. 2020; 20(5):1376. https://doi.org/10.3390/s20051376
Chicago/Turabian StyleLiu, Yang, Yicheng Ye, Qihu Wang, and Weiqi Wang. 2020. "Experimental Research on Shear Failure Monitoring of Composite Rocks Using Piezoelectric Active Sensing Approach" Sensors 20, no. 5: 1376. https://doi.org/10.3390/s20051376
APA StyleLiu, Y., Ye, Y., Wang, Q., & Wang, W. (2020). Experimental Research on Shear Failure Monitoring of Composite Rocks Using Piezoelectric Active Sensing Approach. Sensors, 20(5), 1376. https://doi.org/10.3390/s20051376





