The Algorithm and Structure for Digital Normalized Cross-Correlation by Using First-Order Moment †
Abstract
1. Introduction
2. Normalized Cross-Correlation Based on First-Order Moment
2.1. Cross-Correlation
2.2. Normalized Cross-Correlation
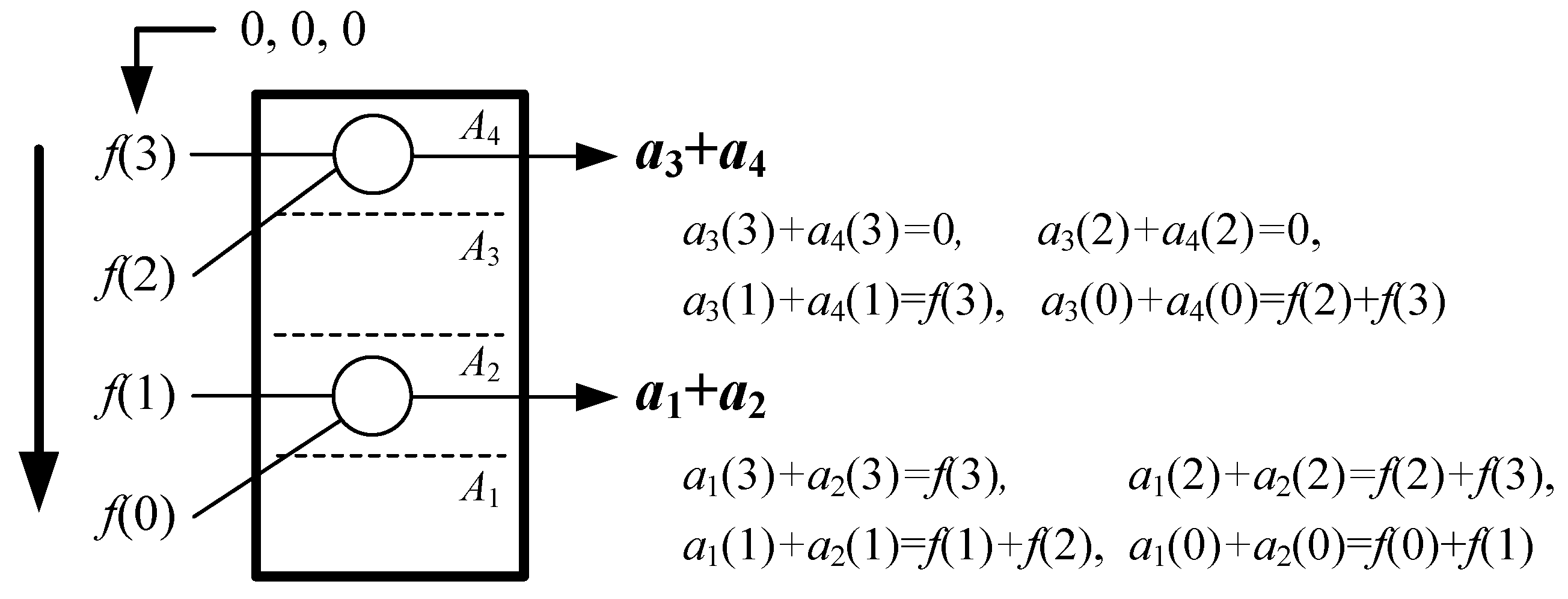
3. The Fast Algorithm and Systolic Array for First-Order Moment
3.1. The Fast Algorithm for First-Order Moment
| Algorithm 1 Moment (aL(n), aL − 1(n), …, a0(n)) |
| Define the array a with two elements |
| Initial a ( aL(n), aL(n) ) |
| for each k [2, L] do // Equation (12) |
| a[1] a[1] + a[0] // 1-network F(a) |
| a[1] a[1] + aL-k+1(n) |
| a[0] a[0] + aL-k+1(n) |
| end for |
| a[0] a[0] + a0(n) |
| return a |
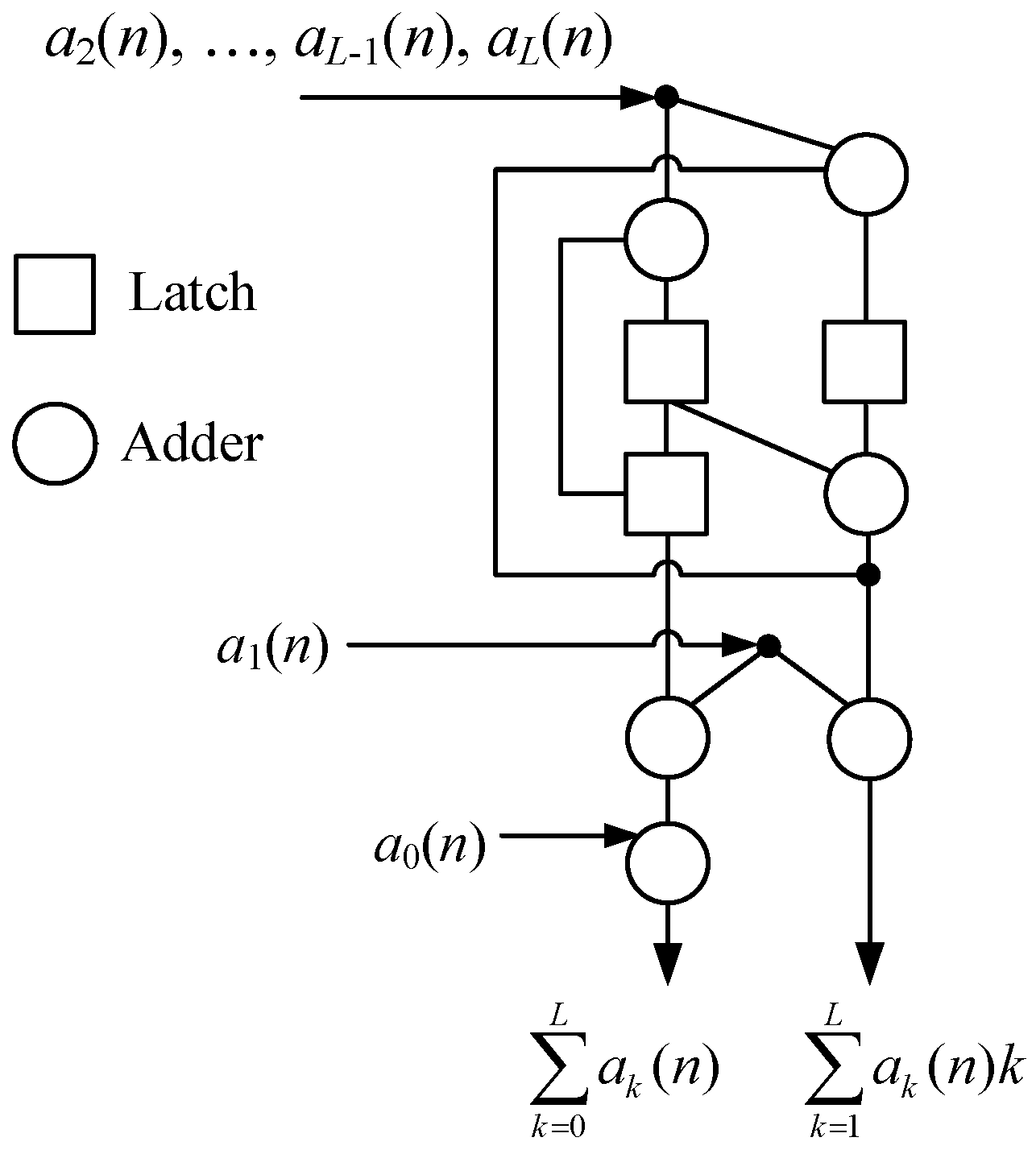
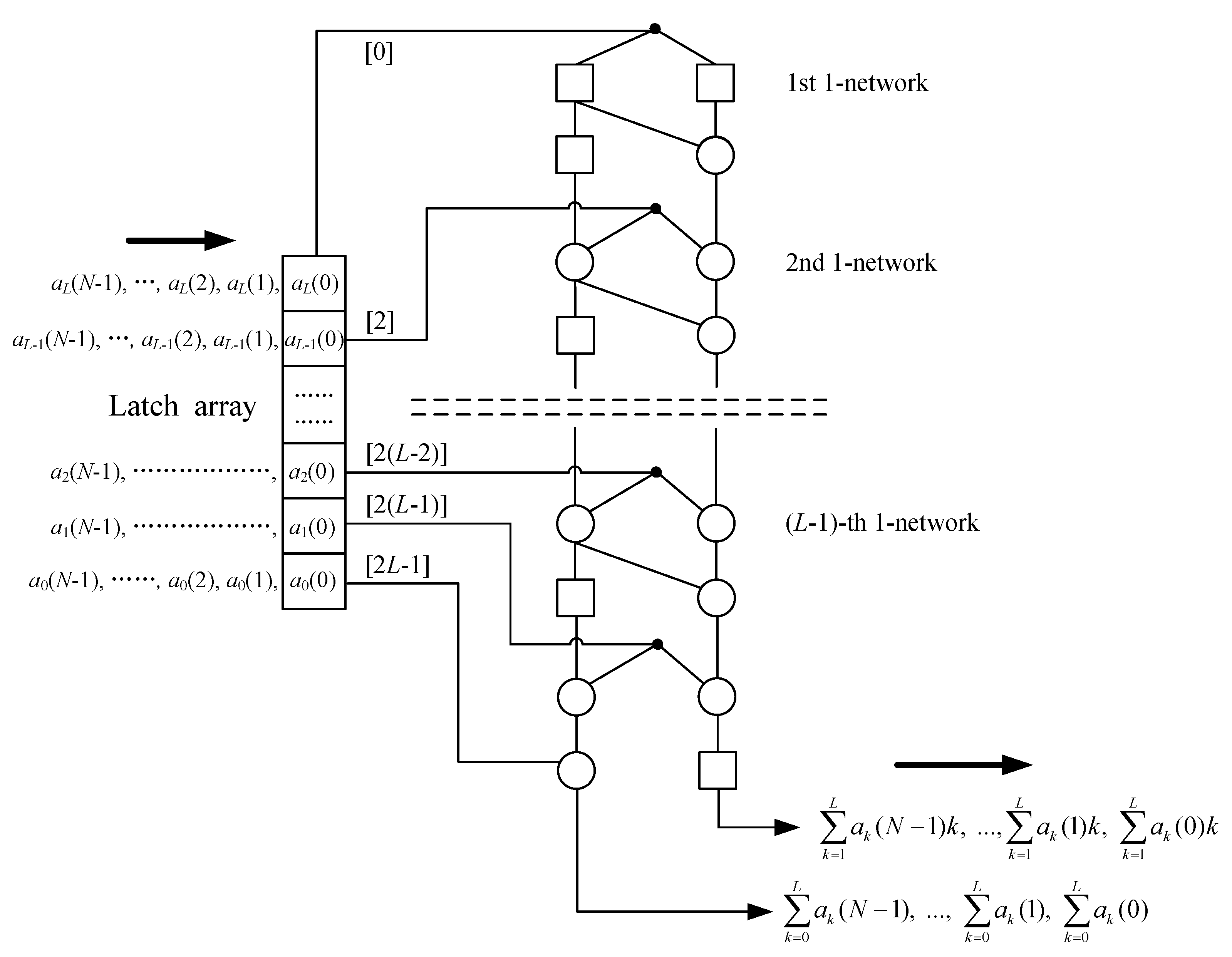
3.2. The Systolic Array for First-Order Moment
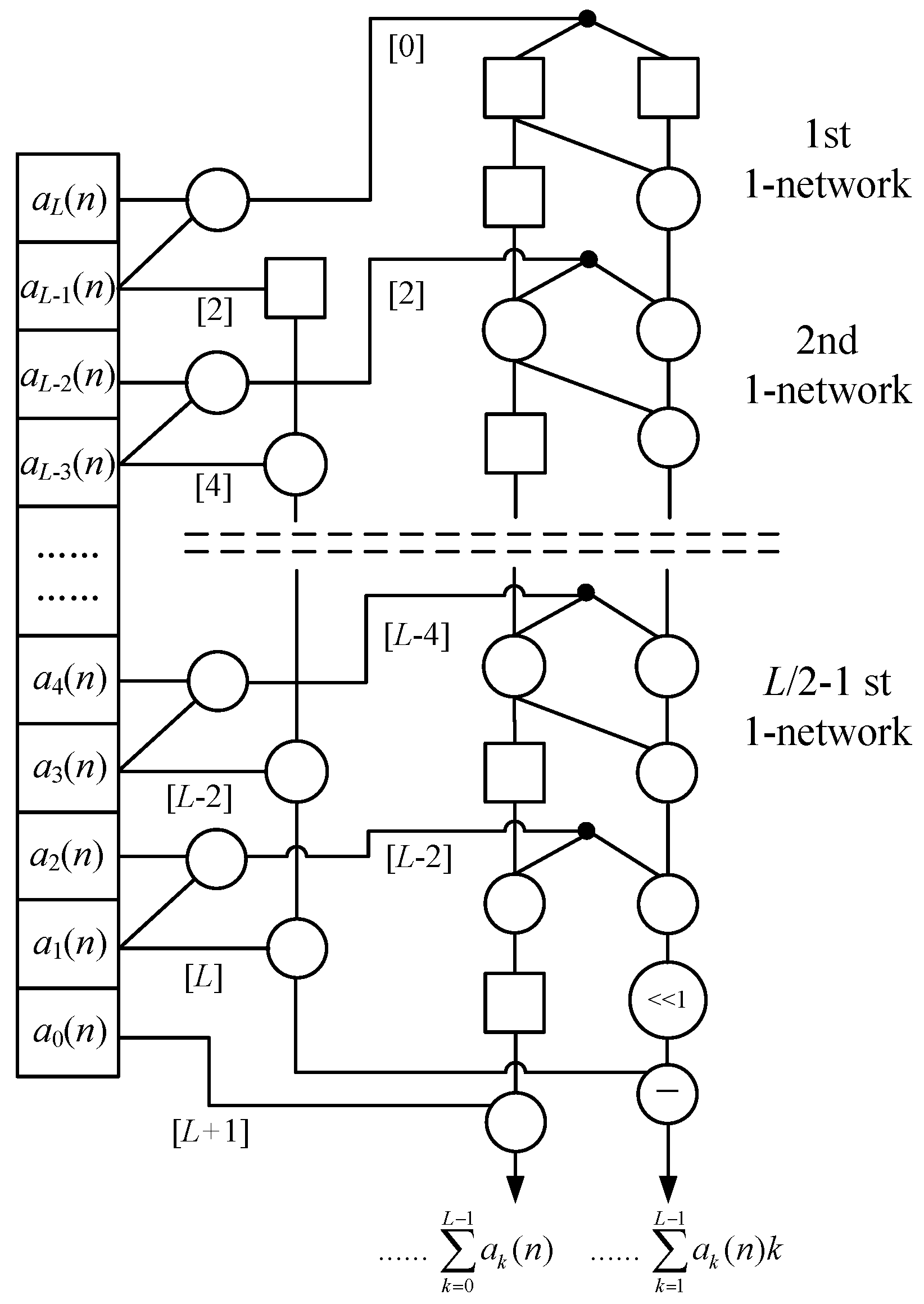
3.3. The Improvement of the Fast Algorithm and Systolic Array for First-Order Moment
4. The Fast Algorithm for Normalized Cross-Correlation
4.1. The Optimization Methods
4.2. The Step of the Fast Algorithm for NCC
- Step 1
- Initializing all ak(n) = 0 (k = 0, 1, …, L), where a0(n) is indispensable for .
- Step 2
- Implementing Equation (3) to acquire the sequence { ak(n) } using N addition.
- Step 3
- Computing , by Equation (13) and Figure 4 with 5L/2 − 1additions.
- Step 4
- Computing b(n) by Equation (14) with 1 multiplication, 2 additions and 1 subtraction.
- Step 5
- Inputting , and b(n) into Equation (9) for a NCC ρ(n), which need 2 subtractions, 4 multiplications, 1 division and 1 square root calculation.
| Algorithm 2 Computing NCC ( n, f, g, b(n-1) ) |
| for each ak in the sequence { ak }: ak 0 |
| for each i [0, N-1] do // Equation (3) |
| k g(i) |
| ak ak + f(n + i) |
| end for |
| for each k [1, L/2] do // Equation (13a) |
| s s + a2k−1 |
| ak a2k−1 + a2k |
| end for |
| a Moment ( aL/2, aL/2−1, …, a2, a1, a0) // Algorithm 1 |
| a[1] a[1] << 1 – s // Equation (13b) |
| Compute b(n) by b(n-1), f(n + N − 1) and f(n − 1) // Equation (14) |
| Compute ρ(n) by a[0], a[1] and b(n) // Equation (9) |
| return ρ(n) |
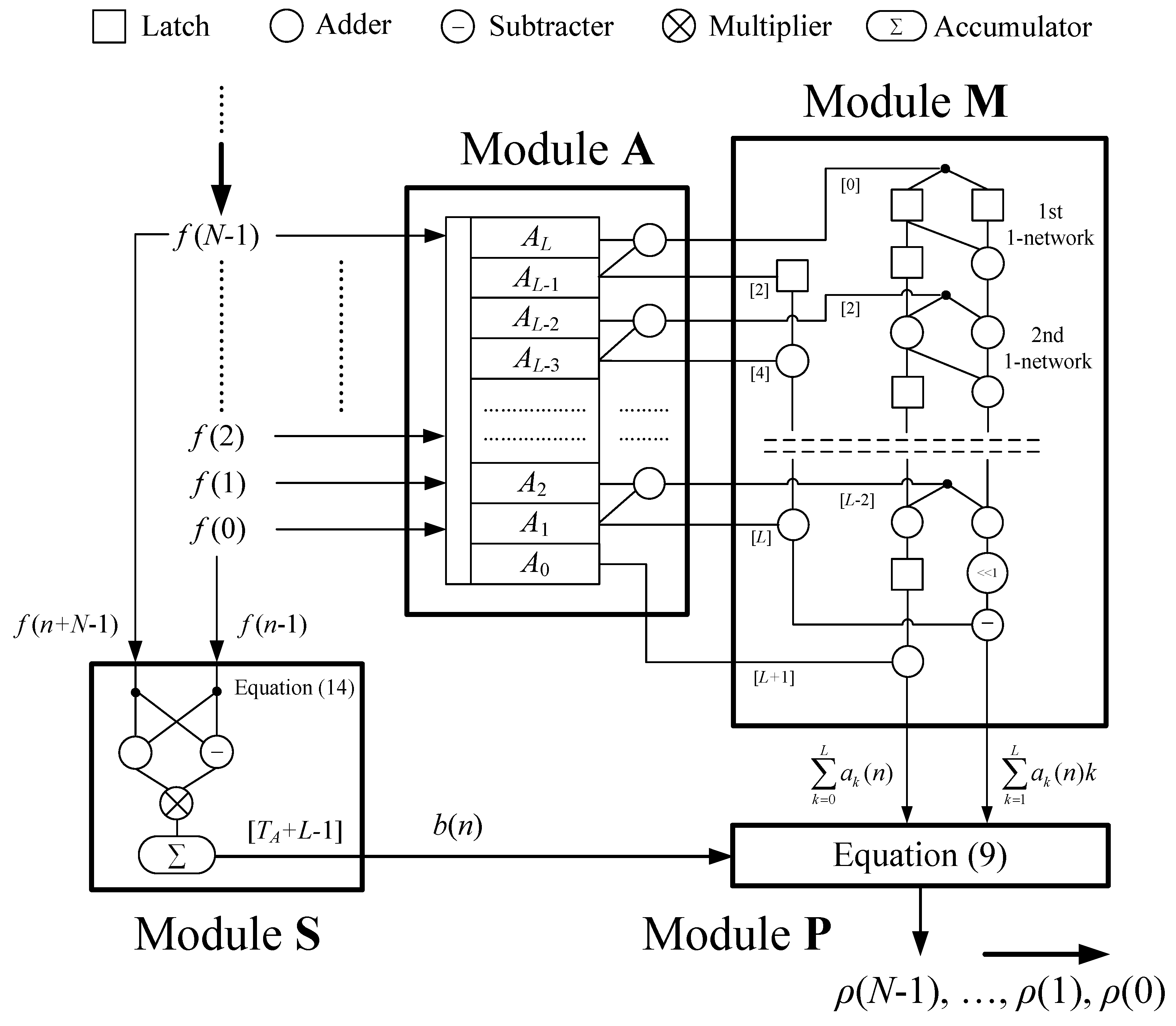
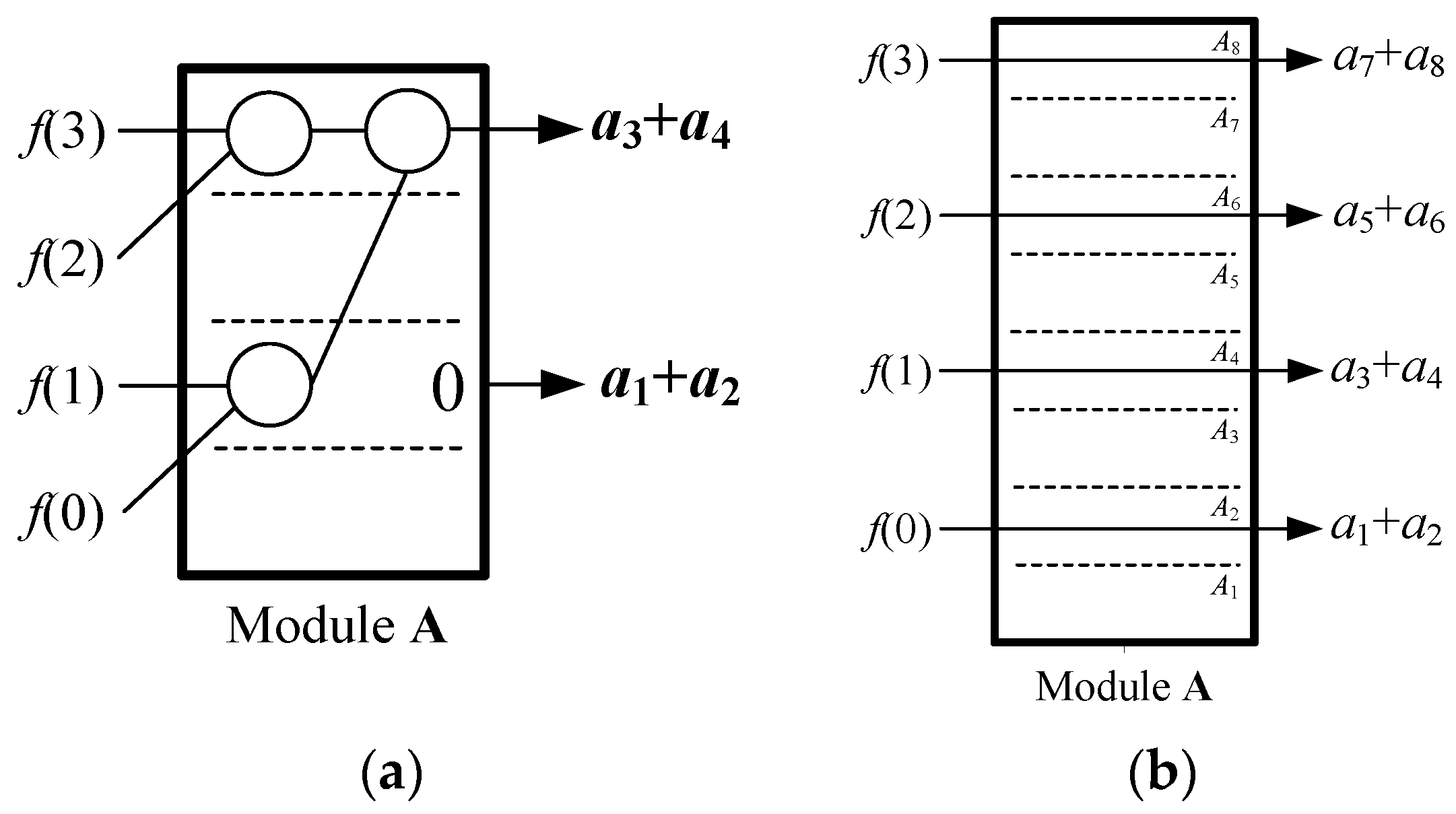
5. The Systolic Array for Normalized Cross-Correlation
5.1. The Module A
5.2. The Model P
5.3. The Systolic Array
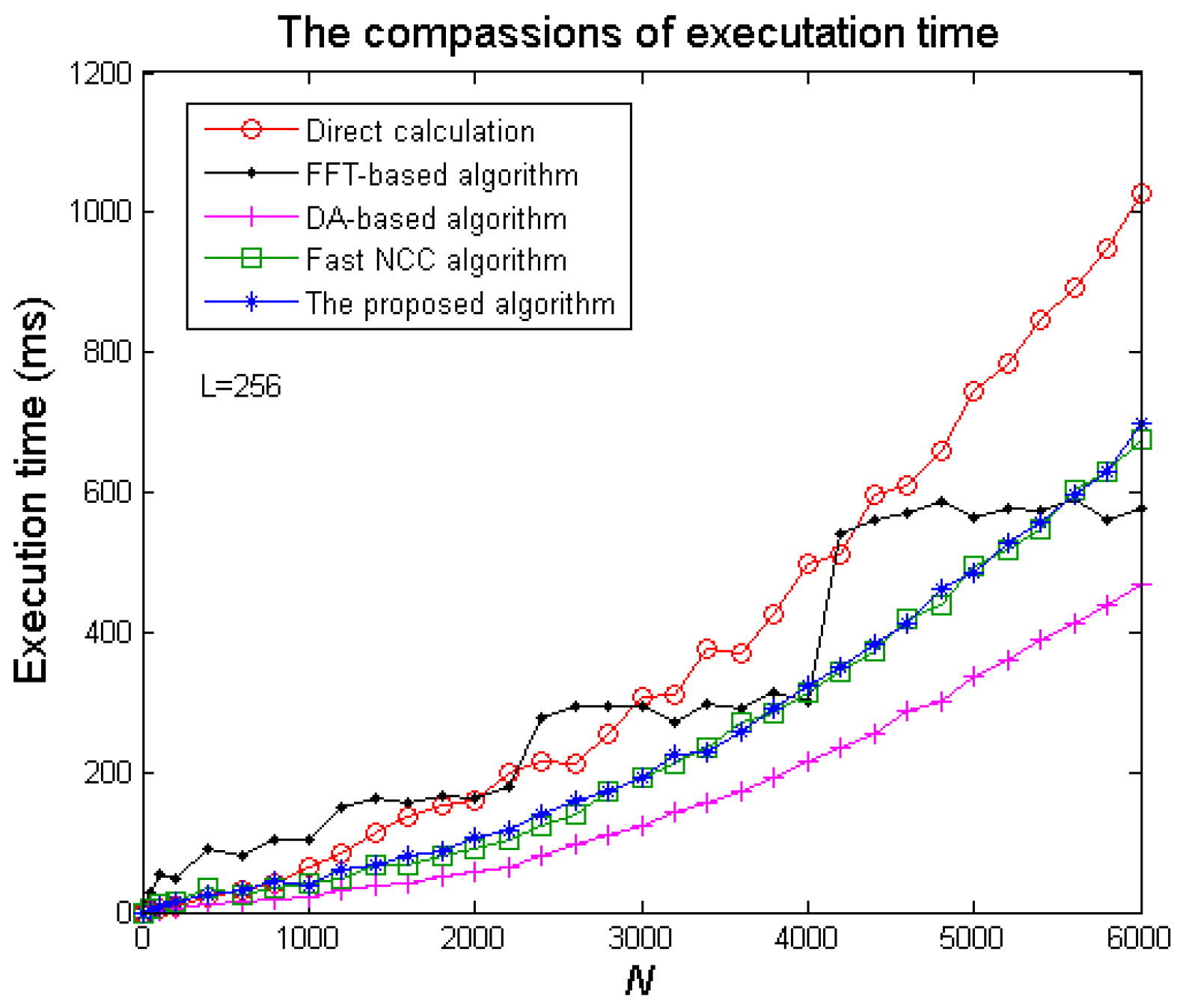
6. Comparisons
6.1. Algorithm Comparison
- (1)
- With less multiplications and memory.
- (2)
- Simple computational structure due to its simple implementation.
- (3)
- Precision and Fit to discrete domain as it uses integer operations [32].
- (4)
- Without limitations on the length of NCC.
- (5)
- Implementation by simple systolic structure.
6.2. Structure Comparison
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Annaby, M.H.; Fouda, Y.M.; Rushdi, M.A. Improved Normalized Cross-Correlation for Defect Detection in Printed-Circuit Boards. IEEE Trans. Semicond. Manuf. 2019, 32, 199–211. [Google Scholar] [CrossRef]
- Duong, D.H.; Chen, C.S.; Chen, L.C. Absolute Depth Measurement Using Multiphase Normalized Cross-Correlation for Precise Optical Profilometry. Sensors 2019, 19, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Banharnsakun, A. Feature point matching based on ABC-NCC algorithm. Evol. Syst. 2018, 9, 71–80. [Google Scholar] [CrossRef]
- Kotenko, I.; Saenko, I.; Branitskiy, A. Applying Big Data Processing and Machine Learning Methods for Mobile Internet of Things Security Monitoring. J. Internet Serv. Inf. Secur. 2018, 8, 54–63. [Google Scholar]
- Sridevi, M.; Sankaranarayanan, N.; Jyothish, A.; Vats, A.; Lalwani, M. Automatic traffic sign recognition system using fast normalized cross correlation and parallel processing. In Proceedings of the 2017 International Conference on Intelligent Communication and Computational Techniques, Jaipur, India, 22–23 December 2017; pp. 200–204. [Google Scholar]
- Bovik, A.C. Basic Tools for Image Fourier Analysis. In The Essential Guide to Image Processing; Academic: San Diego, CA, USA, 2009. [Google Scholar]
- Wu, P.; Li, W.; Song, W.L. Fast, accurate normalized cross-correlation image matching. J. Intell. Fuzzy Syst. 2019, 37, 4431–4436. [Google Scholar] [CrossRef]
- Liu, G.Q.; Kreinovich, V. Fast convolution and Fast Fourier Transform under interval and fuzzy. J. Comput. Syst. Sci. 2010, 76, 63–76. [Google Scholar] [CrossRef][Green Version]
- Kaso, A.; Li, Y. Computation of the normalized cross-correlation by fast Fourier transform. PLoS ONE 2018, 13, e0203434. [Google Scholar] [CrossRef]
- Narasimha, M.J. Linear Convolution Using Skew-Cyclic Convolutions. IEEE Signal. Process. Lett. 2010, 14, 173–176. [Google Scholar] [CrossRef]
- Cheng, L.Z.; Jiang, Z.R. An efficient algorithm for cyclic convolution based on fast-polynomial and fast-W transforms. Circuits Syst. Signal. Process. 2001, 20, 77–88. [Google Scholar]
- Li, H.; Lee, W.S.; Wang, K. Immature green citrus fruit detection and counting based on fast normalized cross correlation (FNCC) using natural outdoor colour images. Precis. Agric. 2016, 17, 678–697. [Google Scholar] [CrossRef]
- Tsai, D.M.; Lin, C.T. Fast normalized cross correlation for defect detection. Pattern Recognit. Lett. 2003, 24, 2625–2631. [Google Scholar] [CrossRef]
- Byard, K. Application of fast cross-correlation algorithms. Electron. Lett. 2015, 51, 242–244. [Google Scholar] [CrossRef]
- Yoo, J.C.; Choi, B.D.; Choi, H.K. 1-D fast normalized cross-correlation using additions. Digit. Signal. Process. 2010, 20, 1482–1493. [Google Scholar] [CrossRef]
- Ismail, L.; Guerchi, D. Performance Evaluation of Convolution on the Cell Broadband Engine Processor. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 337–351. [Google Scholar] [CrossRef]
- Chaudhari, R.E.; Dhok, S.B. An Optimized Approach to Pipelined Architecture for Fast 2D Normalized Cross-Correlation. J. Circuits Syst. Comput. 2019, 28, 1950211. [Google Scholar] [CrossRef]
- Mehendale, M.; Sharma, M.; Peher, P.K. DA-Based Circuits for Inner-Product Computation. In Arithmetic Circuits for DSP Application; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; pp. 77–112. [Google Scholar]
- Cao, L.; Liu, J.G.; Xiong, J.; Zhang, J. Novel structures for cyclic convolution using improved first-order moment algorithm. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 2370–2379. [Google Scholar] [CrossRef]
- Carranza, C.; Llamocca, D.; Pattichis, M. Fast 2D Convolutions and Cross-Correlations Using Scalable Architectures. IEEE Trans. Image Process. 2017, 26, 2230–2245. [Google Scholar] [CrossRef]
- Meher, P.K. Efficient Systolization of Cyclic Convolutions Using Low-Complexity Rectangular Transform Algorithms. In Proceedings of the 2007 International Symposium on Signals, Circuits and Systems ISSCS ’07, Iasi, Romania, 13–14 July 2007; pp. 1–4. [Google Scholar]
- Chen, H.C.; Guo, J.I.; Chang, T.S.; Jen, C.W. A Memory-Efficient Realization of Cyclic Convolution and Its Application to Discrete Cosine Transform. IEEE Trans. Circuits Syst. Video Technol. 2005, 15, 445–453. [Google Scholar] [CrossRef]
- Syed, N.A.A.; Meher, P.K.; Vinod, A.P. Efficient Cross-Correlation Algorithm and Architecture for Robust Synchronization in Frame-Based Communication Systems. Circuits Syst. Signal. Process. 2018, 37, 2548–2573. [Google Scholar] [CrossRef]
- Vun, C.H.; Premkumar, A.B.; Zhang, W. A New RNS based DA Approach for Inner Product Computation. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 2139–2152. [Google Scholar] [CrossRef]
- Liu, J.G.; Pan, C.; Liu, Z.B. Novel Convolutions using First-order Moments. IEEE Trans. Comput. 2012, 61, 1050–1056. [Google Scholar] [CrossRef]
- Hua, X.; Liu, J.G. A Novel Fast Algorithm for the Pseudo Winger-Ville Distribution. J. Commun. Technol. Electron. 2015, 60, 1238–1247. [Google Scholar] [CrossRef]
- Liu, J.G.; Liu, Y.Z.; Wang, G.Y. Fast Discrete W Transforms via Computation of Moments. IEEE Trans. Signal. Process 2005, 53, 654–659. [Google Scholar] [CrossRef]
- Yazdanpanah, H.; Diniz, P.S.R.; Lima, M.V.S. Low-Complexity Feature Stochastic Gradient Algorithm for Block-Lowpass Systems. IEEE Access 2019, 7, 141587–141593. [Google Scholar] [CrossRef]
- Viticchie, A.; Basile, C.; Valenza, F.; Lioy, A. On the impossibility of effectively using likely-invariants for software attestation purposes. J. Wirel. Mob. Netw. Ubiquitous Comput. Dependable Appl. 2018, 9, 1–25. [Google Scholar]
- Adhikari, G.; Sahu, S.; Sahani, S.K.; Das, B.K. Fast normalized cross correlation with early elimination condition. In Proceedings of the 2012 International Conference on Recent Trends in Information Technology, Chennai, India, 19–21 April 2012; pp. 136–140. [Google Scholar]
- Blahut, R.E. Fast Algorithms for Digital Signal Processing; Addison-Wesley: Reading, MA, USA, 1984. [Google Scholar]
- Yuan, Y.; Qin, Z.; Xiong, C.Y. Digital image correlation based on a fast convolution strategy. Opt. Lasers Eng. 2017, 97, 52–61. [Google Scholar] [CrossRef]
- Meher, P.K.; Park, S.Y. A novel DA-based architecture for efficient computation of inner-product of variable vectors. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems, Melbourne, Australia, 1–5 June 2014; pp. 369–372. [Google Scholar]
- Mukherjee, D.; Mukhopadhyay, S. Fast Hardware Architecture for 2-D Separable Convolution Operation. IEEE Trans. Circuits Syst. II Exp. Briefs 2018, 65, 2042–2046. [Google Scholar] [CrossRef]
- Yang, Y.J.; Zhang, Y.H.; Li, D.M.; Wang, Z.J. Parallel Correlation Filters for Real-Time Visual Tracking. Sensors 2019, 19, 1–22. [Google Scholar] [CrossRef]
- Hartl, A.; Annessi, R.; Zseby, T. Subliminal Channels in High-Speed Signature. J. Wirel. Mob. Netw. Ubiquitous Comput. Dependable Appl. 2018, 9, 30–53. [Google Scholar]


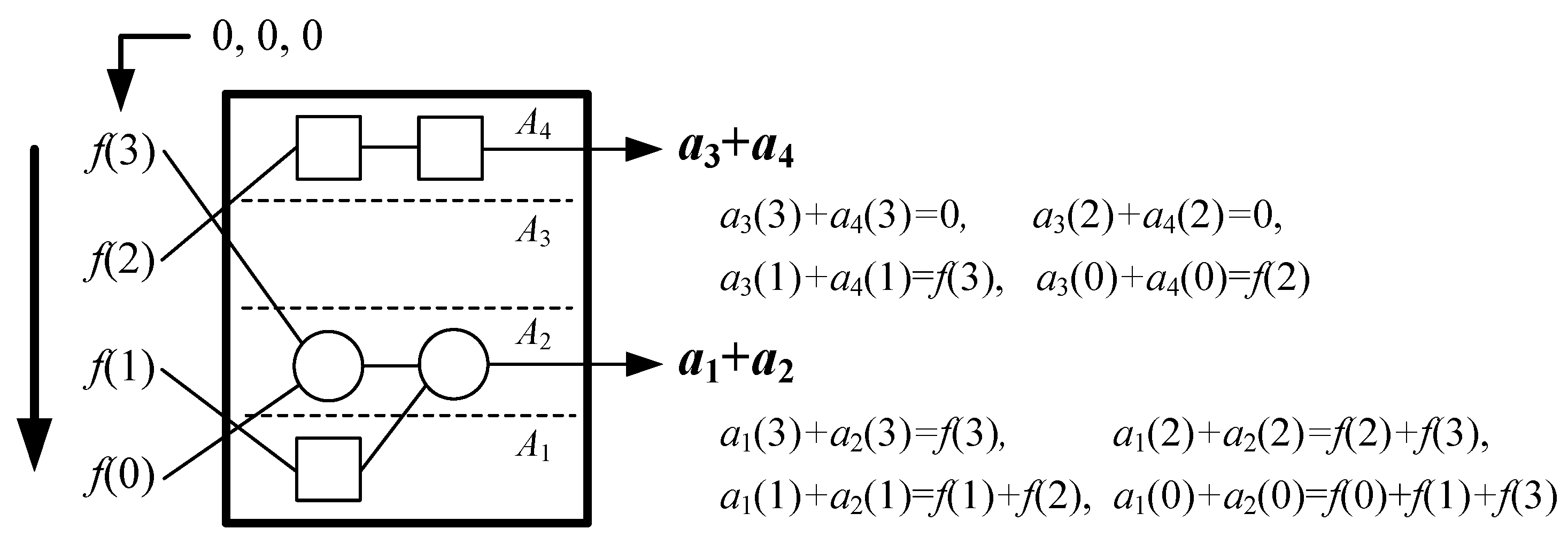


| Algorithm | Multiplication | Addition |
|---|---|---|
| Direct calculation | 2N (N + 1) | 3N (N + 1) |
| FFT-based algorithm [8,9] | (3/2) Nlog2N − (3/2) N + 16 | (7/2) Nlog2N − N/2 + 15 |
| DA-based algorithm [22] | 7N − 1 | (5N − 2) log2L + 8N − 1 |
| Fast NCC algorithm [15] | 0 | 3N (N + 1) |
| The proposed algorithm | 6N − 1 | N (N + 5L/2 + 5) - 4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.; Lv, Z.; Hua, X.; Li, H. The Algorithm and Structure for Digital Normalized Cross-Correlation by Using First-Order Moment. Sensors 2020, 20, 1353. https://doi.org/10.3390/s20051353
Pan C, Lv Z, Hua X, Li H. The Algorithm and Structure for Digital Normalized Cross-Correlation by Using First-Order Moment. Sensors. 2020; 20(5):1353. https://doi.org/10.3390/s20051353
Chicago/Turabian StylePan, Chao, Zhicheng Lv, Xia Hua, and Hongyan Li. 2020. "The Algorithm and Structure for Digital Normalized Cross-Correlation by Using First-Order Moment" Sensors 20, no. 5: 1353. https://doi.org/10.3390/s20051353
APA StylePan, C., Lv, Z., Hua, X., & Li, H. (2020). The Algorithm and Structure for Digital Normalized Cross-Correlation by Using First-Order Moment. Sensors, 20(5), 1353. https://doi.org/10.3390/s20051353




