Multi Criteria Decision Making for the Multi-Satellite Image Acquisition Scheduling Problem
Abstract
1. Introduction
2. Literature Review
3. Model Formulation
- Multi-criteria scoring of all feasible imaging attempts.
- Address biased optimization due to criteria weights specified by decision makers.
- Include operational constraints, e.g., maneuvering, payload specifications, memory capacity.
- Incorporate inter-dependencies in requests due to operational constraints and request specifications, such as large area or stereo imaging.
- Consider weather uncertainty.
- Find solutions in real time.
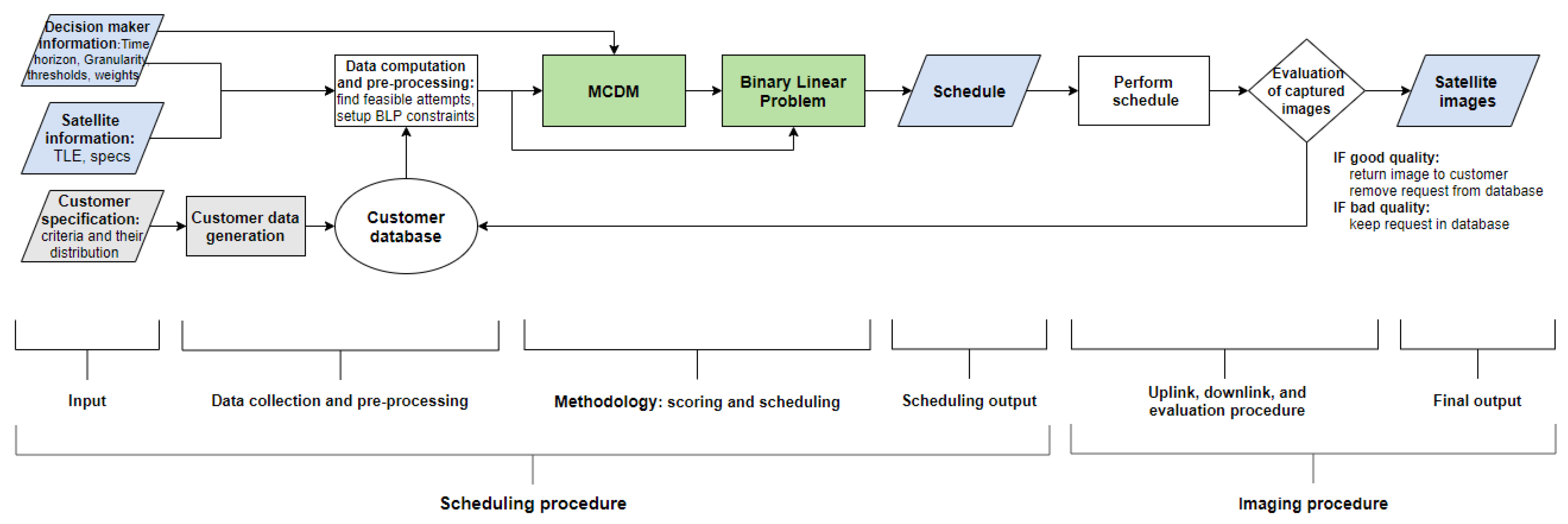
3.1. Input, Data Generation, and Pre-Processing
3.2. Mathematical Optimization Problem
- The payload of each satellite can only perform one task/request at a time.
- Maneuvering time and acquisition duration make a set of attempts infeasible, i.e., some attempts cannot be performed sequentially if there is not enough time for maneuvering the attitude of the satellite. Note that if the payload tries to perform two attempts simultaneously, it will be forbidden as these two attempts are by definition part of a set of infeasible attempts.
- A request must only be acquired once within the time horizon.
- Satellites have limited memory thus affecting the schedule.
- Some requests must be acquired twice and from different angles, these are denoted as stereoscopic requests.
- Attempts must be initiated only if conditions are within some specified quality thresholds.
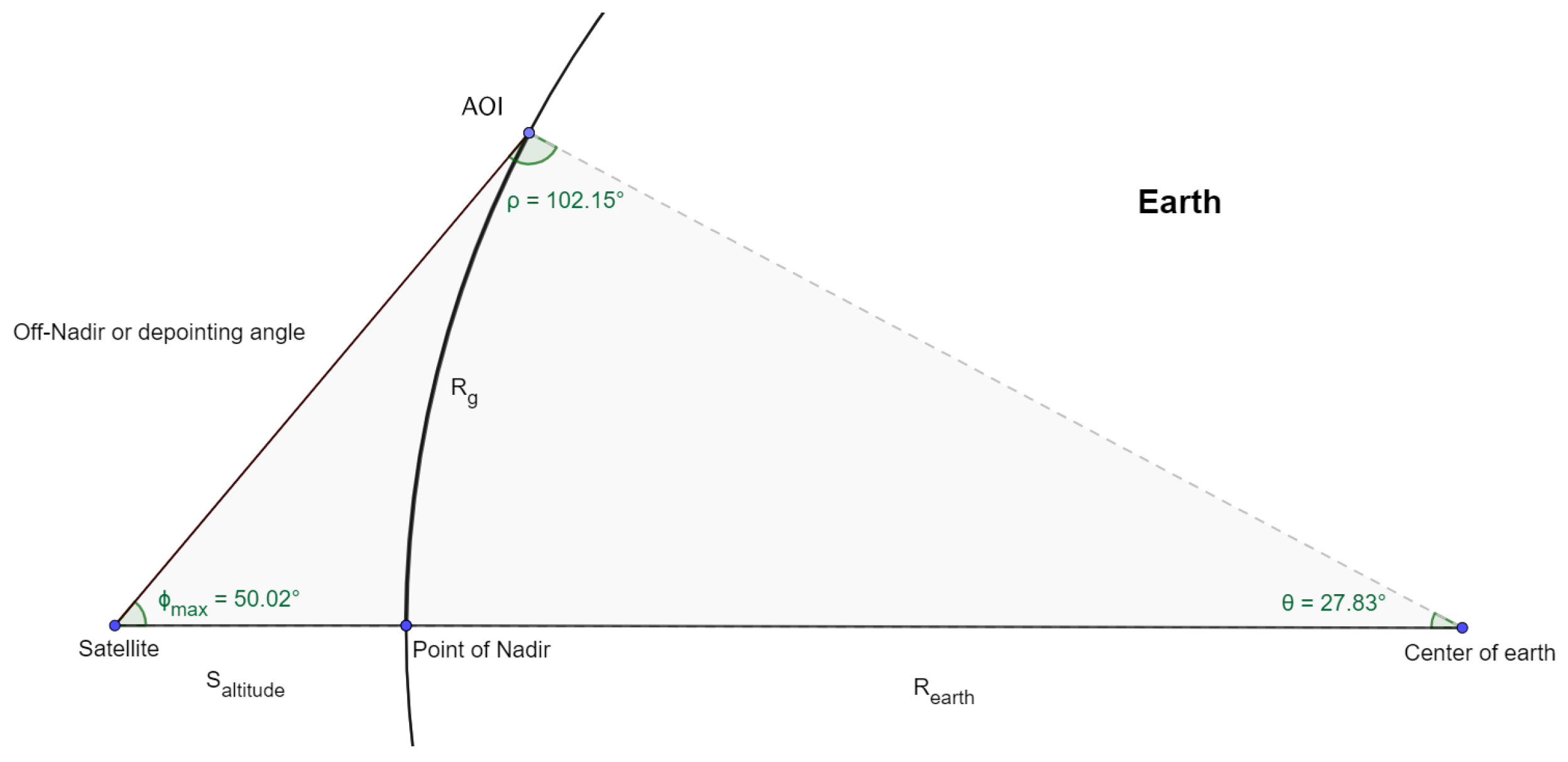
- Off-nadir angle (depointing angle)
- Sun elevation angle
- The effect of real-time uncertainty on cloud coverage and observed cloud coverage
- Price
- Area
- Customer type
- Customer priority
- Age of request
- A request can only be acquired once.
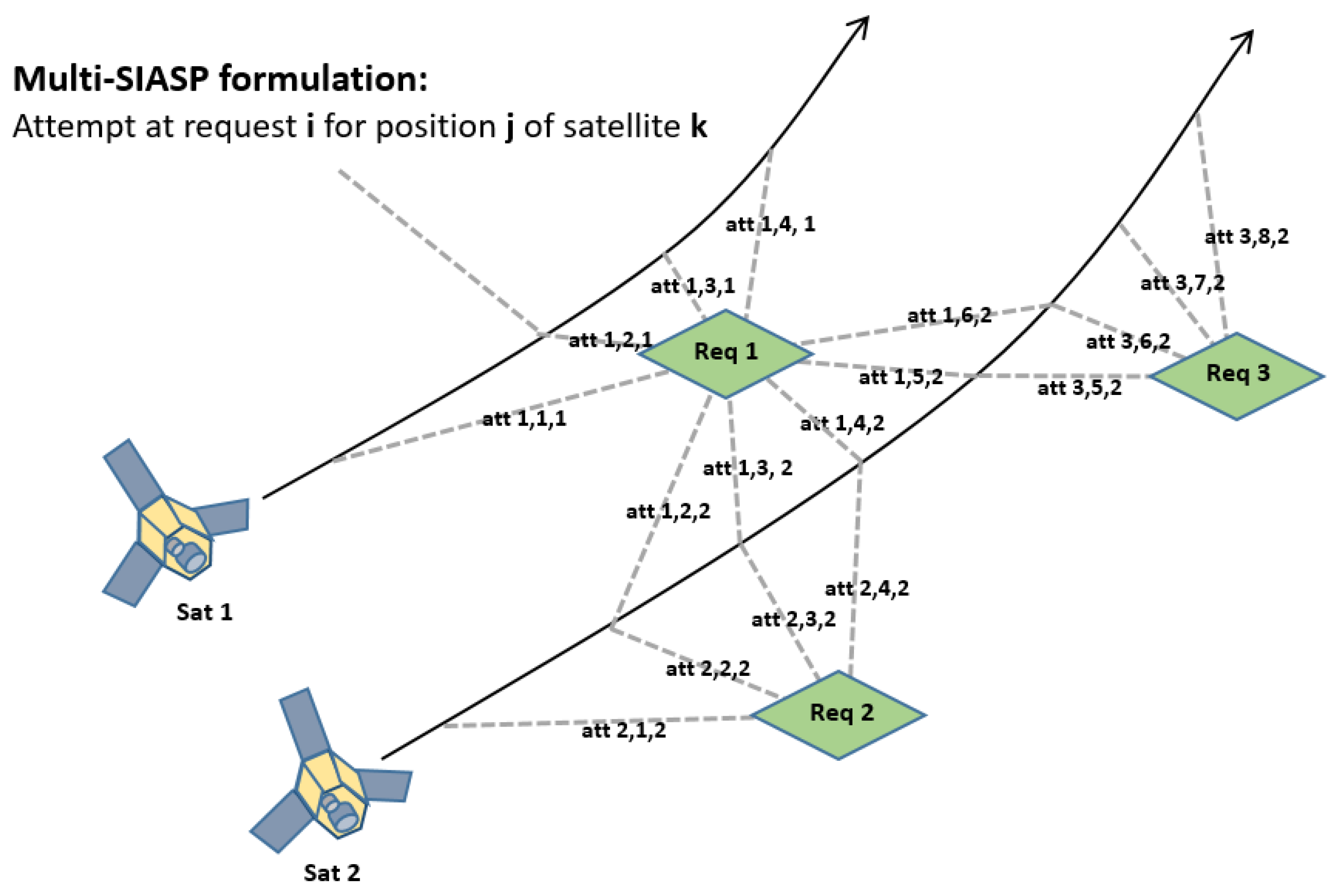
- The maneuvering between requests and the acquisition of a request must be considered while making a feasible schedule. A request acquired from a particular satellite position is considered as an attempt. Incorporating the maneuvering feasibility of the schedule involves considering the satellites consumption of time for the maneuver between that attempt and the next and the acquisition duration of the first attempt. A matrix representing all infeasible pairs of attempts is therefore pursued. Note that all attempts performed by different satellites are independent in terms of maneuverability and acquisition duration.To illustrate the maneuvering feasibility of attempts, we introduce additional variables representing the requests of interest (r and s, for notational convenience), and the specific satellite position where these are performed ( and , respectively). Thereby, investigating whether maneuvers between any two attempts performed by the same satellite is feasible. In this way, a four-dimensional matrix called an infeasibility matrix is generated for each satellite, with , whose dimensions are the first request of interest (r); second request of interest(s); and the satellite position of these attempts ( and ), where , , and .where represents duration of maneuver between attempt to , is the duration of acquiring request r, and is the start time of performing attempt . Additionally, is already computed in the pre-processing. Note, as , we are essentially only interested in the infeasible maneuvers between attempt and future or contemporary attempts. This is because attempts are performed in a time-ordered manner, so we are only interested in which infeasible maneuvers that exist from , as this ultimately represents all infeasible maneuvers present in the satellite network.There is a correlation between the granularity of the SIASP and satellite position, as the granularity directly affects the difference between succeeding satellite positions. However, the granularity could easily have been translated to enforce time instead of distance and thereby directly affect times of acquisition for the satellite.To model the , the rotational speed of the satellite must be known. We disregard the detailed behaviour of the attitude actuators on-board the satellite, and instead assume a constant rotational speed. From industrial partners we have been informed that a good estimate for the rotational speed is 2 degrees per second. To calculate the angle of rotation between two requests, the most direct rotation is made through the plane represented by the two following vectors: vector from position of satellite at to center of request r; vector from position of satellite at to center of request s. To find these vectors we change the longitude-latitude system into the geocentric three-dimensional Cartesian coordinate system. See Appendix B.1 for further explanation. From this, we know that an infeasible maneuver for a pair of attempts will result in , while signifies that the maneuver between two attempts are feasible.Having obtained the infeasibility matrices, we now face the challenge of constructing the feasibility constraint. From Section 2 it is found that the infeasibility constraint is generally included through a pairwise infeasibility constraint or by modelling the SIASP as a maximum clique problem, see, for example [1,4]. Either way the infeasibility constraint is one of the most computationally expensive constraints to consider. As the optimization methodology is not the main focus of this research, and the exact solver is very computationally demanding in the case of either approaches of modelling the feasibility, we choose to over-constrain the solution by assuming that any subset of a set of infeasible attempts with respect to another attempt are also infeasible to each other. This will somewhat restrict the solution space from finding a solution in near real-time even for the larger problem scenarios.Due to the construction of matrix, the similarity of the two sets of attempts and , and the fact that maneuvering between two attempts that are the same attempt must be infeasible, we know that . Accordingly, the following must be true. For simplicity, we assume that the maneuver between a specific attempt and a single other attempt is infeasible, where . That is, , and we know when represents the same attempt as , as a consequence:if the two attempts and are included in the schedule. Furthermore, if additional infeasible attempts in relation to are included in the schedule, then the sum from Equation (3) will be even greater than 2. Analogously, one can observe that only performing a feasible maneuver in the framework of Equation (3) equals one, and not performing any maneuver equals zero. Based on that observation, the following infeasibility constraint is obtained, which if satisfied ensures that no maneuvers violate the physical maneuverability of the satellite.
- The acquisition of images take up storage on the satellites memory. The upper limit for the memory capacity devoted for the particular schedule horizon is known prior. The following formula is used for defining storage of each image.Note, one pixel takes 3 bytes of memory. The upper capacity limit for the kth satellite is denoted, , and the file size of attempt is denoted .The image capacity constraint works as an upper limit constraint of the cumulative file size of the acquired images.
- In this study, we considered the consequence where the satellite operator could deliver stereoscopic images. Given a set of requests, a subset of those requests were assumed to be stereoscopic requests. That subset was denoted , and for the ith stereoscopic request in , we had multiple sets of attempts that satisfied the stereoscopic imaging specifications of a convergence angle between 30 and 60 degrees. Essentially, when considering a stereo request i, and a first attempt at position j of satellite k, we were interested in all other second attempts for the same request i that produced a proper convergence angle. We denote all first attempts that satisfied the conditions of a stereo request i by and all accompanying second attempts that completed a stereo request by . Note,In order to represent all attempts that collectively complete this acquisition, we construct a five-dimensional binary matrix, S.Therefore, the following constraint is proposed to include stereoscopic images.Note, as Equation (6) equals zero, a stereo request should not necessarily be acquired; however, if it is, the complete acquisition of the stereoscopic request must be included in the schedule for the particular planning horizon.
4. Solution Approach
4.1. Reachability and Feasibility Check of Attempts
4.2. MCDM for Scoring Acquisition Attempts
4.3. GLPK Solver
5. Performance Analysis
5.1. Performance Measures Relative to Priority and Scoring Method
5.2. Running Time Relative to Granularity and Requests
5.3. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Multi-Criteria Decision Making
Appendix A.1. ELECTRE-III
- The concordance index for each criterion ,
- The discordance index for each criterion ,
- The credibility index representing the degree of outranking for each criterion . Note, that , where .where . If the discordance index for a relative to b is 1 for any criteria, the credibility index is then 0, representing no confidence in the hypothesis that is as least as good as .
Appendix A.2. TOPSIS
- Calculate normalized decision matrix , representing the normalized criteria values.where − sign and + sign are used for the cost criteria and benefit criteria, respectively.
- Calculate the weighted normalized decision matrix
- Determine the positive ideal and negative ideal solutions and :
- Calculate the Euclidean distances of each alternative to the ideal solutions.for
- Calculate the relative closeness coefficient of each alternative to the ideal solutions, CCi.
- Rank the alternatives according to the relative closeness to the ideal solution. The CCi measures the ratio of the total Euclidean distance to ideal solutions coming from the distance to the negative ideal. The bigger the CCi, the higher the rank.
Appendix B. Additions to Solution Approach
Appendix B.1. Transformation of Vector System
Appendix B.2. Reachability of Requests
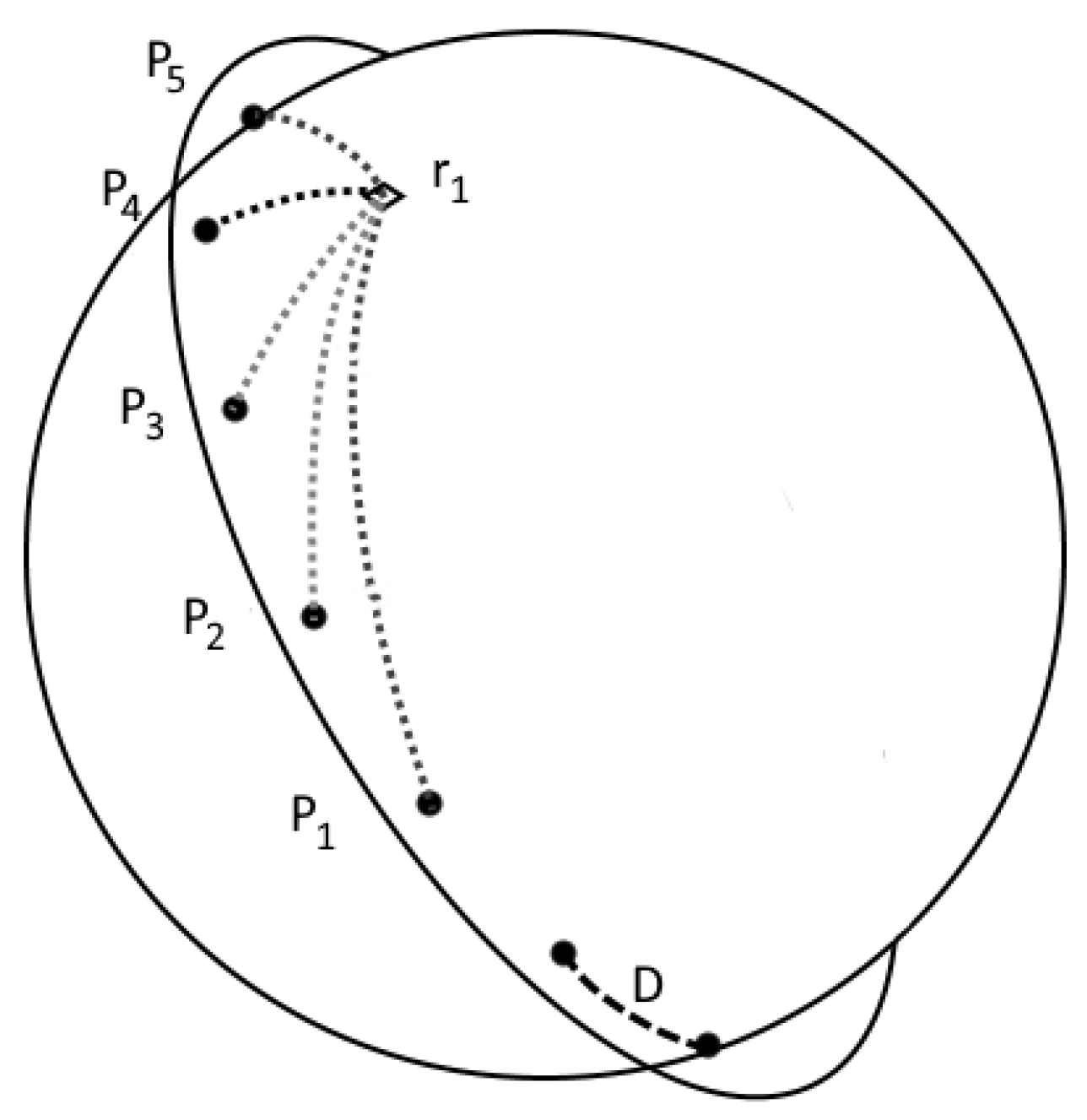
Appendix B.3. Data Input
| Location | Latitude | Longitude |
|---|---|---|
| Copenhagen | 55;56 | 12;13 |
| Aalborg | 56.5;57.5 | 9;10 |
| Entire Denmark | 54.769;57.72 | 8.24;14.70 |
| Toulouse | 43;44 | 1;2 |
| Paris | 48;49.5 | 1.5;3 |
| Nice | 43;44 | 7;8 |
| Entire France | 41.59;51.0 | −4.65;9.45 |
| Variable | Description |
|---|---|
| Start schedule | Date and time of scheduling start. |
| Hours ahead | Defining scheduling horizon. |
| Granularity | Defining the time segmentation of the satellite path. |
| TLEs | Two-line element set defining the satellite path. Note that these should be updated accordingly. |
| Maximum off-nadir angle | Determining the maximum depointing angle a satellite image can be acquired with without its quality being too bad. Set to . |
| Satellite altitude | Set to 645, but could be extracted from TLEs. |
| Earth Radius | 6,371,230 m. |
| Rotation speed | Camera rotation speed. Set to /s. |
| Camera resolution | Set to 1 m2/pixel. |
| Capacity limit of satellite | Set to 1 TB. |
| Data location | See Table A1. |
| Schedule relative criteria | See Table 1. |
References
- Bensana, E.; Verfaillie, G.; Agnese, J.; Bataille, N.; Blumstein, D. Exact and inexact methods for daily management of earth observation satellite. Space Mission Oper. Ground Data Syst. SpaceOps 1996, 394, 507–514. [Google Scholar]
- Vasquez, M.; Hao, J.K. A “logic-constrained” knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observation satellite. Comput. Optim. Appl. 2001, 20, 137–157. [Google Scholar] [CrossRef]
- Jang, J.; Choi, J.; Bae, H.J.; Choi, I.C. Image collection planning for Korea multi-purpose SATellite-2. Eur. J. Oper. Res. 2013, 230, 190–199. [Google Scholar] [CrossRef]
- Malladi, K.T.; Mitrovic-Minic, S.; Punnen, A.P. Clustered maximum weight clique problem: Algorithms and empirical analysis. Comput. Oper. Res. 2017, 85, 113–128. [Google Scholar] [CrossRef]
- Nielsen, L.D.; Sung, I.; Nielsen, P. Convex decomposition for a coverage path planning for autonomous vehicles: Interior extension of edges. Sensors 2019, 19, 4165. [Google Scholar] [CrossRef] [PubMed]
- Ehrgott, M.; Figueira, J.R.; Greco, S. Multiple Criteria Decision Analysis State of the Art Surveys, 2nd ed.; Springer: New York, NY, USA, 2016. [Google Scholar]
- Roy, B. Classement et choix en présence de points de vue multiples. Revue française d’informatique et de recherche opérationnelle 1968, 2, 57–75. Available online: https://www.rairo-ro.org/articles/ro/pdf/1968/01/ro196802V100571.pdf (accessed on 18 December 2019). [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attributes Decision Making Methods and Applications, 198th ed.; Springer: Berlin, Germany, 1981. [Google Scholar]
- Lemaitre, M.; Verfaillie, G.; Jouhaud, F.; Lachiver, J.M.; Bataille, N. Selecting and scheduling observations of agile satellites. Aerosp. Sci. Technol. 2002, 6, 367–381. [Google Scholar] [CrossRef]
- Bianchessi, N.; Cordeau, J.F.; Desrosiers, J.; Laporte, G.; Raymond, V. A heuristic for the multi-satellite, multi-orbit and multi-user management of earth observation satellites. Eur. J. Oper. Res. 2007, 177, 750–762. [Google Scholar] [CrossRef]
- Mansour, M.A.; Dessouky, M.M. A genetic algorithm approach for solving the daily photograph selection problem of the SPOT5 satellite. Comput. Ind. Eng. 2010, 58, 509–520. [Google Scholar] [CrossRef]
- Vasquez, M.; Hao, J.K. Upper bounds for the SPOT 5 daily photograph scheduling problem. J. Comb. Optim. 2003, 7, 87–103. [Google Scholar] [CrossRef]
- Tangpattanakul, P.; Jozefowiez, N.; Lopez, P. A multi-objective local search heuristic for scheduling Earth observations taken by an agile satellite. Eur. J. Oper. Res. 2015, 245, 542–554. [Google Scholar] [CrossRef]
- Wang, J.; Demeulemeester, E.; Hu, X.; Qiu, D.; Liu, J. Exact and heuristic scheduling algorithms for multiple earth observation satellites under uncertainties of clouds. IEEE Syst. J. 2018, 13, 3556–3567. [Google Scholar] [CrossRef]
- Xu, R.; Chen, H.P.; Liang, X.L.; Wang, H.M. Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization. Expert Syst. Appl. 2016, 51, 195–206. [Google Scholar] [CrossRef]
- Barkaoui, M.; Berger, J. A new hybrid genetic algorithm for the collection scheduling problem for a satellite constellation. J. Oper. Res. Soc. 2019, 1–21. [Google Scholar] [CrossRef]
- Wang, J.; Demeulemeester, E.; Hu, X.; Wu, G. Expectation and SAA models and algorithms for scheduling of multiple earth observation satellites under the impact of clouds. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, X. Application of a multi-satellite dynamic mission scheduling model based on mission priority in emergency response. Sensors 2019, 19, 1430. [Google Scholar] [CrossRef]
- Buchanan, J.T.; Sheppard, P.J.; Vanderpooten, D. Project Ranking Using ELECTRE III; University of Waikato: Hamilton, New Zealand, 1999; Available online: https://www.researchgate.net/publication/240195234_Project_ranking_using_Electre_III (accessed on 18 December 2019).
- Bouyssou, D. Outranking methods. In Encyclopedia of Optimization; Njihoff Publishing: Kluwer, Belgium, 2001; pp. 1919–1925. [Google Scholar]
- Corrente, S.; Figueira, J.R.; Greco, S.; Słowiński, R. A robust ranking method extending ELECTRE III to hierarchy of interacting criteria, imprecise weights and stochastic analysis. Omega 2017, 73, 1–17. [Google Scholar] [CrossRef]
- Torlak, G.; Sevkli, M.; Sanal, M.; Zaim, S. Analyzing business competition by using fuzzy TOPSIS method: An example of Turkish domestic airline industry. Expert Syst. Appl. 2011, 38, 3396–3406. [Google Scholar] [CrossRef]
- Greco, S.; Ehrgott, M.; Figueira, J.R. Trends in Multiple Criteria Decision Analysis; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Hoots, F.R. Reformulation of the Brouwer geopotential theory for improved computational efficiency. Celestial Mech. 1981, 24, 367–375. [Google Scholar] [CrossRef]
- Ditzian, Z. A modulus of smoothness on the unit sphere. Journal d’Analyse Mathématique 1999, 79, 189–200. Available online: https://link.springer.com/article/10.1007/BF02788240 (accessed on 18 December 2019). [CrossRef]
- Figueira, J.; Greco, S.R.B.; Słowiński, R. An overview of ELECTRE methods and their recent extensions. J. Multi-Criteria Decisi. Anal. 2013, 20, 61–85. [Google Scholar] [CrossRef]
- Mitchell, J.E. Branch-and-cut algorithms for combinatorial optimization problems. In Handbook of Applied Optimization; Oxford University Press: New York, NY, USA, 2002; pp. 65–77. [Google Scholar]
- Deb, K.; Myburgh, C. A population-based fast algorithm for a billion-dimensional resource allocation problem with integer variables. Eur. J. Oper. Res. 2017, 261, 460–474. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, Y.; Qiao, W.; Chen, X. A Dynamic Composition Mechanism of Security Service Chaining Oriented to SDN/NFV-Enabled Networks. IEEE Access 2018, 6, 53918–53929. [Google Scholar] [CrossRef]
- Nowak, M. Preference and veto thresholds in multicriteria analysis based on stochastic dominance. Eur. J. Oper. Res. 2004, 158, 339–350. [Google Scholar] [CrossRef]

| Data Type | Description |
|---|---|
| Location (Area of Interest) | Uniformly distributed around Denmark and France based on longitude and latitude. The multiple subsets replicate the higher concentration of requests around e.g., urbanized areas, see Table A1. |
| Customer type | Assumed to be uniformly distributed on the set . It represents the different customer types; government and commercial, respectively. |
| Priority | Assumed to only be dependent on customer type, i.e., customer type 1 is further divided into two segments as Priority 1 and Priority 2. Similarly, customer type 2 is divided into Priority 3 and Priority 4. In practice, it depends on the intricate priority of customers within each customer type from the space agency. For example, a four-priority class structure can be arranged as military, government, and commercial one and two. |
| Price | Uniform [1000, 10,000] in euros. Note that these figures are provided for the sake of simulation, but do not reflect any commercial reality. In practice, the price should be correlated with priority, commercial customer types, and location as urbanized areas have a higher demand than ocean-based requests, etc. We assume, only commercial customers to bring profit, e.g., due to collaboration, profit from government organisations are assumed to be zero. |
| Age | Uniform [1, 13], and it represents the days a request have been active. |
| Stereo request | We assume 10% of the customer requests to be stereo requests (3D), and during computation each are considered independently. |
| Area | Uniform [1, 1000] in km2, it represents the area of a particular request. |
| Duration of acquisition | Uniform [2, 8] in seconds. It represents the duration for a satellite to capture a specific request. |
| Problem | Description of Limitation |
|---|---|
| Energy | The satellites energy behaviour when maneuvering and capturing images is neglected. |
| Satellites | Satellites are assumed to be homogeneous in terms of their camera, memory, and maneuverability specifications. Memory of 1 TB. |
| Agility | The maneuverability of the satellite (pitch, roll, yaw) is modeled assuming a constant angular velocity ( per second). |
| Requests | A request can be acquired with the depointing angle being directed at the center of the request. Max depointing angle of 30 degree. |
| Strips | We assume all requests can be acquired in a single strip. That is, we neglect decomposing requests and managing multiple strips for the acquisition of a request. |
| Acquisition | When acquiring a request, the attitude of the satellite is assumed to be locked in that position through the acquisition duration. It is not rotating through the acquisition. |
| Imaging | All satellite camera specifications are assumed to meet requests’ preferences. |
| Stereo | Stereoscopic imaging must be obtained from two different satellite positions with a convergence angle between and . It can be performed by two different satellites. |
| Duration | For analytical tractability it is assumed that the duration is U[2,8] (in seconds). However in practice, it may be correlated with the total area of the request and satellite swath, agility, etc. For example if a satellite is equipped with pushbroom sensors, then a longer image strip requires a longer acquisition duration. |
| Reach | For the reachability of a request relative to a satellite, we only consider the center of that request. |
| Earth | Perfectly spherical. |
| Criteria | Objective | (Indifference/Preference/veto) Threshold Values |
|---|---|---|
| Area (m2) | max | (0/50/1000) |
| Depointing angle (°) | min | (2/5/40) |
| Sun Elevation (°) | max | (2/5/40) |
| Forecasted cloud coverage (%) | min * | (0/5/15) |
| Customer priority | min ** | (0/1/2) |
| Customer type | min ** | (0/0.5/1) |
| Price (monetary value) | max | (0/1000/10,000) |
| Age of request (days) | max | (0/1/5) |
| Weather uncertainty () | min * | (0/2/5) |
| TOPSIS | ELECTRE-III | Naive | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P1 | P2 | P3 | P4 | P1 | P2 | P3 | P4 | |
| Total #acquisitions | 1 | 3 | 10 | 4 | 13 | 3 | 2 | 0 | 6 | 3 | 6 | 3 |
| Total profit | 0.00 | 0.00 | 77,325 | 22,492 | 0.00 | 0.00 | 18,187 | 0.00 | 0.00 | 0.00 | 42,093 | 14111 |
| Avg. observed | 12.000 | 12.000 | 7.600 | 7.250 | 7.230 | 17.333 | 15.000 | - | 6.000 | 12.000 | 12.833 | 5.333 |
| cloud cover | ||||||||||||
| Total area | 788.04 | 1901.69 | 6119.36 | 3333.36 | 8829.06 | 867.90 | 989.68 | 0.00 | 4572.32 | 1901.69 | 3901.24 | 2385.72 |
| Avg. age | 6.000 | 5.666 | 5.100 | 4.250 | 3.769 | 4.000 | 4.000 | - | 3.166 | 5.666 | 4.833 | 3.666 |
| Avg. angle | 11.598 | 16.473 | 16.271 | 23.570 | 19.637 | 23.558 | 25.917 | - | 14.323 | 16.473 | 18.848 | 16.902 |
| Avg. sun | 31.376 | 30.445 | 24.309 | 28.349 | 26.327 | 28.359 | 22.182 | - | 23.880 | 30.445 | 26.297 | 26.998 |
| elevation | ||||||||||||
| Granularity\Requests | 50 | 100 | 200 | 300 | 400 |
|---|---|---|---|---|---|
| 10 | 0.069 | 0.190 | 0.765 | 1.812 | 1.948 |
| 8 | 0.125 | 0.298 | 1.275 | 2.103 | 2.597 |
| 6 | 0.164 | 0.699 | 2.162 | 3.328 | 7.249 |
| 4 | 0.203 | 0.518 | 5.046 | 7.489 | 21.802 |
| 2 | 0.581 | 3.574 | 20.193 | 38.302 | 62.192 |
| Criteria | Weight | Total | P1 | P2 | P3 | P4 | Avg. Obs. | Total | Avg. | Avg. | Avg. Sun |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Acq. | Cloud Cover | Area | Age | Angle | Elevation | ||||||
| Sun elevation | 0.0 | 17.58 | 12.85 | 1.05 | 3.24 | 0.44 | 11.235 | 10,168.958 | 4.181 | 21.989 | 26.093 |
| 0.1 | 17.62 | 12.88 | 1.06 | 3.22 | 0.46 | 11.288 | 10,200.475 | 4.178 | 22.154 | 26.132 | |
| 0.2 | 17.63 | 12.94 | 1.06 | 3.20 | 0.43 | 11.339 | 10,175.572 | 4.191 | 22.329 | 26.168 | |
| 0.3 | 17.63 | 12.94 | 1.03 | 3.22 | 0.44 | 11.369 | 10,146.893 | 4.193 | 22.418 | 26.198 | |
| 0.4 | 17.67 | 12.92 | 1.08 | 3.24 | 0.43 | 11.368 | 10,114.599 | 4.196 | 22.617 | 26.236 | |
| 0.5 | 17.69 | 12.93 | 1.05 | 3.29 | 0.42 | 11.406 | 10,025.724 | 4.196 | 22.839 | 26.281 | |
| 0.6 | 17.69 | 12.89 | 1.06 | 3.31 | 0.43 | 11.534 | 9917.002 | 4.204 | 23.067 | 26.314 | |
| 0.7 | 17.71 | 12.83 | 1.05 | 3.41 | 0.42 | 11.707 | 9806.103 | 4.210 | 23.309 | 26.357 | |
| 0.8 | 17.72 | 12.84 | 1.01 | 3.45 | 0.42 | 11.845 | 9677.122 | 4.253 | 23.455 | 26.396 | |
| 0.9 | 17.72 | 12.80 | 1.01 | 3.50 | 0.41 | 11.984 | 9426.883 | 4.296 | 23.681 | 26.435 | |
| 1.0 | 18.76 | 5.67 | 4.40 | 5.06 | 3.63 | 22.732 | 9838.421 | 4.851 | 24.556 | 27.396 | |
| Cloud cover | 0.0 | 17.71 | 12.88 | 1.08 | 3.29 | 0.46 | 12.561 | 10,351.571 | 4.149 | 21.825 | 26.167 |
| 0.1 | 17.62 | 12.88 | 1.06 | 3.22 | 0.46 | 11.288 | 10,200.475 | 4.178 | 22.154 | 26.132 | |
| 0.2 | 17.61 | 12.84 | 1.06 | 3.26 | 0.45 | 10.699 | 10,125.339 | 4.193 | 22.460 | 26.136 | |
| 0.3 | 17.53 | 12.81 | 1.07 | 3.21 | 0.44 | 10.189 | 9960.712 | 4.206 | 22.624 | 26.127 | |
| 0.4 | 17.50 | 12.85 | 1.04 | 3.17 | 0.44 | 9.880 | 9813.908 | 4.230 | 22.884 | 26.100 | |
| 0.5 | 17.46 | 12.90 | 1.04 | 3.08 | 0.44 | 9.580 | 9695.274 | 4.238 | 23.056 | 26.095 | |
| 0.6 | 17.43 | 12.95 | 1.01 | 3.03 | 0.44 | 9.409 | 9543.410 | 4.251 | 23.271 | 26.084 | |
| 0.7 | 17.40 | 12.86 | 0.99 | 3.11 | 0.44 | 9.198 | 9432.141 | 4.287 | 23.529 | 26.072 | |
| 0.8 | 17.35 | 12.81 | 0.96 | 3.16 | 0.42 | 9.059 | 9270.358 | 4.297 | 23.702 | 26.077 | |
| 0.9 | 17.29 | 12.84 | 0.93 | 3.11 | 0.41 | 8.933 | 9096.544 | 4.326 | 23.902 | 26.077 | |
| 1.0 | 17.83 | 4.55 | 4.81 | 4.07 | 4.40 | 7.112 | 9000.864 | 5.014 | 23.585 | 26.108 | |
| Customer type | 0.0 | 17.61 | 12.78 | 1.08 | 3.29 | 0.46 | 11.276 | 10,259.041 | 4.173 | 22.061 | 26.136 |
| 0.1 | 17.62 | 12.88 | 1.06 | 3.22 | 0.46 | 11.288 | 10,200.475 | 4.178 | 22.154 | 26.132 | |
| 0.2 | 17.62 | 12.96 | 1.05 | 3.17 | 0.44 | 11.287 | 10,138.166 | 4.197 | 22.315 | 26.134 | |
| 0.3 | 17.63 | 13.00 | 1.05 | 3.14 | 0.44 | 11.331 | 10,031.583 | 4.190 | 22.545 | 26.135 | |
| 0.4 | 17.65 | 13.12 | 1.04 | 3.08 | 0.41 | 11.384 | 9962.152 | 4.213 | 22.714 | 26.132 | |
| 0.5 | 17.69 | 13.15 | 1.04 | 3.11 | 0.39 | 11.473 | 9901.817 | 4.225 | 22.849 | 26.116 | |
| 0.6 | 17.69 | 13.17 | 1.03 | 3.09 | 0.40 | 11.542 | 9851.040 | 4.234 | 22.939 | 26.111 | |
| 0.7 | 17.70 | 13.17 | 0.96 | 3.17 | 0.40 | 11.649 | 9786.821 | 4.240 | 23.119 | 26.108 | |
| 0.8 | 17.74 | 13.21 | 0.97 | 3.17 | 0.39 | 11.893 | 9715.841 | 4.237 | 23.214 | 26.110 | |
| 0.9 | 17.75 | 13.24 | 0.96 | 3.16 | 0.39 | 11.987 | 9637.950 | 4.237 | 23.280 | 26.123 | |
| 1.0 | 18.54 | 15.29 | 2.14 | 0.86 | 0.25 | 26.986 | 9229.606 | 5.038 | 24.385 | 26.100 |
| Criteria | (q,p,v) | Total | P1 | P2 | P3 | P4 | Avg. Obs. | Total | Avg. | Avg. | Avg. Sun |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Acq. | Cloud Cover | Area | Age | Angle | Elevation | ||||||
| Cloud cover | (0.0,5,15) | 17.62 | 12.90 | 1.04 | 3.21 | 0.47 | 11.273 | 9997.886 | 4.167 | 22.161 | 26.132 |
| (0.5,5,15) | 17.62 | 12.90 | 1.04 | 3.21 | 0.47 | 11.279 | 9997.886 | 4.167 | 22.160 | 26.132 | |
| (1.0,5,15) | 17.62 | 12.90 | 1.04 | 3.21 | 0.47 | 11.275 | 9998.242 | 4.166 | 22.164 | 26.132 | |
| (1.5,5,15) | 17.62 | 12.90 | 1.04 | 3.21 | 0.47 | 11.282 | 9999.406 | 4.167 | 22.164 | 26.135 | |
| (2.0,5,15) | 17.62 | 12.91 | 1.04 | 3.20 | 0.47 | 11.300 | 9999.536 | 4.164 | 22.166 | 26.130 | |
| (2.5,5,15) | 17.63 | 12.92 | 1.04 | 3.20 | 0.47 | 11.329 | 10,002.442 | 4.166 | 22.170 | 26.133 | |
| (3.0,5,15) | 17.63 | 12.92 | 1.04 | 3.20 | 0.47 | 11.332 | 10,008.931 | 4.169 | 22.166 | 26.132 | |
| (3.5,5,15) | 17.63 | 12.92 | 1.04 | 3.20 | 0.47 | 11.340 | 10,004.778 | 4.168 | 22.170 | 26.131 | |
| (4.0,5,15) | 17.63 | 12.93 | 1.03 | 3.20 | 0.47 | 11.351 | 10,006.516 | 4.173 | 22.162 | 26.131 | |
| (4.5,5,15) | 17.63 | 12.93 | 1.03 | 3.20 | 0.47 | 11.366 | 10,006.516 | 4.173 | 22.159 | 26.131 | |
| Cloud cover | (0,0,15) | 17.62 | 12.86 | 1.04 | 3.26 | 0.46 | 11.054 | 9991.244 | 4.168 | 22.197 | 26.135 |
| (0,1.5,15) | 17.62 | 12.86 | 1.04 | 3.25 | 0.47 | 11.078 | 10,004.304 | 4.168 | 22.189 | 26.134 | |
| (0,3.0,15) | 17.62 | 12.89 | 1.04 | 3.22 | 0.47 | 11.202 | 10,008.823 | 4.168 | 22.142 | 26.128 | |
| (0,4.5,15) | 17.62 | 12.90 | 1.04 | 3.21 | 0.47 | 11.265 | 10,001.395 | 4.168 | 22.159 | 26.133 | |
| (0,6.0,15) | 17.63 | 12.92 | 1.04 | 3.20 | 0.47 | 11.346 | 9998.861 | 4.165 | 22.161 | 26.132 | |
| (0,7.5,15) | 17.65 | 12.92 | 1.04 | 3.22 | 0.47 | 11.430 | 10,014.056 | 4.163 | 22.145 | 26.135 | |
| (0,9.0,15) | 17.64 | 12.95 | 1.04 | 3.20 | 0.45 | 11.503 | 10,019.136 | 4.180 | 22.141 | 26.134 | |
| (0,10.5,15) | 17.64 | 12.94 | 1.04 | 3.21 | 0.45 | 11.559 | 10,037.506 | 4.176 | 22.156 | 26.132 | |
| (0,12.0,15) | 17.65 | 12.98 | 1.04 | 3.18 | 0.45 | 11.700 | 10,046.744 | 4.172 | 22.146 | 26.134 | |
| (0,13.5,15) | 17.65 | 13.02 | 1.04 | 3.15 | 0.44 | 11.791 | 10,063.827 | 4.174 | 22.154 | 26.135 | |
| Cloud cover | (0,5,7.50) | 17.38 | 12.73 | 1.04 | 3.19 | 0.42 | 9.597 | 9743.103 | 4.212 | 22.313 | 26.114 |
| (0,5,9.75) | 17.49 | 12.76 | 1.05 | 3.24 | 0.44 | 10.109 | 9805.737 | 4.197 | 22.324 | 26.129 | |
| (0,5,12.00) | 17.55 | 12.80 | 1.05 | 3.25 | 0.45 | 10.564 | 9868.942 | 4.190 | 22.218 | 26.141 | |
| (0,5,14.25) | 17.62 | 12.85 | 1.05 | 3.26 | 0.46 | 11.132 | 9980.082 | 4.169 | 22.196 | 26.130 | |
| (0,5,16.50) | 17.65 | 12.95 | 1.05 | 3.17 | 0.48 | 11.577 | 10,053.108 | 4.170 | 22.139 | 26.138 | |
| (0,5,18.75) | 17.72 | 13.04 | 1.06 | 3.19 | 0.43 | 12.114 | 10,063.496 | 4.167 | 22.095 | 26.164 | |
| (0,5,21.00) | 17.75 | 13.04 | 1.06 | 3.22 | 0.43 | 12.494 | 10,125.880 | 4.168 | 21.937 | 26.166 | |
| (0,5,23.25) | 17.78 | 13.15 | 1.01 | 3.20 | 0.42 | 13.007 | 10,099.129 | 4.149 | 21.896 | 26.169 | |
| (0,5,25.50) | 17.82 | 13.24 | 1.00 | 3.21 | 0.37 | 13.535 | 10,119.845 | 4.138 | 21.923 | 26.172 | |
| (0,5,27.75) | 17.85 | 13.23 | 1.02 | 3.26 | 0.34 | 13.842 | 10,118.423 | 4.143 | 21.910 | 26.191 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasegaard, A.E.; Picard, M.; Hennart, F.; Nielsen, P.; Saha, S. Multi Criteria Decision Making for the Multi-Satellite Image Acquisition Scheduling Problem. Sensors 2020, 20, 1242. https://doi.org/10.3390/s20051242
Vasegaard AE, Picard M, Hennart F, Nielsen P, Saha S. Multi Criteria Decision Making for the Multi-Satellite Image Acquisition Scheduling Problem. Sensors. 2020; 20(5):1242. https://doi.org/10.3390/s20051242
Chicago/Turabian StyleVasegaard, Alex Elkjær, Mathieu Picard, Florent Hennart, Peter Nielsen, and Subrata Saha. 2020. "Multi Criteria Decision Making for the Multi-Satellite Image Acquisition Scheduling Problem" Sensors 20, no. 5: 1242. https://doi.org/10.3390/s20051242
APA StyleVasegaard, A. E., Picard, M., Hennart, F., Nielsen, P., & Saha, S. (2020). Multi Criteria Decision Making for the Multi-Satellite Image Acquisition Scheduling Problem. Sensors, 20(5), 1242. https://doi.org/10.3390/s20051242






