1. Introduction
As in most endurance sports, the goal of triathlon races is to reach the finish line as quickly as possible. In addition to optimizing training, rest, and nutrition, triathletes can greatly improve their performance by working on a streamlined posture. A huge advantage can also be gained by cycling closely behind another competitor during a race. This other competitor then acts as a wind shield. This technique is called drafting, stayering, or slipstreaming. Recent studies suggest using this technique by riding in a peloton can reduce aerodynamic drag by 90–95% compared to that of an isolated cyclist [
1].
The International Triathlon Union (ITU) makes a distinction between draft-legal and draft-illegal races [
2]. Most long or middle distance races and many standard or sprint distance races fall under the latter category, where it is forbidden to draft behind another athlete or a motor vehicle, i.e., to enter the bicycle or vehicle drafting zone for an extended period of time. For standard and shorter distances the bicycle draft zone is 10 m long measured from the leading edge of the front wheel. An athlete is allowed to enter another athlete’s draft zone but must be progressing through that zone. A maximum of 20 s is allowed to pass through another athlete’s drafting zone. The official regulations regarding middle and long distance events are slightly different, enforcing 12 m distance and 25 s maximal duration. Note that some race organizers enforce even other distances or durations. The experiments in this paper, always assume a 10 m drafting zone and 20 s maximal duration, unless stated otherwise.
Today, drafting regulations are monitored by referees driving a motorbike (
Figure 1). However, monitoring these rules in practice is difficult, hence unpunished drafting violations do occur frequently. In a typical triathlon race, there are not enough referees to check all triathletes all the time. In addition, the referees’ decisions are still subjective as they can only roughly estimate the distances between the bicycles. Furthermore, athletes can typically hear a motorbike approaching them, so they can adjust their behavior momentarily.
The lack of reliable detection of illegal drafting can lead to arbitrariness in the best case, and possibly even to corruption, such as favoring some individuals in the worst case. A drafting detection system based on video taken from a camera mounted under the saddle of a bicycle, equipped with computer vision techniques can offer a solution to these problems. Moreover, when an athlete challenges a referee’s decision, a video based system and its recorded distances can provide supportive data. In summary, by continuously checking compliance with the drafting rules, a camera based detection system will lead to less drafting and consequently ensure fairer triathlon or duathlon races.
In a previous implementation of a drafting detection system, GPS and Web Services are used, yielding an average accuracy of
m for the absolute position of each athlete [
3]. The error can increase in cases of urban canyons and tree lines, because of the limitations of the GPS device, which is a significant deviation, given the drafting distance limit. Two more accessible solutions for a drafting detection system are: Light Detection And Ranging (LiDAR) and RAdio Detection And Ranging (RADAR). The former is a very accurate but expensive and non-compact technique. The latter is more compact and cheaper. However, for object detection with a RADAR system, a sufficient number of reflection points are required at known positions, making this solution potentially less reliable.
Monocular vision based detection and distance estimation algorithms have been demonstrated to successfully estimate the distance between cars in literature for traffic applications. These techniques typically combine object detection networks with geometric techniques but also employ extra information to accurately estimate the distances. These features include the presence of lane markings [
4], or the specific geometry of cars [
5]. However, in the application of detecting bicycles in triathlon races, neither of these additional features can be used.
In this paper, we present a video based solution that automates the task of assessing potential drafting violations and extend the work of Van den Bossche et al. [
6]. A single camera which looks backwards is mounted under the saddle of the bicycle. We do not consider a stereo camera set-up with two or more cameras on one bicycle because this would mitigate the benefit of compactness, and add to the cost.
To be used in a triathlon race context, the mechanical robustness of the system is very important, because road conditions may often cause problems. It must be able to deal with vibrations in the image due to rough road surfaces, such as cobble stones or speed bumps. Furthermore, installing the system on a race bike should be a simple and straightforward procedure. In the proposed system, the mounting of the camera only involves the camera height and the tilt angle, which are easy to control.
The focal point of this paper is the detection of drafting by the camera, whose operation can be summarized as follows. Bicycles are detected in the individual video images with a Convolutional Neural Network (CNN) architecture. The bicycle closest behind the camera is tracked and the distance to the bicycle with the camera is estimated from the apparent height and position of the bicycle. The distance is monitored over an extended time period, which enables an estimate of the probability that a drafting violation (e.g., longer than 20 s in the draft zone) has occurred.
The main contributions of this paper can be summarized as follows:
We trained, applied, and analyzed the performance of real-time CNN-based object detector, specifically for detecting race, time trial, and triathlon bicycles.
We describe two methods for estimating the distance from the camera to the cyclists behind. We performed sensitivity analysis and investigated the systematic errors that can occur which are caused by making simplifying assumptions. The accuracy of the distance estimators is also verified in a realistic scenario using a Light Detection And Ranging (LiDAR) scanner.
We developed an efficient method which determines the probability of violating the drafting rule, based on successive distance estimations and a model of the measurement error. The behavior of this method is rigorously tested in a realistic scenario and through the use of simulations.
2. Drafting Detection
In this section, we discuss all processing steps in our proposed approach. Note that (as a preprocessing step), we assume the camera is intrinsically calibrated and the lens distortion was removed, e.g., with the method of Zhang [
7].
2.1. Bicycle Detection
The first step in the drafting detection system is to detect cyclists in real-time. The aim is to have a robust, real-time detection at least up to 20 m from the camera. To achieve this, a Tiny YOLOv3 (You Only Look Once, version 3) [
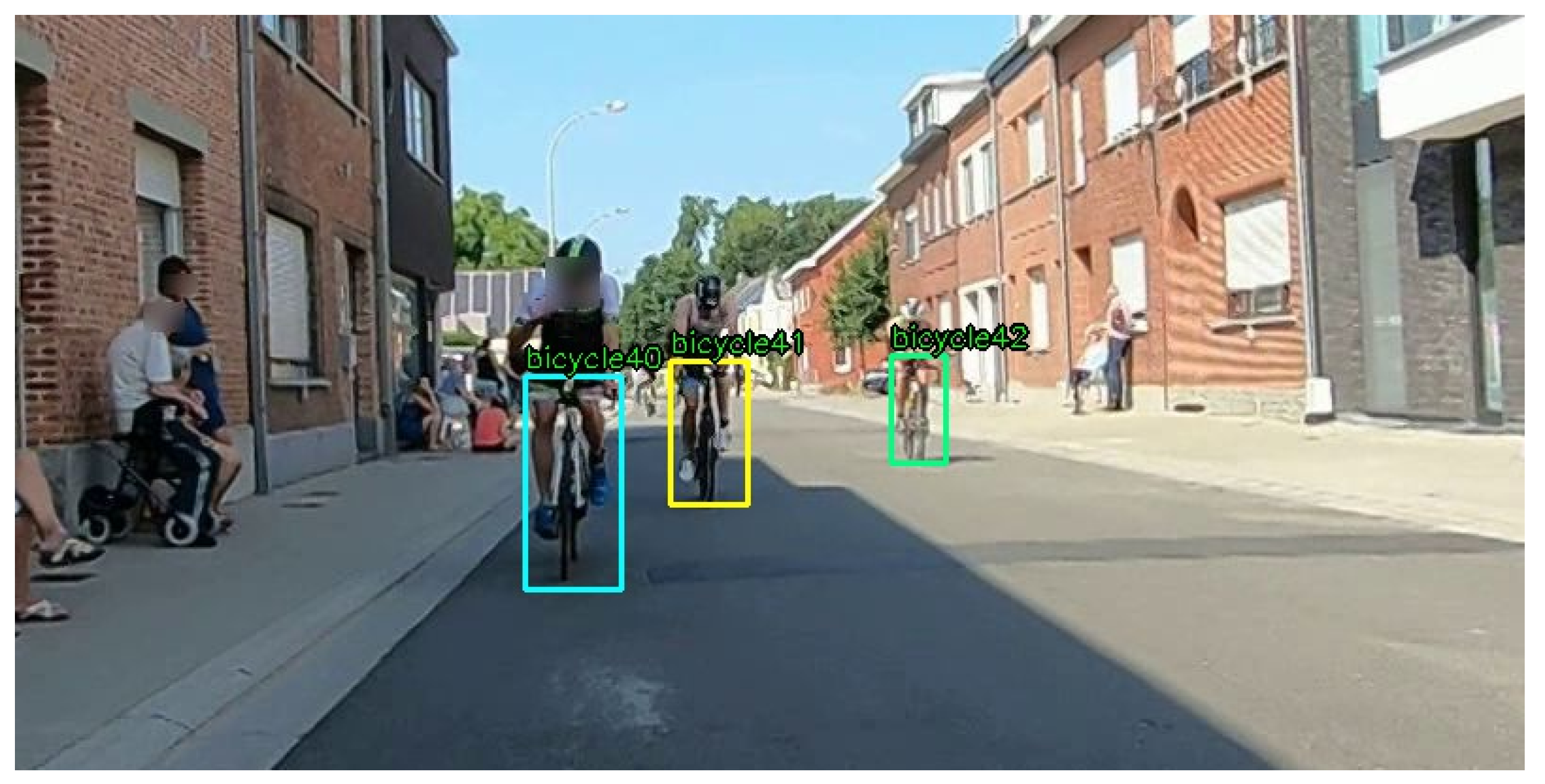
8] network has been trained for specifically detecting triathlon bikes, using 4 different triathlon race recordings of about one hour long each. Our training set for the object detector is very diverse, also including lighting changes (e.g., in tunnels) and poor weather conditions, such as rain. The detector was trained with approximately 60,000 manually annotated ground truth bounding boxes, which overlay the bicycle from the ground (bottom of the front wheel) to the handlebars. An example frame with manually annotated boxes is shown in
Figure 2. This renders the size and position of the bounding boxes useful for distance estimation, as will be shown in
Section 2.3. The training versus test set ratio was 80 to 20%.
The tiny YOLOv3 network obtained an Average Precision (AP) of 77.19% on our dataset, by comparing the detections with manually annotated ground truth bounding boxes. On our hardware (1080p input video and desktop PC with a GeForce GTX 1060 GPU), the detection speed on the test set is 42.57 fps. We note that other object detectors, such as YOLOv3 [
8], Faster RCNN (Region Convolutional Neural Network) [
9], and Mask RCNN [
10], also have the potential to yield high detection rates but are slower, taking 24.58, 7.85, and 6.64 fps, respectively, on the same hardware set-up.
The Single Shot multibox Detector (SSD) [
11] does provide an interesting alternative. It is based on the MobileNet CNN architecture, was specifically designed for constrained devices (e.g., smart phones), and yields a similar processing speed as Tiny YOLOv3 (42.25 fps). Depending on the final application, and whether the processing needs to be executed on the device (i.e., attached to the bicycle) or off-line after the race, a more heavyweight but also more accurate and slower network architecture could be used.
The performance of a re-trained version of this network remains to be investigated in future work. Note that the AP of the detector is further improved by applying object tracking on the detected bicycles, which is discussed in the following subsection.
2.2. Bicycle Tracking
Because the regulations also incorporate a maximal drafting duration, the detected bicycles need to be tracked as long as they are visible throughout the video. We are only interested in tracking a bicycle as long as it stays (visible) behind the camera bicycle. In addition, note that, in order to be robustly detected by Tiny YOLOv3 and tracked, the bicycle should be reasonable close. In our experiments, Tiny YOLOv3 was able to accurately detect bicycles which were further than 20 m away, which is still well above the typical drafting limit.
In our method, the bounding box of the bicycle closest to the camera is not only detected but also tracked and its trajectory is recorded. This results in reliable samples to estimate the distance, which will be discussed in the next section. We note that other potential cyclists (riding further from the camera) are discarded in our current method. To be used in a realistic application, the system should be able to detect multiple cyclists behind. However, due to the increased complexity of the track management of such a system, we have not yet investigated this in our current proposed method.
Tracking increases the robustness of the draft detection considerably. The detection miss rate is lowered by using the predicted position of the tracker in case the detector misses a detection for a certain frame. If a bicycle is detected in the previous frame but not in the current frame, its current position can still be estimated from a tracker’s prediction step. Thus, the effect of missed detections (False Negatives) is mitigated and bicycles in the scene can be better monitored continuously. More specifically, bicycles are linked when they overlap in successive frames. This strategy is simple but accurate (as will be demonstrated further in this subsection), because of the high frame rate and low relative speeds. When no overlapping bounding box is detected at a given point in time, the tracker uses the last detected bounding box as input and then tries to locate it in the current frame. When a new bounding box is detected, a new track is initialized. In this way, the same bicycle can be uniquely identified by its ‘bicycle id’.
In order to make an informed decision with regard to the object tracker, eight object trackers from the literature are benchmarked on our dataset. The success AUC is defined as the Area Under the Curve (AUC) of the success plot, which demonstrates the percentage of the number of frames where the Intersection Over Union (IOU) of the estimated bounding box and the ground truth bounding box is larger than the considered threshold. We evaluated state-of-the-art trackers according to detection speed and success rate as shown in
Figure 3: CSRT (Channel and Spatial Reliability Tracker) [
12], KCF (Kernelized Correlation Filters, Copyright (c) 2012, Piotr Dollar All rights reserved; Copyright (c) 2014, Tomáš Vojíř.) [
13], Boosting [
14], MIL (Multiple Instance Learning) [
15], TLD (Tracking, Learning, and Detection) [
16], Medianflow [
17], MOSSE (Minimum Output Sum of Squared Error) [
18], and DSST (Discriminative Scale Space Tracking) [
19].
According to this benchmark, the Discriminative Scale Space Tracking (DSST) object tracker is the most appropriate solution. It clearly stands out with respect to the AUC of the success plot (0.73 versus 0.44 for the second highest scoring method) and has the third highest processing speed (still well above real time). The DSST tracker builds on the MOSSE tracker (described in Bolme et al. [
18]) and extends it with a multi-scale pyramid to estimate the scale of an object. Note that rotation invariance is less important in our application, since the orientation of the cyclist only typically changes in a road bend.
The Tiny YOLOv3 object detector is tested in combination with the DSST object tracker with regard to improvement in the detection rate. An initial AP of 77.19% for Tiny YOLOv3 was obtained, but, after applying object tracking, an increase of the recall yields an average precision of 88.27% for the bounding boxes. The success plot of this combination is shown in
Figure 4.
Note that this combination is notably very reliable when the IoU threshold is allowed to be low. However, in some cases, a higher IoU threshold is preferred, e.g., if the height of the bounding box needs to be very accurate.
Figure 3 suggests that relying more on the DSST tracker (as opposed to using it mainly for missed detections) could increase the combined detection/tracking performance further. Other configurations could be investigated in future work.
2.3. Distance Estimation
In this section, we discuss two alternatives to estimate the distance between the camera bicycle and the bicycle behind: the Wheel Position-Based method (WPm) and the Handlebar Height-Based method (HHm). Each method has a benefit with respect to the other, which is discussed in detail further in this section. For both methods, we assume a flat road and known geometry of the bicycles, as shown in
Figure 5. At the end of the section, we perform a sensitivity analysis w.r.t. potential violations of the assumptions made and describe systematic errors related to these assumptions.
In both methods, we derive x from the position of the bounding box (with bottom at and height ) of a detected cyclist. The camera tilt angle , the focal length f and the camera height have known values. The camera is mounted at the rear of the saddle and, according to the rules the drafting distance, d is calculated from front wheel to front wheel. Thus, we must add to x to obtain the distance between the two front wheels.
To distinguish between the two models, we will denote the distances estimated by the two methods as and , respectively. In the ideal case, we should have .
2.3.1. Wheel Position-Based Method (WPm)
The first method estimates the location of the bottom of the wheel on the ground plane, starting from a known tilt angle
and camera height
(
Figure 5a). Note that the WPm is closely related to the camera-pose-based trigonometric vehicle distance estimation method described in Reference [
22]. Let
denote the angle between the bottom of the bounding box and the camera center line; thus,
where
is the vertical distance from the image center to the bottom of the bounding box in the image, and
f is the focal length of the camera. The distance
thus equals
The advantage of this method is that is independent of the height of the bicycle behind, which typically can only be estimated. A possible disadvantage of this method is the strong dependence of Equation (4) on the tilt angle of the camera, which will be demonstrated in the sensitivity analysis in
Section 2.3.3.
2.3.2. Handlebar Height-Based Method (HHm)
The second distance estimation method is based on the height of the handlebars above the ground, which is obtained from the height of the detected and tracked bounding box. The expression for the distance of to the object w.r.t. the height of the bounding box is complex and depends on more parameters than the WPm (see
Appendix A). However, this expression can be simplified if we assume that
. From Equation (4),
where
is the height of the bounding box. For realistic recordings a small tilt angle is expected and
when the detected object is far enough from the camera. From
Figure 5, it can be deduced that
. The vertical FOV of commercial cameras is rarely larger than 90°; thus,
when the detected object is entirely visible. Hence, for a small tilt angle
,
. In a typical set-up,
h is more than ten times smaller than the drafting distance limit, so
for the most crucial situations. Thus,
The fact that the tilt angle
can be ignored is a significant advantage of this method. The initial tilt angle must not be measured when setting up the system. Furthermore, due to vibrations, the camera position might change during the recording. Finally, there are situations where the road itself is not perfectly flat, as shown in
Figure 6, which influences the distance estimation in a similar fashion to
that of camera rotation. An in-depth sensitivity analysis is performed in the next section.
2.3.3. Sensitivity Analysis
The parameters in the distance calculation formulae Equations (4)–(6) either depend on the scene geometry ( and ), the intrinsic camera properties (f) or the position or height of the detected and tracked object in the image ( and ). The bicycle’s speed is not included in the distance or probability calculations, so it does not directly contribute the error. However, it might contribute indirectly, e.g., by causing more jitter on an uneven road surface, or when the relative speed between the two bicycles is high, which might (albeit slightly) influence the performance of our tracker.
In practice, all parameters can be prone to errors, each having different potential causes. Hence, we performed sensitivity analysis of
and
w.r.t. these parameters, which is discussed below. The full analysis is performed in
Appendix B. An overview of the results for a small tilt angle
is demonstrated in
Table 1. For example, when there is a small error in the measurements of the height
, the relative error on the distance calculated by the WPm satisfies
.
The sensitivity analysis demonstrates that measured errors w.r.t. camera height , the focal length f, the bottom position bounding box or the height of the bounding box are all (approximately) proportionally propagated to the estimated distances and , i.e., an error of 5% on one of these parameters yields a 5% error on the estimated distance. This also indicates that the absolute error increases linearly with the distance to the cyclist behind.
The partial derivative for
, estimated by the HHm, w.r.t.
is relatively insensitive to tilt angle estimation errors when
(see
Figure 5) is small. This justifies the relaxation from Equation (
5) to Equation (
6). For the WPm, however, even a small estimation error for
can potentially lead to a significant error in the estimation of
, notably when
is small.
If the camera cannot be very tightly fixed in its original position, the tilt angle is the most error-prone parameter. In this scenario, this angle can change (undesirably) throughout a recording, e.g., due to vibrations as demonstrated in
Figure 7. Thus, when using the WPm, this parameter needs to be updated at runtime. This can be realized by optical flow analysis or by utilizing information from an accelerometer and/or a gyroscope.
2.3.4. Systematic Errors
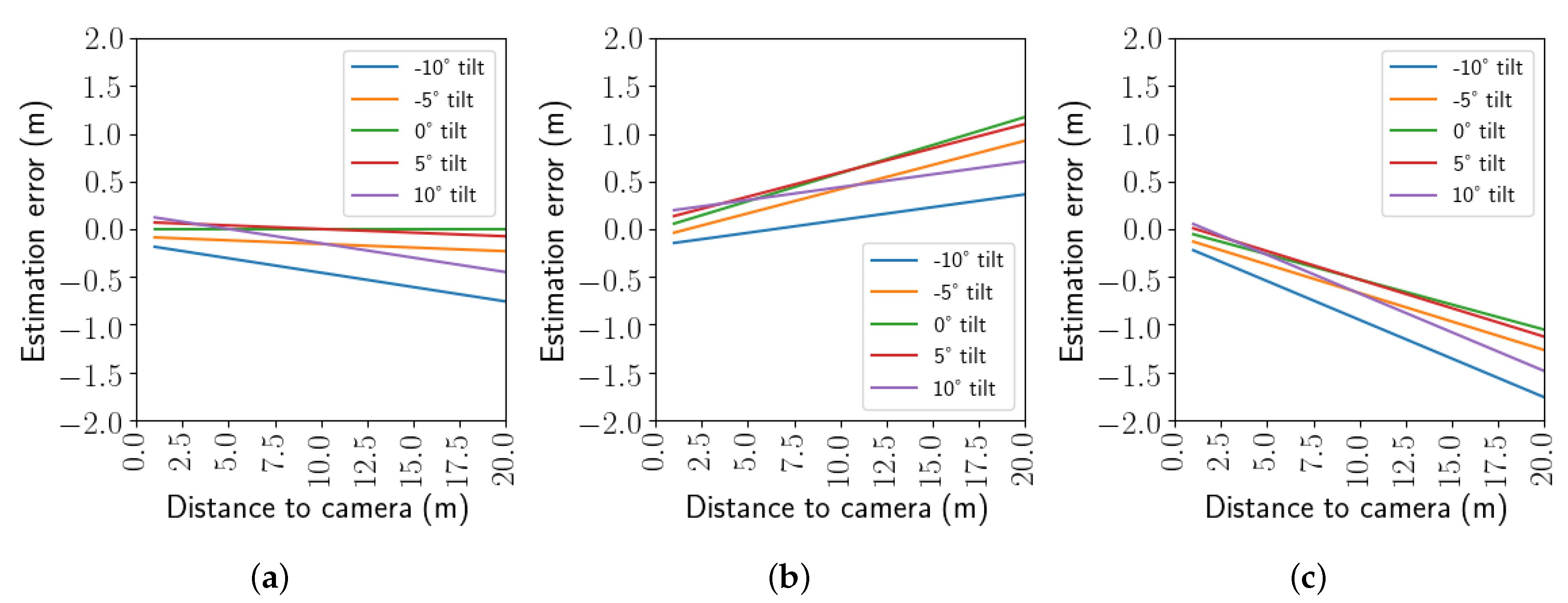
The proposed HHm makes two assumptions; and °. In this section, the effect of the systematic error introduced by these simplifications is investigated.
In practice, there can be a height difference between and of the order of a few centimeters. This issue could be resolved, e.g., by adding a distinctive marker on all bicycles at a predetermined height, which can be detected by the software, and internally adjusting the value of in the detection step accordingly.
The tilt angle
typically differs from 0° when the camera position is either redirected during set-up, or when the angle changes due to vibrations (
Figure 7) during the bike ride. A typical tilted camera has a magnitude of
of up to 10°.
The difference between the exact solution (see
Appendix A, Equation (
A3)) and the approximated solution in Equation (
6) for
is analyzed and demonstrated in
Figure 8 for different realistic values of
,
and
.
The systematic errors vary linearly w.r.t. the distance from the camera. A camera tilt (°) or contributes to an underestimation of the estimated distance, notably for objects further away from the camera. When , the true distance is similarly overestimated.
The WPm is not dependent on
, so it is expected this method performs better when the height of the handlebar of the cyclist behind cannot be accurately estimated. In
Section 3, the performance of both methods is evaluated through simulations and in a realistic scenario.
2.4. Drafting Probability
In the previous sections, methods for determining the distance between two bicycles at a given point in time were explored, based on object detection and tracking. Since the drafting rule also has a temporal component, it is necessary to robustly combine multiple measurements of the distance over a given time period. Given a set of measurements and a certain measurement error probability density function (pdf), our end result is an estimated probability that the cyclist behind violated the drafting rule.
2.4.1. Theoretical Probability Determination
The probability of drafting for a given period of time is closely related to the known theory of ‘success runs’ [
23]. However, the main difference in this application is that the probability of ‘success’ depends on the measured distance, which changes between measurements.
Let be a binary vector of length n. When the distance between the two bicycles d is smaller than the drafting distance limit (e.g., 10 m) at t, ; otherwise, .
We assume that the likelihood function of the real distance
d between two bicycles can be modeled as a distance-dependent normal distribution, with standard deviation
at
. We assume here that the measured distance
is close to the real distance
d. Thus,
. Let
be a distance measurement at time instance
t, with fixed offset
(see
Figure 5). The probability that the bicycle behind is actually closer than
at one time instance can thus be expressed as
Similarly, the probability that the bicycle is not closer than is .
To compute the probability of
given a set of measurements
, we define the index sets
and
. We also assume that all measurements are independent and that the probability that
occurs, given successive measurements
, can be computed as
is defined as a ‘valid drafting pattern’ (
) if it contains at least one instance of at least
successive samples with value 1, where
is the sampling rate and
the maximal time an athlete is allowed to stay in the drafting zone (e.g., 20 s). Since all patterns are mutually exclusive, the probability of drafting over a given period of time (
n samples) is thus the sum of the probabilities of the occurrence of all valid drafting patterns. Let
be the event of a drafting rule violation for
. The probability that such an event has occurred, given distance measurements
is
Note that
always increases over time, i.e., if
, then
. Since
and
, it is easy to show that
Consequently, since
,
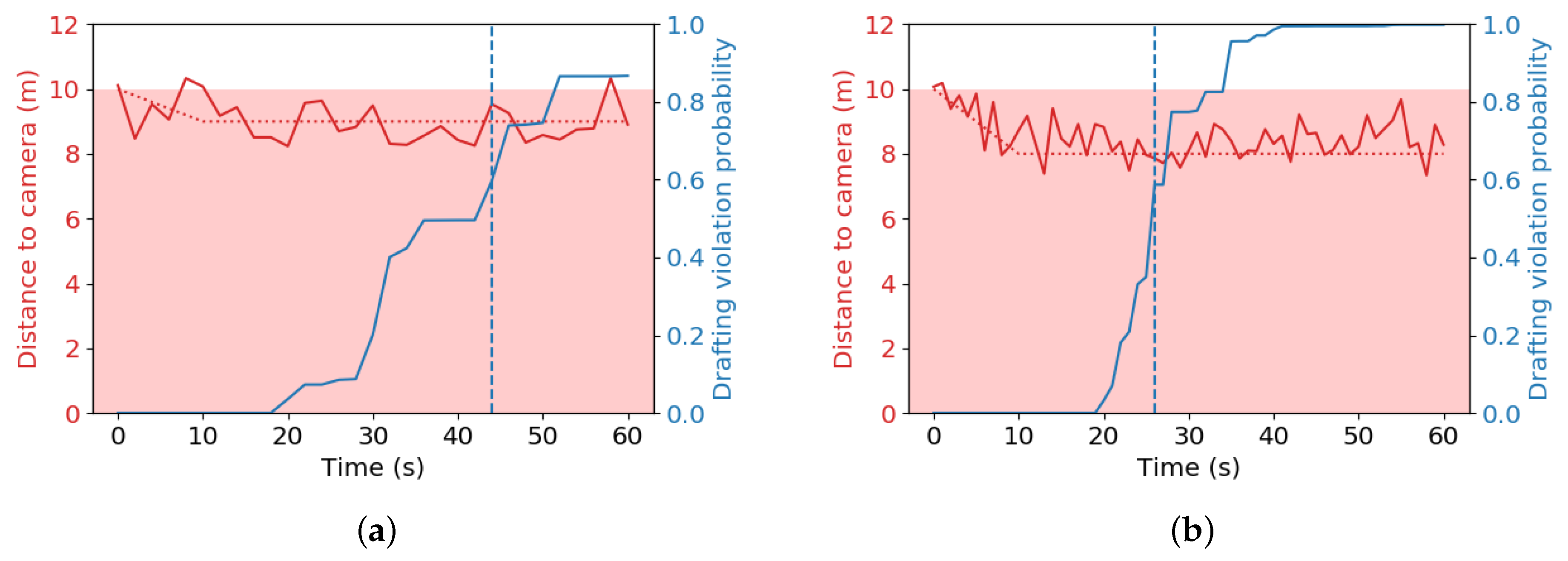
In our application, the drafting violation probability should approach 1 as soon as the cyclist behind spends longer than the drafting time limit in the drafting zone. On the other hand, when a cyclist stays outside of the drafting zone, or is only inside for less than , the probability should stay close to 0. Three factors determine how well follows these considerations:
2.4.2. Efficient Probability Calculation
A naive method of calculating the drafting probability would consist of an exhaustive summation of all probabilities for any given pattern (time complexity
), which in turn require
n multiplications of individual likelihoods, each calculated from Equation (
7).
However, it is also possible to calculate the drafting probability with time complexity
and constant space complexity by re-using previous results. Assume that all earlier probabilities of drafting
for
are known. The updated probability of drafting is now the sum of the probability that drafting had already occurred and the probability that it is the first time the drafting limit has been exceeded for longer than
k successive samples. The drafting limit can only be exceeded for the first time if the last
k samples of
(i.e.,
) are 1, the one before that is equal to 0 and no other valid drafting patterns can be found in
. Hence, the probabilities can be calculated by the following recursive expression:
This equation demonstrates that only the last
k measured distances (or probabilities of momentary drafting with Equation (
7)) and the last
calculated drafting rule violation probabilities need to be kept in memory and a constant number of calculations is done for every new sample.
4. Conclusions
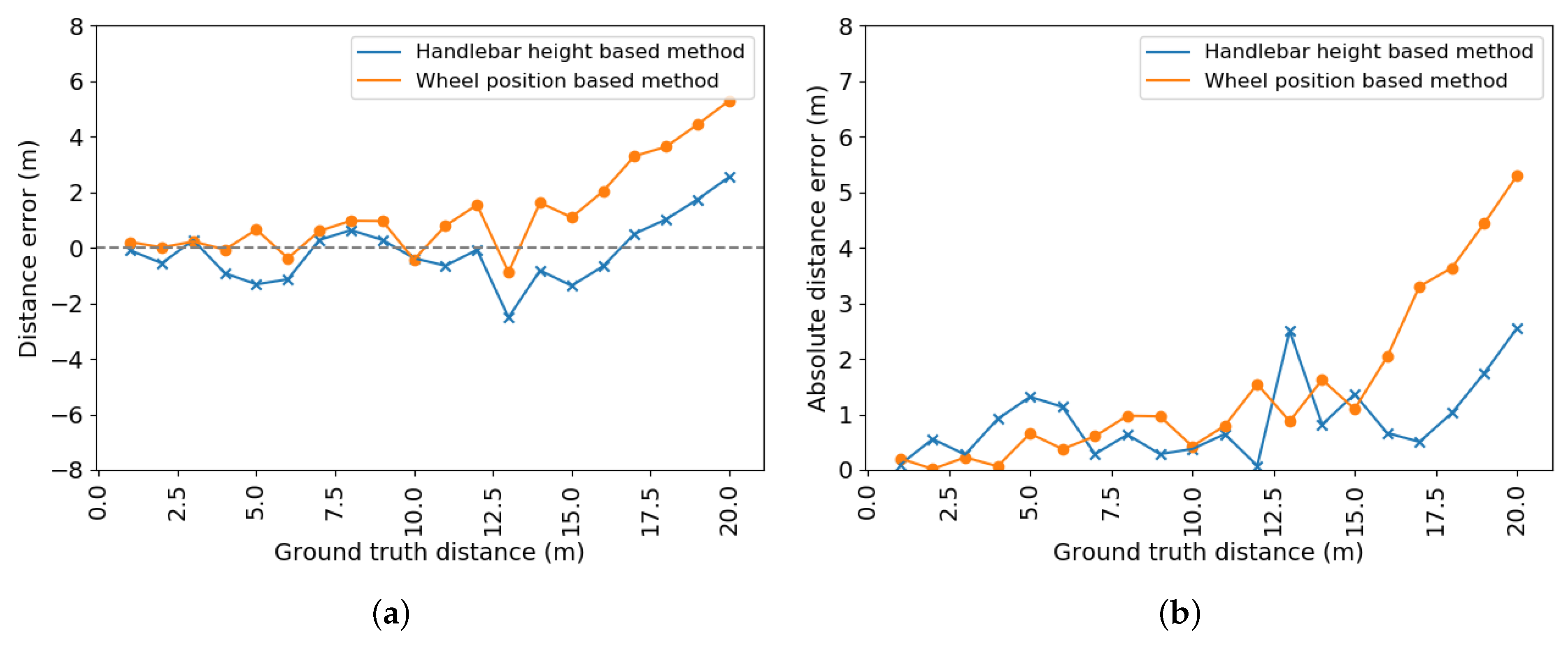
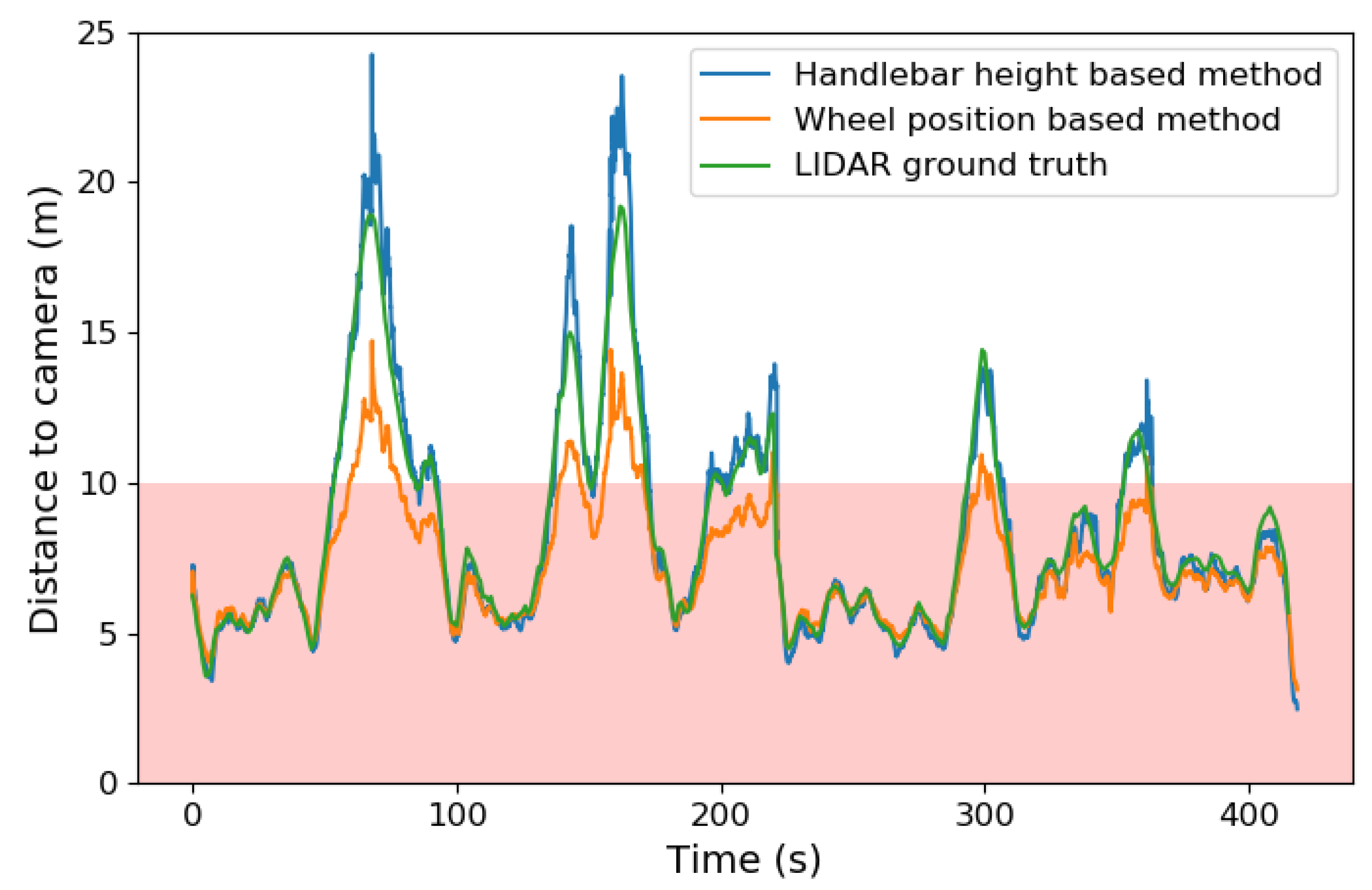
In this paper, a proof of concept for a drafting detection system in triathlon was proposed. The system is composed of four important building blocks: object detection, object tracking, distance determination, and drafting violation probability estimation. Detecting and then following the closest cyclist through the different scenes ensures a continuous monitoring over time. An average precision of % for detected bicycles was obtained on the test set after tracking. The Handlebar Height-Based method (HHm) method appears to be the most accurate one for distance determination, as the Wheel Position-Based method (WPm) is too sensitive to potential tilt angle changes or poor tilt angle estimation. In the static situation test, the average absolute error over all ground truth distances was and m for the HHm and the WPm, respectively. Furthermore, a dynamic test was conducted with LiDAR distances as the ground truth. Over all ground truth distances, this experiment shows that the HHm has an average absolute error of m. For the WPm, this error is m.
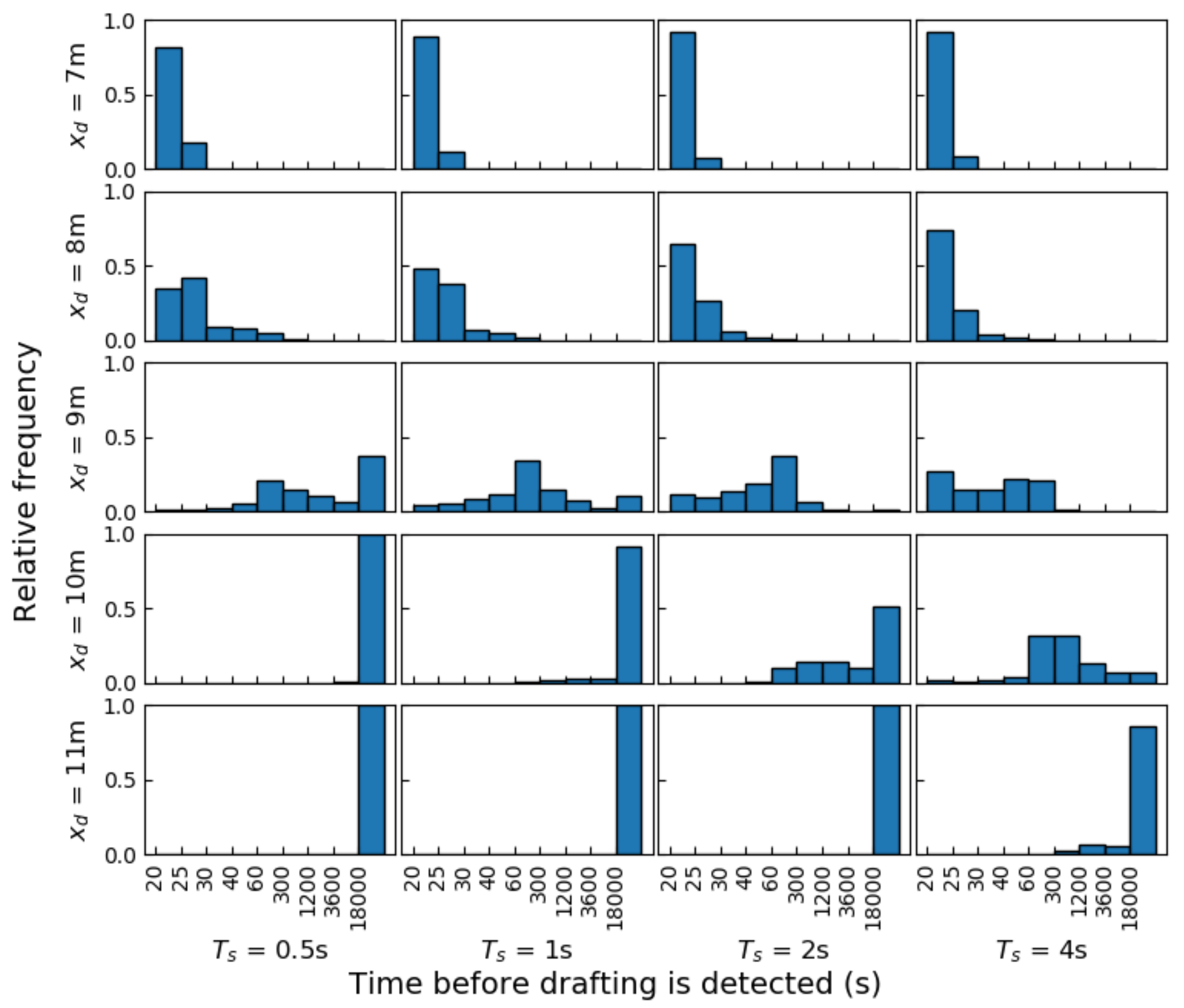
In addition, a drafting violation probability estimation was developed, which checks how likely it is that the drafting rule has been broken over a period of time. When using an appropriate sampling period of at most or 2 s, simulations demonstrate that the calculated probabilities are very useful to detect drafting at 8 m or below. The time before drafting is detected just below the drafting limit is highly variable, however. Nevertheless, with these settings, no unjustified penalties are awarded within a realistic time window. The proposed system shows promise to enter a triathlon and duathlon in order to obtain fairer races when further developed.