Joint Adaptive Sampling Interval and Power Allocation for Maneuvering Target Tracking in a Multiple Opportunistic Array Radar System
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Main Contributions and Innovations
- (1)
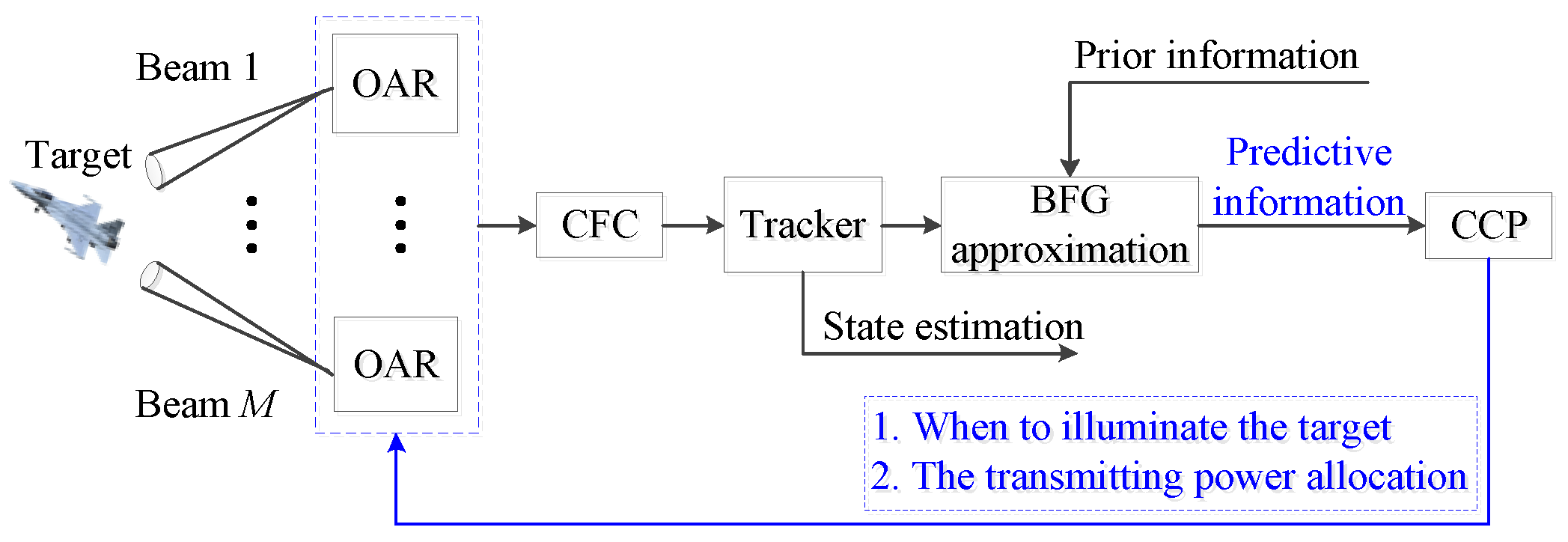
- The BFG approximation is employed so as to allocate the radar resource conveniently. Due to the diversities of motion states of maneuvering targets, it is difficult to predict the target state, and the radar resource allocation has no referenced criterion at the next sampling instant. Guaranteeing that the state vectors have the same mean and covariance under different models, the BFG approximation is introduced to replace the multimodal prior target PDF at each time step. The target state can be predicted easily by a single motion equation, and then accomplish the resource pre-allocation.
- (2)
- A joint adaptive sampling interval and power allocation scheme is presented. The prior CRLB-like as a measurement criteria is compared with the upper boundary of the given tracking error threshold to determine the next optimal sampling interval. The tracking BCRLB-like is computed for power allocation among the distributed radars. The diagonal elements of BCRLB-like provide a referenced boundary on the variances of the estimation of the target’s hybrid state.
- (3)
- The CCP is brought in to handle the uncertainty of target information in a resource management model. The target RCS is regarded as a random variable. The CCP balances the radar resource and the tracking performance by adjusting the confidence level. If the target environment is simple or the tracking performance requirement is low, the confidence level could be lowered appropriately to save more resources for other tasks.
2. System Model
2.1. Signal Model
2.2. Target Motion Model
2.2.1. Constant Velocity Motion Model
2.2.2. Constant Acceleration Motion Model
2.2.3. Coordinated Turn Motion Model
2.3. Measurement Model
3. Resource Management Model for Maneuvering Target Tracking
3.1. Best-Fitting Gaussian Approximation
3.2. Prior Information JP(ξk)
3.3. Data Information JD(ξk)
3.4. Predictive Bayesian Cramér-Rao lower bound (BCRLB-like)
3.5. Modeling of Chance-Constraint Programming (CCP)
4. Resource Allocation Processing Procedure
4.1. Basic of the Technique
4.2. Stochastic Simulation
4.3. Hybrid Intelligent Optimization Algorithm
4.4. Target State Estimation
4.4.1. Process of BFG-UKF
- 1)
- Let Tk+1 = Tk+1+ΔT, and through the BFG approximation in Section 3.1, determine the mode probability pk+1(i), and then calculate Φk+1 and Qp,k+1 (the detailed calculation process is given in Section 3.1).
- 2)
- Predict the prior CRLB-like FP(Tk+1) according to Equations (40) and (45).
- 3)
- If FP(Tk+1) > η2,k+1 (the upper bound of the error threshold), let Tk+1,opt = Tk+1 and go to Step 9. Otherwise, go to Step 1).
4.4.2. Process of Interacting Multiple Model Unscented Kalman Filter (IMM-UKF)
5. Simulation Results and Analysis
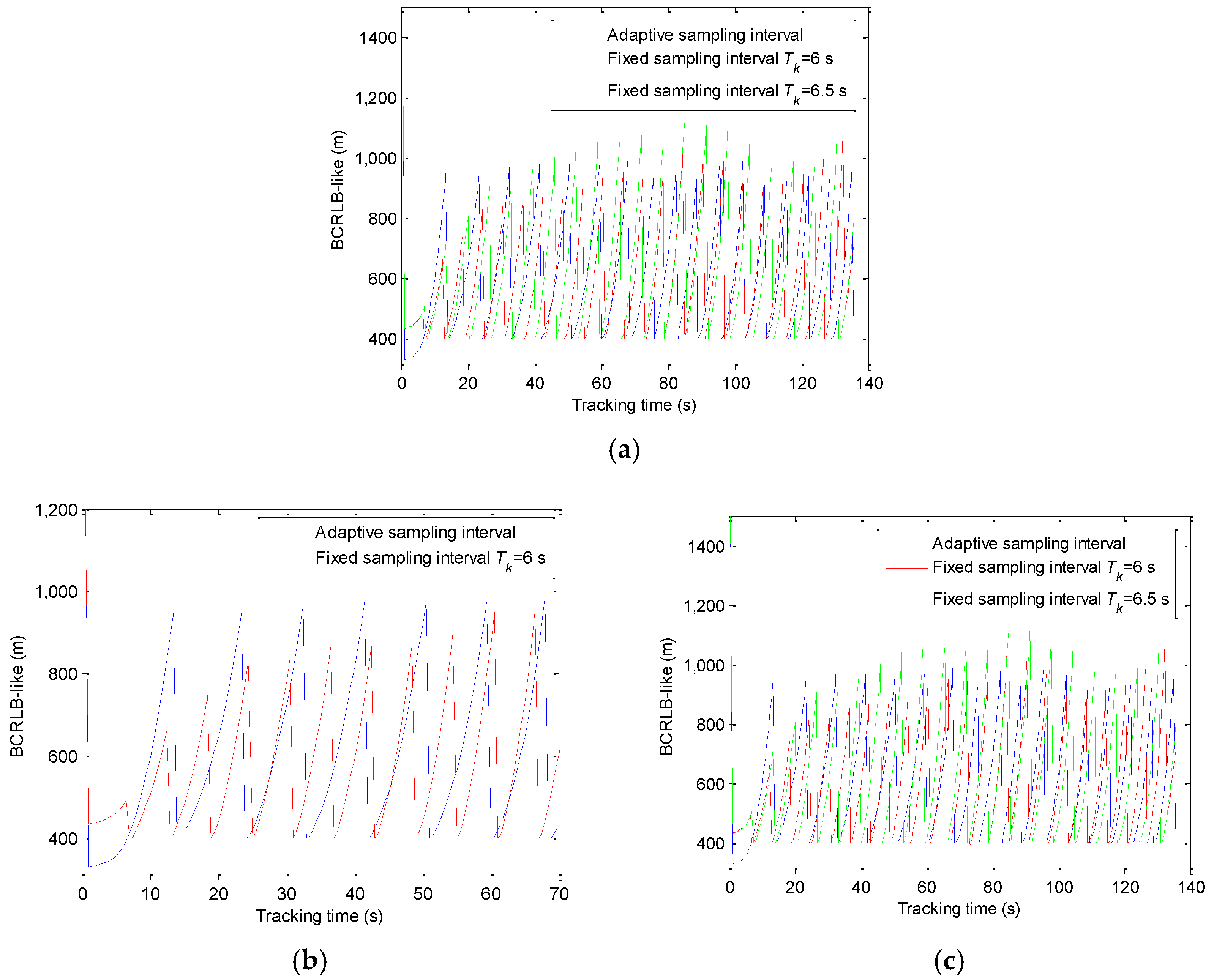
5.1. Adaptive Sampling Interval
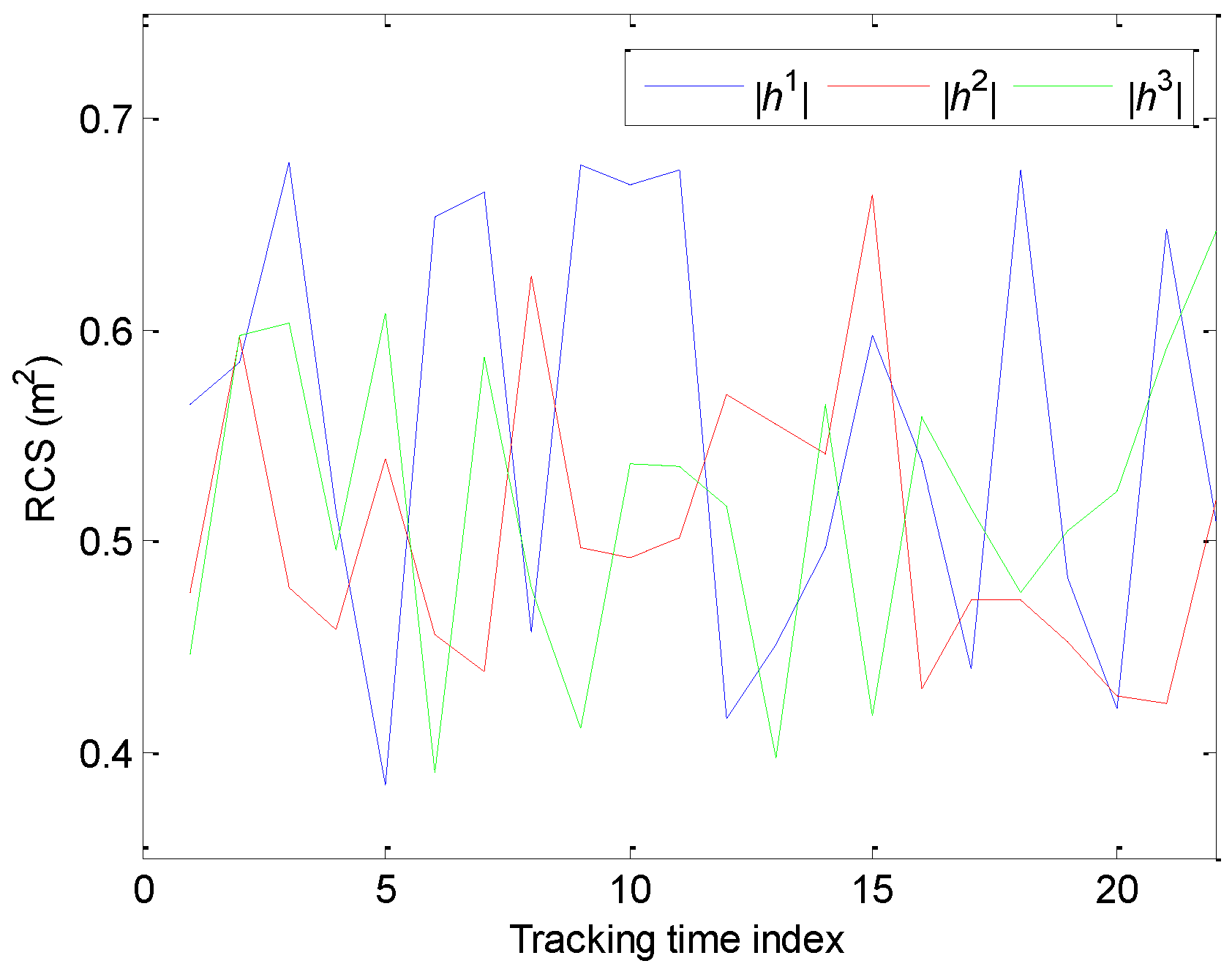
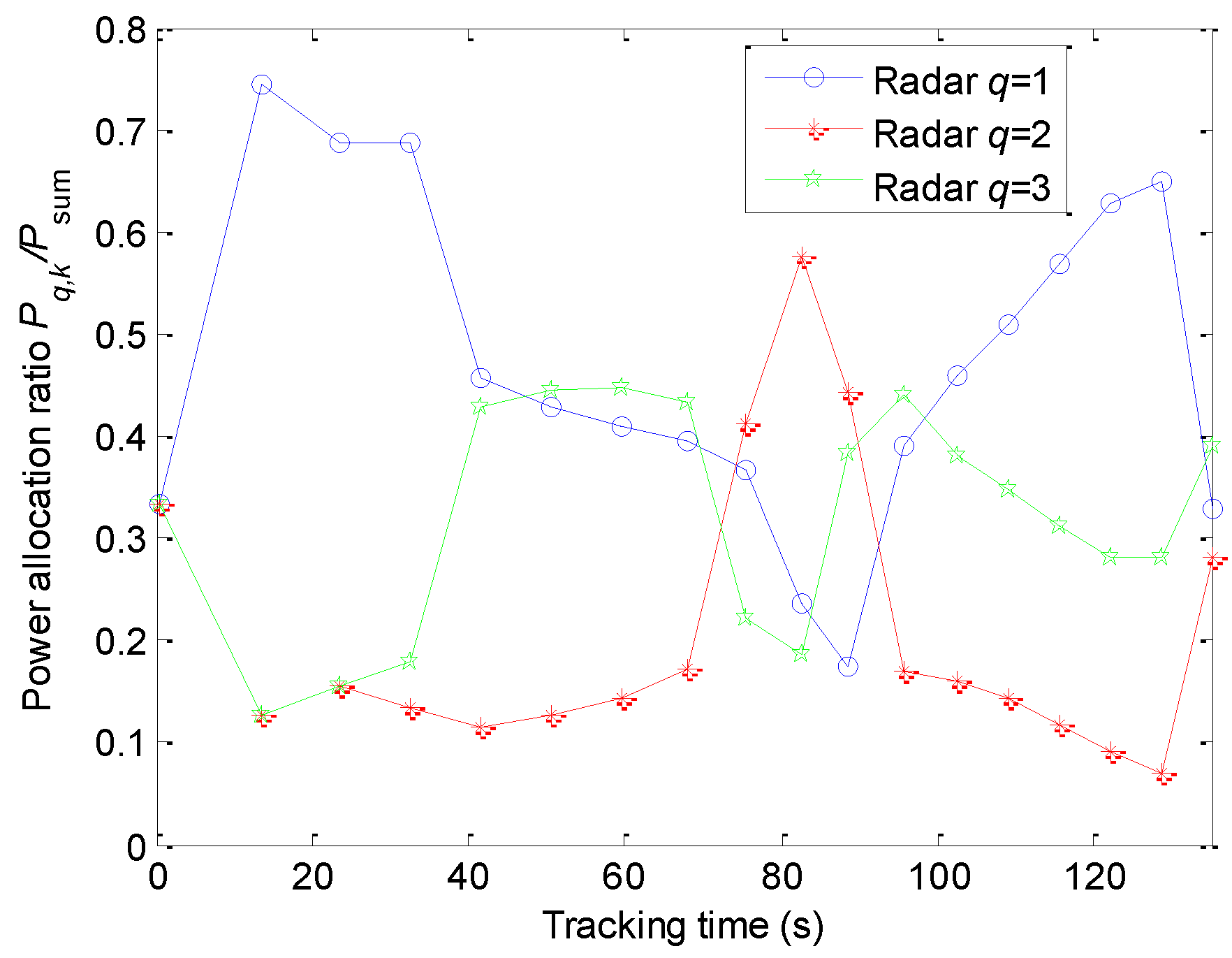
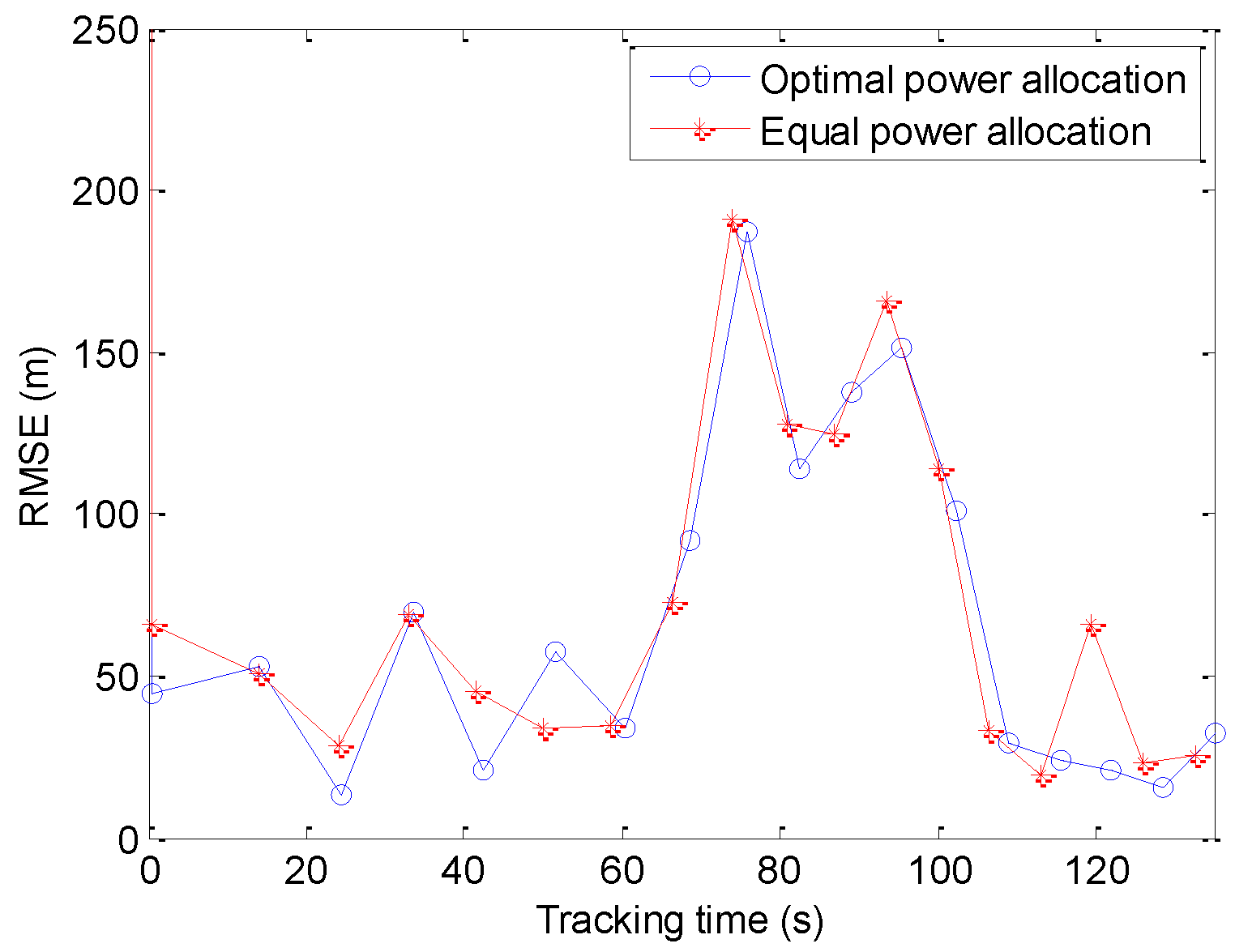
5.2. Optimal Allocation of Power
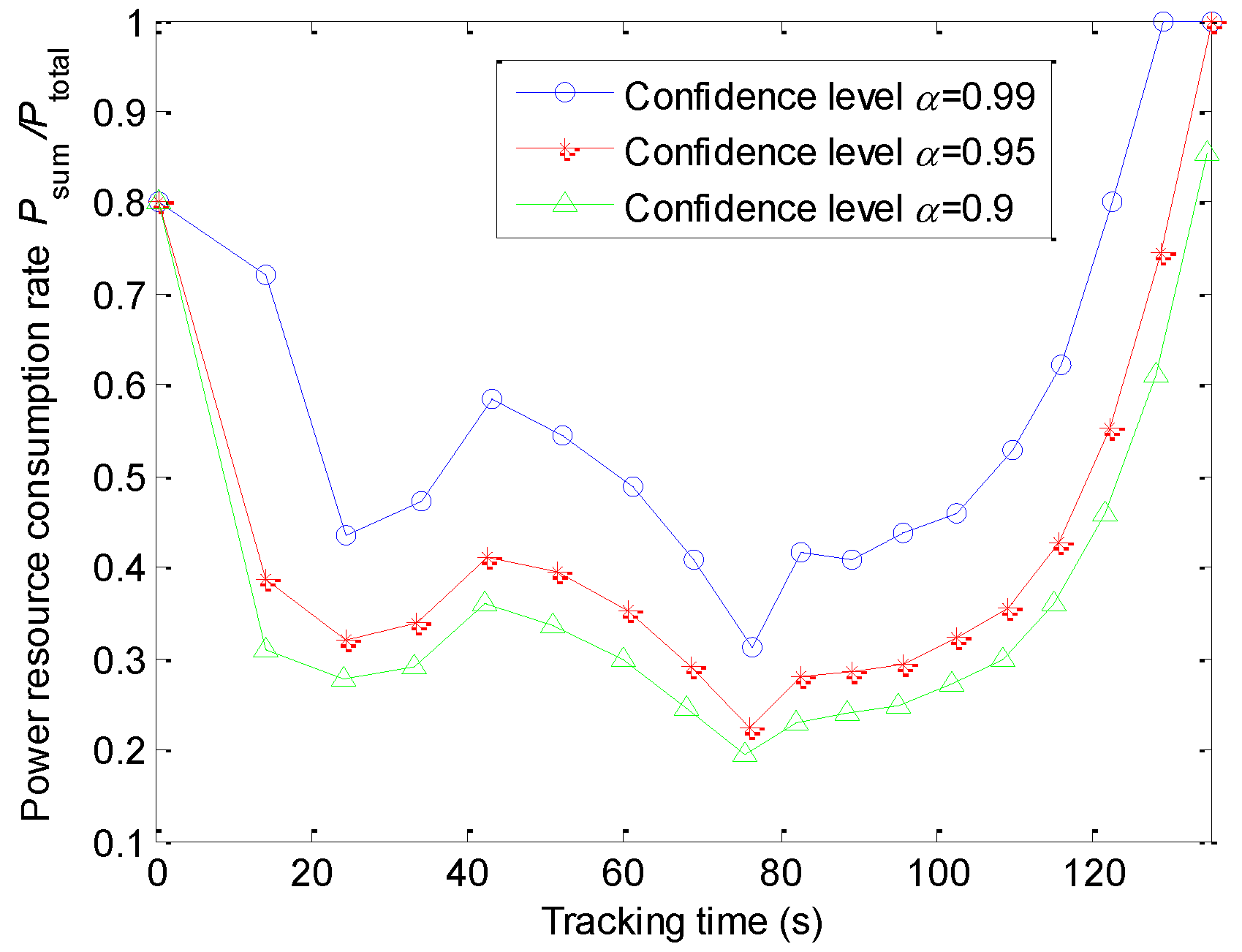
5.3. Chance-Constraint Programming
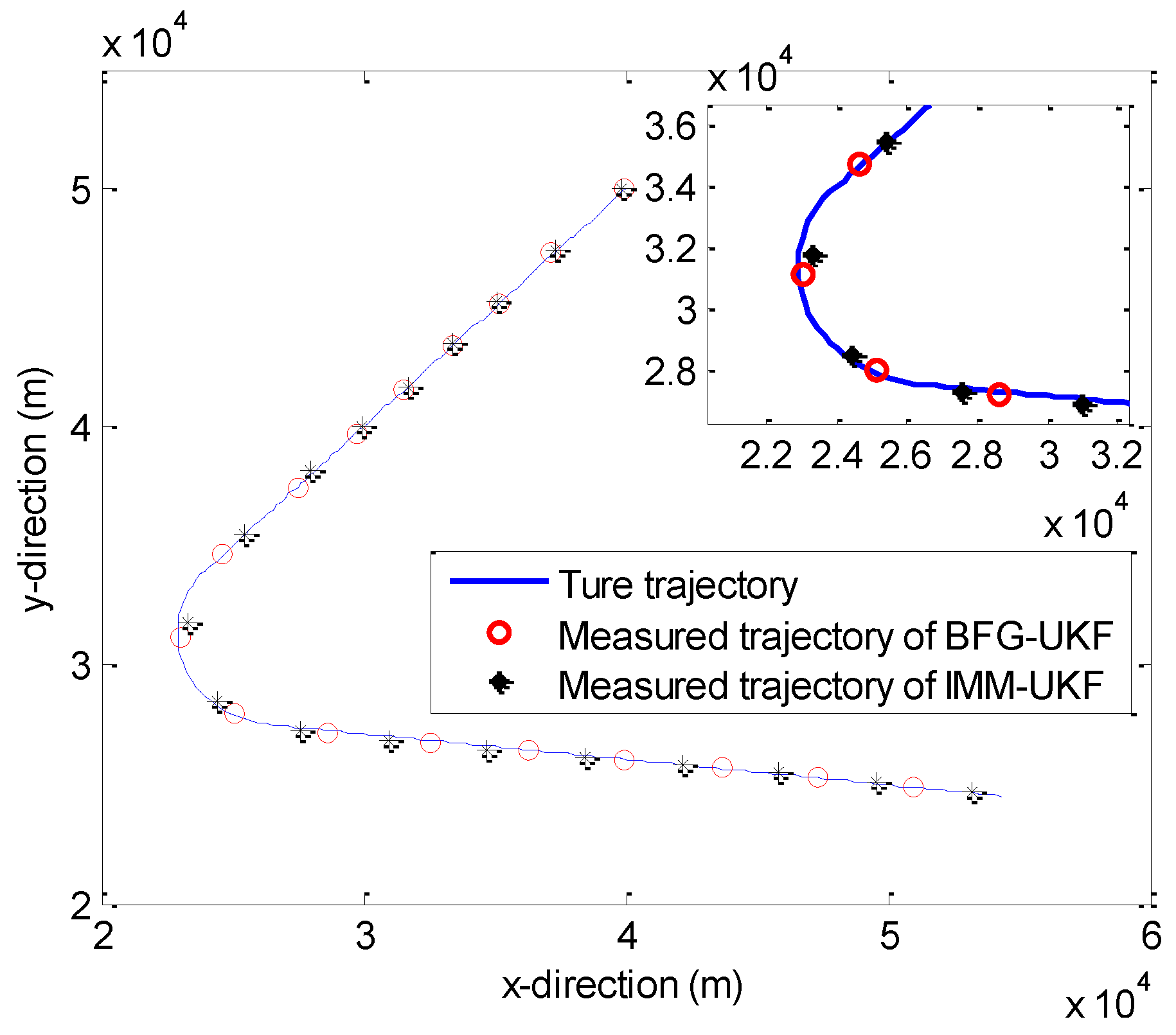
5.4. Target State Estimation with BFG-UKF and IMM-UKF
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Bartee, J.A. Genetic Algorithms as a Tool for Phased Array Radar Design. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2002. [Google Scholar]
- Esswein, L.C. Genetic Algorithm Design and Testing of a Random Element 3-D 2.4 GHz Phased Array Transmit Antenna Constructed of Commercial RF Microchips. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2003. [Google Scholar]
- Kocaman, İ. Distributed Beamforming in a Swarm UAV Network. Master’s thesis, Naval Postgraduate School, Monterey, CA, USA, 2008. [Google Scholar]
- Long, W.J.; Ben, D.; Pan, M.H.; Shu, X.R.; Han, Y.M.; Pan, J.B. Opportunistic digital array radar and its technical characteristic analysis. In Proceedings of the IET International Radar Conference, Guilin, China, 20–22 April 2009; pp. 1–4. [Google Scholar]
- Long, W.J.; Ben, D.; ASIM, B.; Zhang, G. Pattern synthesis optimization of 3-D ODAR based on improved GA using LSFE method. J. Harbin Inst. Technol. (New Ser.) 2011, 18, 96–100. [Google Scholar]
- Visina, R.; Bar-Shalom, Y.; Willett, P. Multiple-Model Estimators for Tracking Sharply Maneuvering Ground Targets. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1–18. [Google Scholar] [CrossRef]
- Han, B.; Huang, H.Q.; Lei, L.; Huang, C.Q. An Improved IMM Algorithm Based on STSRCKF for Maneuvering Target Tracking. IEEE Access 2019, 7, 57795–57804. [Google Scholar] [CrossRef]
- Zhang, H.W.; Xie, W.X. Constrained auxiliary particle filtering for bearings-only maneuvering target tracking. J. Syst. Eng. Electron. 2019, 30, 684–695. [Google Scholar]
- Yu, Y.H. Distributed Multimodel Bernoulli Filters for Maneuvering Target Tracking. IEEE Sens. J. 2018, 18, 5885–5896. [Google Scholar] [CrossRef]
- Godrich, H.; Petropulu, A.P.; Poor, H.V. Sensor selection in distributed multiple-radar architectures for localization: A knapsack problem formulation. IEEE Trans. Signal Process. 2012, 60, 247–260. [Google Scholar] [CrossRef]
- Yan, J.K.; Liu, H.W.; Jiu, B.; Chen, B.; Liu, Z.; Bao, Z. Simultaneous multibeam resource allocation scheme for multiple target tracking. IEEE Trans. Signal Process. 2015, 63, 3110–3122. [Google Scholar] [CrossRef]
- Yan, J.K.; Jiu, B.; Liu, H.W.; Chen, B.; Bao, Z. Prior knowledge-based simultaneous multibeam power allocation algorithm for cognitive multiple targets tracking in clutter. IEEE Trans. Signal Process. 2015, 63, 512–527. [Google Scholar] [CrossRef]
- Yan, J.K.; Liu, H.W.; Jiu, B.; Liu, Z.; Bao, Z. Joint detection and tracking processing algorithm for target tracking in multiple radar system. IEEE Sens. J. 2015, 15, 6534–6541. [Google Scholar] [CrossRef]
- Han, Q.H.; Pan, M.H.; Liang, Z.L. Joint power and beam allocation of opportunistic array radar for multiple target tracking in clutter. Digit. Signal Process. 2018, 78, 136–151. [Google Scholar] [CrossRef]
- Xie, M.C.; Yi, W.; Kirubarajan, T. Joint Node Selection and Power Allocation Strategy for Multitarget Tracking in Decentralized Radar Networks. IEEE Trans. Signal Process. 2018, 66, 729–743. [Google Scholar] [CrossRef]
- Zheng, N.E.; Sun, Y.; Song, X.Y.; Chen, S. Joint resource allocation scheme for target tracking in distributed MIMO radar systems. J. Syst. Eng. Electron. 2019, 30, 709–719. [Google Scholar]
- Van Trees, H.L.; Bell, K.L. Bayesian Bounds for Parameter Estimation and Nonlinear Filtering/Tracking; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Rapoport, I.; Oshman, Y. Recursive Weiss-Weinstein lower bounds for discrete-time nonlinear filtering. In Proceedings of the IEEE Conference Decision Control, Nassau, Bahamas, 14–17 December 2004; pp. 2662–2667. [Google Scholar]
- Reece, S.; Nicholson, D. Tighter alternatives to the Cramér-Rao lower bound for discrete-time filtering. In Proceedings of the International Conference on Information Fusion, Philadelphia, PA, USA, 25–28 July 2005; pp. 717–722. [Google Scholar]
- Tichavsky, P.; Muravchik, C.H.; Nehorai, A. Posterior Cramér-Rao bounds for discrete-time nonlinear filtering. IEEE Trans. Signal Process. 1998, 46, 1386–1396. [Google Scholar] [CrossRef]
- Hernandez, M.; Ristic, B.; Farina, A. A performance bound for manoeuvring target tracking using best-fitting Gaussian distrbutions. In Proceedings of the International Conference on Information Fusion, Philadelphia, PA, USA, 25–28 July 2005; pp. 1–8. [Google Scholar]
- Hernandez, M.L.; Ristic, B.; Farina, A.; SathYan, T.; Kirubarajan, T. Performance Measure for Markovian Switching Systems using Best-Fitting Gaussian Distributions. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 724–747. [Google Scholar] [CrossRef]
- Hernandez, M.; Benavoli, A.; Graziano, A.; Farina, A.; Morelande, M. Performance Measures and MHT for Tracking Move-Stop-Move Targets with MTI Sensors. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 996–1025. [Google Scholar] [CrossRef]
- Ristic, B.; Hernandez, M.; Farina, A.; Ong, H.T. Analysis of radar allocation requirements for an IRST aided tracking of anti-ship missiles. In Proceedings of the International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–8. [Google Scholar]
- Skolnik, M.I. Introduction to Radar System, 3rd ed.; Tata McGraw-Hill Publishing Company Limited: New Delhi, India, 2001; pp. 49–73. [Google Scholar]
- Liu, B.D. Theory and Practice of Uncertain Programming, 2nd ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Chen, X.; Tharmarasa, R.; Kirubarajan, T. Multitarget multisensor tracking. In Academic Press Library in Signal Processing; Sidiropoulos, N.D., Gini, F., Chellappa, R., Theodoridis, S., Eds.; Academic Press: Cambridge, MA, USA, 2014; Volume 2, pp. 759–812. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R. Estimation and Tracking: Principles, Techniques and Software; Artech House: Boston, MA, USA, 1993. [Google Scholar]
- Blackman, S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House: Boston, MA, USA, 1999. [Google Scholar]
- Bessell, A.; Ristic, B.; Farina, A.; Wang, X.; Arulampalam, M.S. Error performance bounds for tracking a manoeuvring target. In Proceedings of the International Conference on Information Fusion, Cairns, Australia, 8–11 July 2003; pp. 903–910. [Google Scholar]
- Van Trees, H.L. Detection, Estimation, Modulation Theory Part III; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Van Trees, H.L. Optimum Array Processing: Detection, Estimation, Modulation Theory IV; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Godrich, H.; Petropulu, A.P.; Poor, H.V. Power allocation strategies for target localization in distributed multiple-radar architecture. IEEE Trans. Signal Process. 2011, 59, 3226–3240. [Google Scholar] [CrossRef]
- Glass, J.D.; Smith, L.D. MIMO radar resource allocation using posterior Cramér-Rao lower bounds. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; pp. 1–9. [Google Scholar]
- Charnes, A.; Cooper, W.W. Chance-constrained programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar] [CrossRef]
- Gustafsson, F.; Gunnarsson, F.; Bergman, N.; Forssell, U.; Jansson, J.; Karlsson, R.; Nordlund, P.J. Particle Filters for Positioning, Navigation, and Tracking. IEEE Trans. Signal Process. 2002, 50, 425–437. [Google Scholar] [CrossRef]
- Míguez, J. Analysis of selection methods for cost-reference particle filtering with applications to maneuvering target tracking and dynamic optimization. Digit. Signal Process. 2007, 17, 787–807. [Google Scholar] [CrossRef]
- Zaitouny, A.; Stemler, T.; Judd, K. Tracking rigid bodies using only position data: A shadowing filter approach based on newtonian dynamics. Digit. Signal Process. 2017, 67, 81–90. [Google Scholar] [CrossRef]
- Zaitouny, A.; Stemler, T.; Algar, S.D. Optimal Shadowing Filter for a Positioning and Tracking Methodology with Limited Information. Sensors 2019, 19, 931. [Google Scholar] [CrossRef] [PubMed]
- Challa, S.; Morelande, M.R.; Mušcki, D.; Evans, R.J. Fundamentals of Object Tracking; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Rong Li, X.; Jilkov, V.P. Survey of maneuvering target tracking. Part V. Multiple-model methods. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1255–1321. [Google Scholar] [CrossRef]
- Babu, V.S.; Shankar, M.R.; Majumdar, S.; Koteswara Rao, S. IMM-unscented Kalman filter based tracking of maneuvering targets using active sonar measurements. In Proceedings of the International Conference on Communications and Signal Processing, Calicut, India, 10–12 February 2011; pp. 126–130. [Google Scholar]
- Wang, X.B.; Pang, X.S.; Wang, D.S. Sequential algorithm for extended H∞ filter-based target tracking in wireless sensor networks. In Proceedings of the Chinese Control Conference, Hangzhou, China, 28–30 July 2015; pp. 7721–7725. [Google Scholar]




| Step 1. Set N′=0; |
| Step 2. Calculate Φk and Qp,k according to the BFG approximation; |
| Step 3. Select a measurement hj,k (j=1, 2, …, NH) from the measurement set and produce F(Tk,Pk,hj,k); |
| Step 4. If F(Tk,Pk,hj,k)≤η1,k, N′= N′+1; |
| Step 5. Repeat the third and fourth steps NH times; |
| Step 6. Pr{F(Tk,Pk,hk)≤η1,k }= N′/NH. |
| (1) Initialize pop_size chromosomes, and check the feasibility of the generated chromosomes by the stochastic simulation in Table 1; |
| (2) Update the chromosomes by crossover and mutation operations in which the feasibility of offspring can be checked by the stochastic simulation in Table 1, and, if they do not satisfy the constraint, correct the chromosomes; |
| (3) Calculate the objective function values of all the chromosomes; |
| (4) Compute the fitness of each chromosome according to the objective function values; |
| (5) Select the chromosomes by spinning the roulette wheel; |
| (6) Repeat the second to fifth steps for a given number of cycles; |
| (7) Report the best chromosome as the optimal solution Pk,opt. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Q.; Pan, M.; Long, W.; Liang, Z.; Shan, C. Joint Adaptive Sampling Interval and Power Allocation for Maneuvering Target Tracking in a Multiple Opportunistic Array Radar System. Sensors 2020, 20, 981. https://doi.org/10.3390/s20040981
Han Q, Pan M, Long W, Liang Z, Shan C. Joint Adaptive Sampling Interval and Power Allocation for Maneuvering Target Tracking in a Multiple Opportunistic Array Radar System. Sensors. 2020; 20(4):981. https://doi.org/10.3390/s20040981
Chicago/Turabian StyleHan, Qinghua, Minghai Pan, Weijun Long, Zhiheng Liang, and Chenggang Shan. 2020. "Joint Adaptive Sampling Interval and Power Allocation for Maneuvering Target Tracking in a Multiple Opportunistic Array Radar System" Sensors 20, no. 4: 981. https://doi.org/10.3390/s20040981
APA StyleHan, Q., Pan, M., Long, W., Liang, Z., & Shan, C. (2020). Joint Adaptive Sampling Interval and Power Allocation for Maneuvering Target Tracking in a Multiple Opportunistic Array Radar System. Sensors, 20(4), 981. https://doi.org/10.3390/s20040981




