Adaptive Repetitive Control of A Linear Oscillating Motor under Periodic Hydraulic Step Load
Abstract
1. Introduction
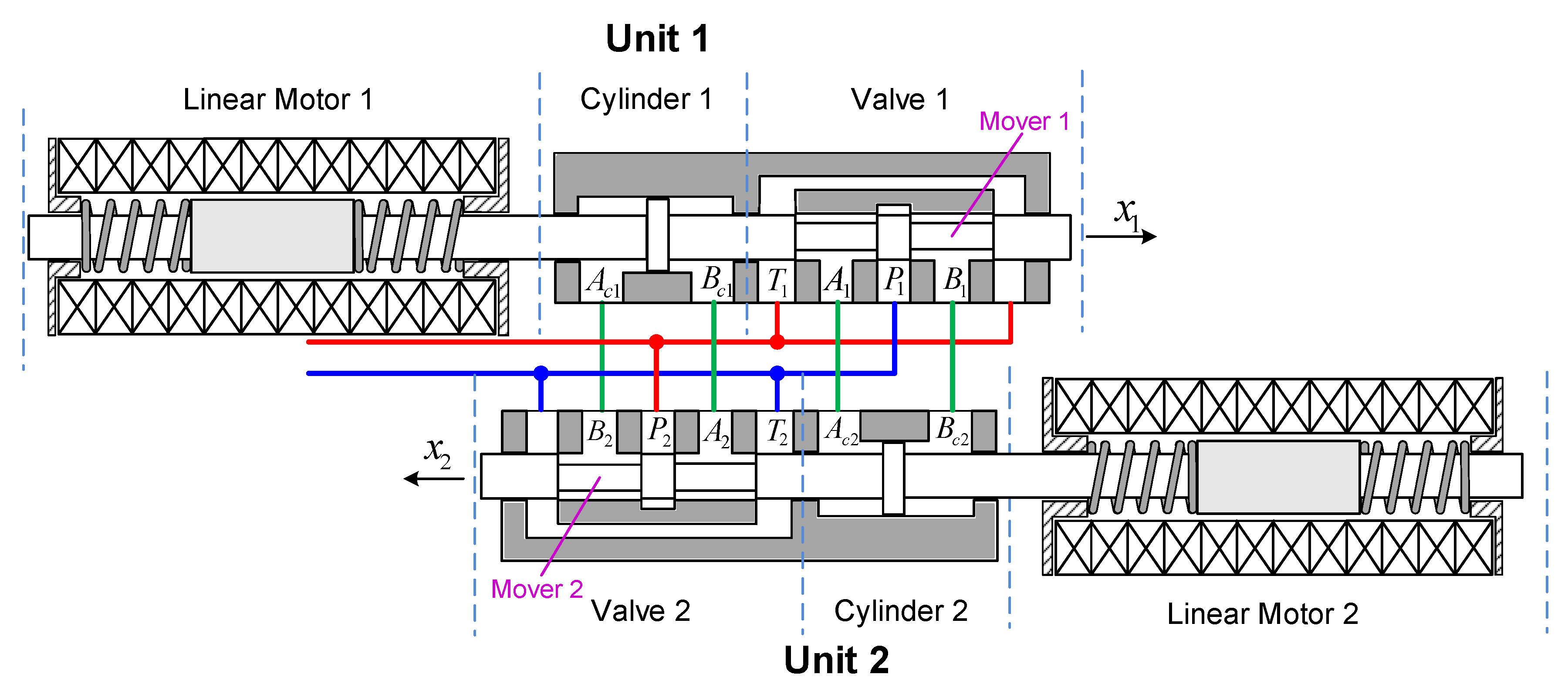
2. Problem Formulation and Dynamic Models
3. Nonlinear Adaptive Repetitive Controller Design
3.1. Design Model and Issues to be Addressed
3.2. Projection Mapping and Parameter Adaptation
3.3. Controller Design
3.4. Main Results
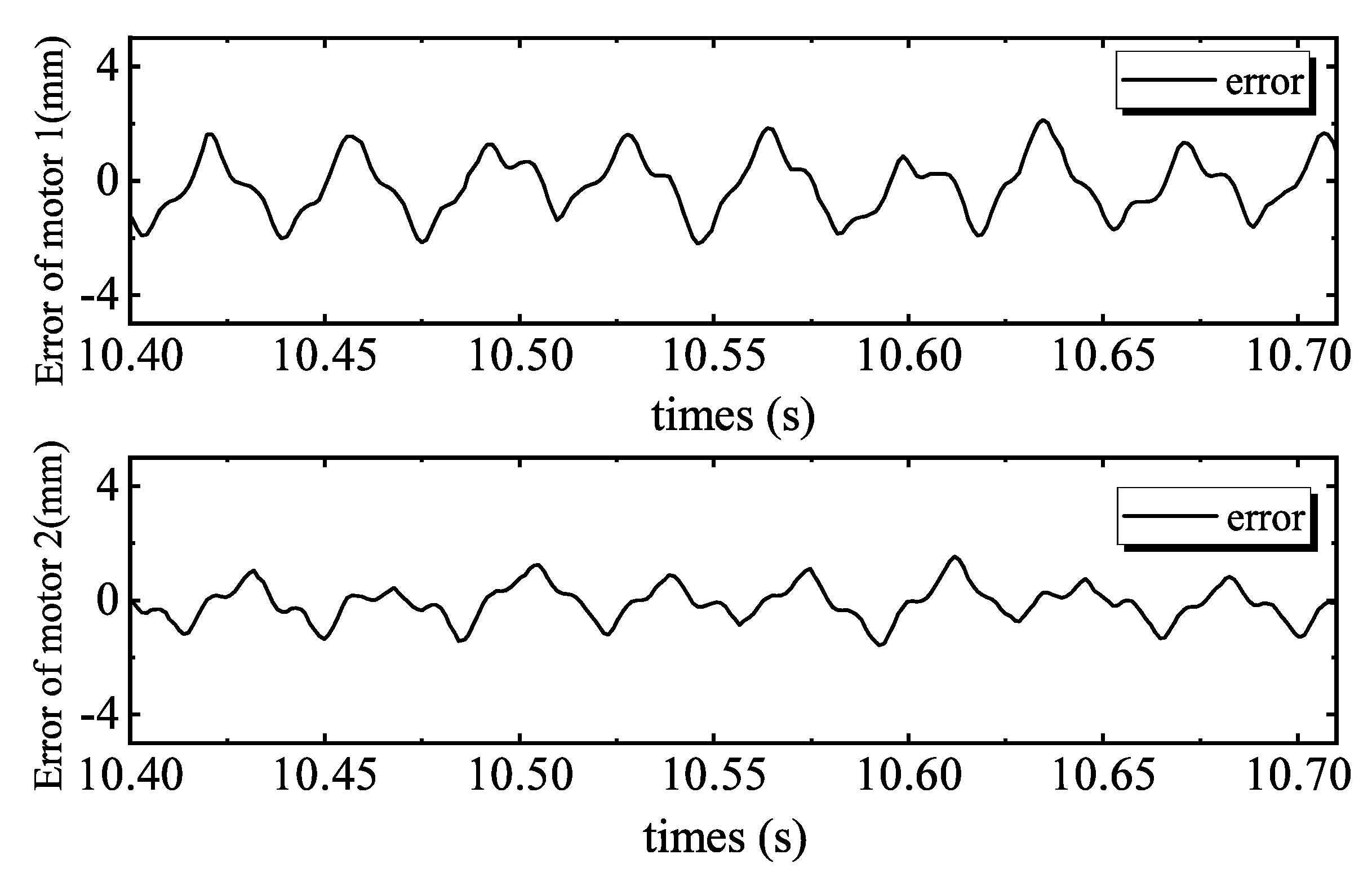
4. Comparative Experimental Results
4.1. Experiment Setup
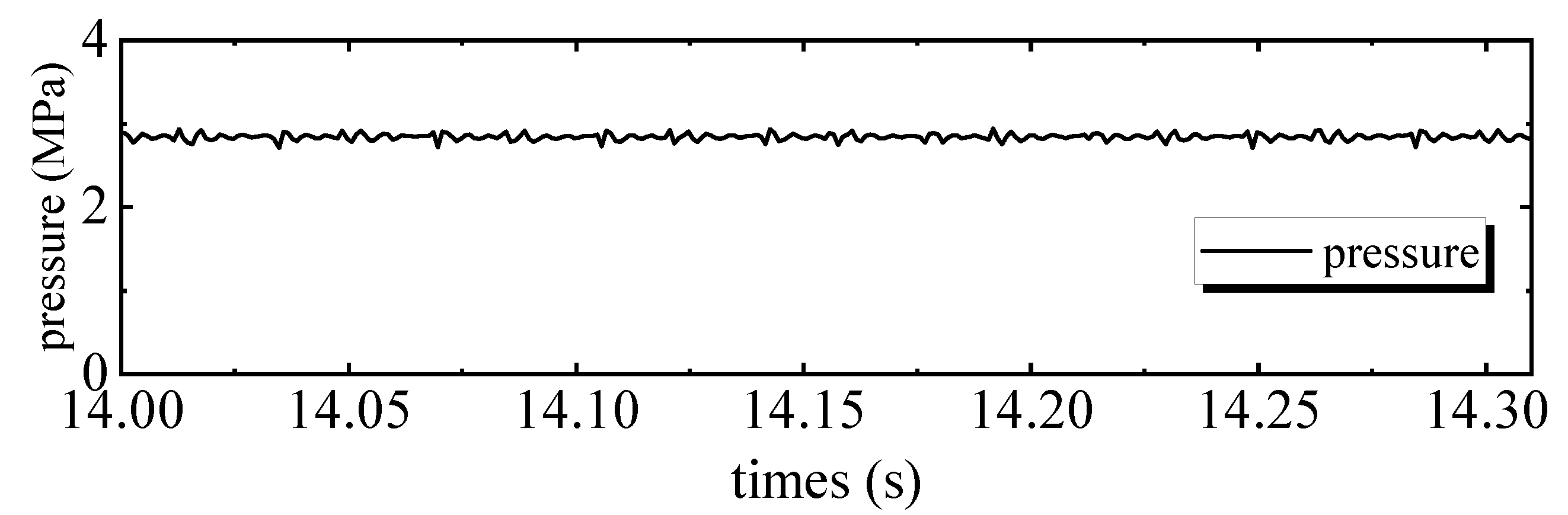
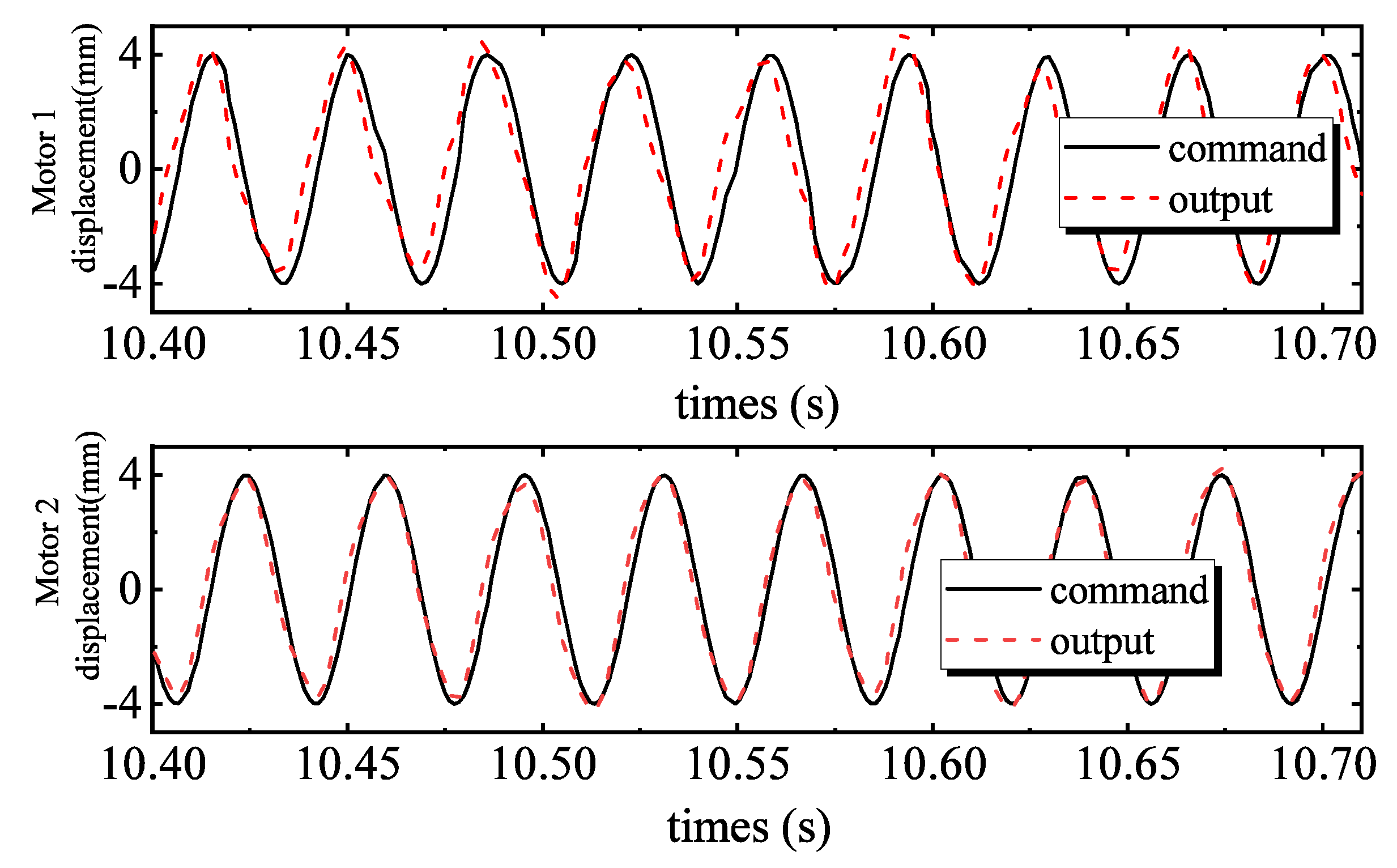
4.2. Comparative Experimental Results
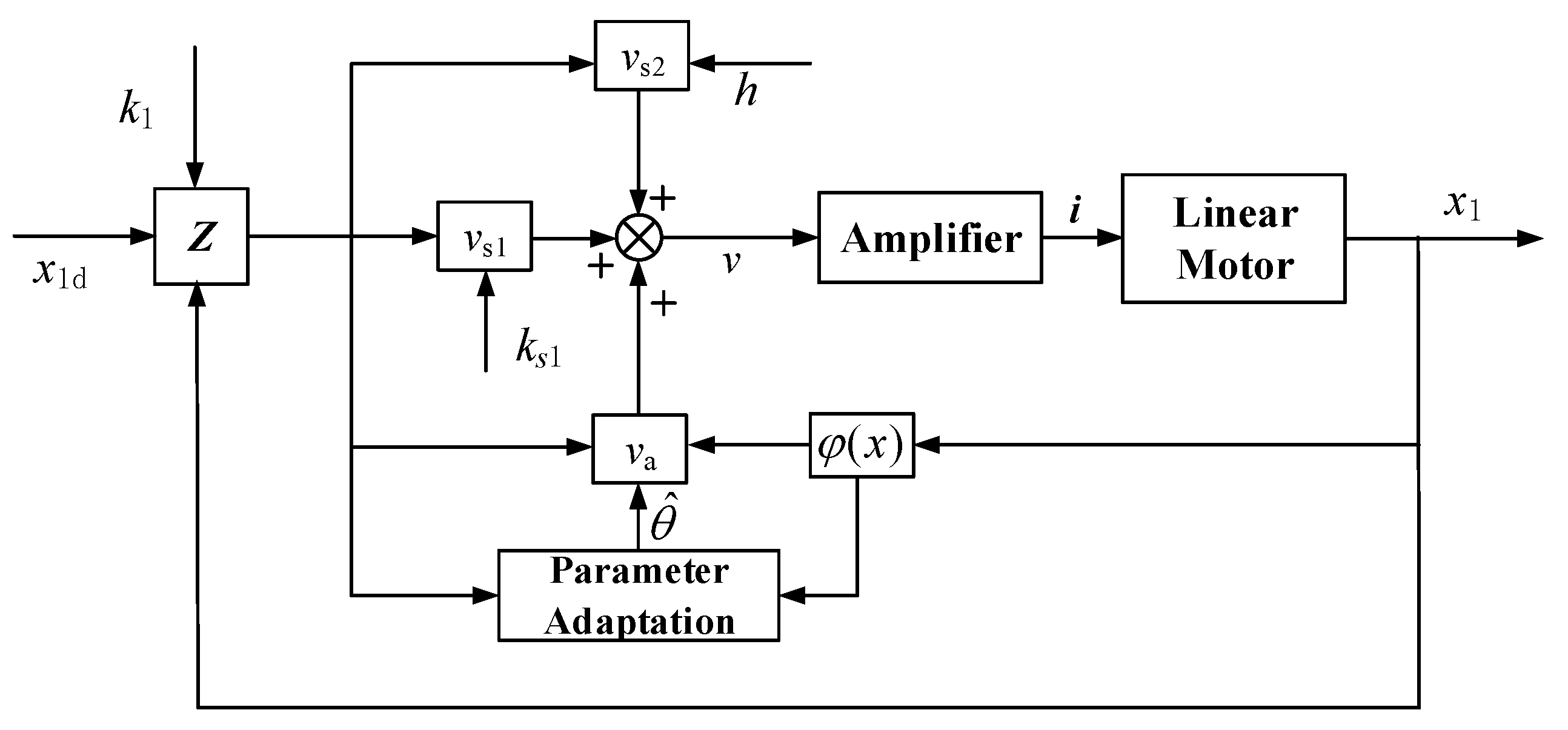
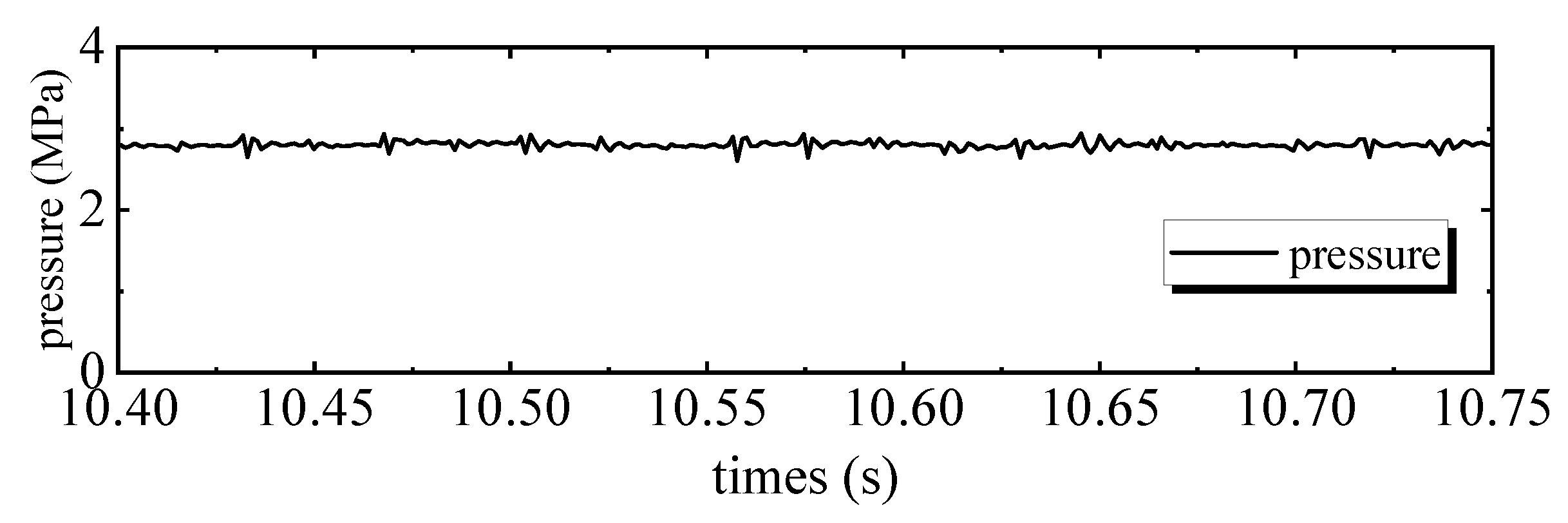
- The nonlinear adaptive repetitive controller in the above section. To simplify the controller and save memory, only a small number of unknown parameters are adapted, i.e., m in Equation (12) is set to 3. So and its counterpart of motor 2 all have seven terms. The initial values for the parameters are set to and . Viscous damping coefficients and as well as the Coulomb friction amplitude were identified by Wang in the design process of the linear oscillating motor [27]. Even if the wear of linear bears and different working conditions change the true values of parameters slightly, it is reasonable to set identified values as the initial values. is the elasticity coefficient of two parallel springs. Its initial value was set to its nominal value. The initial value of the load pressure of the pump was set to 2.8 MPa by adjusting the throttle valve. The hydraulic load of linear motor is periodic. Its initial amplitude can be approximated as the product of load pressure and ram area of piston and its phase is synchronous with displacement of the other linear motor. Initial Fourier coefficients were got by applying Fourier transformation to the periodic initial hydraulic load. The bounds of the parameter variations in the two motor systems are the same and are estimated as and . The magnitude of is assumed to be less than 500, i.e., and . The control gains in two motors are the same: , . The shape function of Coulomb friction [21]. Adaptation rate matrix in the two systems are identically set: . The control diagram is shown in Figure 3.
- Proportional-integral-derivative (PID): A conventional proportional-integral-derivative controller was built. We optimized the PID parameters in experiments. Derivative section is sensitive to interference, whose coefficient was set to zero. Considering the working condition of the LDP, we paid attention to the steady state response of the linear motor, when we optimized PI coefficients. The hydraulic pressure of 2.8 MPa was applied on the LDP. Because of coupling effect of two motors, the amplitude attenuation and phase lag of the single linear motor cannot reflect the control performance. The output flow rate of LDP was measured and recorded, which was used as the optimization objective. We got the optimal PI coefficients when the flow rate was maximum. The controller parameters are , , which represent the P-gain, I-gain and D-gain of two motors, respectively.
- Maximal absolute value of the tracking errors is defined aswhere N is number of the recorded digital signals, and is used as an index of measure of tracking accuracy.
- Average tracking error is defined aswhich is used as a measure of average tracking performance.
- Standard deviation performance index is defined asto measure the deviation level of tracking errors.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LDP | Linear drive collaborative rectification structure pump |
| ARC | Adaptive robust control |
| PID | Proportional-integral-derivative |
| RISE | Robust integral of the sign of the error |
References
- Chaudhuri, A.; Wereley, N. Compact hybrid electrohydraulic actuators using smart materials: A review. J. Intell. Mater. Syst. Struct. 2012, 23, 597–634. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Yoo, J.H.; Wereley, N.M. Design, test and model of a hybrid magnetostrictive hydraulic actuator. Smart Mater. Struct. 2009, 18, 085019. [Google Scholar] [CrossRef]
- Sirohi, J.; Chopra, I. Design and Development of a High Pumping Frequency Piezoelectric-Hydraulic Hybrid Actuator. J. Intell. Mater. Syst. Struct. 2003, 14, 135–147. [Google Scholar] [CrossRef]
- Liang, H.; Jiao, Z.; Liang, Y.; Zhao, L.; Shuai, W.; Yang, L. Design and analysis of a tubular linear oscillating motor for directly-driven EHA pump. Sens. Actuators A Phys. 2014, 210, 107–118. [Google Scholar] [CrossRef]
- Wang, T.; Liang, Y.; Jiao, Z.; Ping, H. Analytical modeling of linear oscillating motor with a mixed method considering saturation effect. Sens. Actuators A Phys. 2015, 234, 375–383. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, Z.; Yan, L.; Dong, W. Conceptual design and composition principles analysis of a novel collaborative rectification structure pump. J. Dyn. Syst. Meas. Control. 2014, 136, 054507. [Google Scholar] [CrossRef]
- Jiao, Z.; Wang, Z.; Li, X. Modeling and Control of a Novel Linear-Driven Electro-Hydrostatic Actuator Using Energetic Macroscopic Representation. J. Dyn. Syst. Meas. Control. 2018, 140, 071002. [Google Scholar] [CrossRef]
- Wang, Z.; Jiao, Z.; Li, X. Design and Testing of a Linear-Driven Electro-Hydrostatic Actuator. J. Dyn. Syst. Meas. Control. 2019, 141, 121009. [Google Scholar] [CrossRef]
- Li, X.; Jiao, Z.; Yan, L.; Shang, Y.; Lei, T. Instantaneous pressure in chambers of the novel collaborative rectification structure pump. In Proceedings of the CSAA/IET International Conference on Aircraft Utility Systems (AUS 2018), Guiyang, China, 19–22 June 2018; pp. 1224–1227. [Google Scholar]
- Feng, Z.; Ling, J.; Ming, M.; Xiao, X. Integrated modified repetitive control with disturbance observer of piezoelectric nanopositioning stages for high-speed and precision motion. J. Dyn. Syst. Meas. Control. 2019, 141, 081006. [Google Scholar] [CrossRef]
- Sabarianand, D.; Karthikeyan, P.; Muthuramalingam, T. A review on control strategies for compensation of hysteresis and creep on piezoelectric actuators based micro systems. Mech. Syst. Signal Process. 2020, 140, 106634. [Google Scholar] [CrossRef]
- Alem, S.F.; Izadi, I.; Sheikholeslam, F.; Ekramian, M. Piezoelectric Actuators with Uncertainty: Observer-Based Hysteresis Compensation and Joint Stability Analysis. IEEE Trans. Control. Syst. Technol. 2019, 1–8. [Google Scholar] [CrossRef]
- Ahn, K.K.; Nam, D.N.C.; Jin, M. Adaptive Backstepping Control of an Electrohydraulic Actuator. IEEE/ASME Trans. Mechatron. 2014, 19, 987–995. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W. Active Disturbance Rejection Adaptive Control of Hydraulic Servo Systems. IEEE Trans. Ind. Electron. 2017, 64, 8023–8032. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W. Active disturbance rejection adaptive control of uncertain nonlinear systems: Theory and application. Nonlinear Dyn. 2017, 89, 1611–1624. [Google Scholar] [CrossRef]
- Guan, C.; Pan, S. Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters. Control. Eng. Pract. 2008, 16, 1275–1284. [Google Scholar] [CrossRef]
- Hara, S.; Omata, T.; Nakano, M. Synthesis of repetitive control systems and its application. In Proceedings of the 1985 24th IEEE Conference on Decision and Control, Fort Lauderdale, FL, USA, 11–13 December 1985; pp. 1387–1392. [Google Scholar]
- Hara, S.; Yamamoto, Y.; Omata, T.; Nakano, M. Repetitive control system: A new type servo system for periodic exogenous signals. IEEE Trans. Autom. Control. 1988, 33, 659–668. [Google Scholar] [CrossRef]
- Yao, B.; Tomizuka, M. Adaptive robust control of SISO nonlinear systems in a semi-strict feedback form. Automatica 1997, 33, 893–900. [Google Scholar] [CrossRef]
- Yao, B. High performance adaptive robust control of nonlinear systems: A general framework and new schemes. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 12 December 1998; pp. 2489–2494. [Google Scholar]
- Yao, J.; Jiao, Z.; Ma, D. A practical nonlinear adaptive control of hydraulic servomechanisms with periodic-like disturbances. IEEE/ASME Trans. Mechatron. 2015, 20, 2752–2760. [Google Scholar] [CrossRef]
- Yao, B.; Xu, L. On the design of adaptive robust repetitive controllers. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition (IMECE’01), IMECE01/DSC-3B, New York, NY, USA, 11–16 November 2001; pp. 1–9. [Google Scholar]
- Merritt, H.E. Hydraulic Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Sastry, S.; Bodson, M. Adaptive Control: Stability, Convergence and Robustness; Courier Corporation: North Chelmsford, MA, USA, 2011. [Google Scholar]
- Yao, B.; Bu, F.; Reedy, J.; Chiu, G.C. Adaptive robust motion control of single-rod hydraulic actuators: Theory and experiments. IEEE/ASME Trans. Mechatron. 2000, 5, 79–91. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Wang, T. Research on High Power Density Linear Oscillating Motor Design and Control Strategy. Ph.D. Thesis, Beihang University, Beijing, China, 2018. [Google Scholar]
- Yao, J.; Jiao, Z.; Ma, D. Extended-state-observer-based output feedback nonlinear robust control of hydraulic systems with backstepping. IEEE Trans. Ind. Electron. 2014, 61, 6285–6293. [Google Scholar] [CrossRef]



| Items | Symbol | Value |
|---|---|---|
| Stroke of cylinder | S | 4 mm |
| Resonant frequency of linear motor | f | 28 Hz |
| ram area of piston | 48 | |
| Force coefficient of linear motor | 27.5 N/A | |
| Motor driver amplification coefficient | 8 A/V | |
| Mass of the mover | m | 1.15 kg |
| Additive elasticity coefficient of two parallel springs | 36,000 N/ |
| Indices | |||
|---|---|---|---|
| Motor 1 with PID | 2.3219 | 1.3354 | 0.7263 |
| Motor 2 with PID | 4.3039 | 2.7644 | 1.2643 |
| Motor 1 with APC | 2.1675 | 0.8506 | 0.6028 |
| Motor 2 with APC | 1.5320 | 0.4887 | 0.3950 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Jiao, Z.; Li, Y.; Cao, Y. Adaptive Repetitive Control of A Linear Oscillating Motor under Periodic Hydraulic Step Load. Sensors 2020, 20, 1140. https://doi.org/10.3390/s20041140
Li X, Jiao Z, Li Y, Cao Y. Adaptive Repetitive Control of A Linear Oscillating Motor under Periodic Hydraulic Step Load. Sensors. 2020; 20(4):1140. https://doi.org/10.3390/s20041140
Chicago/Turabian StyleLi, Xinglu, Zongxia Jiao, Yang Li, and Yuan Cao. 2020. "Adaptive Repetitive Control of A Linear Oscillating Motor under Periodic Hydraulic Step Load" Sensors 20, no. 4: 1140. https://doi.org/10.3390/s20041140
APA StyleLi, X., Jiao, Z., Li, Y., & Cao, Y. (2020). Adaptive Repetitive Control of A Linear Oscillating Motor under Periodic Hydraulic Step Load. Sensors, 20(4), 1140. https://doi.org/10.3390/s20041140





