Development of a Shock and Detonation Velocity Measurement System Using Chirped Fiber Bragg Gratings
Abstract
1. Introduction
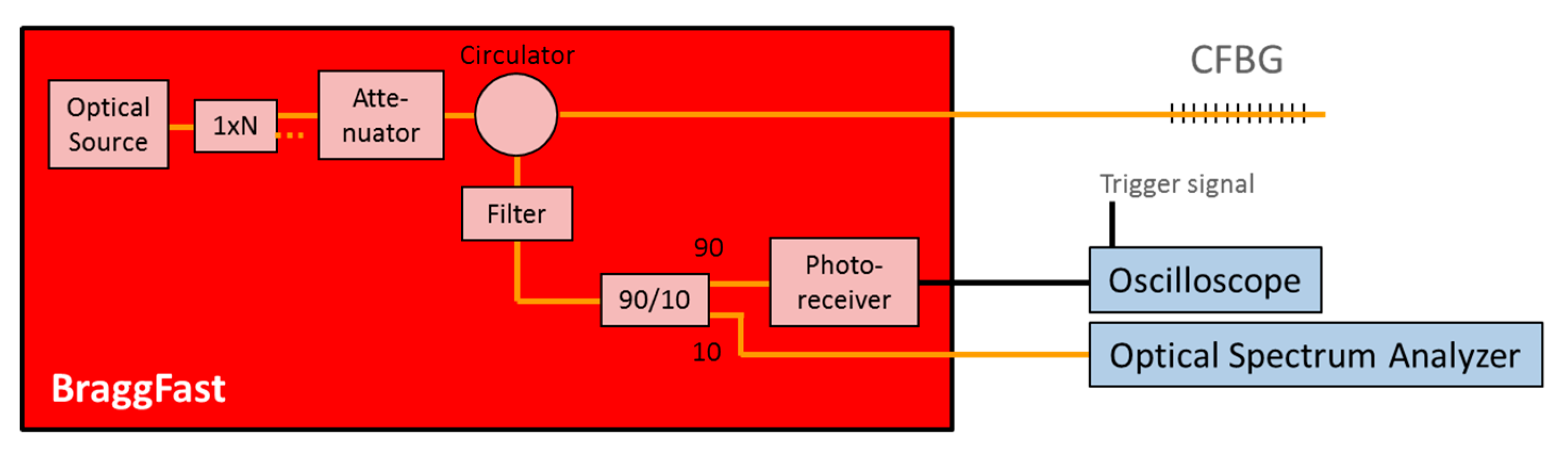
2. BraggFast System
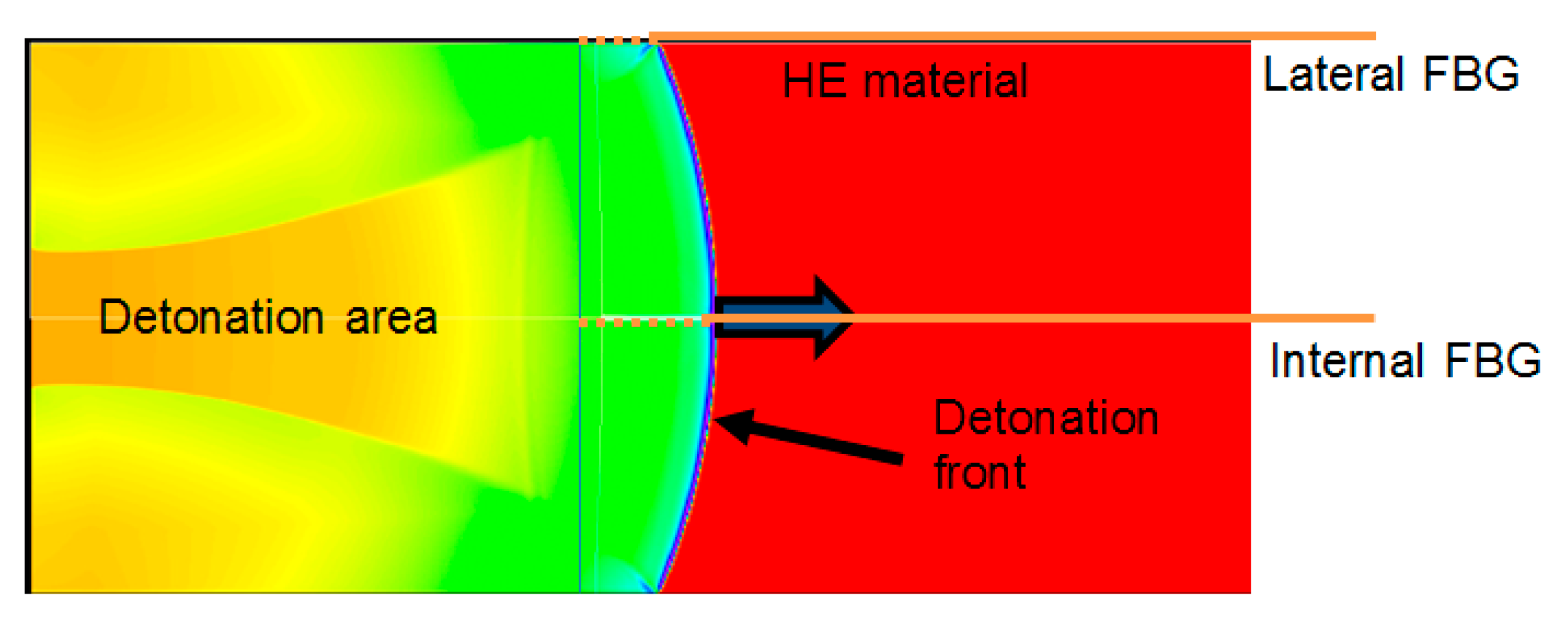
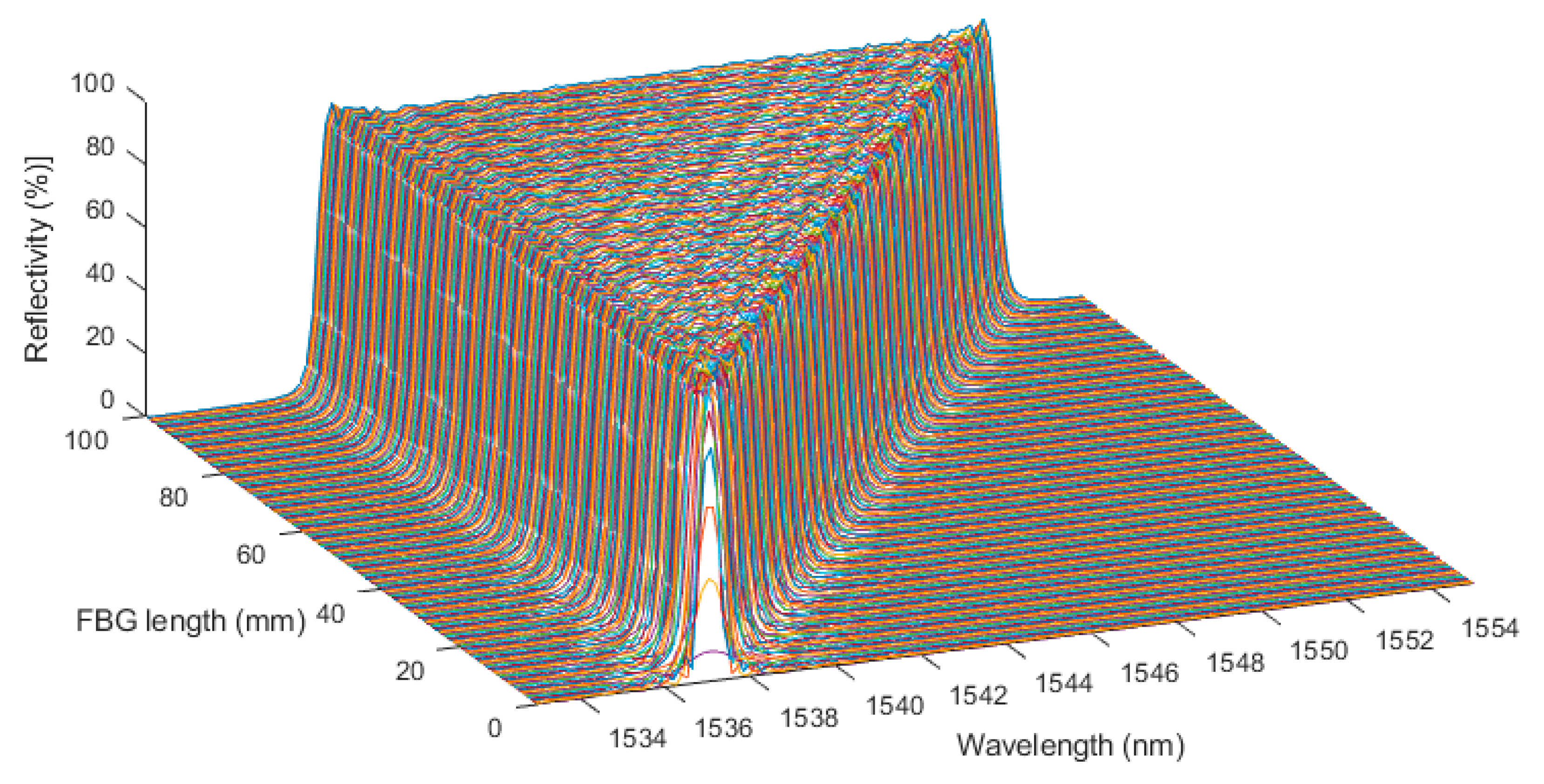
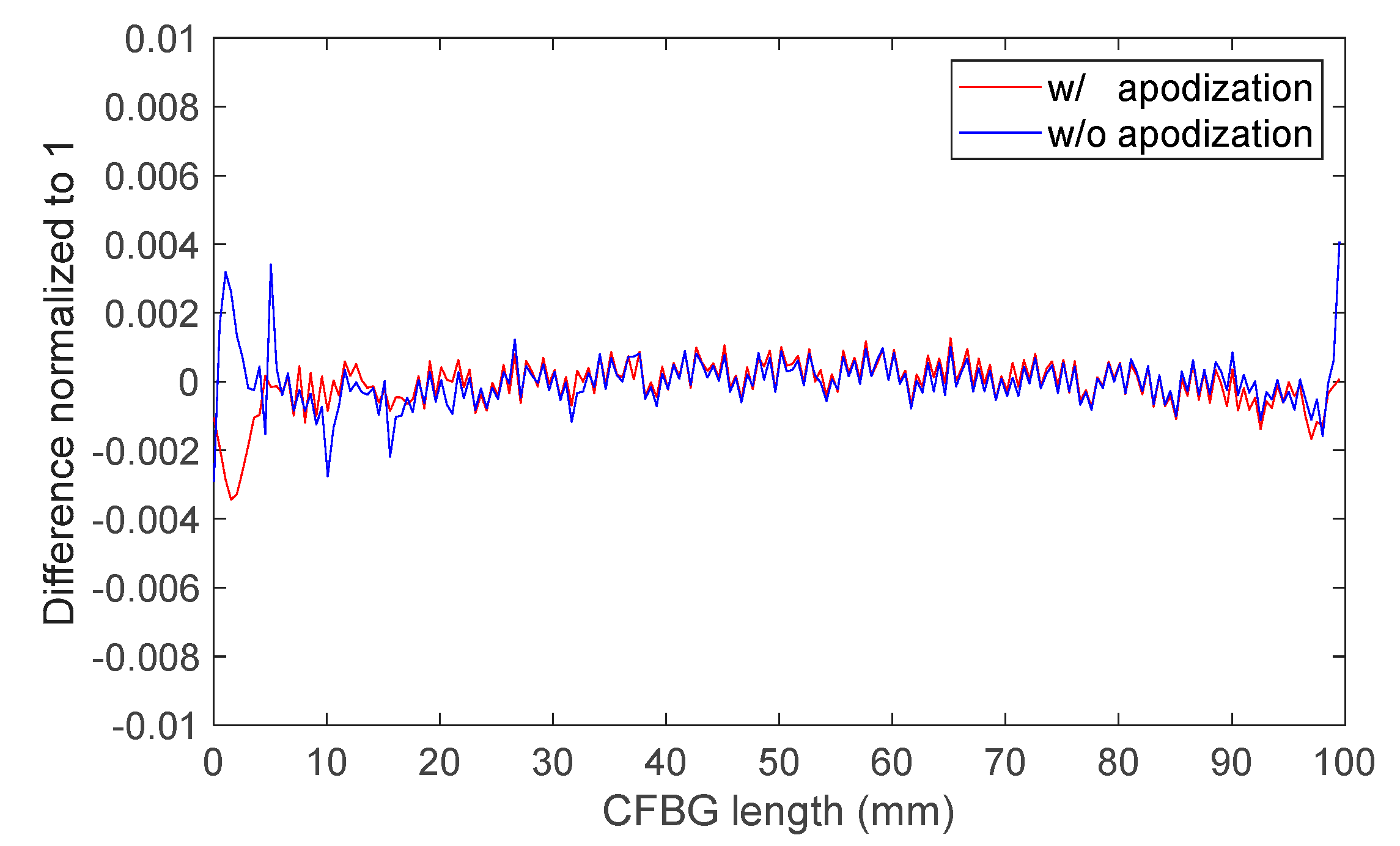
3. Optical Simulation of the CBFG during Detonation
- Central wavelength: 1545 nm;
- Length: 100 mm;
- Chirp rate: 0.16 nm/mm;
- Averaged refractive index: 1.47;
- Refractive index modulation: 2.5 × 10−4;
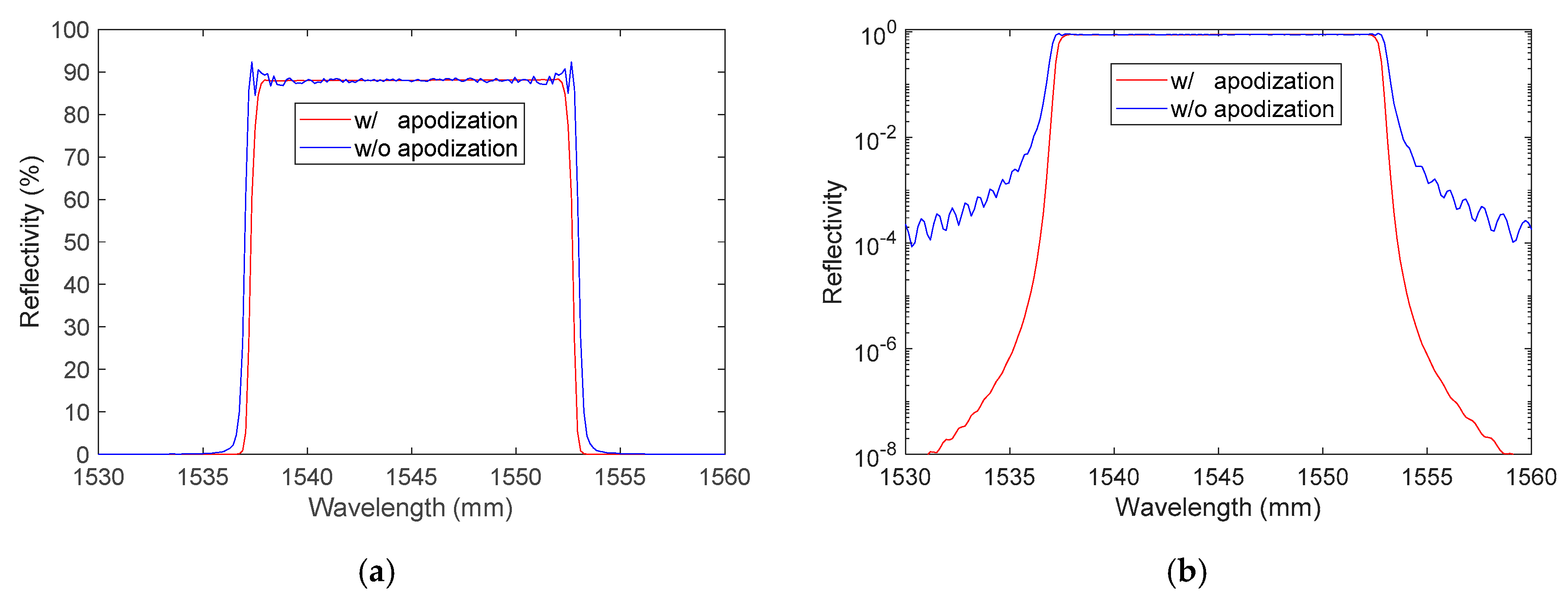
- Apodization: with and without.
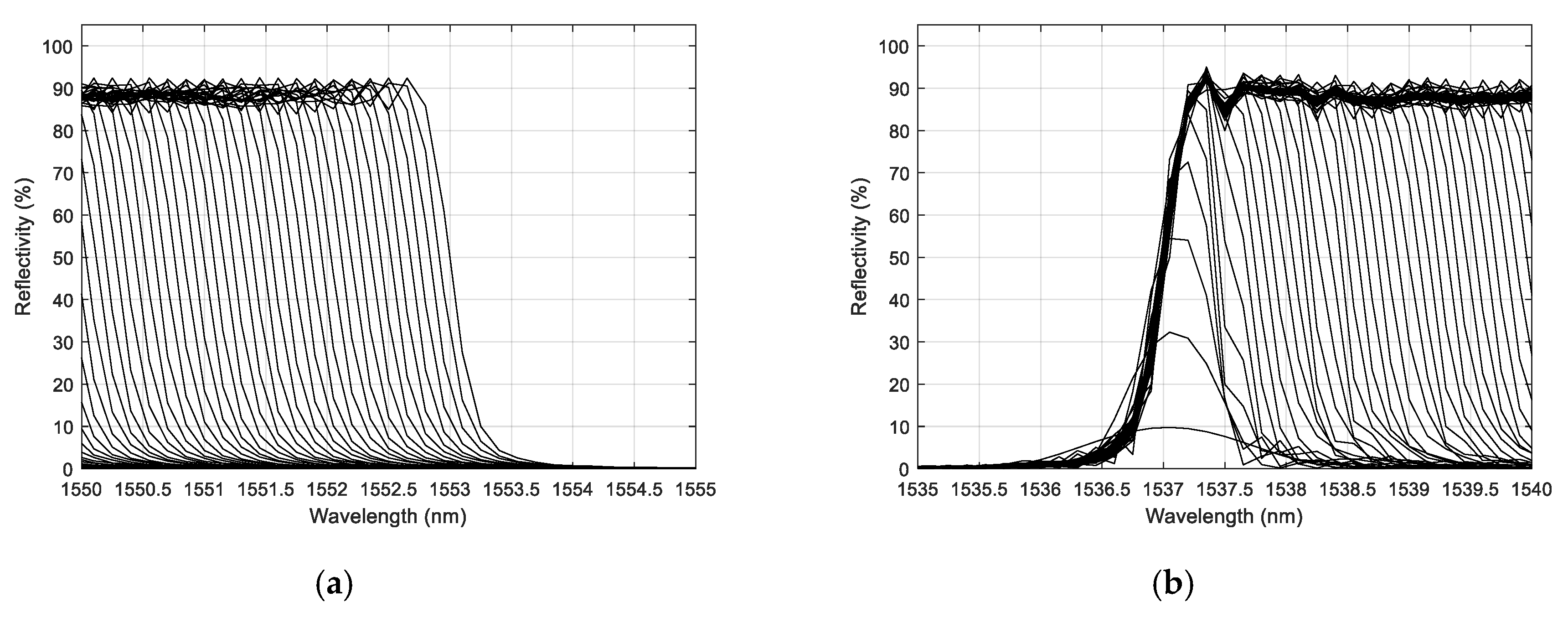
- Center maximum reflectivity: ~88%;
- Spectrum full width at half maximum: 16.2 nm.
- Center maximum reflectivity: ~88%;
- Spectrum full width at half maximum: 15.6 nm.
4. Calibration Procedure Using the Initial Reflected Spectrum
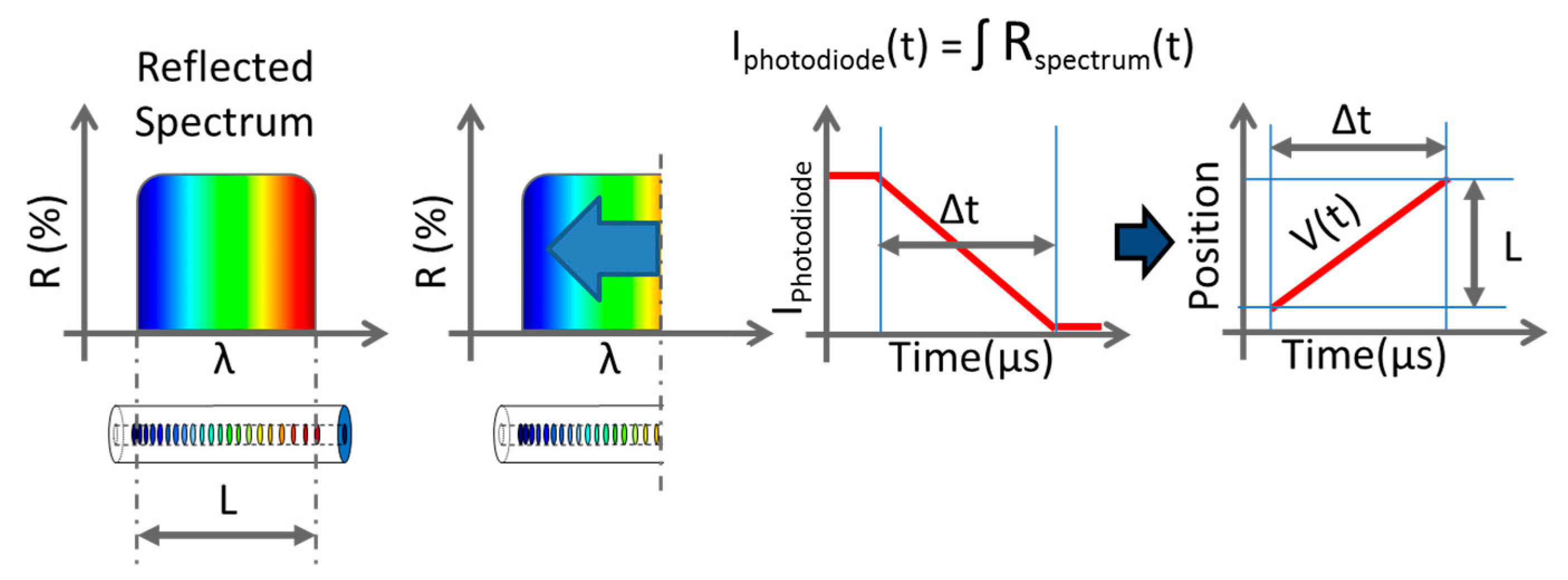
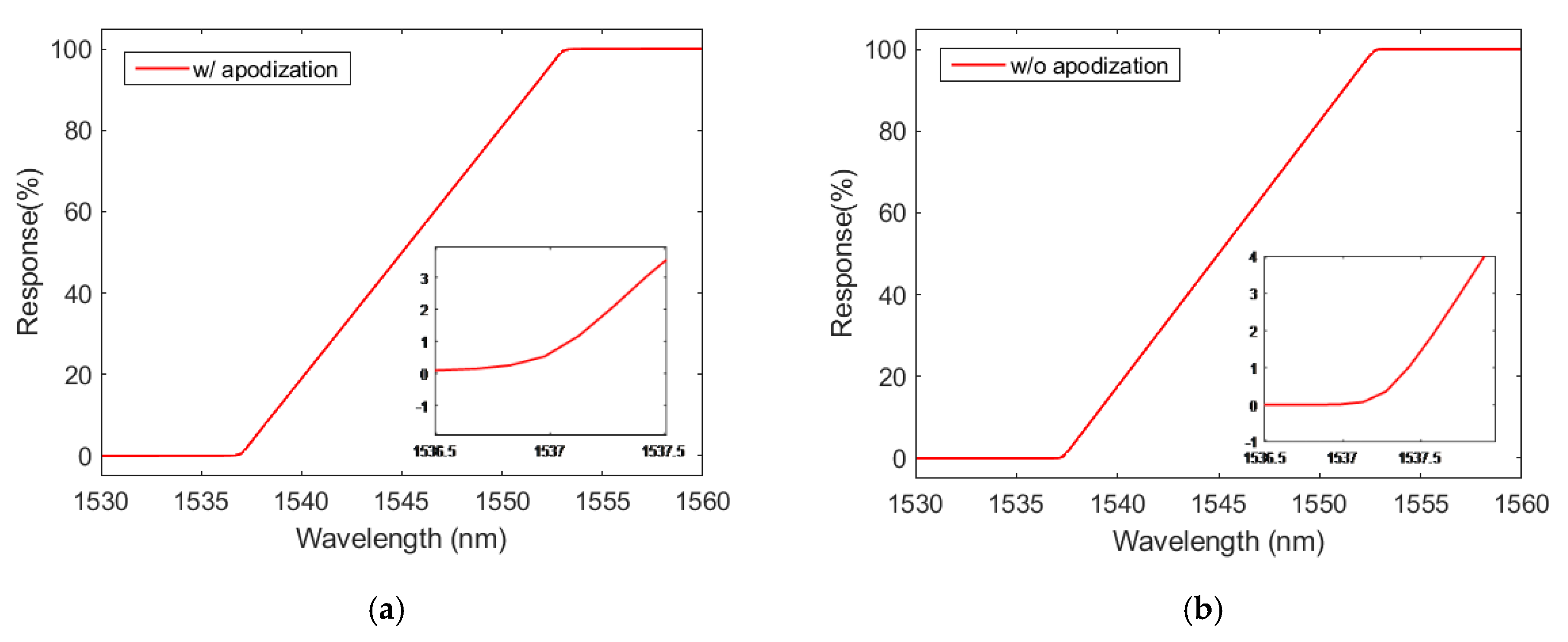
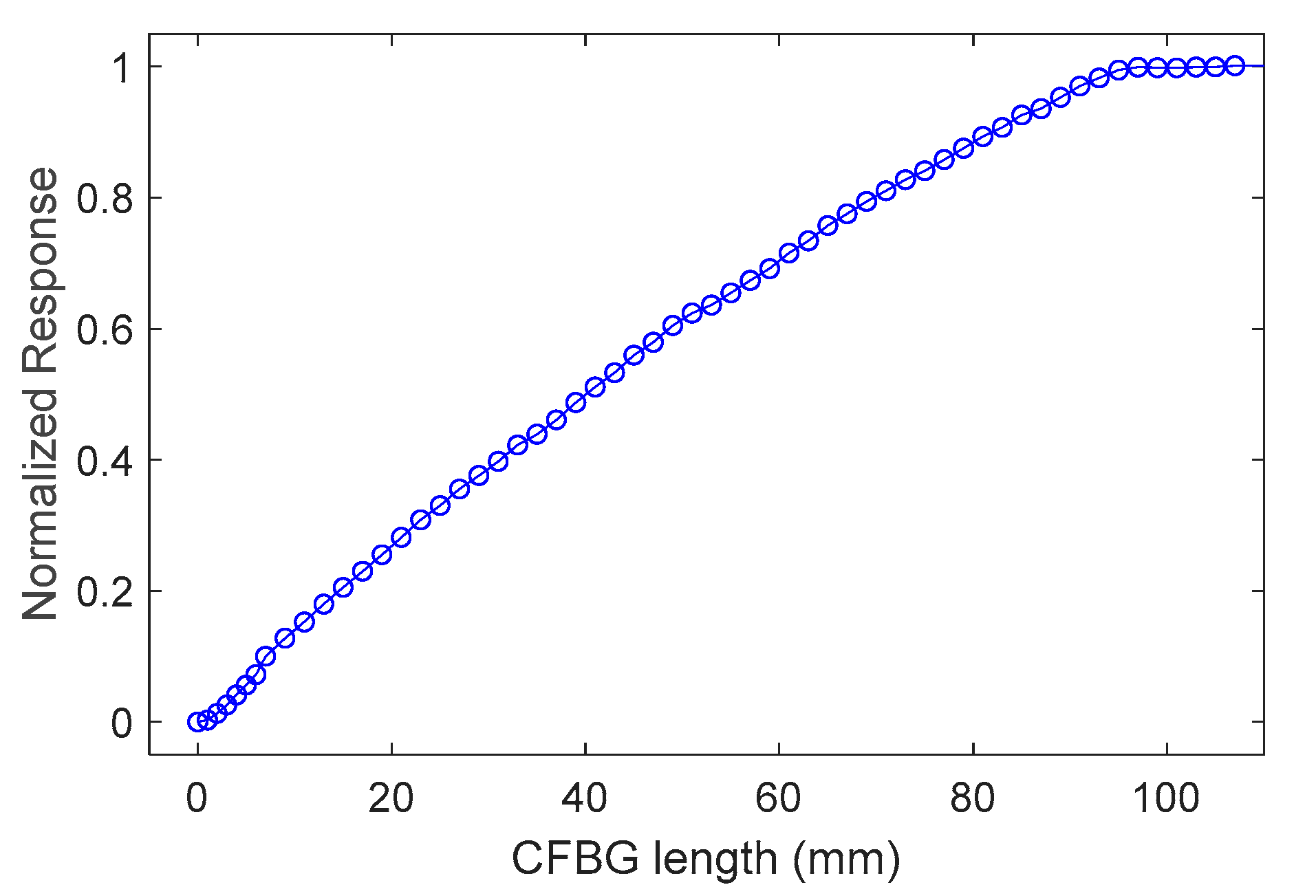
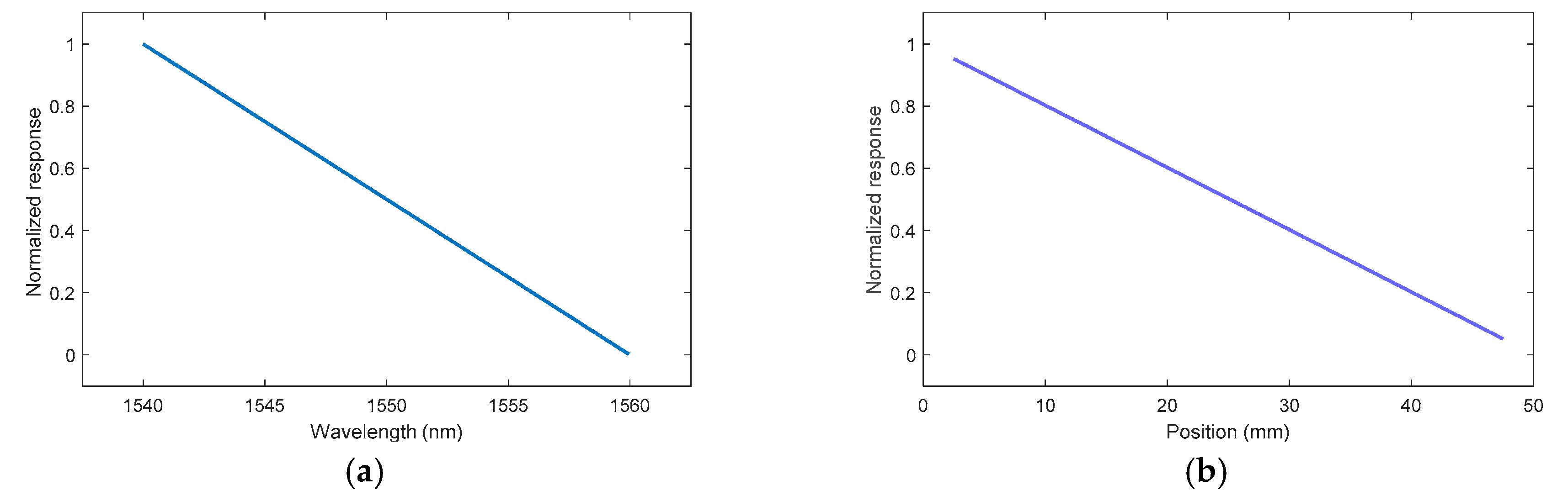
4.1. Theoretical CFBG Response
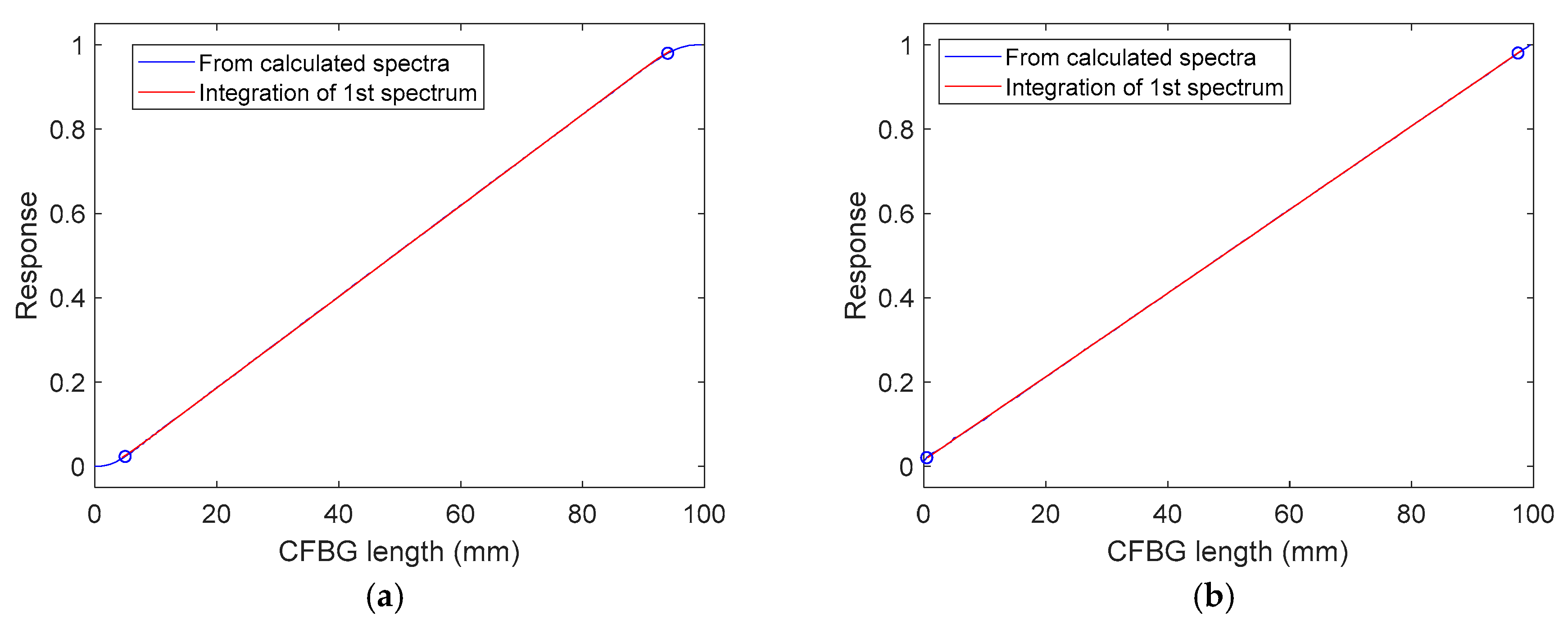
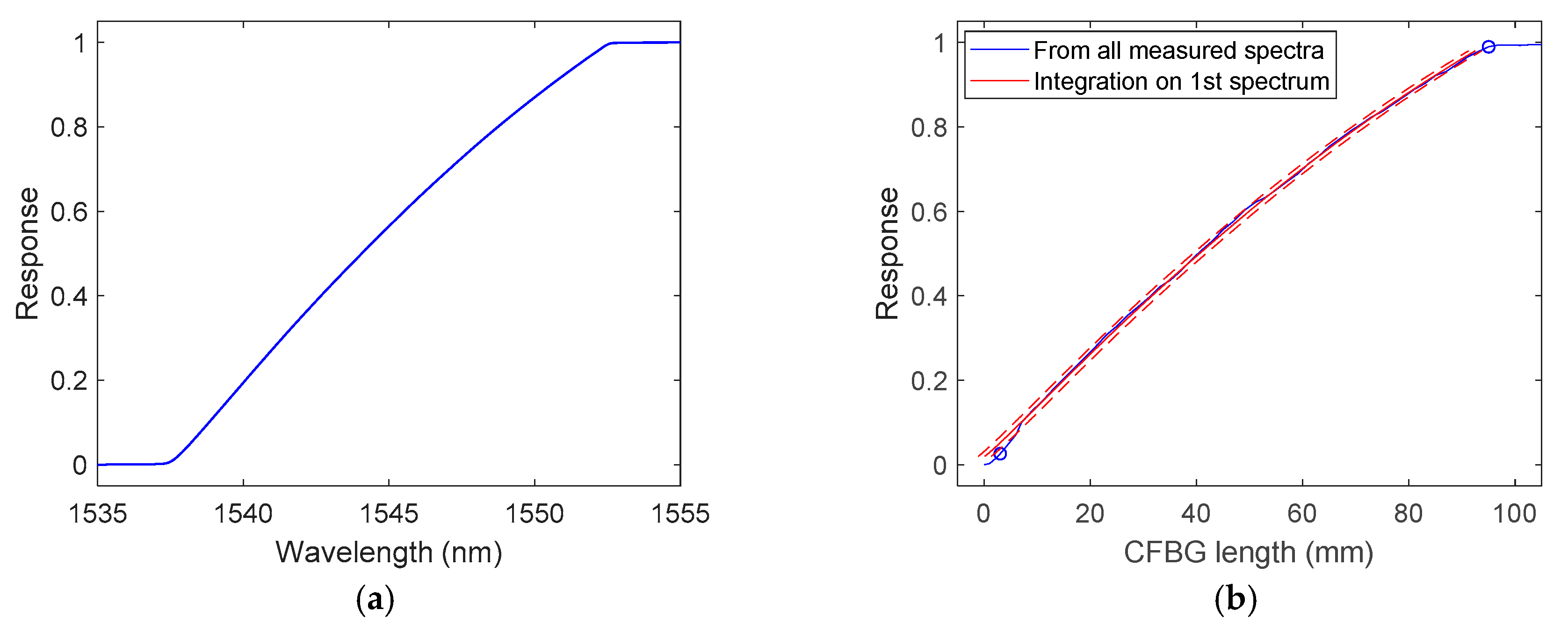
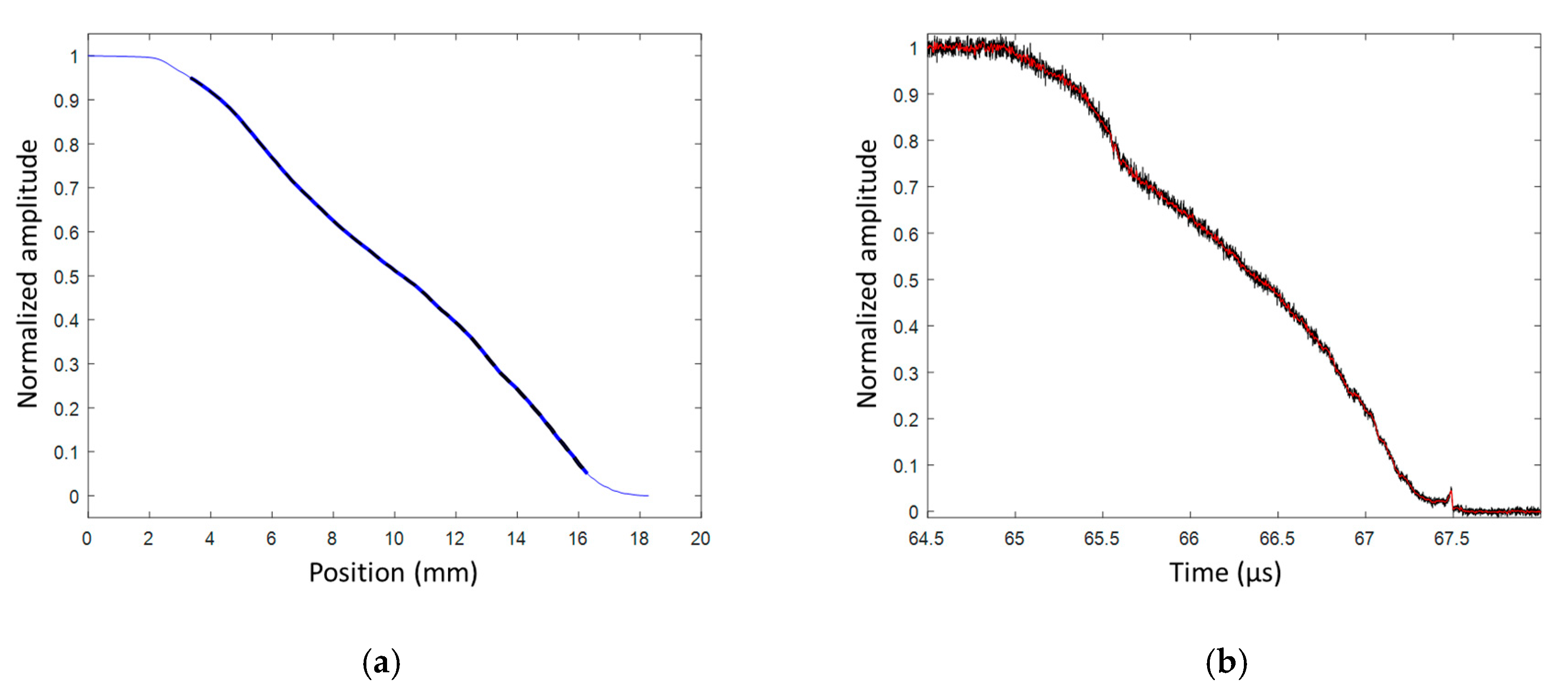
4.2. Simulated CFBG Response from the Initial Spectrum
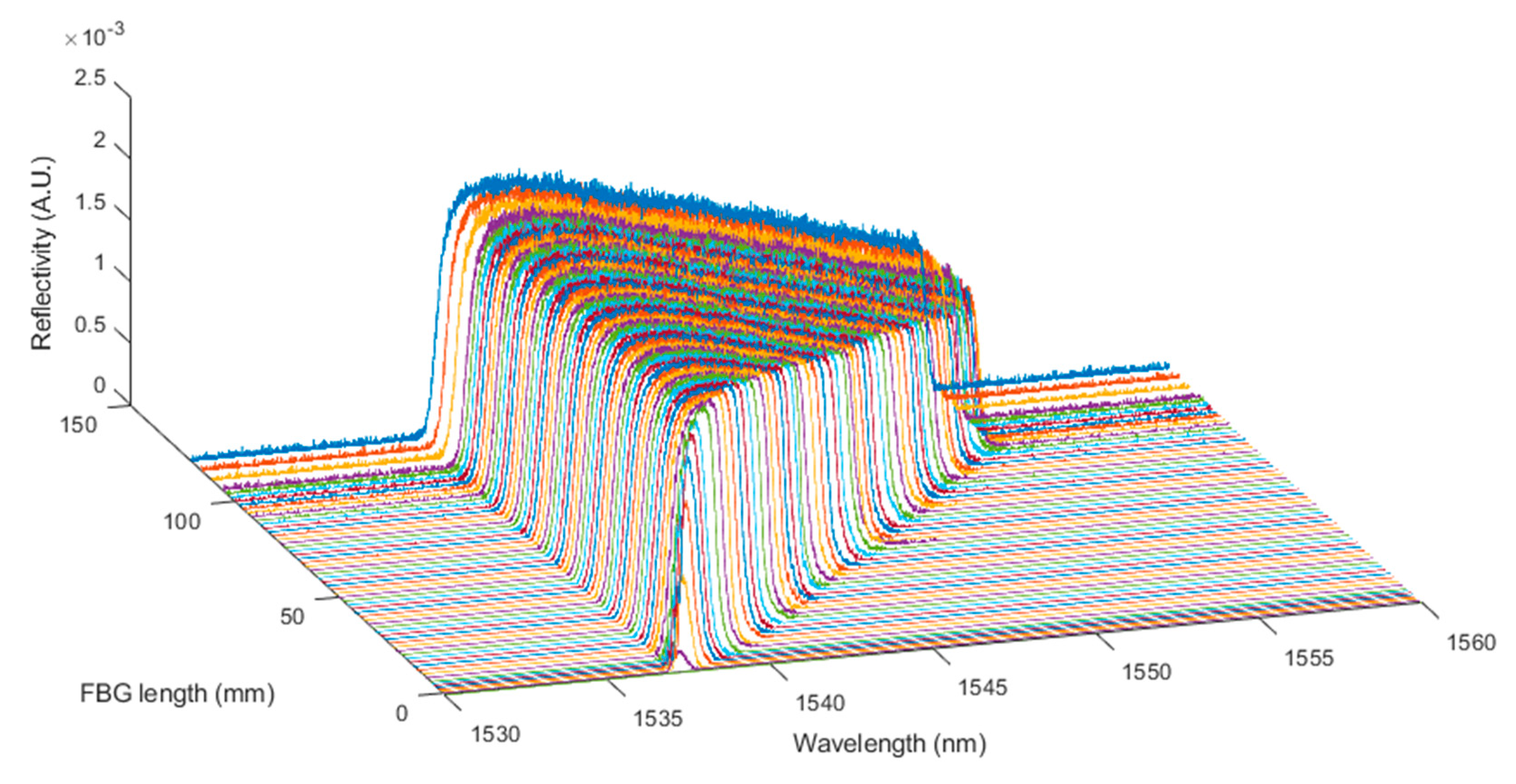
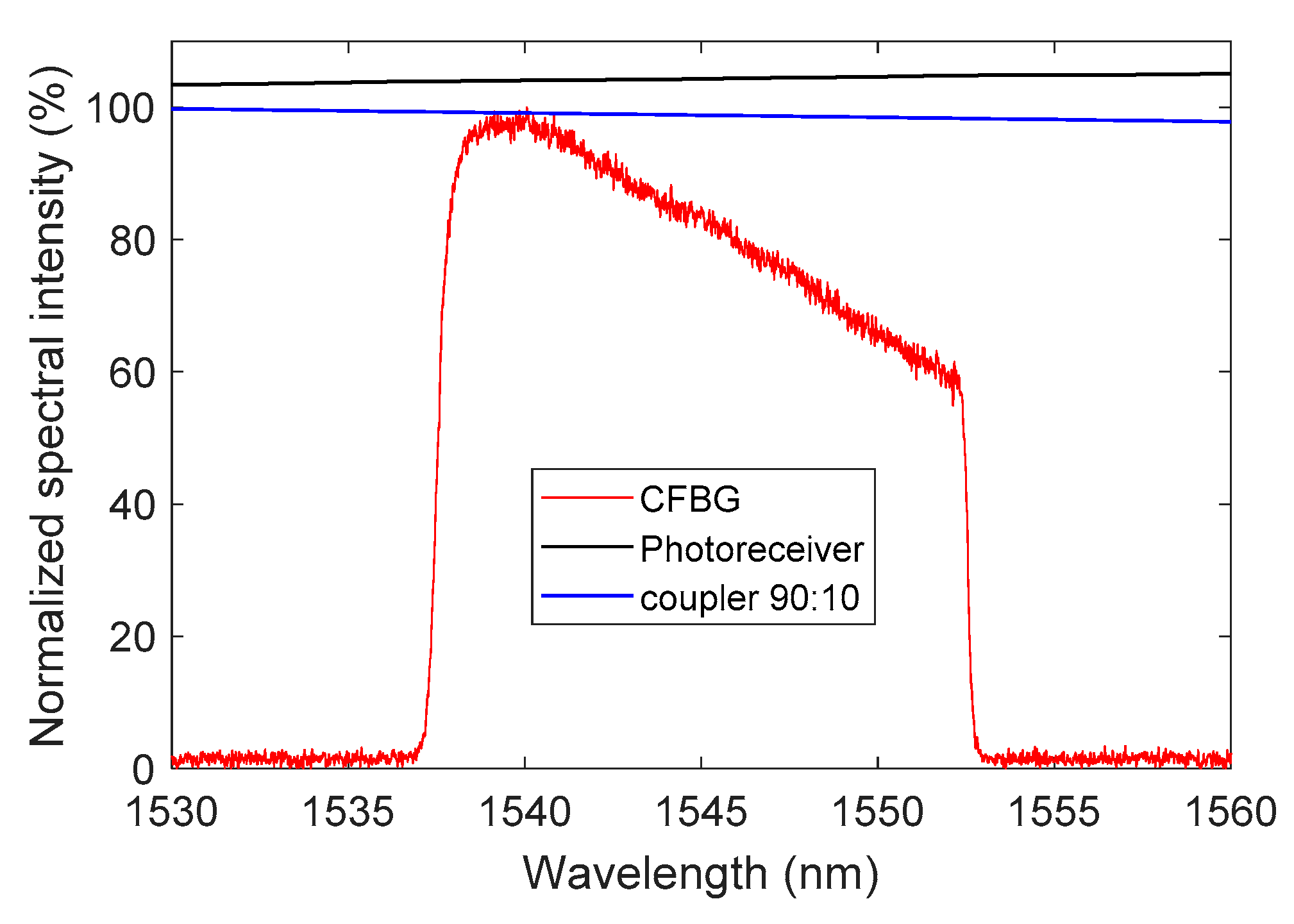
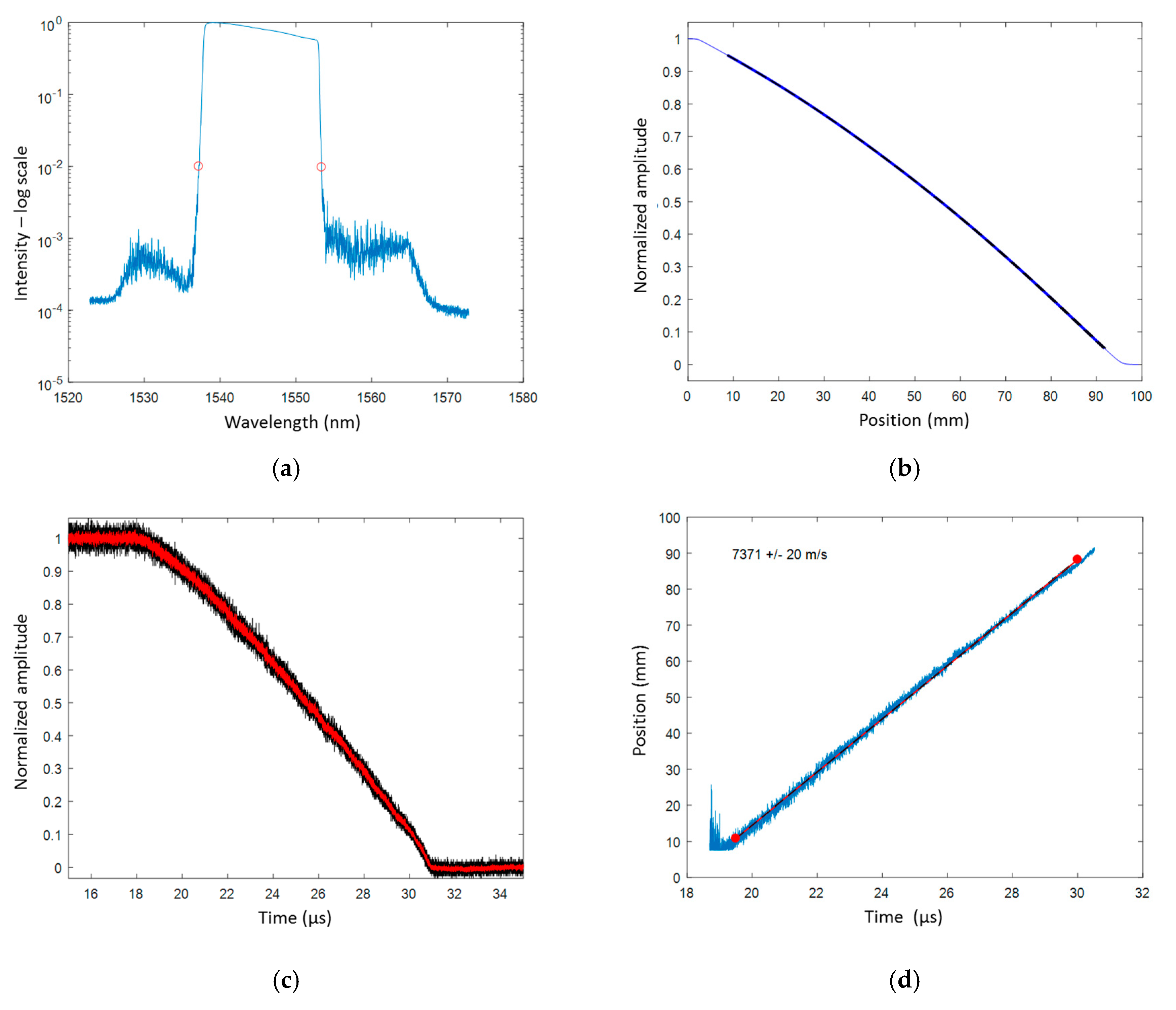
4.3. Experimental CFBG Response from the Initial Spectrum
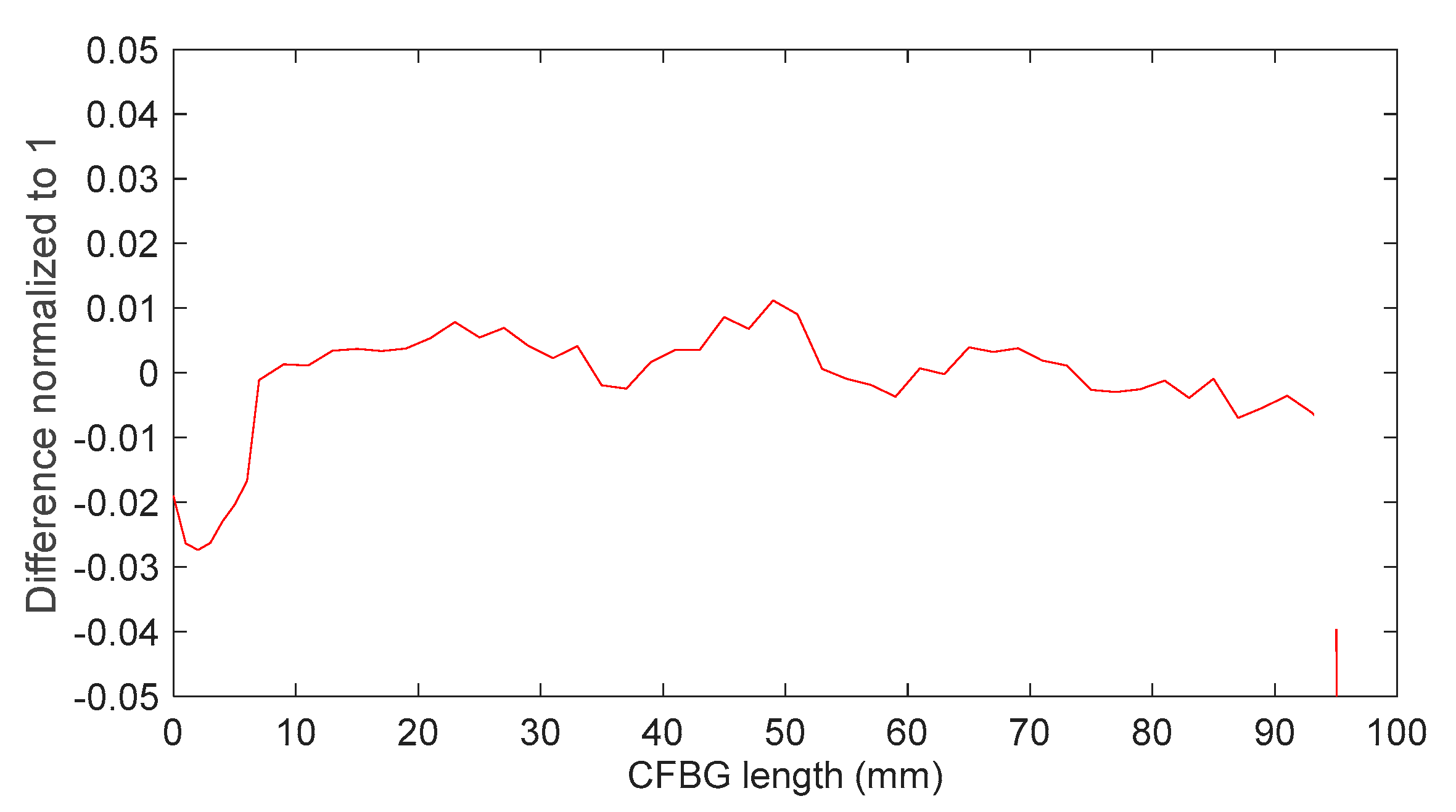
5. Estimation of Experimental Uncertainties by Simulations
5.1. Definition of the Main Parameters
- Steady detonation velocity: 7500 m/s;
- CFBG length: 50 mm;
- Oscilloscope sampling frequency: 1 Gs/s;
- OSA resolution: 0.05 nm;
- Standard deviation on the BraggFast signal SNR: 2%;
- Standard deviation on the optical spectrum SNR: 2%;
- CFBG FWHM: 20 nm;
- Upper CFBG response bound: 0.95;
- Lower CFBG response bound: 0.05;
- Number of points used to smooth the BraggFast signal: 7.
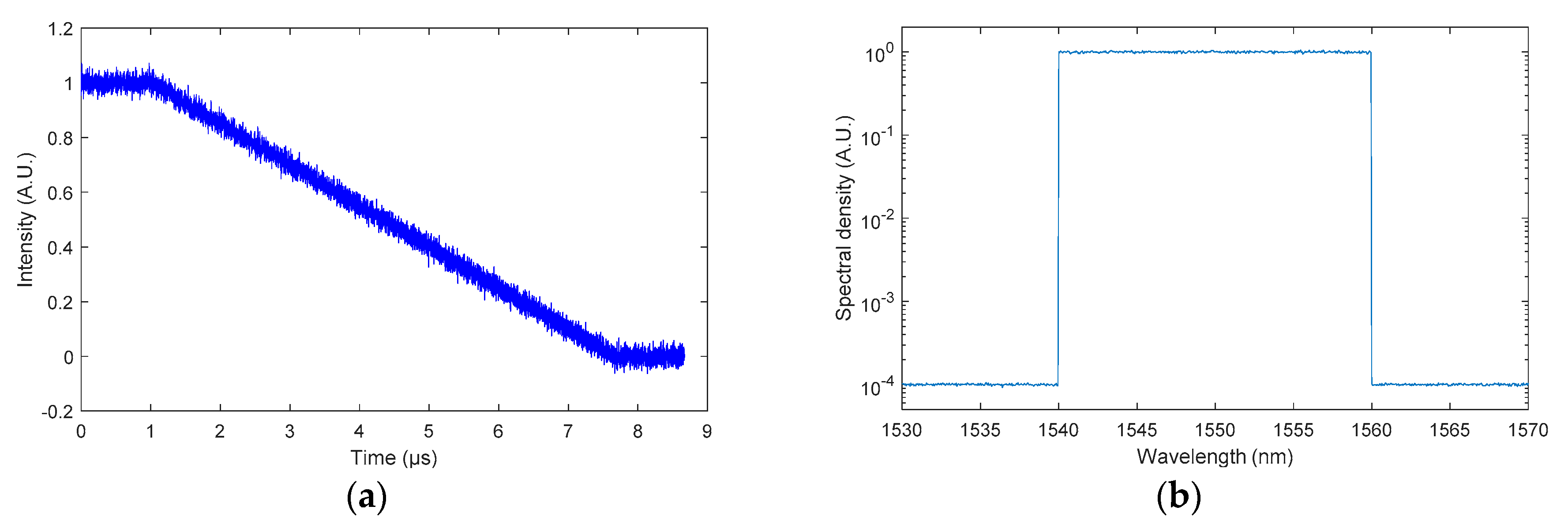
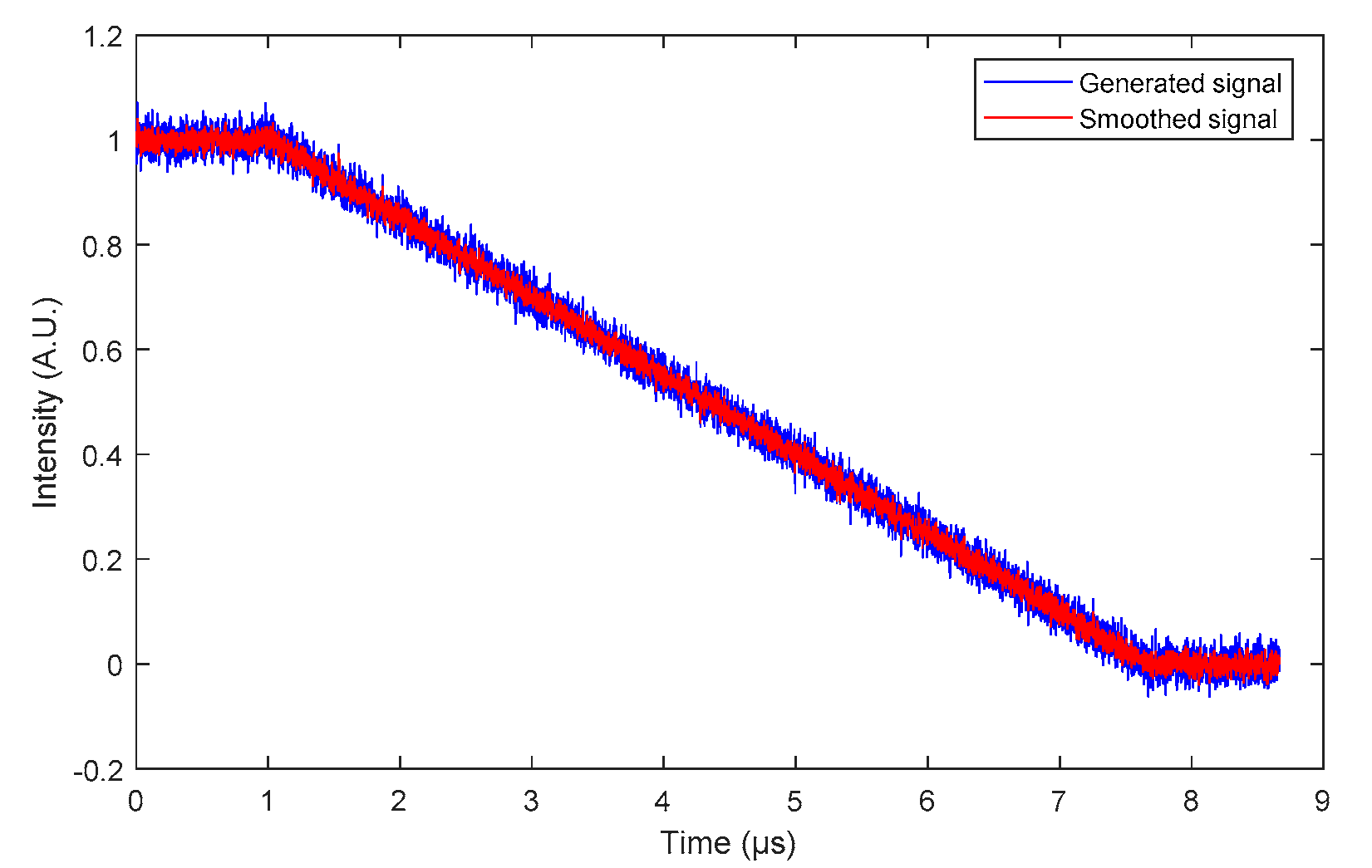
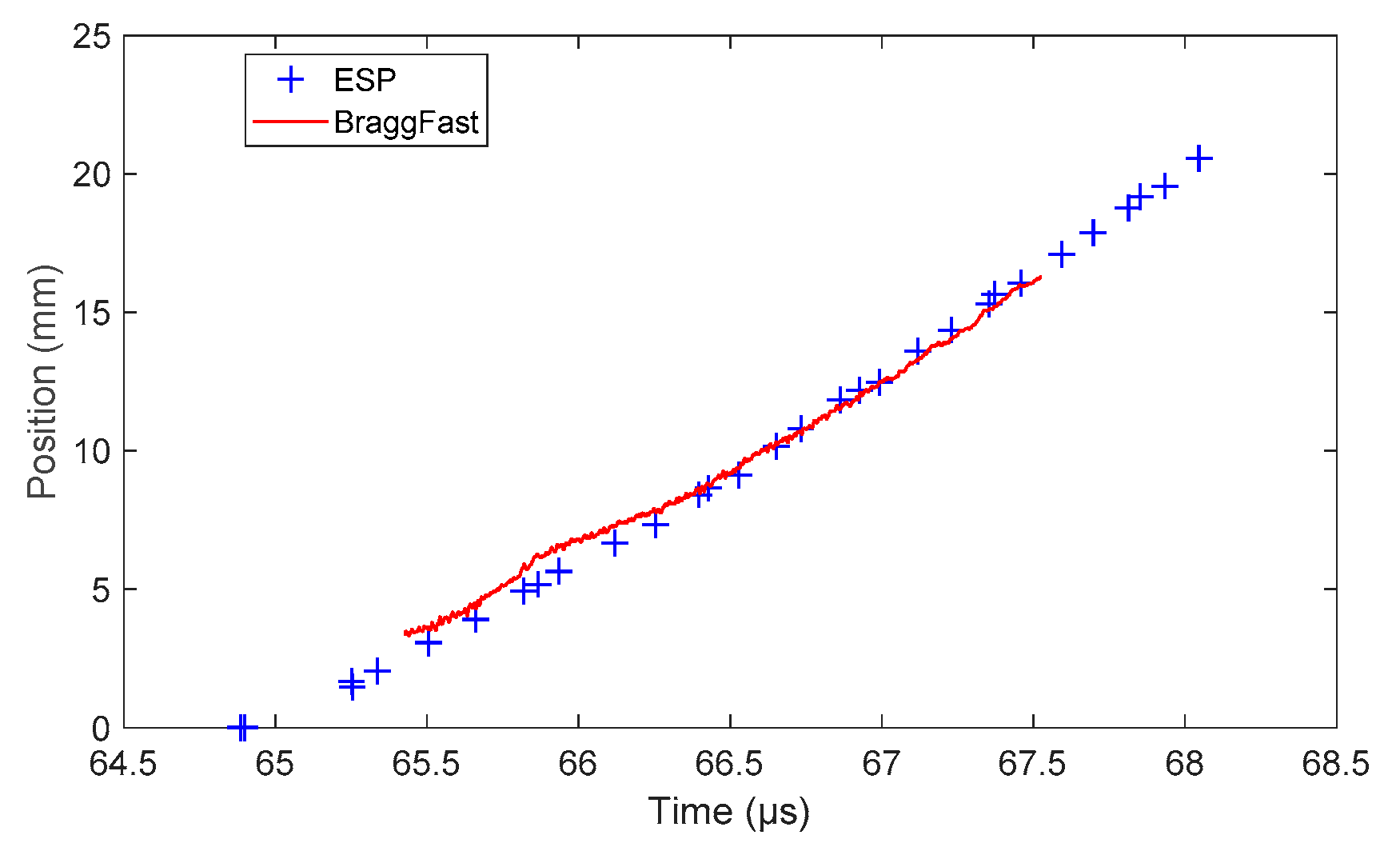
5.2. BraggFast Signal Processing
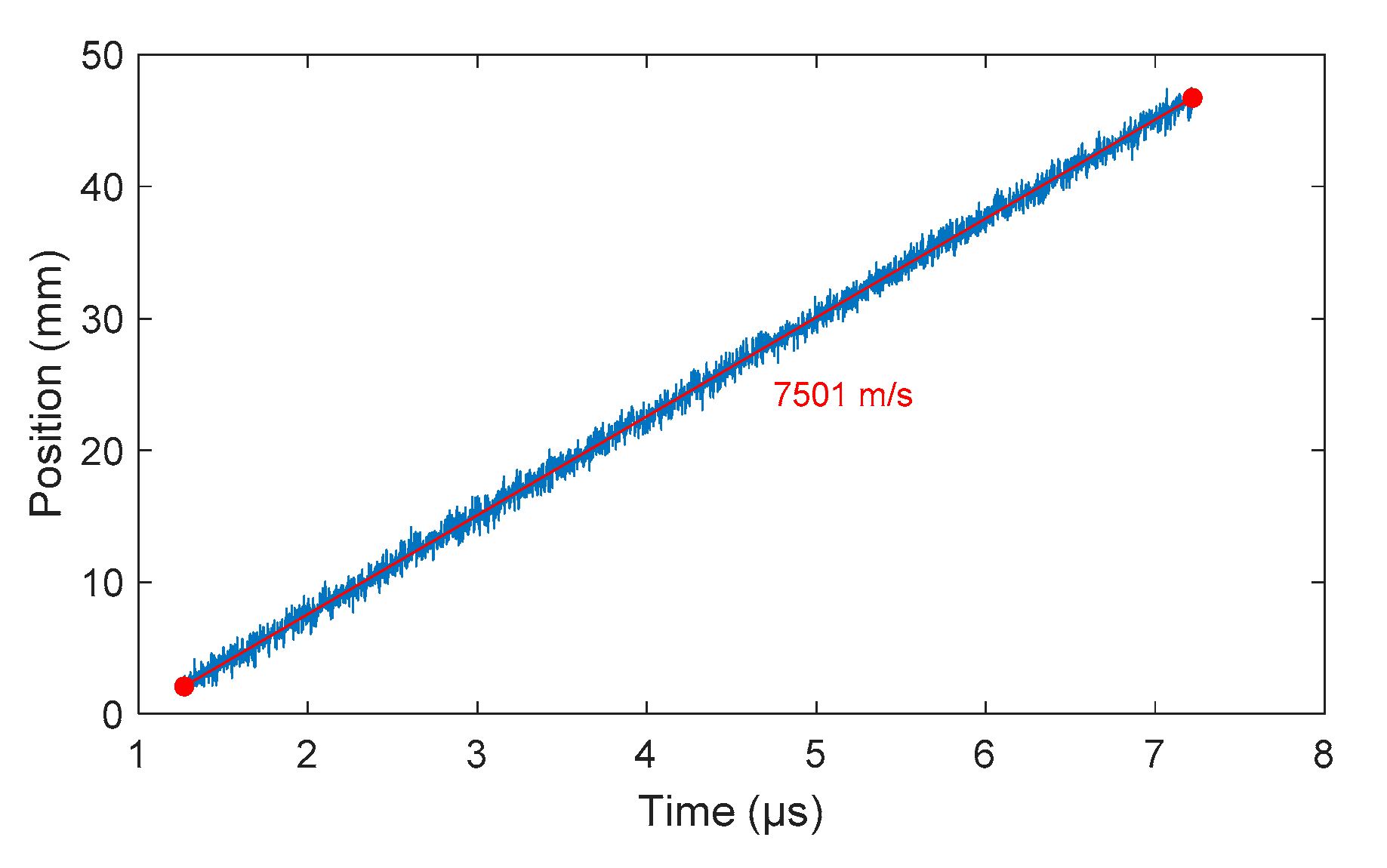
5.3. Detonation Velocity Estimation
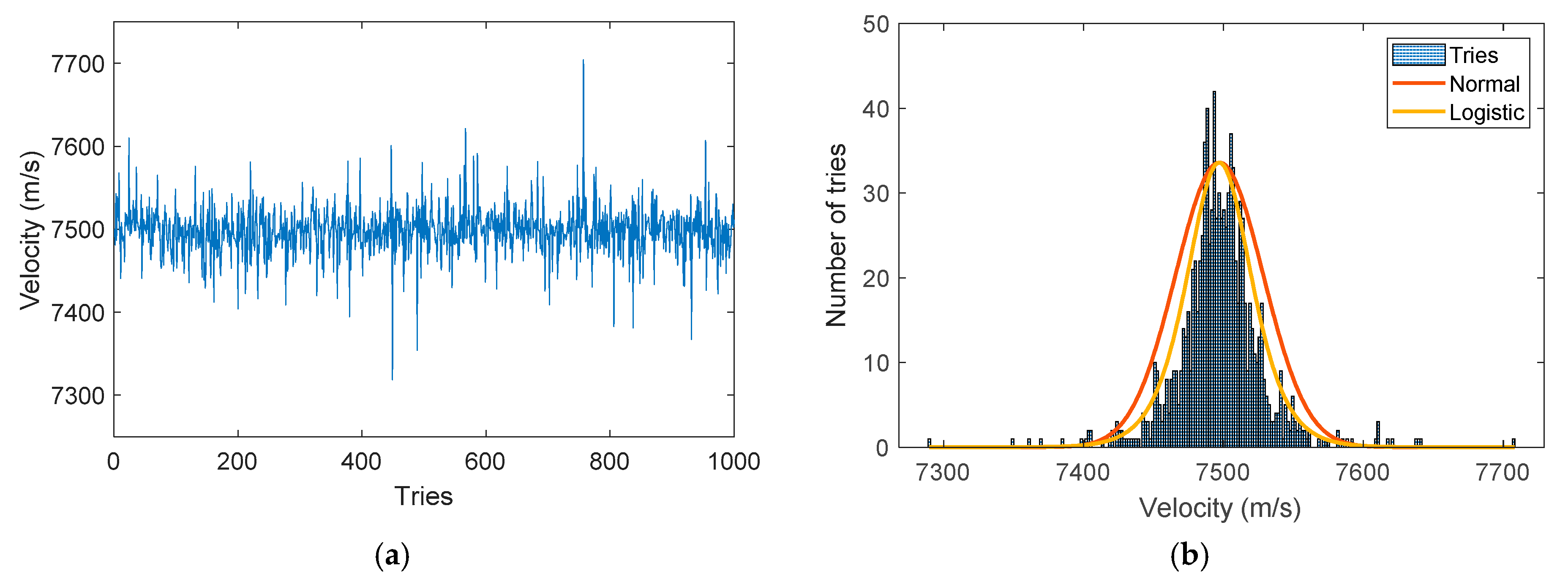
5.4. Influence of the Parameters on the BraggFast Signal Processing
- Series 1: CFBG length variation (10–100 mm);
- Series 2: number of smoothing points (3–20 points);
- Series 3: standard deviation in the BraggFast signal (0.01–3%);
- Series 4: standard deviation in the optical spectrum (0.01–5%).
6. Experimental Results
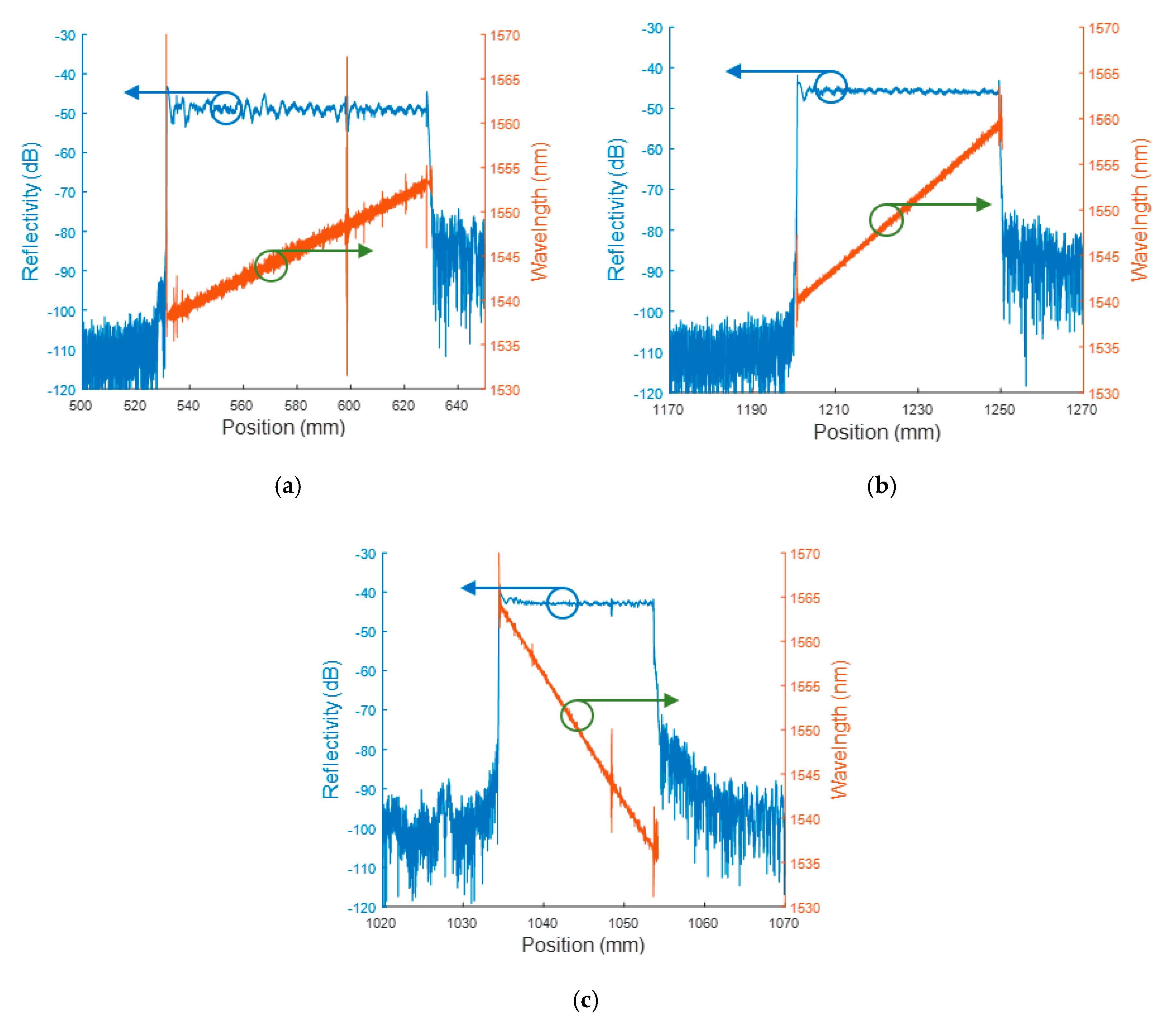
6.1. CFBGs Characterizations
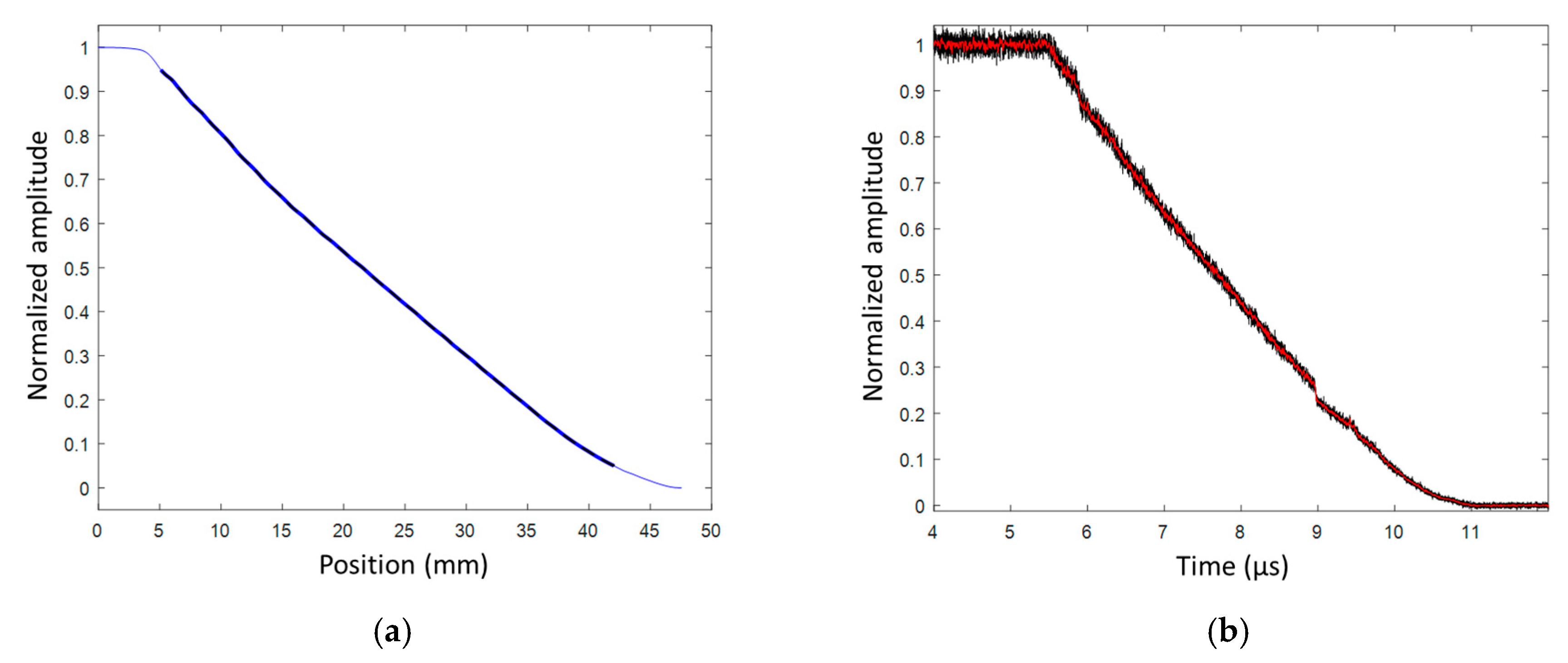
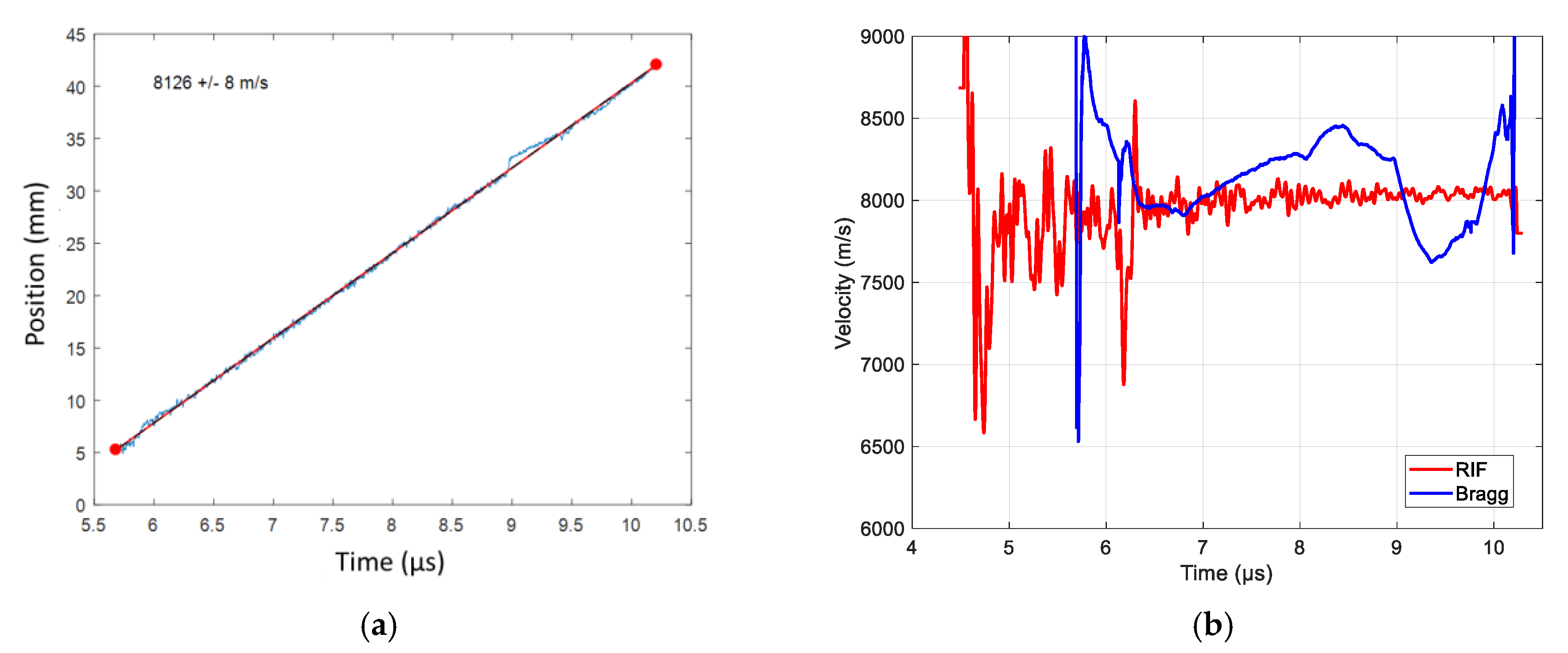
6.2. Steady Detonation Velocity on a Surface Line of a Bare Cylindrical Stick
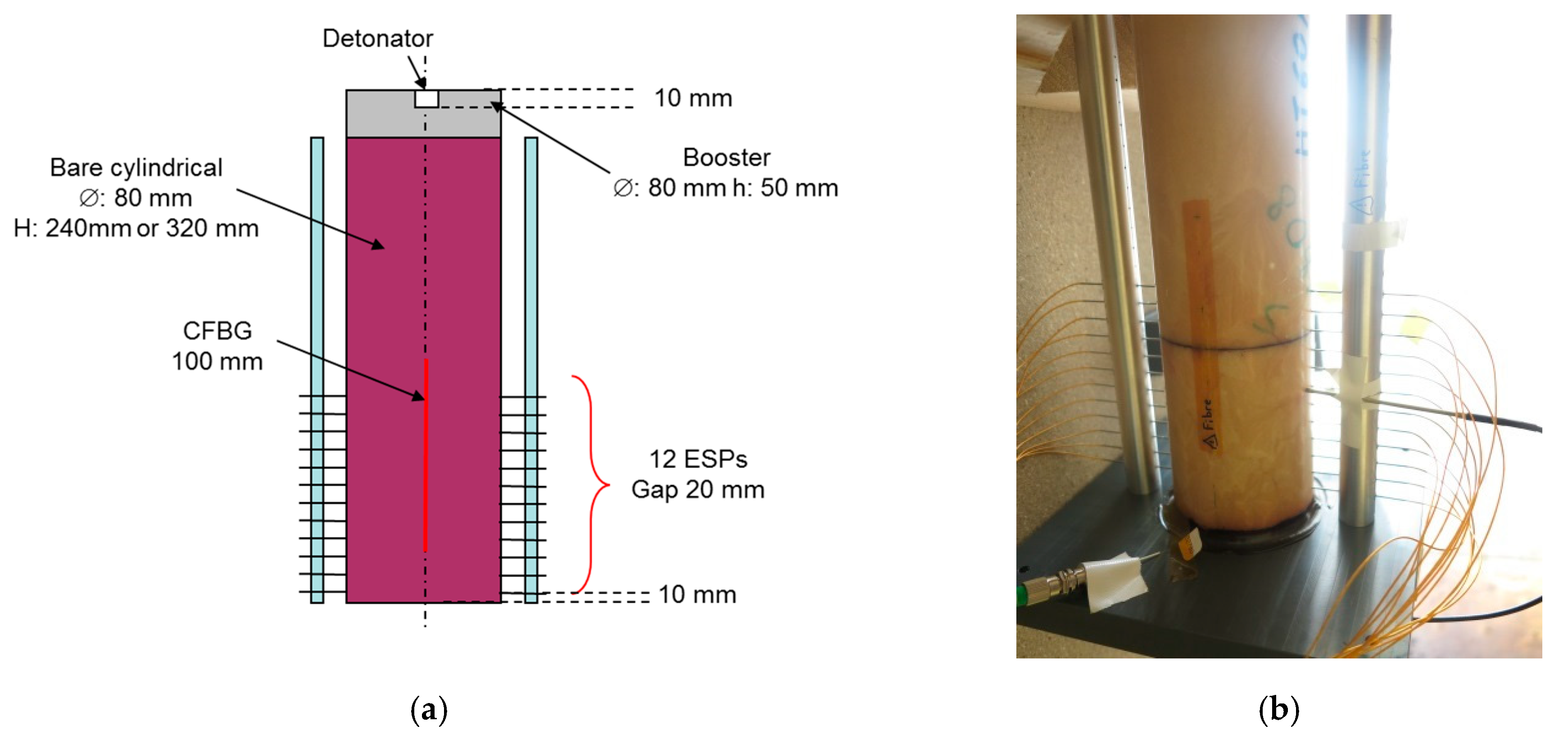
6.2.1. Set-Up
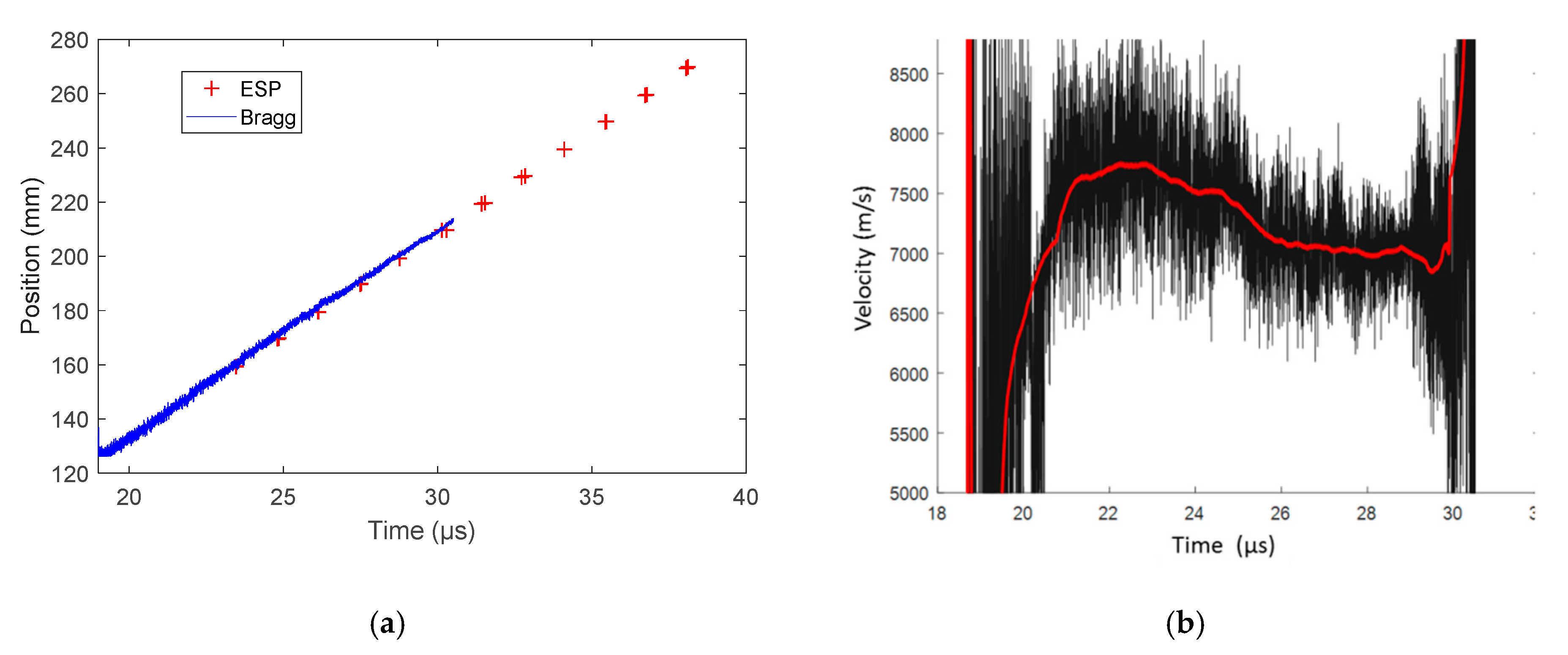
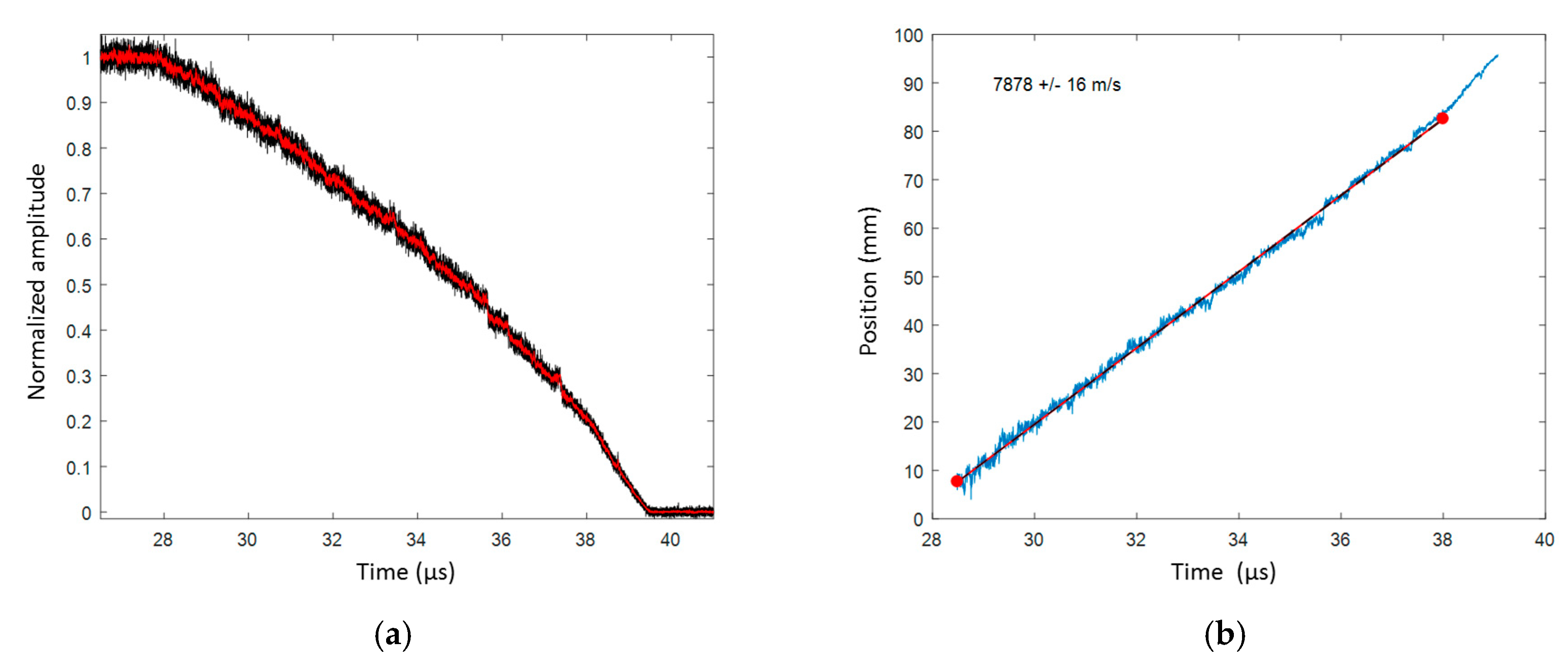
6.2.2. Bare Cylindrical Stick Results with a CFBG on a Surface Line
TNTO Steady Detonation Velocity
Comp B Steady Detonation Velocity
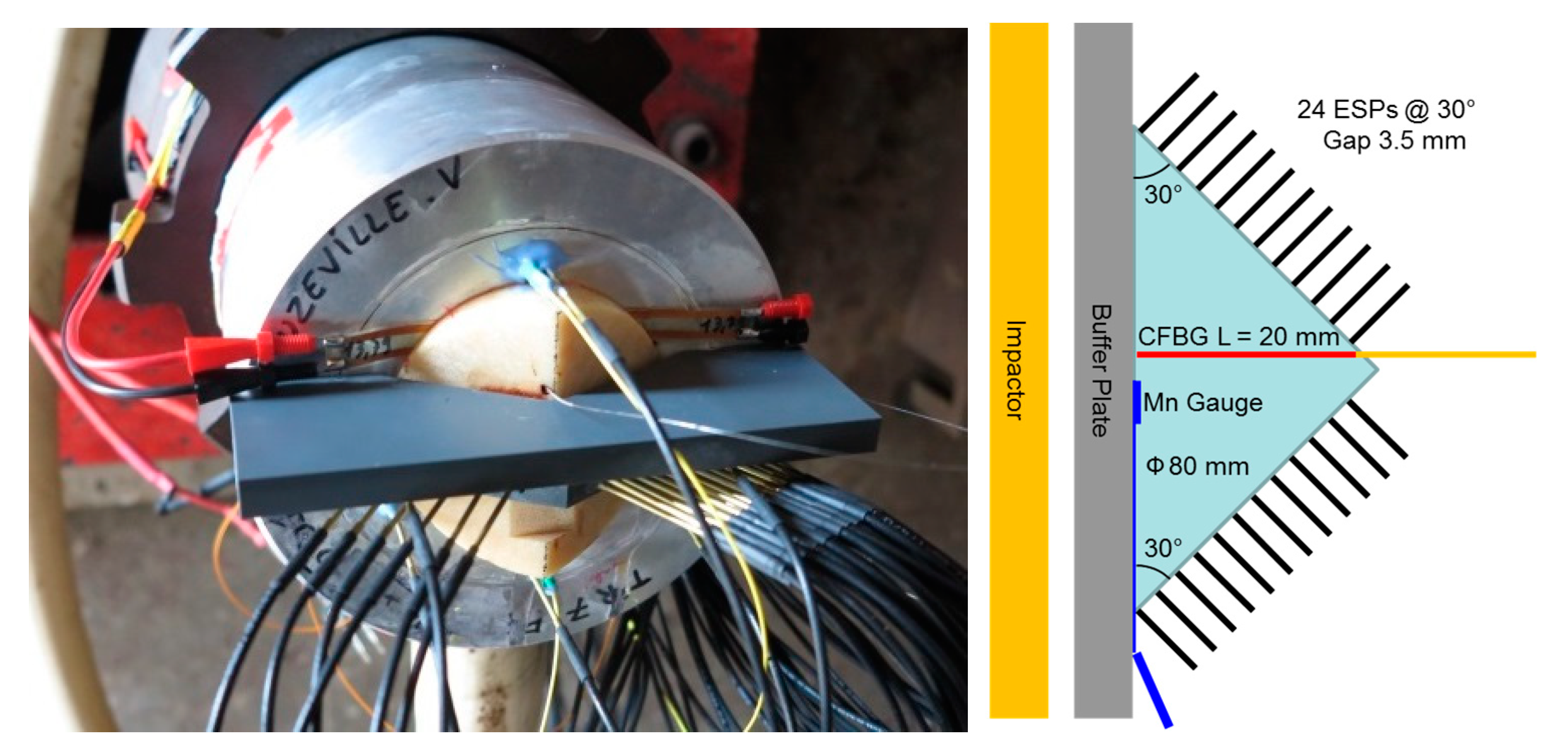
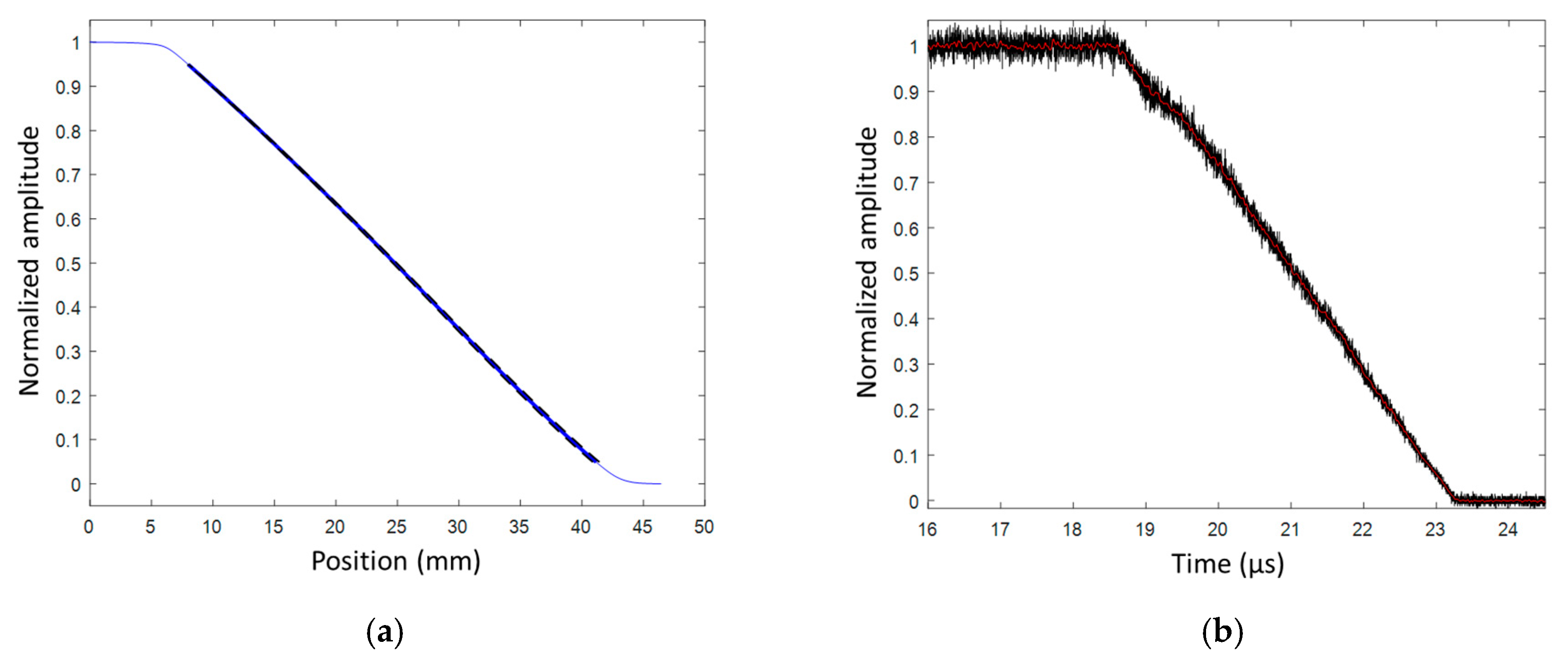
6.3. SDT Characterization in a Wedge Configuration
6.3.1. Set-Up
6.3.2. SDT Results
TNTO SDT
HMX/PBHT (90%/10%) SDT
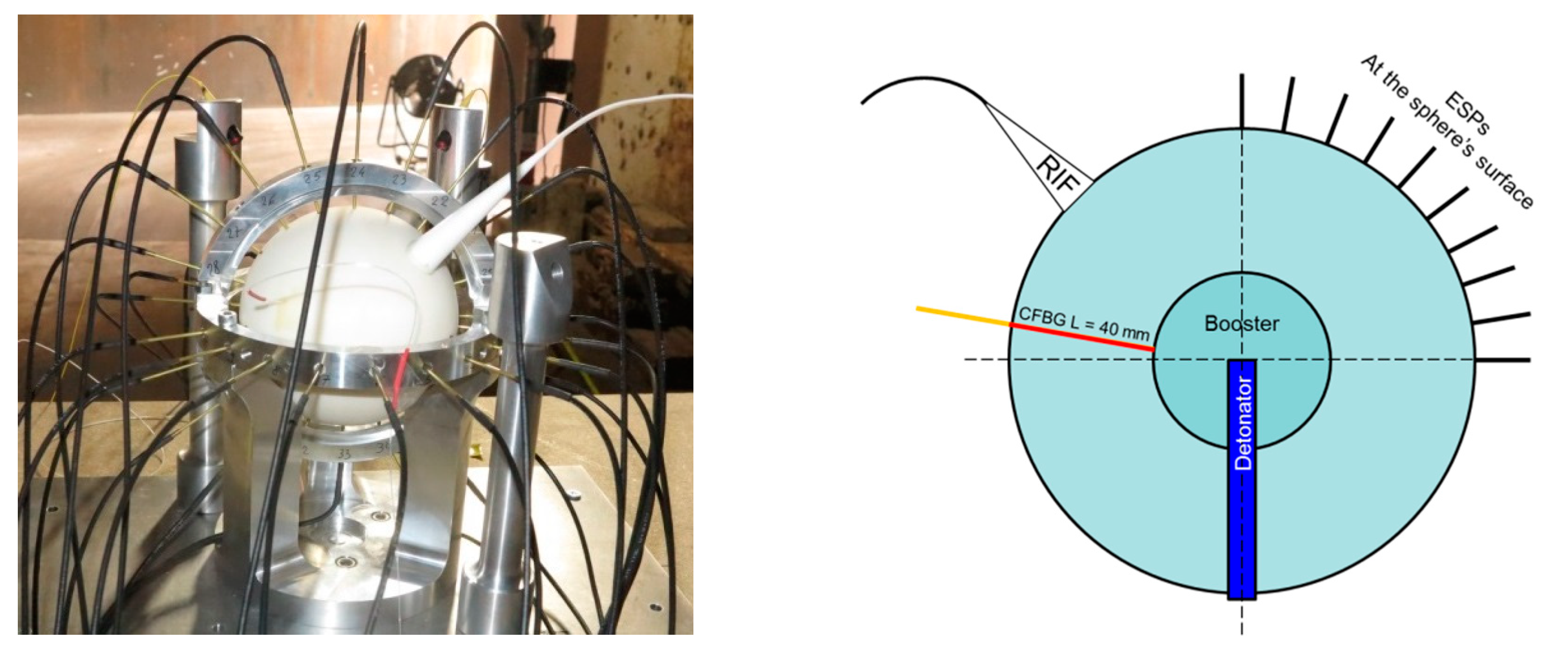
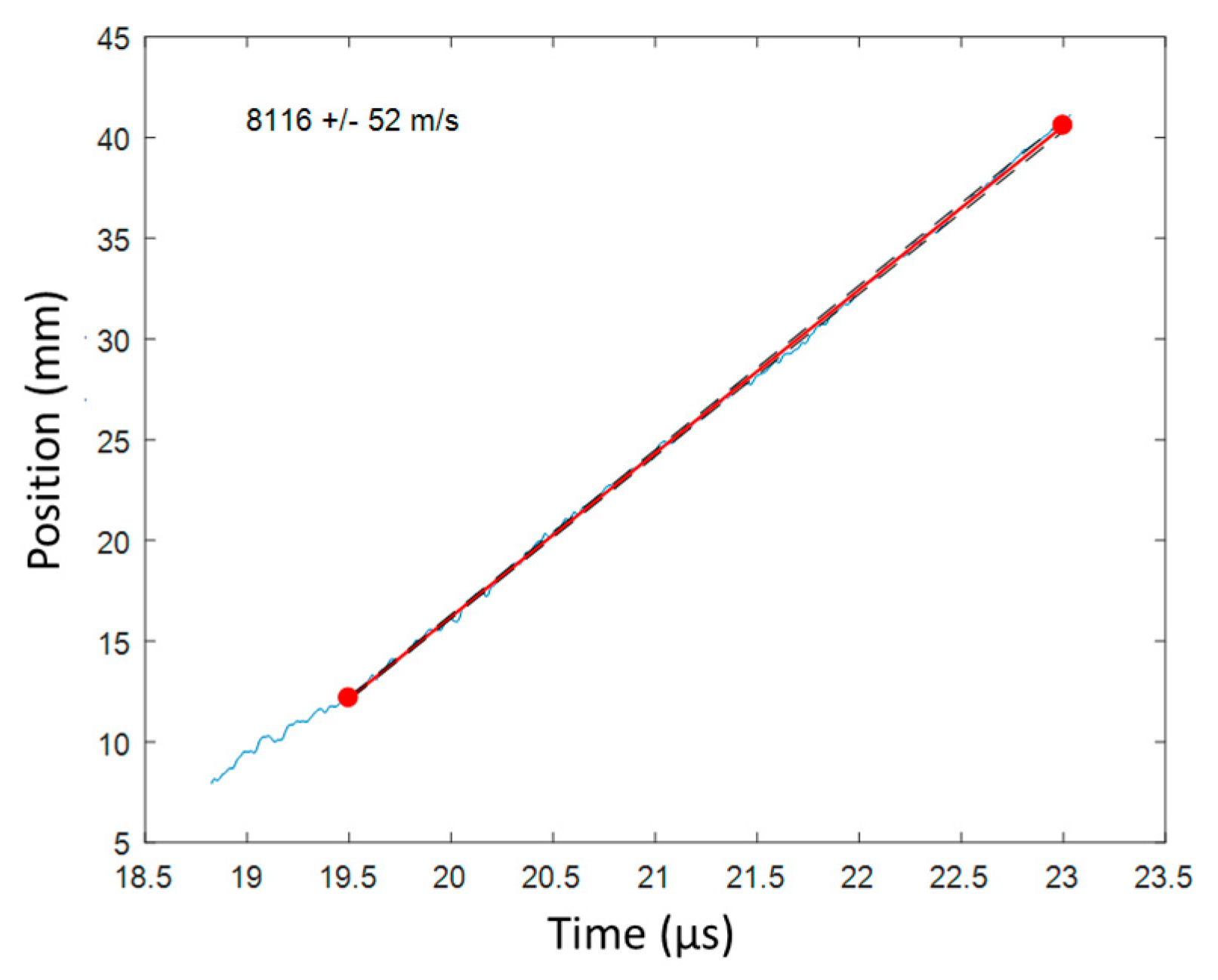
6.4. Steady Detonation Velocity in a Sphere Configuration
6.4.1. Set-Up
6.4.2. RDX/PBHT (82%/18%) Sphere Detonation Results
6.5. Steady Detonation Velocity in Cast-Cured Bare Cylinders
6.5.1. Set-Up
6.5.2. Detonation Velocity Results
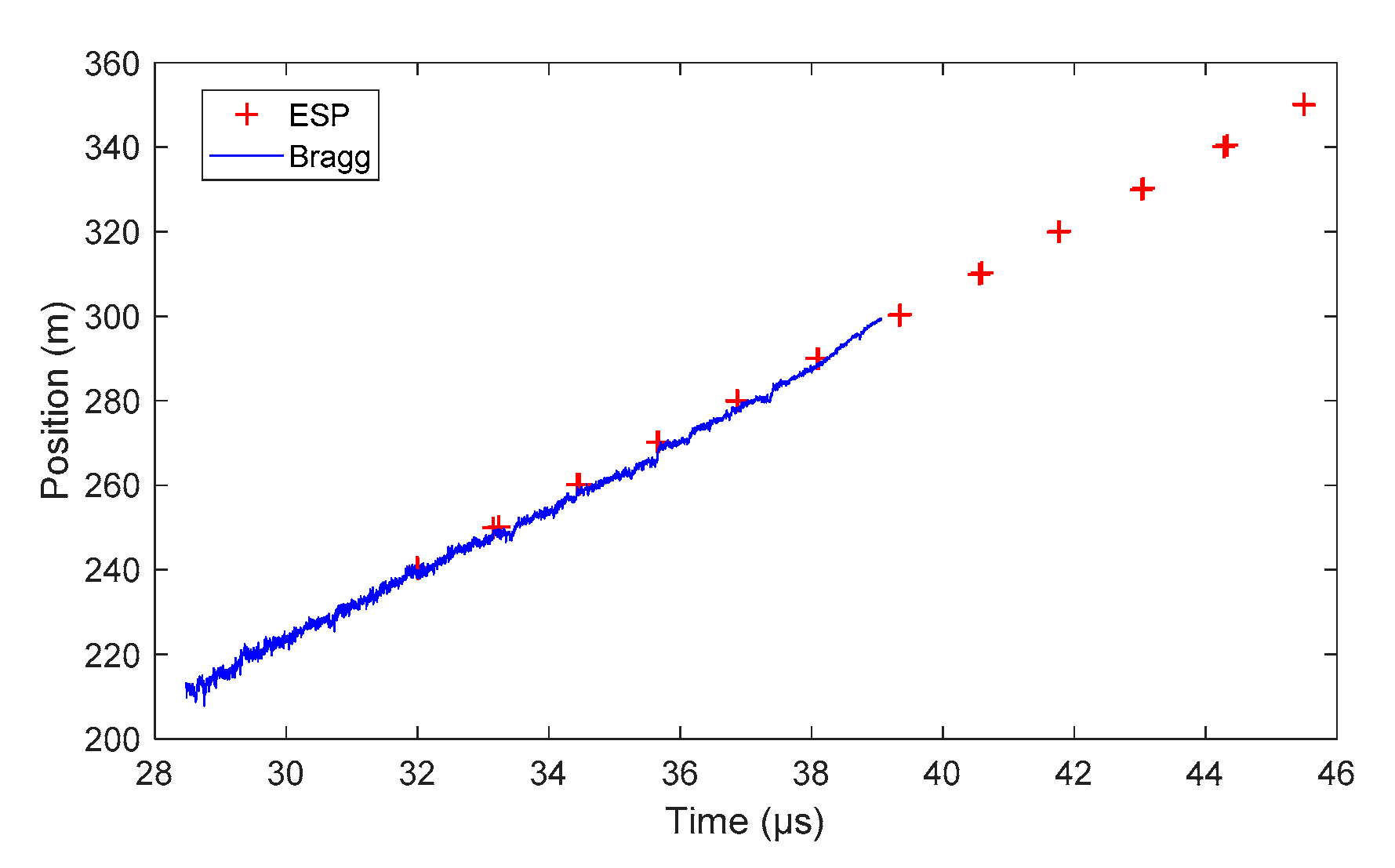
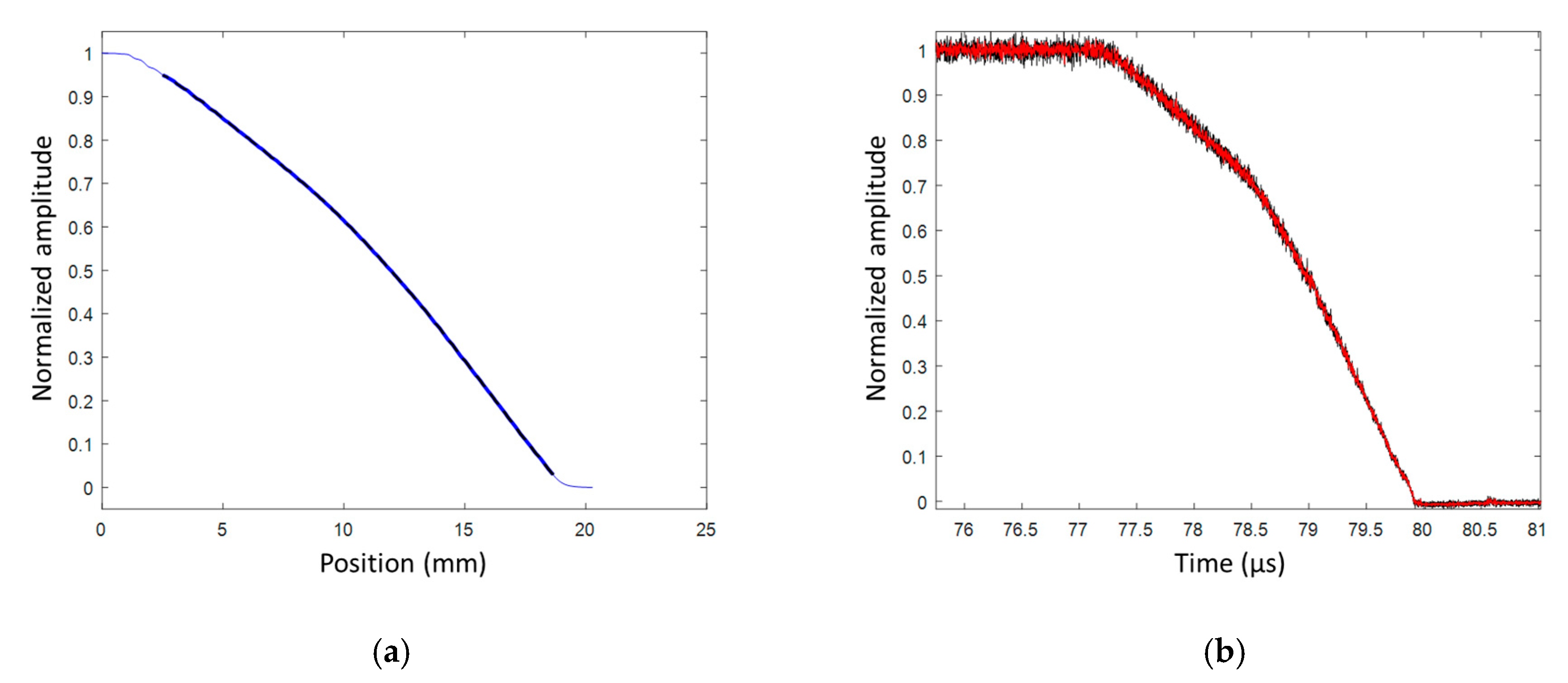
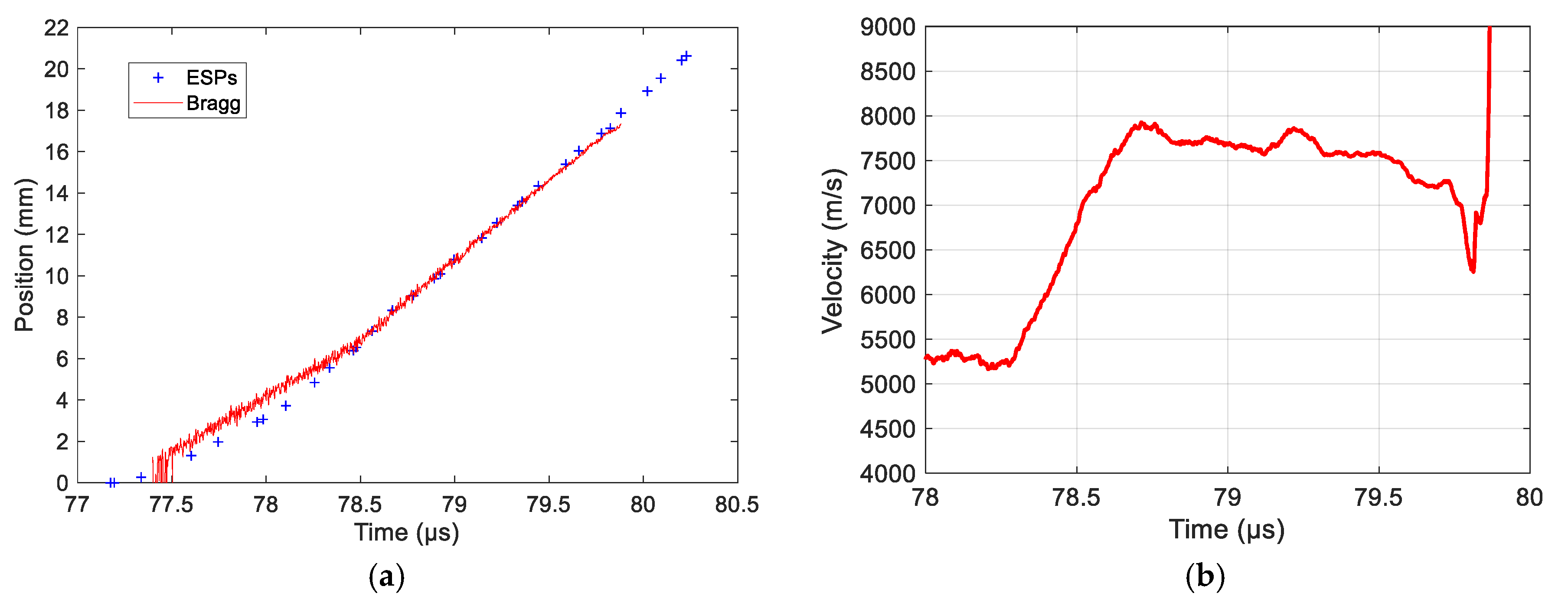
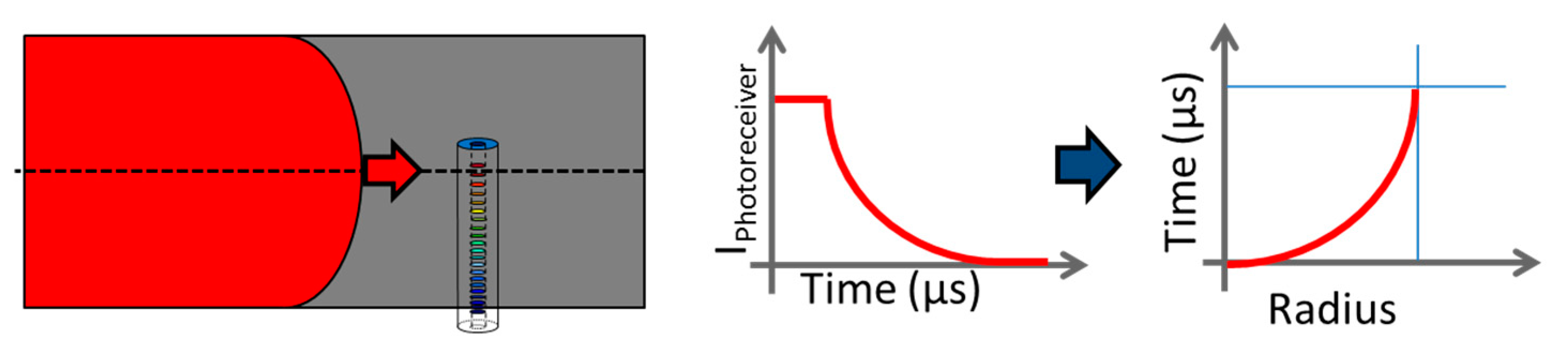
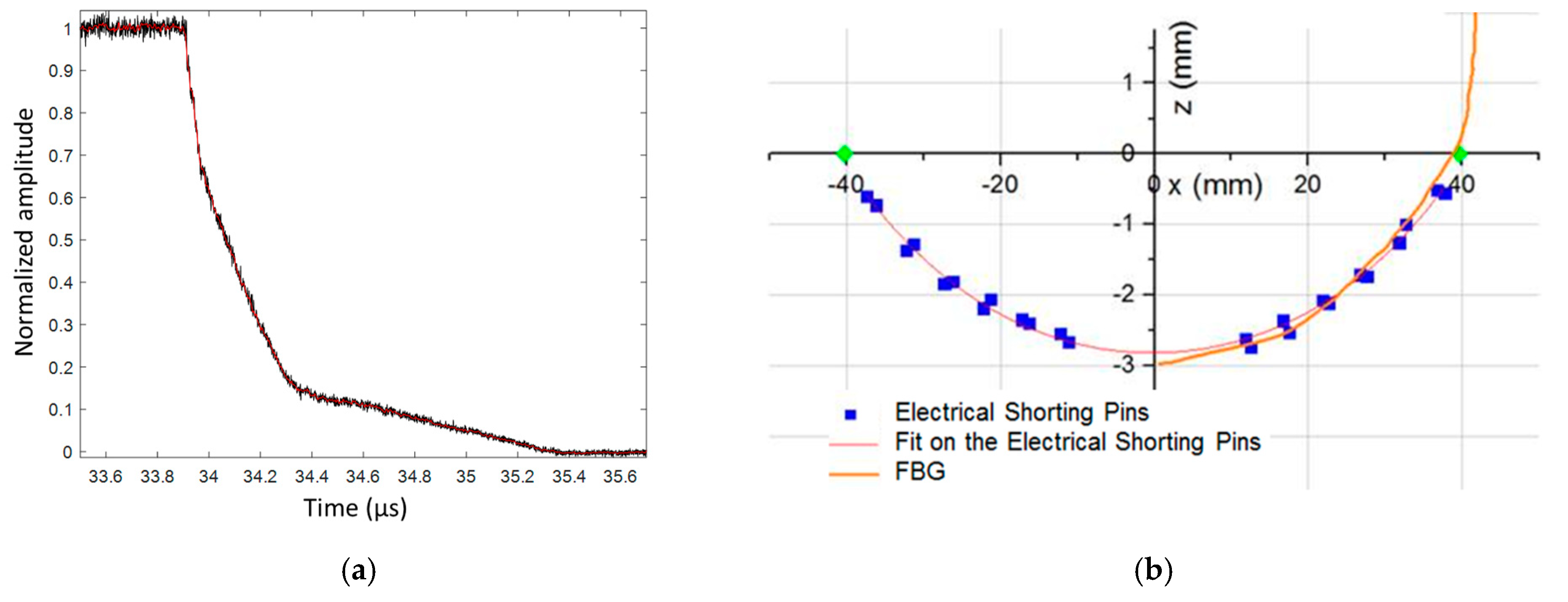
6.6. Detonation Curvature Profile in a Bare Cylinder Stick
6.6.1. Set-Up
6.6.2. Detonation Profile Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goosman, D.; Wade, J.; Garza, R.; Avara, G.; Crabtree, T.; Rivera, A.; Hare, D.; Tolar, D., Jr.; Bratton, B. Optical probes for continuous Fabry-Perot velocimetry inside materials. Proc. SPIE 2004, 5580, 517–528. [Google Scholar]
- Hare, D.E.; Holtkamp, D.B.; Strand, O.T. Embedded fiber optic probes to measure detonation velocities using the Photonic Doppler Velocimeter. In Proceedings of the 14th International Detonation Symposium, Coeur d’Alene, Idaho, 11–16 April 2010. [Google Scholar]
- Benterou, J.; Udd, E.; Wilkins, P.; Roeske, F.; Roos, E.; Jackson, D. In-Situ Continuous Detonation Velocity Measurements Using Fiber-Optic Bragg Grating Sensors; LLNL e-report, UCRL-Proceedings-233137; Lawrence Livermore National Lab. (LLNL): Livermore, CA, USA, 2007. [Google Scholar]
- Benterou, J.; Bennett, C.V.; Cole, G.; Hare, D.E.; May, C.; Udd, E.; Mihailov, S.J.; Lu, P. Embedded fiber optic Bragg grating (FBG) detonation velocity sensor. Proc. SPIE 2009, 7316, 73160E. [Google Scholar]
- Udd, E.; Benterou, J.; May, C.; Mihailov, S.J.; Lu, P. Review of high-speed fiber optic grating sensor systems. Proc. SPIE 2010, 7677, 76770B. [Google Scholar]
- Benterou, J.; May, C.; Udd, E.; Mihailov, S.J.; Lu, P. High speed measurements using fiber-optic Bragg gratings. Proc. SPIE 2011, 8028, 802808. [Google Scholar]
- Rodriguez, G.; Sandberg, R.L.; McCulloch, Q.; Jackson, S.I.; Vincent, S.W.; Udd, E. Chirped fiber Bragg grating detonation velocity sensing. Rev. Sci. Instr. 2015, 84, 015003. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, G.; Sandberg, R.L.; Jackson, S.I.; Dattelbaum, D.M.; Vincent, S.W.; McCulloch, Q.; Martinez, R.M.; Gilbertson, S.M.; Udd, E. Fiber Bragg grating sensing of detonation and shock experiments at Los Alamos National Laboratory. Proc. SPIE 2013, 8722, 872204. [Google Scholar]
- Magne, S.; Lefrançois, A.; Luc, J.; Laffont, G.; Ferdinand, P. Real-time, distributed measurement of detonation velocities inside high explosives with the help of chirped fiber Bragg gratings. Proc. SPIE 2013, 8794, 87942K. [Google Scholar]
- Ravid, A.; Shafir, E.; Zilberman, S.; Berkovic, G.; Glam, B.; Appelbaum, G.; Fedotov, G.A. Fiber Bragg Grating sensor for shock wave diagnostics. J. Phys. Conf. Ser. 2014, 500, 142029–142033. [Google Scholar] [CrossRef]
- Gilbertson, S.; Jackson, S.I.; Vincent, S.W.; Rodriguez, G. Detection of high explosive detonation across material interfaces with chirped fiber Bragg gratings. Appl. Opt. 2015, 54, 3849. [Google Scholar] [CrossRef]
- Barbarin, Y.; Lefrançois, A.; Zaniolo, G.; Chuzeville, V.; Jacquet, L.; Magne, S.; Luc, J.; Osmont, A. Optimization of detonation velocity measurements using a Chirped Fiber Bragg Grating. Proc. SPIE 2015, 9480, 94800S-1. [Google Scholar]
- Udd, E.; Udd, I.; Benterou, J.; Rodriguez, G. Ultrafast fiber grating sensor systems for velocity, position, pressure, and temperature measurements. Proc. SPIE 2016, 9852, 98520Q. [Google Scholar]
- Magne, S.; Laffont, G.; Ferdinand, P.; Barbarin, Y.; Lefrançois, A.; Chuzeville, V.; Luc, J.; Woirin, K. Chirped Fiber Bragg gratings for distributed detonation velocity measurements Bragg gratings. In Proceedings of the Photosensitivity, and Poling in Glass Waveguides, Sydney, Australia, 5–8 September 2016. [Google Scholar]
- Woirin, K.; Barbarin, Y.; Lefrançois, A.; Balbarie, M.; Magne, S.; Collet, C. Transition and detonation processes characterization with Braggfast, a new fiber Bragg grating analysis system for energetic materials. In Proceedings of the 48th International Annual Conference of the Fraunhofer ICT, Karlsruhe, Germany, 27–30 June 2017. [Google Scholar]
- Woirin, K.; Barbarin, Y.; Lefrançois, A.; Balbarie, M.; Magne, S.; Moriceau, J. A new fiber Bragg grating analysis system for transition and detonation processes characterizations. In Proceedings of the 6th International Symposium on Energetic Materials and their applications, Sendai, Japan, 6–10 November 2017. [Google Scholar]
- Barbarin, Y.; Lefrançois, A.; Magne, S.; Chuzeville, V.; Balbarie, M.; Jacquet, L.; Sinatti, F.; Osmont, A.; Luc, J. Dynamic measurements of physical quantities in extreme environment using fiber Bragg grating. In Proceedings of the 25th International Conference on Optical Fiber Sensors, Jeju, South Korea, 24–28 April 2017. [Google Scholar]
- Wei, P.; Lang, H.; Liu, T.; Xia, D. Detonation velocity measurement with Chirped Fiber Bragg Grating. Sensors 2017, 17, 2552. [Google Scholar]
- Udd Scheel, I.; Udd, E. Nanosecond resolution pressure, temperature, position and velocity measurements in energetic materials. In Fiber Optic Sensors and Applications XV; SPIE: Bellingham, WA, USA, 2018; Volume 10654, p. 106540O. [Google Scholar]
- Pooley, J.; Price, E.; Ferguson, J.W.; Ibsen, M. Optimized chirped fibre Bragg gratings for detonation velocity measurements. Sensors 2019, 19, 3333. [Google Scholar] [CrossRef]
- Soller, B.J.; Gifford, D.K.k.; Wolfe, M.S.; Froggatt, M.E. High resolution Optical Frequency-Domain Reflectometry for characterization of components and assemblies. Opt. Express 2005, 13, 666–674. [Google Scholar] [CrossRef]
- Benier, J.; Adolf, L.-M. Development of optical fiber sensor for detonation velocity measurement. In Proceedings of the Europyro Conference, Toulouse, France, 4–7 May 2015. [Google Scholar]
- Pooley, J.; Price, E.; Ferguson, J.W.; Ibsen, M. Detonation velocity measurements with uniform fibre Bragg gratings. Opt. Express 2019, 27, 23464–23475. [Google Scholar] [CrossRef]
- Pooley, J.; Price, E.; Ferguson, J.W.; Ibsen, M. Detonation velocity measurements using rare-earth doped fibres. Sensors 2019, 19, 1697. [Google Scholar] [CrossRef]
- Chuzeville, V.; Baudin, G.; Lefrançois, A.; Genetier, M.; Barbarin, Y.; Jacquet, L.; Lhopitault, J.-L.; Peix, J.; Boulanger, R.; Catoire, L. Detonation initiation of heterogeneous melt-cast high explosives. AIP Conf. Proc. 2017, 1793, 030009. [Google Scholar]
- Chilwell, J.; Hodgkinson, I. Thin films field-transfer matrix theory of planar multilayer waveguides and reflection from prism-loaded waveguides. J. Opt. Soc. Am. A 1984, 1, 742–753. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber grating spectra. J. Lightwave Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Apithy, H.; Bouslimani, Y.; Hamam, H. Simulation methods in optical propagation. Canadian J. Electr. Comput. Eng. 2005, 30, 39–48. [Google Scholar] [CrossRef]
- Magne, S.; Barbarin, Y.; Lefrançois, A.; Balbarie, M.; Sinatti, F.; Osmont, A.; Luc, J.; Woirin, K. Real-time distributed monitoring of pressure and shock velocity by ultrafast spectrometry with Chirped Fiber Bragg Gratings: Experimental vs. calculated wavelength-to-pressure sensitivities in the range [0–4 GPa]. J. Appl. Phys. 2018, 124, 145902. [Google Scholar] [CrossRef]
- Li, H.; Nakamura, Y.; Ogusu, K.; Sheng, Y.; Rothenberg, J.E. Influence of cladding-mode coupling losses on the spectrum of a linearly chirped multi-channel fiber Bragg grating. Opt. Express 2005, 13, 1281–1290. [Google Scholar] [CrossRef] [PubMed]
- Rougier, B.; Lefrançois, A.; Chuzeville, V.; Poeuf, S.; Aubert, H. Static and dynamic permittivity measurement of high explosives in the W band to investigate shock and detonation phenomena. Propellants Explos. Pyrotech. 2019, 44, 153. [Google Scholar] [CrossRef]
- Rougier, B.; Aubert, H.; Lefrançois, A.; Bouton, E.; Luc, J.; Osmont, A.; Barbarin, Y. Simultaneous shock and particle velocities measurement using a single microwave interferometer on pressed TATB composition T2 submitted to plate impact. In Proceedings of the 16th International Symposium on Detonation, Cambridge, MD, USA, 2018. [Google Scholar]
- Ramakrishnan, M.; Rajan, G.; Semenova, Y.; Farrell, G. Overview of Fiber Optic Sensor Technologies for Strain/Temperature Sensing Applications in Composite Materials. Sensors 2016, 16, 99. [Google Scholar] [CrossRef]
- Lefrançois, A.; Baudin, G.; Le Gallic, C..; Boyce, P.; Coudoing, J.-P. Nanometric Aluminium powder influence on the detonation efficiency of explosives. In Proceedings of the 12th International Symposium on Detonation, San Diego, CA, USA, 11–16 August 2002; pp. 22–32. [Google Scholar]
- Elia, T.; Lefrançois, A.; Gnetier, M.; Baudin, G. Diverging spherical run-distance to detonation characterization. In Proceedings of the 16th International Symposium on Detonation, Cambridge, MD, USA, 2018. [Google Scholar]
- Rodriguez, G.; Gilbertson, S. Ultrafast fiber Bragg grating interrogation for sensing in detonation and shock wave experiments. Sensors 2017, 17, 248. [Google Scholar] [CrossRef] [PubMed]
- Barbarin, Y.; Lefrançois, A.; Sinatti, F.; Bey, A.; Balbarie, M.; Osmont, A.; Luc, J. Dynamic dispersive spectrometer using a fiber Bragg grating for high pressure measurements. In Proceedings of the IEEE Sensors, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbarin, Y.; Lefrançois, A.; Chuzeville, V.; Magne, S.; Jacquet, L.; Elia, T.; Woirin, K.; Collet, C.; Osmont, A.; Luc, J. Development of a Shock and Detonation Velocity Measurement System Using Chirped Fiber Bragg Gratings. Sensors 2020, 20, 1026. https://doi.org/10.3390/s20041026
Barbarin Y, Lefrançois A, Chuzeville V, Magne S, Jacquet L, Elia T, Woirin K, Collet C, Osmont A, Luc J. Development of a Shock and Detonation Velocity Measurement System Using Chirped Fiber Bragg Gratings. Sensors. 2020; 20(4):1026. https://doi.org/10.3390/s20041026
Chicago/Turabian StyleBarbarin, Yohan, Alexandre Lefrançois, Vincent Chuzeville, Sylvain Magne, Laurent Jacquet, Thomas Elia, Karol Woirin, Christelle Collet, Antoine Osmont, and Jérôme Luc. 2020. "Development of a Shock and Detonation Velocity Measurement System Using Chirped Fiber Bragg Gratings" Sensors 20, no. 4: 1026. https://doi.org/10.3390/s20041026
APA StyleBarbarin, Y., Lefrançois, A., Chuzeville, V., Magne, S., Jacquet, L., Elia, T., Woirin, K., Collet, C., Osmont, A., & Luc, J. (2020). Development of a Shock and Detonation Velocity Measurement System Using Chirped Fiber Bragg Gratings. Sensors, 20(4), 1026. https://doi.org/10.3390/s20041026





