Predicting Forage Quality of Warm-Season Legumes by Near Infrared Spectroscopy Coupled with Machine Learning Techniques
Abstract
1. Introduction
2. Materials and Methods
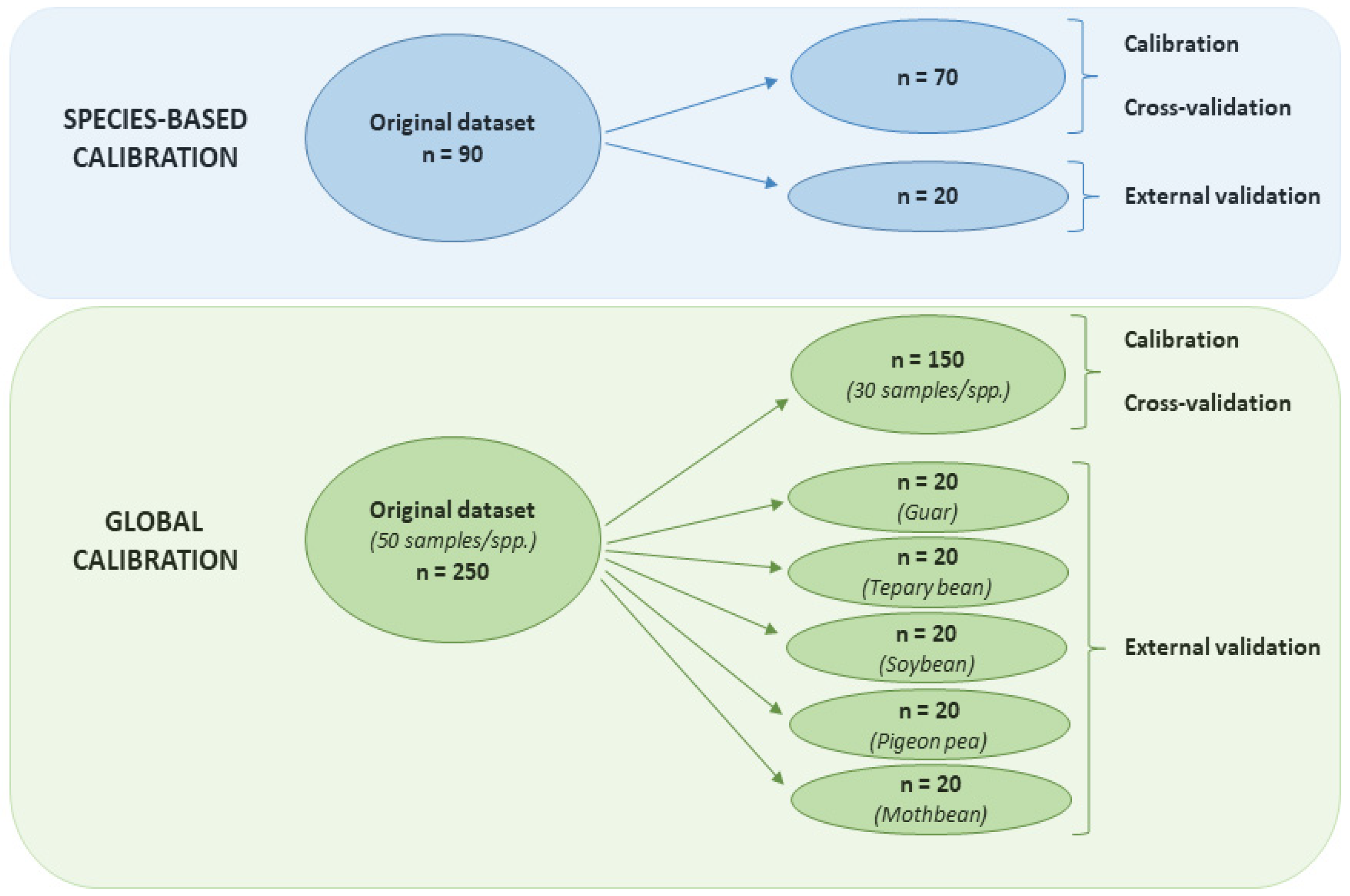
2.1. Materials
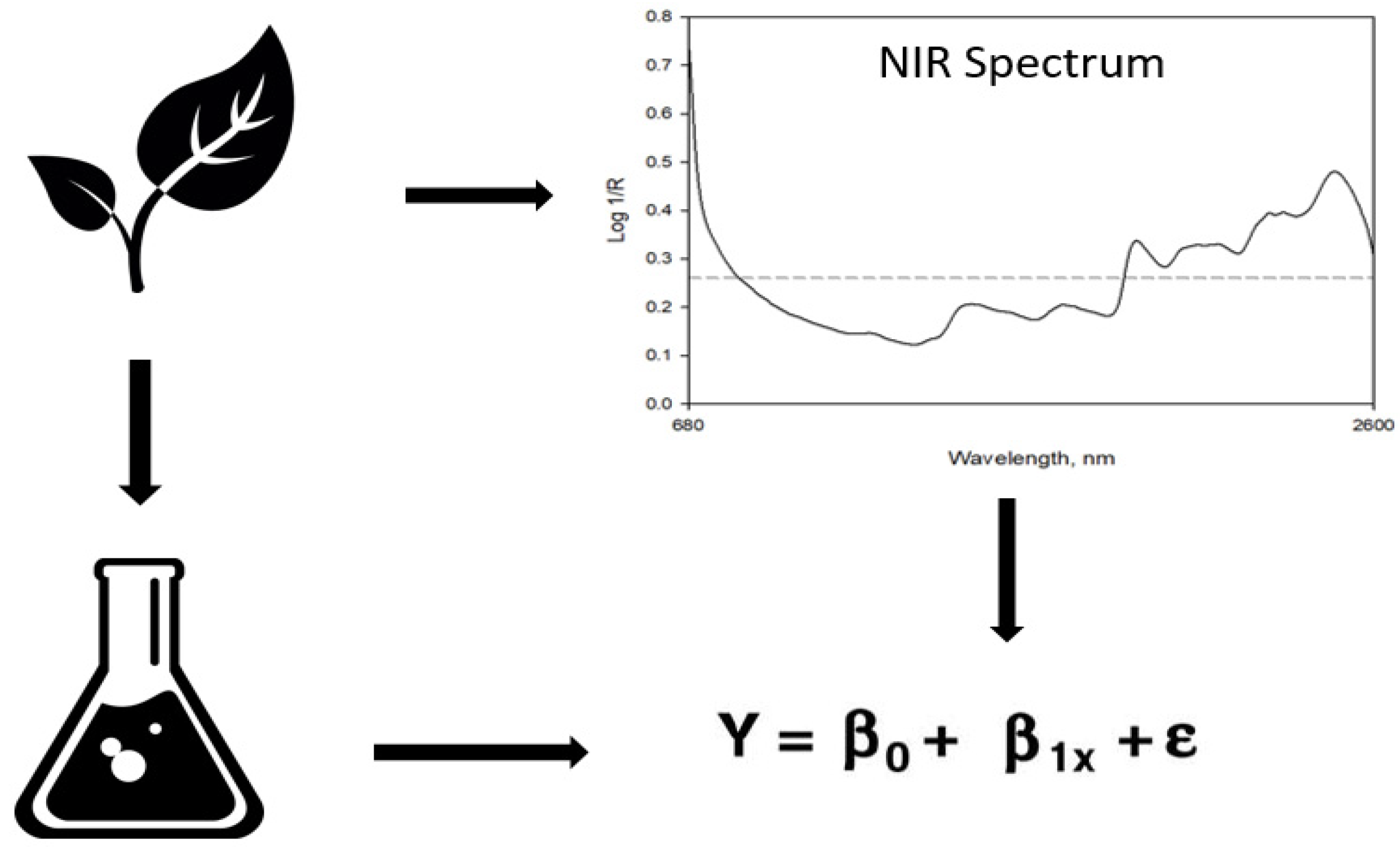
2.2. Laboratory and NIRS Analysis
2.3. Calibration Techniques
2.4. Performance Evaluation
2.5. Software
3. Results and Discussion
3.1. Guar
3.2. Tepary Bean
3.3. Soybean
3.4. Pigeon Pea
3.5. Global Calibrations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Disclaimer
Abbreviations
References
- Phillips, W.; Coleman, S. Productivity and economic return of three warm season grass stocker systems for the Southern Great Plains. J. Prod. Agric. 1995, 8, 334–339. [Google Scholar] [CrossRef]
- Williams, M.; HaLmmond, A. Rotational vs. continuous intensive stocking management of bahiagrass pasture for cows and calves. Agron. J. 1999, 91, 11–16. [Google Scholar] [CrossRef]
- Rao, S.C.; Northup, B.K. Capabilities of four novel warm-season legumes in the southern Great Plains: Biomass and forage quality. Crop Sci. 2009, 49, 1096–1102. [Google Scholar] [CrossRef]
- Rao, S.C.; Northup, B.K. Pigeon pea potential for summer grazing in the southern Great Plains. Agron. J. 2012, 104, 199–203. [Google Scholar] [CrossRef]
- Rao, S.C.; Northup, B.K. Biomass production and quality of indian-origin forage guar in Southern Great Plains. Agron. J. 2013, 105, 945–950. [Google Scholar] [CrossRef]
- Foster, J.; Adesogan, A.; Carter, J.; Sollenberger, L.; Blount, A.; Myer, R.; Phatak, S.; Maddox, M. Annual legumes for forage systems in the United States Gulf Coast region. Agron. J. 2009, 101, 415–421. [Google Scholar] [CrossRef]
- Baath, G.S.; Northup, B.K.; Gowda, P.H.; Turner, K.E.; Rocateli, A.C. Mothbean: A potential summer crop for the Southern Great Plains. Am. J. Plant Sci. 2018, 9, 1391. [Google Scholar] [CrossRef]
- Rushing, J.B.; Saha, U.K.; Lemus, R.; Sonon, L.; Baldwin, B.S. Analysis of some important forage quality attributes of Southeastern Wildrye (Elymus glabriflorus) using near-infrared reflectance spectroscopy. Am. J. Anal. Chem. 2016, 7, 642. [Google Scholar] [CrossRef]
- Brogna, N.; Pacchioli, M.T.; Immovilli, A.; Ruozzi, F.; Ward, R.; Formigoni, A. The use of near-infrared reflectance spectroscopy (NIRS) in the prediction of chemical composition and in vitro neutral detergent fiber (NDF) digestibility of Italian alfalfa hay. Ital. J. Anim. Sci. 2009, 8, 271–273. [Google Scholar] [CrossRef]
- Volkers, K.; Wachendorf, M.; Loges, R.; Jovanovic, N.; Taube, F. Prediction of the quality of forage maize by near-infrared reflectance spectroscopy. Anim. Feed Sci. Technol. 2003, 109, 183–194. [Google Scholar] [CrossRef]
- Yang, Z.; Nie, G.; Pan, L.; Zhang, Y.; Huang, L.; Ma, X.; Zhang, X. Development and validation of near-infrared spectroscopy for the prediction of forage quality parameters in Lolium multiflorum. PeerJ 2017, 5, e3867. [Google Scholar] [CrossRef] [PubMed]
- Hill, N.; Cabrera, M.; Agee, C. Morphological and climatological predictors of forage quality in tall fescue. Crop Sci. 1995, 35, 541–549. [Google Scholar] [CrossRef]
- Muir, J.P.; Pitman, W.D.; Dubeux Jr, J.C.; Foster, J.L. The future of warm-season, tropical and subtropical forage legumes in sustainable pastures and rangelands. Afr. J. Range Forage Sci. 2014, 31, 187–198. [Google Scholar] [CrossRef]
- Baath, G.S.; Northup, B.K.; Rocateli, A.C.; Gowda, P.H.; Neel, J.P. Forage potential of summer annual grain legumes in the southern great plains. Agron. J. 2018, 110, 2198–2210. [Google Scholar] [CrossRef]
- Agelet, L.E.; Hurburgh, C.R., Jr. A tutorial on near infrared spectroscopy and its calibration. Crit. Rev. Anal. Chem. 2010, 40, 246–260. [Google Scholar] [CrossRef]
- Roggo, Y.; Chalus, P.; Maurer, L.; Lema-Martinez, C.; Edmond, A.; Jent, N. A review of near infrared spectroscopy and chemometrics in pharmaceutical technologies. J. Pharm. Biomed. Anal. 2007, 44, 683–700. [Google Scholar] [CrossRef]
- Wang, K.; Chi, G.; Lau, R.; Chen, T. Multivariate calibration of near infrared spectroscopy in the presence of light scattering effect: A comparative study. Anal. Lett. 2011, 44, 824–836. [Google Scholar] [CrossRef]
- Cui, C.; Fearn, T. Comparison of partial least squares regression, least squares support vector machines, and Gaussian process regression for a near infrared calibration. J. Near Infrared Spectrosc. 2017, 25, 5–14. [Google Scholar] [CrossRef]
- Rao, S.; Mayeux, H.; Northup, B. Performance of forage soybean in the southern Great Plains. Crop Sci. 2005, 45, 1973–1977. [Google Scholar] [CrossRef]
- Rosipal, R.; Kramer, N. Subspace, latent structure and feature selection techniques. Lect. Notes Comput. Sci. Chap. Overv. Recent Adv. Part. Least Sq. 2006, 2940, 34–51. [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Huang, C.-L.; Wang, C.-J. A GA-based feature selection and parameters optimizationfor support vector machines. Expert Syst. Appl. 2006, 31, 231–240. [Google Scholar] [CrossRef]
- Platt, J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv. Large Margin Classif. 1999, 10, 61–74. [Google Scholar]
- Frank, E.; Hall, M.A.; Witten, I.H. The WEKA Workbench; Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques”, 4th ed.; Morgan Kaufmann: Cambridge, MA, USA, 2016. [Google Scholar]
- Malley, D.; Martin, P.; Ben-Dor, E. Application in analysis of soils. In Near-Infrared Spectroscopy in Agriculture, 1st ed.; Roberts, C.A., Workman, J., Jr., Reeves, J.B., III, Eds.; American Society of Agronomy; Crop Science Society of America; Soil Science Society of America: Madison, WI, USA, 2004; pp. 729–783. [Google Scholar]
- Baath, G.S.; Kakani, V.G.; Gowda, P.H.; Rocateli, A.C.; Northup, B.K.; Singh, H.; Katta, J.R. Guar responses to temperature: Estimation of cardinal temperatures and photosynthetic parameters. Ind. Crop. Prod. 2019. [Google Scholar] [CrossRef]
- Wittkop, B.; Snowdon, R.J.; Friedt, W. New NIRS calibrations for fiber fractions reveal broad genetic variation in Brassica napus seed quality. J. Agric. Food Chem. 2012, 60, 2248–2256. [Google Scholar] [CrossRef]
- Kong, X.; Xie, J.; Wu, X.; Huang, Y.; Bao, J. Rapid prediction of acid detergent fiber, neutral detergent fiber, and acid detergent lignin of rice materials by near-infrared spectroscopy. J. Agric. Food Chem. 2005, 53, 2843–2848. [Google Scholar] [CrossRef]
- Nielsen, D.C. Forage soybean yield and quality response to water use. Field Crop. Res. 2011, 124, 400–407. [Google Scholar] [CrossRef]
- Beck, P.; Hubbell, D., III; Hess, T.; Wilson, K.; Williamson, J.A. Effect of a forage-type soybean cover crop on wheat forage production and animal performance in a continuous wheat pasture system. Prof. Anim. Sci. 2017, 33, 659–667. [Google Scholar] [CrossRef]
- Asekova, S.; Han, S.-I.; Choi, H.-J.; Park, S.-J.; Shin, D.-H.; Kwon, C.-H.; Shannon, J.G.; LEE, J.D. Determination of forage quality by near-infrared reflectance spectroscopy in soybean. Turk. J. Agric. For. 2016, 40, 45–52. [Google Scholar] [CrossRef]
- Rao, S.; Coleman, S.; Mayeux, H. Forage production and nutritive value of selected pigeonpea ecotypes in the southern Great Plains. Crop Sci. 2002, 42, 1259–1263. [Google Scholar] [CrossRef]
- Berardo, N.; Dzowela, B.; Hove, L.; Odoardi, M. Near infrared calibration of chemical constituents of Cajanus cajan (pigeon pea) used as forage. Anim. Feed Sci. Technol. 1997, 69, 201–206. [Google Scholar] [CrossRef]
- Roberts, C.A.; Stuth, J.; Flinn, P. Analysis of forages and feedstuffs. In Near-Infrared Spectroscopy in Agriculture, 1st ed.; Roberts, C.A., Workman, J., Jr., Reeves, J.B., III, Eds.; American Society of Agronomy; Crop Science Society of America; Soil Science Society of America: Madison, WI, USA, 2004; pp. 231–267. [Google Scholar]
| Species | Parameter | Calibration and Cross-Validation (n = 70) | External Validation (n = 20) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | Min | Max | Mean | SD | ||
| ------------------------- (%) ------------------------- | |||||||||
| Guar | CP | 3.94 | 34.87 | 17.66 | 8.66 | 3.69 | 33.56 | 15.07 | 9.50 |
| NDF | 16.83 | 70.80 | 37.57 | 16.95 | 22.95 | 75.78 | 45.94 | 17.82 | |
| ADF | 8.90 | 58.39 | 27.19 | 15.29 | 12.79 | 62.93 | 34.70 | 16.57 | |
| IVTD | 40.35 | 95.22 | 79.27 | 14.11 | 42.96 | 94.37 | 73.38 | 16.08 | |
| Tepary bean | CP | 4.50 | 31.12 | 15.76 | 7.78 | 5.94 | 30.25 | 19.35 | 8.13 |
| NDF | 22.90 | 71.57 | 48.34 | 12.31 | 25.52 | 60.95 | 43.90 | 10.21 | |
| ADF | 15.32 | 59.16 | 34.92 | 11.99 | 17.08 | 48.16 | 30.36 | 10.39 | |
| IVTD | 55.88 | 93.16 | 75.50 | 10.83 | 60.23 | 92.56 | 81.34 | 8.56 | |
| Soybean | CP | 4.15 | 39.75 | 21.16 | 11.03 | 6.31 | 36.12 | 19.73 | 8.94 |
| IVTD | 42.45 | 99.30 | 78.25 | 16.28 | 57.66 | 98.31 | 80.21 | 12.38 | |
| Pigeon pea | CP | 4.52 | 32.48 | 16.30 | 8.77 | 6.24 | 28.64 | 15.62 | 7.41 |
| IVTD | 30.71 | 91.08 | 61.55 | 19.28 | 33.31 | 82.89 | 59.76 | 16.40 | |
| Parameter | Method | Calibration (n = 70) | Cross-Validation (n = 70) | External Validation (n = 20) | |||
|---|---|---|---|---|---|---|---|
| R2c | RMSEc | R2cv | RMSEcv | R2v | RMSEv | ||
| CP | GP | 0.95 | 1.84 | 0.93 | 2.20 | 0.96 | 2.12 |
| PLS | 0.99 | 0.78 | 0.95 | 1.97 | 0.93 | 2.52 | |
| SVM | 0.98 | 1.23 | 0.97 | 1.56 | 0.98 | 1.27 | |
| NDF | GP | 0.90 | 5.53 | 0.84 | 6.73 | 0.90 | 6.98 |
| PLS | 0.98 | 2.17 | 0.85 | 6.66 | 0.93 | 5.52 | |
| SVM | 0.94 | 3.98 | 0.91 | 5.08 | 0.94 | 4.67 | |
| ADF | GP | 0.91 | 4.79 | 0.86 | 5.77 | 0.92 | 6.02 |
| PLS | 0.99 | 1.18 | 0.95 | 3.36 | 0.94 | 4.23 | |
| SVM | 0.97 | 2.46 | 0.95 | 3.51 | 0.96 | 3.78 | |
| IVTD | GP | 0.88 | 4.92 | 0.81 | 6.10 | 0.93 | 5.63 |
| PLS | 0.98 | 2.15 | 0.81 | 6.69 | 0.87 | 5.66 | |
| SVM | 0.94 | 3.51 | 0.83 | 5.88 | 0.94 | 4.19 | |
| Parameter | Method | Calibration (n = 70) | Cross-Validation (n = 70) | External Validation (n = 20) | |||
|---|---|---|---|---|---|---|---|
| R2c | RMSEc | R2cv | RMSEcv | R2v | RMSEv | ||
| CP | GP | 0.94 | 1.89 | 0.90 | 2.42 | 0.94 | 2.20 |
| PLS | 0.99 | 0.68 | 0.93 | 2.03 | 0.98 | 1.35 | |
| SVM | 0.97 | 1.35 | 0.95 | 1.74 | 0.94 | 1.94 | |
| NDF | GP | 0.85 | 4.96 | 0.75 | 6.22 | 0.75 | 5.10 |
| PLS | 0.98 | 1.64 | 0.84 | 5.09 | 0.75 | 5.53 | |
| SVM | 0.94 | 2.97 | 0.72 | 7.01 | 0.84 | 4.03 | |
| ADF | GP | 0.87 | 4.60 | 0.78 | 5.62 | 0.86 | 3.90 |
| PLS | 0.98 | 1.47 | 0.89 | 3.97 | 0.92 | 3.34 | |
| SVM | 0.96 | 2.45 | 0.86 | 4.52 | 0.95 | 2.23 | |
| IVTD | GP | 0.87 | 4.02 | 0.75 | 5.39 | 0.75 | 4.25 |
| PLS | 0.98 | 1.55 | 0.79 | 5.00 | 0.88 | 2.89 | |
| SVM | 0.93 | 2.86 | 0.75 | 5.70 | 0.82 | 3.82 | |
| Parameter | Method | Calibration (n = 70) | Cross-Validation (n = 70) | External Validation (n = 20) | |||
|---|---|---|---|---|---|---|---|
| R2c | RMSEc | R2cv | RMSEcv | R2v | RMSEv | ||
| CP | GP | 0.92 | 4.63 | 0.87 | 5.78 | 0.92 | 3.78 |
| PLS | 0.98 | 2.16 | 0.84 | 6.92 | 0.93 | 3.46 | |
| SVM | 0.94 | 3.92 | 0.89 | 5.28 | 0.89 | 4.09 | |
| IVTD | GP | 0.96 | 2.14 | 0.94 | 2.71 | 0.92 | 2.53 |
| PLS | 0.99 | 0.80 | 0.96 | 2.05 | 0.94 | 2.24 | |
| SVM | 0.99 | 1.26 | 0.97 | 1.85 | 0.96 | 1.78 | |
| Parameter | Method | Calibration (n = 70) | Cross-Validation (n = 70) | External Validation (n = 20) | |||
|---|---|---|---|---|---|---|---|
| R2c | RMSEc | R2cv | RMSEcv | R2v | RMSEv | ||
| CP | GP | 0.98 | 1.37 | 0.96 | 1.73 | 0.96 | 1.69 |
| PLS | 1.00 | 0.43 | 0.97 | 1.46 | 0.98 | 1.02 | |
| SVM | 0.99 | 0.84 | 0.98 | 1.17 | 0.98 | 1.12 | |
| IVTD | GP | 0.95 | 4.51 | 0.86 | 7.18 | 0.97 | 2.95 |
| PLS | 0.99 | 1.93 | 0.92 | 5.49 | 0.96 | 3.09 | |
| SVM | 0.97 | 3.31 | 0.91 | 5.86 | 0.97 | 2.85 | |
| Method | Calibration (n = 150) | Cross-Validation (n = 150) | External Validation (n = 20) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Guar | Tepary Bean | Soybean | Pigeon Pea | Mothbean | |||||||||||
| R2c | RMSEc | R2cv | RMSEcv | R2v | RMSEv | R2v | RMSEv | R2v | RMSEv | R2v | RMSEv | R2v | RMSEv | ||
| CP | GP | 0.92 | 2.15 | 0.89 | 2.46 | 0.93 | 2.42 | 0.95 | 2.72 | 0.91 | 3.95 | 0.98 | 2.21 | 0.94 | 3.36 |
| PLS | 0.97 | 1.15 | 0.92 | 2.02 | 0.94 | 2.36 | 0.94 | 2.49 | 0.94 | 2.47 | 0.98 | 2.03 | 0.94 | 3.10 | |
| SVM | 0.96 | 1.48 | 0.94 | 1.87 | 0.92 | 2.77 | 0.95 | 2.36 | 0.94 | 3.16 | 0.99 | 1.29 | 0.97 | 2.54 | |
| IVTD | GP | 0.86 | 5.09 | 0.81 | 5.84 | 0.65 | 6.16 | 0.91 | 4.41 | 0.82 | 7.93 | 0.91 | 4.75 | 0.42 | 5.40 |
| PLS | 0.94 | 3.28 | 0.85 | 5.28 | 0.81 | 5.00 | 0.90 | 5.53 | 0.88 | 5.19 | 0.98 | 2.21 | 0.69 | 4.50 | |
| SVM | 0.91 | 3.98 | 0.86 | 4.98 | 0.77 | 5.12 | 0.92 | 4.74 | 0.86 | 5.60 | 0.97 | 2.77 | 0.65 | 4.29 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baath, G.S.; Baath, H.K.; Gowda, P.H.; Thomas, J.P.; Northup, B.K.; Rao, S.C.; Singh, H. Predicting Forage Quality of Warm-Season Legumes by Near Infrared Spectroscopy Coupled with Machine Learning Techniques. Sensors 2020, 20, 867. https://doi.org/10.3390/s20030867
Baath GS, Baath HK, Gowda PH, Thomas JP, Northup BK, Rao SC, Singh H. Predicting Forage Quality of Warm-Season Legumes by Near Infrared Spectroscopy Coupled with Machine Learning Techniques. Sensors. 2020; 20(3):867. https://doi.org/10.3390/s20030867
Chicago/Turabian StyleBaath, Gurjinder S., Harpinder K. Baath, Prasanna H. Gowda, Johnson P. Thomas, Brian K. Northup, Srinivas C. Rao, and Hardeep Singh. 2020. "Predicting Forage Quality of Warm-Season Legumes by Near Infrared Spectroscopy Coupled with Machine Learning Techniques" Sensors 20, no. 3: 867. https://doi.org/10.3390/s20030867
APA StyleBaath, G. S., Baath, H. K., Gowda, P. H., Thomas, J. P., Northup, B. K., Rao, S. C., & Singh, H. (2020). Predicting Forage Quality of Warm-Season Legumes by Near Infrared Spectroscopy Coupled with Machine Learning Techniques. Sensors, 20(3), 867. https://doi.org/10.3390/s20030867





