Abstract
Optical camera communications (OCC) research field has grown recently, aided by ubiquitous digital cameras; however, atmospheric conditions can restrict their feasibility in outdoor scenarios. In this work, we studied an experimental OCC system under environmental phenomena emulated in a laboratory chamber. We found that the heat-induced turbulence does not affect our system significantly, while the attenuation caused by fog does decrease the signal quality. For this reason, a novel strategy is proposed, using the camera’s built-in amplifier to overcome the optical power loss and to decrease the quantization noise induced by the analog-digital converter of the camera. The signal quality has been evaluated using the Pearson’s correlation coefficient with respect to a reference template signal, along with the signal-to-noise ratio that has been empirically evaluated. The amplification mechanism introduced allows our system to receive the OCC signal under heavy fog by gradually increasing the camera gain up to 16 dB, for meteorological visibility values down to 10 m, with a correlation coefficient of 0.9 with respect to clear conditions.
1. Introduction
Digital cameras are ubiquitous consumer electronics and are being explored to deliver extra capabilities beyond traditional photography and video. A new optical communication technique using cameras as receivers has been studied in the IEEE 802.15 SG7a within the framework of optical wireless communications and considered as a candidate of IEEE 802.15.7r1, which is called Optical Camera Communication (OCC). OCC has been investigated as one of the Visible Light Communication (VLC) schemes [1]. OCC implemented within internet of things (IoT) environments provides multiple functionalities of vision, data communications, localization and motion detection (MD) [2,3] used in various IoT-based network applications including device-to-device communications [4], mobile atto-cells [5], vehicular communications [6,7,8], and smart cities, offices, and homes (SCOH) [9].
The majority of new generation smart devices have built-in Complementary Metal-Oxide-Semiconductor (CMOS) image sensors, providing the ability to capture photos and videos [10,11]. The strategy behind using a CMOS camera for OCC is that the image sensor performs an acquisition mechanism known as Rolling Shutter (RS), in which it sequentially integrates light on rows of pixels [12] starting the scanning of each line with a delay with respect to the previous one. In other words, the timings of the line-wise scanning make the imaging sensor to capture different windows of time of the optical signal coming from a Light Emitting Diode (LED) transmitter (). Then, each line of the image can hold a distinct portion of information.
The use of LEDs available in SCOH’s lighting infrastructures, along with optical receivers, for making VLC systems is particularly challenging in outdoor environments. The potential applications of OCC in these scenarios are related to the creation and improvement of communication networks for the vehicular and pedestrian infrastructures [13], where a large number of LED lights and CMOS cameras can be found. The desirable distance coverage of the different services that can take advantage of OCC ranges from a few meters for hand-held receiver devices based on smartphones, and tens of meters for vehicular networks that support Intelligent Transportation Systems (ITS). The achievable link distance in OCC depends partly on the signal-to-noise ratio (SNR) at the receiver, which in turn depends on the transmitted power, the attenuation caused by the channel, the optical lens array of the camera and various sources of noise and interference. In the case of RS-based systems, the maximum link distance is also restricted by the number of lines of pixels covered by the transmitter. For this, the geometry of the transmitting surface, as well as the image forming lens array configuration, determine the image area in pixels [14]. The modulation and packet scheme may have an impact on the maximum link distance if the image frames must contain a number of visible symbols for demodulation. Depending on the case of application, the LED and camera-based transceivers can either have static or mobile positions and orientations, making mobility support essential, which relies on the effective detection of the pixels that have an SNR level suitable for demodulation.
The vehicular VLC (VVLC) are a significant application case with challenging conditions of relative position and motion between nodes. An analysis based on a comparison of VVLC with radio frequency (RF) vehicle-to-vehicle (V2V) links in terms of channel time variation was proposed in [15]. It was shown that the VVLC links have much slower channel time variation as compared to RF V2V links. On the other hand, the VVLC investigation in [16] obtained link duration for VVLC between neighboring vehicles are more than 5 s while in certain other cases the average link duration can be up to 15 s. The safety regulations in [17,18] provide the speed limits and inter-vehicle distance in different weather conditions for the estimation of the desired distance of coverage. Table 1 shows the speed limit based on the European Commission regarding mobility and transport standards, which may vary slightly from one European country to the other. The inter-vehicle distances outlined have been calculated based on the 2 s driving rule for good to bad weather conditions, according to the Government of Ireland, which recommends that a driver maintains a minimum of two seconds apart form the leading vehicle for good weather conditions, which is doubled to four seconds in bad weather.

Table 1.
Inter-vehicle distances based on the weather condition based on regulations in [17,18].
The performance of intensity-modulation and direct-detection method employed by LED-to-Photodiode (PD) VLC [9,19], is highly restricted by external light sources such as sunlight, public lighting, and signaling. Moreover, weather conditions, such as the presence of fog, or high temperatures, cause substantial optical distortions [20]. Addressing these challenges, authors in [21] derived a path-loss model for PD-to-LED VLC using Mie’s theory and simulating rain and fog conditions in a vehicular VLC setting. They determined the maximum achievable distances as a function of the desired bit-error-ratio (BER) using pulse amplitude modulation (PAM). They found that, for a 32-PAM system, the maximum distance achievable for the desired BER of is reduced from 72.21 m in clear weather, to 69.13 m in rainy conditions, and 52.85 m and 25.93 m in foggy conditions of different densities. The same Mie’s theory is also used in [22] to evaluate a PD-based VLC link under maritime fog conditions. Scattering and phase functions are derived, as well as the spectrum of the attenuation of optical signals for different distances. In [23], the authors experimented with a LED-to-PD VLC link of 1 m distance based on a single 1 W red LED and multiple PDs attached to a Fresnel lens under dense fog conditions in a laboratory chamber. The lens allows them to maintain a 25 dB signal-to-noise ratio (SNR) varying the optical gain it provides to compensate the attenuation due to the fog presence.
Atmospheric turbulence, and oceanic turbulence in the case of Underwater Wireless Optical Communication (UWOC), has been extensively studied. Guo et al. introduced the traditional lognormal model into a simulated VLC link for ITS [24]. The authors proved that VLC wavelengths in ITS performed worse than longer ones (e.g., 1550 nm), which is straightforward, taking into account that the turbulence measured by Rytov’s variance has a dependence on the wavelength. In the case of UWOC, in which the use of visible-range wavelengths is mandatory due to the water absorption spectrum, Kolmogorov’s turbulence spectrum is substituted by Nikishov’s [25]. This turbulence spectrum fits better with the experimental measurements since it takes into account not only temperature but salinity variations.
Although the impact of turbulence has been characterized for classical optical detectors, its effect on OCC systems has not been adequately addressed yet. Works addressing channel characterization in outdoor OCC links [20] are still scarce compared to the amount of research on PD-based VLC. In the previous work [26], we evaluated the feasibility of a global shutter-based OCC link under fog conditions by the success rate of bits of vehicular link experimentally tested with a red brake light and a digital reflex camera. For a modulation index of 75%, the system showed high reliability under dense fog conditions up to a meteorological visibility of 20 m.
The contribution of this paper is to experimentally derive the feasibility of OCC in emulated outdoor conditions of fog and heat-induced turbulence using commercially available LEDs and cameras. This work is the first to report an experimental investigation on the effects of such conditions on an RS-based system. The experiments carried out for this work were done using a laboratory chamber, and the conditions emulated were of heat-induced turbulence and the presence of fog in the air. The refractive index structure parameter () [27] is used to estimate the level of turbulence and the meteorological visibility () as a measure of the level of fog. The fog experiments are especially relevant because we utilize the camera’s built-in amplifier to overcome the fog attenuation and mitigate the relative contribution of the quantization noise induced by the analog-to-digital conversion stage, ensuring an improvement of the signal quality without increasing the exposure time, and, thus, keeping a high bandwidth.
This paper is structured as follows. Section 2 describes the used methodology, including the channel modeling, the model for the meteorological phenomena studied, and it presents the experimental design. Section 3 presents the experimental setup, describing the laboratory chamber and the OCC system employed. Section 4 shows the obtained results for heat-induced turbulence and fog experiments and performs an in-depth discussion. Finally, conclusions are drawn in Section 5.
2. Methodology
In this section, we describe the relevant processes involved in the CMOS camera mechanism of acquisition in RS-based OCC employed by our system and derive the analytical tools used for the evaluation of its performance in the experimental setting.
2.1. Channel Modelling
In CMOS image sensors, the red-green-blue (RGB) light from a Bayer filter impinges the subpixels. These entities are integrated by PDs and their driving circuit and are grouped by rows connected in parallel to amplifiers and analog/digital converter (ADC) units that are shared by columns. The output of these hardware blocks are image matrices that are sent to the camera digital signal processor (DSP), where data is compressed and delivered to the user as a media file. The sensor performs RS acquisition, in which the start and end of the exposure of each row of pixels are determined by the circuit’s fixed row-shift time () and the software-defined exposure time () [28]. The time parameters and circuitry mentioned are shown in Figure 1. Since is fixed, in order to increase the data rate, must be set as low as possible to make the sensor capture the highest diversity of states of the transmitter within each frame. The received power at a camera coming from a Lambertian light source of order m and transmitted power can be expressed as
where and are the emission and incident angles, respectively, is the area of the camera’s external lens, and d is the link span. From the RS mechanism shown in Figure 1, we can express the energy captured by the row as
where h (columns), v (rows) are the dimensions of the image sensor, and is the mask of pixels where the source shape is projected. From the integral limits, it can be derived that the bandwidth of the system decreases with the augment of the exposure time. In other words, the longer is , the more lines are simultaneously exposed, and the received signal is integrated in longer and less diverse time windows. For this reason, frames in OCC have to be acquired within short periods.
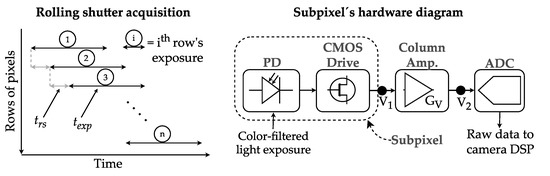
Figure 1.
Typical configuration of Complementary Metal-Oxide-Semiconductor (CMOS) camera sub-pixels.
Note that low values of , along with the attenuation factor in outdoor channels caused by the presence of particles such as fog or by the light refraction by turbulence can result in lower than the sensor’s lowest threshold of detection. For overcoming this, we can take advantage of the amplifying stage in the subpixel circuitry shown in Figure 1. The voltage-ratio gain of the column amplifier block behaves as
where is the voltage obtained from the pixel integration of light during exposure, and is the voltage value that is sampled by the ADC. In the case of the IMX219 sensor and of other CMOS sensors with the architecture shown in Figure 1, a software-defined analog gain configuration can set the value of for each capture. The typical values of range from 0 dB to 20.6 dB, as shown in [29].
The column gain of the CMOS sensor amplifies the received signal and all the noises up to the ADC. This includes the shot noise at the PD, and the thermal noises of the circuits, which can be modeled as random variables of Normal distributions with variances , and , as:
where is the Boltzmann’s constant, is noise temperature, is the bandwidth, is the electron charge, is the dark current of the camera’s pixels, and is the PD current at pixel in the color band . This current is determined by the emitted spectrum of the light source, the corresponding Bayer filter, and the substrate’s responsivity. Finally, models the contribution of the background illumination level to the shot noise. Nonetheless, since reduced exposure times are generally used, the contribution of can be neglected.
The signal is then sampled by the ADC, introducing quantization noise (), that is usually modeled as a zero-mean random normal contribution whose variance depends on the resolution of the converter. This results in the SNR, which is referred at the DSP’s input as:
Considering the SNR as a function of , it can be observed that it has an increasing behaviour with an upper asymptote given by . Especially in the cases when the signal entering the ADC is weak, e.g., as in high attenuation scenarios such as in the presence of dense fog, the relative loss due to quantization noise can be minimized by increasing the column amplification. In other words, the SNR can be optimized by the camera analog gain, unless the ADC is saturated.
Our system employs an On-off keying (OOK) modulation for each of the color bands with a fixed data input that is used as a beacon signal. For bit error ratio (BER) derivation, let us assume the system now works with a random data input of as the probabilities of value 0 and 1, respectively. The Maximum Likelihood Estimator (MLE) threshold at the detection stage of the OOK demodulation is given by
where and are the expected values of the received signal for the cases of transmitted signal equal to bits 0 and 1, respectively. If the receiver’s DSP applied a digital gain , the resulting MLE threshold would be . In this case, if , where is the bit depth, and is the maximum digital value of the signal coming from the ADC, the BER would tend to the worst case of a coin flip (error probability equal to 0.5).
2.2. Meteorological Phenomena
The presence of fog particles and turbulence in the air are known as relevant sources of signal distortion in outdoor optical systems. These conditions can be emulated in a laboratory chamber, and well-known parameters can estimate their degree, as explained in the following derivations.
Beer’s law [30] can describe the attenuation of propagating optical signals caused by fog. Generally, in optical systems, visibility in km is used to characterize fog attenuation (). Using the Mie’s scattering model [31], can be related to as:
where denotes wavelength in nm and parameter q is the distribution size of scattering particles given by Kim’s model [32], which is in the short range of visibility (<0.5 km) considered equal to zero. Thus, is given by:
The channel coefficient for fog can be determined by applying Beer’s law describing light scattering and absorption in a medium as:
Consequently, the average received optical power for the LOS link at the under fog is expressed as:
where denotes the addition of noises associated with and .
The coefficient depends on the value of the product of fog-attenuation and distance (), which is known as the optical density of the link. This variable can have the same value for different combinations of fog level and link span, allowing to infer the influence of both variables varying only one of them.
The heat-induced turbulence of air results from variations in temperature and pressure of the atmosphere along the path of transmission. Consequently, this leads to variations of the refractive index of the air, resulting in amplitude and phase fluctuations of the propagating optical beam [33]. For describing the strength of atmospheric turbulence, the parameter most commonly used is the refractive index structure parameter () (in units of m) [34,35], given by:
where T represents temperature in Kelvin, P is pressure in millibar, is the temperature structure parameter which is related to the universal 2/3 power law of temperature variations [35] given by:
where is the temperature difference between two points separated by distance , while the outer and inner scales of the small temperature variations are denoted by and , respectively.
2.3. Experimental Design
For the OCC system to be tested under emulated meteorological phenomena, the following conditions were considered. The signal transmitted by the VLC lamp was chosen to be a repetitive beacon, formed by a sequence of on-off pulses of each of the RGB channels, and followed by a black (off state) pulse denoted as K, then, the beacon was arbitrarily set to the following: G-R-B-K. The K pulse allows measuring the dark intensity in the pixels that cover the lamp image, while the pure color pulses allow to estimate the inter-channel cross-talk between the LED RGB colors and the RGB subpixels of the camera, as explained in our previous work [36]. The camera equipment was configured to take captures with fixed and different sequentially. After taking reference measurements, the atmospheric conditions were emulated while the beacon transmission and capture processes were sustained. The reference and test image sequences are processed through the stages shown in Figure 2, including the extraction of relevant pixels area in the picture, the estimation and enhancing of inter-channel cross-talk, and finally, the computation correlation between the signals obtained in clear conditions and under emulated weather conditions.
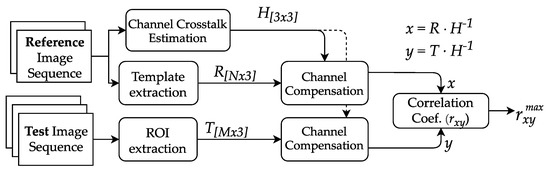
Figure 2.
Flow diagram of the offline processing of data captured by cameras.
The extraction of the relevant group of pixels in OCC image frames, known as Region of Interest (ROI) detection, consists of locating the projection of the source in the image. In this case, we first manually locate and extract the ROI from the reference sequence. Then, since the test group is taken with the same alignment, the ROI stays fixed. Thus, the same coordinates of it are re-utilized. The pixels containing data are then averaged by row, giving the three-channel (RGB) signal , where N is the number of rows of the ROI. From the reference ROI, a template of one G-R-B-K beacon signal is saved as , where M is the number of rows used by one beacon in the RS acquisition.
As shown in previous work [36], the inter-channel cross-talk (ICCT), which is caused by the mismatch between the LEDs and the camera’s Bayer filter spectra, is estimated from clear frames and then compensated in all datasets. We separately analyze R, G, and B pulses from the beacon signal. A matrix is obtained by averaging the contribution of each pure-LED pulse at the three RGB subpixels. In other words, a component from is the average measure from the subpixel when the LED is illuminating it, where . The inverse matrix is used to clean all the datasets from ICCT found at this configuration. Finally, ICCT cleaned signals and are compared using the Pearson’s correlation coefficient , which is defined as:
where are the reference sample points from R, of size N, are N consecutive samples of T, and are the mean values. The correlation is calculated for all possible consecutive subsets and the maximum value is considered the similarity of the frame compared to the reference.
3. Experimental Setup
In this section, we describe the full setup of our experiments, which is shown in Figure 3, including the laboratory chamber used, the tools used for emulating hot and foggy weather conditions, the measurement devices used for estimating the levels of each condition, and the and devices that comprise the OCC link. The key experiment parameters are listed in Table 2 and the block diagram of the experimental setup is shown in Figure 4.
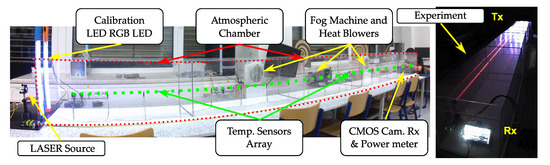
Figure 3.
Photos of the laboratory setup utilized in the experiments.

Table 2.
Experiment key parameters.
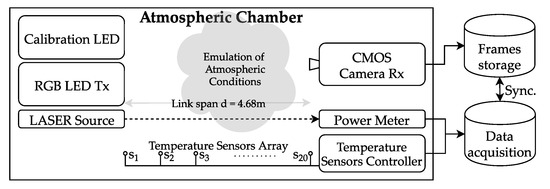
Figure 4.
Block diagram of the experimental setup.
3.1. Laboratory Chamber
The atmospheric chamber set up for measurements in the facilities of the Czech Technical University in Prague [27] features two heater fans, and one Glycerine machine, that can blow hot air and fog into the chamber, respectively. For the characterization of turbulence and light scintillation in the chamber, an array of 20 temperature sensors were set up equidistantly. A laser source of 625 nm and 2 mW, and an optical power meter placed on each end of the chamber are used to measure the fog attenuation.
3.2. OCC System
The transmitter unit was built using strips of RGB LEDs connected to a microcontroller (model ATmega328p [37]) through a switching circuit based on transistors. The LED arrays were installed on aluminum rails with a white meth-acrylate diffuser. The circuitry makes the RGB channels to emit the beacon signal (idle state) repeatedly, or to send arbitrary data coming from a serial port (this feature was not used in this experiment). The chip time or the pulse width is set by software in the microcontroller. In the case of the experiments, this parameter was set to s.
The receiver was made using an Element14 Raspberry Pi board with its official camera device PiCamera V2. The firmware allows to set from 1 to 16 dB and exposure time from 20 ns up to the time elapsed between frame captures, which in case of 30 fps video is approximately 33.3 ms. The fixed internal structure of the CMOS sensor (Sony IMX219) featured by the PiCamera is set to have a row-shift time = 18.904 s [29]. The exposure time was set to = 60 s.
Given the hardware configuration of our system in the laboratory, as shown in Figure 3, each of the image frames can contain up to 64 symbols. Since the modulation uses RGB channels, each symbol then is formed by 3 bits. The maximum throughput of this configuration at 30 fps is then 5.76 kbps.
4. Results
In this section, we show the results from the analysis of the images obtained from heat-turbulence and fog experiments carried out, as shown in Section 3. The maximum values of the correlation coefficient were computed between the ICCT-compensated reference image sequence and the images captured under different conditions, as explained in Section 2. The values obtained are analyzed together with the experimental parameters set: in the case of heat-induced turbulence, and , , in the case of fog.
4.1. Heat-Turbulence Experiments
The heat-turbulence experiment’s reference image sequence was captured using the chamber heaters off at a stabilized laboratory temperature of 21.7 C. Thus, the template signal extracted from these captures is the result of operating the system under a negligible level of turbulence. The remaining test image sequence was captured under the thermal influence of channel in two parts, one under a higher laboratory temperature of 32.3 C, and a second part with the heaters of the chamber working at full power, setting another turbulence level. The parameter value is then calculated using the temperature sensors samples. The values between the frames of the test image sequence and the template are calculated. With these values, we infer the influence of this phenomenon.
The refractive index structure parameter values during the first part of the test image sequence capture ranged from m to m in high room temperature with the heaters off. In the second part, the range of turbulence increased to m m. The obtained between the signals from each part of the experiment and the template are shown as histograms in Figure 5. To estimate the similarity between the data from the reference and from each part of the test image sequence, a Kolmogórov-Smirnov (KS) statistical test was done, which consists of a non-parametric tool that estimates if two data sets are samples from the same distribution with a confidence p-value [38]. The result is that the first part of the test image sequence has confidence value of having the same distribution as the reference, and the second has . It can be seen an almost negligible influence of turbulence on OCC systems.
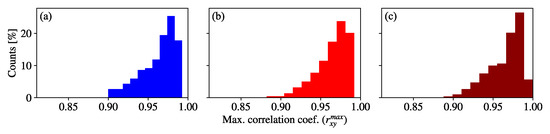
Figure 5.
Distribution of maximum correlation coefficient values of image sequences taken (a) under a cool room temperature of 21.7 C (no turbulence), (b) under a warm room temperature of 32.3 C and with heaters off, and (c) with turbulence induced by the heaters.
The different ranges of turbulence analyzed presumably have the same distribution of values, according to the KS statistical test, and also the vast amount of them meet that , which means that the experimental setup’s behavior is considerably similar to the reference, regardless of the turbulence ranges that were induced. This robustness of the system can be attributed to the short link distance and the big field of view of the camera. Both make the refraction effects unnoticeable in the received signal of our system.
4.2. Fog Experiments
For the fog emulation experiment, the reference image sequence was taken under clear air in the laboratory chamber while the optical power meter measured the power of the laser without fog attenuation. The test image sequence was taken while the chamber was arbitrarily supplied with fog from the Antari F-80Z, while the laser power was measured in synchronicity in order to label each image with the current . The value of of the images was sequentially modified from 0 to 16 dB by steps of 1 dB during the test image sequence, while for the reference, it was set to zero as default.
The values obtained for the test images sequence varying and are shown as a contour plot in Figure 6. The high correlation area () determines three important regions (highlighted in Figure 6 by dashed circles). For the high values of visibility, the signal coming from the transmitter is not affected by the fog attenuation and is received with the highest power. Then, the increase of gain causes saturation of the ADC, affecting the correlation. In the low visibility region, the presence of dense fog attenuates the received signal and lowers the correlation. It can be seen that, in this low-visibility region, the increase of gain gives a high correlation, meaning that the camera amplifier compensates the attenuation from fog. The region in between, around 50 m visibility, shows high values of correlation regardless of the variations of gain. The three regions described are shown in Figure 7, and a non-parametric locally estimated scatterplot smoothing (LOESS) regression [39] is performed with parameter span to show the trend of the data points. Examples of the ROI extraction from test images sequence are included to depict the effect of visibility and gain over the frames.
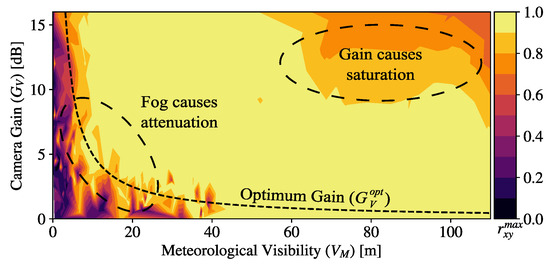
Figure 6.
Maximum correlation between test and reference signals varying camera gain under emulated fog conditions of different values of meteorological visibility.
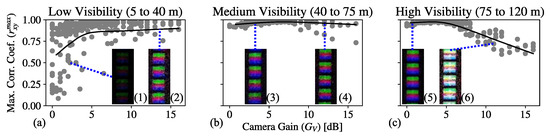
Figure 7.
Maximum correlation data (gray dots) from fog-emulation experiments, separated by levels of (a) low, (b) medium, and (c) high visibility and their respective locally estimated scatterplot smoothing (LOESS) regression for (black curves). The area encircled in (a) is the region of image frames affected by the fog attenuation and in (b) by gain saturation. Insets are Region of Interest (ROI) extraction examples: (1) for low visibility and low gain, (2) low visibility and high gain, (3) medium visibility and low gain, (4) medium visibility and high gain, (5) high visibility and low gain, and (6) high visibility and high gain.
From the minimum gain values in the area of , an optimum gain curve is derived providing that there is an inverse proportionality relationship between meteorological visibility and camera gain as follows:
where is an empirical parameter. Using curve fitting, the value dB·km was derived for our experimental setup.
In order to calculate the SNR from the empirical data obtained, we have considered that OOK modulation is used. The following approximation of the SNR has been derived (note the factor due to OOK):
where comprises the samples of pixels that fall within the ROI mask as described in Equation (2), which was determined from reference images and since the and are static it is the same for the whole experiment. , and denote the statistical expected value and variance, respectively.
The empirical SNR definition was calculated for all the image sequences of the fog experiments. The results for the frames taken with = 11 dB are shown in Figure 8 for the three RGB channels. This value of gain was chosen because, as shown in Figure 6, the level = 11 dB is affected by the dense fog and also by the saturation. The SNR values in Figure 8 are plotted against optical density in logaritmic scale. They show that higher attenuation values, or alternatively, longer link spans, cause a decay of the SNR. Therefore, a curve fitting was carried out assuming that the SNR decays at a rate of dB per decade of optical density, as follows:
where SNR(1) is the estimated signal-to-noise ratio at unitary optical density.
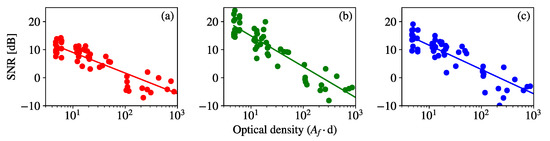
Figure 8.
Empirical signal-to-noise ratio (SNR) values obtained from captures at = 11 dB plotted against optical density values at fixed link range d and with values emulated by the presence of fog. The plot in (a) corresponds to R channel, (b) to G channel, and (c) to B channel, and their respective fitted curves.
The SNR values obtained from the image sequences were also evaluated on their influence over , as shown in Figure 9. A LOESS regression also shows the trend of the scatterplots in the figure, and it can be seen that increases with the SNR, except for the highest SNR values in the blue channel, which are affected by saturation of the ADC. It can also be seen that SNR values higher than 5 dB make for most of the samples. From this, it can be concluded that is a valid metric for the quality of the signal in OCC, although SNR is more robust.
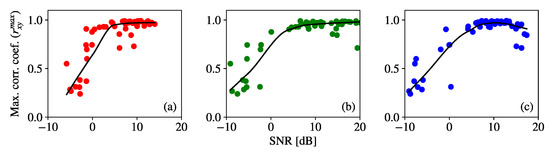
Figure 9.
Values of from test image sequence of the fog-emulation experiment plotted against empirical SNR. The values are for frames taken with = 11 dB. The scatter plot in (a) corresponds to R channel, (b) to G channel, and (c) to B channel, and the curves in black are their corresponding LOESS regression for span value 0.7.
The results obtained in this experiment show that the fog attenuation can make the power of the optical signal weaken down to the point that the noise induced by the ADC considerably affects the SNR. In other words, the conversion to digital corrupts the weak optical signal from dense fog conditions or long link spans. In these cases, the column amplifier of the camera is crucial to keep a high amplitude input at the ADC and reduce the effect of quantization.
5. Conclusions
In this paper, we presented an experimental study of the influence of two kinds of atmospheric conditions over an RS-based OCC link: the heat-induced turbulence due to random fluctuations of the refractive index of the air along the path, and the attenuation caused by the presence of fog particles in the air. The image sequences captured under the two different conditions were compared to a reference sequence of images taken under clear conditions. For this, we used the maximum value of Pearson’s correlation coefficient to determine their similarity. We have also evaluated the signal quality by the empirical SNR obtained from the image frames and showed its relationship with and its dependence on the product between fog attenuation and link span, known as the optical density. The most important findings in this work are, first, that the turbulence levels emulated do not affect the signal quality considerably. For the fog experiments, we have derived an expression for the theoretical SNR as a function of the analog camera gain, showing that a CMOS camera-based OCC system can improve the SNR by using the column amplifier. In the fog experiments, the correlation was impaired in two different cases: for high values of , when the gain is increased, the correlation drops because of the saturation of the signal, and, for low visibility, the attenuation caused by the fog impairs the similarity to the reference when the gain is low, because of the loss due to quantization noise at the ADC. It was found for the latter case that by increasing the gain of the camera, the attenuation can be compensated, allowing the OCC link to receive signal with a for values down to 10 m. Our findings show that there is an inverse proportionality relationship between the optimum camera gain and the visibility, and that the empirical SNR decays at a rate with the optical density. This utilization of the CMOS camera’s built-in amplifier opens a new possibility for OCC systems, extending the control strategy, and allowing to keep low exposure times and, thus, a high bandwidth, even in dense fog scenarios.
Author Contributions
The contributions of the authors in this paper are the following: conceptualization, V.M., S.R.T., E.E.; investigation, V.M., S.R.T.; methodology, V.M., E.E.; project administration, S.Z., R.P.-J.; software V.M.; and validation, S.Z., R.P.-J. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 764461, and from the Spanish Research Administration (MINECO project: OSCAR, ref.: TEC 2017-84065-C3-1-R)
Acknowledgments
V. M. thanks the technical support given by Jan Bohata, Petr Chvojka, and Dmytro Suslov at the Czech Technical University in Prague, and by Victor Guerra, and Cristo Jurado-Verdu at IDeTIC - Universidad de Las Palmas de Gran Canaria.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Cahyadi, W.A.; Kim, Y.H.; Chung, Y.H.; Ahn, C.J. Mobile phone camera-based indoor visible light communications with rotation compensation. IEEE Photonics J. 2016, 8, 1–8. [Google Scholar] [CrossRef]
- Teli, S.R.; Zvanovec, S.; Ghassemlooy, Z. Performance evaluation of neural network assisted motion detection schemes implemented within indoor optical camera based communications. Opt. Express 2019, 27, 24082–24092. [Google Scholar] [CrossRef] [PubMed]
- Chavez-Burbano, P.; Vitek, S.; Teli, S.; Guerra, V.; Rabadan, J.; Perez-Jimenez, R.; Zvanovec, S. Optical camera communication system for Internet of Things based on organic light emitting diodes. Electron. Lett. 2019, 55, 334–336. [Google Scholar] [CrossRef]
- Tiwari, S.V.; Sewaiwar, A.; Chung, Y.H. Optical bidirectional beacon based visible light communications. Opt. Express 2015, 23, 26551–26564. [Google Scholar] [CrossRef] [PubMed]
- Pergoloni, S.; Biagi, M.; Colonnese, S.; Cusani, R.; Scarano, G. Coverage optimization of 5G atto-cells for visible light communications access. In Proceedings of the 2015 IEEE International Workshop on Measurements & Networking (M&N), Coimbra, Portugal, 12–13 October 2015; pp. 1–5. [Google Scholar]
- Boban, M.; Kousaridas, A.; Manolakis, K.; Eichinger, J.; Xu, W. Connected roads of the future: Use cases, requirements, and design considerations for vehicle-to-everything communications. IEEE Veh. Technol. Mag. 2018, 13, 110–123. [Google Scholar] [CrossRef]
- Yamazato, T.; Takai, I.; Okada, H.; Fujii, T.; Yendo, T.; Arai, S.; Andoh, M.; Harada, T.; Yasutomi, K.; Kagawa, K.; et al. Image-sensor-based visible light communication for automotive applications. IEEE Commun. Mag. 2014, 52, 88–97. [Google Scholar] [CrossRef]
- Takai, I.; Ito, S.; Yasutomi, K.; Kagawa, K.; Andoh, M.; Kawahito, S. LED and CMOS image sensor based optical wireless communication system for automotive applications. IEEE Photonics J. 2013, 5, 6801418. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Alves, L.N.; Zvanovec, S.; Khalighi, M.A. Visible Light Communications: Theory and Applications; CRC Press: Borarton, FL, USA, 2017. [Google Scholar]
- Boubezari, R.; Le Minh, H.; Ghassemlooy, Z.; Bouridane, A. Smartphone camera based visible light communication. J. Lightwave Technol. 2016, 34, 4121–4127. [Google Scholar] [CrossRef]
- Nguyen, T.; Islam, A.; Hossan, T.; Jang, Y.M. Current status and performance analysis of optical camera communication technologies for 5G networks. IEEE Access 2017, 5, 4574–4594. [Google Scholar] [CrossRef]
- Nguyen, T.; Hong, C.H.; Le, N.T.; Jang, Y.M. High-speed asynchronous Optical Camera Communication using LED and rolling shutter camera. In Proceedings of the 2015 Seventh International Conference on Ubiquitous and Future Networks, Sapporo, Japan, 7–10 July 2015; pp. 214–219. [Google Scholar]
- Chavez-Burbano, P.; Guerra, V.; Rabadan, J.; Perez-Jimenez, R. Optical camera communication for smart cities. In Proceedings of the 2017 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Qingdao, China, 22–24 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Chavez-Burbano, P.; Guerra, V.; Rabadan, J.; Rodriguez-Esparragon, D.; Perez-Jimenez, R. Experimental characterization of close-emitter interference in an optical camera communication system. Sensors 2017, 17, 1561. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Wang, C.; Tsai, H.M. Characterizing channel fading in vehicular visible light communications with video data. In Proceedings of the 2014 IEEE Vehicular Networking Conference (VNC), Paderborn, Germany, 3–5 December 2014; pp. 226–229. [Google Scholar]
- Wu, L.C.; Tsai, H.M. Modeling vehicle-to-vehicle visible light communication link duration with empirical data. In Proceedings of the 2013 IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 1103–1109. [Google Scholar]
- Mobility and Transport (European Comission). Current Speed Limit Policies. Available online: https://ec.europa.eu/transport/road_safety/specialist/knowledge/speed/speed_limits/current_speed_limit_policies_en (accessed on 28 January 2020).
- Road Safety Authority (Government of Ireland). The Two-Second Rule. Available online: http://www.rotr.ie/rules-for-driving/speed-limits/speed-limits_2-second-rule.html (accessed on 28 January 2020).
- Kim, Y.H.; Chung, Y.H. Experimental outdoor visible light data communication system using differential decision threshold with optical and color filters. Opt. Eng. 2015, 54, 040501. [Google Scholar] [CrossRef]
- Islam, A.; Hossan, M.T.; Jang, Y.M. Convolutional neural networkscheme–based optical camera communication system for intelligent Internet of vehicles. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718770153. [Google Scholar] [CrossRef]
- Elamassie, M.; Karbalayghareh, M.; Miramirkhani, F.; Kizilirmak, R.C.; Uysal, M. Effect of fog and rain on the performance of vehicular visible light communications. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–6. [Google Scholar]
- Tian, X.; Miao, Z.; Han, X.; Lu, F. Sea Fog Attenuation Analysis of White-LED Light Sources for Maritime VLC. In Proceedings of the 2019 IEEE International Conference on Computational Electromagnetics (ICCEM), Shanghai, China, 20–22 March 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Kim, Y.H.; Cahyadi, W.A.; Chung, Y.H. Experimental demonstration of VLC-based vehicle-to-vehicle communications under fog conditions. IEEE Photonics J. 2015, 7, 1–9. [Google Scholar] [CrossRef]
- Guo, L.-D.; Cheng, M.-J.; Guo, L.-X. Visible light propagation characteristics under turbulent atmosphere and its impact on communication performance of traffic system. In Proceedings of the 14th National Conference on Laser Technology and Optoelectronics (LTO 2019), Shanghai, China, 17 May 2019; p. 1117047. [Google Scholar] [CrossRef]
- Nikishov, V.V.; Nikishov, V.I. Spectrum of Turbulent Fluctuations of the Sea-Water Refraction Index. Int. J. Fluid Mech. Res. 2000, 27, 82–98. [Google Scholar] [CrossRef]
- Eso, E.; Burton, A.; Hassan, N.B.; Abadi, M.M.; Ghassemlooy, Z.; Zvanovec, S. Experimental Investigation of the Effects of Fog on Optical Camera-based VLC for a Vehicular Environment. In Proceedings of the 2019 15th International Conference on Telecommunications (ConTEL), Graz, Austria, 3–5 July 2019; pp. 1–5. [Google Scholar]
- Bohata, J.; Zvanovec, S.; Korinek, T.; Abadi, M.M.; Ghassemlooy, Z. Characterization of dual-polarization LTE radio over a free-space optical turbulence channel. Appl. Opt. 2015, 54, 7082–7087. [Google Scholar] [CrossRef] [PubMed]
- Kuroda, T. Essential Principles of Image Sensors; CRC Press: Borarton, FL, USA, 2017. [Google Scholar]
- IMX219PQH5-C Datasheet. Available online: https://datasheetspdf.com/pdf/1404029/Sony/IMX219PQH5-C/1 (accessed on 28 January 2020).
- Weichel, H. Laser Beam Propagation in the Atmosphere; SPIE Press: Bellingham, WA, USA, 1990; Volume 3. [Google Scholar]
- Henniger, H.; Wilfert, O. An Introduction to Free-space Optical Communications. Radioengineering 2010, 19, 203–212. [Google Scholar]
- Kim, I.I.; McArthur, B.; Korevaar, E.J. Comparison of laser beam propagation at 785 nm and 1550 nm in fog and haze for optical wireless communications. In Proceedings of the Optical Wireless Communications III. International Society for Optics and Photonics, Boston, MA, USA, 6 February 2001; pp. 26–37. [Google Scholar]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with Matlab; CRC Press: Borarton, FL, USA, 2019. [Google Scholar]
- Nor, N.A.M.; Fabiyi, E.; Abadi, M.M.; Tang, X.; Ghassemlooy, Z.; Burton, A. Investigation of moderate-to-strong turbulence effects on free space optics—A laboratory demonstration. In Proceedings of the 2015 13th International Conference on Telecommunications (ConTEL), Graz, Austria, 13–15 July 2015; pp. 1–5. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media; SPIE Press: Bellingham, WA, USA, 2005; Volume 152. [Google Scholar]
- Jurado-Verdu, C.; Matus, V.; Rabadan, J.; Guerra, V.; Perez-Jimenez, R. Correlation-based receiver for optical camera communications. Opt. Express 2019, 27, 19150–19155. [Google Scholar] [CrossRef] [PubMed]
- Atmel Corporation. ATmega328p, 8-bit AVR Microcontroller with 32K Bytes In-System Programmable Flash, Datasheet; Atmel Corporation: San Jose, CA, USA, 2015; 328p. [Google Scholar]
- Massey, F.J., Jr. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Locally weighted regression: An approach to regression analysis by local fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).