Optical Fiber FP Sensor for Simultaneous Measurement of Refractive Index and Temperature Based on the Empirical Mode Decomposition Algorithm
Abstract
1. Introduction
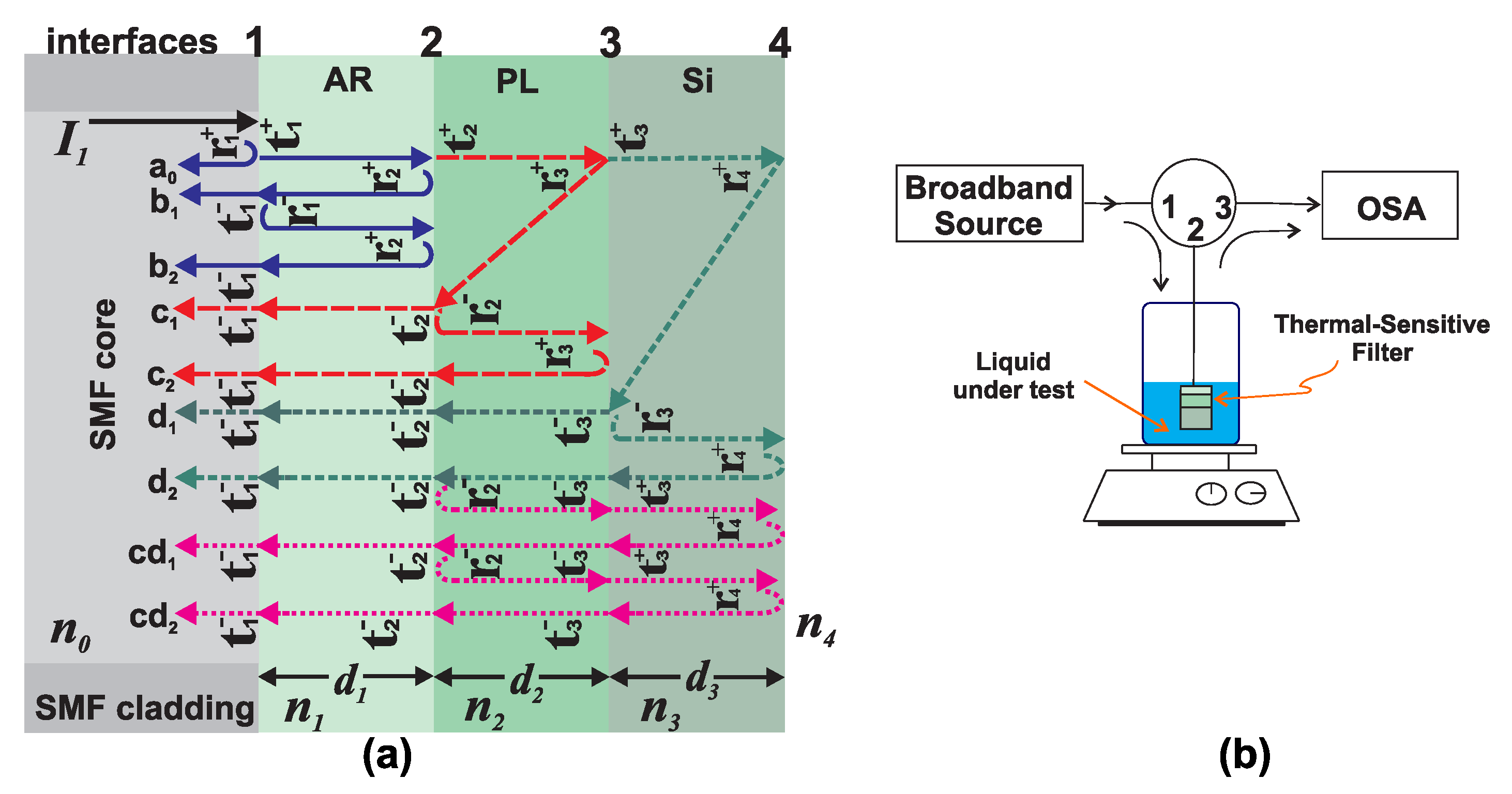
2. Sensing Element Design and Fabrication
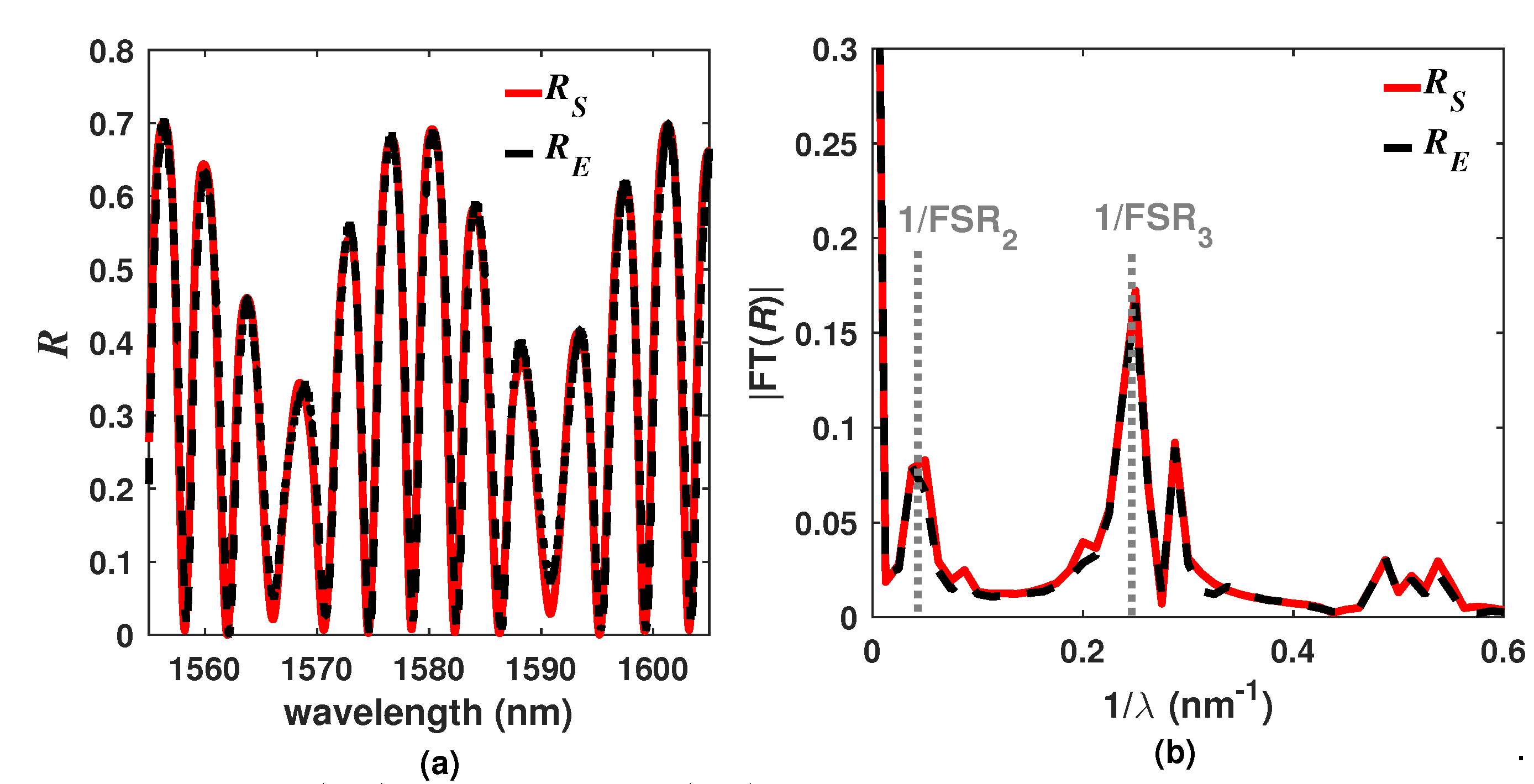
2.1. Characterization of Reflected Intensity Distribution Pattern of the Fabricated Filter
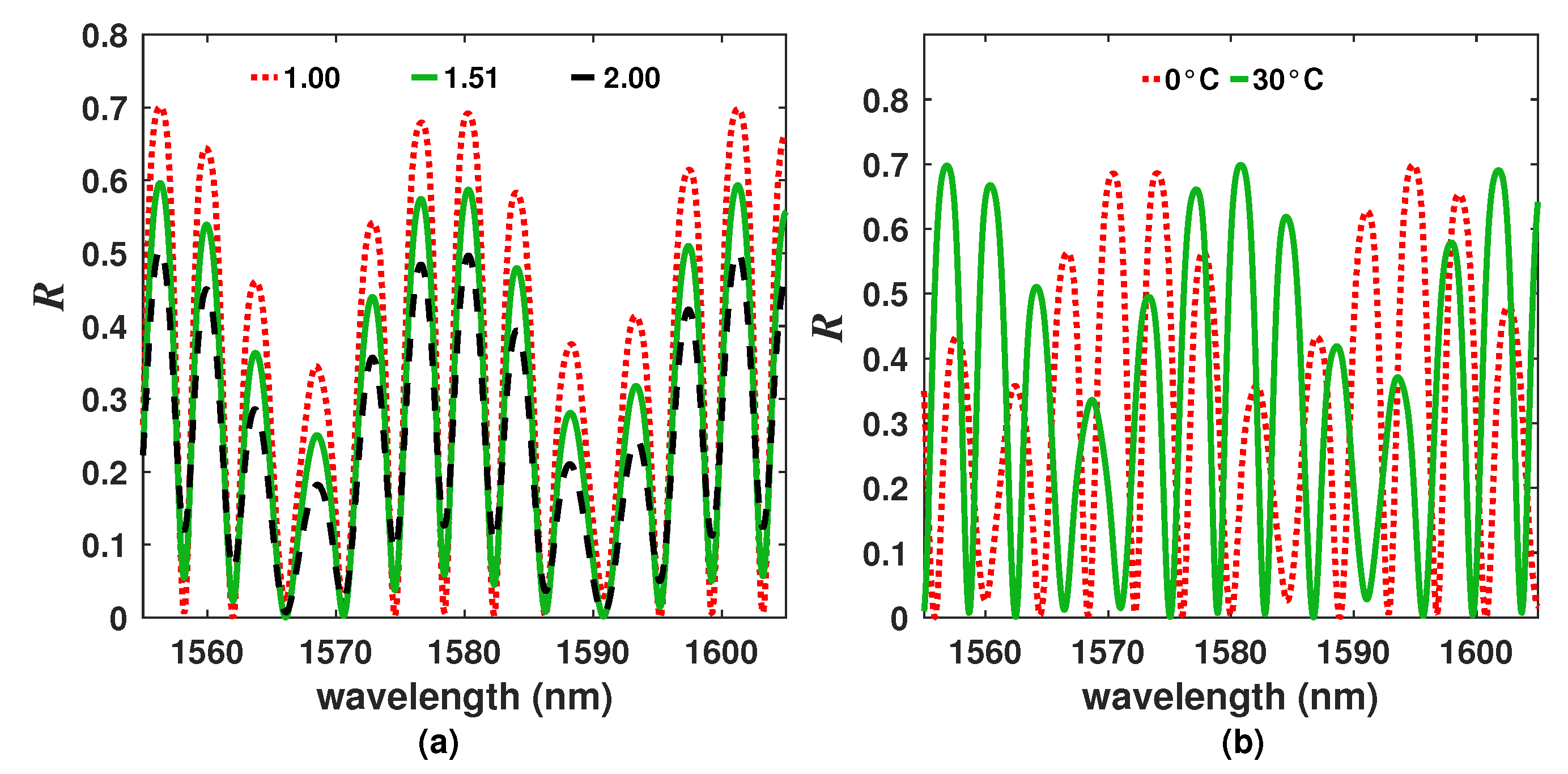
2.2. Characterization of the Refractive Index Effects
2.3. Characterization of the Temperature Effects
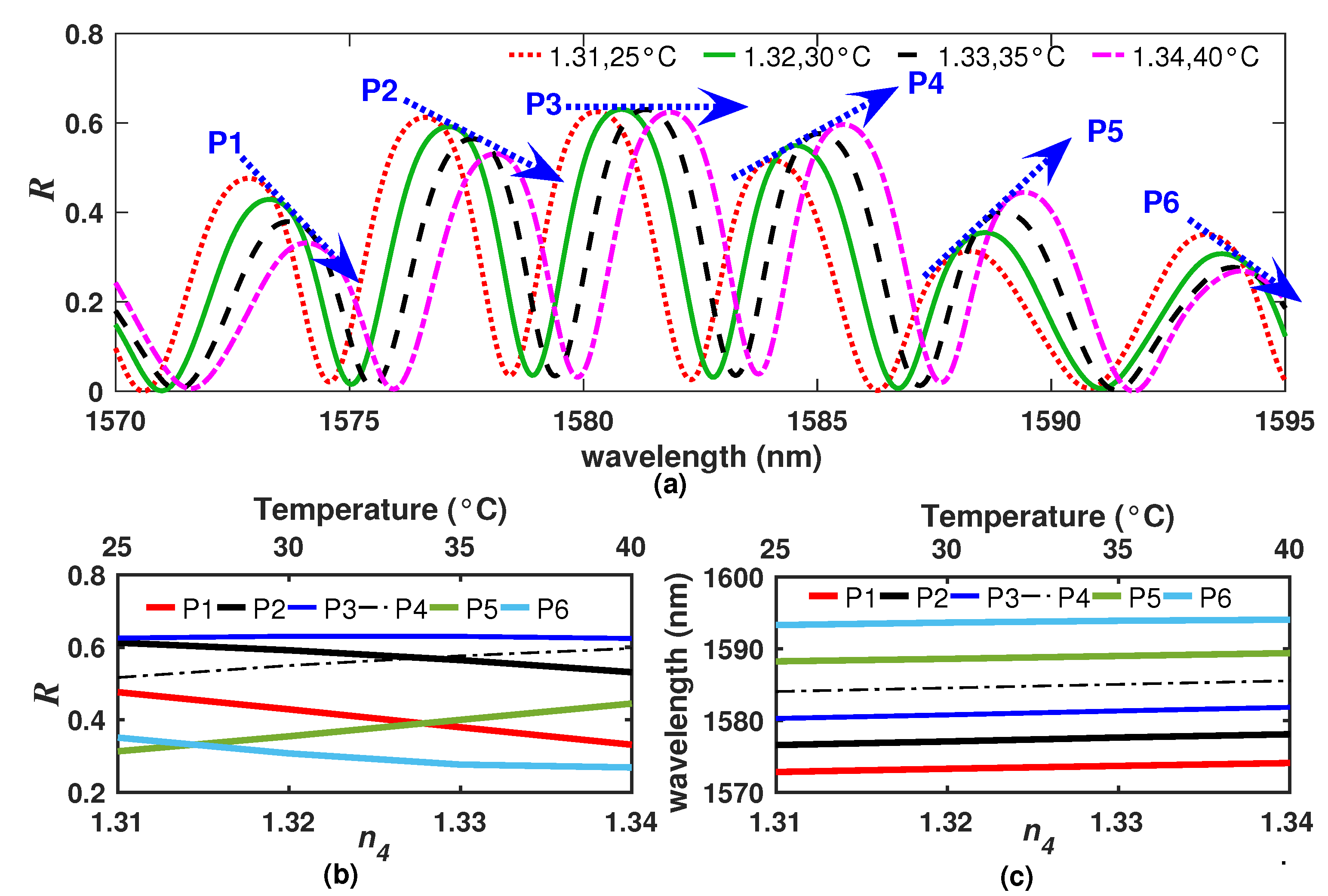
2.4. Simultaneous Refractive Index and Temperature Effects
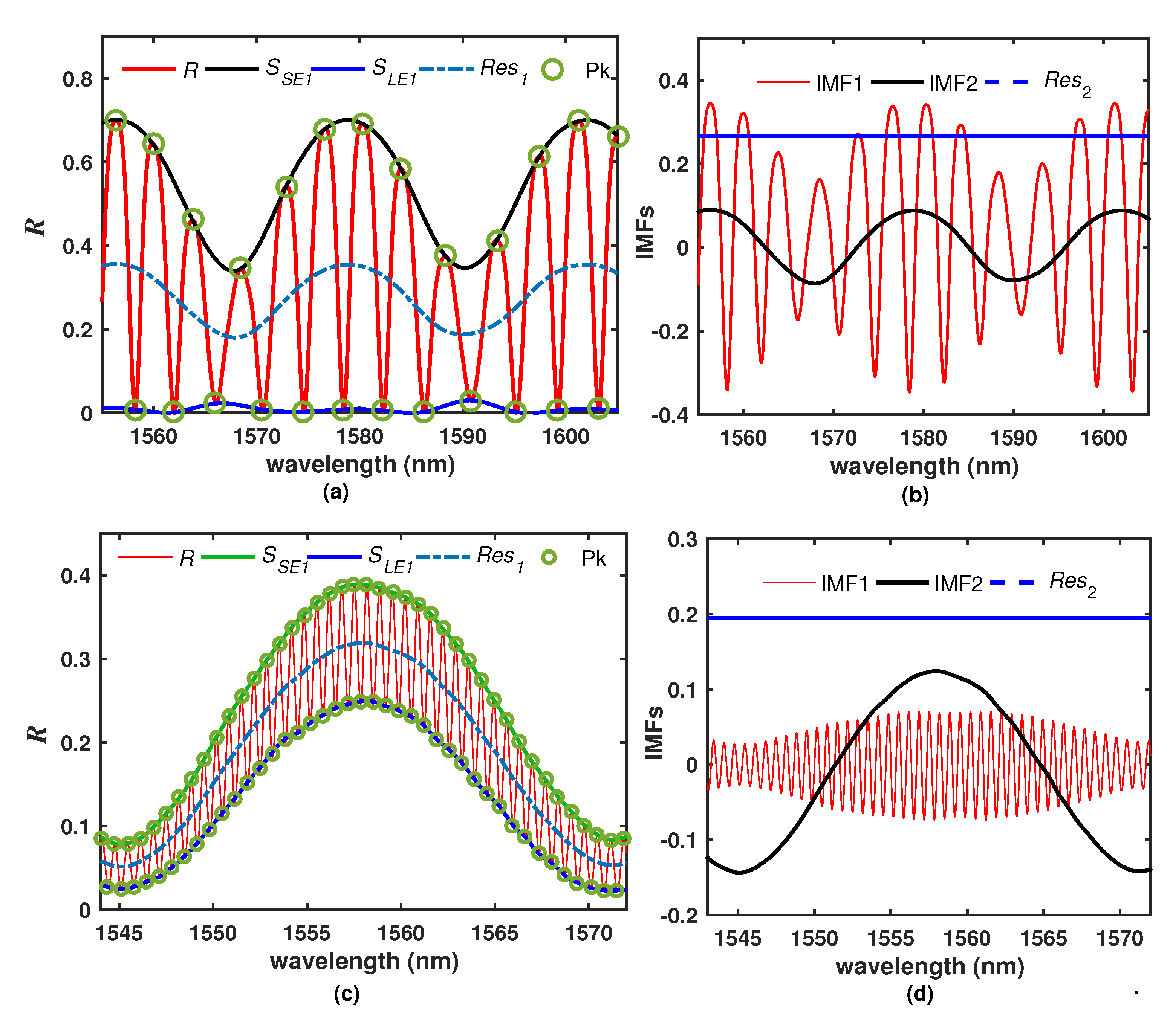
3. Spectrum Decomposition
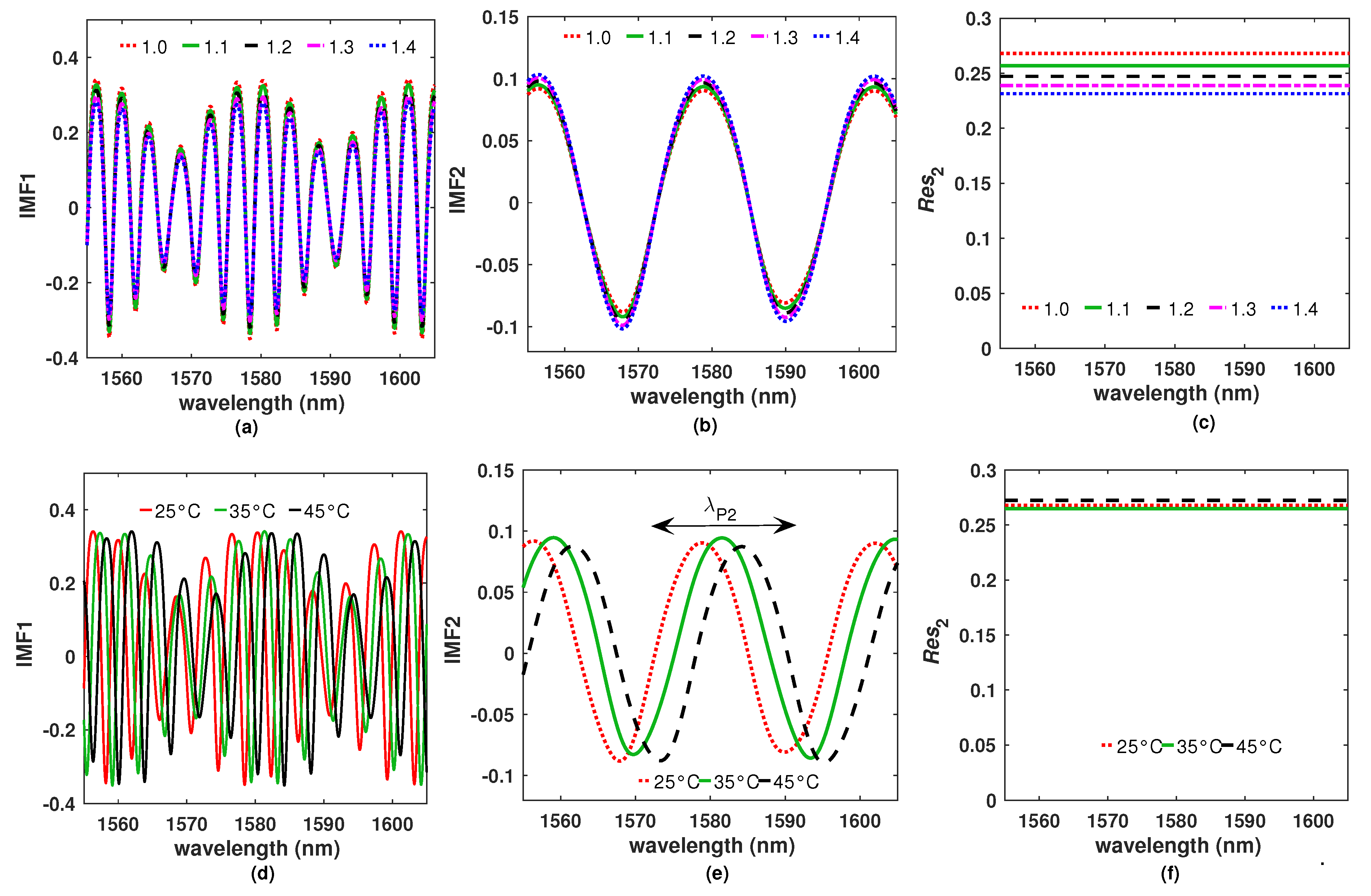
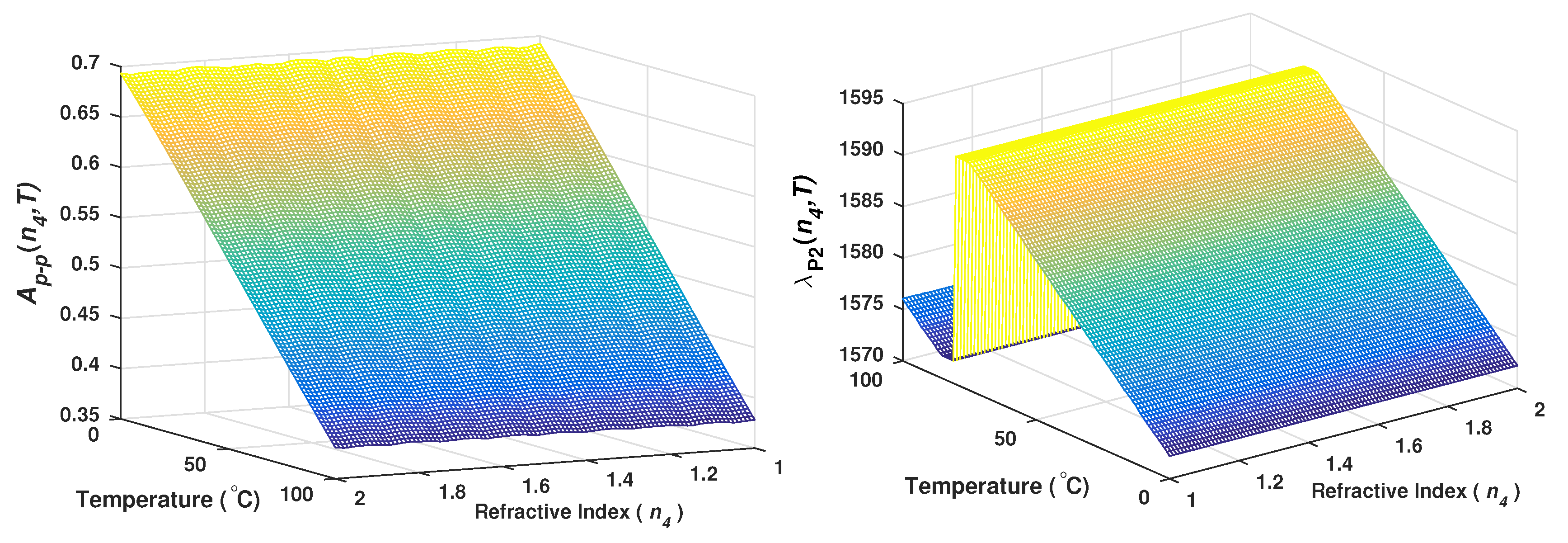
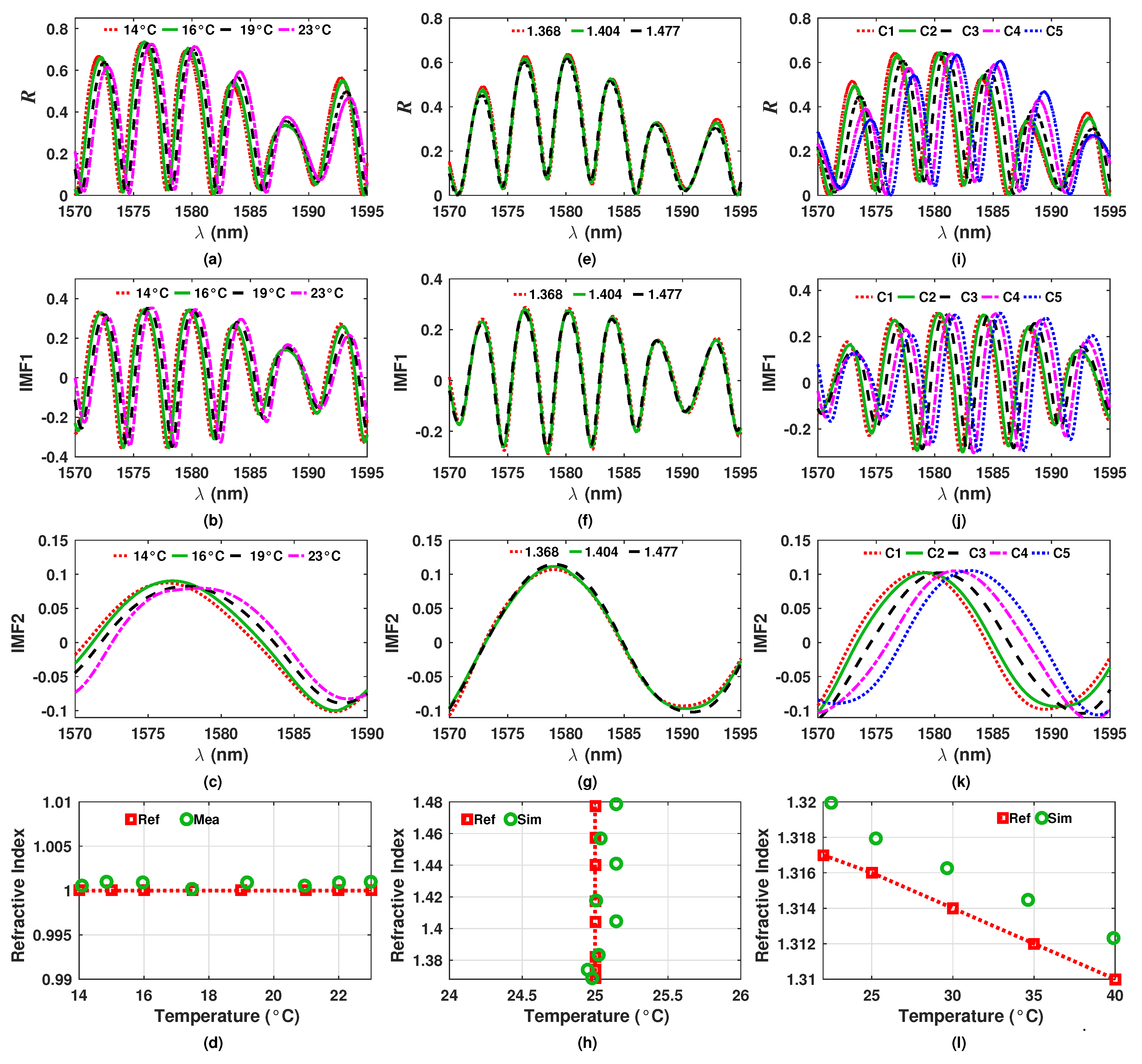
4. Effects of the Refractive Index and the Temperature over the IMFs
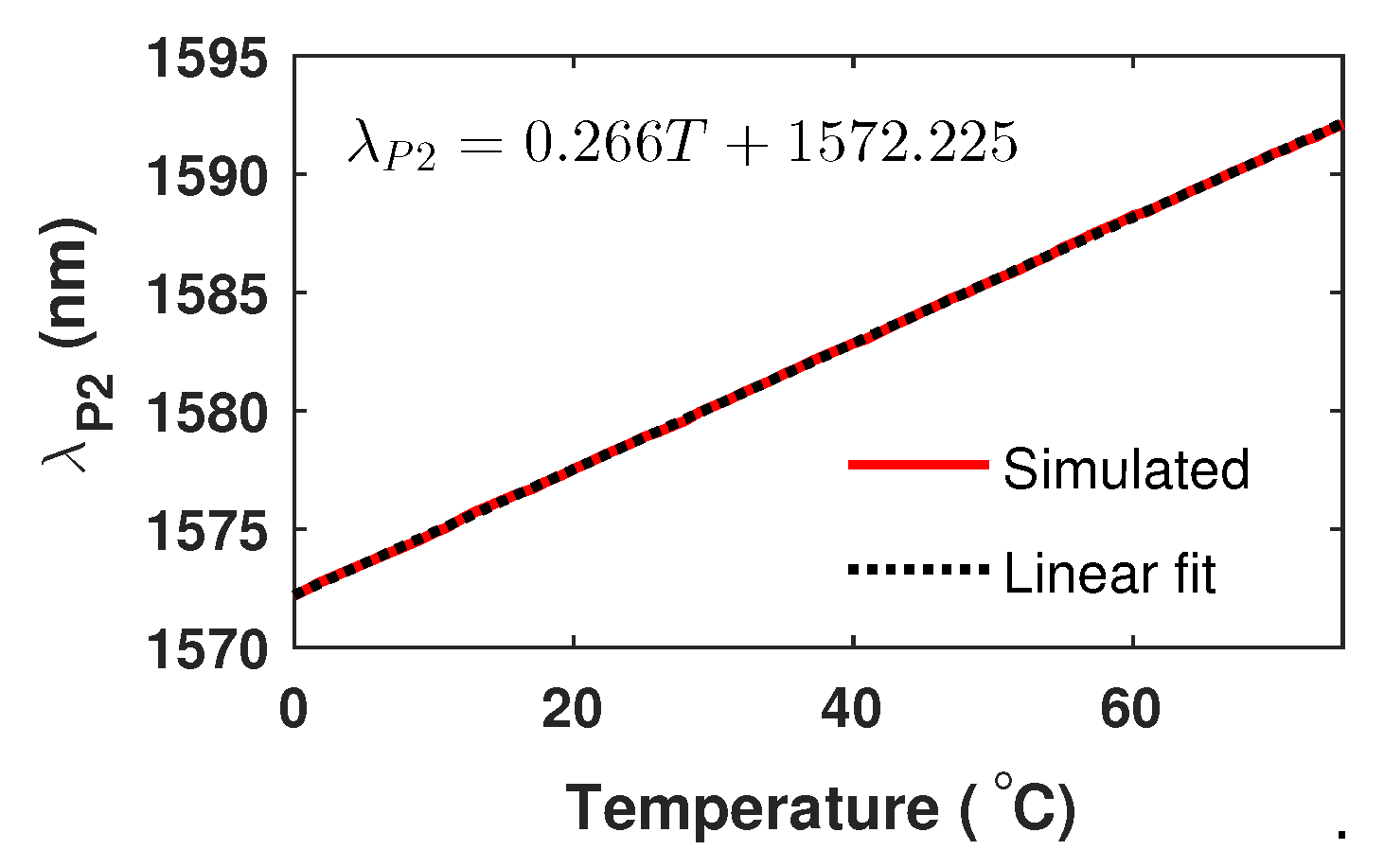
5. Experimental Measurement of Refractive Index and Temperature
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Urrutia, A.; Del Villar, I.; Zubiate, P.; Zamarreño, C.R. A Comprehensive Review of Optical Fiber Refractometers: Toward a Standard Comparative Criterion. Laser Photonics Rev. 2019, 13, 1900094. [Google Scholar] [CrossRef]
- Dash, J.N.; Jha, R. Fabry-Perot based strain insensitive photonic crystal fiber modal interferometer for inline sensing of refractive index and temperature. Appl. Opt. 2015, 54, 10479–10486. [Google Scholar] [CrossRef] [PubMed]
- Frazão, O.; Baptista, J.M.; Santos, J.L.; Kobelke, J.; Schuster, K. Refractive index tip sensor based on Fabry-Perot cavities formed by a suspended core fibre. J. Eur. Opt. Soc.-Rapid Publ. 2009, 4, 1–4. [Google Scholar] [CrossRef]
- Ran, Z.L.; Rao, Y.J.; Liu, W.J.; Liao, X.; Chiang, K.S. Laser-micromachined Fabry-Perot optical fiber tip sensor for high-resolution temperature-independent measurement of refractive index. Opt. Express 2008, 16, 2252–2263. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Yang, Y.; Jia, Z.; Wang, D.N. Hybrid Fabry-Perot interferometer for simultaneous liquid refractive index and temperature measurement. Opt. Express 2017, 25, 14483–14493. [Google Scholar] [CrossRef]
- Vargas-Rodriguez, E.; Guzman-Chavez, A.D.; Cano-Contreras, M.; Gallegos-Arellano, E.; Jauregui-Vazquez, D.; Hernández-García, J.C.; Estudillo-Ayala, J.M.; Rojas-Laguna, R. Analytical Modelling of a Refractive Index Sensor Based on an Intrinsic Micro Fabry-Perot Interferometer. Sensors 2015, 15, 26128–26142. [Google Scholar] [CrossRef]
- Pevec, S.; Donlagic, D. MultiParameter Fiber-Optic Sensor for Simultaneous Measurement of Thermal Conductivity, Pressure, Refractive Index, and Temperature. IEEE Photonics J. 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Wei, T.; Han, Y.; Li, Y.; Tsai, H.L.; Xiao, H. Temperature-insensitive miniaturized fiber inline Fabry-Perot interferometer for highly sensitive refractive index measurement. Opt. Express 2008, 16, 5764–5769. [Google Scholar] [CrossRef]
- Lee, C.L.; Liu, K.W.; Luo, S.H.; Wu, M.S.; Ma, C.T. A Hot-Polymer Fiber Fabry–Perot Interferometer Anemometer for Sensing Airflow. Sensors 2017, 17, 2015. [Google Scholar] [CrossRef]
- Ma, C.T.; Chang, Y.W.; Yang, Y.J.; Lee, C.L. A Dual-Polymer Fiber Fizeau Interferometer for Simultaneous Measurement of Relative Humidity and Temperature. Sensors 2017, 17, 2659. [Google Scholar] [CrossRef]
- Vargas-Rodriguez, E.; Guzman-Chavez, A.D.; Garcia-Ramirez, M.A. Tunable Optical Filter Based on Two Thermal Sensitive Layers. IEEE Photonics Technol. Lett. 2018, 30, 1776–1779. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.; Li, L.; Xiong, L.; Shum, P.P. Liquid core fiber interferometer for simultaneous measurement of refractive index and temperature. IEEE Photonics Technol. Lett. 2018, 31, 189–192. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, Y.; Zhu, C.; Chen, C.; Yang, R.; Xue, Y.; Chen, Q.; Sun, H. Miniature End-Capped Fiber Sensor for Refractive Index and Temperature Measurement. IEEE Photonics Technol. Lett. 2014, 26, 7–10. [Google Scholar] [CrossRef]
- Tan, X.L.; Geng, Y.F.; Li, X.J.; Deng, Y.L.; Yin, Z.; Gao, R. UV-Curable Polymer Microhemisphere-Based Fiber-Optic Fabry–Perot Interferometer for Simultaneous Measurement of Refractive Index and Temperature. IEEE Photonics J. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Hasar, U.C.; Ozbek, I.Y.; Karacali, T. Nondestructive Optical Characterization of Fabry-Pérot Cavities by Full Spectra Fitting Method. IEEE Photonics Technol. Lett. 2018, 30, 1404–1407. [Google Scholar] [CrossRef]
- Industrias Kola Loka SA de CV. Personal communication. 2018. Available online: www.krazykolaloka.com.mx/index.html (accessed on 5 January 2020).
- Lyon, K.G.; Salinger, G.L.; Swenson, C.A.; White, G.K. Linear thermal expansion measurements on silicon from 6 to 340 K. J. Appl. Phys. 1977, 48, 865–868. [Google Scholar] [CrossRef]
- Komma, J.; Schwarz, C.; Hofmann, G.; Heinert, D.; Nawrodt, R. Thermo-optic coefficient of silicon at 1550 nm and cryogenic temperatures. Appl. Phys. Lett. 2012, 101, 041905. [Google Scholar] [CrossRef]
- Tuominen, J.; Niemi, T.; Ludvigsen, H. Wavelength reference for optical telecommunications based on a temperature-tunable silicon etalon. Rev. Sci. Instrum. 2003, 74, 3620–3623. [Google Scholar] [CrossRef]
- Cardona-Maya, Y.; Botero-Cadavid, J.F. Refractive index desensitized optical fiber temperature sensor. Revista Facultad de Ingeniería Universidad de Antioquia 2017, 85, 86–90. [Google Scholar] [CrossRef]
- Khodier, S.A. Refractive index of standard oils as a function of wavelength and temperature. Opt. Laser Technol. 2002, 34, 125–128. [Google Scholar] [CrossRef]
- Xu, W.; Huang, X.G.; Pan, J.S. Simple Fiber-Optic Refractive Index Sensor Based On Fresnel Reflection and Optical Switch. IEEE Sens. J. 2013, 13, 1571–1574. [Google Scholar] [CrossRef]
- Maheshwari, S.; Kumar, A. Empirical Mode Decomposition: Theory & Applications. Int. J. Electron. Eng. 2014, 7, 873–878. [Google Scholar]
- Ge, H.; Chen, G.; Yu, H.; Chen, H.; An, F. Theoretical Analysis of Empirical Mode Decomposition. Symmetry 2018, 10, 623. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]

| Description | Parameter |
|---|---|
| Refractive index | |
| Layer thickness | |
| Thermo-optic coefficient | |
| Thermo-expansion coefficient | |
| Phase difference | |
| Optical losses | |
| Refractive index change | |
| Layer thickness variation | |
| Transmission coefficients | |
| Reflection coefficients |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargas-Rodriguez, E.; Guzman-Chavez, A.D.; Baeza-Serrato, R.; Garcia-Ramirez, M.A. Optical Fiber FP Sensor for Simultaneous Measurement of Refractive Index and Temperature Based on the Empirical Mode Decomposition Algorithm. Sensors 2020, 20, 664. https://doi.org/10.3390/s20030664
Vargas-Rodriguez E, Guzman-Chavez AD, Baeza-Serrato R, Garcia-Ramirez MA. Optical Fiber FP Sensor for Simultaneous Measurement of Refractive Index and Temperature Based on the Empirical Mode Decomposition Algorithm. Sensors. 2020; 20(3):664. https://doi.org/10.3390/s20030664
Chicago/Turabian StyleVargas-Rodriguez, Everardo, Ana Dinora Guzman-Chavez, Roberto Baeza-Serrato, and Mario Alberto Garcia-Ramirez. 2020. "Optical Fiber FP Sensor for Simultaneous Measurement of Refractive Index and Temperature Based on the Empirical Mode Decomposition Algorithm" Sensors 20, no. 3: 664. https://doi.org/10.3390/s20030664
APA StyleVargas-Rodriguez, E., Guzman-Chavez, A. D., Baeza-Serrato, R., & Garcia-Ramirez, M. A. (2020). Optical Fiber FP Sensor for Simultaneous Measurement of Refractive Index and Temperature Based on the Empirical Mode Decomposition Algorithm. Sensors, 20(3), 664. https://doi.org/10.3390/s20030664






