3D Hermite Transform Optical Flow Estimation in Left Ventricle CT Sequences
Abstract
1. Introduction
2. The 3D Hermite Transform
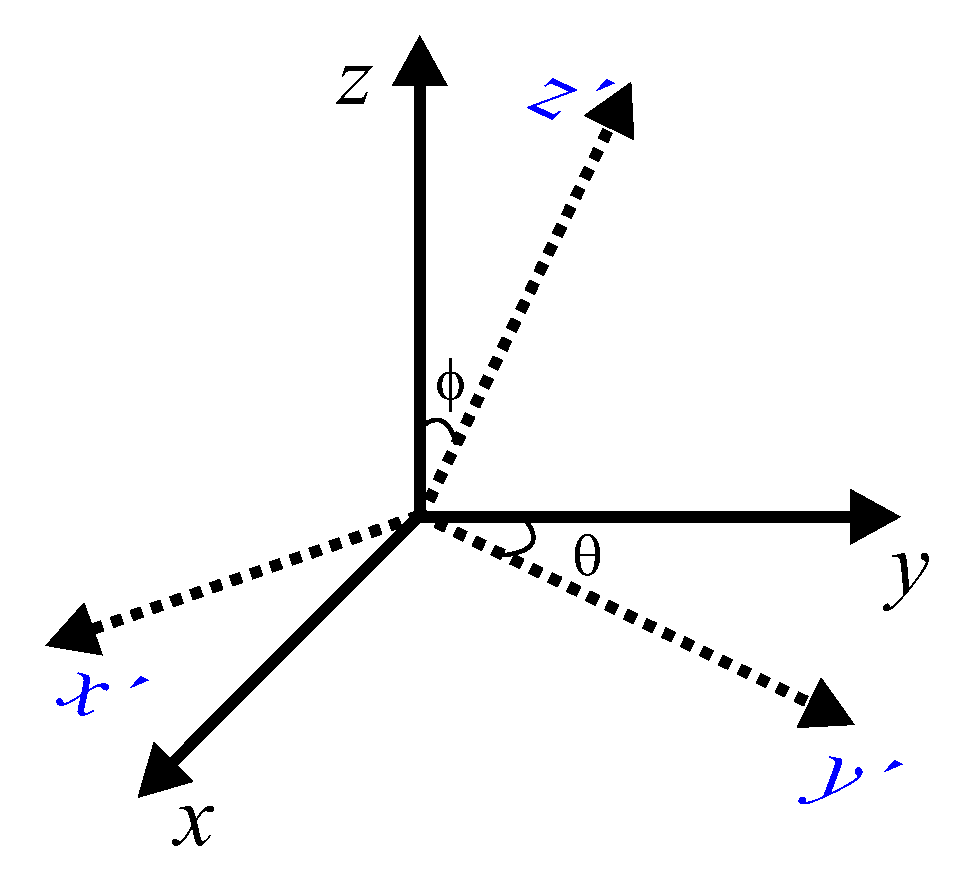
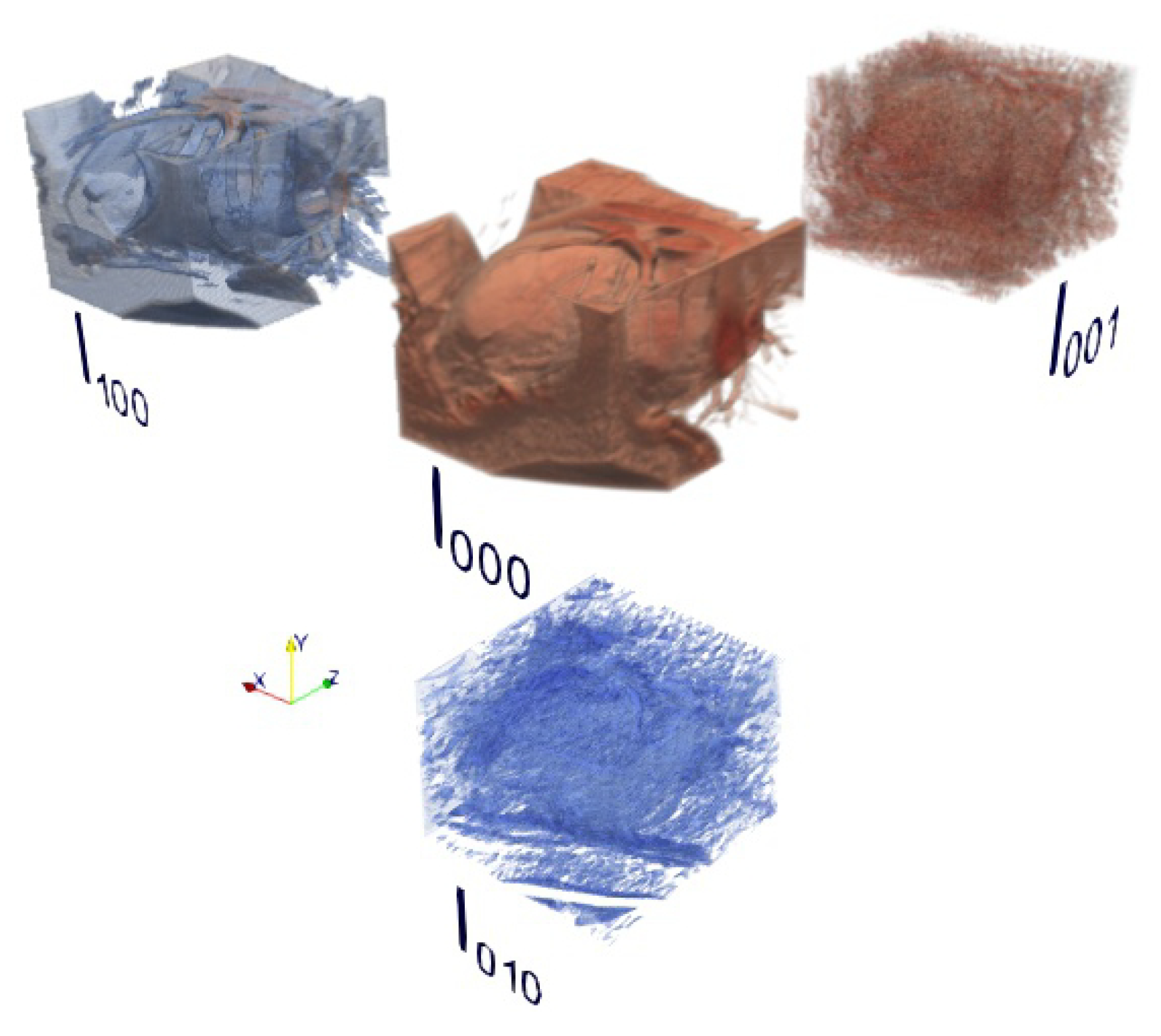
3D Steered Hermite Transform
3. Optical Flow using the Hermite Transform
Model
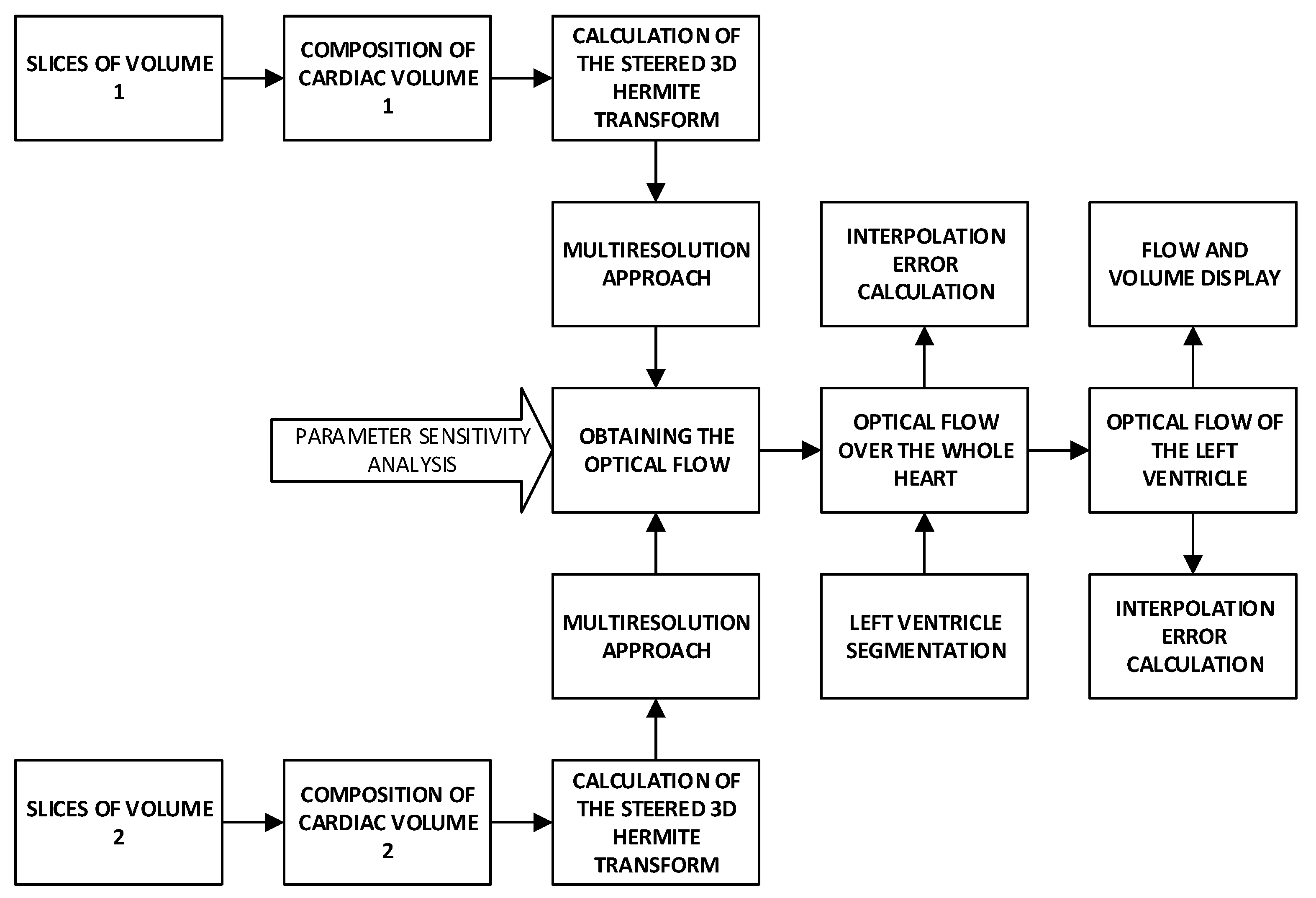
4. Materials and Overview of the Method
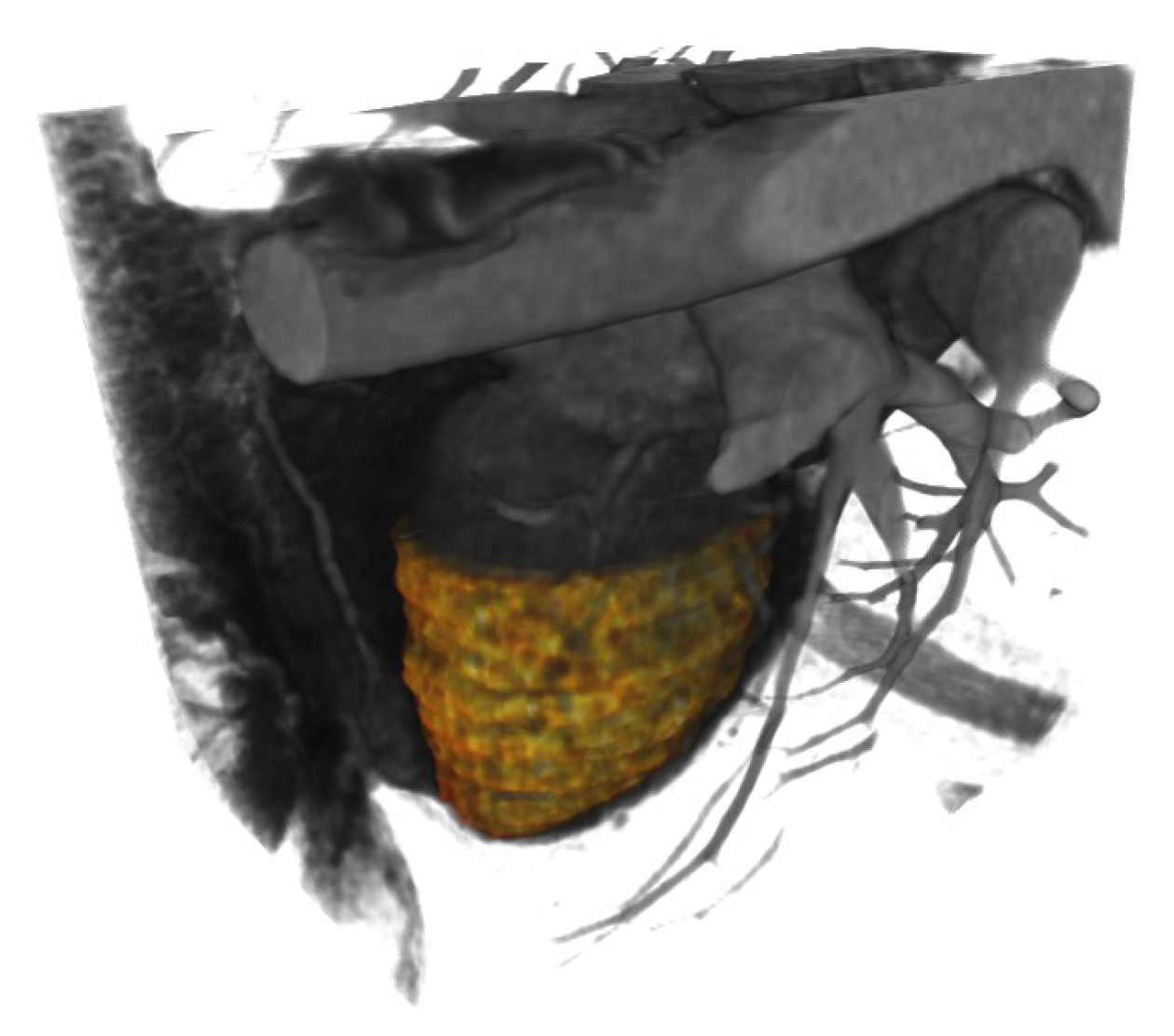
4.1. Dataset Description
4.2. Ethical Approval
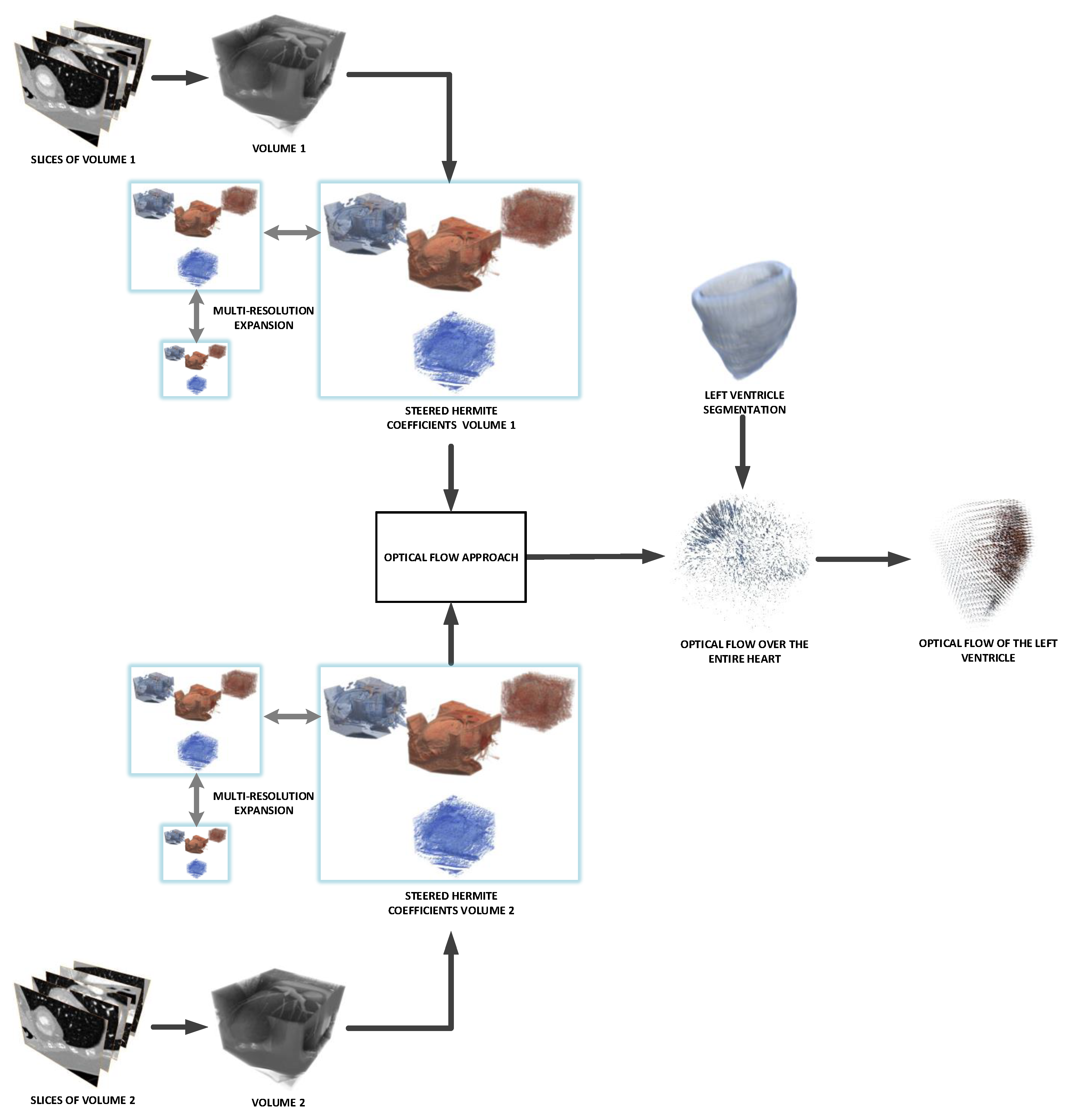
4.3. Overview of the Method
5. Experiments and Results
5.1. Validation
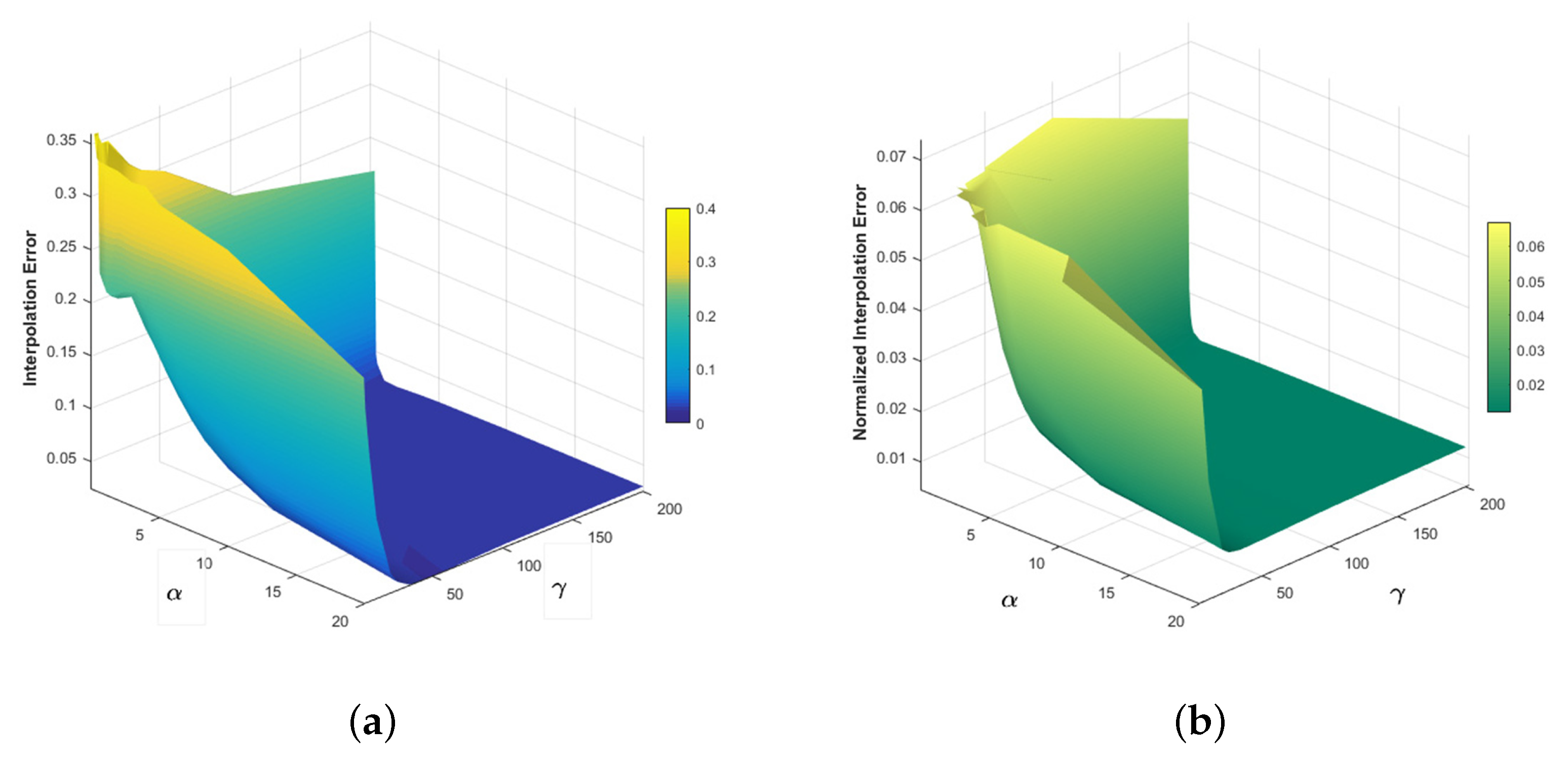
5.1.1. Hermite Transform Parameter Tuning
5.1.2. Optical Flow Parameter Sensitivity Analysis
5.1.3. 2D Interpolation Errors
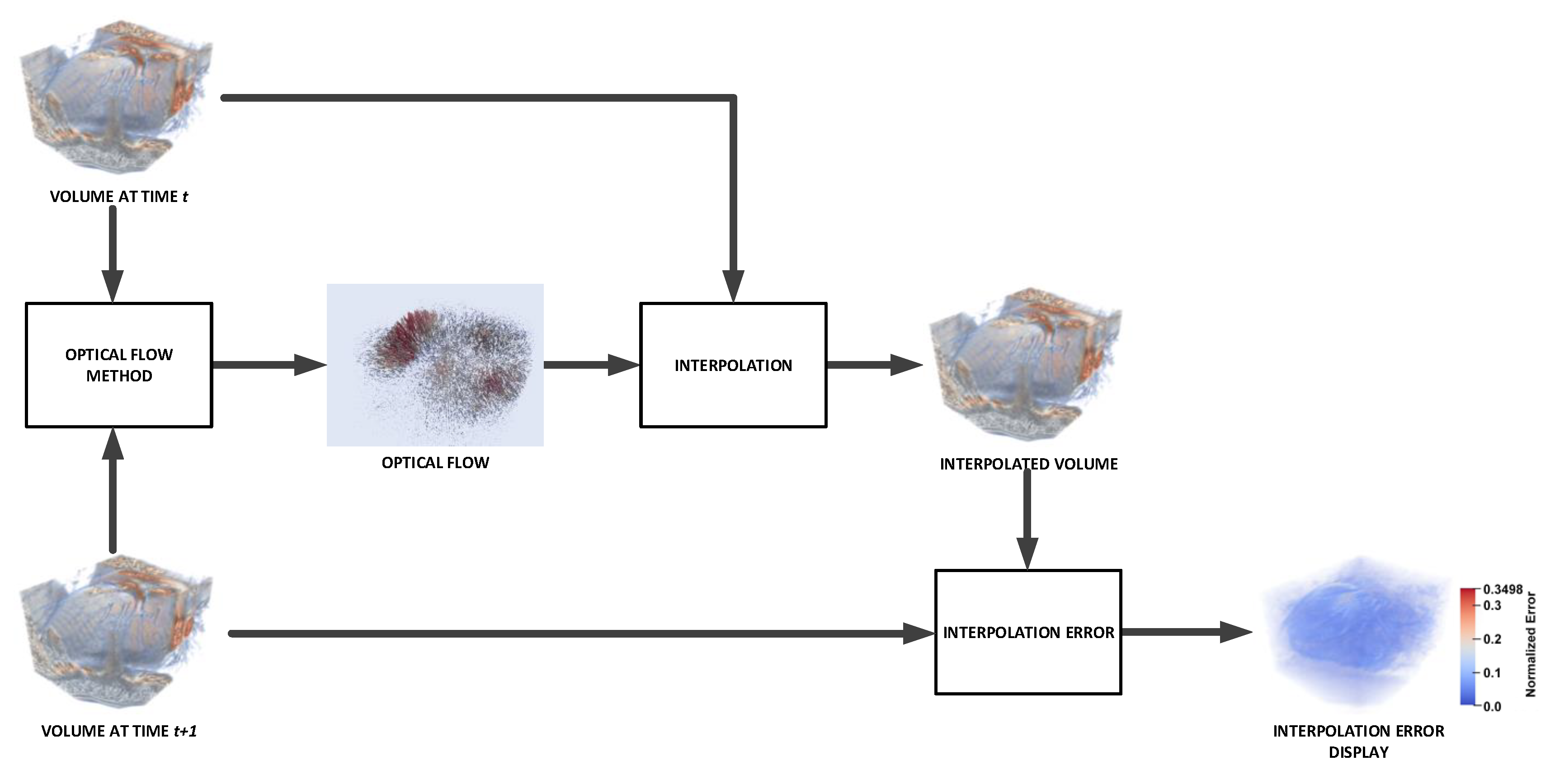
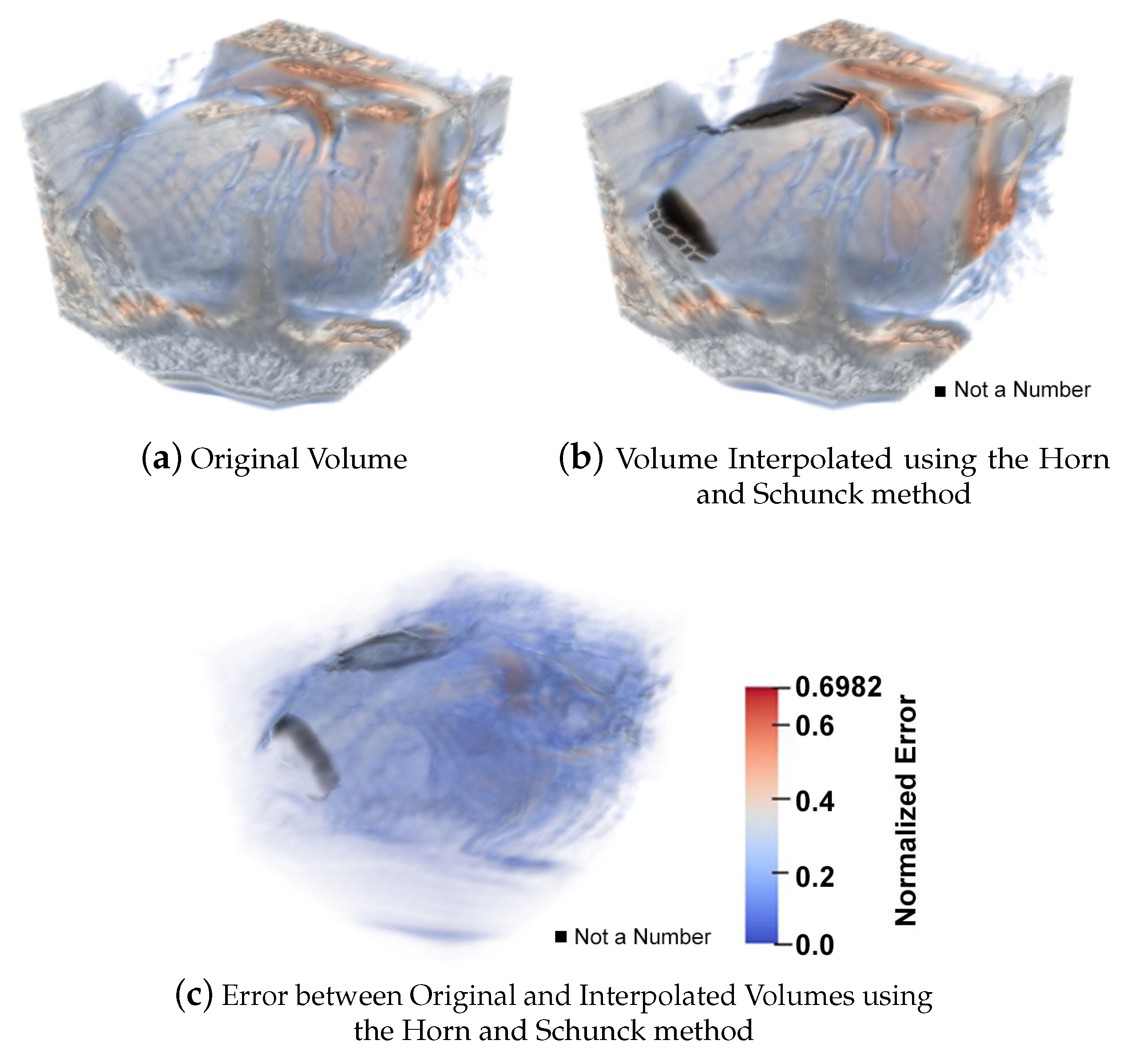
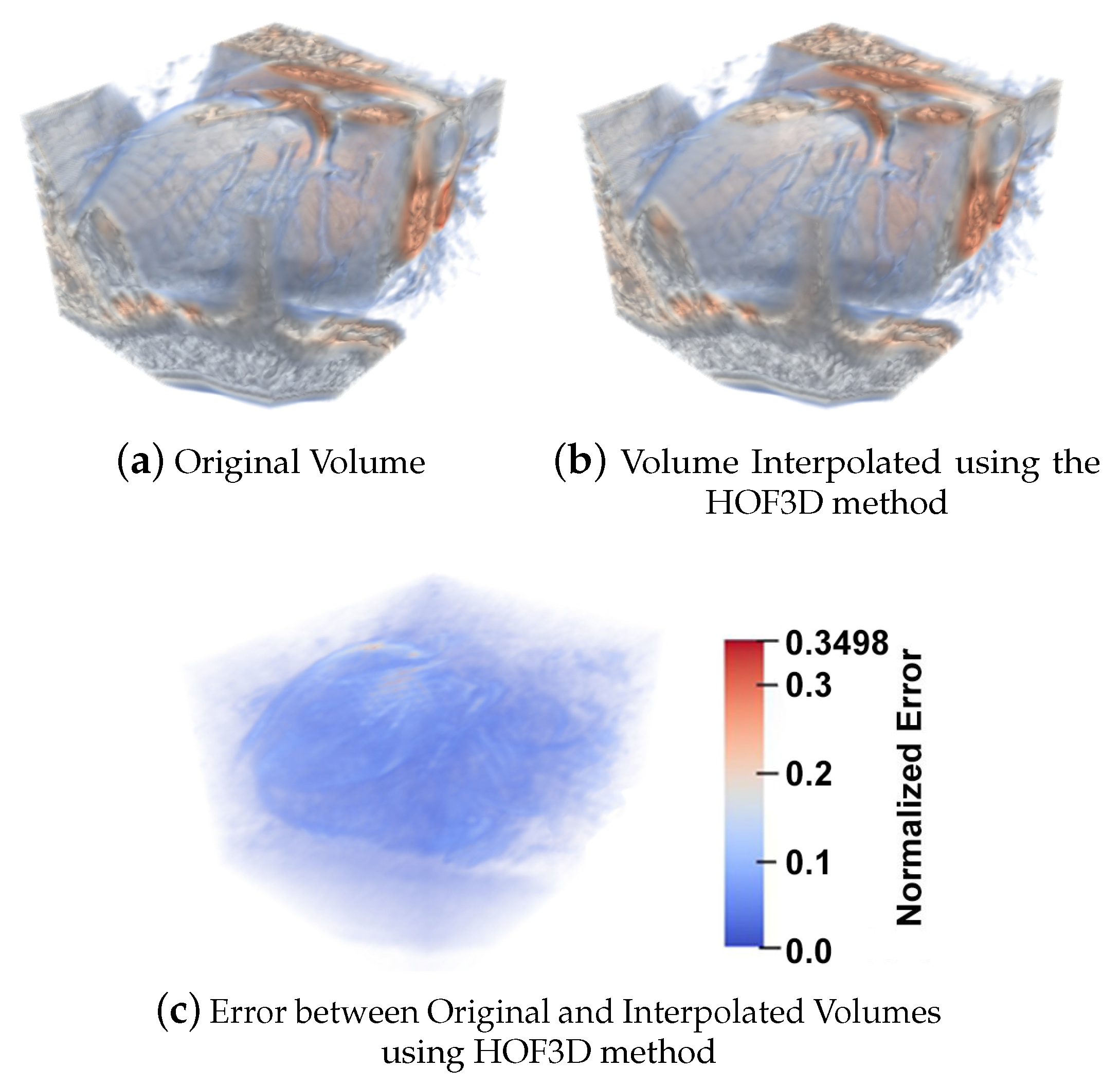
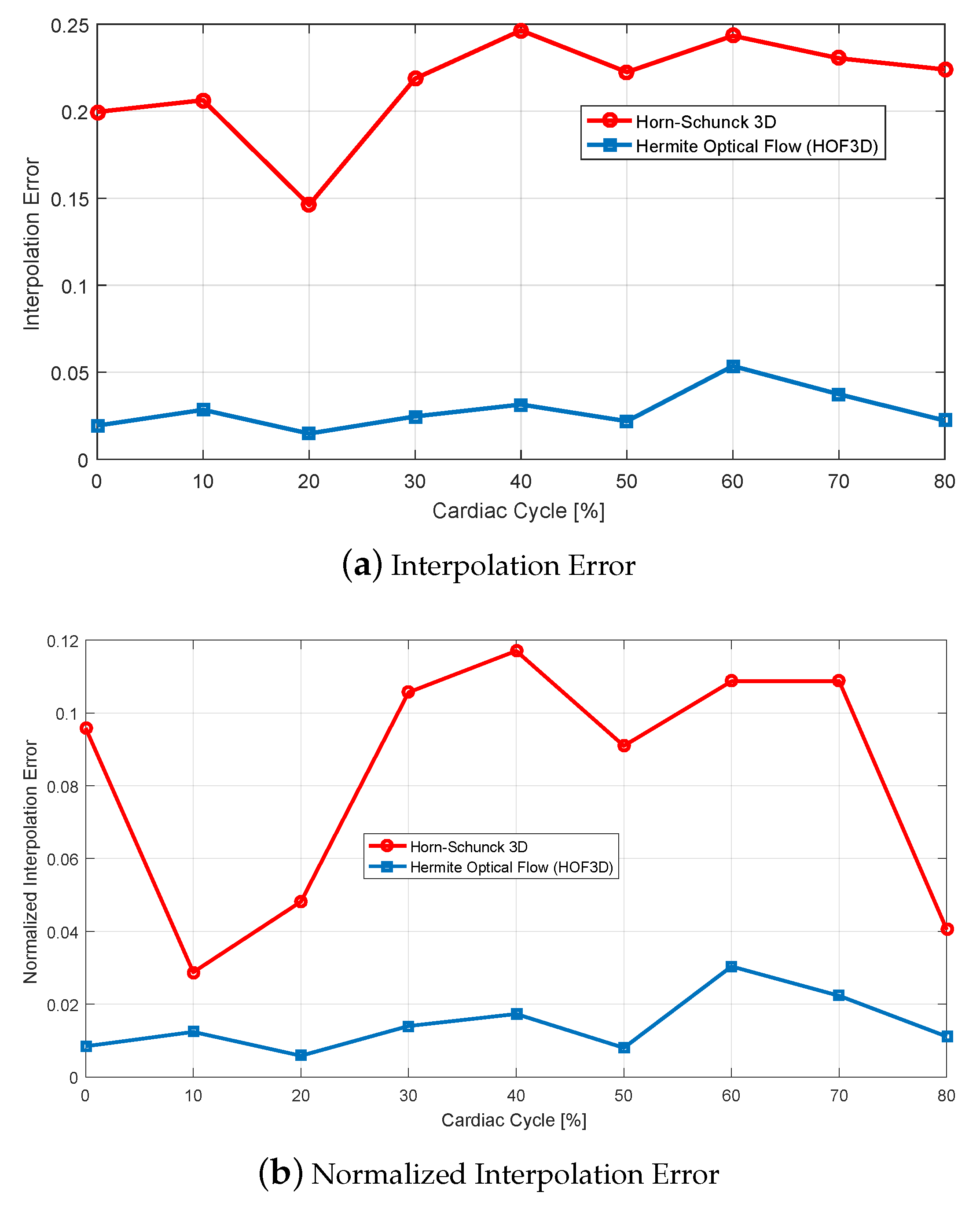
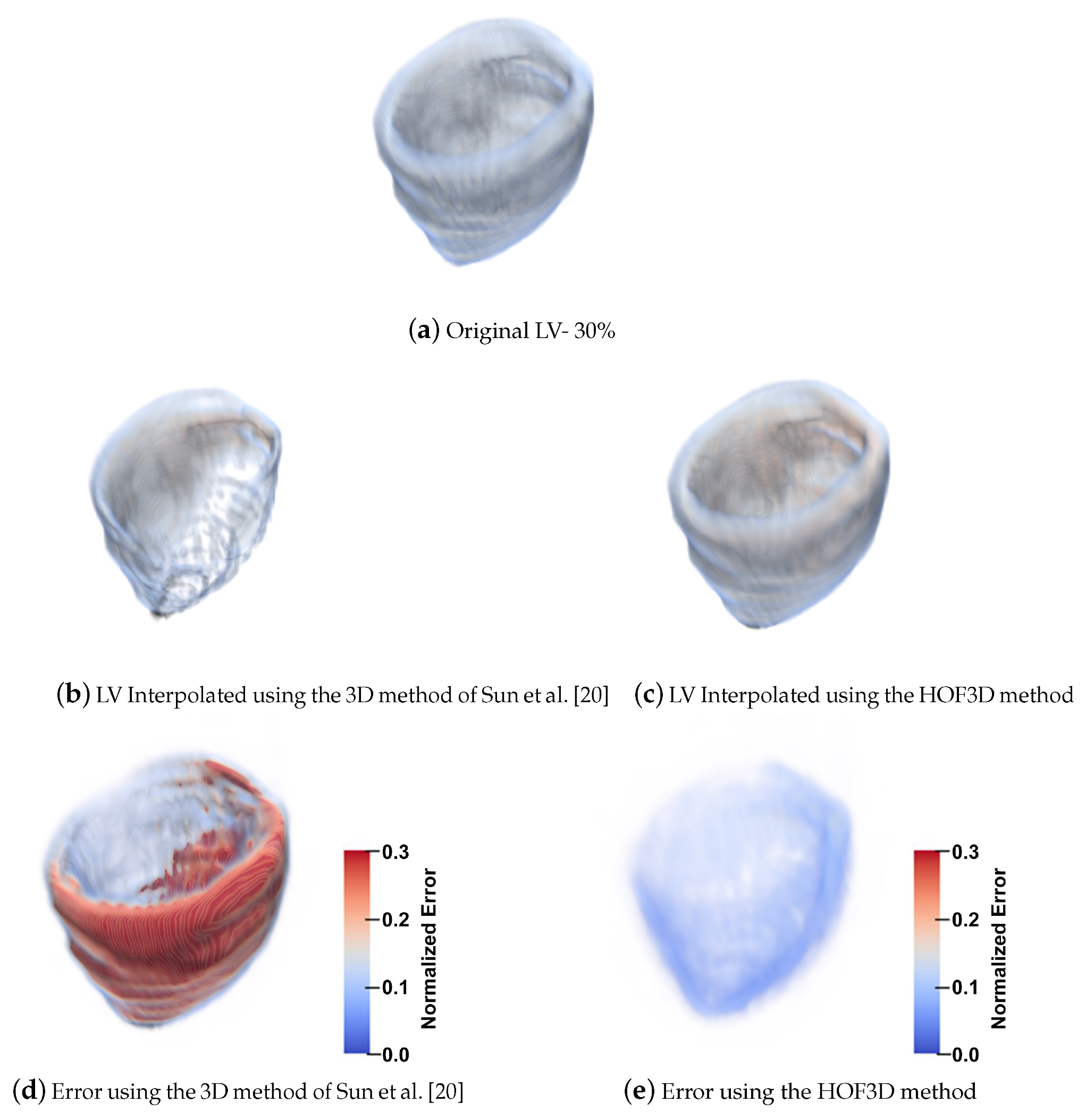
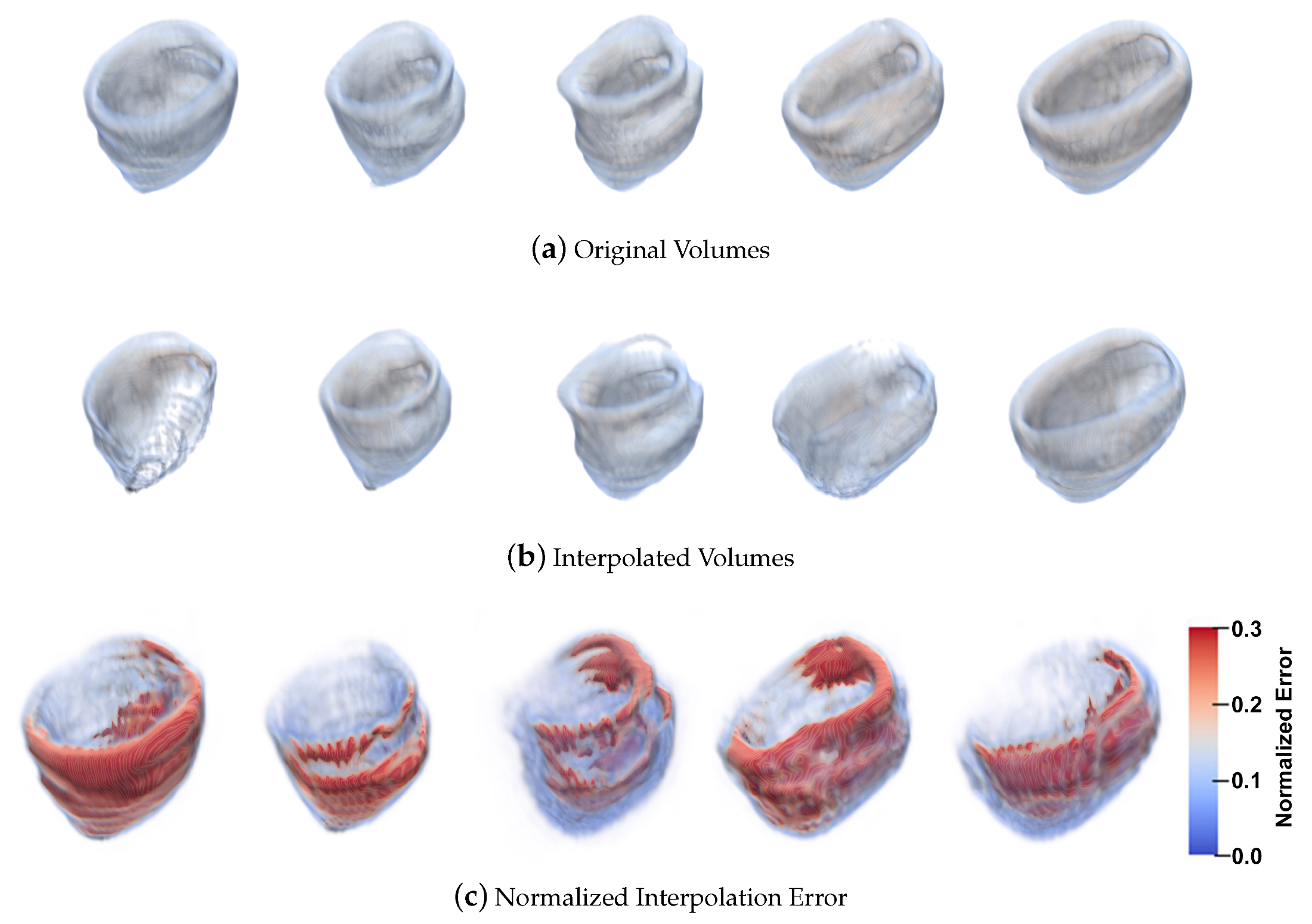
5.1.4. 3D Interpolation Errors
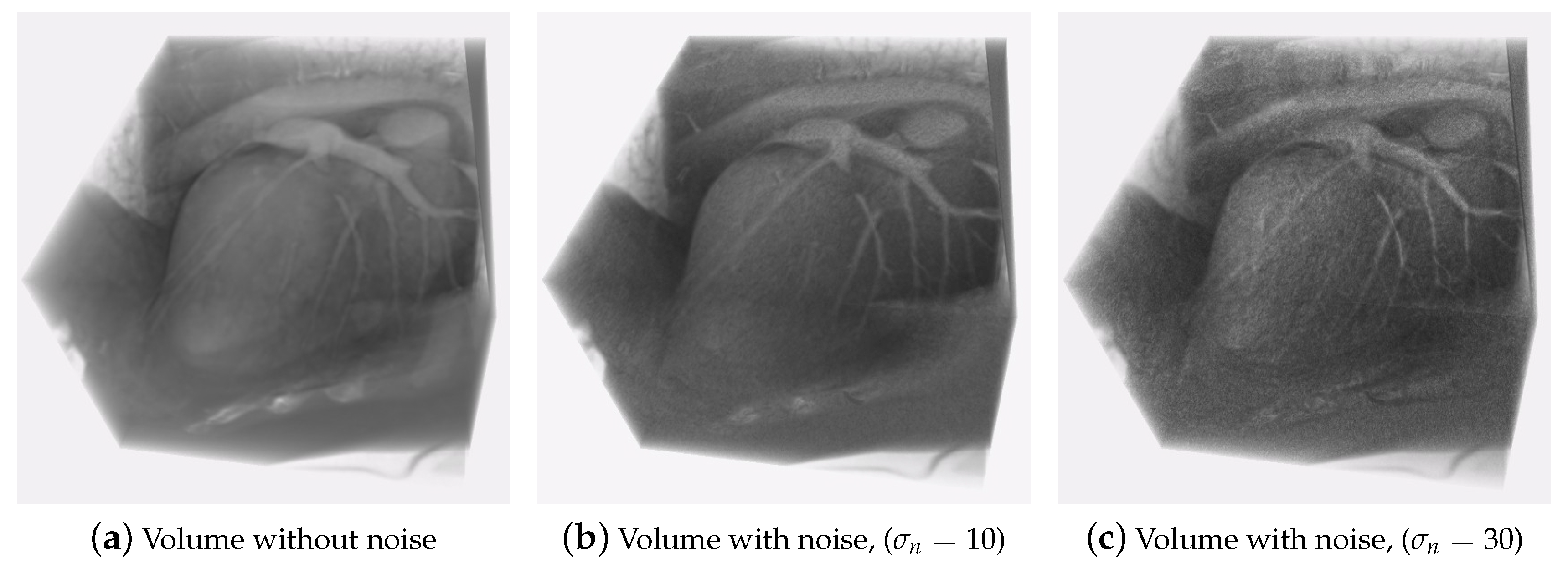
5.1.5. Robustness to Noise
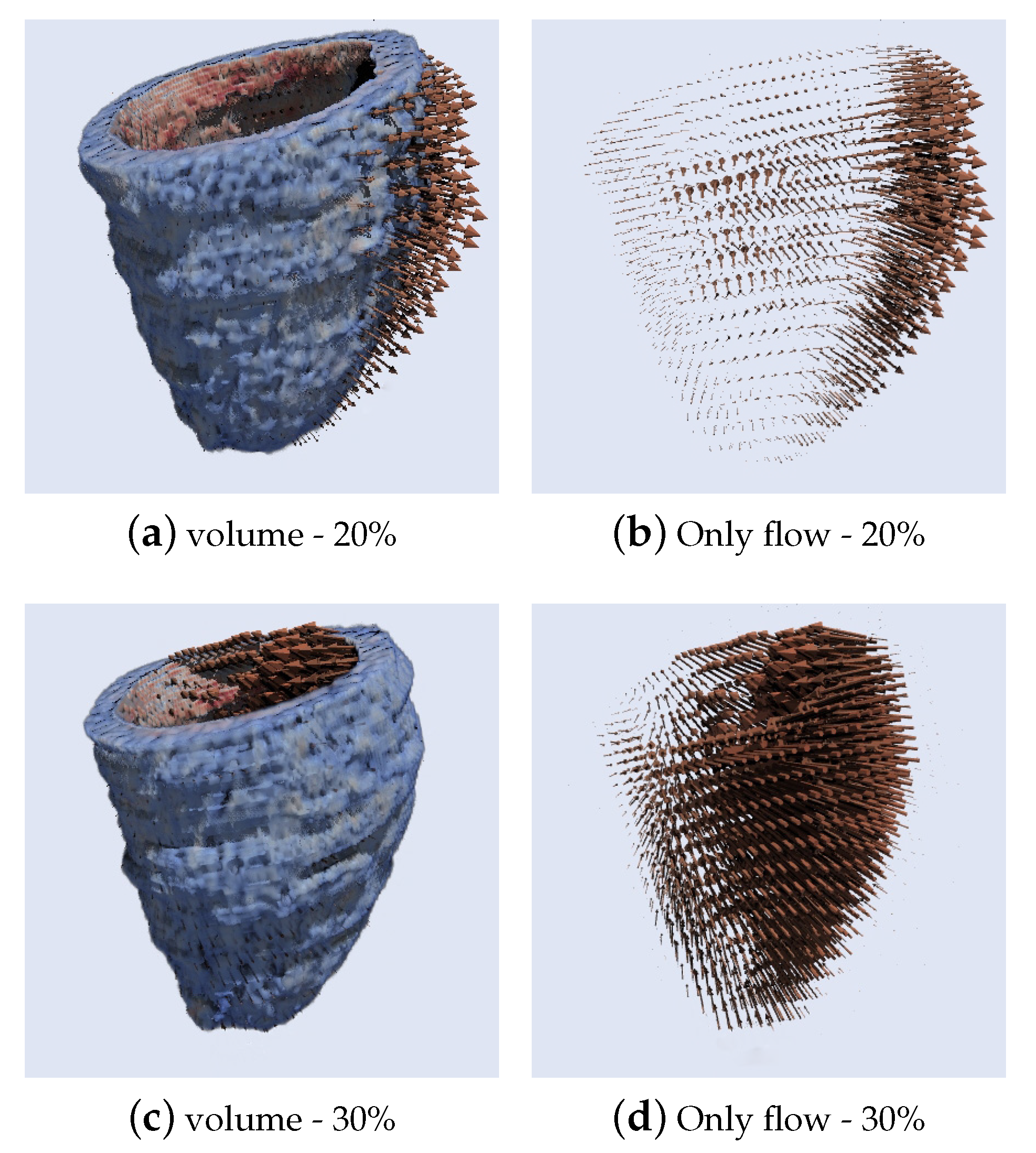
5.2. 3D Optical Flow Results
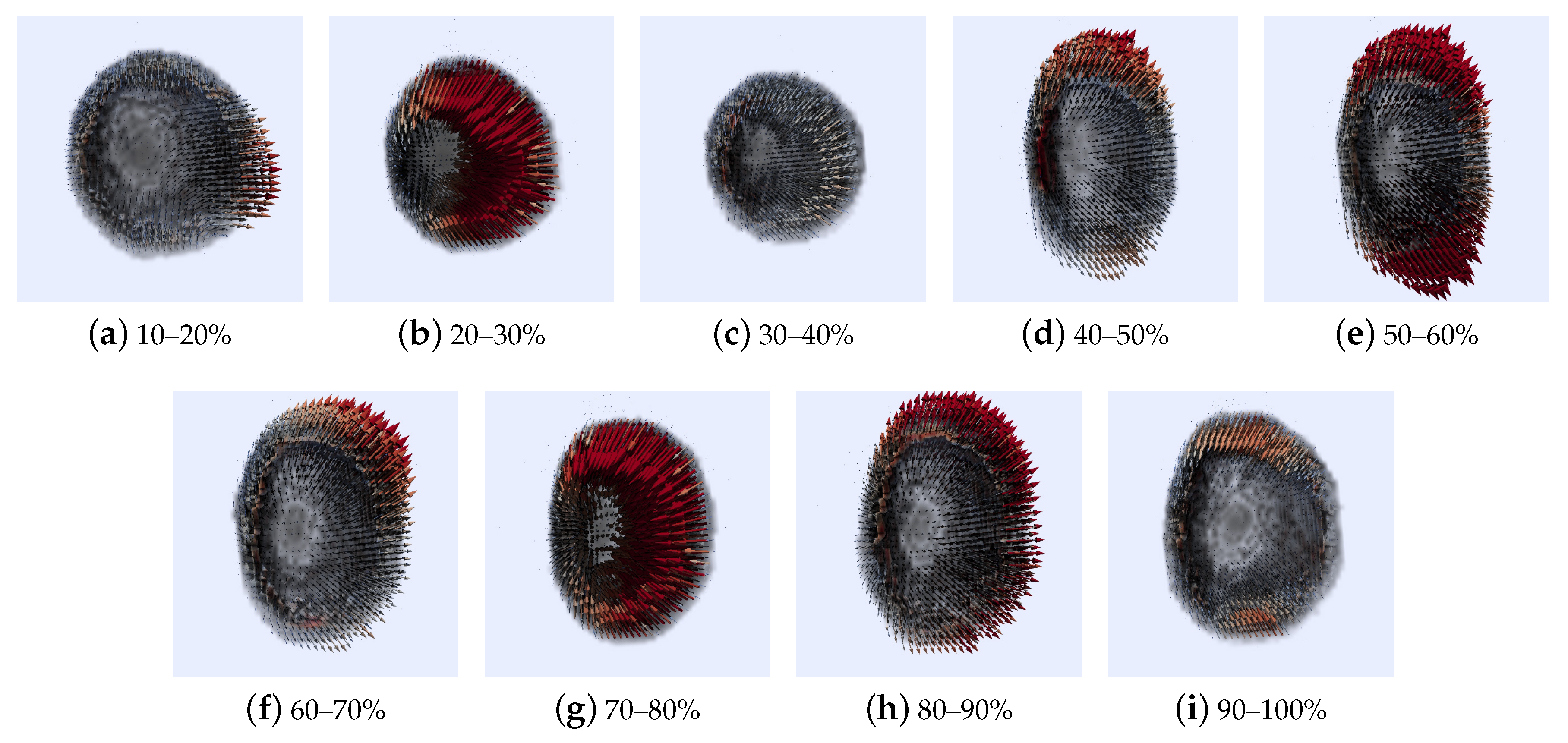
5.2.1. 3D Optical Flow Estimation of the Left Ventricle
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Three-dimensional space plus time | |
| Two-dimensional space plus time | |
| HT | Hermite transform |
| SHT | Steered Hermite transform |
| HVS | Human vision system |
| CT | Computed tomography |
| CVD | Cardiovascular diseases |
| LV | Left ventricular |
| MRI | Magnetic resonance imaging |
| HT3D | Hermite transform in 3D |
| IHT3D | Inverse Hermite transform in 3D |
| SHT3D | Steered Hermite transform in 3D |
| HOF3D | Horn-Hermite optical flow in 3D |
| ECG | Electrocardiography |
| IE | Interpolation error |
| NE | Normalized interpolation error |
| CNN | Convolutional Neural Network |
References
- World Health Organization. Cardiovascular diseases (CVD). 2019. Available online: http://www.who.int/mediacentre/factsheets/fs317/en/ (accessed on 22 November 2019).
- Cheung, Y.F. The role of 3D wall motion tracking in heart failure. Nat. Rev. Cardiol. 2012, 9, 644. [Google Scholar] [CrossRef] [PubMed]
- Xiong, G.; Sun, P.P.; Zhou, H.; Ha, S.; o Hartaigh, B.; Truong, Q.A.; Min, J.K. Comprehensive Modeling and Visualization of Cardiac Anatomy and Physiology from CT Imaging and Computer Simulations. IEEE Trans. Vis. Comput. Graph. 2017, 23, 1014–1028. [Google Scholar] [CrossRef] [PubMed]
- Min, J.K.; Shaw, L.; Berman, D. The Present State of Coronary Computed Tomography Angiography A Process in Evolution. Am. Coll. Cardiol. 2010, 55, 957–965. [Google Scholar] [CrossRef] [PubMed]
- Schoenhagen, P.; Stillman, A.; Halliburton, S.; White, R. CT of the heart: Principles, advances, clinical uses. Clevel. Clin. J. Med. 2005, 72, 127–140. [Google Scholar] [CrossRef] [PubMed]
- Barron, J.L.; Fleet, D.J.; Beauchemin, S.S.; Burkitt, T.A. Performance of optical flow techniques. In Proceedings of the 1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Champaign, IL, USA, 15–18 June 1992; pp. 236–242. [Google Scholar] [CrossRef]
- Nagel, H.H.; Enkelmann, W. An Investigation of Smoothness Constraints for the Estimation of Displacement Vector Fields from Image Sequences. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 565–593. [Google Scholar] [CrossRef] [PubMed]
- Nagel, H.H. Displacement vectors derived from second-order intensity variations in image sequences. Comput. Vis. Graph. Image Process. 1983, 21, 85–117. [Google Scholar] [CrossRef]
- TRETIAK, O. Velocity estimation form image sequences with second order differential operators. In Proceedings of the International Conference on Pattern Recognition, Montreal, QC, Canada, 30 July–2 August 1984. [Google Scholar]
- Haralick, R.M.; Lee, J.S. The Facet Approach to Optic Flow; Technical Report; Virginia Polytechnic Inst and State Univ Blacksburg Dept of Computer Science: Blacksburg, VA, USA, 1983. [Google Scholar]
- Horn, B.K.P.; Schunck, B.G. Determining Optical Flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Hildreth, E.C. Computations underlying the measurement of visual motion. Artif. Intell. 1984, 23, 309–354. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA; Volume 2, pp. 674–679. [Google Scholar]
- Uras, S.; Girosi, F.; Verri, A.; Torre, V. A computational approach to motion perception. Biol. Cybern. 1988, 60, 79–87. [Google Scholar] [CrossRef]
- Anandan, P. A computational framework and an algorithm for the measurement of visual motion. Int. J. Comput. Vis. 1989, 2, 283–310. [Google Scholar] [CrossRef]
- Little, J.; Bulthoff, H.; Poggio, T. Parallel Optical Flow Using Local Voting; IEEE: New York, NY, USA, 1988; pp. 454–459. [Google Scholar]
- Adelson, E.H.; Bergen, J.R. Spatiotemporal energy models for the perception of motion. J. Opt. Soc. Am. A 1985, 2, 284–299. [Google Scholar] [CrossRef]
- Heeger, D.J. Optical flow using spatiotemporal filters. Int. J. Comput. Vis. 1988, 1, 279–302. [Google Scholar] [CrossRef]
- Fleet, D.J.; Jepson, A.D. Computation of component image velocity from local phase information. Int. J. Comput. Vis. 1990, 5, 77–104. [Google Scholar] [CrossRef]
- Sun, D.; Roth, S.; Black, M.J. Secrets of optical flow estimation and their principles. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2432–2439. [Google Scholar] [CrossRef]
- Haag, M.; Nagel, H.H. Combination of Edge Element and Optical Flow Estimates for 3D-Model-Based Vehicle Tracking in Traffic Image Sequences. Int. J. Comput. Vis. 1999, 35, 295–319. [Google Scholar] [CrossRef]
- Amat, F.; Myers, E.W.; Keller, P.J. Fast and robust optical flow for time-lapse microscopy using super-voxels. Bioinformatics 2013, 29, 373–380. [Google Scholar] [CrossRef] [PubMed]
- Barranco, F.; Fermüller, C.; Aloimonos, Y.; Ros, E. Joint direct estimation of 3D geometry and 3D motion using spatio temporal gradients. arXiv 2018, arXiv:1805.06641. [Google Scholar]
- Patil, G.; Suja, P. Emotion recognition from 3D videos using optical flow method. In Proceedings of the 2017 International Conference On Smart Technologies For Smart Nation (SmartTechCon), Bengaluru, India, 17–19 August 2017; pp. 825–829. [Google Scholar] [CrossRef]
- Rodriguez, M.P.; Nygren, A. Motion Estimation in Cardiac Fluorescence Imaging With Scale-Space Landmarks and Optical Flow: A Comparative Study. IEEE Trans. Biomed. Eng. 2015, 62, 774–782. [Google Scholar] [CrossRef]
- Saleh, R.H.; Bakr, H.M.A.; Zidan, I.; Hadhoud, M.M.A. An innovate automatic heart localization method in cardiac Cine MRI using optical flow. In Proceedings of the 8th Cairo International Biomedical Engineering Conference (CIBEC), Cairo, Egypt, 15–17 December 2016; pp. 106–109. [Google Scholar] [CrossRef]
- Liu, H.; Hong, T.H.; Herman, M.; Chellappa, R. A General Motion Model and Spatio-Temporal Filters for Computing Optical Flow. Int. J. Comput. Vis. 1997, 22, 141–172. [Google Scholar] [CrossRef]
- Silvan-Cardenas, J.L.; Escalante-Ramirez, B. Optic-flow information extraction with directional Gaussian-derivatives. In Proceedings of the 15th International Conference on Pattern Recognition ICPR-2000, Barcelona, Spain, 3–7 September 2000; Volume 3, pp. 190–193. [Google Scholar] [CrossRef]
- Moya-Albor, E.; Escalante-RamíRez, B.; Vallejo, E. Optical Flow Estimation in Cardiac CT Images Using the Steered Hermite Transform. Image Commun. 2013, 28, 267–291. [Google Scholar] [CrossRef]
- Baghaie, A.; DSouza, R.M.; Yu, Z. Dense correspondence and optical flow estimation using gabor, schmid and steerable descriptors. In International Symposium on Visual Computing; Springer: Cham, Switzerland, 2015; pp. 406–415. [Google Scholar]
- Satriano, A.; Heydari, B.; Narous, M.; Exner, D.V.; Mikami, Y.; Attwood, M.M.; Tyberg, J.V.; Lydell, C.P.; Howarth, A.G.; Fine, N.M.; et al. Clinical feasibility and validation of 3D principal strain analysis from cine MRI: Comparison to 2D strain by MRI and 3D speckle tracking echocardiography. Int. J. Cardiovasc. Imaging 2017, 33, 1979–1992. [Google Scholar] [CrossRef]
- Pedrizzetti, G.; Sengupta, S.; Caracciolo, G.; Park, C.S.; Amaki, M.; Goliasch, G.; Narula, J.; Sengupta, P.P. Three-Dimensional Principal Strain Analysis for Characterizing Subclinical Changes in Left Ventricular Function. J. Am. Soc. Echocardiogr. 2014, 27, 1041–1050.e1. [Google Scholar] [CrossRef] [PubMed]
- Barba-J, L.; Moya-Albor, E.; Escalante-Ramírez, B.; Brieva, J.; Venegas, E.V. Segmentation and optical flow estimation in cardiac CT sequences based on a spatiotemporal PDM with a correction scheme and the Hermite transform. Comput. Biol. Med. 2016, 69, 189–202. [Google Scholar] [CrossRef] [PubMed]
- Ranjan, A.; Romero, J.; Black, M.J. Learning human optical flow. arXiv 2018, arXiv:1806.05666. [Google Scholar]
- Alexiadis, D.S.; Mitianoudis, N.; Stathaki, T. Multidimensional directional steerable filters—Theory and application to 3D flow estimation. Image Vis. Comput. 2018, 71, 38–67. [Google Scholar] [CrossRef]
- Ha, I.Y.; Wilms, M.; Handels, H.; Heinrich, M.P. Model-based sparse-to-dense image registration for realtime respiratory motion estimation in image-guided interventions. IEEE Trans. Biomed. Eng. 2018, 66, 302–310. [Google Scholar] [CrossRef]
- Yoon, S.; Katsevich, A.; Frenkel, M.; Munro, P.; Paysan, P.; Seghers, D.; Strzelecki, A. A motion estimation and compensation algorithm for 4D CBCT of the abdomen. In Proceedings of the 15th International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine, Philadelphia, PA, USA, 2–6 June 2019; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11072, p. 110720E. [Google Scholar]
- Cha, J.; Farhangi, M.M.; Dunlap, N.; Amini, A.A. Segmentation and tracking of lung nodules via graph-cuts incorporating shape prior and motion from 4D CT. Med. Phys. 2018, 45, 297–306. [Google Scholar] [CrossRef]
- Prevost, R.; Salehi, M.; Jagoda, S.; Kumar, N.; Sprung, J.; Ladikos, A.; Bauer, R.; Zettinig, O.; Wein, W. 3D freehand ultrasound without external tracking using deep learning. Med. Image Anal. 2018, 48, 187–202. [Google Scholar] [CrossRef]
- Gorce, J.; Friboulet, D.; Magnin, I. Estimation of three-dimensional cardiac velocity fields: Assessment of a differential method and application to 3D CT data. Med. Image Anal 1997, 1, 127–140. [Google Scholar] [CrossRef]
- Queirós, S.; Vilaça, J.L.; Morais, P.; Fonseca, J.C.; D’hooge, J.; Barbosa, D. Fast left ventricle tracking using localized anatomical affine optical flow. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2871. [Google Scholar] [CrossRef]
- Krishnaswamy, D.; Hareendranathan, A.R.; Suwatanaviroj, T.; Boulanger, P.; Becher, H.; Noga, M.; Punithakumar, K. A Novel 4D Semi-Automated Algorithm for Volumetric Segmentation in Echocardiography. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 1119–1122. [Google Scholar]
- Tek, H.; Georgescu, B.; Mansi, T.; Sauer, F.; Comaniciu, D.; Houle, H.C.; Voigt, I. Cardiac Flow Detection Based on Morphological Modeling in Medical Diagnostic Ultrasound Imaging. U.S. Patent Application No. 15/797,161, 2 May 2019. [Google Scholar]
- Duan, Q.; Angelini, E.D.; Herz, S.L.; Ingrassia, C.M.; Gerard, O.; Costa, K.D.; Holmes, J.W.; Laine, A.F. Evaluation of optical flow algorithms for tracking endocardial surfaces on three-dimensional ultrasound data. Proc. SPIE 2005, 5750, 159–169. [Google Scholar] [CrossRef]
- Duan, Q.; Angelini, E.D.; Homma, S.; Laine, A. Validation of Optical-Flow for Quantification of Myocardial Deformations on Simulated Rt3d Ultrasound. In Proceedings of the 2007 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Washington, DC, USA, 12–16 April 2007; pp. 944–947. [Google Scholar] [CrossRef]
- Leung, E.; Danilouchkine, M.; van Stralen, M.; de Jong, N.; van der Steen, A.; Bosch, J. Tracking left ventricular borders in 3D echocardiographic sequences using motion-guided optical flow. SPIE 2009. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, X.; Ma, J.; Jing, Y.; Gonzales, M.J.; Villongco, C.; Krishnamurthy, A.; Frank, L.R.; Nigam, V.; Stark, P.; et al. An atlas-based geometry pipeline for cardiac Hermite model construction and diffusion tensor reorientation. Med. Image Anal. 2012, 16, 1130–1141. [Google Scholar] [CrossRef] [PubMed]
- Thirion, J.P. Image matching as a diffusion process: An analogy with Maxwell’s demons. Med. Image Anal. 2018, 2, 243–260. [Google Scholar] [CrossRef]
- Moya-Albor, E.; Mira, C.; Brieva, J.; Escalante-Ramirez, B.; Venegas, E.V. 3D optical flow estimation in cardiac CT images using the Hermite transform. SPIE 2017, 10160. [Google Scholar] [CrossRef]
- Martens, J.B. The Hermite Transform-Theory. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1595–1606. [Google Scholar] [CrossRef]
- Sakitt, B.; Barlow, H. A Model for the Economical Encoding of the Visual Image in Cerebral Cortex. Biol. Cybern. 1982, 43, 97–108. [Google Scholar] [CrossRef]
- Young, R. The Gaussian Derivative Theory of Spatial Vision: Analysis of Cortical Cell Receptive Field Line–Weighting Profiles; Research publication; General Motors Research Laboratories: Warren, MI, USA, 1985. [Google Scholar]
- Martens, J.B. The Hermite Transform-Applications. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1607–1618. [Google Scholar] [CrossRef]
- Young, R. Gaussian derivative model of spatial vision: I. Retinal mechanisms. Spat. Vis. 1987, 2, 273–293. [Google Scholar] [CrossRef]
- Brackx, F.; De Schepper, N.; Sommen, F. The higher dimensional Hermite transform: A new approach. Complex Var. 2003, 48, 189–210. [Google Scholar] [CrossRef]
- Abramowitz, M. Handbook of Mathematical Functions, With Formulas, Graphs, and Mathematical Tables; Dover Publications: Mineola, NY, USA, 1974. [Google Scholar]
- Van Dijk, A.M.; Martens, J. Image representation and compression with steered Hermite transforms. Signal Process. 1997, 56, 1–16. [Google Scholar] [CrossRef]
- Freeman, W.T.; Adelson, E.H. The Design and Use of Steerable Filters. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 891–906. [Google Scholar] [CrossRef]
- Escalante-Ramírez, B.; Silván-Cárdenas, J.L. Multiresolution directional-oriented image transform based on Gaussian derivatives. Proc. SPIE 2001, 4478, 315–322. [Google Scholar] [CrossRef]
- Escalante-Ramírez, B.; Silván-Cárdenas, J.L. Advanced modeling of visual information processing: A multiresolution directional-oriented image transform based on Gaussian derivatives. Signal Process. Image Commun. 2005, 20, 801–812. [Google Scholar] [CrossRef]
- Wu, X.; Ding, G.; Taylor, V. Parallel Optical Flow Processing of 4D Cardiac CT Data on Multicore Clusters. In Proceedings of the 2014 IEEE 17th International Conference on Computational Science and Engineering, Chengdu, China, 19–21 December 2014; pp. 113–120. [Google Scholar]
- Otte, M.; Nagel, H.H. Optical flow estimation: Advances and comparisons. In European Conference on Computer Vision; Eklundh, J.O., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; Volume I, pp. 49–60. [Google Scholar] [CrossRef]
- Baker, S.; Scharstein, D.; Lewis, J.P.; Roth, S.; Black, M.J.; Szeliski, R. A Database and Evaluation Methodology for Optical Flow. Int. J. Comput. Vis. 2011, 92, 1–31. [Google Scholar] [CrossRef]
- Mathworks, T. Computer Vision System Toolbox. 2018. Available online: https://mathworks.com/products/computer-vision (accessed on 22 November 2019).
- Bigun, J.; Granlund, G.H.; Wiklund, J. Multidimensional orientation estimation with applications to texture analysis and optical flow. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 775–790. [Google Scholar] [CrossRef]
- Koren, M.J.; Devereux, R.B.; Casale, P.N.; Savage, D.D.; Laragh, J.H. Relation of left ventricular mass and geometry to morbidity and mortality in uncomplicated essential hypertension. Ann. Intern. Med. 1991, 114, 345–352. [Google Scholar] [CrossRef]
- McDonald, I.G. The shape and movements of the human left ventricle during systole: A study by cineangiography and by cineradiography of epicardial markers. Am. J. Cardiol. 1970, 26, 221–230. [Google Scholar] [CrossRef]
- Chen, C.W.; Huang, T.S. Epicardial motion and deformation estimation from coronary artery bifurcation points. In Proceedings of the Third International Conference on Computer Vision, Osaka, Japan, 4–7 December 1990; pp. 456–459. [Google Scholar]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- CIBC. Seg3D: Volumetric Image Segmentation and Visualization. Scientific Computing and Imaging Institute (SCI). 2016. Available online: Http://www.seg3d.org (accessed on 22 November 2019).
- Ahrens, J.; Geveci, B.; Law, C. Paraview: An end-user tool for large data visualization. In The Visualization Handbook; Elsevier: Amsterdam, The Netherlands, 2005; Volume 717, ISBN 978-0123875822. [Google Scholar]
- Ayachit, U. The Paraview Guide: A Parallel Visualization Application; Kitware, Inc.: Clifton Park, NY, USA, 2015. [Google Scholar]
- Song, S.M.; Leahy, R.M. Computation of 3-D velocity fields from 3-D cine CT images of a human heart. IEEE Trans. Med. Imaging 1991, 10, 295–306. [Google Scholar] [CrossRef]
- Chan, K.G.; Liebling, M. Estimation of divergence-free 3D cardiac blood flow in a zebrafish larva using multi-view microscopy. In Proceedings of the 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), New York, NY, USA, 16–19 April 2015; pp. 385–388. [Google Scholar]
- Gutierrez, M.; Moura, L.; Melo, C.; Alens, N. Computing optical flow in cardiac images for 3D motion analysis. In Proceedings of the Computers in Cardiology Conference, London, UK, 5–8 September 1993; pp. 37–40. [Google Scholar]
- Condell, J.; Barron, L. 3D Optical Flow Methods in Cardiac Imaging. In Proceedings of the Irish Machine Vision and Image Processing Conference, Belfast, UK, 30–31 August 2005; Volume 30, p. 227. [Google Scholar]
- Silván-Cárdenas, J.L.; Escalante-Ramírez, B. The Multiscale Hermite Transform for Local Orientation Analysis. IEEE Trans. Image Process. 2006, 15, 1236–1253. [Google Scholar] [CrossRef]






| Paper | OF Model | Method | Application | Evaluation Metric |
|---|---|---|---|---|
| Proposed method | 3D | Using the 3D Steered Hermite Transform | Left ventricle CT sequences | Interpolation errors in 3D |
| Ranjan et al. [34] | 3D | A 3D model human body and a CNN | Estimate human flow fields | End point error |
| Alexiadis et al. [35] | 2D | Minimizing a cost functional | 3D flow estimation | Mean angular error on synthetic images |
| Queiros et al. [41] | 3D | Anatomically affine optical flow | Left ventricle tracking | Distance and Dice metrics |
| Patil et al. [24] | 2D | Farnebäck | Emotion recognition | Accuracy of 6 emotions |
| Saleh et al. [26] | 2D | Lucas-Kanade | Heart Localization | Accuracy on localizing |
| Baghaie et al. [30] | 2D | Gabor, Schmid and steerable filters | 2D flow estimation | Angular and interpolation errors |
| Rodriguez et al. [25] | 2D | Horn & Schunck | Cardiac motion estimation | Mean square error |
| Ground Truth Images | Ground Truth Flow | Horn-Schunck [64] | Farnebäck [64] | HOF2D |
|---|---|---|---|---|
| dimetrodon | 2.641 | 8.589 | 3.127 | 2.865 |
| groove2 | 10.439 | 23.492 | 8.831 | 10.353 |
| groove3 | 19.401 | 32.351 | 15.703 | 17.460 |
| urban3 | 9.870 | 17.727 | 9.489 | 8.122 |
| venus | 8.813 | 20.659 | 5.847 | 8.835 |
| Ground Truth Images | Ground Truth Flow | Horn-Schunck [64] | Farnebäck [64] | HOF2D |
|---|---|---|---|---|
| dimetrodon | 0.207 | 0.546 | 0.382 | 0.270 |
| groove2 | 0.418 | 0.860 | 0.385 | 0.329 |
| groove3 | 0.990 | 1.622 | 0.626 | 0.532 |
| urban3 | 2.325 | 2.452 | 1.342 | 0.700 |
| venus | 0.801 | 1.376 | 0.434 | 0.348 |
| Gaussian Noise () | Interpolation Error | Normalized Interpolation Error |
|---|---|---|
| 0 | 0.03190 | 0.01696 |
| 5 | 0.03499 | 0.01954 |
| 10 | 0.03778 | 0.02168 |
| 15 | 0.04295 | 0.02563 |
| 20 | 0.04597 | 0.02779 |
| 30 | 0.05468 | 0.03387 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mira, C.; Moya-Albor, E.; Escalante-Ramírez, B.; Olveres, J.; Brieva, J.; Vallejo, E. 3D Hermite Transform Optical Flow Estimation in Left Ventricle CT Sequences. Sensors 2020, 20, 595. https://doi.org/10.3390/s20030595
Mira C, Moya-Albor E, Escalante-Ramírez B, Olveres J, Brieva J, Vallejo E. 3D Hermite Transform Optical Flow Estimation in Left Ventricle CT Sequences. Sensors. 2020; 20(3):595. https://doi.org/10.3390/s20030595
Chicago/Turabian StyleMira, Carlos, Ernesto Moya-Albor, Boris Escalante-Ramírez, Jimena Olveres, Jorge Brieva, and Enrique Vallejo. 2020. "3D Hermite Transform Optical Flow Estimation in Left Ventricle CT Sequences" Sensors 20, no. 3: 595. https://doi.org/10.3390/s20030595
APA StyleMira, C., Moya-Albor, E., Escalante-Ramírez, B., Olveres, J., Brieva, J., & Vallejo, E. (2020). 3D Hermite Transform Optical Flow Estimation in Left Ventricle CT Sequences. Sensors, 20(3), 595. https://doi.org/10.3390/s20030595








