Compressive Sensing Spectroscopy Using a Residual Convolutional Neural Network
Abstract
1. Introduction
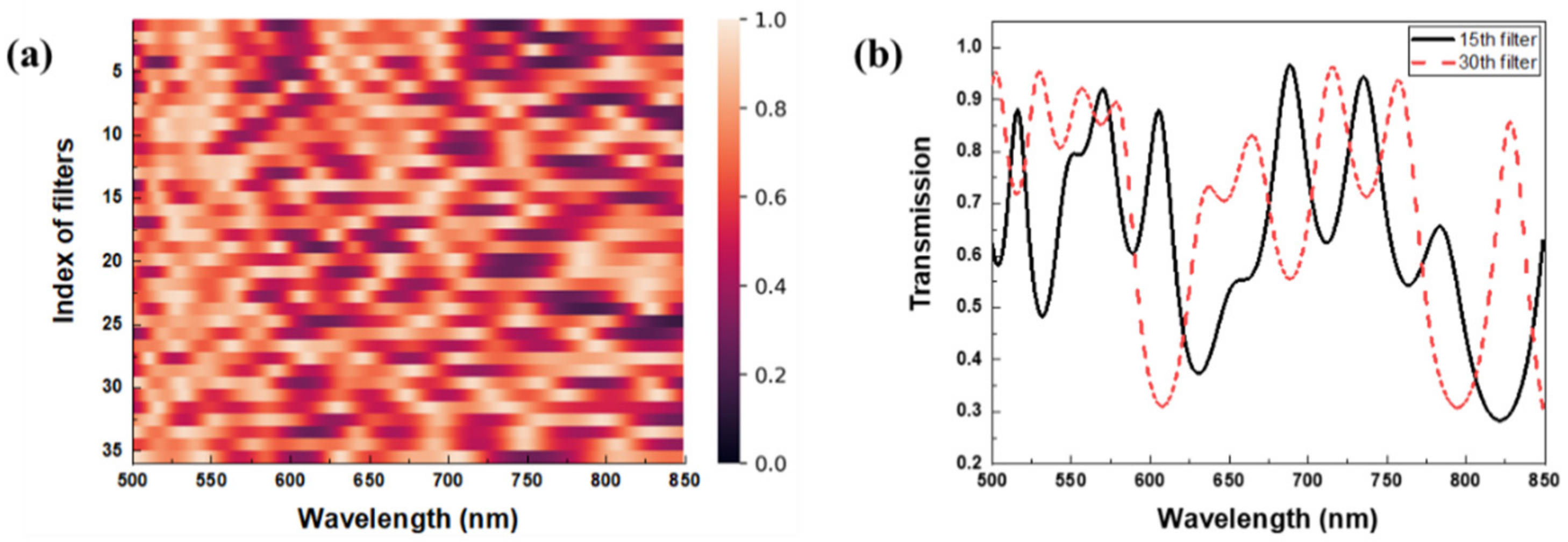
2. Optical Structure
| Algorithm 1: Recursive processes for amplitude reflection coefficients. | |
| Input: | |
| Structure parameters: | |
| Step 1: | Calculate and using structure parameters. |
| for k = 2, 3, ..., l. for k = 2, 3, ..., l. for k = 2, 3, ..., l. | |
| Step 2: | Obtain by setting |
| For k = l-1 to 2 | |
| Step 3: | Compute |
| Output: | |
3. Compressive Sensing (CS) Spectrometers Using the Proposed Residual Convolutional Neural Network (ResCNN)
3.1. CS Spectrometers
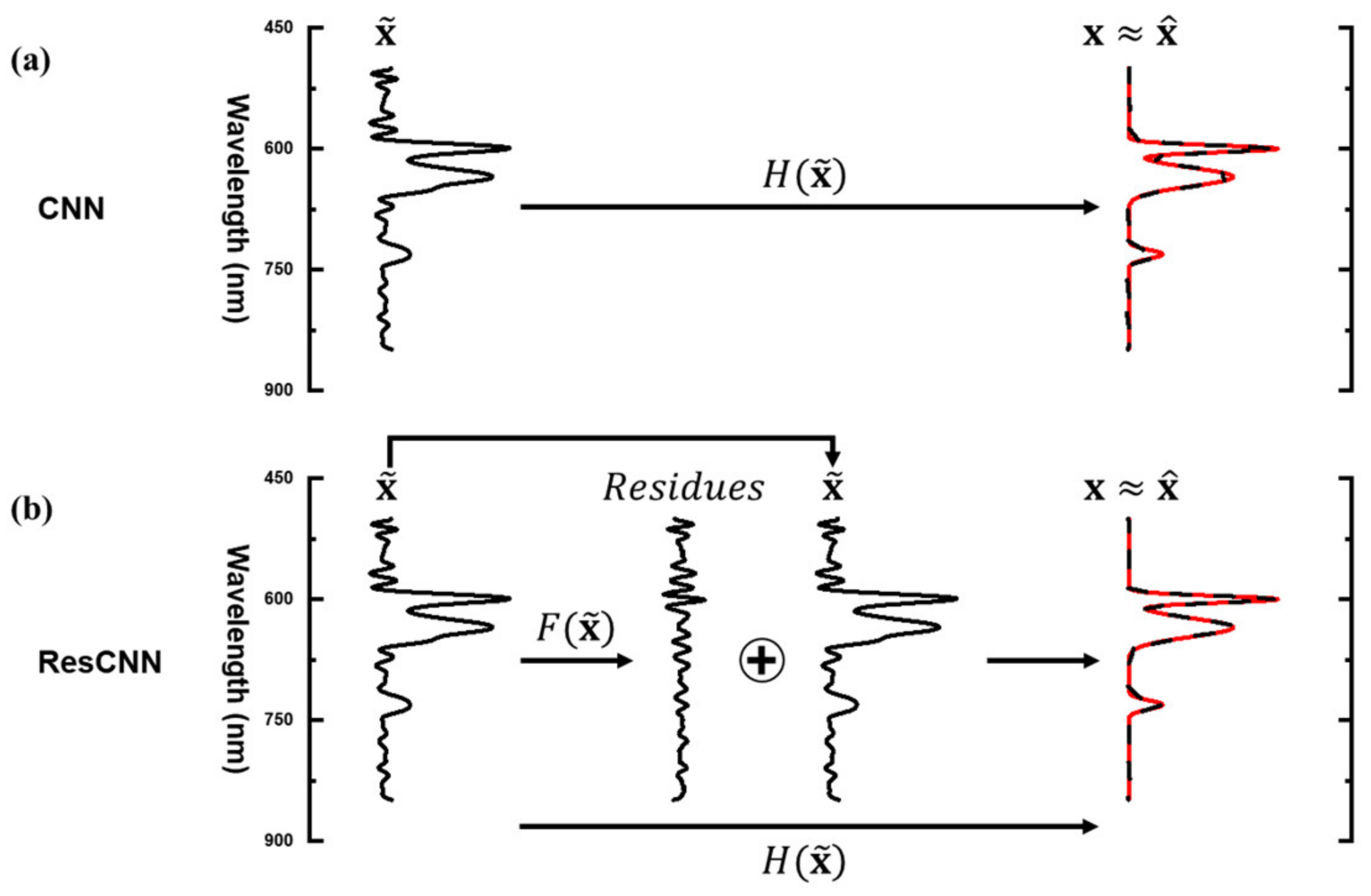
3.2. The Proposed ResCNN
4. Simulated Experiments
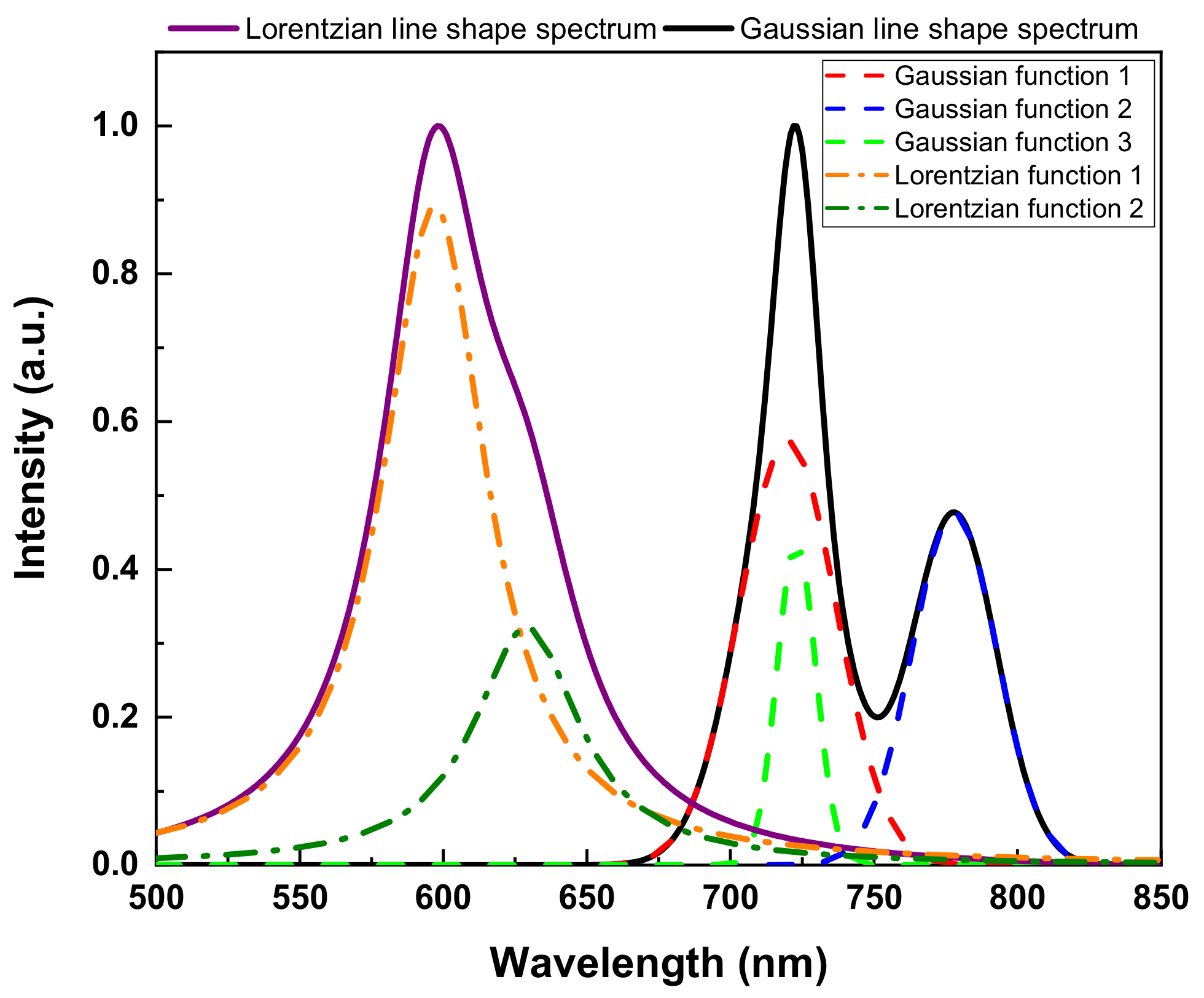
4.1. Spectral Datasets
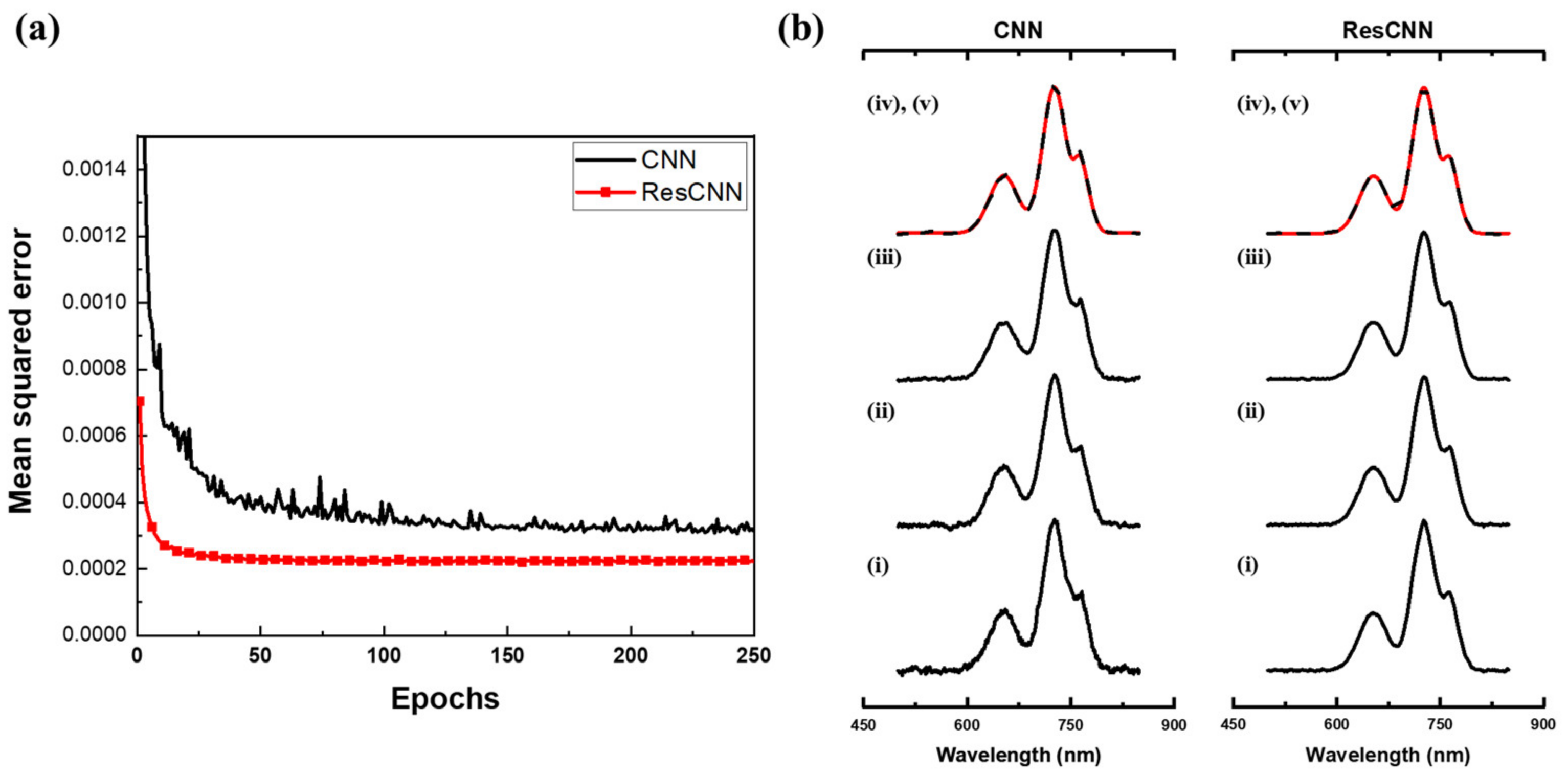
4.2. Data Preprocessing and Training
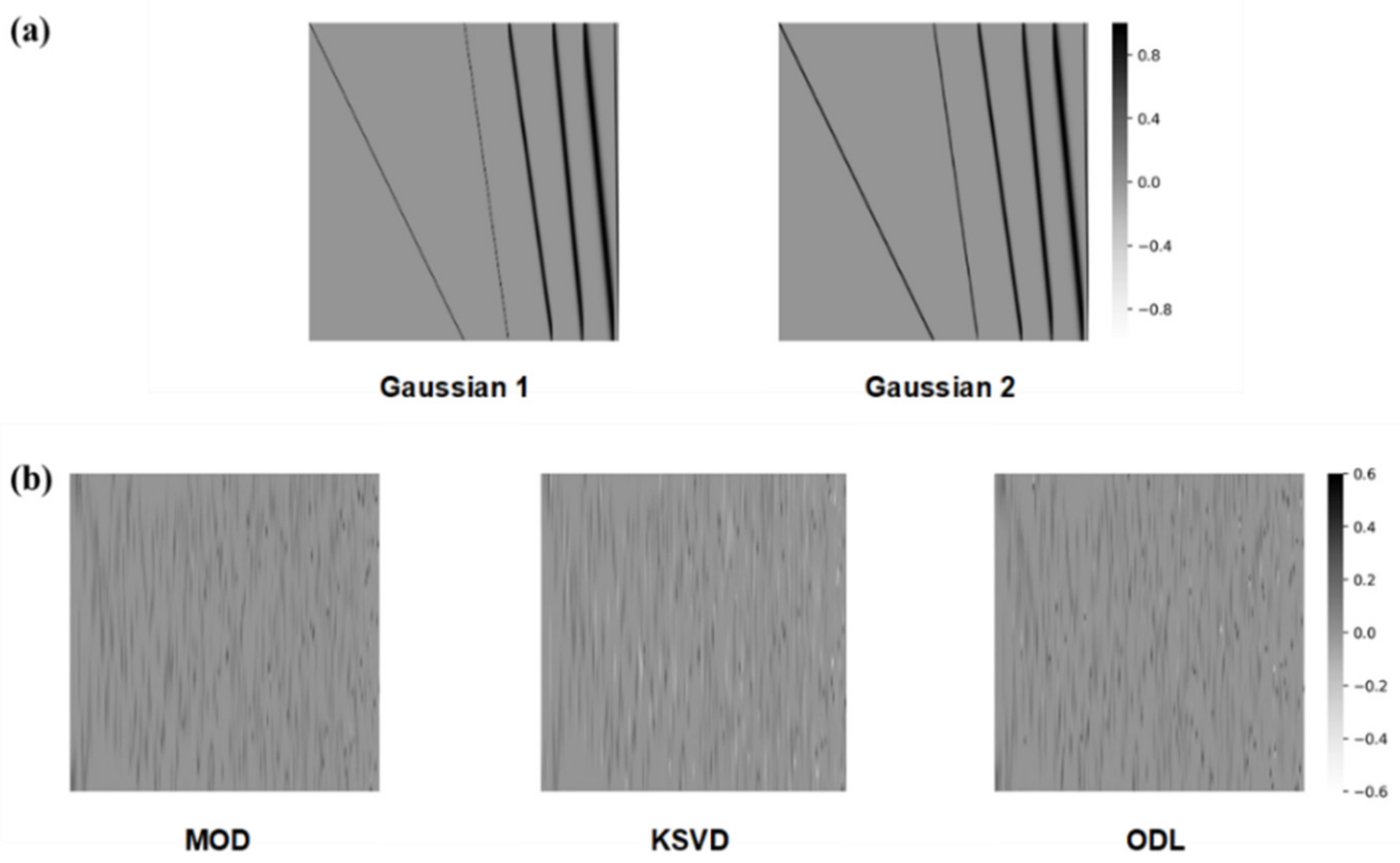
4.3. Sparsifying Bases for Spare Recovery
5. Results
5.1. Synthetic Datasets
5.2. Noisy Synthetic Datasets
5.3. Measured Datasets
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Izake, E.L. Forensic and homeland security applications of modern portable Raman spectroscopy. Forensic Sci. Int. 2010, 202, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Cho, D.; Kim, J.; Kim, M.; Youn, S.; Jang, J.E.; Je, M.; Lee, D.H.; Lee, B.; Farkas, D.L.; et al. Smartphone-based multispectral imaging: System development and potential for mobile skin diagnosis. Biomed. Opt. Express 2016, 7, 5294–5307. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kutyniok, G. Compressed Sensing: Theory and Applications; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Candes, E.J.; Eldar, Y.C.; Needell, D.; Randall, P. Compressed sensing with coherent and redundant dictionaries. Appl. Comput. Harm. Anal. 2011, 31, 59–73. [Google Scholar] [CrossRef]
- Oiknine, Y.; August, I.; Blumberg, D.G.; Stern, A. Compressive sensing resonator spectroscopy. Opt. Lett. 2017, 42, 25–28. [Google Scholar] [CrossRef]
- Kurokawa, U.; Choi, B.I.; Chang, C.-C. Filter-based miniature spectrometers: Spectrum reconstruction using adaptive regularization. IEEE Sens. J. 2011, 11, 1556–1563. [Google Scholar] [CrossRef]
- Cerjan, B.; Halas, N.J. Toward a Nanophotonic Nose: A Compressive Sensing-Enhanced, Optoelectronic Mid-Infrared Spectrometer. ACS Photonics 2018, 6, 79–86. [Google Scholar] [CrossRef]
- Oiknine, Y.; August, I.; Stern, A. Multi-aperture snapshot compressive hyperspectral camera. Opt. Lett. 2018, 43, 5042–5045. [Google Scholar] [CrossRef]
- Kim, C.; Lee, W.-B.; Lee, S.K.; Lee, Y.T.; Lee, H.-N. Fabrication of 2D thin-film filter-array for compressive sensing spectroscopy. Opt. Lasers Eng. 2019, 115, 53–58. [Google Scholar] [CrossRef]
- Oliver, J.; Lee, W.-B.; Lee, H.-N. Filters with random transmittance for improving resolution in filter-array-based spectrometers. Opt. Express 2013, 21, 3969–3989. [Google Scholar] [CrossRef] [PubMed]
- August, Y.; Stern, A. Compressive sensing spectrometry based on liquid crystal devices. Opt. Lett. 2013, 38, 4996–4999. [Google Scholar] [CrossRef] [PubMed]
- Huang, E.; Ma, Q.; Liu, Z. Etalon Array Reconstructive Spectrometry. Sci. Rep. 2017, 7, 40693. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yu, Z. Spectral analysis based on compressive sensing in nanophotonic structures. Opt. Express 2014, 22, 25608–25614. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yi, S.; Chen, A.; Zhou, M.; Luk, T.S.; James, A.; Nogan, J.; Ross, W.; Joe, G.; Shahsafi, A. Single-shot on-chip spectral sensors based on photonic crystal slabs. Nat. Commun. 2019, 10, 1020. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Dai, W.; Milenkovic, O. Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans. Inf. Theory 2009, 55, 2230–2249. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. Decoding by linear programming. arXiv 2005, arXiv:math/0502327. [Google Scholar] [CrossRef]
- Oliver, J.; Lee, W.; Park, S.; Lee, H.-N. Improving resolution of miniature spectrometers by exploiting sparse nature of signals. Opt. Express 2012, 20, 2613–2625. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Mousavi, A.; Baraniuk, R.G. Learning to invert: Signal recovery via deep convolutional networks. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2272–2276. [Google Scholar]
- Li, Y.; Xue, Y.; Tian, L. Deep speckle correlation: A deep learning approach toward scalable imaging through scattering media. Optica 2018, 5, 1181–1190. [Google Scholar] [CrossRef]
- Lee, D.; Yoo, J.; Ye, J.C. Deep residual learning for compressed sensing MRI. In Proceedings of the 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, VIC, Australia, 18–21 April 2017; pp. 15–18. [Google Scholar]
- Mardani, M.; Gong, E.; Cheng, J.Y.; Vasanawala, S.S.; Zaharchuk, G.; Xing, L.; Pauly, J.M. Deep Generative Adversarial Neural Networks for Compressive Sensing MRI. IEEE Trans. Med. Imaging 2019, 38, 167–179. [Google Scholar] [CrossRef] [PubMed]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.; Park, D.; Lee, H.-N. Convolutional neural networks for the reconstruction of spectra in compressive sensing spectrometers. In Optical Data Science II; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 10937, p. 109370L. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Macleod, H.A. Thin-Film Optical Filters; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Barry, J.R.; Kahn, J.M. Link design for nondirected wireless infrared communications. Appl. Opt. 1995, 34, 3764–3776. [Google Scholar] [CrossRef] [PubMed]
- Kokaly, R.F.; Clark, R.N.; Swayze, G.A.; Livo, K.E.; Hoefen, T.M.; Pearson, N.C.; Wise, R.A.; Benzel, W.M.; Lowers, H.A.; Driscoll, R.L. USGS Spectral Library Version 7 Data: US Geological Survey Data Release; United States Geological Survey (USGS): Reston, VA, USA, 2017. [Google Scholar]
- University of Eastern Finland. Spectral Color Research Group. Available online: http://www.uef.fi/web/spectral/-spectral-database (accessed on 2 August 2019).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Chen, G.; Needell, D. Compressed sensing and dictionary learning. Finite Fram. Theory 2016, 73, 201. [Google Scholar]
- Engan, K.; Aase, S.O.; Husoy, J.H. Method of optimal directions for frame design. In Proceedings of the 1999 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings. ICASSP99 (Cat. No. 99CH36258), Phoenix, AZ, USA, 15–19 March 1999; Volume 5, pp. 2443–2446. [Google Scholar]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal. Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online dictionary learning for sparse coding. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–17 June 2009; pp. 689–696. [Google Scholar]
- Koh, K.; Kim, S.-J.; Boyd, S. An interior-point method for large-scale l1-regularized logistic regression. J. Mach. Learn. Res. 2007, 8, 1519–1555. [Google Scholar]
- Martino, L.; Elvira, V. Compressed Monte Carlo for distributed Bayesian inference. arXiv 2018, arXiv:1811.0505. [Google Scholar]
- Liu, S.; Wu, H.; Huang, Y.; Yang, Y.; Jia, J. Accelerated Structure-Aware Sparse Bayesian Learning for 3D Electrical Impedance Tomography. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Tsiligianni, E.; Deligiannis, N. Deep coupled-representation learning for sparse linear inverse problems with side information. IEEE Signal. Process. Lett. 2019, 26, 1768–1772. [Google Scholar] [CrossRef]
- Diamond, S.; Sitzmann, V.; Heide, F.; Wetzstein, G. Unrolled optimization with deep priors. arXiv 2017, arXiv:1705.08041. [Google Scholar]
- Gilton, D.; Ongie, G.; Willett, R. Neumann Networks for Linear Inverse Problems in Imaging. IEEE Trans. Comput. Imaging 2019. [Google Scholar] [CrossRef]

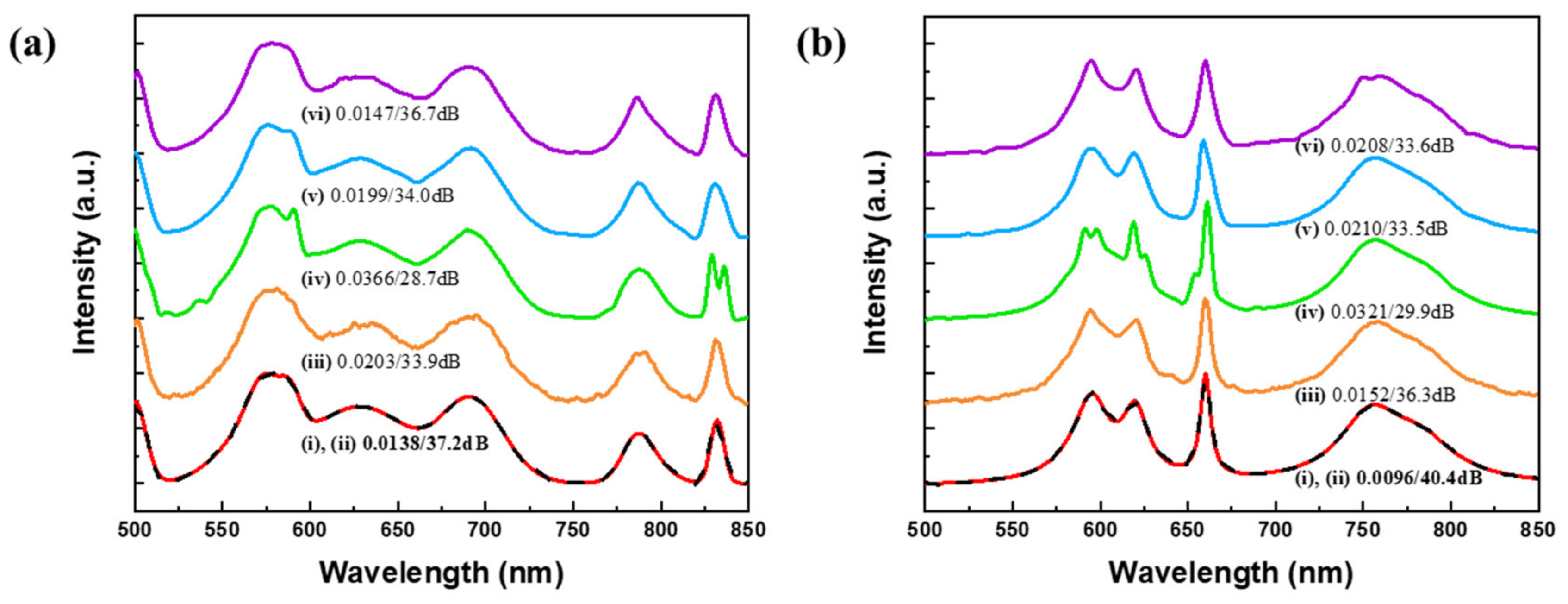

| Dataset | Training/Validation/Test | Avg. Number of Nonzero Values | Description |
|---|---|---|---|
| Gaussian dataset | 8000/2000/2000 | 336.8/350 | FWHM (nm) on the interval [2, 50], Height on the interval [0, 1] |
| Lorentzian dataset | 8000/2000/2000 | 349/350 | FWHM (nm) on the interval [2, 50], Height on the interval [0, 1] |
| US Geological Survey [32] | 982/246/245 | 348.9/350 | 350–2500 nm, 2151 spectral bands (we use 350 spectral bands in 500–849 nm) |
| Munsell colors [33] | 1066/267/267 | 349/350 | 380–780 nm, 401 spectral bands (we use 350 spectral bands in 400–749 nm) |
| Sparse Recovery | Deep Learning | ||||||
|---|---|---|---|---|---|---|---|
| Dataset | Gaussian 1 | Gaussian 2 | K-SVD | MOD | ODL | CNN | ResCNN |
| Gaussian dataset | 0.0226 (43.1 dB) | 0.0112 (49.7 dB) | 0.0172 (40.3 dB) | 0.0174 (40.3 dB) | 0.0161 (41.1 dB) | 0.0132 (40.5 dB) | 0.0094 (47.2 dB) |
| Lorentzian dataset | 0.0146 (44.9 dB) | 0.0094 (47.5 dB) | 0.0136 (42.3 dB) | 0.0137 (42.3 dB) | 0.0127 (42.9 dB) | 0.0101 (42.8 dB) | 0.0073 (49.0 dB) |
| SNR (dB) | |||||||
| Dataset | Method | 15 dB | 20 dB | 25 dB | 30 dB | 35 dB | 40 dB |
| Gaussian Dataset | Sparse recovery + Gaussian 2 | 0.0796 (22.7 dB) | 0.0482 (27.1 dB) | 0.0308 (31.2 dB) | 0.0215 (34.8 dB) | 0.0166 (37.9 dB) | 0.0138 (40.7 dB) |
| ResCNN | 0.0671 (24.2 dB) | 0.0401 (28.7 dB) | 0.0251 (32.9 dB) | 0.0171 (36.6 dB) | 0.0130 (39.8 dB) | 0.0110 (42.4 dB) | |
| Lorentzian Dataset | Sparse recovery + Gaussian 2 | 0.0817 (22.6 dB) | 0.0483 (27.1 dB) | 0.0300 (31.2 dB) | 0.0201 (35.0 dB) | 0.0147 (38.5 dB) | 0.0119 (41.4 dB) |
| ResCNN | 0.0689 (24.1 dB) | 0.0404 (28.7 dB) | 0.0243 (33.1 dB) | 0.0157 (37.1 dB) | 0.0113 (40.6 dB) | 0.0091 (43.4 dB) | |
| Sparse Recovery | Deep Learning | ||||||
|---|---|---|---|---|---|---|---|
| Dataset | Gaussian 1 | Gaussian 2 | K-SVD | MOD | ODL | CNN | ResCNN |
| USGS [32] | 0.0081 (45.3 dB) | 0.0061 (48.4 dB) | 0.0070 (48.5 dB) | 0.0081 (47.4 dB) | 0.0074 (47.6 dB) | 0.0116 (40.8 dB) | 0.0048 (52.4 dB) |
| Munsell colors [33] | 0.0068 (44.6 dB) | 0.0050 (47.5 dB) | 0.0040 (49.8 dB) | 0.0040 (49.9 dB) | 0.0042 (49.5 dB) | 0.0076 (43.0 dB) | 0.0040 (50.0 dB) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Park, D.; Lee, H.-N. Compressive Sensing Spectroscopy Using a Residual Convolutional Neural Network. Sensors 2020, 20, 594. https://doi.org/10.3390/s20030594
Kim C, Park D, Lee H-N. Compressive Sensing Spectroscopy Using a Residual Convolutional Neural Network. Sensors. 2020; 20(3):594. https://doi.org/10.3390/s20030594
Chicago/Turabian StyleKim, Cheolsun, Dongju Park, and Heung-No Lee. 2020. "Compressive Sensing Spectroscopy Using a Residual Convolutional Neural Network" Sensors 20, no. 3: 594. https://doi.org/10.3390/s20030594
APA StyleKim, C., Park, D., & Lee, H.-N. (2020). Compressive Sensing Spectroscopy Using a Residual Convolutional Neural Network. Sensors, 20(3), 594. https://doi.org/10.3390/s20030594





