A Cross-Regional Analysis of the COVID-19 Spread during the 2020 Italian Vacation Period: Results from Three Computational Models Are Compared
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.1.1. COVID-19 Data
2.1.2. Tourist Data
2.1.3. Other Relevant Data
- The population density for each region (available for the year 2019);
- The annual expenditure on healthcare for each region (available for the year 2019);
- The percentage of population with more than 65 years of age (available for the year 2019);
- A categorical variable representing the geographical position of each region in Italy. ISTAT dictates that each region can belong to one of these following areas: North-West, North-East, Center, South, Islands.
2.2. Methodologies
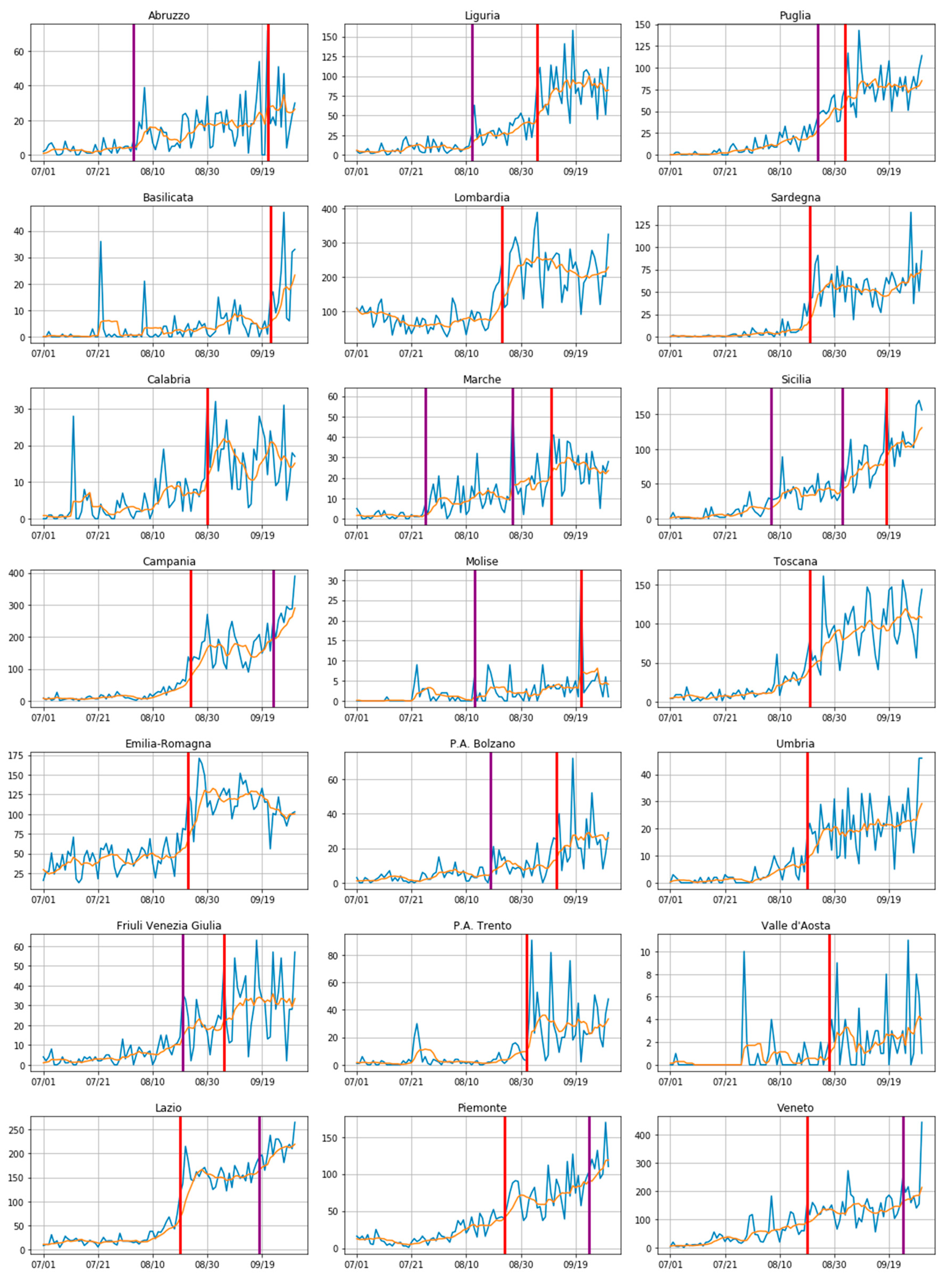
2.2.1. A Changepoint Detection Method
2.2.2. A Simple Toy Model
2.2.3. A Statistical Model with a Negative Binomial Regression
- is the cumulative number of the new infection cases, occurring in a region, during the time comprised within the (black) window, w;
- is the sum of inbound and outbound tourists for a given region, , during the aforementioned window, ;
- is the population density for each region, , measured as the number of inhabitants per km2;
- is the healthcare expenditure for the region, , expressed as a percentage of the region’s GDP;
- is the ratio between the total population and the population over the age of 65;
- is a variable that takes into account the area to which a given region belongs, as shown in Table 2;
- stands for the natural logarithm. We used logarithms at the right-hand side of the formula above, in accordance with the model proposed in [15], where this choice is mainly motivated by an increase in the performance prediction.
2.2.4. A Cognitive Model
3. Results
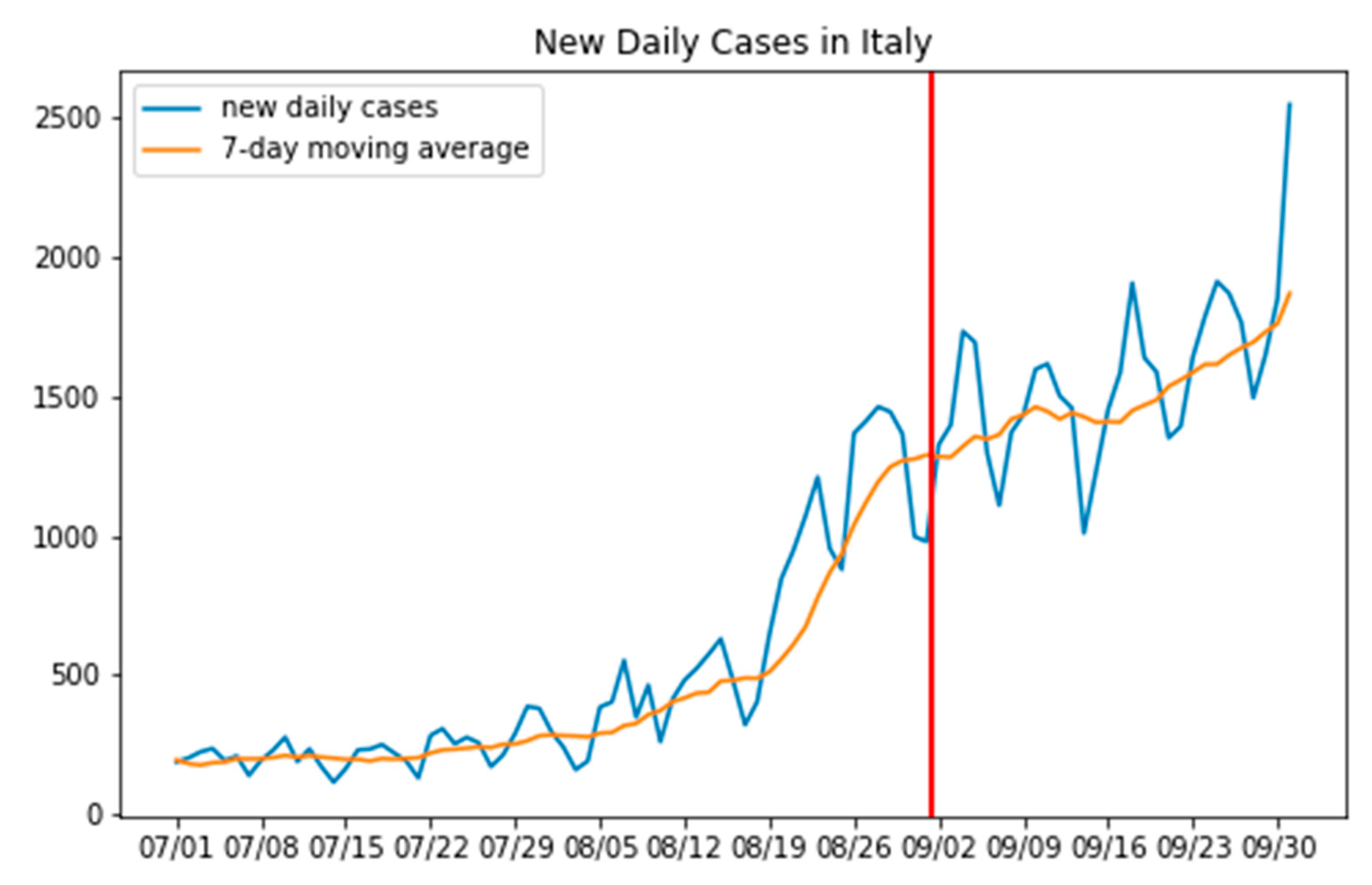
3.1. Where the Infection Curve Starts to Change
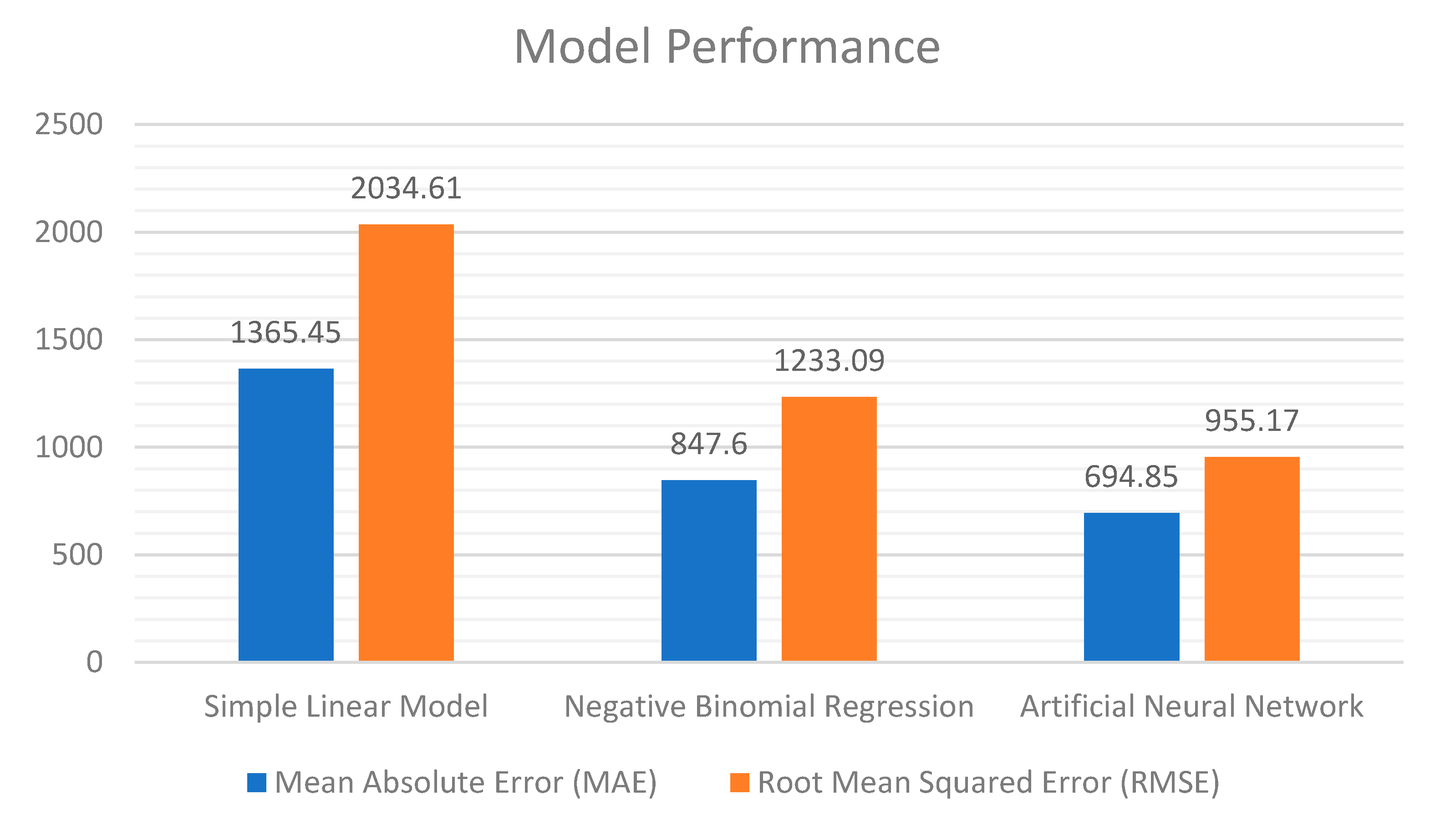
3.2. Predicting How Big This Change Is
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Zhang, A.; Wang, J. Exploring the roles of high-speed train, air and coach services in the spread of COVID-19 in China. Transp. Policy 2020, 94, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Pueyo, T.; Lash, N.; Serkez, Y. Opinion | This Is Why We Couldn’t Control the Pandemic. N. Y. Times 2020. Available online: https://www.nytimes.com/interactive/2020/09/14/opinion/politics/coronavirus-close-borders-travel-quarantine.html (accessed on 30 October 2020).
- Presidenza del Consiglio dei Ministri Decreto del Presidente del Consiglio dei Ministri, 8 Marzo. Gazz. Uff. Della Repubb. Ital. 2020, 59, 1–6.
- Civil Protection Department. COVID-19 Italian Data Repository; Presidenza del Consiglio dei Ministri—Dipartimento della Protezione Civile: Roma, Italy, 2020. [Google Scholar]
- Pietromarchi, V. Italy’s Busy Summer Lights Fuse on Coronavirus Resurgence Fears. AL Jazeera 2020. Available online: https://www.aljazeera.com/news/2020/8/28/italys-busy-summer-lights-fuse-on-coronavirus-resurgence-fears (accessed on 30 October 2020).
- Matthews, L. Italy Reopens to European Travelers—but Not to Americans Yet. AFAR Media 2020. Available online: https://www.afar.com/magazine/is-italy-reopening-and-when-will-i-be-able-to-visit (accessed on 30 October 2020).
- Giuffrida, A. How Sardinia went from safe haven to Covid-19 hotspot. Guardian 2020. Available online: https://www.theguardian.com/world/2020/sep/06/how-sardinia-went-from-safe-haven-to-covid-19-hotspot (accessed on 30 October 2020).
- Rigaill, G.; Lebarbier, E.; Robin, S. Exact posterior distributions and model selection criteria for multiple change-point detection problems. Stat. Comput. 2012, 22, 917–929. [Google Scholar] [CrossRef]
- Istituto Italiano di Statistica Una Breve Guida Alle Statistiche sul Turismo 2020. Available online: https://www.istat.it/it/archivio/243826 (accessed on 30 October 2020).
- Piegorsch, W.W. Maximum likelihood estimation for the negative binomial dispersion parameter. Biometrics 1990, 46, 863–867. [Google Scholar] [CrossRef] [PubMed]
- Furuya, H. Risk of transmission of airborne infection during train commute based on mathematical model. Environ. Health Prev. Med. 2007, 12, 78–83. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hu, M.; Lin, H.; Wang, J.; Xu, C.; Tatem, A.J.; Meng, B.; Zhang, X.; Liu, Y.; Wang, P.; Wu, G.; et al. Risk of Coronavirus Disease 2019 Transmission in Train Passengers: An Epidemiological and Modeling Study. Clin. Infect. Dis. 2020. [Google Scholar] [CrossRef] [PubMed]
- Krisztin, T.; Piribauer, P.; Wögerer, M. The spatial econometrics of the coronavirus pandemic. Lett. Spat. Resour. Sci. 2020. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, S.; Wheeler, D. Modeling and Predicting the Spread of Covid-19: Comparative Results for the United States, the Philippines, and South Africa; World Bank Group: Washington, DC, USA, 2020. [Google Scholar]
- Farzanegan, M.R.; Gholipour, H.F.; Feizi, M.; Nunkoo, R.; Andargoli, A.E. International Tourism and Outbreak of Coronavirus (COVID-19): A Cross-Country Analysis. J. Travel Res. 2020, 0047287520931593. [Google Scholar] [CrossRef]
- Falk, M.T.; Hagsten, E. The unwanted free rider: Covid-19. Curr. Issues Tour. 2020, 1–6. [Google Scholar] [CrossRef]
- Gössling, S.; Scott, D.; Hall, C.M. Pandemics, tourism and global change: A rapid assessment of COVID-19. J. Sustain. Tour. 2020, 29, 1–20. [Google Scholar] [CrossRef]
- D’Orazio, M.; Bernardini, G.; Quagliarini, E. Sustainable and resilient strategies for touristic cities against COVID-19: An agent-based approach. arXiv 2020, arXiv:2005.12547. [Google Scholar]
- Roda, W.C.; Varughese, M.B.; Han, D.; Li, M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020, 5, 271–281. [Google Scholar] [CrossRef] [PubMed]
- Carli, A.; Rosano, A.; Sindoni, A. Rapporto Osservasalute 2019, Osservatorio sulla Salute 2019. Available online: https://www.osservatoriosullasalute.it/osservasalute/rapporto-osservasalute-2019 (accessed on 30 October 2020).
- Truong, C.; Oudre, L.; Vayatis, N. Selective review of offline change point detection methods. Signal Process. 2020, 167, 107299. [Google Scholar] [CrossRef]
- Regione Toscana Focus: Gli Italiani nelle Regioni Italiane. 2019. Available online: https://servizi.toscana.it/RT/statistichedinamiche/Turismo_matrice_2019/ (accessed on 30 October 2020).
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28–30 June 2010; pp. 92–96. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S.; Statistics and Computing, 4th ed.; Springer: New York, NY, USA, 2002; ISBN 978-0-387-95457-8. [Google Scholar]
- Lau, M.S.Y.; Grenfell, B.; Thomas, M.; Bryan, M.; Nelson, K.; Lopman, B. Characterizing superspreading events and age-specific infectiousness of SARS-CoV-2 transmission in Georgia, USA. Proc. Natl. Acad. Sci. USA 2020, 117, 22430–22435. [Google Scholar] [CrossRef] [PubMed]
- Lloyd-Smith, J.O.; Schreiber, S.J.; Kopp, P.E.; Getz, W.M. Superspreading and the effect of individual variation on disease emergence. Nature 2005, 438, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Hilbe, J. Negative Binomial Regression, 2nd ed.; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Chollet, F. Deep Learning with Python; Manning Publications: Greenwich, CT, USA, 2018; ISBN 978-1-61729-443-3. [Google Scholar]
- Roccetti, M.; Delnevo, G.; Casini, L.; Cappiello, G. Is bigger always better? A controversial journey to the center of machine learning design, with uses and misuses of big data for predicting water meter failures. J. Big Data 2019, 6, 70. [Google Scholar] [CrossRef]
- Mirri, S.; Delnevo, G.; Roccetti, M. Is a COVID-19 Second Wave Possible in Emilia-Romagna (Italy)? Forecasting a Future Outbreak with Particulate Pollution and Machine Learning. Computation 2020, 8, 74. [Google Scholar] [CrossRef]
- Delnevo, G.; Mirri, S.; Roccetti, M. Particulate Matter and COVID-19 Disease Diffusion in Emilia-Romagna (Italy). Already a Cold Case? Computation 2020, 8, 59. [Google Scholar] [CrossRef]
- Roccetti, M.; Casini, L.; Delnevo, G.; Orrù, V.; Marchetti, N. Potential and Limitations of Designing a Deep Learning Model for Discovering New Archaeological Sites: A Case with the Mesopotamian Floodplain. In Proceedings of the ACM International Conference Proceeding Series; ACM: New York, NY, USA, 2020; pp. 216–221. [Google Scholar]
- Casini, L.; Marfia, G.; Roccetti, M. Some Reflections on the Potential and Limitations of Deep Learning for Automated Music Generation. In Proceedings of the 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Bologna, Italy, 9–12 September 2018; pp. 27–31. [Google Scholar]
- Zou, F.; Shen, L.; Jie, Z.; Zhang, W.; Liu, W. A Sufficient Condition for Convergences of Adam and RMSProp. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11127–11135. [Google Scholar]
- Meotti, G. L’Occidente in lockdown. Sul Covid abbiamo solo opzioni difficili. Ci aspetta un tempo spaventoso ma affascinante (In Italian). Il Foglio 2020. Available online: https://www.ilfoglio.it/cultura/2020/10/27/news/l-occidente-in-lockdown-sul-covid-abbiamo-solo-opzioni-difficili-ci-aspetta-un-tempo-spaventoso-ma-affascinante--1303510/ (accessed on 30 October 2020).
- Carbonaro, A.; Piccinini, F.; Reda, R. Integrating Heterogeneous Data of Healthcare Devices to enable Domain Data Management. J. e-Learn. Knowl. Soc. 2018, 14, 45–56. [Google Scholar]
- Salomoni, P.; Mirri, S.; Ferretti, S.; Roccetti, M. Profiling Learners with Special Needs for Custom e-Learning Experiences, a Closed Case? In Proceedings of the ACM International Conference Proceedings Series, Banff, AB, Canada, 7–8 May 2007; ACM: New York, NY, USA, 2007; pp. 84–92. [Google Scholar]



| Classification | Regions |
|---|---|
| North-West | Valle d’Aosta, Piedmont, Lombardy, Liguria |
| North-East | Veneto, Emilia-Romagna, Friuli-Venezia Giulia, Trentino Alto-Adige |
| Center | Tuscany, Lazio, Umbria, Marche |
| South | Campania, Abruzzo, Molise, Puglia, Basilicata, Calabria |
| Islands | Sardinia, Sicily |
| Coefficients | Estimate | Std. Error | z-Value | Pr(>|z|) |
|---|---|---|---|---|
| (Intercept) | −9.93064 | 2.10982 | −4.707 | 2.52 × 10−6 |
| log(T) | 0.85395 | 0.12426 | 6.872 | 6.31 × 10−12 |
| log(D) | 0.82921 | 0.14986 | 5.533 | 3.14 × 10−8 |
| log(H) | −1.19588 | 0.59292 | −2.017 | 0.04370 |
| O | 11.12581 | 3.68649 | 3.018 | 0.00254 |
| (A) Islands | 1.33754 | 0.35277 | 3.792 | 0.00015 |
| (A) North-Est | 0.06887 | 0.17690 | 0.389 | 0.69705 |
| (A) North-West | −0.31216 | 0.19199 | −1.626 | 0.10397 |
| (A) South | 0.65365 | 0.27646 | 2.364 | 0.01806 |
| Layer (Type) | Neurons | # of Parameters |
|---|---|---|
| layer_1 (ReLU) | 16 | 160 (16 × 10) |
| layer_2 (ReLU) | 8 | 136 (17 × 8) |
| layer_3 (ReLU) | 8 | 72 (9 × 8) |
| output | 1 | 9 (9 × 1) |
| Region | Real Cases | Simple Toy Model | Negative Binomial | Cognitive |
|---|---|---|---|---|
| Abruzzo | 480 | 270 | 463 | 293 |
| Basilicata | 135 | 101 | 91 | 117 |
| Calabria | 383 | 275 | 298 | 270 |
| Campania | 3959 | 391 | 1466 | 2007 |
| Emilia-Romagna | 3325 | 1430 | 2133 | 2484 |
| Friuli Venezia Giulia | 677 | 195 | 362 | 348 |
| Lazio | 4303 | 334 | 1619 | 2168 |
| Liguria | 1504 | 405 | 907 | 889 |
| Lombardia | 6239 | 571 | 3349 | 4329 |
| Marche | 542 | 379 | 513 | 470 |
| Molise | 84 | 18 | 37 | 101 |
| Piemonte | 1817 | 229 | 781 | 983 |
| Puglia | 1689 | 560 | 922 | 857 |
| Sardegna | 1452 | 395 | 491 | 610 |
| Sicilia | 1625 | 372 | 1254 | 1034 |
| Toscana | 2412 | 907 | 1314 | 1557 |
| Trentino-Alto Adige | 869 | 1105 | 472 | 778 |
| Umbria | 546 | 212 | 223 | 199 |
| Valle d’Aosta | 46 | 138 | 40 | 67 |
| Veneto | 3852 | 999 | 2252 | 2557 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casini, L.; Roccetti, M. A Cross-Regional Analysis of the COVID-19 Spread during the 2020 Italian Vacation Period: Results from Three Computational Models Are Compared. Sensors 2020, 20, 7319. https://doi.org/10.3390/s20247319
Casini L, Roccetti M. A Cross-Regional Analysis of the COVID-19 Spread during the 2020 Italian Vacation Period: Results from Three Computational Models Are Compared. Sensors. 2020; 20(24):7319. https://doi.org/10.3390/s20247319
Chicago/Turabian StyleCasini, Luca, and Marco Roccetti. 2020. "A Cross-Regional Analysis of the COVID-19 Spread during the 2020 Italian Vacation Period: Results from Three Computational Models Are Compared" Sensors 20, no. 24: 7319. https://doi.org/10.3390/s20247319
APA StyleCasini, L., & Roccetti, M. (2020). A Cross-Regional Analysis of the COVID-19 Spread during the 2020 Italian Vacation Period: Results from Three Computational Models Are Compared. Sensors, 20(24), 7319. https://doi.org/10.3390/s20247319






