Monitoring and Landscape Dynamic Analysis of Alpine Wetland Area Based on Multiple Algorithms: A Case Study of Zoige Plateau
Abstract
1. Introduction
2. Materials and Methods
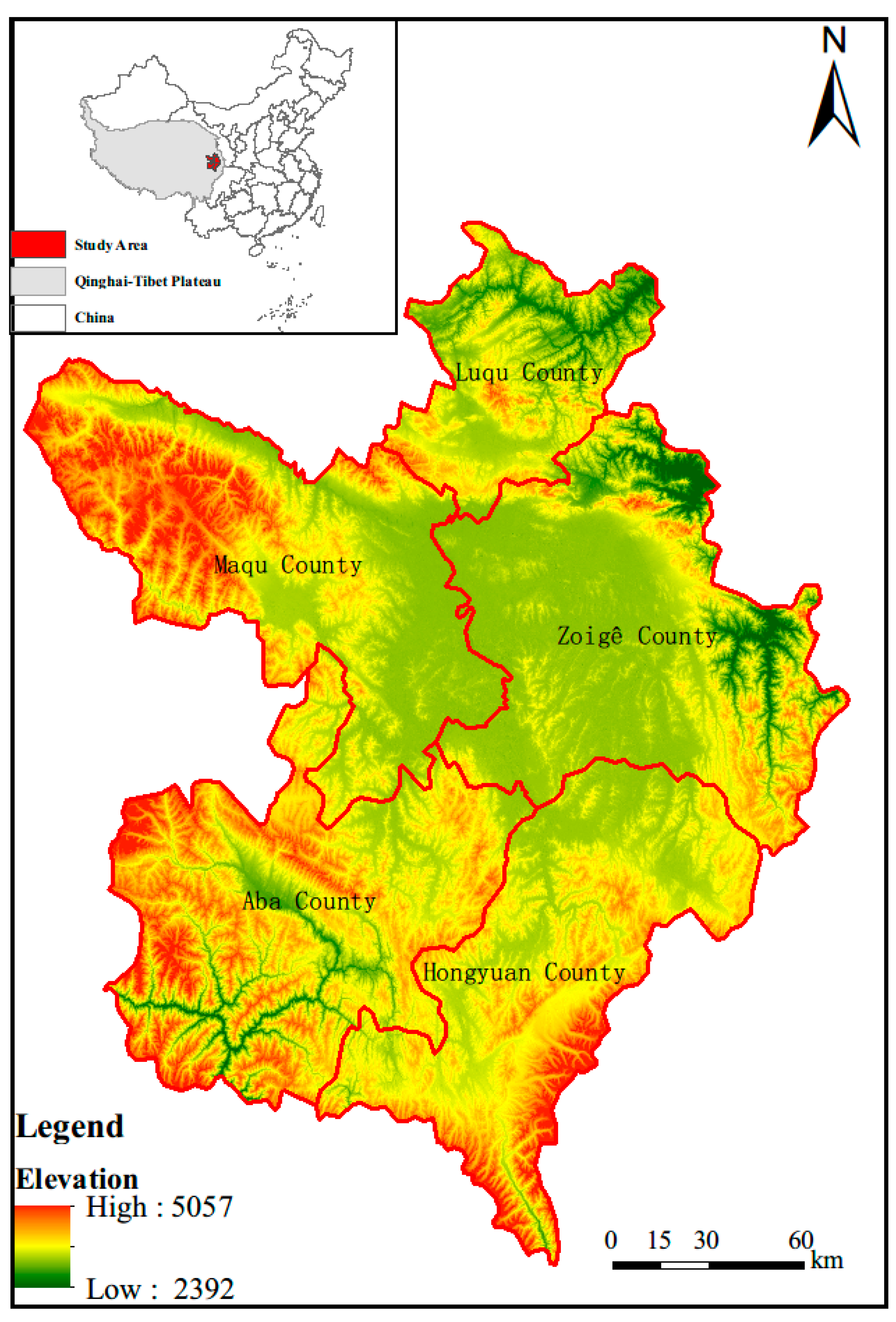
2.1. Study Area
2.2. Data Preparation
2.2.1. Satellite Imagery Process
2.2.2. Classification Feature Collection
2.2.3. Sample Selection
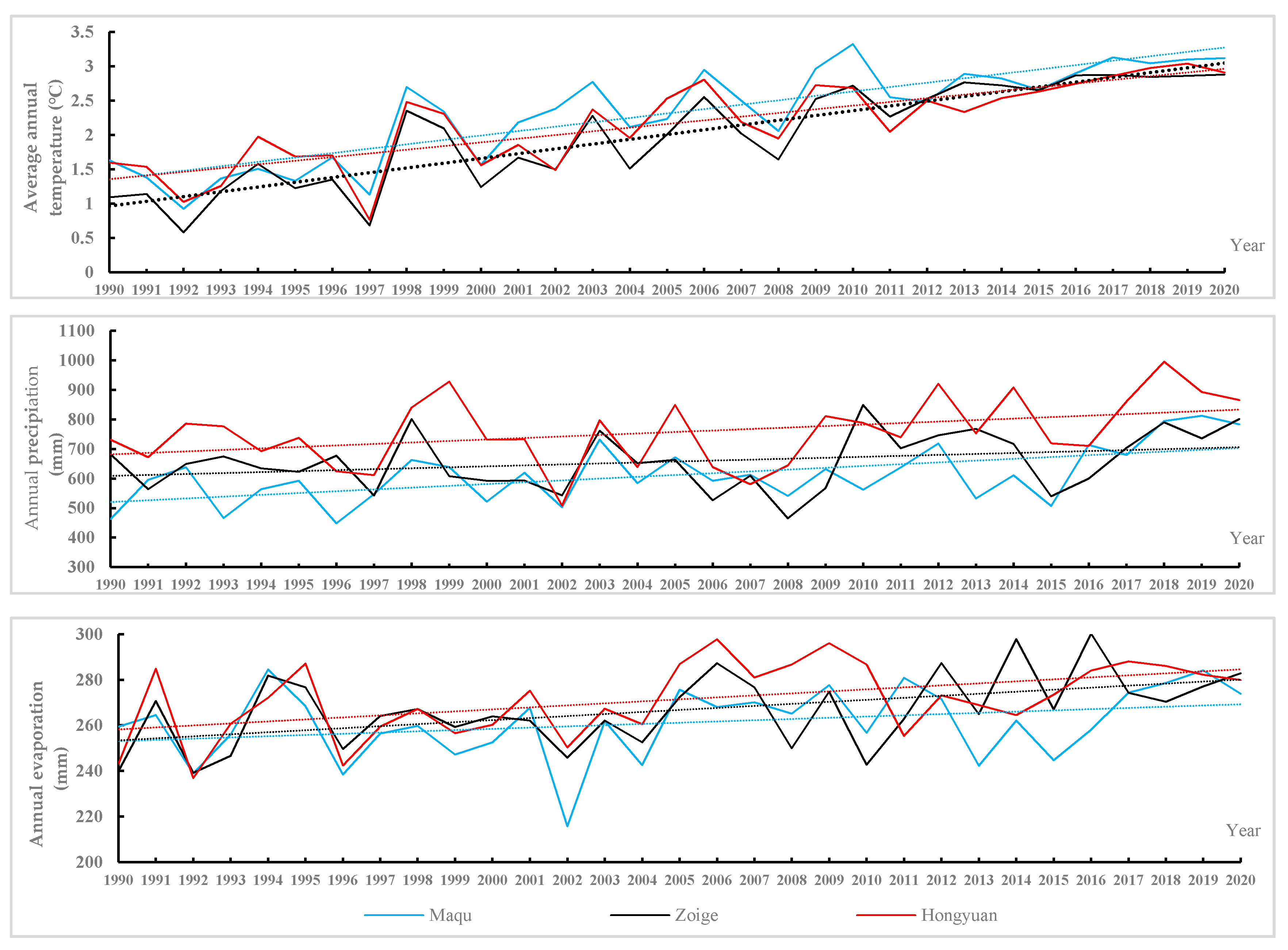
2.2.4. Meteorological and Socio-Economic Data
2.3. Methods
2.3.1. Calculation Methods of Landscape Indices
2.3.2. Grey Relational Analysis
- (1)
- the original data sequence includes characteristic target sequence (x0) and related factor order (xi):
- (2)
- calculation of correlation coefficient:where εi (k) is the relative difference between the sequence of related factors xi and the characteristic target sequence x0 at time k, called the correlation coefficient of xi to x0 at time k; 0.5 is the resolution coefficient; min (Δi(min)), the minimum difference between the two levels; max (Δi(max)), the maximum difference between the two levels.
- (3)
- The grey correlation calculation is:where ri, the correlation degree between the characteristic target sequence (x0) and the related factor sequence (xi).
3. Results
3.1. Classification Results and Accuracy
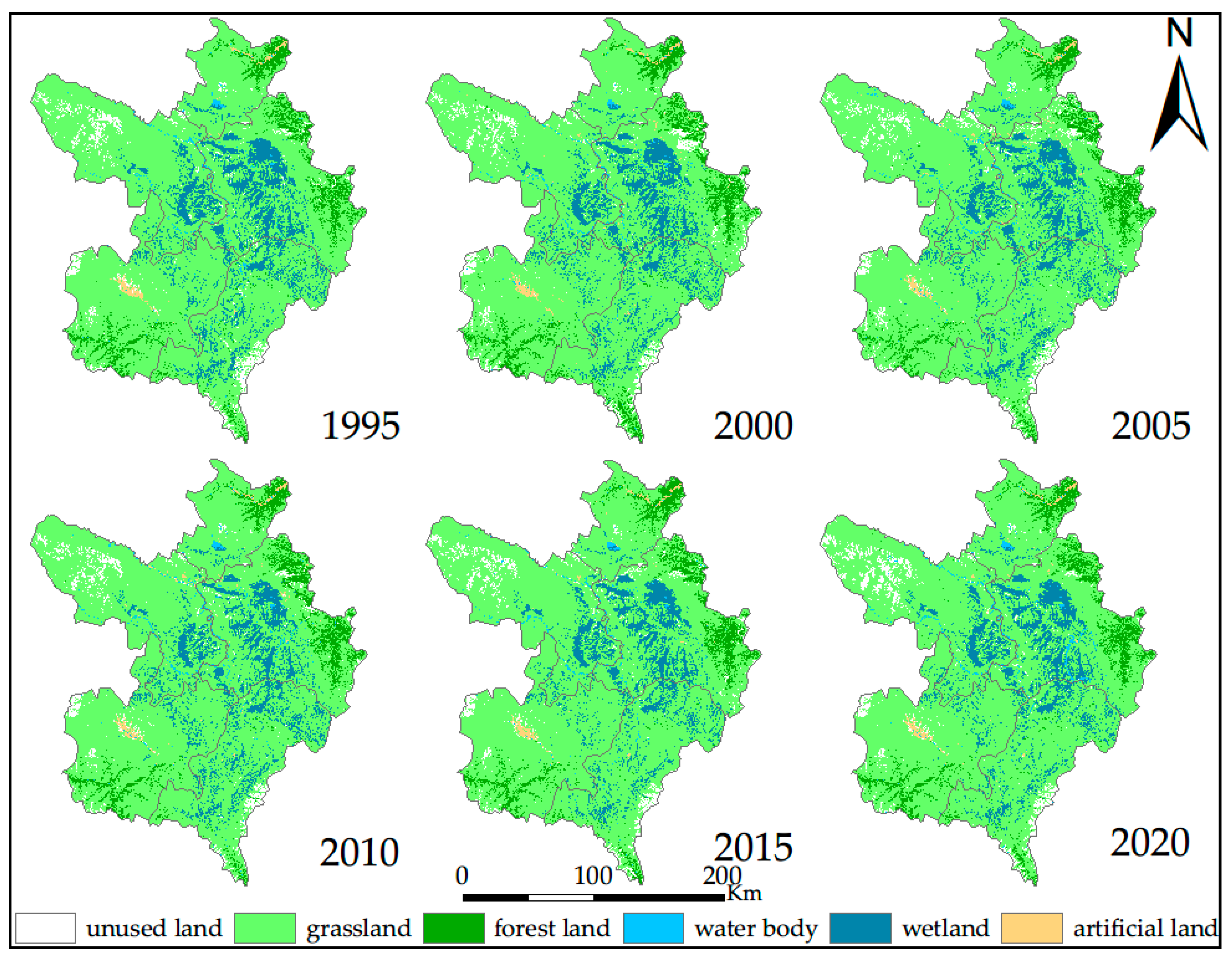
3.2. Dynamics Change, from 1995 to 2020
3.3. Results of Dynamic Landscape Changes
3.4. Grey Relational Analysis
4. Discussion
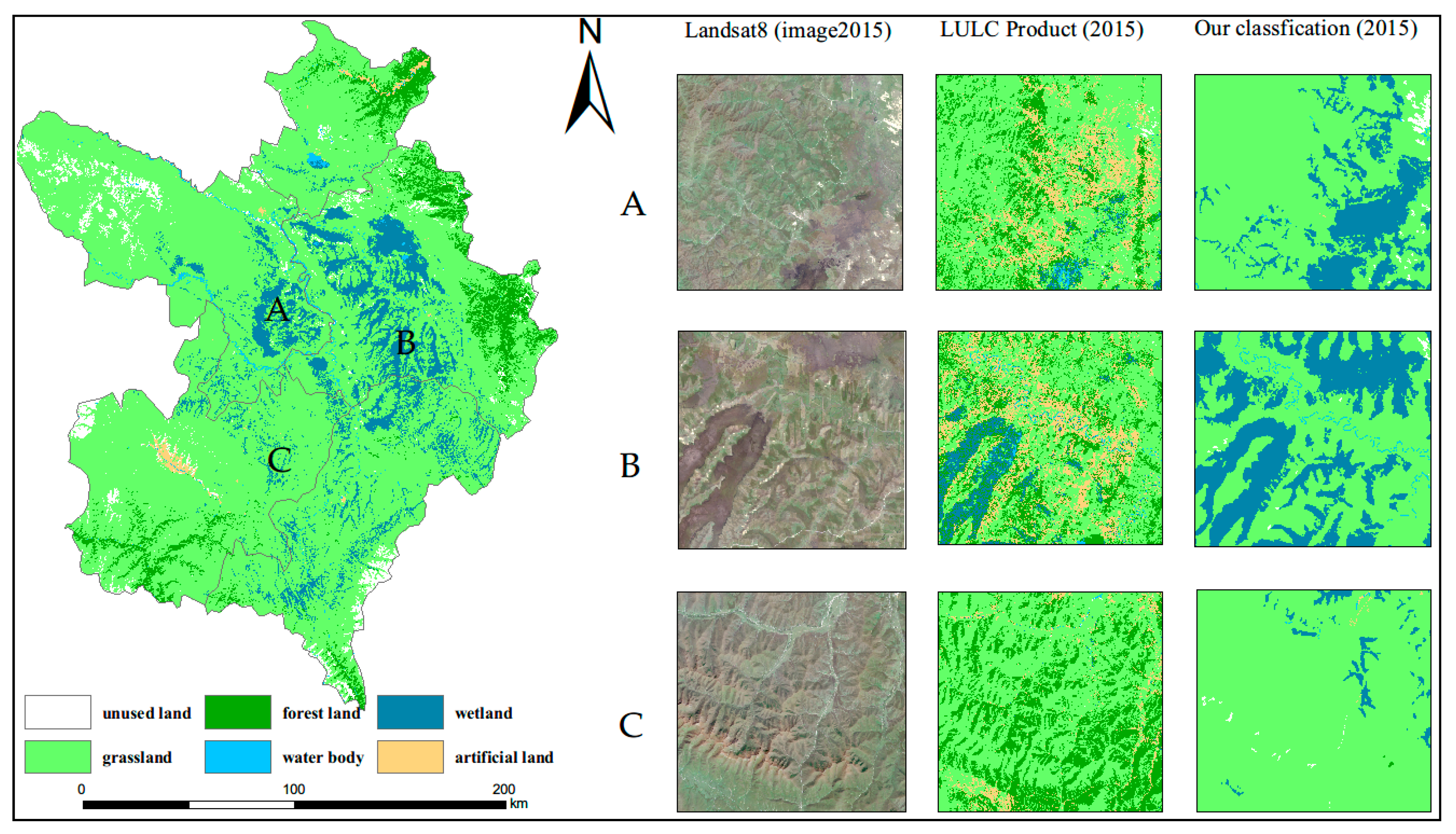
4.1. Comparison of Classification Results and Analysis of Classification Variable Importance
4.2. Analysis of Landscape Dynamics and Drivers of Wetland Changes
4.3. Limitations of the Current Study and Platforms Selection
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rezaee, M.; Mahdianpari, M.; Zhang, Y.; Salehi, B. Deep Convolutional Neural Network for Complex Wetland Classification Using Optical Remote Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3030–3039. [Google Scholar] [CrossRef]
- Agboola, J.I.; Ndimele, P.E.; Odunuga, S.; Akanni, A.; Kosemani, B.; Ahove, M.A. Ecological health status of the Lagos wetland ecosystems: Implications for coastal risk reduction. Estuar. Coast. Shelf Sci. 2016, 183, 73–81. [Google Scholar] [CrossRef]
- Castano-Castano, S.; Martinez-Santos, P.; Martinez-Alfaro, P.E. Evaluating infiltration losses in a Mediterranean wetland: Las Tablas de Daimiel National Park, Spain. Hydrol. Process. 2008, 22, 5048–5053. [Google Scholar] [CrossRef]
- Eskandari-Damaneh, H.; Noroozi, H.; Ghoochani, O.M.; Taheri-Reykandeh, E.; Cotton, M. Evaluating rural participation in wetland management: A contingent valuation analysis of the set-aside policy in Iran. Sci. Total Environ. 2020, 747, 141127. [Google Scholar] [CrossRef] [PubMed]
- Wan, R.R.; Wang, P.; Wang, X.L.; Yao, X.; Dai, X. Modeling wetland aboveground biomass in the Poyang Lake National Nature Reserve using machine learning algorithms and Landsat-8 imagery. J. Appl. Remote Sens. 2018, 12, 046029. [Google Scholar] [CrossRef]
- Boys, C.A.; Williams, R.J. Succession of fish and crustacean assemblages following reinstatement of tidal flow in a temperate coastal wetland. Ecol. Eng. 2012, 49, 221–232. [Google Scholar] [CrossRef]
- Dong, Z.; Hu, G.; Yan, C.; Wang, W.; Lu, J. Aeolian desertification and its causes in the Zoige Plateau of China’s Qinghai-Tibetan Plateau. Environ. Earth Sci. 2010, 59, 1731–1740. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.; Wang, Y. Changes in alpine wetland ecosystems of the Qinghai-Tibetan plateau from 1967 to 2004. Environ. Monit. Assess. 2011, 180, 189–199. [Google Scholar] [CrossRef]
- Liu, L.; Cao, W.; Shao, Q.; Huang, L.; He, T. Characteristics of Land Use/Cover and Macroscopic Ecological Changes in the Headwaters of the Yangtze River and of the Yellow River over the Past 30 Years. Sustainability 2016, 8, 237. [Google Scholar] [CrossRef]
- Wang, X.; Chen, R.; Yang, Y. Effects of Permafrost Degradation on the Hydrological Regime in the Source Regions of the Yangtze and Yellow Rivers, China. Water 2017, 9, 897. [Google Scholar] [CrossRef]
- Zhi, W.; Ji, G. Constructed wetlands, 1991-2011: A review of research development, current trends, and future directions. Sci. Total Environ. 2012, 441, 19–27. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, M.J.; Colna, K.E.; El-Mezayen, M.M.; Laureano-Rosario, A.E.; Mendez-Lazaro, P.; Otis, D.B.; Toro-Farmer, G.; Vega-Rodriguez, M.; Muller-Karger, F.E. Satellite Remote Sensing for Coastal Management: A Review of Successful Applications. Environ. Manag. 2017, 60, 323–339. [Google Scholar] [CrossRef] [PubMed]
- Adeli, S.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.J.; Brisco, B.; Tamiminia, H.; Shaw, S. Wetland Monitoring Using SAR Data: A Meta-Analysis and Comprehensive Review. Remote Sens. 2020, 12, 2190. [Google Scholar] [CrossRef]
- Gong, P.; Li, X.C.; Zhang, W. 40-Year (1978–2017) human settlement changes in China reflected by impervious surfaces from satellite remote sensing. Sci. Bull. 2019, 64, 756–763. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Han, X.; Chen, X.; Feng, L. Four decades of winter wetland changes in Poyang Lake based on Landsat observations between 1973 and 2013. Remote Sens. Environ. 2015, 156, 426–437. [Google Scholar] [CrossRef]
- Ge, J.; Meng, B.; Liang, T.; Feng, Q.; Gao, J.; Yang, S.; Huang, X.; Xie, H. Modeling alpine grassland cover based on MODIS data and support vector machine regression in the headwater region of the Huanghe River, China. Remote Sens. Environ. 2018, 218, 162–173. [Google Scholar] [CrossRef]
- Han, X.; Feng, L.; Hu, C.; Chen, X. Wetland changes of China’s largest freshwater lake and their linkage with the Three Gorges Dam. Remote Sens. Environ. 2018, 204, 799–811. [Google Scholar] [CrossRef]
- Rapinel, S.; Mony, C.; Lecoq, L.; Clément, B.; Thomas, A.; Hubert-Moy, L. Evaluation of Sentinel-2 time-series for mapping floodplain grassland plant communities. Remote Sens. Environ. 2019, 223, 115–129. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.; Adeli, S.; Brisco, B. Google Earth Engine for geo-big data applications: A meta-analysis and systematic review. ISPRS J. Photogramm. Remote Sens. 2020, 164, 152–170. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Zhang, D.-D.; Zhang, L. Land Cover Change in the Central Region of the Lower Yangtze River Based on Landsat Imagery and the Google Earth Engine: A Case Study in Nanjing, China. Sensors 2020, 20, 2091. [Google Scholar] [CrossRef]
- Hao, B.; Ma, M.; Li, S.; Li, Q.; Hao, D.; Huang, J.; Ge, Z.; Yang, H.; Han, X. Land Use Change and Climate Variation in the Three Gorges Reservoir Catchment from 2000 to 2015 Based on the Google Earth Engine. Sensors 2019, 19, 2118. [Google Scholar] [CrossRef]
- Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Xu, M.; Watanachaturaporn, P.; Varshney, P.K.; Arora, M.K. Decision tree regression for soft classification of remote sensing data. Remote Sens. Environ. 2005, 97, 322–336. [Google Scholar] [CrossRef]
- Wang, C.; Yang, W.; Zhu, Y.; Ren, Y. Analysis of the impact of ancient city walls on urban landscape patterns by remote sensing. Landsc. Ecol. Eng. 2020. [Google Scholar] [CrossRef]
- Bai, J.-H.; Lu, Q.-Q.; Wang, J.-J.; Zhao, Q.-Q.; Ouyang, H.; Deng, W.; Li, A.-N. Landscape pattern evolution processes of alpine wetlands and their driving factors in the Zoige Plateau of China. J. Mt. Sci. 2013, 10, 54–67. [Google Scholar] [CrossRef]
- Tang, J.; Li, Y.; Cui, S.; Xu, L.; Ding, S.; Nie, W. Linking land-use change, landscape patterns, and ecosystem services in a coastal watershed of southeastern China. Glob. Ecol. Conserv. 2020, 23, e01177. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Hsu, C.-C.; Chiou, M.-L.; Chen, C.-I. The main factors affecting Taiwan’s economic growth rate via dynamic grey relational analysis. PLoS ONE 2020, 15, e0240065. [Google Scholar] [CrossRef]
- Almetwally, A.A. Multi-objective Optimization of Woven Fabric Parameters Using Taguchi-Grey Relational Analysis. J. Nat. Fibers 2020, 17, 1468–1478. [Google Scholar] [CrossRef]
- Xie, W.; Ma, Y.; Li, S.; Zhang, S.; Ruan, L.; Yang, M.; Shi, W.; Zhang, H.; Zhang, L. Optimizing soil dissolved organic matter extraction by grey relational analysis. Pedosphere 2020, 30, 589–596. [Google Scholar] [CrossRef]
- Li, B.; Wu, Q.; Zhang, W.; Liu, Z. Water resources security evaluation model based on grey relational analysis and analytic network process: A case study of Guizhou Province. J. Water Process Eng. 2020, 37, 101429. [Google Scholar] [CrossRef]
- Shen, G.; Yang, X.C.; Jin, Y.X.; Xu, B.; Zhou, Q.B. Remote sensing and evaluation of the wetland ecological degradation process of the Zoige Plateau Wetland in China. Ecol. Indic. 2019, 104, 48–58. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Hobart, G.W.; Luther, J.E.; Hermosilla, T.; Griffiths, P.; Coops, N.C.; Hall, R.J.; Hostert, P.; Dyk, A.; et al. Pixel-Based Image Compositing for Large-Area Dense Time Series Applications and Science. Can. J. Remote Sens. 2014, 40, 192–212. [Google Scholar] [CrossRef]
- Flood, N. Seasonal Composite Landsat TM/ETM plus Images Using the Medoid (a Multi-Dimensional Median). Remote Sens. 2013, 5, 6481–6500. [Google Scholar] [CrossRef]
- Huang, H.; Chen, Y.; Clinton, N.; Wang, J.; Wang, X.; Liu, C.; Gong, P.; Yang, J.; Bai, Y.; Zheng, Y.; et al. Mapping major land cover dynamics in Beijing using all Landsat images in Google Earth Engine. Remote Sens. Environ. 2017, 202, 166–176. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.C.; Kline, K.; Scaramuzza, P.L.; Kovalskyy, V.; Hansen, M.; Loveland, T.R.; Vermote, E.; Zhang, C.S. Web-enabled Landsat Data (WELD): Landsat ETM plus composited mosaics of the conterminous United States. Remote Sens. Environ. 2010, 114, 35–49. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, L.; Wang, W.; Cao, R.; Zhang, Y.; Shen, W. Spatio-temporal analysis of vegetation variation in the Yellow River Basin. Ecol. Indic. 2015, 51, 117–126. [Google Scholar] [CrossRef]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Zhang, S.; Wu, J. Detecting, Extracting, and Monitoring Surface Water from Space Using Optical Sensors: A Review. Rev. Geophys. 2018, 56, 333–360. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar]
- Langat, P.K.; Kumar, L.; Koech, R. Monitoring river channel dynamics using remote sensing and GIS techniques. Geomorphology 2019, 325, 92–102. [Google Scholar] [CrossRef]
- Wang, H.; Liu, C.; Zang, F.; Yang, J.; Li, N.; Rong, Z.; Zhao, C. Impacts of Topography on the Land Cover Classification in the Qilian Mountains, Northwest China. Can. J. Remote Sens. 2020, 46, 344–359. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Srinet, R.; Nandy, S.; Padalia, H.; Ghosh, S.; Watham, T.; Patel, N.R.; Chauhan, P. Mapping plant functional types in Northwest Himalayan foothills of India using random forest algorithm in Google Earth Engine. Int. J. Remote Sens. 2020, 41, 7296–7309. [Google Scholar] [CrossRef]
- Shen, G.; Yang, X.; Jin, Y.; Luo, S.; Xu, B.; Zhou, Q. Land Use Changes in the Zoige Plateau Based on the Object-Oriented Method and Their Effects on Landscape Patterns. Remote Sens. 2019, 12, 14. [Google Scholar] [CrossRef]
- Liu, C.; Li, W.; Zhu, G.; Zhou, H.; Yan, H.; Xue, P. Land Use/Land Cover Changes and Their Driving Factors in the Northeastern Tibetan Plateau Based on Geographical Detectors and Google Earth Engine: A Case Study in Gannan Prefecture. Remote Sens. 2020, 12, 3139. [Google Scholar] [CrossRef]
- Berhane, T.M.; Costa, H.; Lane, C.R.; Anenkhonov, O.A.; Chepinoga, V.V.; Autrey, B.C. The Influence of Region of Interest Heterogeneity on Classification Accuracy in Wetland Systems. Remote Sens. 2019, 11, 551. [Google Scholar] [CrossRef]
- Damtea, W.; Kim, D.; Im, S. Spatiotemporal Analysis of Land Cover Changes in the Chemoga Basin, Ethiopia, Using Landsat and Google Earth Images. Sustainability 2020, 12, 3607. [Google Scholar] [CrossRef]
- Ji, H.; Li, X.; Wei, X.; Liu, W.; Zhang, L.; Wang, L. Mapping 10-m Resolution Rural Settlements Using Multi-Source Remote Sensing Datasets with the Google Earth Engine Platform. Remote Sens. 2020, 12, 2832. [Google Scholar] [CrossRef]
- Krajewski, P.; Solecka, I.; Mrozik, K. Forest Landscape Change and Preliminary Study on Its Driving Forces in Sleza Landscape Park (Southwestern Poland) in 1883–2013. Sustainability 2018, 10, 4526. [Google Scholar] [CrossRef]
- Teluguntla, P.; Thenkabail, P.S.; Oliphant, A.; Xiong, J.; Gumma, M.K.; Congalton, R.G.; Yadav, K.; Huete, A. A 30-m landsat-derived cropland extent product of Australia and China using random forest machine learning algorithm on Google Earth Engine cloud computing platform. ISPRS J. Photogramm. Remote Sens. 2018, 144, 325–340. [Google Scholar] [CrossRef]
- Belgiu, M.; Dragut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Na, X.; Zhang, S.; Li, X.; Yu, H.; Liu, C. Improved Land Cover Mapping using Random Forests Combined with Landsat Thematic Mapper Imagery and Ancillary Geographic Data. Photogramm. Eng. Remote Sens. 2010, 76, 833–840. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ma, L.; Fu, T.; Blaschke, T.; Li, M.; Tiede, D.; Zhou, Z.; Ma, X.; Chen, D. Evaluation of Feature Selection Methods for Object-Based Land Cover Mapping of Unmanned Aerial Vehicle Imagery Using Random Forest and Support Vector Machine Classifiers. ISPRS Int. J. Geo-Inf. 2017, 6, 51. [Google Scholar] [CrossRef]
- Karlson, M.; Gålfalk, M.; Crill, P.; Bousquet, P.; Saunois, M.; Bastviken, D. Delineating northern peatlands using Sentinel-1 time series and terrain indices from local and regional digital elevation models. Remote Sens. Environ. 2019, 231, 111252. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, X.; Zou, Z.; Chen, B.; Ma, J.; Dong, J.; Doughty, R.B.; Zhong, Q.; Qin, Y.; Dai, S.; et al. Tracking annual changes of coastal tidal flats in China during 1986–2016 through analyses of Landsat images with Google Earth Engine. Remote Sens. Environ. 2020, 238, 110987. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Qiu, P.; Wu, N.; Luo, P.; Wang, Z.; Li, M. Analysis of dynamics and driving factors of wetland landscape in Zoige, Eastern Qinghai-Tibetan Plateau. J. Mt. Sci. 2009, 6, 42–55. [Google Scholar] [CrossRef]
- Lei, G.; Li, A.; Zhang, Z.; Bian, J.; Hu, G.; Wang, C.; Nan, X.; Wang, J.; Tan, J.; Liao, X. The Quantitative Estimation of Grazing Intensity on the Zoige Plateau Based on the Space-Air-Ground Integrated Monitoring Technology. Remote Sens. 2020, 12, 1399. [Google Scholar] [CrossRef]
- Rashid, I.; Aneaus, S. Landscape transformation of an urban wetland in Kashmir Himalaya, India using high-resolution remote sensing data, geospatial modeling, and ground observations over the last 5 decades (1965–2018). Environ. Monit. Assess. 2020, 192, 635. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Zhong, R.; Sun, H.; Wu, Q.; Du, L.; Geng, Y.; Cao, S. Integrated Airborne LiDAR Data and Imagery for Suburban Land Cover Classification Using Machine Learning Methods. Sensors 2019, 19, 1996. [Google Scholar] [CrossRef] [PubMed]
- Tavares, P.A.; Santos Beltrao, N.E.; Guimaraes, U.S.; Teodoro, A.C. Integration of Sentinel-1 and Sentinel-2 for Classification and LULC Mapping in the Urban Area of Belem, Eastern Brazilian Amazon. Sensors 2019, 19, 1140. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Zhong, R.; Zhao, W.; Song, K.; Du, L. Land-cover classification using GF-2 images and airborne lidar data based on Random Forest. Int. J. Remote Sens. 2018, 40, 2410–2426. [Google Scholar] [CrossRef]
- Tobón-Marín, A.; Cañón Barriga, J. Analysis of changes in rivers planforms using google earth engine. Int. J. Remote Sens. 2020, 41, 8654–8681. [Google Scholar] [CrossRef]
| Year | Gross Domestic Product (104 Yuan) | I Primary Industry (104 Yuan) | II Secondary Industry (104 Yuan) | III Tertiary Industry (104 Yuan) | Industrial Structure % | Population (104) | Number of Livestock (104) | Per Capita GDP (104 Yuan) |
|---|---|---|---|---|---|---|---|---|
| 1995 | 62,420 | 42,268 | 9881 | 10,271 | 68:16:16 | 21.5 | 203.42 | 0.3054 |
| 2000 | 87,261 | 49,939 | 17,953 | 19,369 | 57:21:22 | 22.65 | 295.38 | 0.402 |
| 2005 | 156,655 | 70,133 | 38,493 | 48,029 | 45:24:31 | 25.09 | 336.4 | 0.6481 |
| 2010 | 335,526 | 133,604 | 82,011 | 119,911 | 40:24:36 | 27.84 | 387.22 | 1.2753 |
| 2015 | 587,772 | 214,098 | 129,436 | 244,238 | 36:22:42 | 29.01 | 355.08 | 2.0902 |
| 2020 | 798,323 | 316,934 | 210,757 | 270,632 | 40:24:36 | 30.26 | 320.52 | 2.6913 |
| Types | Platform-Classifier | 6 Periods | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1995 | 2000 | 2005 | 2010 | 2015 | 2020 | ||||||||
| UA | PA | UA | PA | UA | PA | UA | PA | UA | PA | UA | PA | ||
| Grassland | RF-GEE | 89.74% | 97.36% | 90.38% | 96.64% | 88.48% | 96.75% | 89.45% | 93.15% | 93.81% | 96.72% | 90.26% | 93.83% |
| SVM-GEE | 86.86% | 96.04% | 87.57% | 90.84% | 85.71% | 96.34% | 80.59% | 88.36% | 90.20% | 88.89% | 88.36% | 88.51% | |
| DT-Envi | 92.60% | 95.89% | 88.68% | 96.04% | 89.45% | 96.04% | 89.06% | 96.13% | 92.76% | 96.74% | 88.39% | 92.90% | |
| Wetland | RF-GEE | 94.23% | 89.42% | 89.12% | 86.94% | 93.25% | 85.14% | 87.79% | 85.50% | 94.92% | 94.92% | 89.96% | 87.59% |
| SVM-GEE | 88.85% | 90.15% | 88.00% | 89.80% | 90.66% | 84.42% | 91.71% | 83.12% | 93.33% | 91.30% | 82.87% | 89.10% | |
| DT-Envi | 89.24% | 91.43% | 91.79% | 89.78% | 92.80% | 86.25% | 91.51% | 89.86% | 92.51% | 92.86% | 92.66% | 86.96% | |
| Forest | RF-GEE | 97.37% | 95.36% | 98.21% | 97.06% | 96.24% | 94.21% | 96.65% | 97.74% | 96.59% | 96.05% | 96.02% | 95.54% |
| SVM-GEE | 98.88% | 90.72% | 96.73% | 87.06% | 97.31% | 95.26% | 94.48% | 90.96% | 88.37% | 85.88% | 95.79% | 90.10% | |
| DT-Envi | 97.63% | 97.06% | 97.93% | 97.42% | 94.94% | 96.02% | 98.40% | 96.86% | 96.45% | 95.48% | 93.18% | 92.66% | |
| Water | RF-GEE | 92.45% | 79.67% | 91.18% | 78.81% | 90.35% | 83.74% | 93.20% | 82.76% | 98.13% | 88.24% | 93.50% | 87.12% |
| SVM-GEE | 84.40% | 74.80% | 76.61% | 80.50% | 89.38% | 82.11% | 84.72% | 78.74% | 93.46% | 84.03% | 86.07% | 79.55% | |
| DT-Envi | 97.85% | 77.12% | 95.00% | 77.24% | 96.08% | 84.48% | 93.14% | 77.24% | 92.62% | 85.61% | 93.97% | 91.60% | |
| Artificial land | RF-GEE | 89.76% | 89.06% | 91.82% | 90.18% | 93.40% | 86.84% | 94.34% | 95.26% | 97.89% | 93.94% | 94.12% | 89.60% |
| SVM-GEE | 87.25% | 69.53% | 92.40% | 65.18% | 85.71% | 84.21% | 73.33% | 69.18% | 88.76% | 79.80% | 93.75% | 72.00% | |
| DT-Envi | 88.24% | 93.75% | 88.98% | 82.03% | 94.06% | 90.48% | 89.38% | 88.60% | 96.52% | 88.80% | 93.33% | 84.85% | |
| Unused land | RF-GEE | 96.43% | 91.53% | 95.95% | 89.31% | 93.83% | 93.25% | 89.36% | 85.71% | 92.99% | 92.99% | 88.36% | 88.36% |
| SVM-GEE | 91.91% | 89.83% | 75.28% | 84.28% | 96.35% | 80.98% | 84.80% | 88.96% | 71.72% | 90.45% | 75.80% | 87.83% | |
| DT-Envi | 96.08% | 92.45% | 94.80% | 92.66% | 94.25% | 90.34% | 93.33% | 88.05% | 94.02% | 92.02% | 83.75% | 84.81% | |
| Overall accuracy | RF-GEE | 92.57% | 91.93% | 91.61% | 90.72% | 94.92% | 91.32% | ||||||
| SVM-GEE | 89.20% | 86.33% | 89.62% | 84.39% | 88.09% | 86.57% | |||||||
| DT-Envi | 92.98% | 91.73% | 92.10% | 91.65% | 93.64% | 90.06% | |||||||
| Kappa coefficient | RF-GEE | 90.32% | 89.30% | 89.11% | 87.65% | 93.27% | 88.63% | ||||||
| SVM-GEE | 85.86% | 81.94% | 86.49% | 81.25% | 84.33% | 82.47% | |||||||
| DT-Envi | 90.73% | 89.22% | 89.42% | 89.17% | 91.65% | 86.81% | |||||||
| Year | PN/n | WA/hm2 | WP/% |
|---|---|---|---|
| 1995 | 7093 (*) | 450,642.87 (*) | 10.61 (*) |
| 2000 | 7515 (+5.9%) | 437,998.77 (−2.8%) | 10.31 (−2.8%) |
| 2005 | 9410 (+25.2%) | 420,869.7 (−3.9%) | 9.91 (−3.9%) |
| 2010 | 8403 (−11.7%) | 409,675.86 (−2.6%) | 9.65 (−2.6%) |
| 2015 | 5703 (−32.1%) | 397,207.44 (−3.1%) | 9.35 (−3.1%) |
| 2020 | 6323 (+10.9%) | 407,560.05 (+2.7%) | 9.60 (+2.7%) |
| Time Interval | Wetland LCI |
|---|---|
| 1995–2000 | 0.150 |
| 2000–2005 | 0.200 |
| 2005–2010 | 0.130 |
| 2010–2015 | 0.150 |
| 2015–2020 | 0.125 |
| Number of Patches/n | 1995 | 2000 | 2005 | 2010 | 2015 | 2020 | |
|---|---|---|---|---|---|---|---|
| Area/hm2 | |||||||
| <10 | 5579 (*) | 5773 (+3.5%) | 7817 (+35.4%) | 6634 (−15.1%) | 4000 (−39.7%) | 4601 (+15.0%) | |
| 10~25 | 580 (*) | 719 (+24.0%) | 622 (−13.5%) | 693 (+11.4%) | 680 (−1.9%) | 701 (+3.1%) | |
| 25~50 | 361 (*) | 372 (+3.0%) | 366 (−1.6%) | 376 (+2.7%) | 387 (+2.9%) | 363 (−6.2%) | |
| 50~100 | 221 (*) | 271 (+22.6%) | 251 (−7.4%) | 290 (+15.5%) | 293 (+1.0%) | 288 (−1.7%) | |
| 100~300 | 195 (*) | 233 (+19.5%) | 224 (−3.9%) | 233 (+4.0%) | 211 (−9.4%) | 234 (+10.9%) | |
| 300~600 | 73 (*) | 60 (−17.8%) | 54 (−10%) | 77 (+42.6%) | 59 (−23.4%) | 57 (−3.4%) | |
| 600~1000 | 31 (*) | 40 (+29.0%) | 23 (−42.5%) | 39 (+69.6%) | 24 (−38.5%) | 26 (+8.3%) | |
| 1000~3000 | 34 (*) | 32 (−5.9%) | 33 (+3.1%) | 42 (+27.3%) | 32 (−23.8%) | 35 (+9.4%) | |
| 3000~10,000 | 12 (*) | 9 (−25.0%) | 13 (+44.4%) | 14 (+7.7%) | 10 (−28.6%) | 11 (+10%) | |
| >10,000 | 7 (*) | 6 (−14.3%) | 7 (+16.7%) | 5 (−28.6%) | 7 (+40%) | 7 (0) | |
| 1995 | 2000 | 2005 | 2010 | 2015 | 2020 | |
|---|---|---|---|---|---|---|
| <1000 hm2 (small) | 131,056.67 (*) | 145,567.17 (+11.0%) | 127,784.52 (−12.2%) | 156,258.81 (+22.3%) | 131,129.28 (−16.1%) | 139,128.06 (+6.1%) |
| 1000–10,000 hm2 (middle) | 116,713.17 (*) | 101,714.04 (−12.9%) | 120,763.89 (+18.7%) | 140,681.34 (+16.5%) | 102,240.45 (−27.3%) | 103,977.55 (+1.7%) |
| >10,000 hm2 (large) | 202,873 (*) | 190,717.5 (−6%) | 172,321.3 (−16%) | 112,735.7 (−34.6%) | 163,837.89 (+45.3%) | 164,454.4 (+0.4%) |
| all | 450,642.87 (*) | 437,998.77 (−2.8%) | 420,869.7 (−3.9%) | 409,675.86 (−2.7%) | 397,207.44 (−3.1%) | 407,560.05 (+2.6%) |
| Year | PD | LSI | SHDI | SHEI |
|---|---|---|---|---|
| 1995 | 0.1667 (*) | 93.3986 (*) | 0.3379 (*) | 0.4875 (*) |
| 2000 | 0.1767 (+6.0%) | 97.421 (+4.3%) | 0.3316 (−1.9%) | 0.4783 (−1.9%) |
| 2005 | 0.2212 (+25.2%) | 98.4492 (+1.1%) | 0.3227 (−2.7%) | 0.4656 (−2.7%) |
| 2010 | 0.1975 (−11.7%) | 107.8013 (+9.5%) | 0.3169 (−1.8%) | 0.4572 (−1.8%) |
| 2015 | 0.1341 (−32.1%) | 88.8969 (−17.5%) | 0.3103 (−2.1%) | 0.4476 (−2.1%) |
| 2020 | 0.1549 (+15.5%) | 90.0597 (+1.3%) | 0.3177 (+2.3%) | 0.4584 (+2.4%) |
| Transfer Type/Time | Change Area (hm2) | ||||
|---|---|---|---|---|---|
| 1995–2000 | 2000–2005 | 2005–2010 | 2010–2015 | 2015–2020 | |
| Wetland to grassland | 77,471.8 | 107,182.2 | 99,318 | 105,216.8 | 88,084.9 |
| Grassland to wetland | 65,066.7 | 89,893.4 | 89,119.9 | 92,147.1 | 97,577.4 |
| Wetland to others | 80,619.2 | 109,085.8 | 101,734.9 | 106,992.4 | 89,614.4 |
| Influencing Factor | Annual Evaporation | Annual Precipitation | Total Population | Large Livestock Inventory | Average Annual Temperature | Primary Industry | Secondary Industry | Tertiary Industry |
|---|---|---|---|---|---|---|---|---|
| Correlation degree | 0.953 | 0.875 | 0.851 | 0.837 | 0.758 | 0.607 | 0.572 | 0.548 |
| Sort | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Xue, P.; Liu, C.; Yan, H.; Zhu, G.; Cao, Y. Monitoring and Landscape Dynamic Analysis of Alpine Wetland Area Based on Multiple Algorithms: A Case Study of Zoige Plateau. Sensors 2020, 20, 7315. https://doi.org/10.3390/s20247315
Li W, Xue P, Liu C, Yan H, Zhu G, Cao Y. Monitoring and Landscape Dynamic Analysis of Alpine Wetland Area Based on Multiple Algorithms: A Case Study of Zoige Plateau. Sensors. 2020; 20(24):7315. https://doi.org/10.3390/s20247315
Chicago/Turabian StyleLi, Wenlong, Pengfei Xue, Chenli Liu, Hepiao Yan, Gaofeng Zhu, and Yapeng Cao. 2020. "Monitoring and Landscape Dynamic Analysis of Alpine Wetland Area Based on Multiple Algorithms: A Case Study of Zoige Plateau" Sensors 20, no. 24: 7315. https://doi.org/10.3390/s20247315
APA StyleLi, W., Xue, P., Liu, C., Yan, H., Zhu, G., & Cao, Y. (2020). Monitoring and Landscape Dynamic Analysis of Alpine Wetland Area Based on Multiple Algorithms: A Case Study of Zoige Plateau. Sensors, 20(24), 7315. https://doi.org/10.3390/s20247315





