Towards Continuous and Ambulatory Blood Pressure Monitoring: Methods for Efficient Data Acquisition for Pulse Transit Time Estimation
Abstract
1. Introduction
1.1. Rationale
1.2. Data Compression Background
1.3. Contributions
2. Materials and Methods
2.1. Algorithm
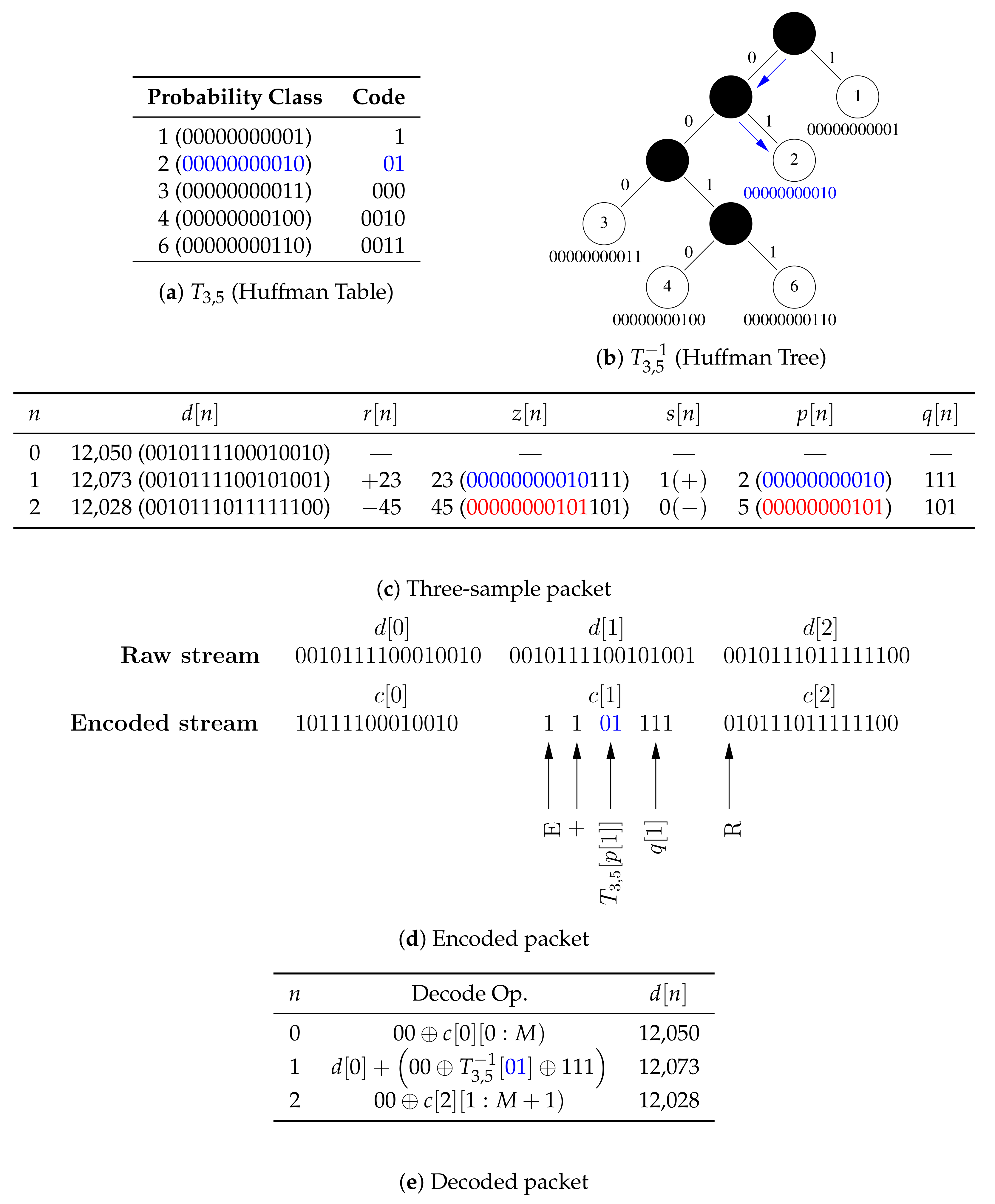
2.1.1. Encoder
| Algorithm 1. encode. |
| Input: |
| Output: |
|
| Comments:(1) Denotes the magnitude or cardinality (size) of its given argument when applied to a scalar or a set, respectively; (2) ⊕ Denotes bitwise concatenation; and (3) Leading superscript explicitly indicates the size (in bits) |
2.1.2. Hyperparameter Search
| Algorithm 2 Fast hyperparameter optimization and Huffman table construction. |
| Input: |
| Output: |
|
| Comments: (1)is the sequence of magnitudes of the first backward difference of; (2)denotes the sequence; and (3)is computed with the recurrence relation in Equation (14) |
- Algorithm 2 does not invoke the encoder because only the knowledge of a sample’s probability class, but not its actual code, is required to compute its code length, which implies that number of primitive operations within each loop is reduced.
- There is no need to explicitly compute the code lengths for samples whose probability classes are not in the compression table because they have already been implicitly accounted for by the first term in Equation (12).
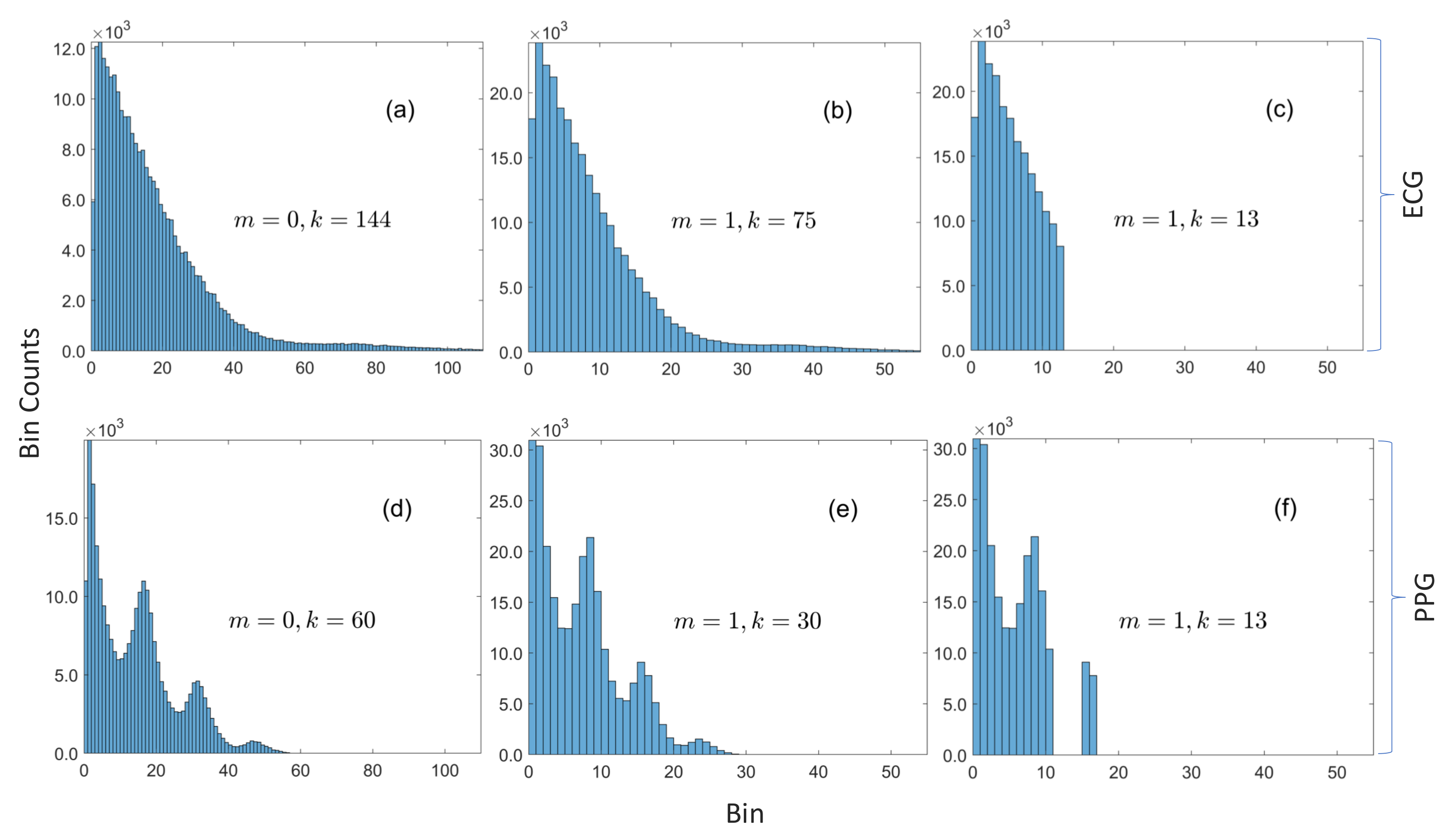
- In Algorithm 2, the innermost for-all-loop over the k entries in the compression table replaces the for-loop over the N samples in the validation dataset with the naive implementation. The table size is several orders of magnitude smaller than the size of the validation data. Moreover, the predicates in the innermost for-all-loop and its associated if-statement may be interchanged if , i.e., the size of the histogram is smaller than the size of the table, so that the cost of evaluating is , where (in contrast to the cost with the naive method). For instance, the worst case cost of given in the simulated example in Figure 3 is proportional to 5—whether the size of the validation dataset is or is irrelevant.
- is the number of bits saved by compressing a sample within the probability class a. However, instead of computing those values one-at-a-time, the histogram is used to compute the total number of bits saved by all samples within the probability class a.
- Huffman tables for sorted data can be computed in linear time, and the size of the table is typically very small, so the cost of computing is low.
- is independent of k, so is only computed once to evaluate with , .
- The cost of the do-while-loop, which executes the brute-force search, is decoupled from the size of the data (and becomes fixed) once the number of nonzero bins in and converge because the loop only depends on through and . One important consequence of this result (which was not exploited in this work) is that the algorithm can be made to be very memory efficient because there is no need to explicitly store the raw data. may be constructed by incrementally updating the histogram for the first N samples received from the embedded system, while may be similarly constructed from the latter N samples. Moreover, the cost of computing the histograms in this manner is negligible because it is spread out over time.
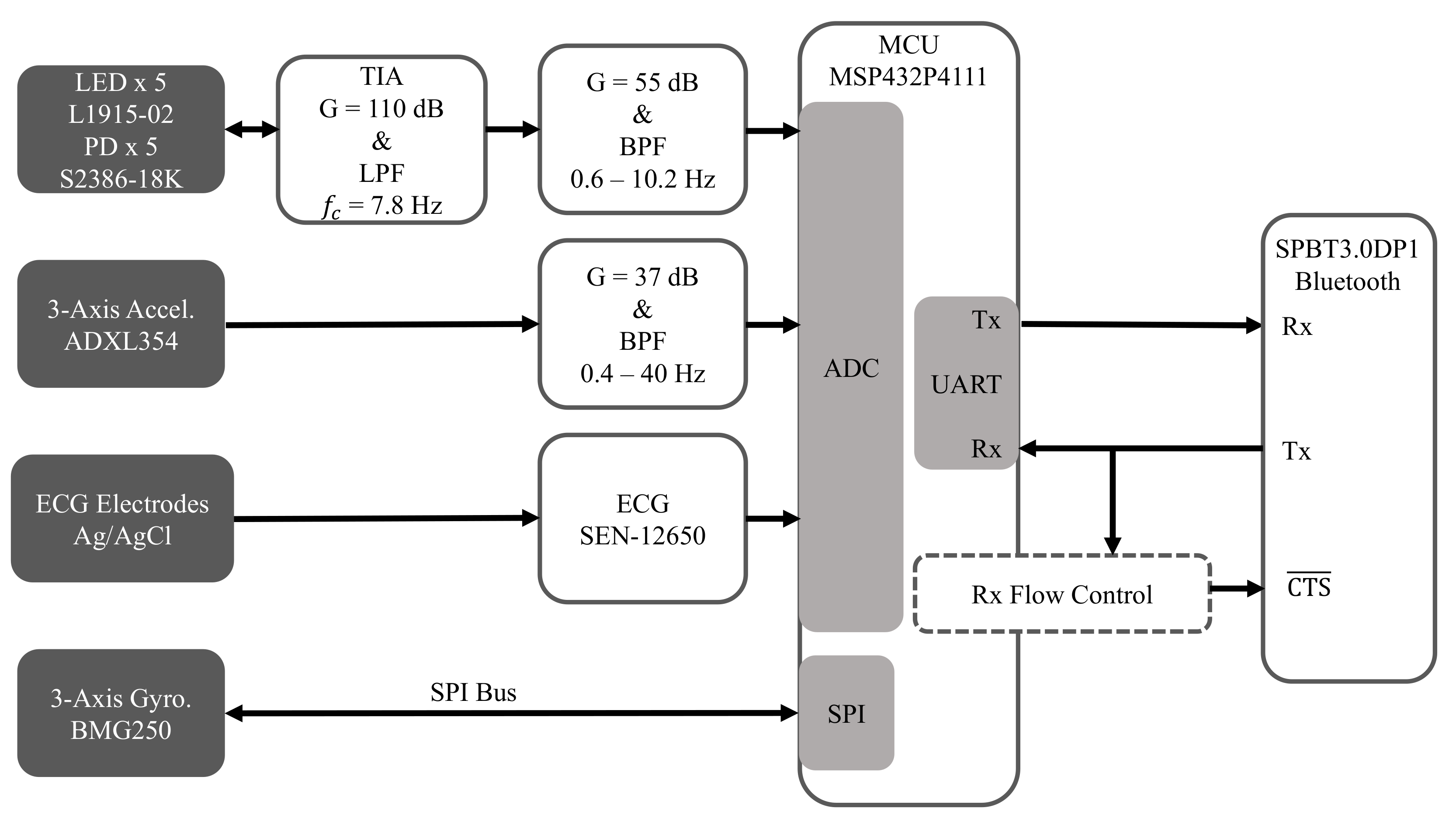
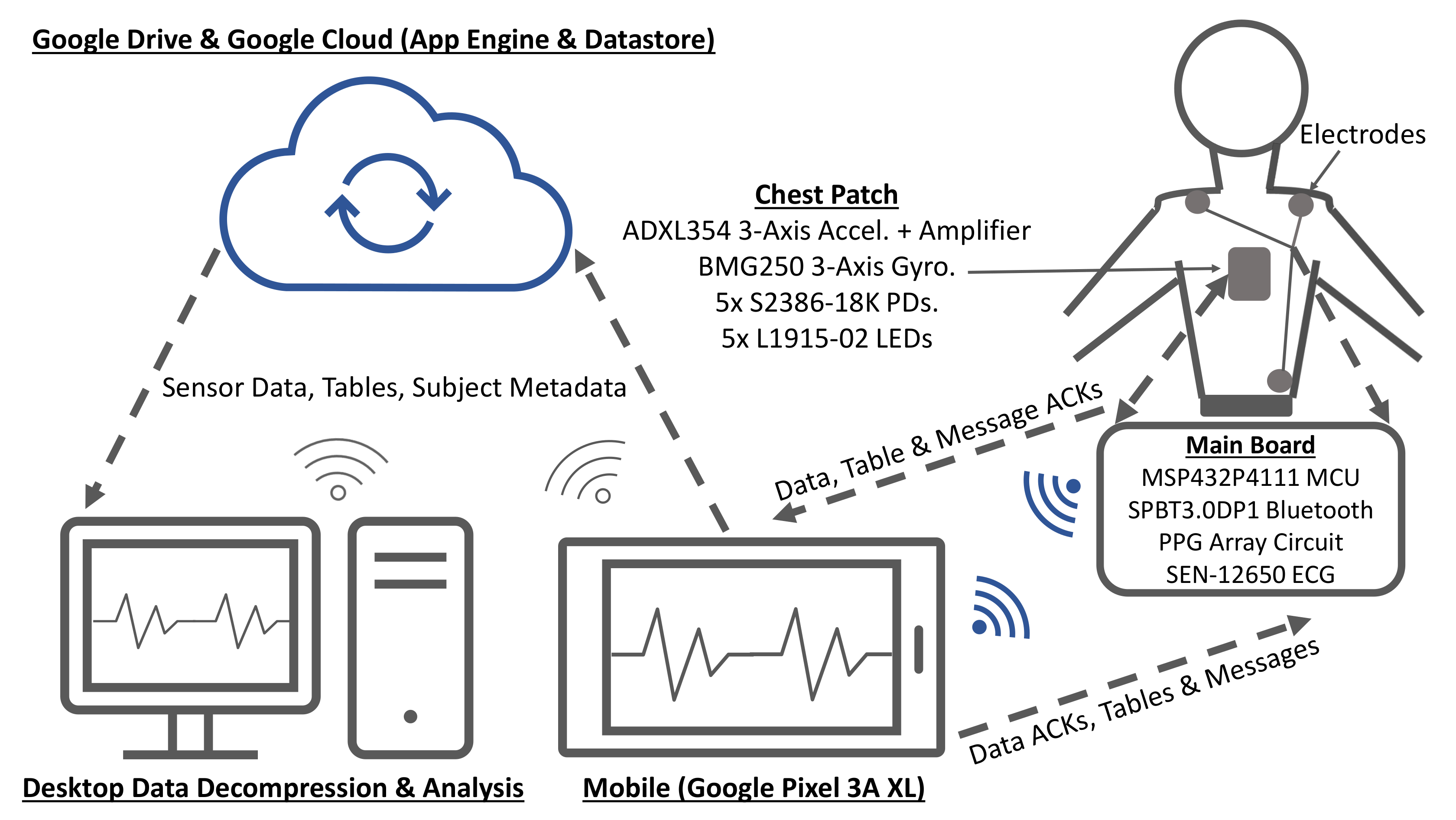
2.2. Hardware
2.2.1. Electrocardiogram (ECG)
2.2.2. Seismocardiogram (SCG)
2.2.3. Gyrocardiogram (GCG)
2.2.4. Reflectance Mode Photoplethysmogram (rPPG)
2.2.5. Microcontroller
2.2.6. Bluetooth Module
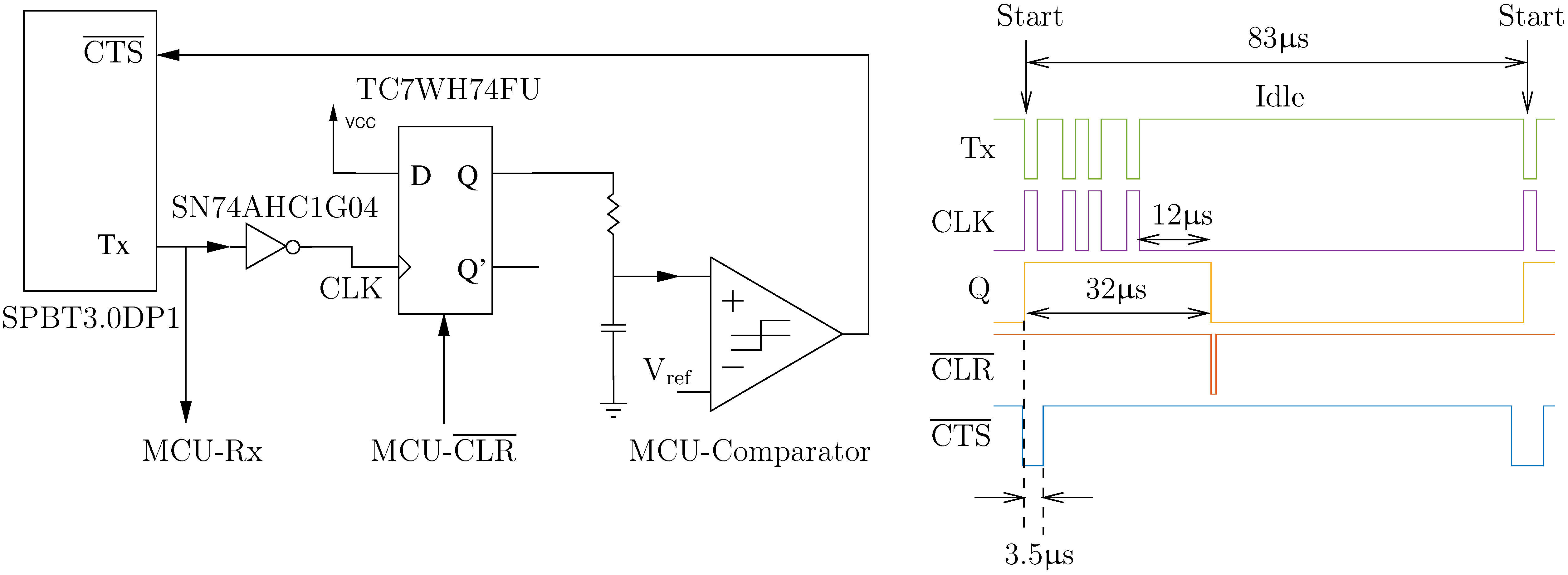
2.2.7. UART Flow Control
2.3. Software
2.4. Subject Demographics
2.5. Measurements
2.5.1. Data Acquisition at below the Theoretical Channel Capacity
2.5.2. Data Acquisition at above the Theoretical Channel Capacity
2.5.3. Experimental Protocol
2.6. Post-Processing
3. Results and Discussion
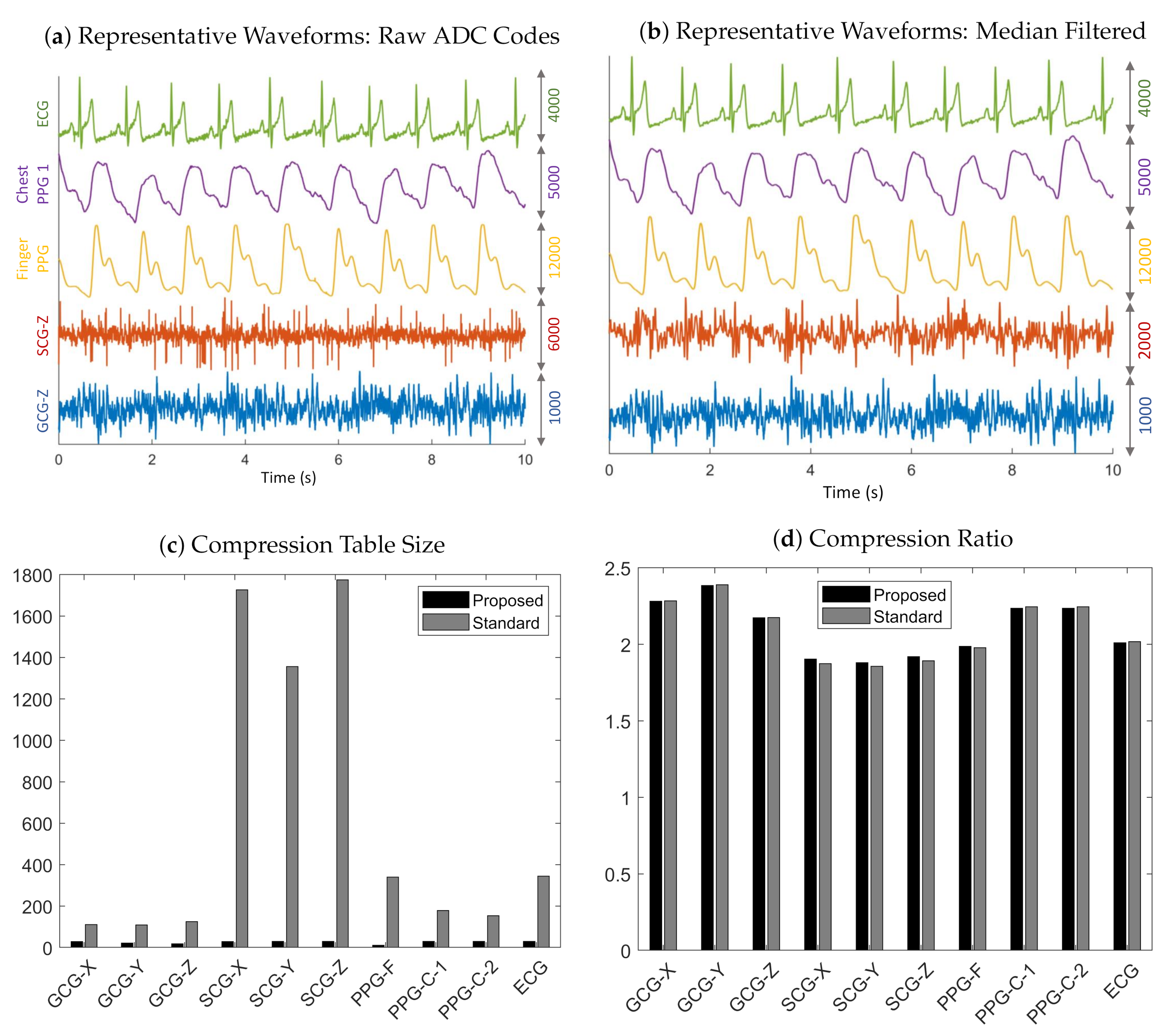
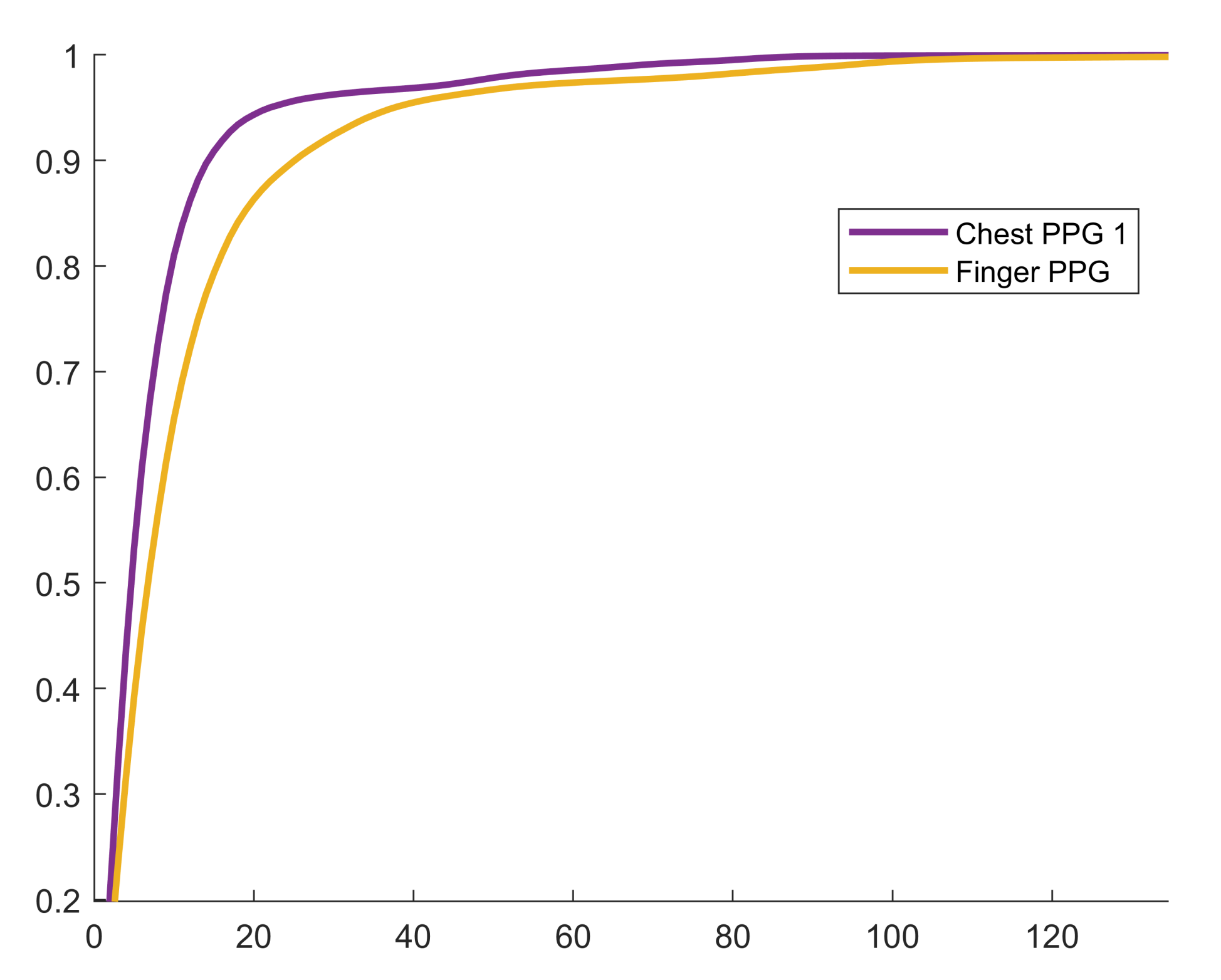
3.1. Compression
3.2. UART Flow Control
3.3. Limitations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Table Size Check
Appendix A.2. Alternative Proof for Proposition 1
Appendix A.3. Huffman Codes for ECG (Bin → Code (Counts))
References
- Affordable Technology: Blood Pressure Measuring Devices for Low Resource Settings; World Health Organization: Geneva, Switzerland, 2005; Available online: http://www.who.int/iris/handle/10665/43115 (accessed on 9 December 2020).
- Burt, V.L.; Whelton, P.; Roccella, E.J.; Brown, C.; Cutler, J.A.; Higgins, M.; Horan, M.J.; Labarthe, D. Prevalence of hypertension in the US adult population. Hypertension 1995, 25, 305–313. [Google Scholar] [CrossRef]
- Mukkamala, R.; Hahn, J.O.; Inan, O.T.; Mestha, L.K.; Kim, C.S.; Töreyin, H.; Kyal, S. Toward ubiquitous blood pressure monitoring via pulse transit time: Theory and practice. IEEE Trans. Biomed. Eng. 2015, 62, 1879–1901. [Google Scholar] [CrossRef]
- Gesche, H.; Grosskurth, D.; Küchler, G.; Patzak, A. Continuous blood pressure measurement by using the pulse transit time: Comparison to cuff-based method. Eur. J. Appl. Physiol. 2012, 112, 309–315. [Google Scholar] [CrossRef] [PubMed]
- Gholamhosseini, H.; Meintjes, A.; Baig, M.M.; Lindén, M. Smartphone-based Continuous Blood Pressure Measurement Using Pulse Transit Time. Stud. Health Technol. Inform. 2016, 224, 84–89. [Google Scholar] [PubMed]
- Carek, A.M.; Conant, J.; Joshi, A.; Kang, H.; Inan, O.T. SeismoWatch: Wearable Cuffless Blood Pressure Monitoring Using Pulse Transit Time. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2017, 1, 40. [Google Scholar] [CrossRef] [PubMed]
- Töreyin, H.; Javaid, A.Q.; Ashouri, H.; Ode, O.; Inan, O.T. Towards ubiquitous blood pressure monitoring in an armband using pulse transit time. In Proceedings of the 2015 IEEE Biomedical Circuits and Systems Conference (BioCAS), Atlanta, GA, USA, 22–24 October 2015; pp. 1–4. [Google Scholar]
- Zhang, G.; Gao, M.; Xu, D.; Olivier, N.B.; Mukkamala, R. Pulse arrival time is not an adequate surrogate for pulse transit time as a marker of blood pressure. J. Appl. Physiol. 2011, 111, 1681–1686. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Al-Ali, A.; Mohamed, A.; Ward, R. Improving Remote Health Monitoring: A Low-Complexity ECG Compression Approach. Diagnostics 2018, 8, 10. [Google Scholar] [CrossRef]
- Yildirim, O.; Tan, R.S.; Acharya, R. An efficient compression of ECG signals using deep convolutional autoencoders. Cogn. Syst. Res. 2018, 52, 198–211. [Google Scholar] [CrossRef]
- Said, A.B.; Mohamed, A.; Elfouly, T. Deep learning approach for EEG compression in mHealth system. In Proceedings of the 13th International Wireless Communications and Mobile Computing Conference, Valencia, Spain, 26–30 June 2017; pp. 1508–1512. [Google Scholar]
- Jalaleddine, S.M.S.; Hutchens, C.G.; Strattan, R.D.; Coberly, W.A. ECG data compression techniques-a unified approach. IEEE Trans. Biomed. Eng. 1990, 37, 329–343. [Google Scholar] [CrossRef]
- Craven, D.; McGinley, B.; Kilmartin, L.; Glavin, M.; Jones, E. Adaptive Dictionary Reconstruction for Compressed Sensing of ECG signals. IEEE J. Biomed. Health Inform. 2017, 21, 645–654. [Google Scholar] [CrossRef]
- Shaw, L.; Rahman, D.; Routray, A. Highly Efficient Compression Algorithms for Multichannel EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 957–968. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Kumar, A.; Pandey, R.K. Beta wavelet based ECG signal compression using lossless encoding with modified thresholding. Comput. Electr. Eng. 2013, 39, 130–140. [Google Scholar] [CrossRef]
- Duda, K.; Turcza, P.; Zielinski, T.P. Lossless ECG compression with lifting wavelet transform. In Proceedings of the 18th IEEE Instrumentation and Measurement Technology, Budapest, Hungary, 21–23 May 2001; pp. 640–644. [Google Scholar]
- Surekha, K.S.; Patil, B.P. Hybrid Compression Technique Using Linear Predictive Coding for Electrocardiogram Signals. Int. J. Eng. Technol. Sci. Res. 2017, 4, 497–500. [Google Scholar]
- Chua, E.; Fang, W. Mixed bio-signal lossless data compressor for portable brain-heart monitoring systems. IEEE Trans. Consum. Electron. 2011, 57, 267–273. [Google Scholar] [CrossRef]
- Hejrati, B.; Fathi, A.; Abdali-Mohammadi, F. Efficient lossless multi-channel EEG compression based on channel clustering. Biomed. Signal Process. Control 2017, 31, 295–300. [Google Scholar] [CrossRef]
- Huffman, D. A Method for the Construction of Minimum-Redundancy Codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Witten, I.H.; Neal, R.M.; Cleary, J.G. Arithmetic coding for data compression. Commun. ACM 1987, 30, 520–540. [Google Scholar] [CrossRef]
- Chang, G.C.; Lin, Y.D. An Efficient Lossless ECG Compression Method Using Delta Coding and Optimally Selective Huffman Coding. In Proceedings of the 6th World Congress of Biomechanics (WCB 2010), Singapore, 1–6 August 2010; IFMBE Proceedings. Lim, C.T., Goh, J.C.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Voume 31, pp. 1327–1330. [Google Scholar]
- Cover, M.C.; Thomas, J.A. Entropy, Relative Entropy, and Mutual Information. In Elements of Information Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991; p. 27. [Google Scholar]
- Scardulla, F.; D’Acquisto, L.; Colombarini, R.; Hu, S.; Pasta, S.; Bellavia, D. A Study on the Effect of Contact Pressure during Physical Activity on Photoplethysmographic Heart Rate Measurements. Sensors 2020, 20, 5052. [Google Scholar] [CrossRef]
- Shaltis, P.; Reisner, A.; Asada, H. Calibration of the Photoplethysmogram to Arterial Blood Pressure: Capabilities and Limitations for Continuous Pressure Monitoring. In Proceedings of the IEEE EMBC 27th Annual Conference, Shanghai, China, 17–18 January 2006; pp. 3970–3973. [Google Scholar]
- Tamura, T.; Maeda, Y.; Sekine, M.; Yoshida, M. Wearable Photoplethsysmographic Sensors—Past and Present. Electronics 2014, 3, 282–302. [Google Scholar] [CrossRef]
- Pigeon, S. Huffman Coding. In Lossless Compression Handbook; Academic Press: New York, NY, USA, 2003; pp. 1–33. [Google Scholar]
- Pahlm, O.; Börjesson, P.O.; Werner, O. Compact digital storage of ECGs. Comput. Programs Biomed. 1979, 9, 293–300. [Google Scholar] [CrossRef]
- Tsai, T.; Kuo, W. An Efficient ECG Lossless Compression System for Embedded Platforms With Telemedicine Applications. IEEE Access 2018, 6, 42207–42215. [Google Scholar] [CrossRef]
- Rai, Y.; Le Callet, P. Visual attention, visual salience, and perceived interest in multimedia applications. In Academic Press Library in Signal Processing; Elsevier: Amsterdam, The Netherlands, 2018; pp. 113–161. [Google Scholar]
- Sutherland, A. Elliptic Curves. In Massachusetts Institute of Technology: MIT OpenCourseWare; License: Creative Commons BY-NC-SA; Spring: Berlin/Heidelberg, Germany, 2019; Available online: https://math.mit.edu/classes/18.783/2017/LectureNotes3.pdf (accessed on 9 December 2020).
- ISO/IEC. ISO International Standard ISO/IEC 14882:2014-Programming Language C++ [Working Draft]; International Organization for Standardization (ISO): Geneva, Switzerland, 2014. [Google Scholar]
- Inan, O.T.; Migeotte, P.F.; Park, K.S.; Etemadi, M.; Tavakolian, K.; Casanella, R.; Zanetti, J.; Tank, J.; Funtova, I.; Prisk, G.K.; et al. Ballistocardiography and Seismocardiography: A Review of Recent Advances. IEEE J. Biomed. Health Inform. 2015, 19, 1414–1427. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, K.; Verma, A.K.; Blaber, A.; Zanetti, J.; Schmidt, S.E.; Struijk, J.J.; Tavakolian, K. Challenges in using seismocardiography for blood pressure monitoring. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar]
- Di Rienzo, M.; Meriggi, P.; Rizzo, F.; Vaini, E.; Faini, A.; Merati, G.; Parati, G.; Castiglioni, P. A wearable system for the seismocardiogram assessment in daily life conditions. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 4263–4266. [Google Scholar]
- Zanetti, J.; Salerno, D. Seismocardiography: A technique for recording precordial acceleration. In Proceedings of the Fourth Annual IEEE Symposium Computer-Based Medical Systems, Baltimore, MD, USA,, 12–14 May 1991; IEEE Computer Society: Los Alamitos, CA, USA, 1991; pp. 4–9. [Google Scholar]
- Tadi, M.J.; Lehtonen, E.; Saraste, A.; Tuominen, J.; Koskinen, J.; Teräs, M.; Airaksinen, J.; Pänkäälä, M.; Koivisto, T. Gyrocardiography: A New Non-invasive Monitoring Method for the Assessment of Cardiac Mechanics and the Estimation of Hemodynamic Variables. Sci. Rep. 2017, 7, 6823. [Google Scholar] [CrossRef] [PubMed]
- Dehkordi, P.; Tavakolian, K.; Tadi, M.J.; Zakeri, V. Khosrow-khavar, F. Investigating the estimation of cardiac time intervals using gyrocardiography. Physiol. Meas. 2020, 41. [Google Scholar] [CrossRef]
- Yang, C.; Tavassolian, N. Combined Seismo- and Gyro-Cardiography: A more Comprehensive Evaluation of Heart-Induced Chest Vibrations. IEEE J. Biomed. Health Inform. 2018, 22, 1466–1475. [Google Scholar] [CrossRef]
- Inan, O.T.; Baran Pouyan, M.; Javaid, A.Q.; Dowling, S.; Etemadi, M.; Dorier, A.; Heller, J.A.; Bicen, A.O.; Roy, S.; De Marco, T.; et al. Novel Wearable Seismocardiography and Machine Learning Algorithms Can Access Clinical Status of Heart Failure Patients. Circ. Heart Failure 2018, 11, e004313. [Google Scholar] [CrossRef]
- Shandhi, M.M.H.; Hersek, S.; Fan, J.; Sander, E.; De Marco, T.; Heller, J.A.; Etemadi, M.; Klein, L.; Inan, O.T. Wearable Patch-Based Estimation of Oxygen Uptake and Assessment of Clinical Status during Cardiopulmonary Exercise Testing in Patients With Heart Failure: Wearable Monitoring of Cardiovascular Health in Heart Failure Patients. J. Card. Fail. 2020, 26, 948–958. [Google Scholar] [CrossRef]


| 1600 Hz | 3200 Hz | |||
|---|---|---|---|---|
| Sensor | Proposed | Standard | Proposed | Standard |
| GCG-X | ||||
| GCG-Y | ||||
| GCG-Z | ||||
| SCG-X | ||||
| SCG-Y | ||||
| SCG-Z | ||||
| PPG-F | ||||
| PPG-C-1 | ||||
| PPG-C-2 | ||||
| ECG | ||||
| 1600 Hz | 3200 Hz | |||
|---|---|---|---|---|
| Sensor | Proposed | Standard | Proposed | Standard |
| GCG-X | ||||
| GCG-Y | ||||
| GCG-Z | ||||
| SCG-X | ||||
| SCG-Y | ||||
| SCG-Z | ||||
| PPG-F | ||||
| PPG-C-1 | ||||
| PPG-C-2 | ||||
| ECG | ||||
| 1600 Hz | 3200 Hz | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sensor | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
| GCG-X | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| GCG-Y | 2 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 2 |
| GCG-Z | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 |
| SCG-X | 2 | 2 | 0 | 2 | 1 | 2 | 2 | 0 | 1 | 0 |
| SCG-Y | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 0 | 1 | 0 |
| SCG-Z | 2 | 2 | 1 | 2 | 1 | 2 | 2 | 1 | 1 | 1 |
| PPG-F | 2 | 2 | 3 | 2 | 2 | 1 | 1 | 3 | 3 | 3 |
| PPG-C-1 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| PPG-C-2 | 2 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| ECG | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ode, O.; Orlandic, L.; Inan, O.T. Towards Continuous and Ambulatory Blood Pressure Monitoring: Methods for Efficient Data Acquisition for Pulse Transit Time Estimation. Sensors 2020, 20, 7106. https://doi.org/10.3390/s20247106
Ode O, Orlandic L, Inan OT. Towards Continuous and Ambulatory Blood Pressure Monitoring: Methods for Efficient Data Acquisition for Pulse Transit Time Estimation. Sensors. 2020; 20(24):7106. https://doi.org/10.3390/s20247106
Chicago/Turabian StyleOde, Oludotun, Lara Orlandic, and Omer T. Inan. 2020. "Towards Continuous and Ambulatory Blood Pressure Monitoring: Methods for Efficient Data Acquisition for Pulse Transit Time Estimation" Sensors 20, no. 24: 7106. https://doi.org/10.3390/s20247106
APA StyleOde, O., Orlandic, L., & Inan, O. T. (2020). Towards Continuous and Ambulatory Blood Pressure Monitoring: Methods for Efficient Data Acquisition for Pulse Transit Time Estimation. Sensors, 20(24), 7106. https://doi.org/10.3390/s20247106





