Epistemic Network Analyses of Economics Students’ Graph Understanding: An Eye-Tracking Study
Abstract
1. Introduction
2. Conceptual and Methodological Background
2.1. Response Processes of Solving Graph Tasks
2.2. Eye-Tracking Research on Students’ Difficulties in Graph Understanding
2.3. Transitions between AOIs as a Predictor of the Quality of Graph Understanding
2.4. Research Questions
3. Method
3.1. Background Information
3.2. Commonalities
3.2.1. Tasks
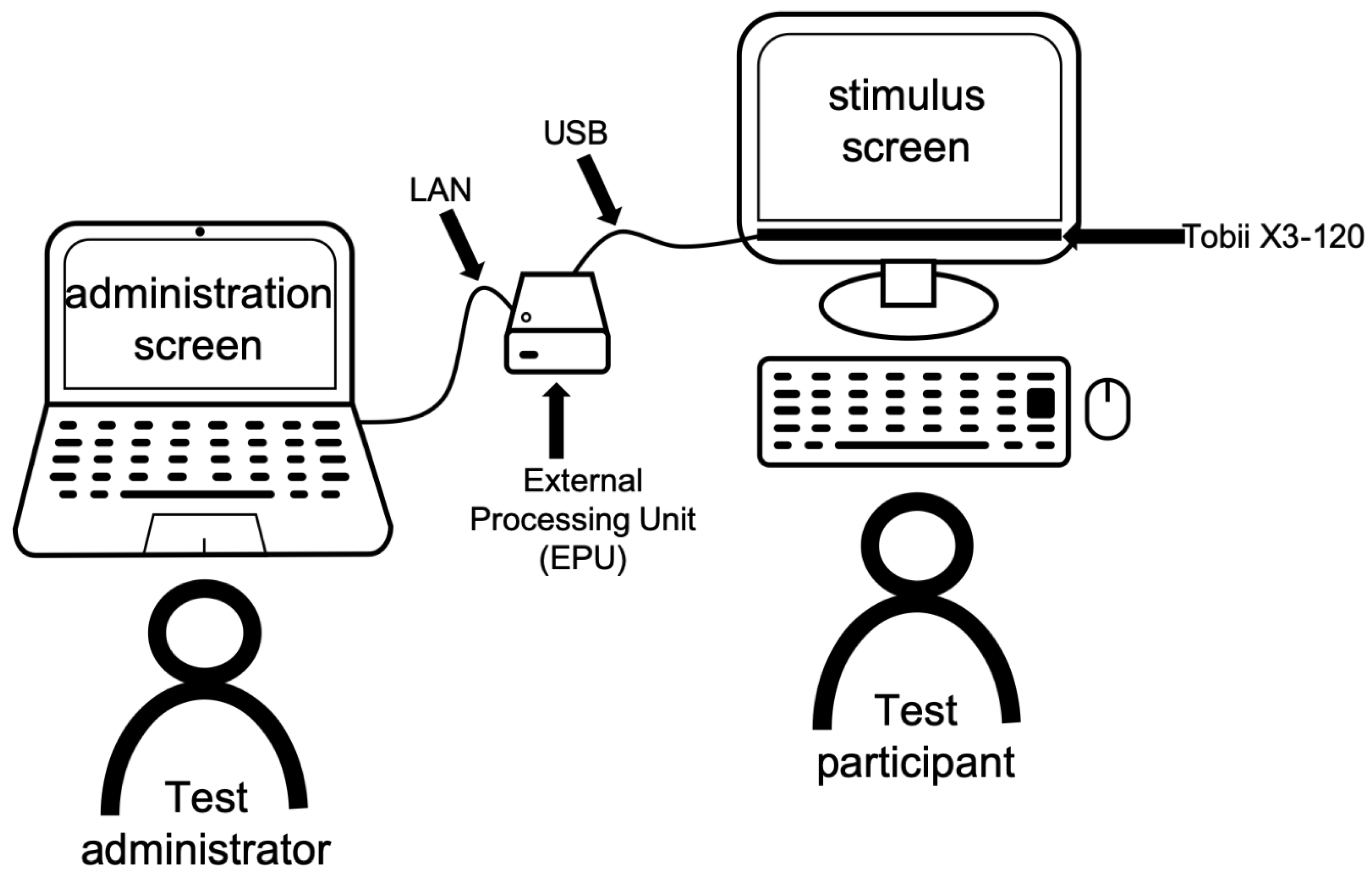
3.2.2. Procedure and Apparatus
3.3. Differences and Extensions
3.4. Participants
3.5. AOIs
- AOI_Question represents the area of the screen where the task question was displayed.
- AOI_yaxislab represents the area of the screen where the label for the y-axis was displayed.
- AOI_xaxislab represents the area of the screen where the x-axis label was displayed.
- AOI_graph represents the area of the screen where the graph was displayed.
- AOI_Attractor represents the area of the screen where the correct answer (attractor) was displayed.
- AOI_yaxis represents the area of the screen where the y-axis was displayed.
- AOI_xaxis represents the area of the screen where the x-axis was displayed.
- AOI_Distractor represents the areas of the screen where the incorrect answers (distractors) were displayed.
3.6. Data and Analysis
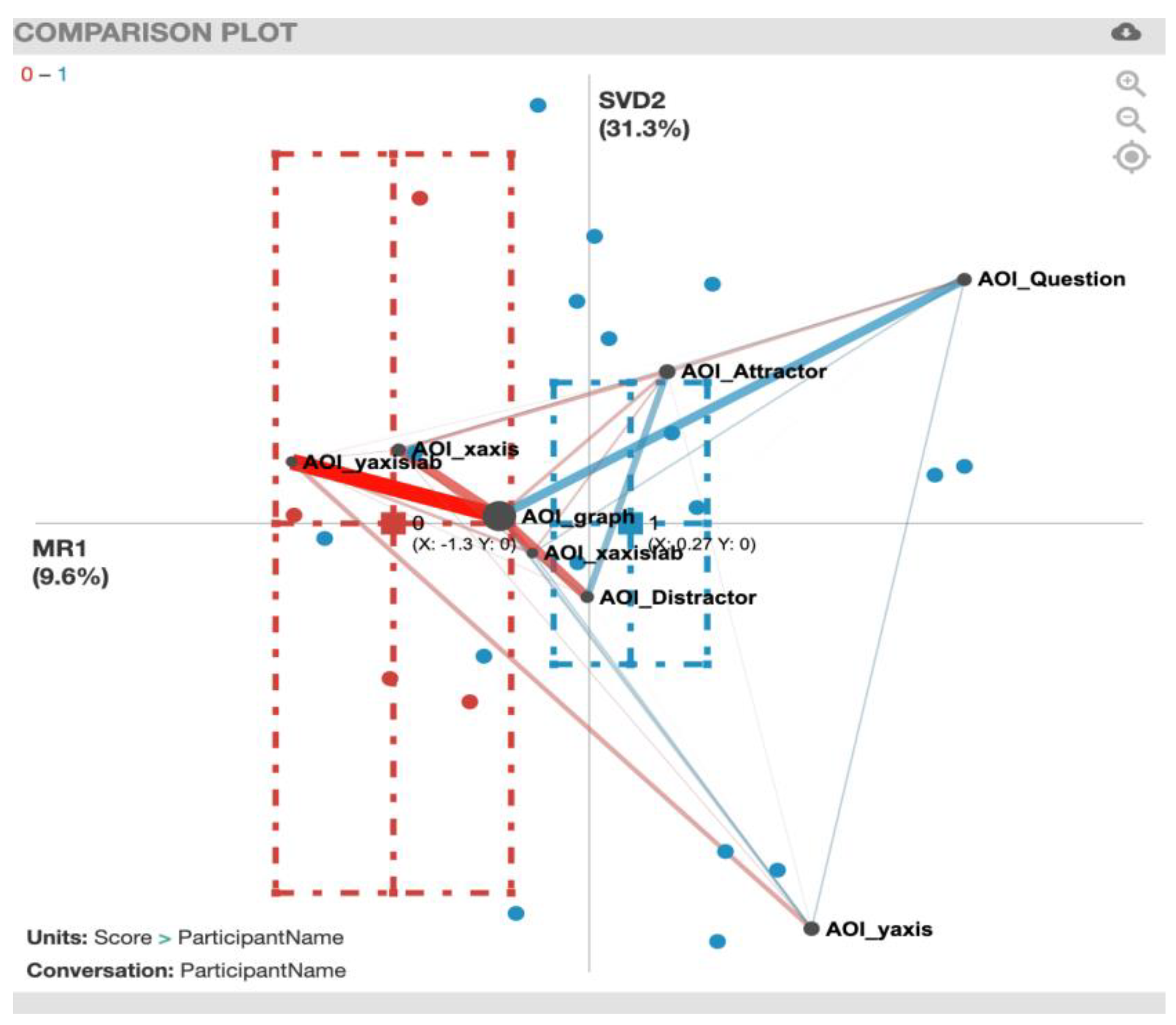
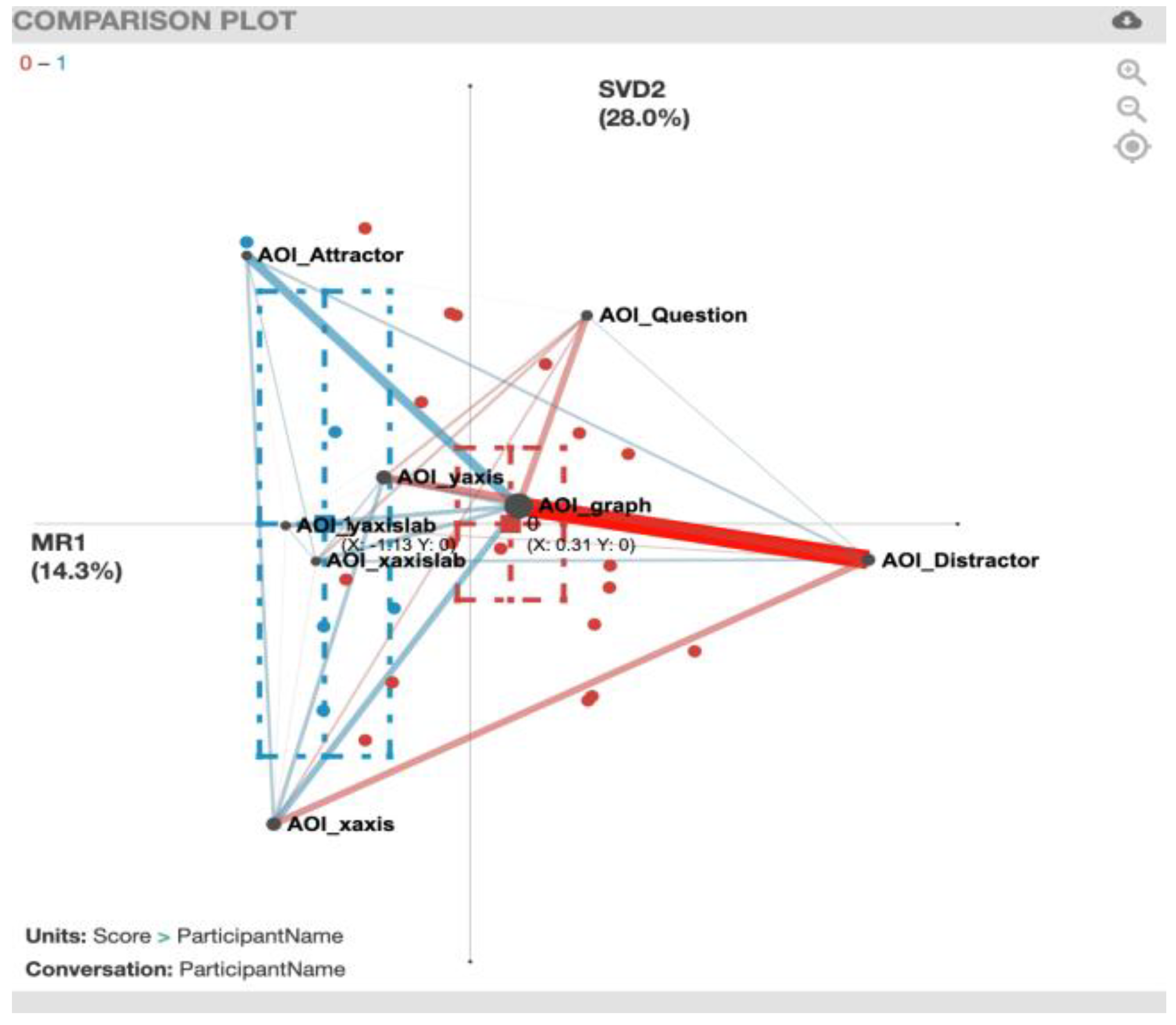
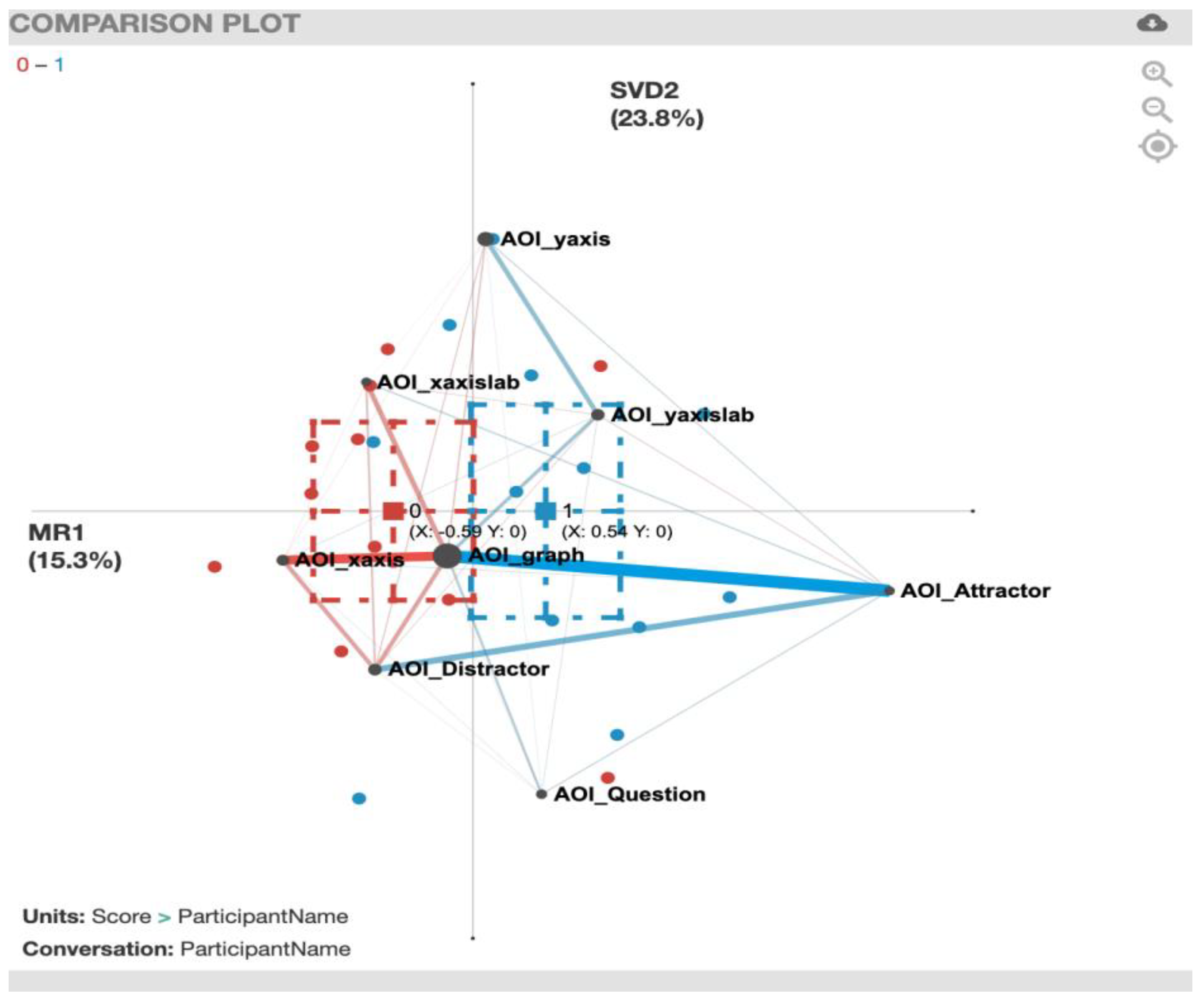
3.7. Epistemic Network Analysis (ENA)
4. Results
4.1. Comparison of Fixation Frequencies between Correct and Incorrect Solvers
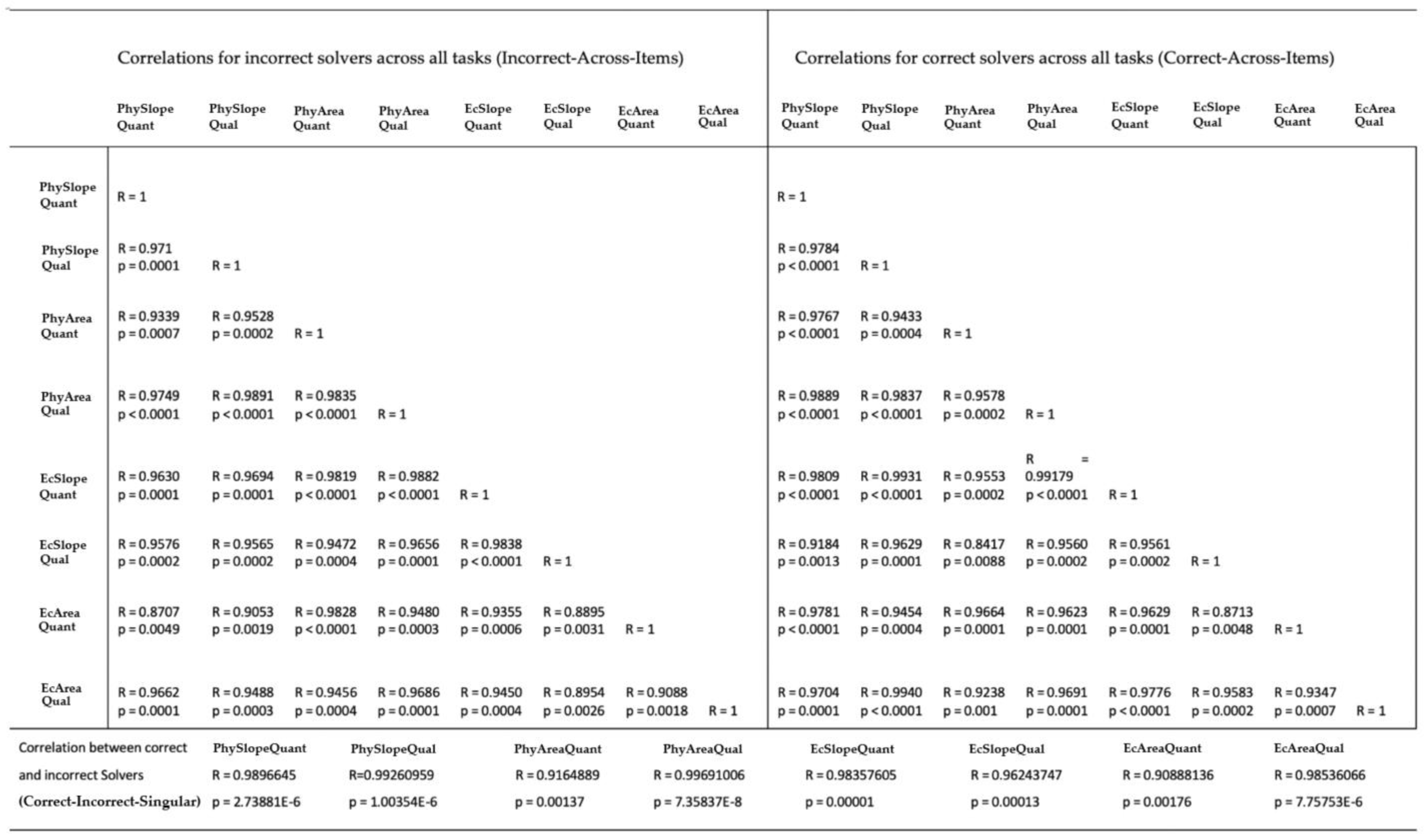
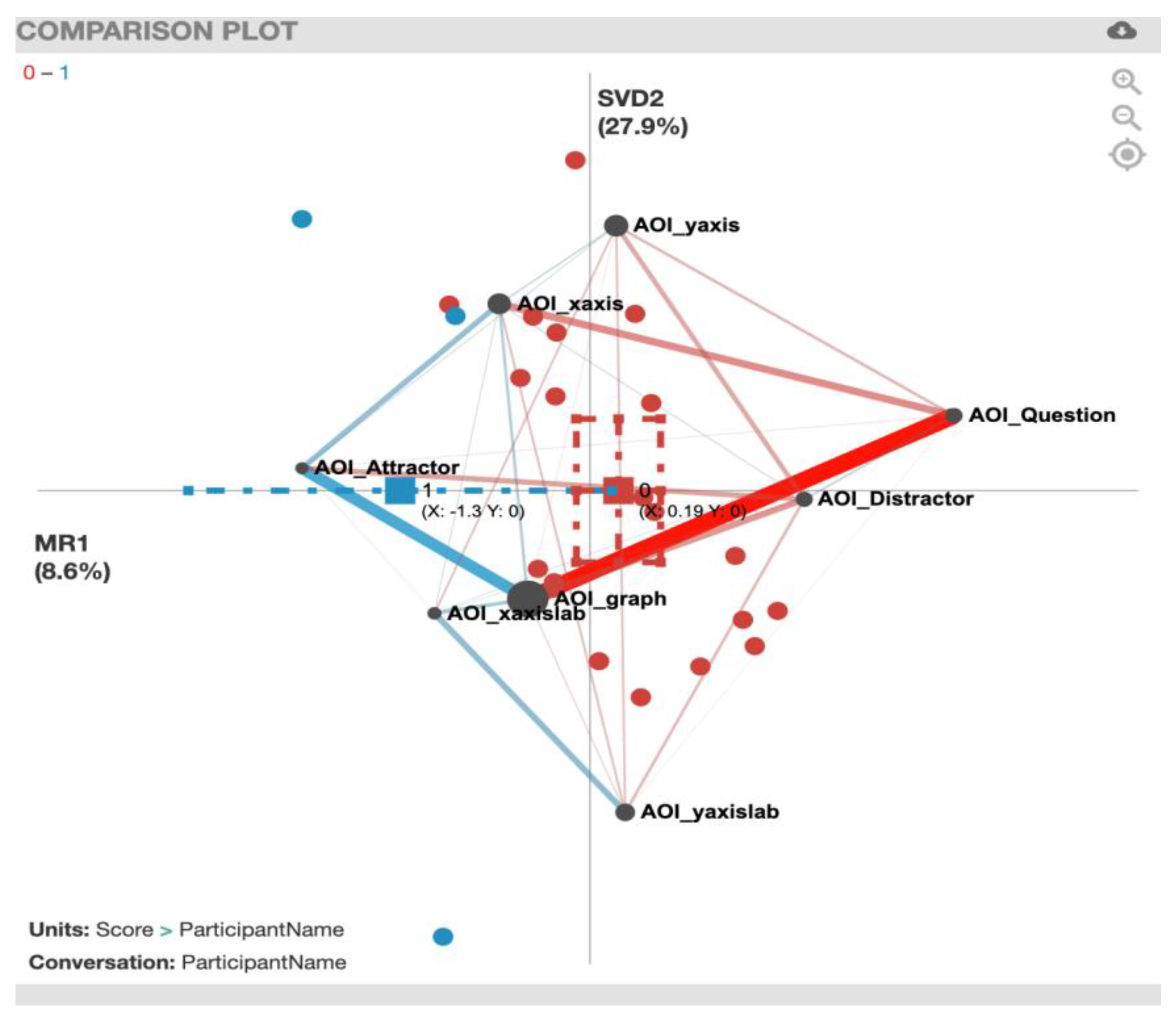
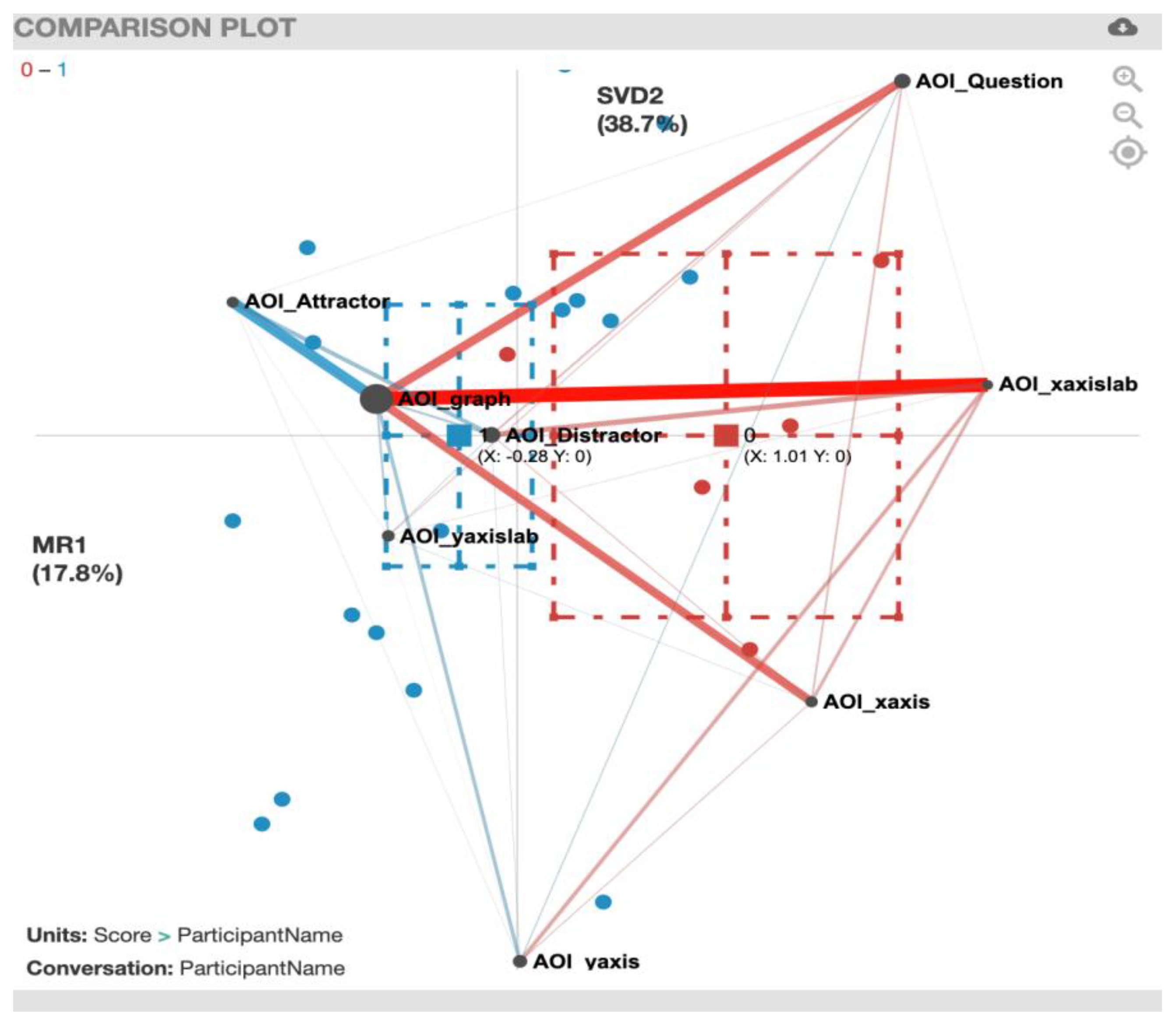
4.2. Gaze Transition Comparison between Correct and Incorrect Responses
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| AOI | ECAreaQual | PhyAreaQual | EcAreaQuant | PhyAreaQuant | EcSlopeQual | PhylopeQual | EcSlopeQuant | PhySlopeQuant | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| incorrect | correct | incorrect | correct | incorrect | correct | incorrect | correct | incorrect | correct | incorrect | correct | incorrect | correct | incorrect | correct | |
| AOI_Question | 30.4% | 25.5% | 23.5% | 21.6% | 36.2% | 19.9% | 28.9% | 13.5% | 21.8% | 30.2% | 20.4% | 24.2% | 25.3% | 24.1% | 15.6% | 18.4% |
| t(21) = 1.05; p = 0.3 | t(21) = 0.65; p = 0.52 | t(21) = 2.22; p = 0.04 | t(21) = 1.86; p = 0.04 | t(21) = −1.6; p = 0.13 | t(21) = −0.7; p = 0.49 | t(21) = 0.18; p = 0.86 | t(21) = 0.61; p = 0.55 | |||||||||
| AOI_yaxislab | 6.8% | 7.7% | 5.7% | 5.5% | 11.7% | 7.6% | 6.8% | 9.3% | 2.6% | 2.1% | 3.9% | 2.8% | 3.4% | 2.9% | 6.9% | 8.0% |
| t(21) = −0.7; p = 0.49 | t(21) = 0.32; p = 0.75 | t(21) = 1.24; p = 0.23 | t(21) = −0.87; p = 0.23 | t(21) = 0.69; p = 0.55 | t(21) = 0.48; p = 0.63 | t(21) = 0.49; p = 0.63 | t(21) = 0.55; p = 0.59 | |||||||||
| AOI_xaxislab | 1.5% | 1.7% | 2.4% | 1.7% | 1.0% | 0.6% | 1.7% | 4.1% | 2.4% | 0.6% | 2.0% | 1.1% | 2.6% | 2.8% | 4.1% | 2.2% |
| t(21) = 0.39; p = 0.7 | t(21) = 1.36; p = 0.19 | t(21) = 0.66; p = 0.52 | t(21) = −1.58; p = 0.52 | t(21) = 3.82; p < 0.01 | t(21) = 1.29; p = 0.21 | t(21) = 0.31; p = 0.76 | t(21) = 1.42; p = 0.17 | |||||||||
| AOI_graph | 50.3% | 53.9% | 54.9% | 53.7% | 52.5% | 64.0% | 50.8% | 64.8% | 49.6% | 46.1% | 57.4% | 56.5% | 51.5% | 55.6% | 62.5% | 59.7% |
| t(21) = −0.64; p = 0.52 | t(21) = 0.38; p = 0.7 | t(21) = −1.65; p = 0.11 | t(21) = −1.67; p = 0.11 | t(21) = 0.50; p = 0.62 | t(21) = 0.14; p = 0.89 | t(21) = −0.58; p = 0.56 | t(21) = 0.56; p = 0.58 | |||||||||
| AOI_Attractor | 8.3% | 11.9% | 5.4% | 5.1% | 1.5% | 3.7% | 1.9% | 5.8% | 1.5% | 6.7% | 10.2% | 8.2% | 3.6% | 7.5% | 2.8% | 6.6% |
| t(21) = −2.04; p = 0.05 | t(21) = 0.4; p = 0.69 | t(21) = −2.6; p = 0.02 | t(21) = −3.4; p = 0.03 | t(21) = −2.53; p = 0.02 | t(21) = 0.87; p = 0.39 | t(21) = −2.3; p = 0.03 | t(21) = −3.7; p < 0.01 | |||||||||
| AOI_yaxis | 5.9% | 6.6% | 8.9% | 7.8% | 10.4% | 20.1% | 9.2% | 9.5% | 2.7% | 3.4% | 5.3% | 4.2% | 9.6% | 8.8% | 9.9% | 10.0% |
| t(21) = 0.27; p = 0.79 | t(21) = 0.88; p = 0.39 | t(21) = −2.7; p = 0.01 | t(21) = −0.101; p = 0.9 | t(21) = −0.35; p = 0.73 | t(21) = 0.66; p = 0.52 | t(21) = −0.34; p = 0.7 | t(21) = −0.05; p = 0.96 | |||||||||
| AOI_xaxis | 2.9% | 1.5% | 5.3% | 6.7% | 6.2% | 7.4% | 8.3% | 12.5% | 3.1% | 1.8% | 4.9% | 2.4% | 7.1% | 7.9% | 6.1% | 4.0% |
| t(21) = 2.01; p = 0.049 | t(21) = −1.44; p = 0.17 | t(21) = −0.80; p = 0.43 | t(21) = −1.73; p = 0.09 | t(21) = 1.57; p = 0.13 | t(21) = 2.36; p = 0.03 | t(21) = −0.32; p = 0.8 | t(21) = 1.72; p = 0.09 | |||||||||
| AOI_Distractor | 8.8% | 5.2% | 9.0% | 11.7% | 3.2% | 5.6% | 7.6% | 5.2% | 17.5% | 12.0% | 3.0% | 4.2% | 14.2% | 7.7% | 13.8% | 9.2% |
| t(21) = 1.75; p = 0.09 | t(21) = 2.19; p = 0.04 | t(21) = −1.47; p = 0.16 | t(21) = 0.94; p = 0.36 | t(21) = 2.74; p = 0.01 | t(21) = 2.42; p = 0.03 | t(21) = 2.6; p = 0.02 | t(21) = 2.5; p = 0.019 | |||||||||
References
- Klein, P.; Küchemann, S.; Brückner, S.; Zlatkin-Troitschanskaia, O.; Kuhn, J. Student understanding of graph slope and area under a curve: A replication study comparing first-year physics and economics students. Phys. Rev. Phys. Educ. Res. 2019, 15, 1–17. [Google Scholar] [CrossRef]
- Ring, M.; Brahm, T.; Randler, C. Do difficulty levels matter for graphical literacy? A performance assessment study with authentic graphs. Int. J. Sci. Educ. 2019, 41, 1787–1804. [Google Scholar] [CrossRef]
- Susac, A.; Bubic, A.; Kazotti, E.; Planinic, M.; Palmovic, M. Student understanding of graph slope and area under a graph: A comparison of physics and nonphysics students. Phys. Rev. Phys. Educ. Res. 2018, 14, 20109. [Google Scholar] [CrossRef]
- Curcio, F.R. Comprehension of Mathematical Relationships Expressed in Graphs. J. Res. Math. Edu. 1987, 18, 382. [Google Scholar] [CrossRef]
- Freedman, E.G.; Shah, P. Toward a Model of Knowledge-Based Graph Comprehension. In Proceedings of the International Conference on Theory and Application of Diagrams, Callaway Gardens, GA, USA, 18–20 April 2002; Hegarty, M., Meyer, B., Narayanan, N.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Pinker, S. A theory of graph comprehension. In Artificial Intelligence and the Future of Testing; Routledge: London, UK, 1990; pp. 73–126. [Google Scholar]
- Strobel, B.; Lindner, M.A.; Saß, S.; Köller, O. Task-irrelevant data impair processing of graph reading tasks: An eye tracking study. Learn. Instr. 2018, 55, 139–147. [Google Scholar] [CrossRef]
- Beichner, R.J. Testing student interpretation of kinematics graphs. Am. J. Phys. 1994, 62, 750–762. [Google Scholar] [CrossRef]
- Benedict, M.E.; Hoag, J. Factors influencing performance in Economics: Graphs and quantitative useage. In International Handbook on Teaching and Learning in Economics; Hoyt, G.M., McGoldrick, K., Eds.; Edward Elgar: Cheltenham, UK, 2012; pp. 334–340. [Google Scholar]
- Bowen, G.M.; Roth, W.M. Lecturing graphing: What features of lectures contribute to student difficulties in learning to interpret graph? Res. Sci. Educ. 1998, 28, 77–90. [Google Scholar] [CrossRef]
- Stern, E.; Aprea, C.; Ebner, H.G. Improving cross-content transfer in text processing by means of active graphical representation. Learn. Instr. 2003, 13, 191–203. [Google Scholar] [CrossRef]
- Madsen, A.M.; Larson, A.M.; Loschky, L.C.; Rebello, N.S. Differences in visual attention between those who correctly and incorrectly answer physics problems. Phys. Rev. Phys. Educ. Res. 2012, 8, 10122. [Google Scholar] [CrossRef]
- McDermott, L.C.; Rosenquist, M.L.; van Zee, E.H. Student difficulties in connecting graphs and physics: Examples from kinematics. Am. J. Phys. 1987, 55, 503–513. [Google Scholar] [CrossRef]
- Planinic, M.; Ivanjek, L.; Susac, A.; Milin-Sipus, Z. Comparison of university students’ understanding of graphs in different contexts. Phys. Rev. Spec. Top. Phys. Educ. Res. 2013, 9, 020103. [Google Scholar] [CrossRef]
- Wemyss, T.; van Kampen, P. Categorization of first-year university students’ interpretations of numerical linear distance-time graphs. Phys. Rev. Spec. Top. Phys. Educ. Res. 2013, 9, 34. [Google Scholar] [CrossRef]
- Cohn, E.; Cohn, S.; Balch, D.C.; Bradley, J. Do graphs promote learning in principles of economics? J. Econ. Educ. 2001, 32, 299–310. [Google Scholar] [CrossRef]
- Jensen, U. Wozu Mathe in den Wirtschaftswissenschaften? Eine Einführung für Studienanfänger; Springer: Wiesbaden, Germany, 2011. [Google Scholar]
- Vöttiner, A.; Woisch, A. Studienqualitätsmonitor 2010. Available online: https://www.dzhw.eu/forschung/governance/sqm/berichte/sqm_2010 (accessed on 30 November 2020).
- Hill, C.D.; Stegner, T. Which Students Benefit from Graphs in a Principles of Economics Class? Am. Econ. 2003, 47, 69–77. [Google Scholar] [CrossRef]
- Brückner, S.; Zlatkin-Troitschanskaia, O.; Küchemann, S.; Klein, P.; Kuhn, J. Changes in Students’ Understanding of and Visual Attention on Digitally Represented Graphs across Two Domains in Higher Education: A Postreplication Study. Front. Psychol. 2020, 11, 2090. [Google Scholar] [CrossRef]
- Bergey, B.W.; Cromley, J.G.; Newcombe, N.S. Teaching high school biology students to coordinate text and diagrams: Relations with transfer, effort, and spatial skill. Int. J. Sci. Educ. 2015, 37, 2476–2502. [Google Scholar] [CrossRef]
- Kekule, M. Students’ Approaches When Dealing with Kinematics Graphs Explored by Eye-Tracking Research Method. Available online: http://scimath.net/fiser2014/presentations/Martina%20Kekule.pdf (accessed on 30 November 2020).
- Tsai, M.-J.; Hou, H.-T.; Lai, M.-L.; Liu, W.-Y.; Yang, F.-Y. Visual attention for solving multiple-choice science problem: An eye-tracking analysis. Comput. Educ. 2012, 58, 375–385. [Google Scholar] [CrossRef]
- Shaffer, D.W. Quantitative Ethnography; Cathcart Press: Madison, WI, USA, 2017. [Google Scholar]
- Shaffer, D.W.; Collier, W.; Ruis, A.R. A tutorial on epistemic network analysis: Analyzing the structure of connections in cognitive, social, and interaction data. J. Learn. Anal. 2016, 3, 9–45. [Google Scholar] [CrossRef]
- Shaffer, D.W.; Ruis, A.R. Epistemic Network Analysis: A Worked Example of Theory-Based Learning Analytics. Available online: https://par.nsf.gov/servlets/purl/10060304 (accessed on 30 November 2020).
- Friel, S.N.; Curcio, F.R.; Bright, G.W. Making sense of graphs: Critical factors influencing comprehension and instructional implications. J. Res. Math. Educ. 2001, 32, 124–158. [Google Scholar] [CrossRef]
- Schnotz, W.; Baadte, C. Surface and deep structures in graphics comprehension. Mem. Cognit. 2015, 43, 605–618. [Google Scholar]
- Schüler, A. Investigating gaze behavior during processing of inconsistent text-picture information: Evidence for text-picture integration. Learn. Instr. 2017, 49, 218–231. [Google Scholar] [CrossRef]
- Ainsworth, S. DeFT: A conceptual framework for considering learning with multiple representations. Learn. Instr. 2006, 16, 183–198. [Google Scholar] [CrossRef]
- Carpenter, P.A.; Shah, P. A Model of the Perceptual and Conceptual Processes in Graph Comprehension. J. Exp. Psychol. Gen. 1998, 4, 75–100. [Google Scholar] [CrossRef]
- Schnotz, W.; Bannert, M. Construction and interference in learning from multiple representation. Learn. Instr. 2003, 13, 141–156. [Google Scholar] [CrossRef]
- Leinhardt, G.; Zaslavsky, O.; Stein, M.K. Functions, Graphs, and Graphing: Tasks, Learning, and Teaching. Rev. Educ. Res. 1990, 60, 1–64. [Google Scholar] [CrossRef]
- Holmqvist, K.; Nyström, M.; Andersson, R.; Dewhurst, R.; Jarodzka, H.; van de Weijer, J. Eye Tracking: A Comprehensive Guide to Methods and Measures, 1st ed.; Oxford University Press: Oxford, UK; New York, NY, USA; Auckland, New Zealand, 2011. [Google Scholar]
- Orquin, J.; Loose, S. Attention and Choice: A Review on Eye Movements in Decision Making. Acta Psychol. 2013, 144, 190–206. [Google Scholar] [CrossRef] [PubMed]
- Raney, G.E.; Campbell, S.J.; Bovee, J.C. Using eye movements to evaluate the cognitive processes involved in text comprehension. J. Vis. Exp. 2014, 83, 1–7. [Google Scholar] [CrossRef]
- Schwonke, R.; Berthold, K.; Renkl, A. How multiple external representations are used and how they can be made more useful. Appl. Cogn. Psychol. 2009, 23, 1227–1243. [Google Scholar] [CrossRef]
- Klein, P.; Kuhn, J.; Müller, A. Förderung von Repräsentationskompetenz und Experimentbezug in den vorlesungsbegleitenden Übungen zur Experimentalphysik. Zeitschrift für Didaktik der Naturwissenschaften 2018, 24, 17–34. [Google Scholar] [CrossRef]
- Mason, L.; Pluchino, P.; Tornatora, M.C.; Ariasi, N. An Eye-Tracking Study of Learning From Science Text With Concrete and Abstract Illustrations. J. Exp. Educ. 2013, 81, 356–384. [Google Scholar] [CrossRef]
- Rosengrant, D.; Thomson, C.; Mzoughi, T.; Sabella, M.; Henderson, C.; Singh, C. Comparing Experts and Novices in Solving Electrical Circuit Problems with the Help of Eye-Tracking. Available online: https://aip.scitation.org/doi/abs/10.1063/1.3266728 (accessed on 30 November 2020).
- Klein, P.; Viiri, J.; Kuhn, J. Visual cues improve students’ understanding of divergence and curl: Evidence from eye movements during reading and problem solving. Phys. Rev. Spec. Top. Phys. Educ. Res. 2019, 15. [Google Scholar] [CrossRef]
- Blascheck, T.; Kurzhals, K.; Raschke, M.; Burch, M.; Weiskopf, D.; Ertl, T. Visualization of eye tracking data: A taxonomy and survey. Comput. Graph. Forum 2017, 36, 260–284. [Google Scholar] [CrossRef]
- Saß, S.; Schütte, K.; Lindner, M.A. Test-takers’ eye movements: Effects of integration aids and types of graphical representations. Comput. Educ. 2017, 109, 85–97. [Google Scholar] [CrossRef]
- Jian, Y.-C.; Wu, C.-J.; Su, J.-H. Learners’ eye movements during construction of mechanical kinematic representations from static diagrams. Learn. Instr. 2014, 32, 51–62. [Google Scholar] [CrossRef]
- Smith, A.D.; Mestre, J.P.; Ross, B.H. Eye-gaze patterns as students study worked-out examples in mechanics. Phys. Rev. Spec. Top. Phys. Educ. Res. 2010, 6, 020118. [Google Scholar] [CrossRef]
- Schuhen, M.; Kunde, F. Informelles Lernen und ökonomische Bildung. In Informelles Lernen; Rohs, M., Ed.; Springer: Wiesbaden, Germany, 2016; pp. 455–466. [Google Scholar]
- Kühling-Thees, C.; Happ, R.; Zlatkin-Troitschanskaia, O.; Pant, H.A. The Impact of Entry Preconditions on Student Dropout and Subject Change in Business and Economics. In Student Learning in German Higher Education; Springer: Wiesbaden, Germany, 2020; pp. 351–370. [Google Scholar]
- Zlatkin-Troitschanskaia, O.; Jitomirski, J.; Happ, R.; Molerov, D.; Schlax, J.; Kühling-Thees, C.; Förster, M.; Brückner, S. Validating a test for measuring knowledge and understanding of economics among university students. Zeitschrift für Pädagogische Psychologie 2019, 33, 119–133. [Google Scholar] [CrossRef]
- Schlax, J.; Zlatkin-Troitschanskaia, O.; Kühling-Thess, C.; Brückner, S. Influences on the Development of Economic Knowledge over the First Academic Year. Results of a Germany-Wide Longitudinal Study. In Student Learning in German Higher Education. Innovative Measurement Approaches and Research Results; Zlatkin-Troitschanskaia, O., Pant, H.A., Toepper, M., Lautenbach, C., Eds.; Springer: Wiesbaden, Germany, 2020; pp. 371–400. [Google Scholar]
- Salvucci, D.D.; Goldberg, J.H. Identifying fixations and saccades in eye-tracking protocols. In Proceedings of the Symposium on Eye Tracking Research and Applications; Duchowski, A.T., Ed.; ACM Press: New York, NY, USA, 2000; pp. 71–78. [Google Scholar]
- Marquart, C.L.; Hinojosa, C.; Swiecki, Z.; Eagan, B.; Shaffer, D.W. Epistemic Network Analysis (Version 1.6.0) [Software]. 2018. Available online: http://app.epistemicnetwork.org (accessed on 30 November 2020).
- Ruis, A.R.; Rosser, A.A.; Quandt-Walle, C.; Nathwani, J.N.; Shaffer, D.W.; Pugh, C.M. The hands and head of a surgeon: Modeling operative competency with multimodal epistemic network analysis. Am. J. Surg. Pathol. 2018, 216, 835–840. [Google Scholar] [CrossRef]
- Andrist, S.; Collier, W.; Gleicher, M.; Mutlu, B.; Shaffer, D. Look together: Analyzing gaze coordination with epistemic network analysis. Front. Behav. Neurosci. 2015, 6, 1016. [Google Scholar] [CrossRef]
- Sullivan, S.A.; Warner-Hillard, C.; Eagan, B.R.; Thompson, R.; Ruis, A.R.; Haines, K.; Pugh, C.M.; Shaffer, D.W.; Jung, H.S. Using epistemic network analysis to identify targets for educational interventions in trauma team communication. Surgery 2018, 4, 938–943. [Google Scholar] [CrossRef]
- Wooldridge, A.R.; Carayon, P.; Eagan, B.R.; Shaffer, D.W. Quantifying the qualitative with epistemic network analysis: A human factors case study of task-allocation communication in a primary care team. IISE Trans. Healthc. Syst. Eng. 2018, 1, 72–82. [Google Scholar] [CrossRef]
- Siebert-Evenstone, A.; Arastoopour Irgens, G.; Collier, W.; Swiecki, Z.; Ruis, A.R.; Williamson Shaffer, D. In Search of Conversational Grain Size: Modelling Semantic Structure Using Moving Stanza Windows. J. Learn. Anal. 2017, 4, 123–139. [Google Scholar] [CrossRef]
- Eraslan, S.; Yesilada, Y.; Harper, S. Eye tracking scanpath analysis techniques on web pages: A survey, evaluation and comparison. J. Eye Mov. Res. 2016, 9, 1–19. [Google Scholar]
- Kang, Z.; Landry, S.J. An eye movement analysis algorithm for a multielement target tracking task: Maximum transition-based agglomerative hierarchical clustering. IEEE Trans. Man-Mach. Syst. 2014, 45, 13–24. [Google Scholar] [CrossRef]
- Golebiowska, I.; Opach, T.; Rød, J.K. Breaking the Eyes: How Do Users Get Started with a Coordinated and Multiple View Geovisualization Tool? Available online: https://www.tandfonline.com/doi/full/10.1080/00087041.2019.1660513 (accessed on 30 November 2020).
- Prokop, M.; Pilař, L.; Tichá, I. Impact of Think-Aloud on Eye-Tracking: A Comparison of Concurrent and Retrospective Think-Aloud for Research on Decision-Making in the Game Environment. Sensors 2020, 20, 2750. [Google Scholar] [CrossRef] [PubMed]
- Andrienko, G.; Andrienko, N.; Burch, M.; Weiskopf, D. Visual Analytics Methodology for Eye Movement Studies. IEEE Trans. Vis. Comput. Graph. 2012, 18, 2889–2898. [Google Scholar] [CrossRef] [PubMed]






| Case | Participant | Media | Record.T. | Start | End | Fix.Index | Process | AOI_Quest. | AOI_Yaxisl. | AOI_Graph | … |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ae04rcVe | AreaQualfin | 370589 | 12:25:22.46 | 12:25:22.65 | 1112 | AOI_Question | 1 | 0 | 0 | … |
| 1 | ae04rcVe | AreaQualfin | 370781 | 12:25:22.65 | 12:25:22.90 | 1113 | AOI_Question | 1 | 0 | 0 | … |
| 1 | ae04rcVe | AreaQualfin | 371031 | 12:25:22.90 | 12:25:23.06 | 1114 | AOI_Question | 1 | 0 | 0 | … |
| 1 | ae04rcVe | AreaQualfin | 371189 | 12:25:23.06 | 12:25:23.14 | 1115 | AOI_graph | 0 | 0 | 1 | … |
| 1 | ae04rcVe | AreaQualfin | 371272 | 12:25:23.14 | 12:25:23.38 | 1116 | AOI_graph | 0 | 0 | 1 | … |
| 1 | ae04rcVe | AreaQualfin | 371514 | 12:25:23.38 | 12:25:23.62 | 1117 | AOI_Question | 1 | 0 | 0 | … |
| 1 | ae04rcVe | AreaQualfin | 371756 | 12:25:23.62 | 12:25:23.77 | 1118 | AOI_Question | 1 | 0 | 0 | … |
| … | … | … | … | … | … | … | … | … | … | … | … |
| Question | Yaxislab | Xaxislab | Graph | Attractor | Yaxis | Xaxis | Distractor |
|---|---|---|---|---|---|---|---|
| 1328 | 1753 | 793 | 6987 | 1192 | 3004 | 1815 | 1539 |
| AOI | ECAreaQual | PhyAreaQual | EcAreaQuant | PhyAreaQuant | EcSlopeQual | PhylopeQual | EcSlopeQuant | PhySlopeQuant | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | |
| AOI_Question | 30.4% | 25.5% | 23.5% | 21.6% | 36.2% | 19.9% * | 28.9% | 13.5% * | 21.8% | 30.2% | 20.4% | 24.2% | 25.3% | 24.1% | 15.6% | 18.4% |
| AOI_yaxislab | 6.8% | 7.7% | 5.7% | 5.5% | 11.7% | 7.6% | 6.8% | 9.3% | 2.6% | 2.1% | 3.9% | 2.8% | 3.4% | 2.9% | 6.9% | 8.0% |
| AOI_xaxislab | 1.5% | 1.7% | 2.4% | 1.7% | 1.0% | 0.6% | 1.7% | 4.1% | 2.4% | 0.6% ** | 2.0% | 1.1% | 2.6% | 2.8% | 4.1% | 2.2% |
| AOI_graph | 50.3% | 53.9% | 54.9% | 53.7% | 52.5% | 64.0% | 50.8% | 64.8% | 49.6% | 46.1% | 57.4% | 56.5% | 51.5% | 55.6% | 62.5% | 59.7% |
| AOI_Attractor | 8.3% | 11.9% | 5.4% | 5.1% | 1.5% | 3.7% * | 1.9% | 5.8% * | 1.5% | 6.7% * | 10.2% | 8.2% | 3.6% | 7.5% * | 2.8% | 6.6% ** |
| AOI_yaxis | 5.9% | 6.6% | 8.9% | 7.8% | 10.4% | 20.1% * | 9.2% | 9.5% | 2.7% | 3.4% | 5.3% | 4.2% | 9.6% | 8.8% | 9.9% | 10.0% |
| AOI_xaxis | 2.9% | 1.5% * | 5.3% | 6.7% | 6.2% | 7.4% | 8.3% | 12.5% | 3.1% | 1.8% | 4.9% | 2.4% * | 7.1% | 7.9% | 6.1% | 4.0% |
| AOI_Distractor | 8.8% | 5.2% | 9.0% | 11.7% * | 3.2% | 5.6% | 7.6% | 5.2% | 17.5% | 12.0% * | 3.0% | 4.2% * | 14.2% | 7.7% * | 13.8% | 9.2% |
| Number of solvers | 14 | 9 | 11 | 12 | 18 | 5 | 20 | 3 | 5 | 18 | 4 | 19 | 18 | 5 | 11 | 12 |
| Incorrect Solvers | Correct Solvers | |||
|---|---|---|---|---|
| Correlation R | p-Value | Correlation R | p-Value | |
| AOI_Question | 0.98826 | 4.01 × 10−1 | 0.99264 | 9.90 × 10−2 |
| AOI_yaxislab | 0.96159 | 0.00014 | 0.92150 | 0.00114 |
| AOI_xaxislab | 0.96236 | 0.00013 | 0.96873 | 0.00007 |
| AOI_graph | 0.98055 | 0.00002 | 0.98529 | 7.87 × 10−1 |
| AOI_Attractor | 0.93042 | 0.00080 | 0.94725 | 0.00035 |
| AOI_yaxis | 0.99497 | 3.17 × 10−2 | 0.99882 | 4.10 × 10−4 |
| AOI_xaxis | 0.98343 | 0.00001 | 0.99320 | 7.83 × 10−2 |
| AOI_Distractor | 0.90852 | 0.00179 | 0.99200 | 1.27 × 10−1 |
| AreaQualFin | AreaQualPhys | AreaQuantFin | AreaQuantPhys | SlopeQualFin | SlopeQualPhys | SlopeQuantFin | SlopeQuantPhys | |
|---|---|---|---|---|---|---|---|---|
| AOI_AttractorAOI_Distractor | −0.763 | −0.133 | −2.155 * | 0.440 | −1.129 | 0.309 | −0.633 | 0.626 |
| AOI_AttractorAOI_graph | −1.943 | 1.817 | −2.371 * | −2.418 * | −2.315 * | 1.645 | −1.118 | −1.809 |
| AOI_AttractorAOI_question | −2.280 * | 1.914 | −0.755 | - | - | 1.518 | −0.131 | −0.518 |
| AOI_AttractorAOI_xaxis | −0.195 | −1.130 | −0.961 | −0.641 | - | 1.873 | 0.091 | −1.915 |
| AOI_AttractorAOI_xaxislab | −0.442 | −0.518 | 0.518 | 0.552 | - | 3.370 ** | −1.348 | 0.062 |
| AOI_AttractorAOI_yaxis | −0.693 | 1.929 | −1.552 | −1.000 | −0.755 | 0.757 | −1.166 | 0.589 |
| AOI_AttractorAOI_yaxislab | −1.254 | −1.915 | 0.812 | −1.000 | −1.844 | −0.655 | −1.000 | 0.749 |
| AOI_DistractorAOI_graph | 1.294 | 0.176 | −0.885 | −0.039 | −0.513 | 2.473 | 1.258 | 2.361 * |
| AOI_DistractorAOI_question | 0.211 | 0.077 | −1.100 | −0.601 | 1.201 | −0.450 | −0.901 | 0.677 |
| AOI_DistractorAOI_xaxis | 1.749 | −0.309 | −0.916 | −0.863 | 0.916 | −0.450 | 0.825 | 2.362 * |
| AOI_DistractorAOI_xaxislab | 0.795 | 1.060 | −0.131 | 2.517 * | 1.968 | −0.450 | −1.230 | 1.763 |
| AOI_DistractorAOI_yaxis | 1.472 | 2.257 * | −1.149 | 0.823 | −0.102 | 1.525 | 1.223 | 1.785 |
| AOI_DistractorAOI_yaxislab | 1.385 | 2.084 | −0.641 | 0.828 | 0.166 | −0.450 | 2.715 * | 1.454 |
| AOI_graphAOI_question | −0.274 | 0.176 | −0.351 | 2.325 * | 1.694 | 2.396 | 0.210 | 0.334 |
| AOI_graphAOI_xaxis | 0.314 | 1.066 | −2.284 * | −0.769 | 0.667 | 1.313 | −0.859 | 2.380 * |
| AOI_graphAOI_xaxislab | −1.308 | 1.512 | −1.551 | −0.395 | 0.901 | 1.070 | −0.178 | 1.824 |
| AOI_graphAOI_yaxis | −0.707 | 1.811 | −0.974 | −0.193 | −0.583 | 0.653 | −0.297 | 2.029 |
| AOI_graphAOI_yaxislab | −1.833 | 1.588 | −0.076 | −0.168 | −0.596 | 3.642 | 0.052 | 1.523 |
| AOI_questionAOI_xaxis | 1.546 | 0.380 | −0.797 | 0.812 | −0.518 | 0.951 | 0.493 | 0.086 |
| AOI_questionAOI_xaxislab | 0.324 | 0.594 | - | −0.757 | −0.518 | −0.655 | 1.314 | 1.000 |
| AOI_questionAOI_yaxis | −1.060 | 1.112 | 0.215 | 3.249 ** | −2.204 * | −0.450 | 0.961 | 1.191 |
| AOI_questionAOI_yaxislab | 0.921 | 2.390 * | 0.268 | −0.546 | −0.377 | 1.072 | 0.709 | 1.269 |
| AOI_xaxisAOI_xaxislab | −1.023 | 1.129 | 1.330 | −0.849 | 1.804 | 1.633 | 0.337 | 0.915 |
| AOI_xaxisAOI_yaxis | −0.055 | −0.547 | −1.421 | 1.326 | 0.166 | 1.217 | −0.266 | 1.510 |
| AOI_xaxisAOI_yaxislab | 0.211 | 0.481 | −0.033 | −2.671 * | - | - | 2.204 * | −1.393 |
| AOI_xaxislabAOI_yaxis | −0.615 | 1.234 | −0.166 | 0.552 | 0.904 | −0.772 | −0.828 | 2.506 * |
| AOI_xaxislabAOI_yaxislab | −1.284 | 0.362 | −0.502 | −0.734 | −1.000 | 0.691 | −1.188 | 0.156 |
| AOI_yaxisAOI_yaxislab | 0.230 | 1.899 | −0.404 | −0.279 | 0.777 | 0.856 | 0.458 | 1.172 |
| EcArea Qual | PhyArea Qual | EcArea Quant | PhyArea Quant | EcSlope Qual | PhySlope Qual | EcSlope Quant | PhySlope Quant | Total | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strong Transition Associations | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ |
| AOI_graph and AOI_Attractor | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | ||||||||
| AOI_graph and AOI_yaxislab | 1 | 1 | 1 | 1 | 1 | 2 | 3 | |||||||||||
| AOI_graph and AOI_xaxislab | 1 | 1 | 1 | 1 | 1 | 3 | ||||||||||||
| AOI_graph and AOI_xaxis | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 4 | ||||||||||
| AOI_graph and AOI_yaxis | 1 | 1 | 1 | 1 | 2 | 2 | ||||||||||||
| AOI_graph and AOI_Distractor | 1 | 1 | 1 | 1 | 1 | 0 | 5 | |||||||||||
| AOI_graph and AOI_Question | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 5 | |||||||||
| AOI_Attractor and AOI_Distractor | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | ||||||||
| AOI_xaxis and AOI_yaxis | 1 | 1 | 0 | |||||||||||||||
| AOI_xaxislab and AOI_yaxislab | 1 | 1 | 1 | 2 | 1 | |||||||||||||
| AOI_xaxislab and AOI_Distractor | 1 | 0 | 1 | |||||||||||||||
| AOI_xaxis and AOI_Attractor | 1 | 1 | 2 | 0 | ||||||||||||||
| AOI_yaxislab and AOI_xaxis | 1 | 1 | 0 | |||||||||||||||
| AOI_yaxislab and AOI_yaxis | 1 | 1 | 1 | 1 | 2 | |||||||||||||
| AOI_yaxis and AOI_Attractor | 1 | 1 | 0 | |||||||||||||||
| AOI_Distractor and AOI_yaxis | 1 | 0 | 1 | |||||||||||||||
| AOI_Question and AOI_xaxis | 1 | 1 | 1 | 1 | 2 | |||||||||||||
| AOI_Question and AOI_yaxis | 1 | 0 | 1 | |||||||||||||||
| AOI_Question and AOI_yaxislab | 1 | 0 | 1 | |||||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brückner, S.; Schneider, J.; Zlatkin-Troitschanskaia, O.; Drachsler, H. Epistemic Network Analyses of Economics Students’ Graph Understanding: An Eye-Tracking Study. Sensors 2020, 20, 6908. https://doi.org/10.3390/s20236908
Brückner S, Schneider J, Zlatkin-Troitschanskaia O, Drachsler H. Epistemic Network Analyses of Economics Students’ Graph Understanding: An Eye-Tracking Study. Sensors. 2020; 20(23):6908. https://doi.org/10.3390/s20236908
Chicago/Turabian StyleBrückner, Sebastian, Jan Schneider, Olga Zlatkin-Troitschanskaia, and Hendrik Drachsler. 2020. "Epistemic Network Analyses of Economics Students’ Graph Understanding: An Eye-Tracking Study" Sensors 20, no. 23: 6908. https://doi.org/10.3390/s20236908
APA StyleBrückner, S., Schneider, J., Zlatkin-Troitschanskaia, O., & Drachsler, H. (2020). Epistemic Network Analyses of Economics Students’ Graph Understanding: An Eye-Tracking Study. Sensors, 20(23), 6908. https://doi.org/10.3390/s20236908






