Adaptive Quasi-Unsupervised Detection of Smoke Plume by LiDAR
Abstract
1. Introduction
2. Materials and Methods
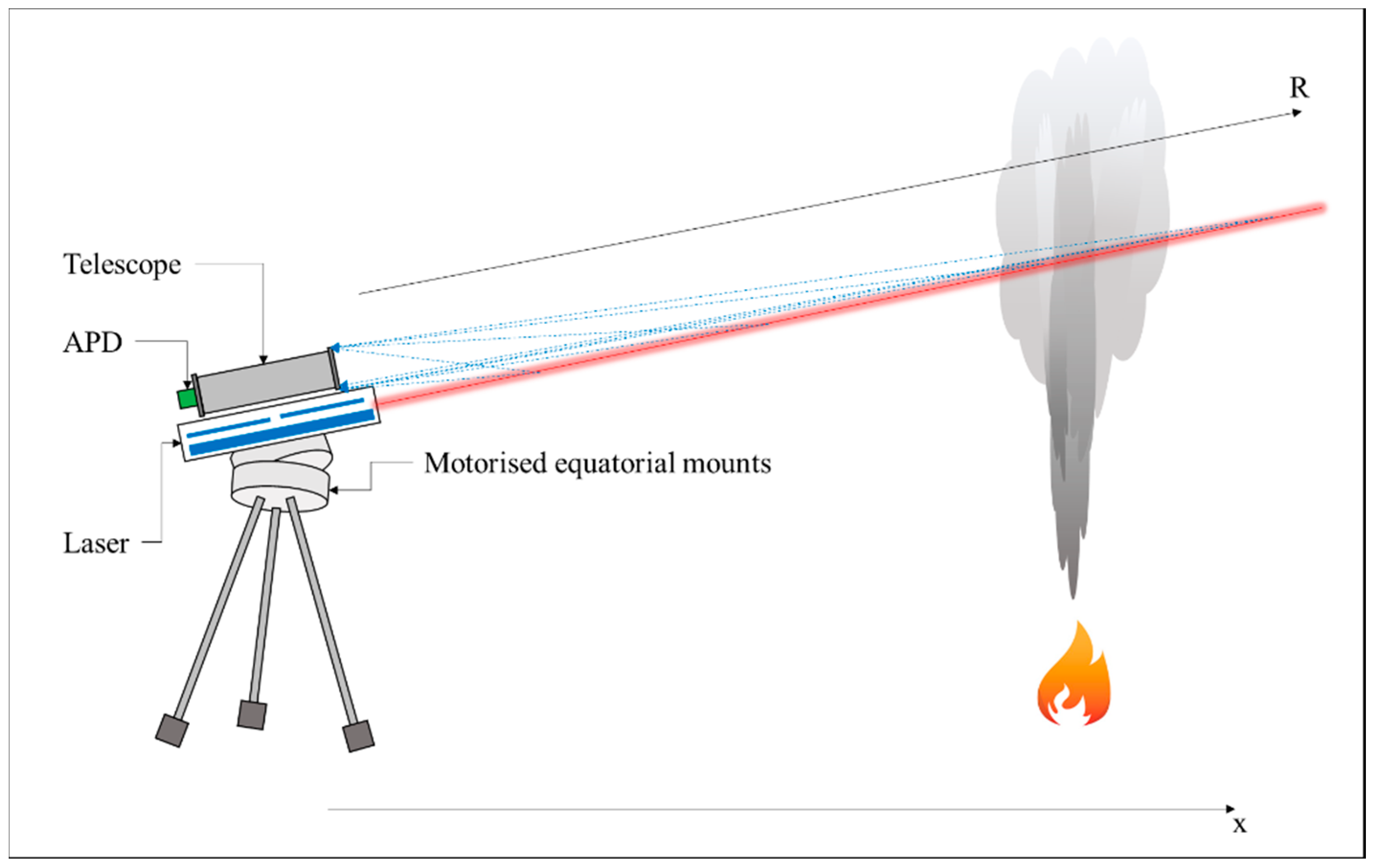
2.1. LiDAR Apparatus and Measurement Scheme
2.2. LiDAR Inversion
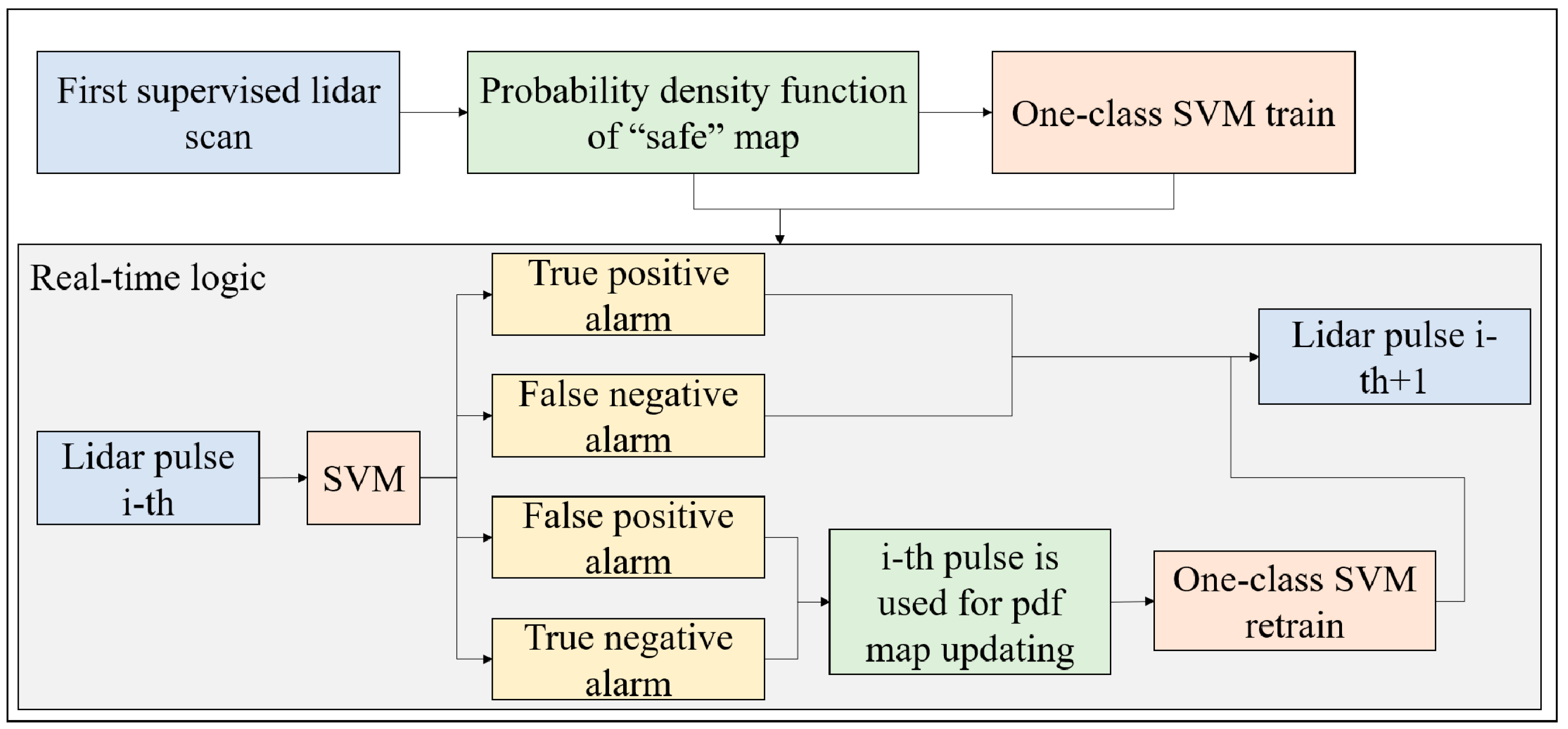
2.3. Quasi-Unsupervised Classification Algorithm
- True positive alarm: the SVM classifies an alarm, the operator takes the countermeasures and confirms the presence of smoke and fire. In this case, the LiDAR continues the monitoring and goes to the i-th + 1 pulse.
- False positive alarm: the SVM classifies an alarm, the operator takes the countermeasures and negates the presence of smoke and fire. In this case, the data of the i-th pulse, which is a “safe” pulse, is used to update the map and retrain the SVM.
- True negative alarm: the SVM does not classify an alarm, no fires and smokes are observed in the following minutes. The pulse is a “safe” pulse and it is used to update the map and retrain the SVM.
- False negative alarm: the SVM does not classify an alarm, but within the next minutes, smokes and fires are observed. The pulse is not a “safe” pulse and cannot be used to update the map and retrain the SVM.
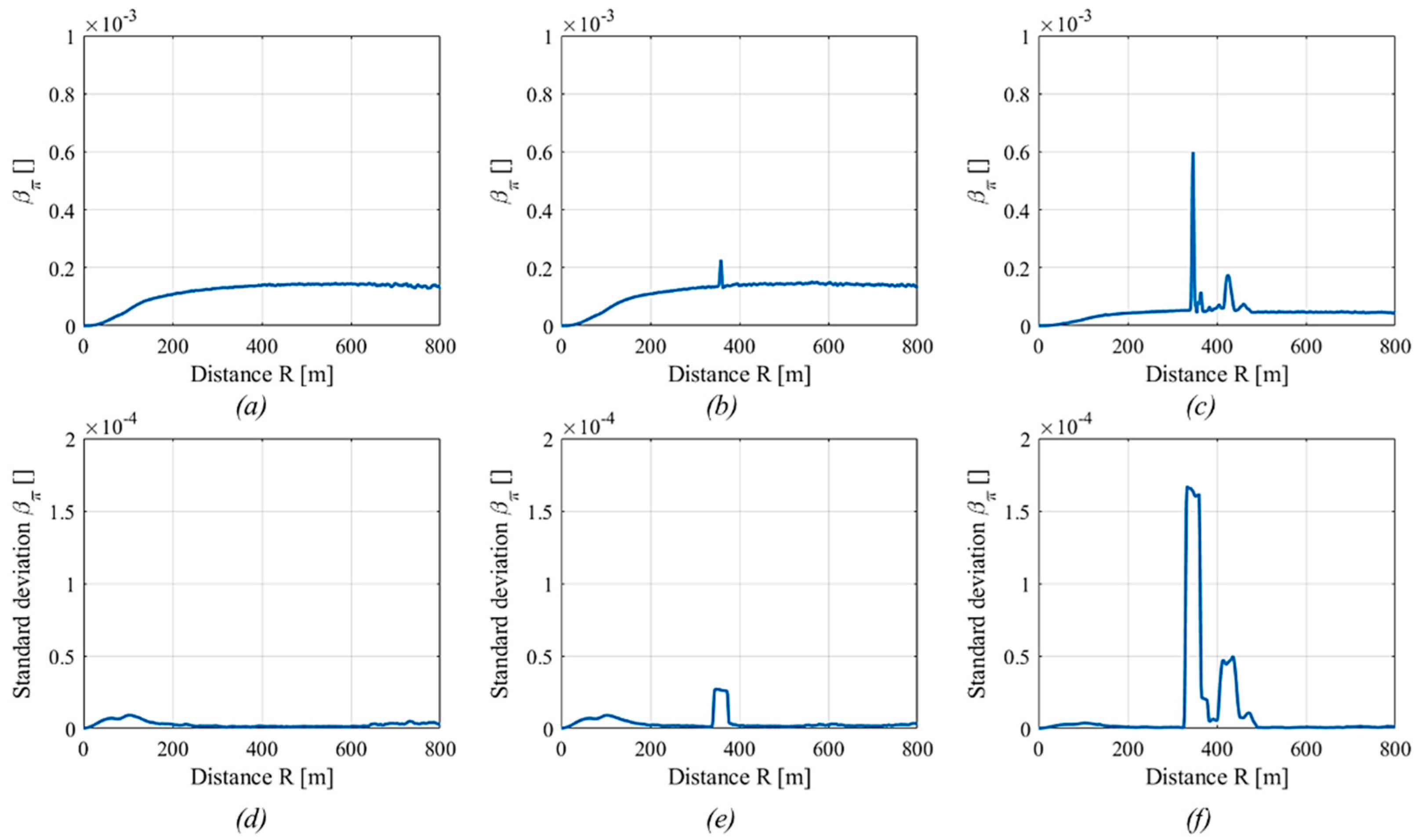
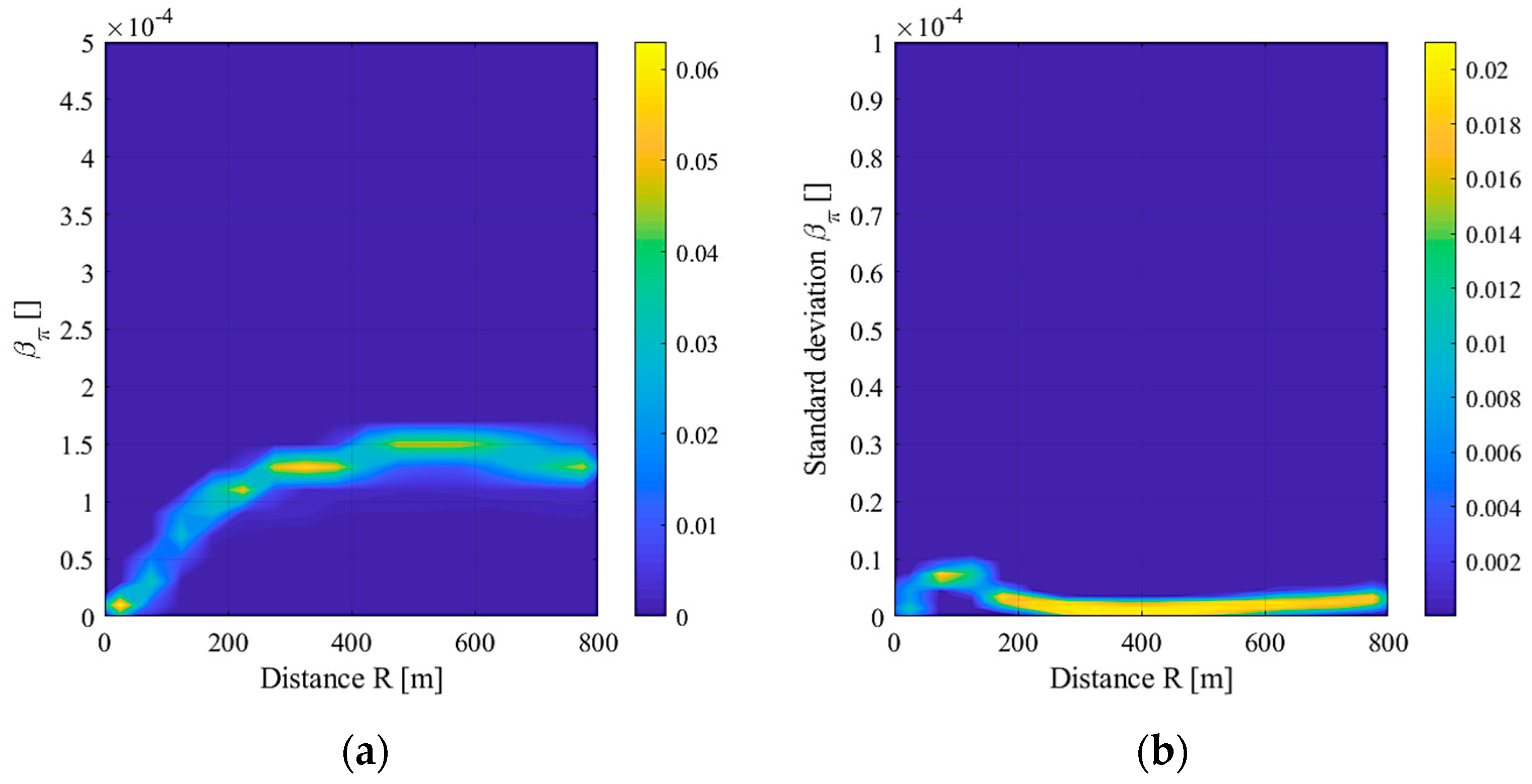
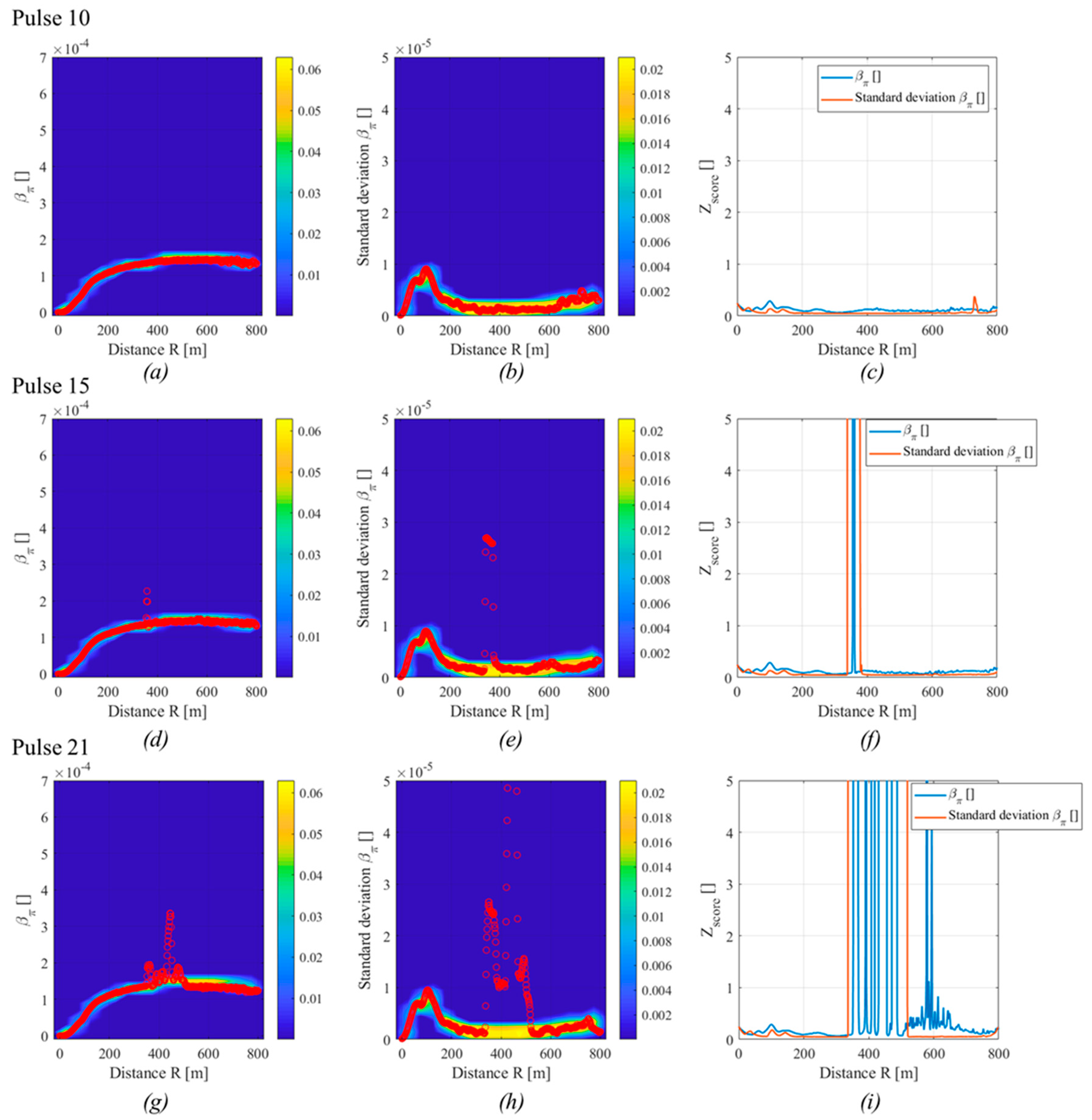
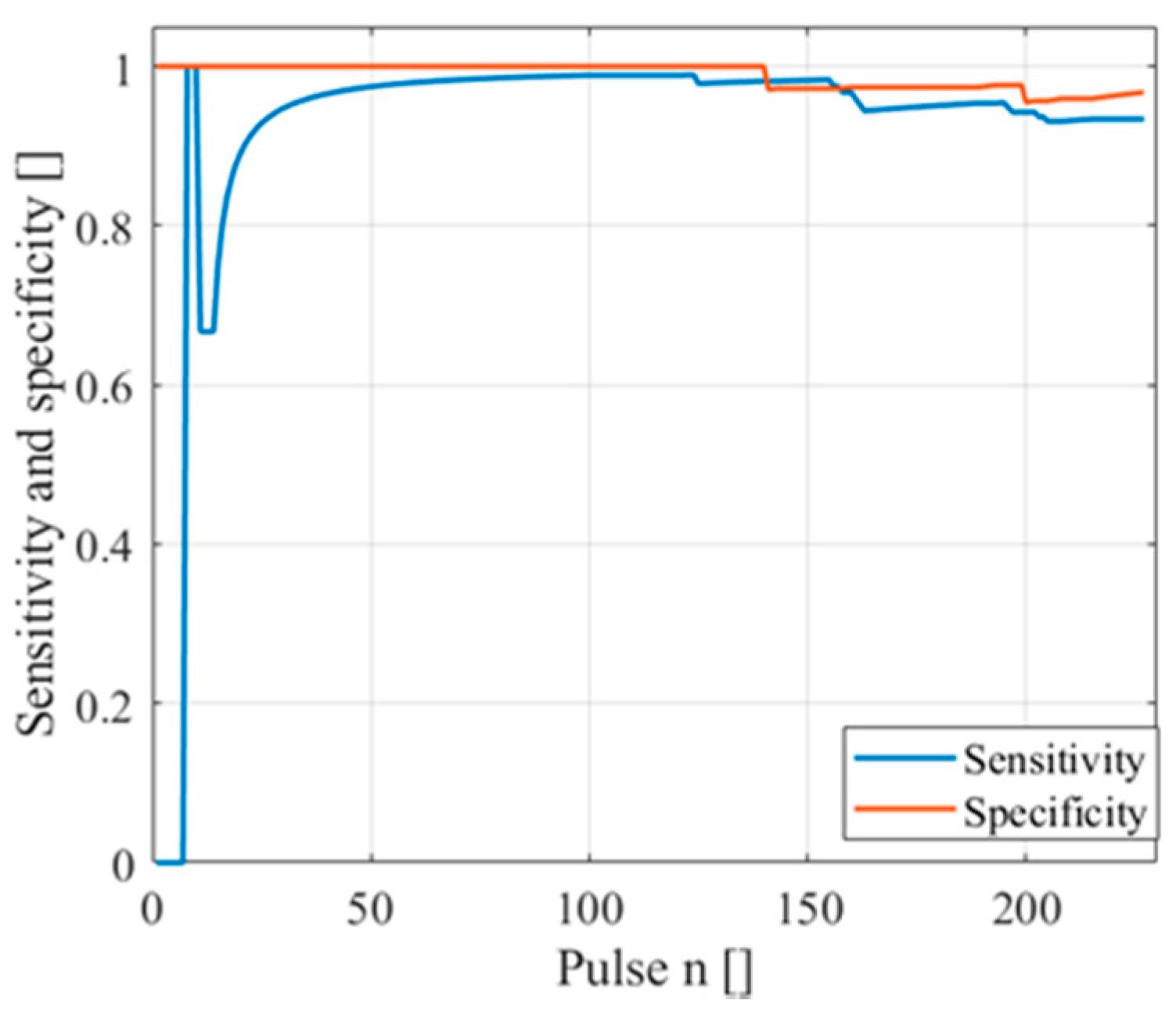
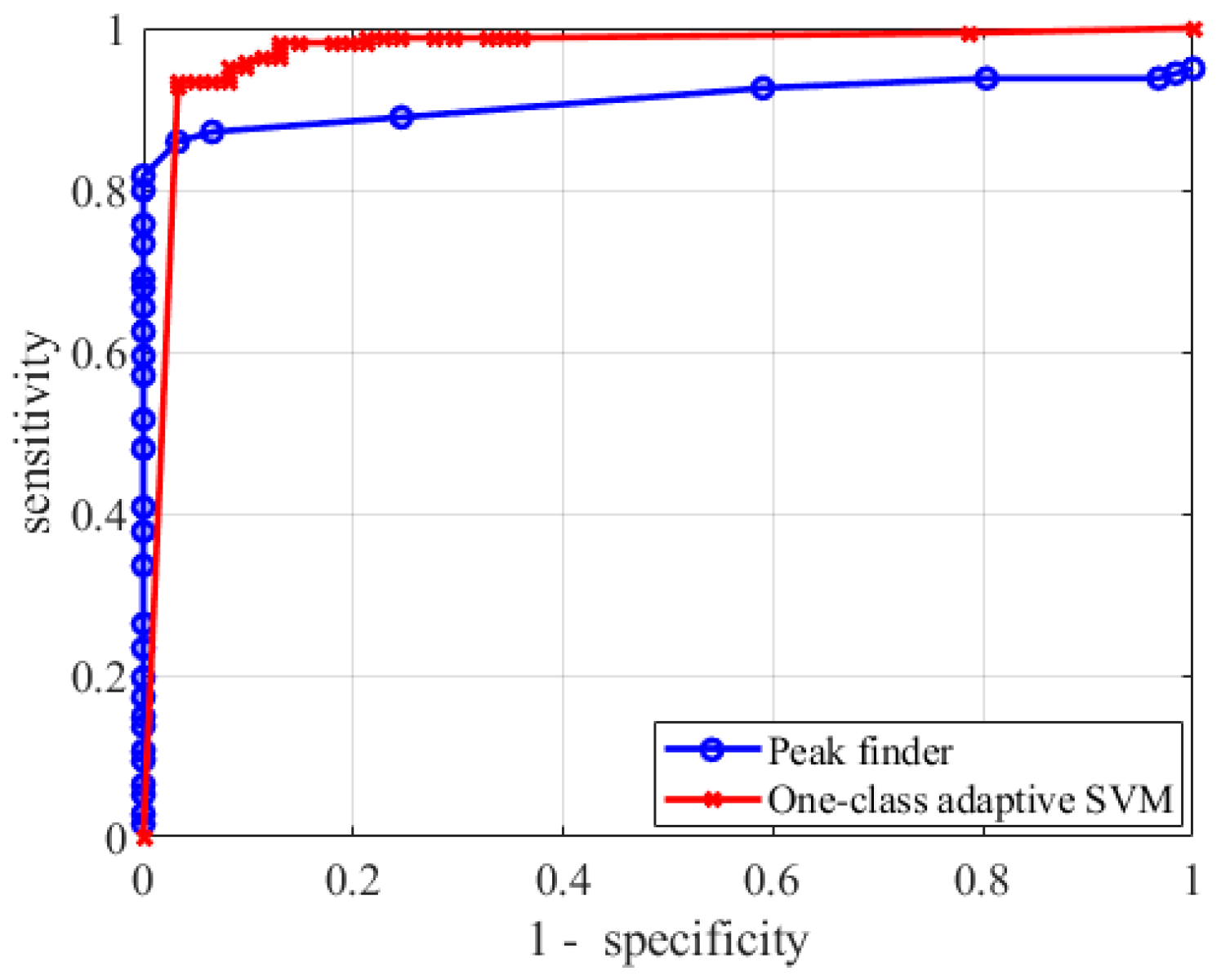
3. Results
- The sensitivity does not reach very high performances, even for very small specificity (and thus a high number of false alarms);
- The specificity is very high only for very small sensitivity;
- The algorithm is very unstable in the “best performances” region, i.e., where both specificity and sensitivity are large enough (>80%). A variation of the 5% of the prominence lead to a variation of the performances of 10%, making the choice of the prominence very critical.
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weitkamp, C. Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Springer Science+Business Media: New York, NY, USA, 2005. [Google Scholar]
- Gondal, M.A. Lidar system for remote environmental studies. Talanta 2000, 53, 147–154. [Google Scholar] [CrossRef]
- Browell, E.V.; Ismail, S.; Shipley, S.T. Ultraviolet DIAL measurements of O3 profiles in regions of spatially inhomogeneous aerosols. Appl. Opt. 1985, 24, 2827–2836. [Google Scholar] [CrossRef] [PubMed]
- De Young, R.J.; Barnes, N.P. Profiling atmospheric water vapor using a fiber laser lidar system. Appl. Opt. 2010, 49, 562–567. [Google Scholar] [CrossRef] [PubMed]
- Fredriksson, K.A.; Hertz, H.M. Evaluation of the DIAL technique for studies on NO2 using a mobile lidar system. Appl. Opt. 1984, 23, 1403–1411. [Google Scholar] [CrossRef] [PubMed]
- Weibring, P.; Edner, H.; Svanberg, S. Versatile mobile lidar system for environmental monitoring. Appl. Opt. 2003, 42, 3583–3594. [Google Scholar] [CrossRef] [PubMed]
- Bellecci, C.; Caputi, G.E.M.L.; De Donato, F.; Gaudio, P.; Valentíni, M. CO2 dial for monitoring atmospheric pollutants at the University of Calabria. Il Nuovo Cimento C. 1995, 18, 463–472. [Google Scholar] [CrossRef]
- Cook, C.S.; Bethke, G.W.; Conner, W.D. Remote Measurement of Smoke Plume Transmittance Using Lidar. Appl. Opt. 1972, 11, 1742–1748. [Google Scholar] [CrossRef] [PubMed]
- Utkin, A.; Lavrov, A.; Costa, L.; Simões, F.; Vilar, R. Detection of small forest fires by lidar. Appl. Phys. A 2002, 74, 77–83. [Google Scholar] [CrossRef]
- Uthe, E.E. Lidar evaluation of smoke and dust clouds. Appl. Opt. 1981, 20, 1503–1510. [Google Scholar] [CrossRef] [PubMed]
- Gelfusa, M.; Malizia, A.; Murari, A.; Parracino, S.; Lungaroni, M.; Peluso, E.; Vega, J.; DeLeo, L.; Perrimezzi, C.; Gaudio, P. First attempts at measuring widespread smoke with a mobile lidar system. In Proceedings of the 2015 Fotonica AEIT Italian Conference on Photonics Technologies, Turin, Italy, 6–8 May 2015. [Google Scholar]
- Bellecci, C.; Francucci, M.; Gaudio, P.; Gelfusa, M.; Martellucci, S.; Richetta, M. Early detection of small forest fire by dial technique. In Proceedings of the SPIE 5976, Remote Sensing for Agriculture, Ecosystems, and Hydrology VII, Bruges, Belgium, 19–22 September 2005. [Google Scholar]
- Bellecci, C.; De Leo, L.; Gaudio, P.; Gelfusa, M.; Feudo, T.L.; Martellucci, S.; Richetta, M. Reduction of false alarms in forest fire surveillance using water vapour concentration measurements. Opt. Laser Technol. 2009, 41, 374–379. [Google Scholar] [CrossRef]
- Utkin, A.B.; Lavrov, A.V.; Vilar, R.M. A Simple Neural-network Algorithm for Classification of Lidar Signals Applied to Forest-fire Detection. In Proceedings of the International Joint Conference on Computational Intelligence (IJCCI), Madeira, Portugal, 5–7 October 2009. [Google Scholar]
- Kovalev, V.A.; Eichinger, W.E. Elastic Lidar: Theory, Practice, and Analysis Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Klett, J.D. Stable analytical inversion solution for processing lidar returns. Appl. Opt. 1981, 20, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Klett, J.D. Lidar inversion with variable backscatter/extinction ratios. Appl. Opt. 1985, 24, 1638–1643. [Google Scholar] [CrossRef] [PubMed]
- Shettle, E.; Fenn, R.W. Models for the Aerosols of the Lower Atmosphere and the Effects of Humidity Variations on Their Optical Properties; Optical Physics Division, Air Force Geophysics Laboratory: Hanscom AFB, MA, USA, 1979. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote. Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Shin, H.J.; Eom, D.-H.; Kim, S.-S. One-class support vector machines—An application in machine fault detection and classification. Comput. Ind. Eng. 2005, 48, 395–408. [Google Scholar] [CrossRef]
- Vaughan, M.A.; Powell, K.A.; Winker, D.M.; Hostetler, C.A.; Kuehn, R.E.; Hunt, W.H.; Getzewich, B.J.; Young, S.A.; Liu, Z.; McGill, M.J. Fully Automated Detection of Cloud and Aerosol Layers in the CALIPSO Lidar Measurements. J. Atmospheric Ocean. Technol. 2009, 26, 2034–2050. [Google Scholar] [CrossRef]
- Dai, G.; Wu, S.; Song, X. Depolarization Ratio Profiles Calibration and Observations of Aerosol and Cloud in the Tibetan Plateau Based on Polarization Raman Lidar. Remote. Sens. 2018, 10, 378. [Google Scholar] [CrossRef]
| Light Source | |||
|---|---|---|---|
| Laser type | ND:YaG | Pulse width | 8 ns |
| Functioning | Pulsed | Beam diameter | 5 mm |
| Mean wavelength | 1064 nm | Beam divergence | 4 mrad |
| Max repetition rate | 10 Hz | ||
| Telescope | |||
| Nominal focal length | 1300 mm | Primary mirror diameter | 102 mm |
| f-number | f/12.7 | Field of view | 1.2 mrad |
| Photodiode | |||
| Time response | 5 ns | ||
| Gain | 100 | ||
| Quantum Efficiency | 38% | ||
| DAQ—Card PXI 5122 | |||
| Resolution | 14 bit | ||
| Sampling rate | 100 Msample/s | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossi, R.; Gelfusa, M.; Malizia, A.; Gaudio, P. Adaptive Quasi-Unsupervised Detection of Smoke Plume by LiDAR. Sensors 2020, 20, 6602. https://doi.org/10.3390/s20226602
Rossi R, Gelfusa M, Malizia A, Gaudio P. Adaptive Quasi-Unsupervised Detection of Smoke Plume by LiDAR. Sensors. 2020; 20(22):6602. https://doi.org/10.3390/s20226602
Chicago/Turabian StyleRossi, Riccardo, Michela Gelfusa, Andrea Malizia, and Pasqualino Gaudio. 2020. "Adaptive Quasi-Unsupervised Detection of Smoke Plume by LiDAR" Sensors 20, no. 22: 6602. https://doi.org/10.3390/s20226602
APA StyleRossi, R., Gelfusa, M., Malizia, A., & Gaudio, P. (2020). Adaptive Quasi-Unsupervised Detection of Smoke Plume by LiDAR. Sensors, 20(22), 6602. https://doi.org/10.3390/s20226602








