Fiber Bragg Grating Sensors for Performance Evaluation of Fast Magnetic Resonance Thermometry on Synthetic Phantom
Abstract
1. Introduction
2. Theoretical Background
2.1. Fiber Bragg Grating Sensors
2.2. Magnetic Resonance Thermometry
3. Materials and Methods
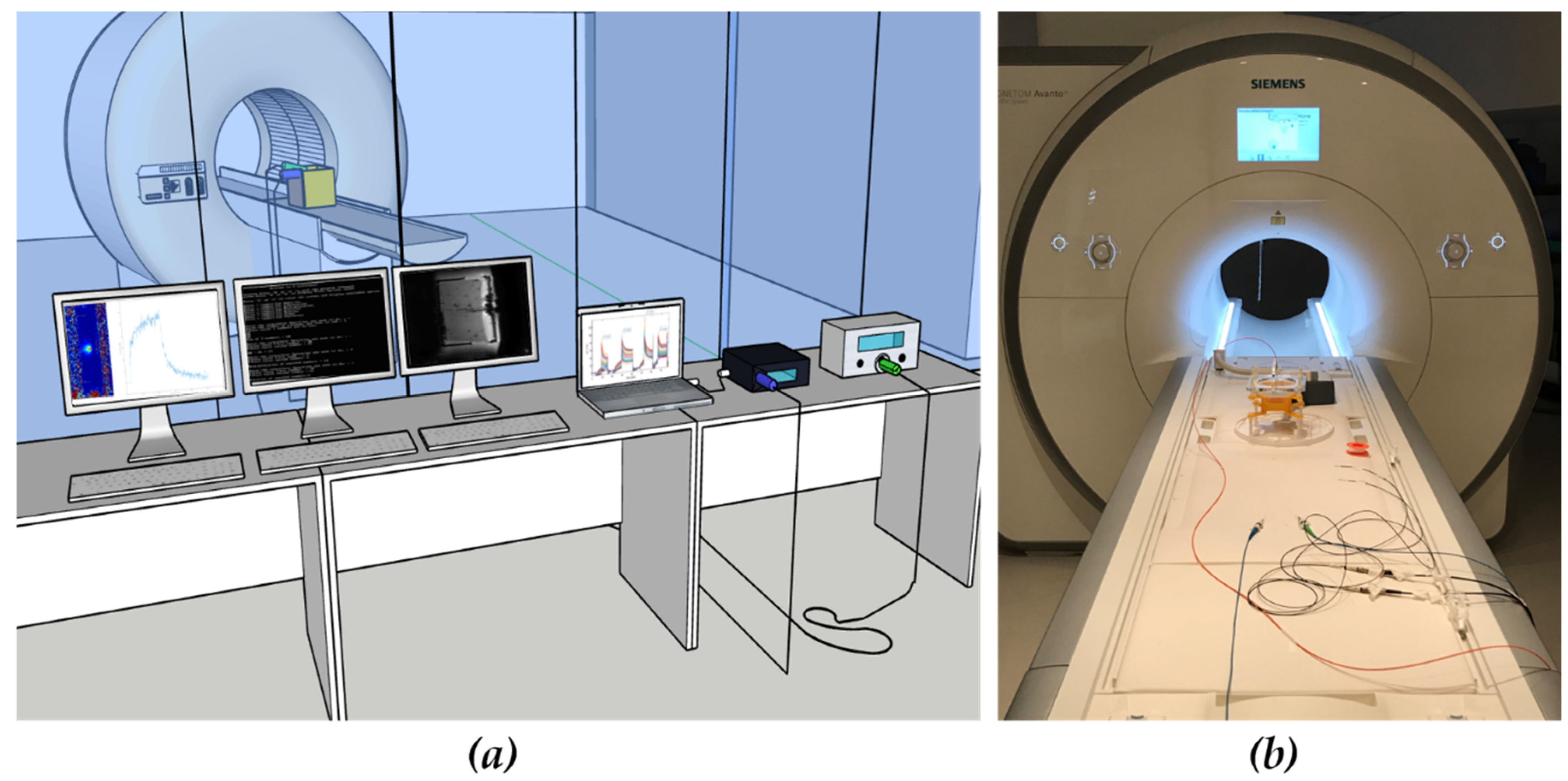
3.1. Experimental Setup
3.1.1. Agar Gel
3.1.2. Customized Box
3.1.3. Laser
3.1.4. Fiber Bragg Grating Sensors Setup
3.1.5. MR Scanner and Sequences
3.2. MRTI Analysis
3.3. Data Analysis for FBGs and MRTI Comparison
4. Results
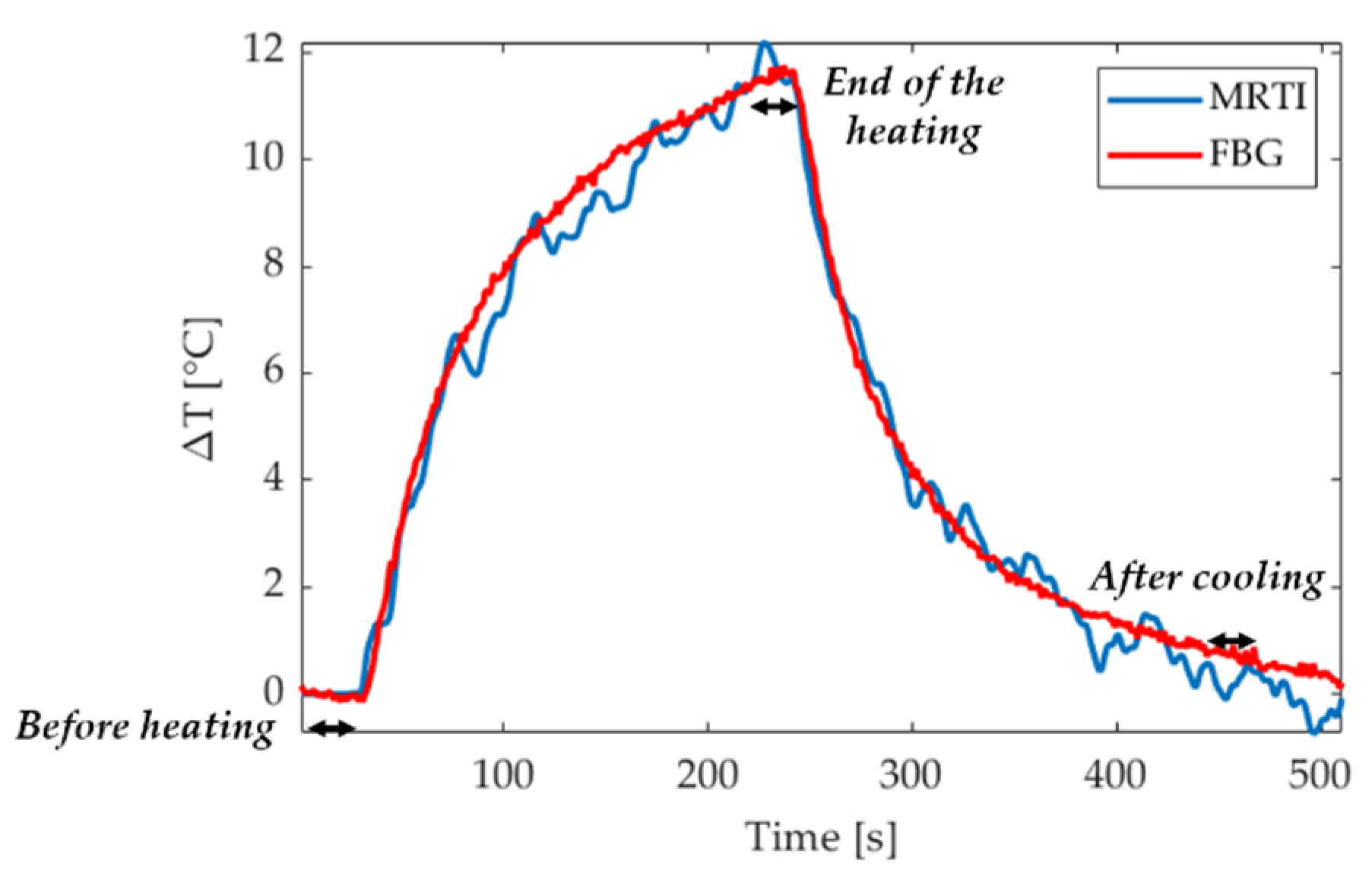
4.1. Analysis of MRTI during Laser Heating
4.2. MRTI Precision
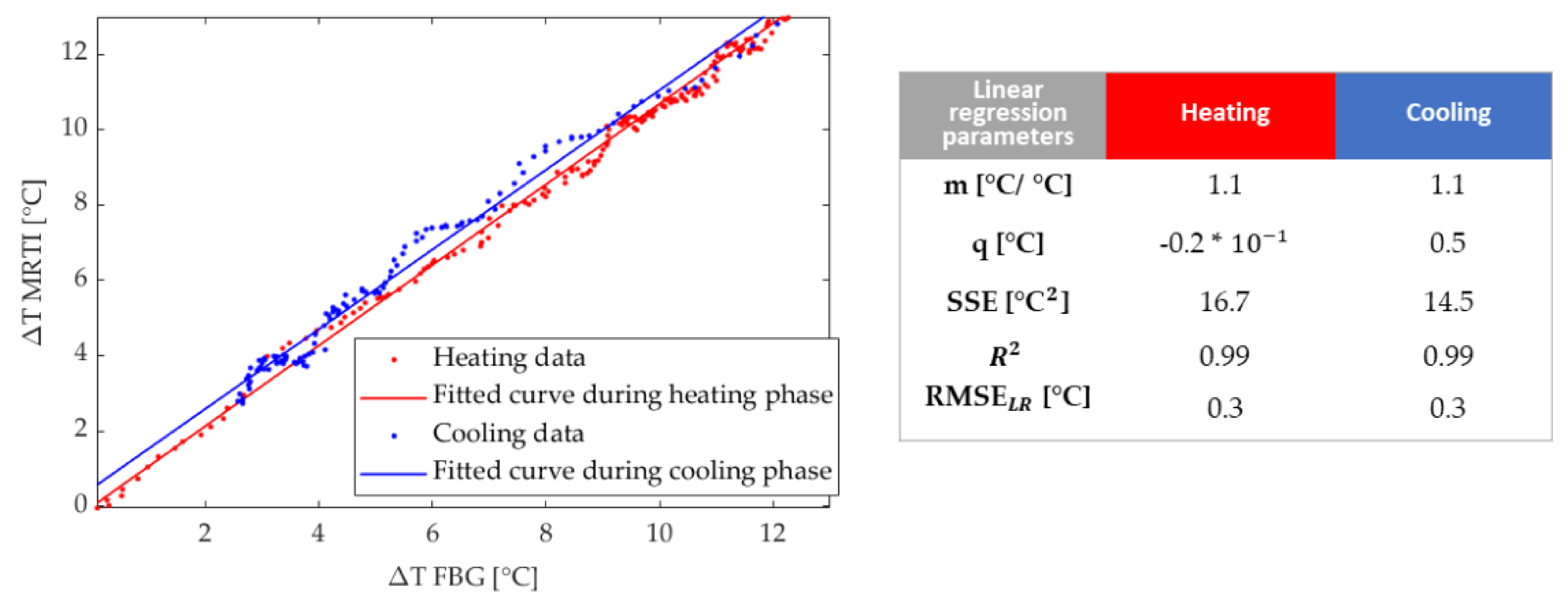
4.3. Comparison between FBGs and MRTI Temperature Values
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goldberg, S.N.; Gazelle, G.S.; Mueller, P.R. Thermal Ablation Therapy for Focal Malignancy. Am. J. Roentgenol. 2000, 174, 323–331. [Google Scholar] [CrossRef] [PubMed]
- Izzo, F. Other Thermal Ablation Techniques: Microwave and Interstitial Laser Ablation of Liver Tumors. Ann. Surg. Oncol. 2003, 10, 491–497. [Google Scholar] [CrossRef] [PubMed]
- Bowman, R. A Probe for Measuring Temperature in Radio-Frequency-Heated Material (Short Papers). IEEE Trans. Microw. Theory Tech. 1976, 24, 43–45. [Google Scholar] [CrossRef]
- Welch, A.J.; Van Gemert, M.J.C. Optical-Thermal Response of Laser-Irradiated Tissue; Springer: New York, NY, USA, 2011; Volume 2. [Google Scholar]
- Saccomandi, P.; Schena, E.; Massaroni, C.; Fong, Y.; Grasso, R.F.; Giurazza, F.; Zobel, B.B.; Buy, X.; Palussiere, J.; Cazzato, R.L. Temperature monitoring during microwave ablation in ex vivo porcine livers. Eur. J. Surg. Oncol. 2015, 41, 1699–1705. [Google Scholar] [CrossRef] [PubMed]
- Denys, A.; De Baere, T.; Kuoch, V.; Dupas, B.; Chevallier, P.; Madoff, D.C.; Schnyder, P.; Doenz, F. Radio-frequency tissue ablation of the liver: In vivo and ex vivo experiments with four different systems. Eur. Radiol. 2003, 13, 2346–2352. [Google Scholar] [CrossRef] [PubMed]
- Quesson, B.; De Zwart, J.A.; Moonen, C.T.W. Magnetic resonance temperature imaging for guidance of thermotherapy. J. Magn. Reson. Imaging 2000, 12, 525–533. [Google Scholar] [CrossRef]
- Bloembergen, N.; Purcell, E.M.; Pound, R.V. Relaxation Effects in Nuclear Magnetic Resonance Absorption. Phys. Rev. 1948, 73, 679–712. [Google Scholar] [CrossRef]
- Parker, D.L.; Smith, V.; Sheldon, P.; Crooks, L.E.; Fussell, L. Temperature distribution measurements in two-dimensional NMR imaging. Med Phys. 1983, 10, 321–325. [Google Scholar] [CrossRef]
- Odéen, H.; Parker, D.L. Magnetic resonance thermometry and its biological applications—Physical principles and practical considerations. Prog. Nucl. Magn. Reson. Spectrosc. 2019, 110, 34–61. [Google Scholar] [CrossRef]
- Ishihara, Y.; Calderon, A.; Watanabe, H.; Okamoto, K.; Suzuki, Y.; Kuroda, K.; Suzuki, Y. A precise and fast temperature mapping using water proton chemical shift. Magn. Reson. Med. 1995, 34, 814–823. [Google Scholar] [CrossRef]
- De Senneville, B.D.; Mougenot, C.; Quesson, B.; Dragonu, I.; Grenier, N.; Moonen, C.T. MR thermometry for monitoring tumor ablation. Eur. Radiol. 2007, 17, 2401–2410. [Google Scholar] [CrossRef] [PubMed]
- Rieke, V.; Pauly, K.B. MR thermometry. J. Magn. Reson. Imaging 2008, 27, 376–390. [Google Scholar] [CrossRef] [PubMed]
- Odéen, H.; Parker, D.L. Improved MR thermometry for laser interstitial thermotherapy. Lasers Surg. Med. 2019, 51, 286–300. [Google Scholar] [CrossRef] [PubMed]
- Frich, L. Non-invasive thermometry for monitoring hepatic radiofrequency ablation. Minim. Invasive Ther. Allied Technol. 2006, 15, 18–25. [Google Scholar] [CrossRef]
- Kickhefel, A.; Roland, J.; Weiss, C.; Schick, F. Accuracy of real-time MR temperature mapping in the brain: A comparison of fast sequences. Phys. Medica 2010, 26, 192–201. [Google Scholar] [CrossRef]
- Ozenne, V.; Bour, P.; De Senneville, B.D.; Toupin, S.; Vaussy, A.; Lepetit-Coiffé, M.; Jaïs, P.; Cochet, H.; Quesson, B. Assessment of left ventricle magnetic resonance temperature stability in patients in the presence of arrhythmias. NMR Biomed. 2019, 32, e4160. [Google Scholar] [CrossRef]
- Cernicanu, A.; Lepetit-Coiffe, M.; Roland, J.; Becker, C.; Terraz, S. Validation of fast MR thermometry at 1.5 T with gradient-echo echo planar imaging sequences: Phantom and clinical feasibility studies. NMR Biomed. 2008, 21, 849–858. [Google Scholar] [CrossRef]
- Stehling, M.K.; Turner, R.; Mansfield, P. Echo-planar imaging: Magnetic resonance imaging in a fraction of a second. Science 1991, 254, 43–50. [Google Scholar] [CrossRef]
- Griswold, M.A.; Fromm, M.; Heidemann, R.M.; Nittka, M.; Jellus, V.; Wang, J.; Kiefer, B.; Haase, A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002, 47, 1202–1210. [Google Scholar] [CrossRef]
- A Feinberg, D.; Hale, J.D.; Watts, J.C.; Kaufman, L.; Mark, A. Halving MR imaging time by conjugation: Demonstration at 3.5 kG. Radiology 1986, 161, 527–531. [Google Scholar] [CrossRef]
- Toupin, S.; Bour, P.; Lepetit-Coiffé, M.; Ozenne, V.; De Senneville, B.D.; Schneider, R.; Vaussy, A.; Chaumeil, A.; Cochet, H.; Sacher, F.; et al. Feasibility of real-time MR thermal dose mapping for predicting radiofrequency ablation outcome in the myocardium in vivo. J. Cardiovasc. Magn. Reson. 2017, 19, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Conturo, T.E.; Smith, G.D. Signal-to-noise in phase angle reconstruction: Dynamic range extension using phase reference offsets. Magn. Reson. Med. 1990, 15, 420–437. [Google Scholar] [CrossRef] [PubMed]
- Bazrafshan, B.; Hübner, F.; Farshid, P.; Hammerstingl, R.; Paul, J.; Vogel, V.; Mäntele, W.; Vogl, T.J. Temperature imaging of laser-induced thermotherapy (LITT) by MRI: Evaluation of different sequences in phantom. Lasers Med. Sci. 2013, 29, 173–183. [Google Scholar] [CrossRef] [PubMed]
- Taffoni, F.; Formica, D.; Saccomandi, P.; Di Pino, G.; Schena, E. Optical Fiber-Based MR-Compatible Sensors for Medical Applications: An Overview. Sensors 2013, 13, 14105–14120. [Google Scholar] [CrossRef] [PubMed]
- Wehrle, G.; Nohama, P.; Kalinowski, H.J.; Torres, P.I.; Valente, L.C.G. A fibre optic Bragg grating strain sensor for monitoring ventilatory movements. Meas. Sci. Technol. 2001, 12, 805–809. [Google Scholar] [CrossRef]
- Witt, J.; Narbonneau, F.; Schukar, M.; Krebber, K.; De Jonckheere, J.; Jeanne, M.; Kinet, D.; Paquet, B.; Depre, A.; D’Angelo, L.T.; et al. Medical Textiles With Embedded Fiber Optic Sensors for Monitoring of Respiratory Movement. IEEE Sensors J. 2011, 12, 246–254. [Google Scholar] [CrossRef]
- Tosi, D.; Macchi, E.G.; Cigada, A. Fiber-Optic Temperature and Pressure Sensors Applied to Radiofrequency Thermal Ablation in Liver Phantom: Methodology and Experimental Measurements. J. Sensors 2015, 2015, 1–22. [Google Scholar] [CrossRef]
- Samset, E.; Mala, T.; Edwin, B.; Gladhaug, I.; Søreide, O.; Fosse, E. Validation of estimated 3D temperature maps during hepatic cryo surgery. Magn. Reson. Imaging 2001, 19, 715–721. [Google Scholar] [CrossRef]
- Jelbuldina, M.; Korganbayev, S.; Seidagaliyeva, Z.; Sovetov, S.; Tuganbekov, T.; Tosi, D. Fiber Bragg Grating Sensor for Temperature Monitoring During HIFU Ablation of Ex Vivo Breast Fibroadenoma. IEEE Sensors Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Schena, E.; Tosi, D.; Saccomandi, P.; Lewis, E.; Kim, T. Fiber Optic Sensors for Temperature Monitoring during Thermal Treatments: An Overview. Sensors 2016, 16, 1144. [Google Scholar] [CrossRef]
- Gowardhan, B.; Greene, D. Cryotherapy for the prostate: An in vitro and clinical study of two new developments; advanced cryoneedles and a temperature monitoring system. BJU Int. 2007, 100, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Samset, E.; Mala, T.; Ellingsen, R.; Gladhaug, I.; Søreide, O.; Fosse, E. Temperature measurement in soft tissue using a distributed fibre Bragg-grating sensor system. Minim. Invasive Ther. Allied Technol. 2001, 10, 89–93. [Google Scholar] [CrossRef] [PubMed]
- Saccomandi, P.; Giraudau, C.; Davrieux, C.F.; Quero, G.; Schena, E.; Breschi, L.; Di Matteo, F.M.; Costamagna, G.; Marescaux, J. In vivo image-guided MR thermometry during laser ablation: Experience in kidney and liver. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Morra, F.; De Landro, M.; Korganbayev, S.; Wolf, A.; Dostovalov, A.; Cigada, A.; Saccomandi, P. Spatially resolved thermometry during laser ablation in tissues: Distributed and quasi-distributed fiber optic-based sensing. Opt. Fiber Technol. 2020, 58, 102295. [Google Scholar] [CrossRef]
- Allegretti, G.; Saccomandi, P.; Giurazza, F.; Caponero, M.; Frauenfelder, G.; Di Matteo, F.; Zobel, B.B.; Silvestri, S.; Schena, E. Magnetic resonance-based thermometry during laser ablation on ex-vivo swine pancreas and liver. Med. Eng. Phys. 2015, 37, 631–641. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J.; Member IEEE. Fiber grating sensors. J. Light. Technol. 1997, 15, 1442–1462. [Google Scholar] [CrossRef]
- Othonos, A.; Kalli, K.; Kohnke, G.E. Fiber Bragg Gratings: Fundamentals and Applications in Telecommunications and Sensing. Phys. Today 2000, 53, 61–62. [Google Scholar] [CrossRef]
- Dostovalov, A.V.; Wolf, A.; Parygin, A.; Zyubin, V.; Babin, S. Femtosecond point-by-point inscription of Bragg gratings by drawing a coated fiber through ferrule. Opt. Express 2016, 24, 16232–16237. [Google Scholar] [CrossRef]
- De Zwart, J.A.; Van Gelderen, P.; Kelly, D.J.; Moonen, C.T. Fast Magnetic-Resonance Temperature Imaging. J. Magn. Reson. Ser. B 1996, 112, 86–90. [Google Scholar] [CrossRef]
- Ozenne, V.; Toupin, S.; Bour, P.; De Senneville, B.D.; Lepetit-Coiffé, M.; Boissenin, M.; Benois-Pineau, J.; Hansen, M.S.; Inati, S.J.; Govari, A.; et al. Improved cardiac magnetic resonance thermometry and dosimetry for monitoring lesion formation during catheter ablation. Magn. Reson. Med. 2016, 77, 673–683. [Google Scholar] [CrossRef]
- Walker, P.; Lerski, R.; Vré, R.M.-D.; Binet, J.; Yane, F., VI. Preparation of agarose gels as reference substances for NMR relaxation time measurement. Magn. Reson. Imaging 1988, 6, 215–222. [Google Scholar] [CrossRef]
- Ernst, R.R.; Anderson, W.A. Application of Fourier Transform Spectroscopy to Magnetic Resonance. Rev. Sci. Instruments 1966, 37, 93–102. [Google Scholar] [CrossRef]
- Nelson, T.; Tung, S. Temperature dependence of proton relaxation times in vitro. Magn. Reson. Imaging 1987, 5, 189–199. [Google Scholar] [CrossRef]
- Hansen, M.S.; Sørensen, T.S. Gadgetron: An open source framework for medical image reconstruction. Magn. Reson. Med. 2013, 69, 1768–1776. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Saccomandi, P.; Massaroni, C.; Silvestri, S.; Giurazza, F.; Frauenfelder, G.; Zobel, B.B.; Schena, E. Feasibility assessment of magnetic resonance-thermometry on pancreas undergoing laser ablation: Sensitivity analysis of three sequences. Meas. J. Int. Meas. Confed. 2016, 80, 21–28. [Google Scholar] [CrossRef]







| Parameters | Experiments |
|---|---|
| Field of view [mm] | 96 × 96 |
| Matrix size [pixel] | 96 × 96 |
| Spatial resolution [mm3] | 1 × 1 × 2 |
| Pixel size after zero filling [mm3] | 0.5 × 0.5 × 2 |
| TR [ms] | 1000 |
| TE [ms] | 23 |
| Flip angle [°] | 45 |
| Bandwidth in read direction [Hz/pixel] | 1086 |
| Bandwidth in phase direction [Hz] | 666 |
| Total experiment duration [s] | 510 |
| Parameters | High Resolution 2D GRE |
|---|---|
| Field of view [mm] | 96 × 96 |
| Matrix size [pixel] | 416 × 416 |
| Spatial resolution [mm3] | 0.23 × 0.23 × 2 |
| TR [ms] | 100 |
| TE [ms] | 9.7 |
| Flip angle [°] | 35 |
| Bandwidth [Hz/pixel] | 100 |
| TA [s] | 703 |
| Number of slices | 3 |
| GRAPPA acceleration | 2 |
| Number of averages | 32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Landro, M.; Ianniello, J.; Yon, M.; Wolf, A.; Quesson, B.; Schena, E.; Saccomandi, P. Fiber Bragg Grating Sensors for Performance Evaluation of Fast Magnetic Resonance Thermometry on Synthetic Phantom. Sensors 2020, 20, 6468. https://doi.org/10.3390/s20226468
De Landro M, Ianniello J, Yon M, Wolf A, Quesson B, Schena E, Saccomandi P. Fiber Bragg Grating Sensors for Performance Evaluation of Fast Magnetic Resonance Thermometry on Synthetic Phantom. Sensors. 2020; 20(22):6468. https://doi.org/10.3390/s20226468
Chicago/Turabian StyleDe Landro, Martina, Jacopo Ianniello, Maxime Yon, Alexey Wolf, Bruno Quesson, Emiliano Schena, and Paola Saccomandi. 2020. "Fiber Bragg Grating Sensors for Performance Evaluation of Fast Magnetic Resonance Thermometry on Synthetic Phantom" Sensors 20, no. 22: 6468. https://doi.org/10.3390/s20226468
APA StyleDe Landro, M., Ianniello, J., Yon, M., Wolf, A., Quesson, B., Schena, E., & Saccomandi, P. (2020). Fiber Bragg Grating Sensors for Performance Evaluation of Fast Magnetic Resonance Thermometry on Synthetic Phantom. Sensors, 20(22), 6468. https://doi.org/10.3390/s20226468







