Blind Estimation Methods for BPSK Signal Based on Duffing Oscillator
Abstract
1. Introduction
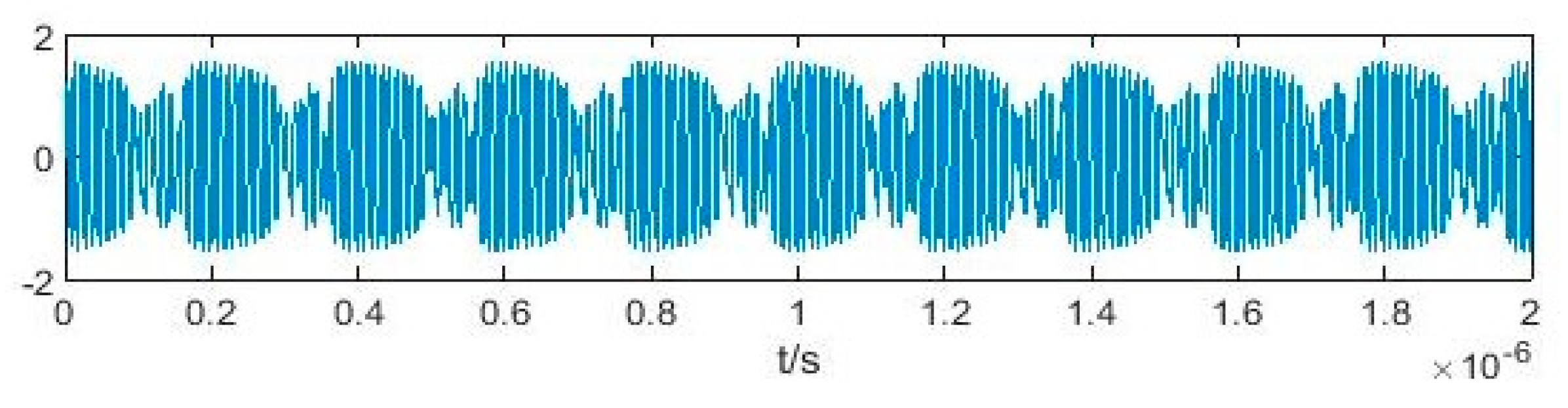
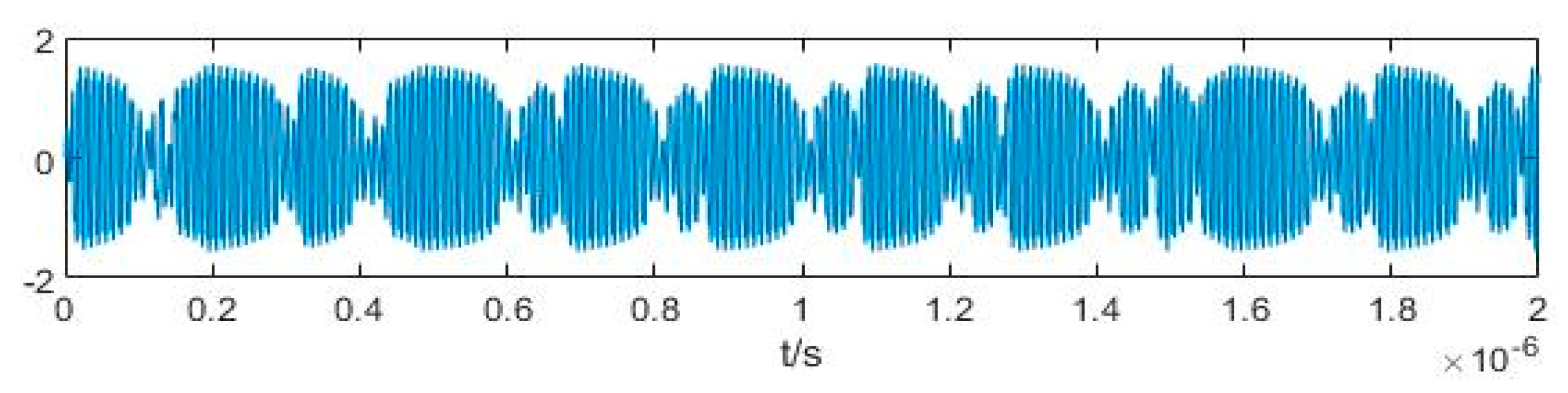
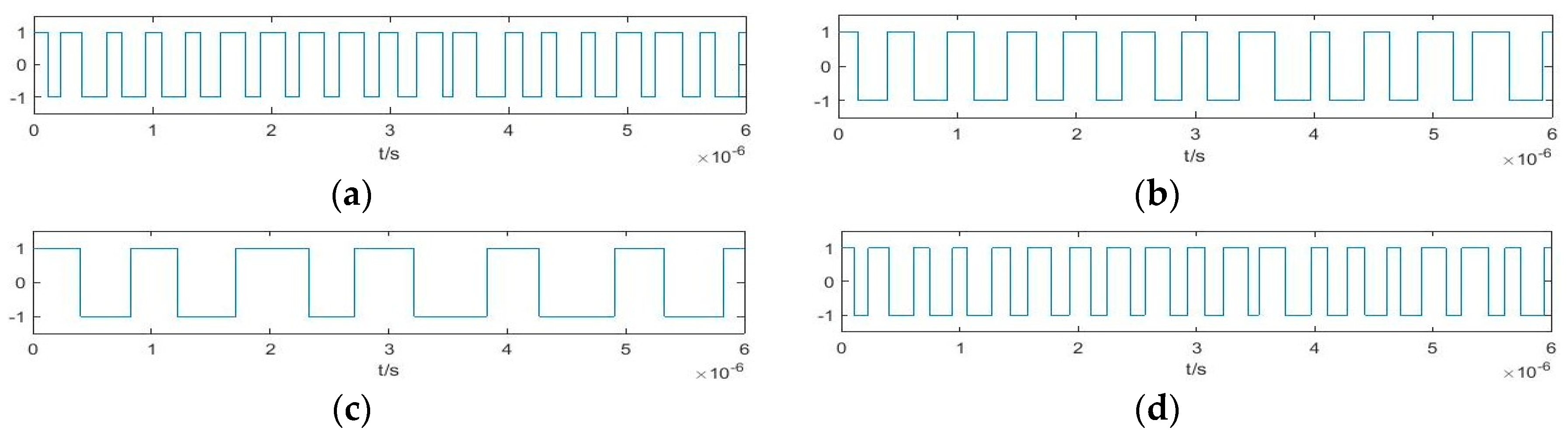
2. Relationship among Functions in Duffing Oscillator System under Intermittent Chaotic State Excited by BPSK Signal
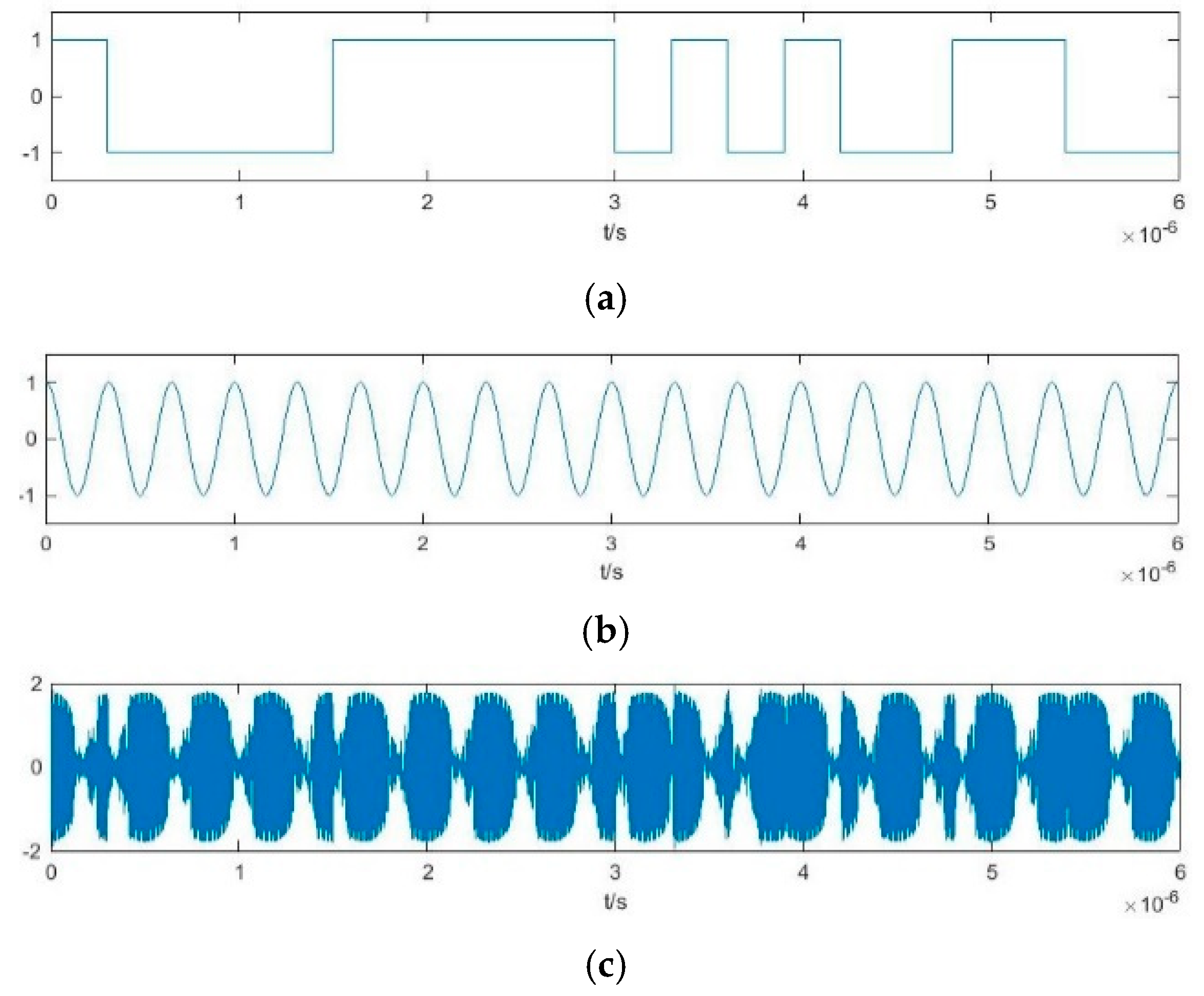
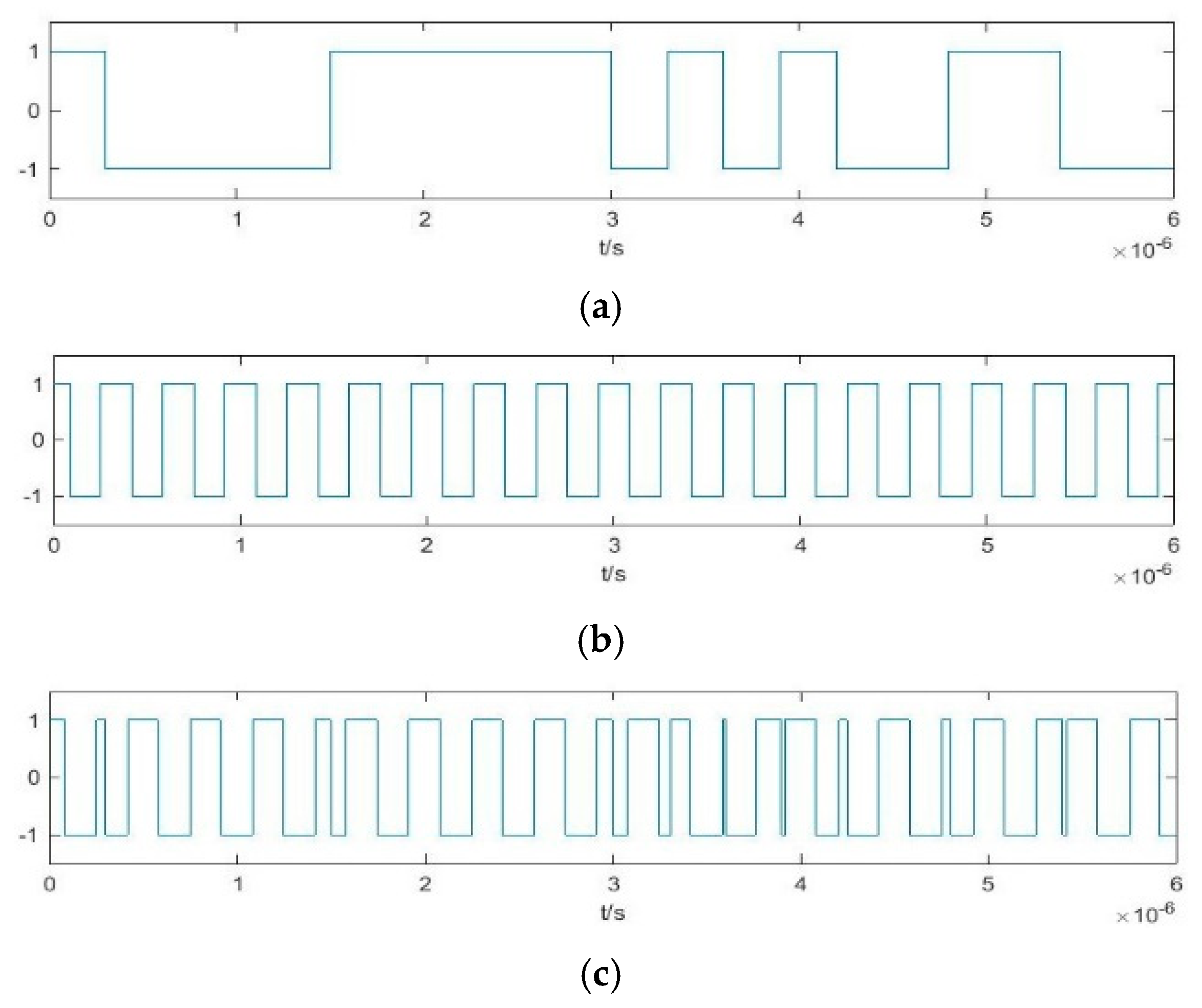
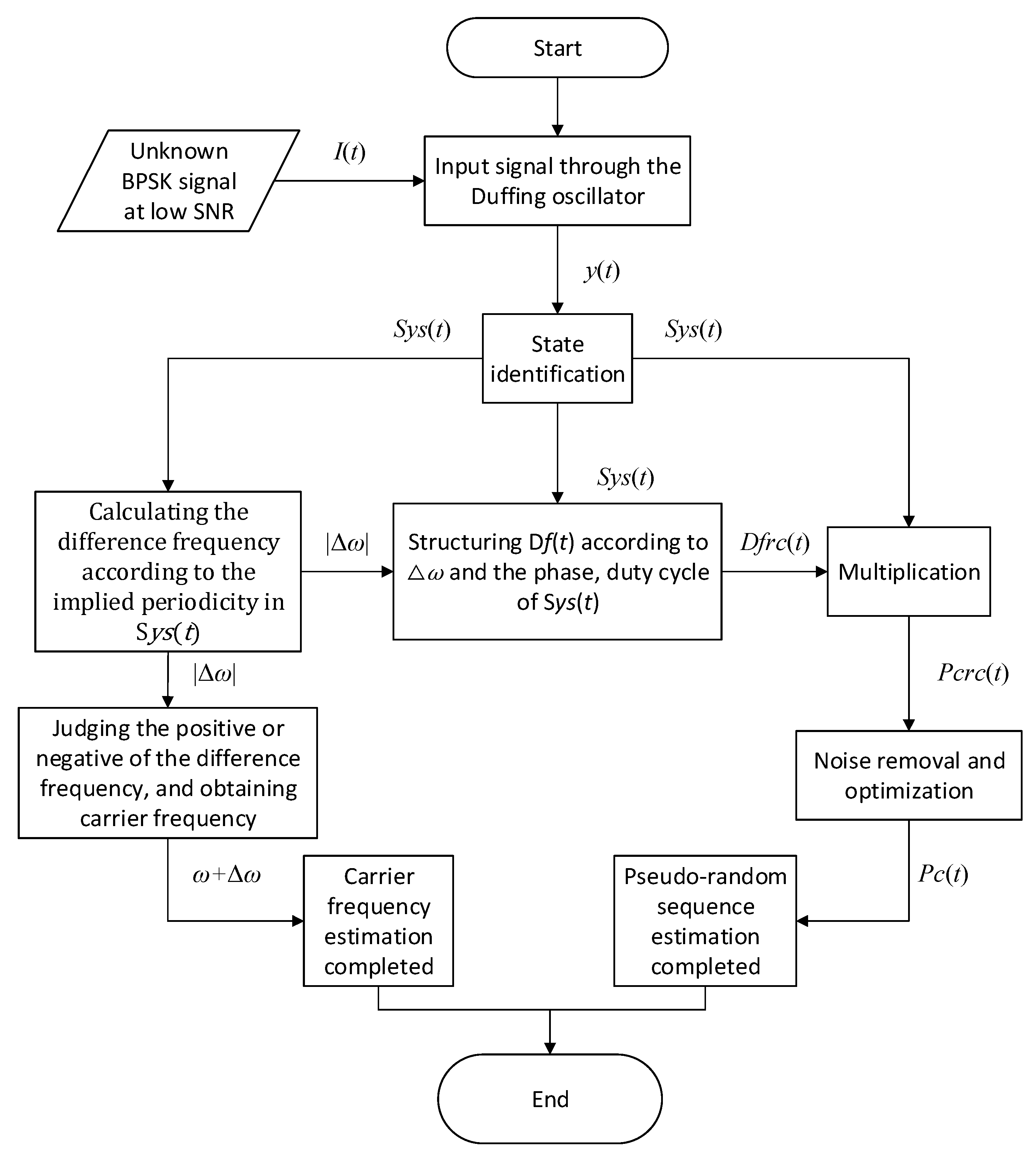
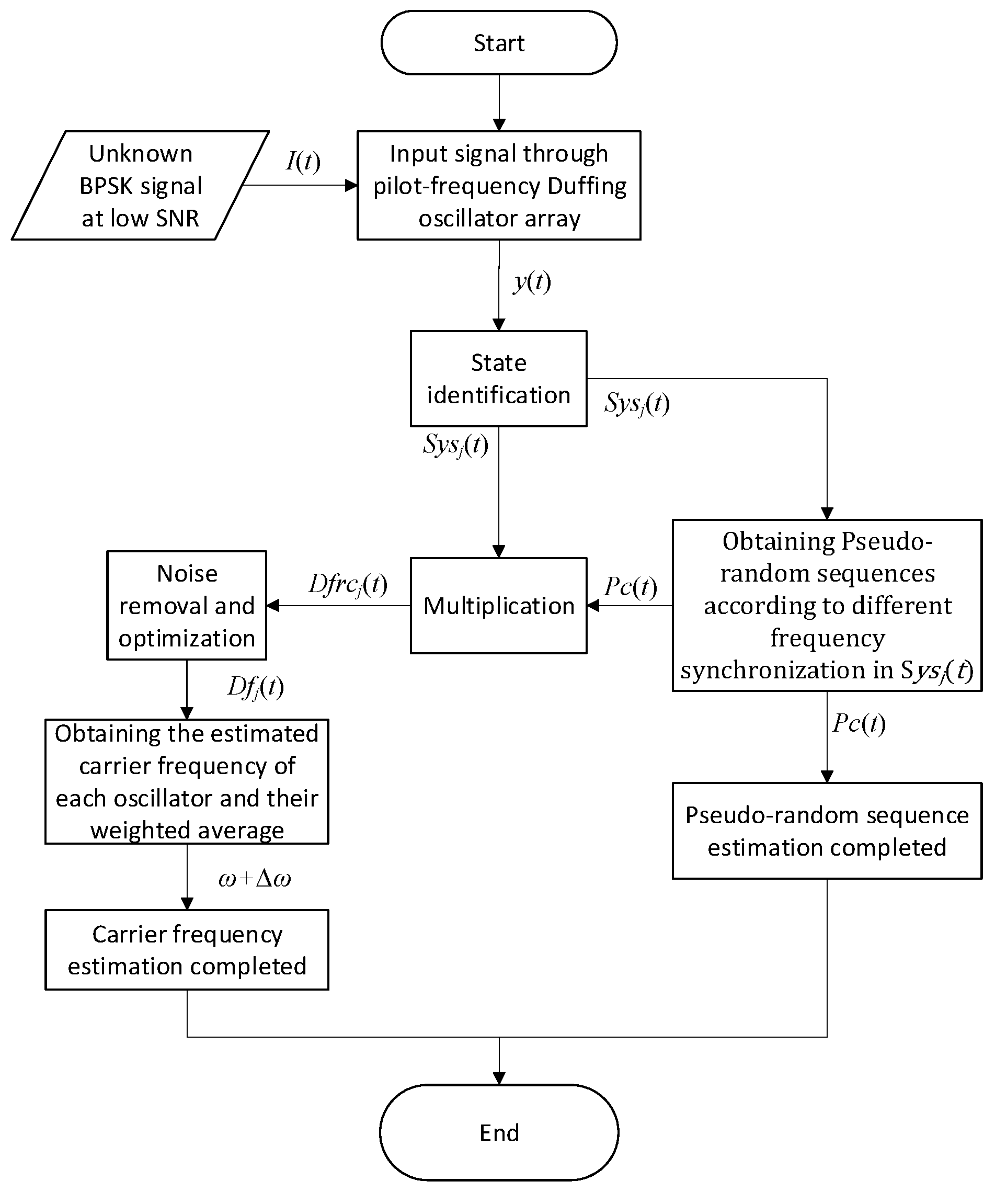
3. Parameter Estimation Method for BPSK Signals Based on Output Characteristics Including Implied Periodicity and Array Synchronization of Duffing Oscillator
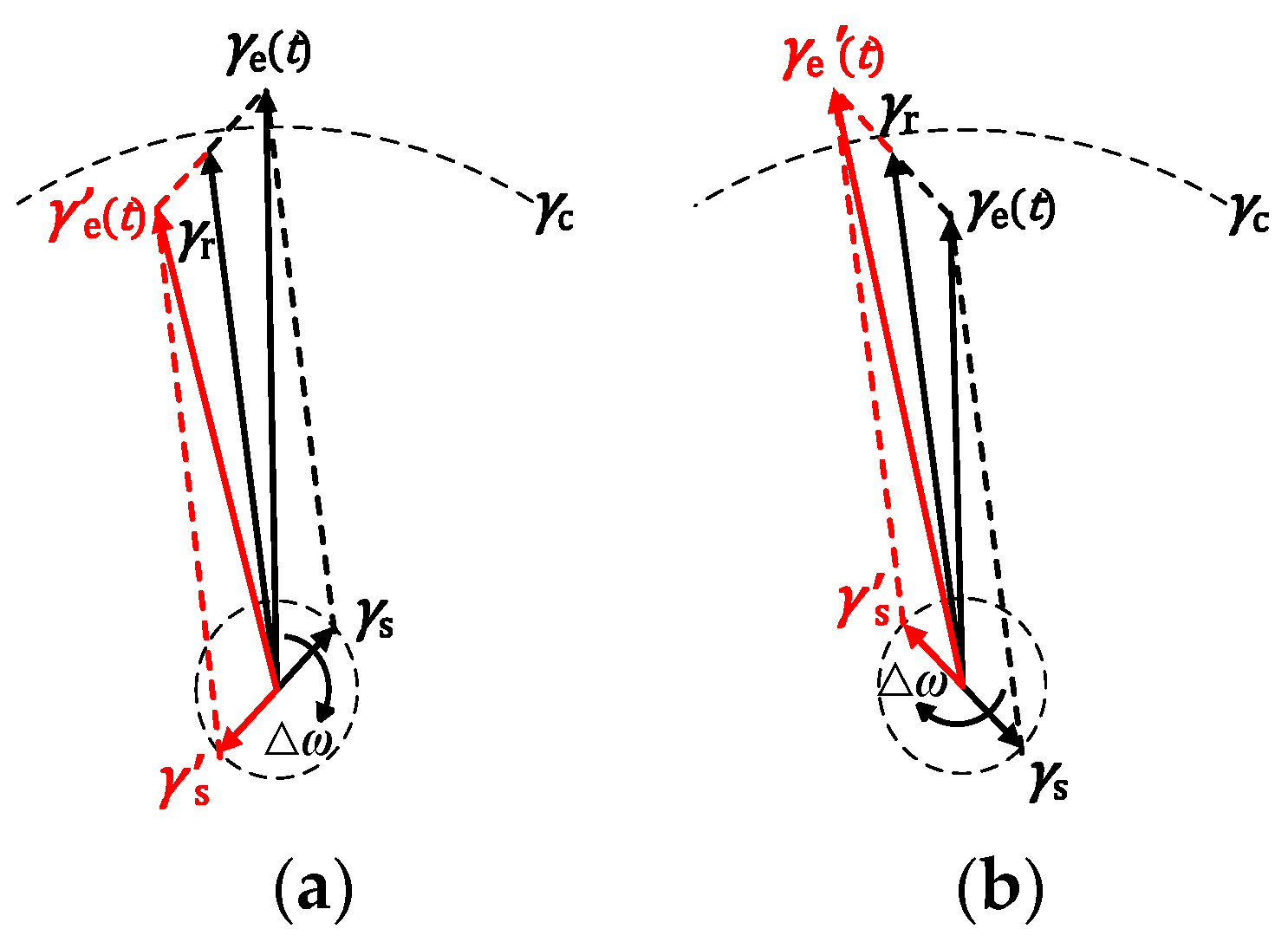
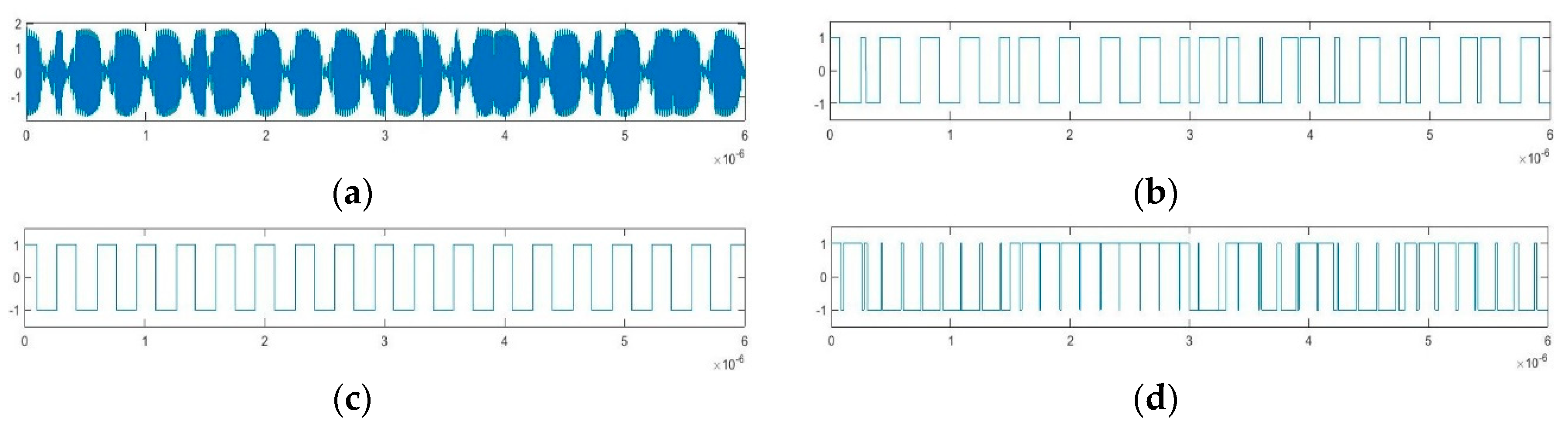
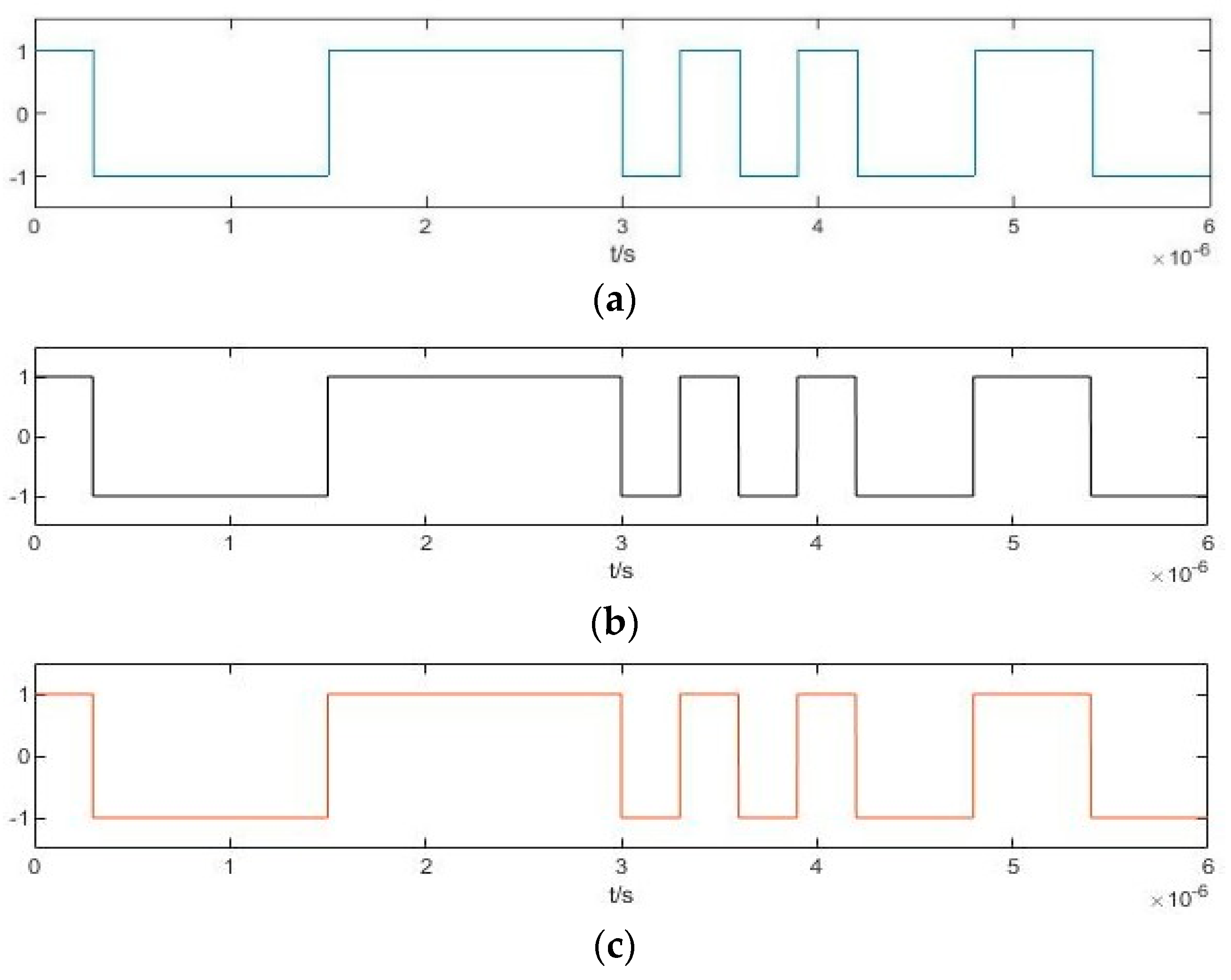
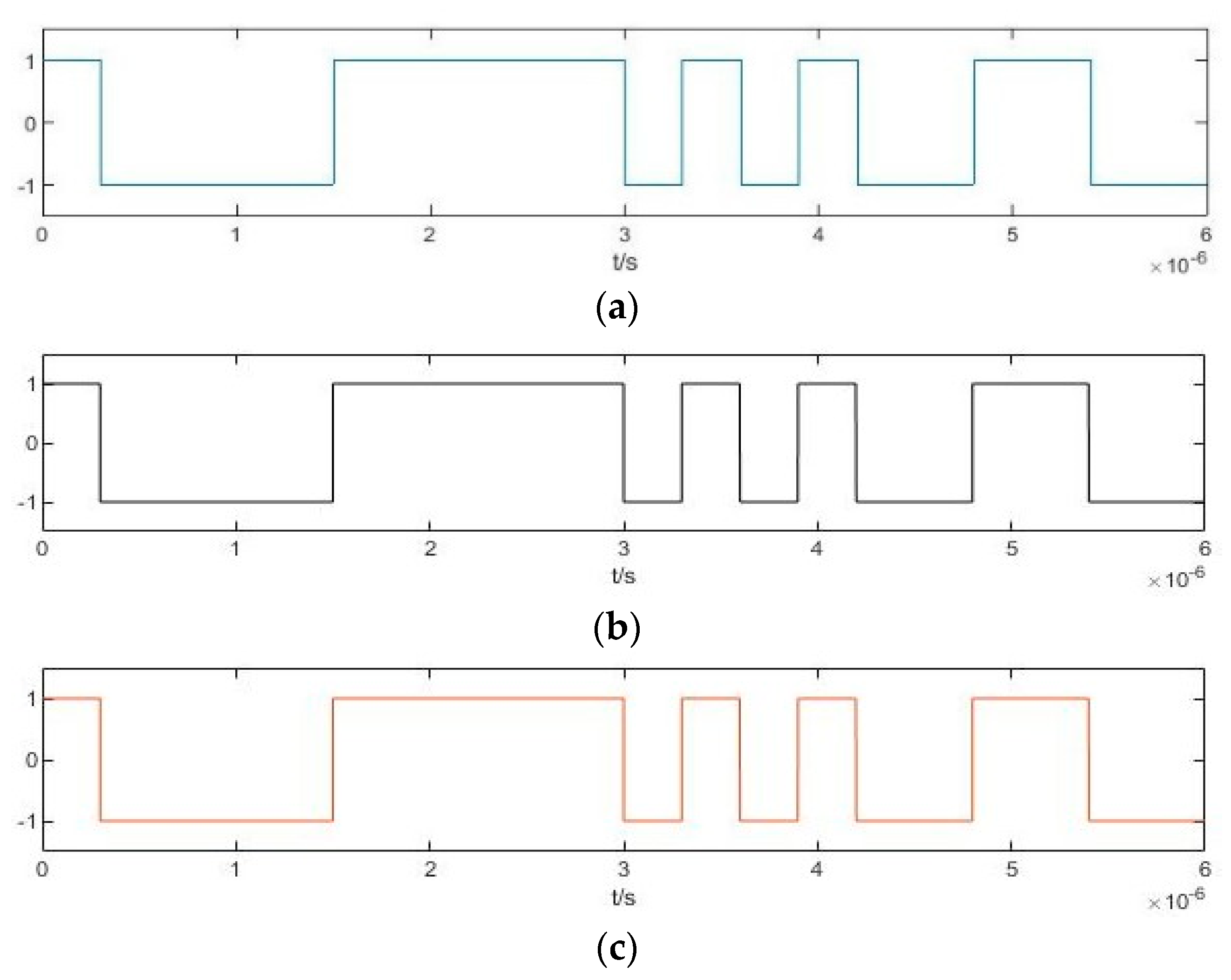
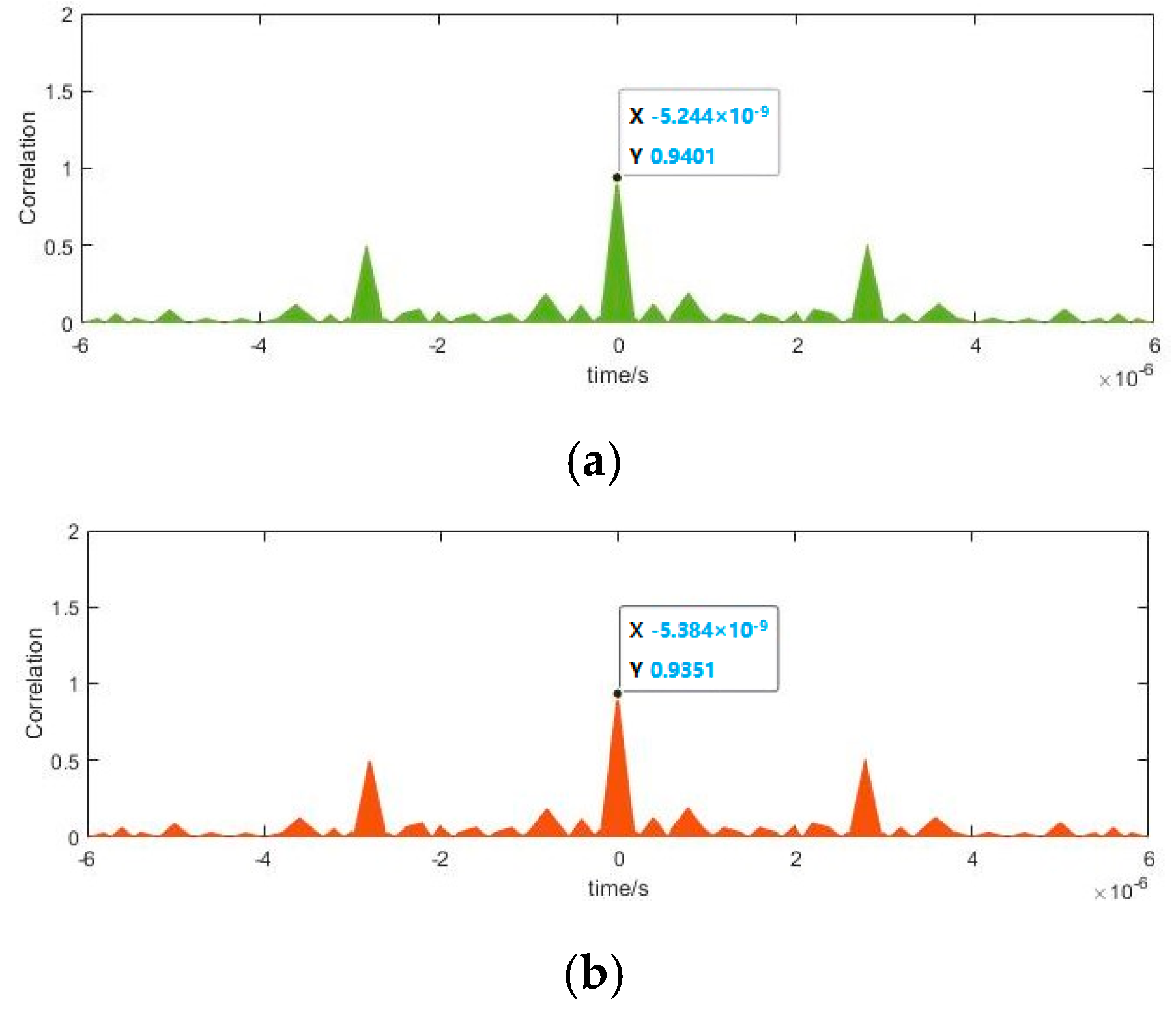
3.1. Parameter Estimation Method for BPSK Signals Based on Implied Periodicity
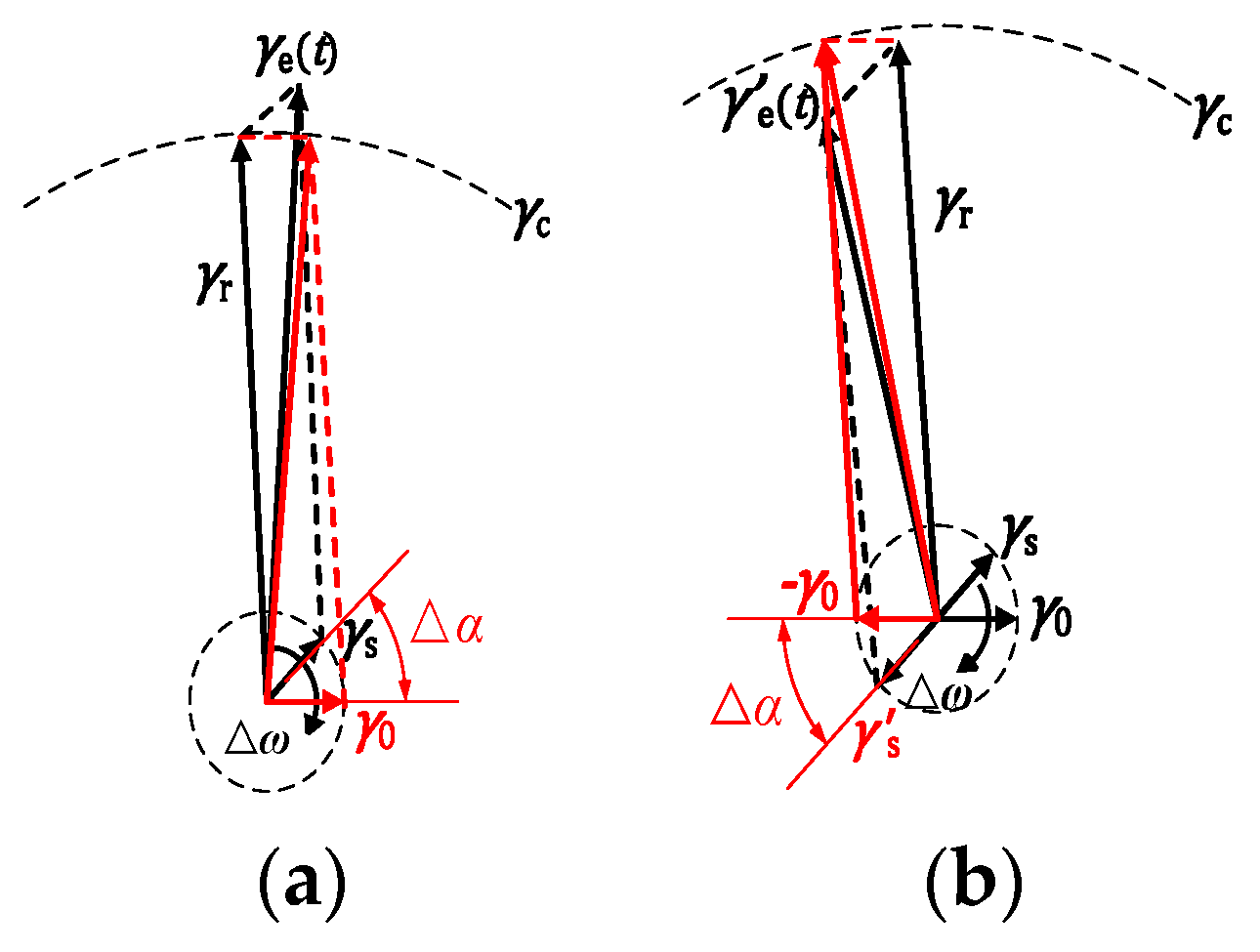
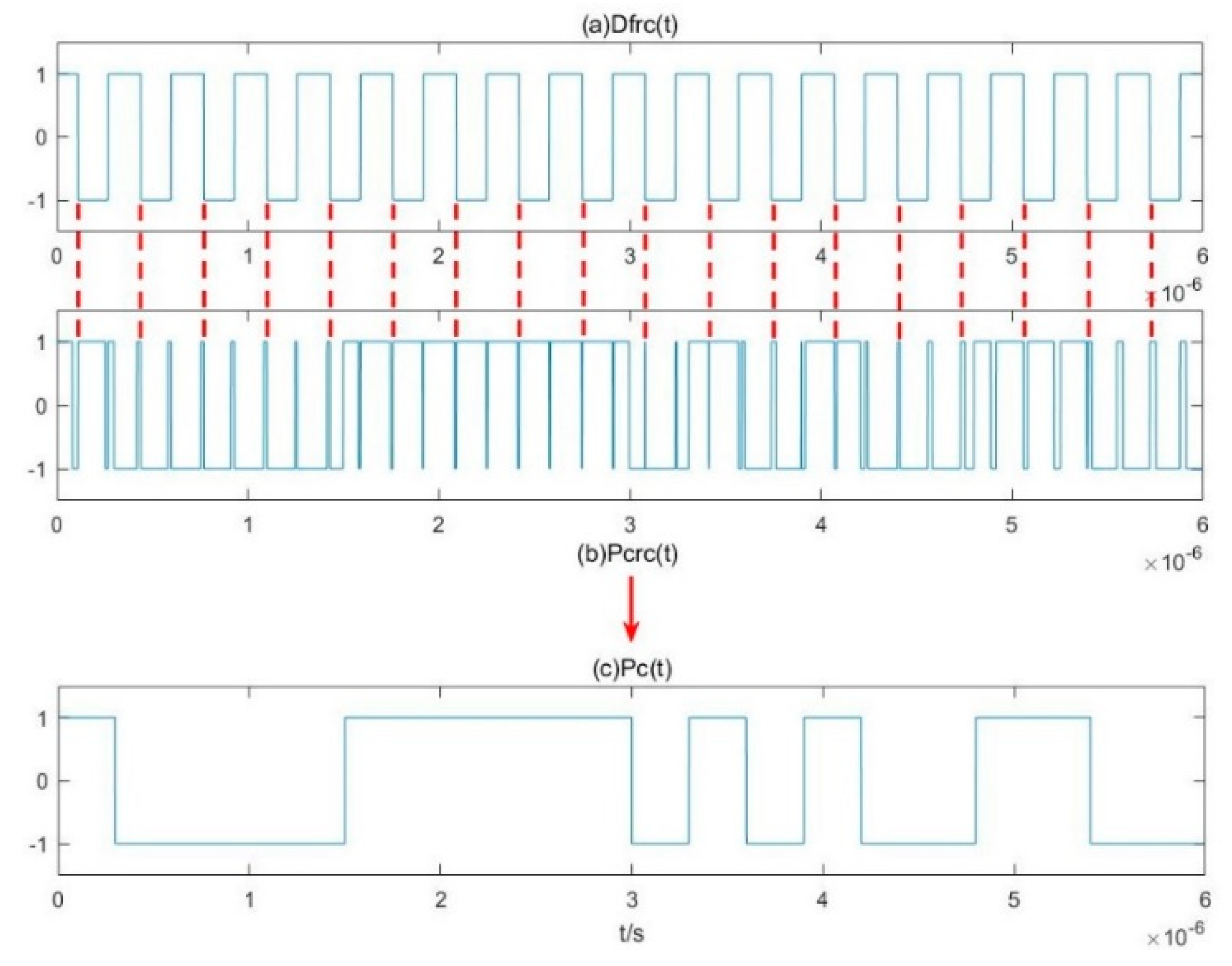
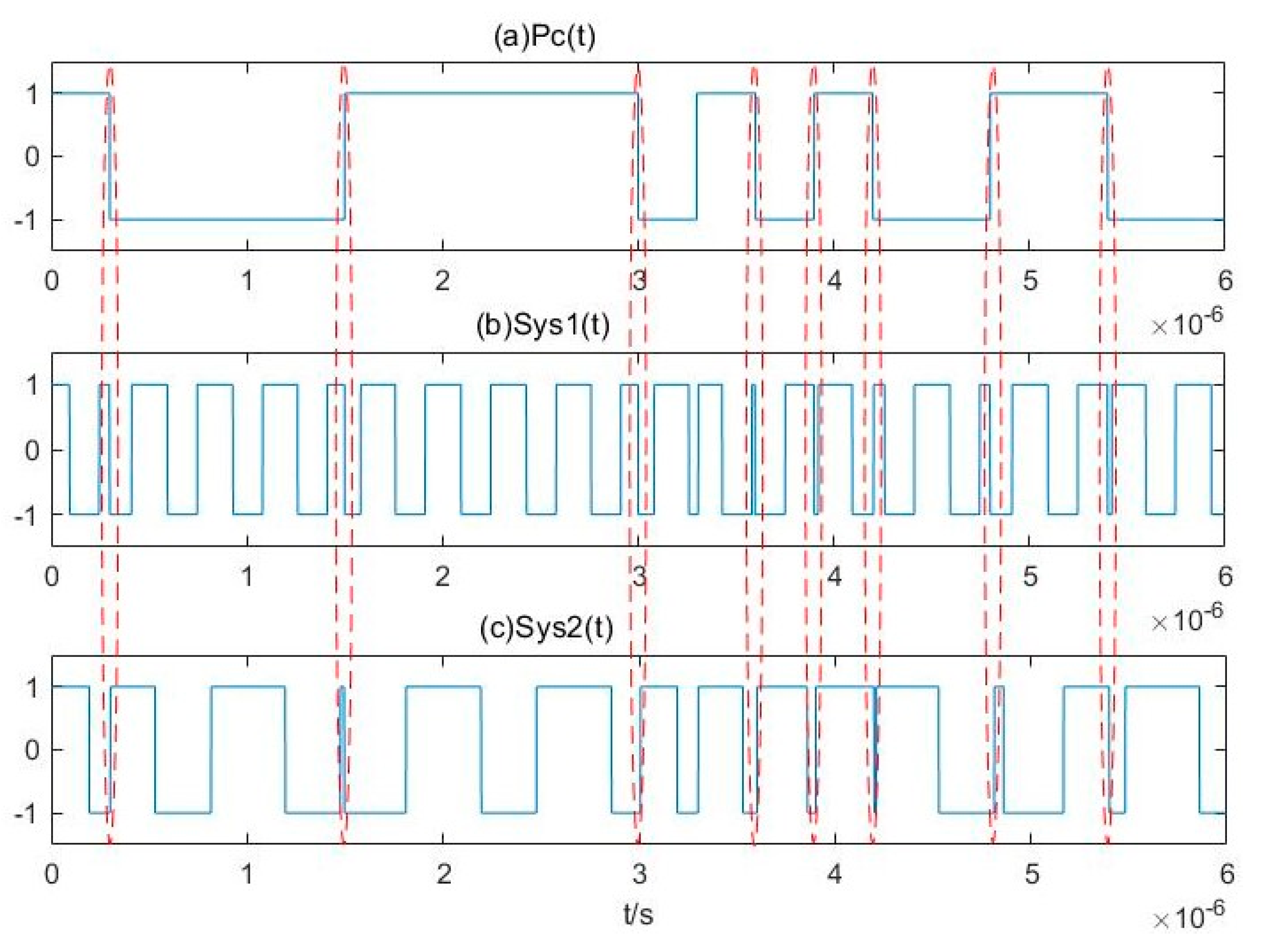
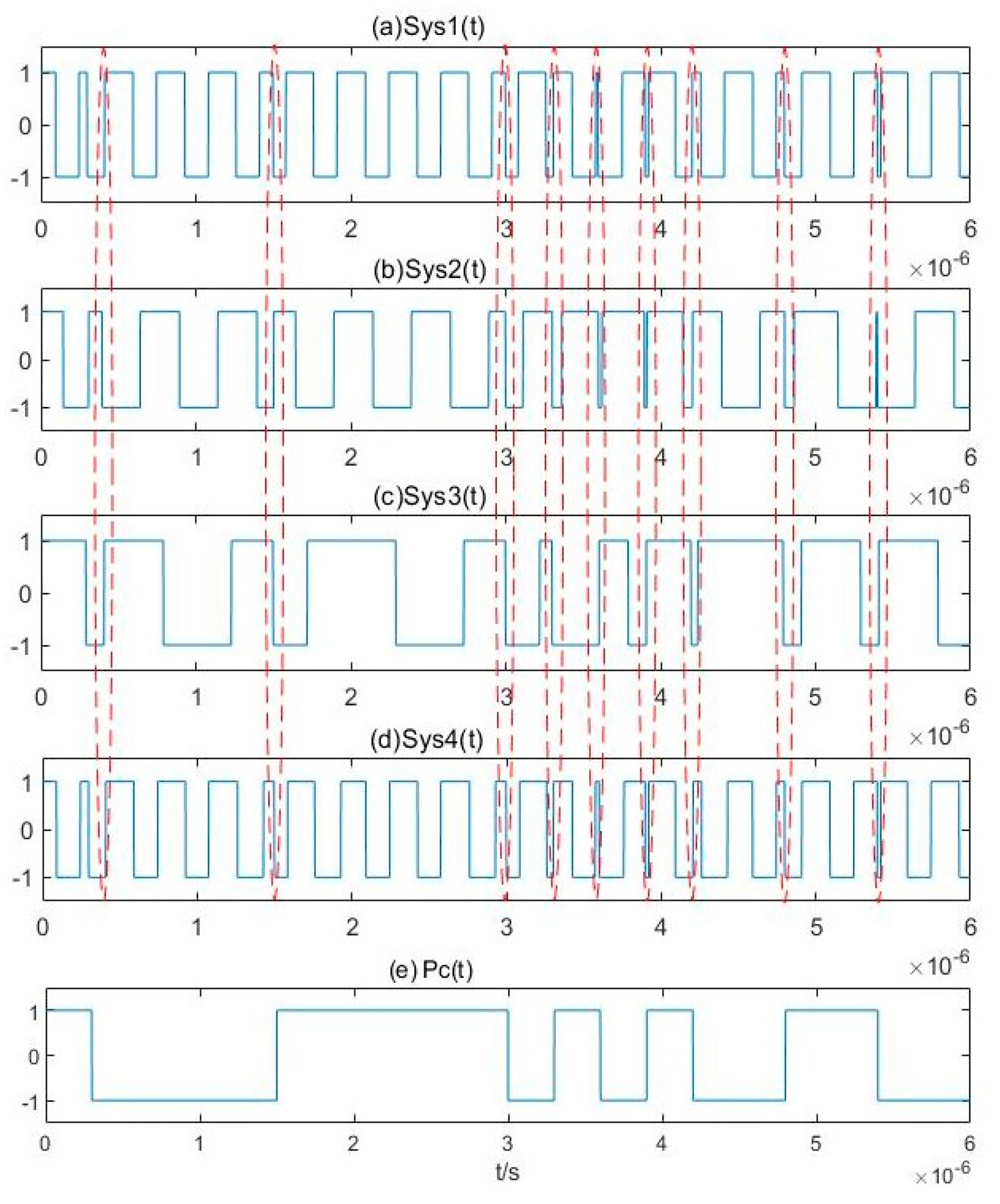
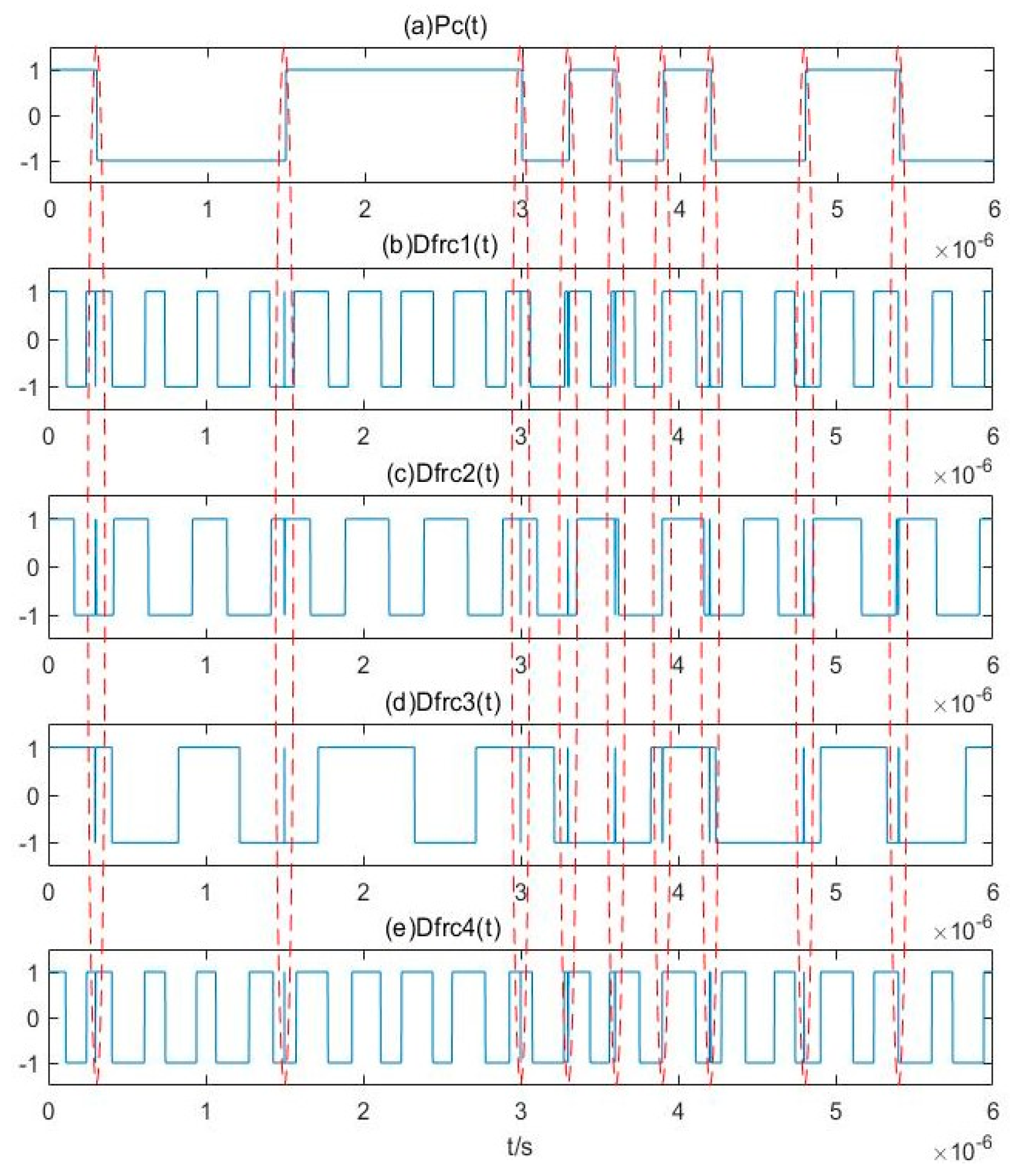
3.2. Parameter Estimation Method for BPSK Signals Based on Pilot Frequency Array Synchronization
4. Experimental Validation Using the BPSK Signal Parameter Estimation Method
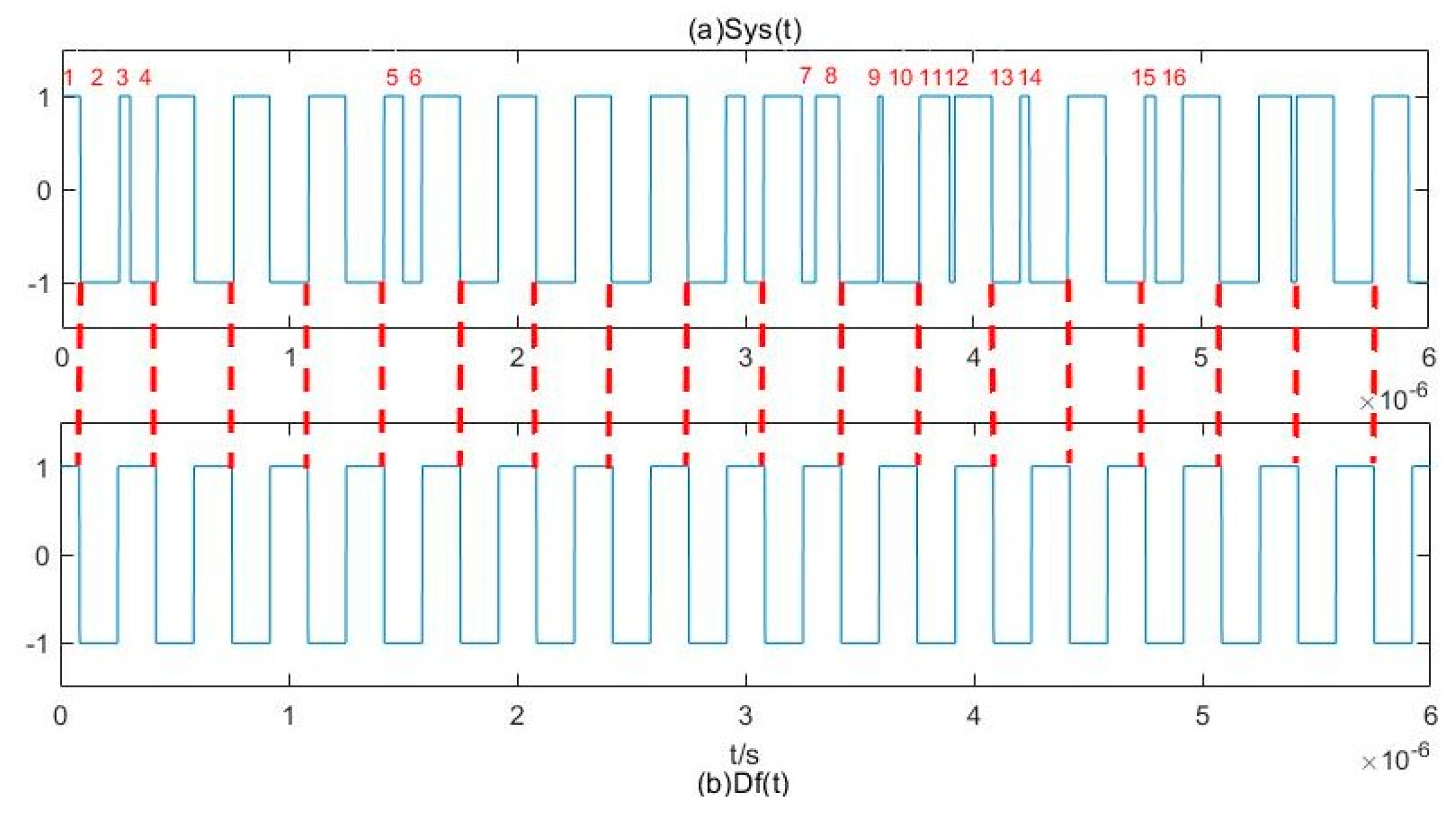
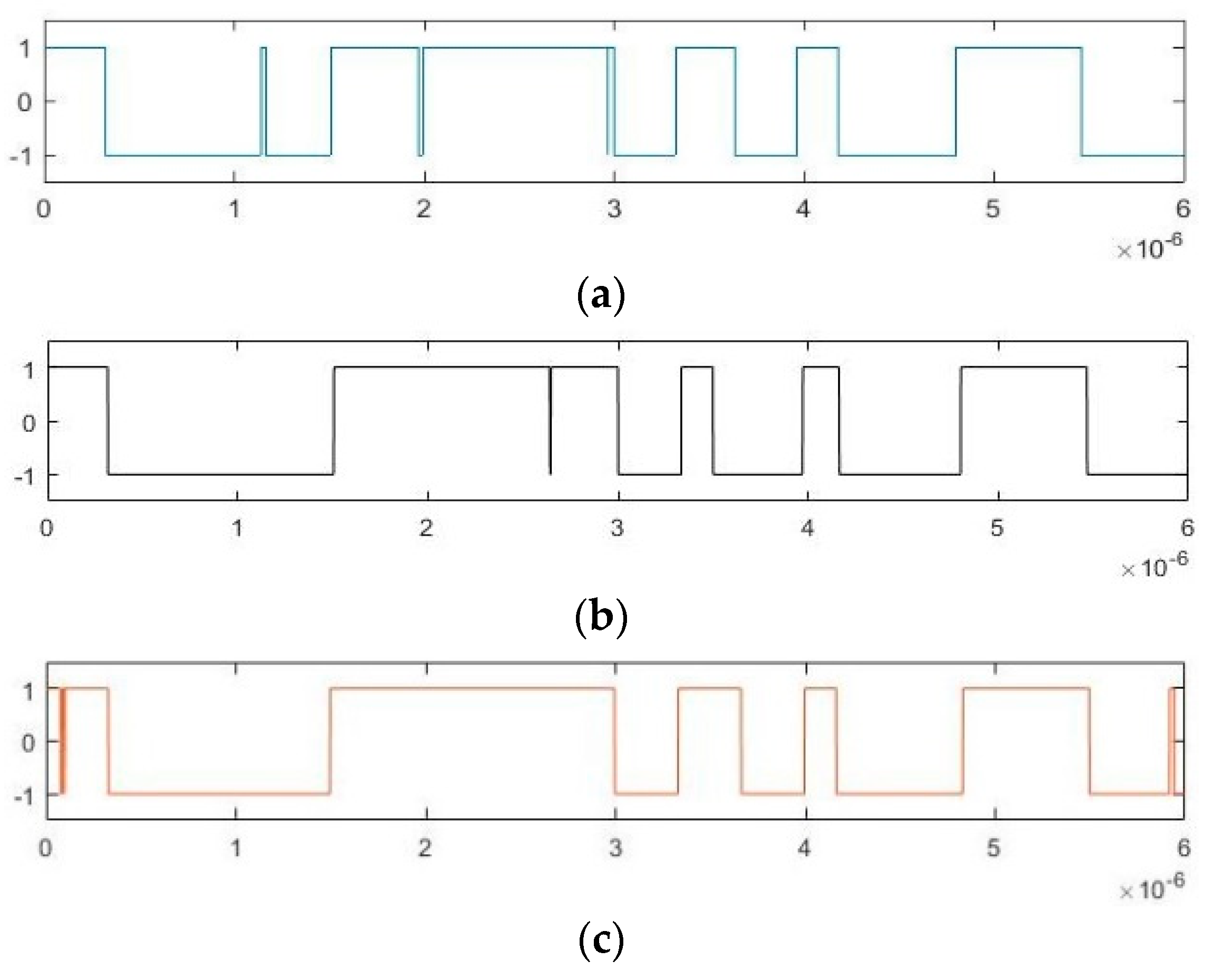
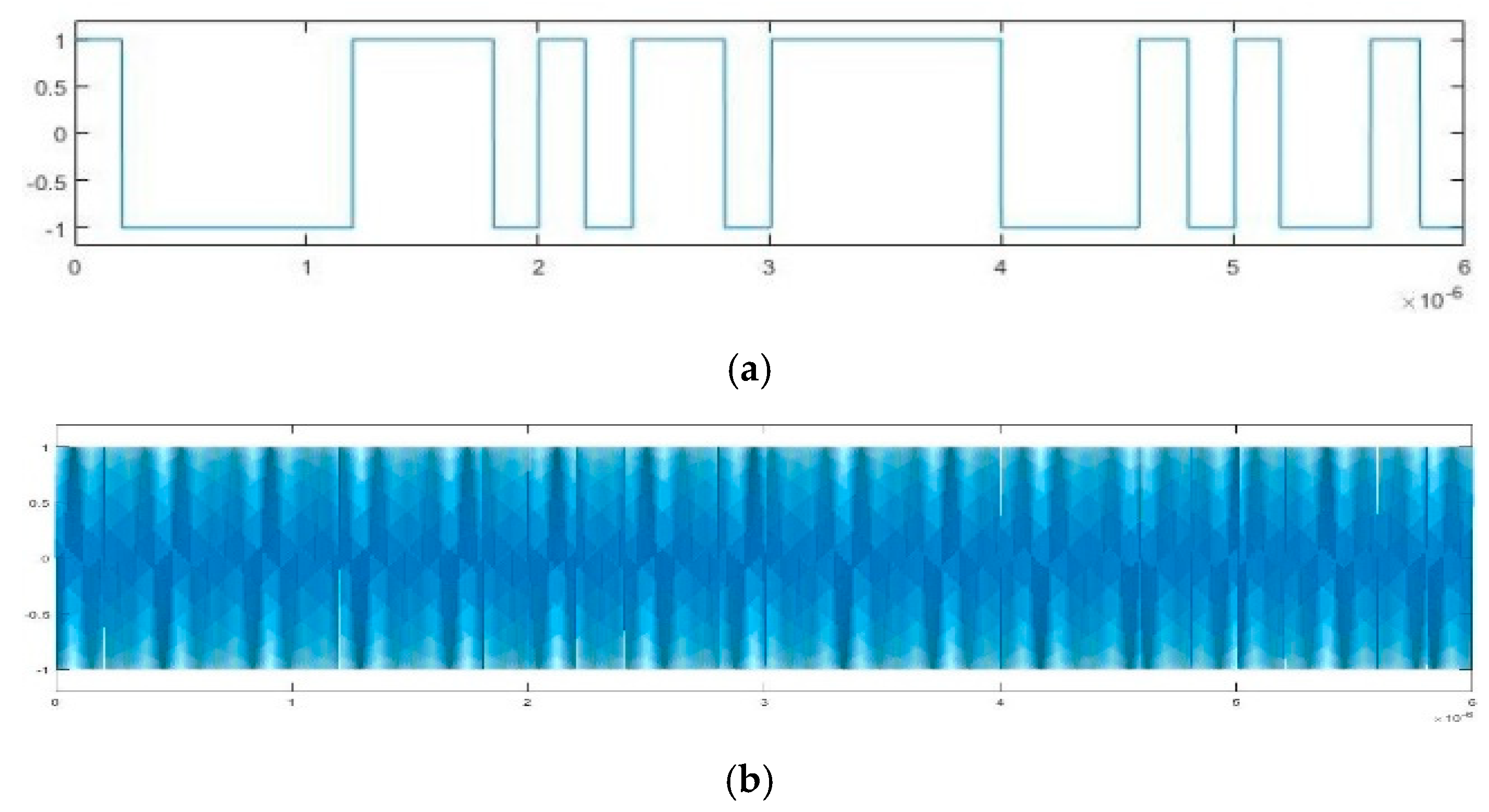
4.1. Simulation Experiment
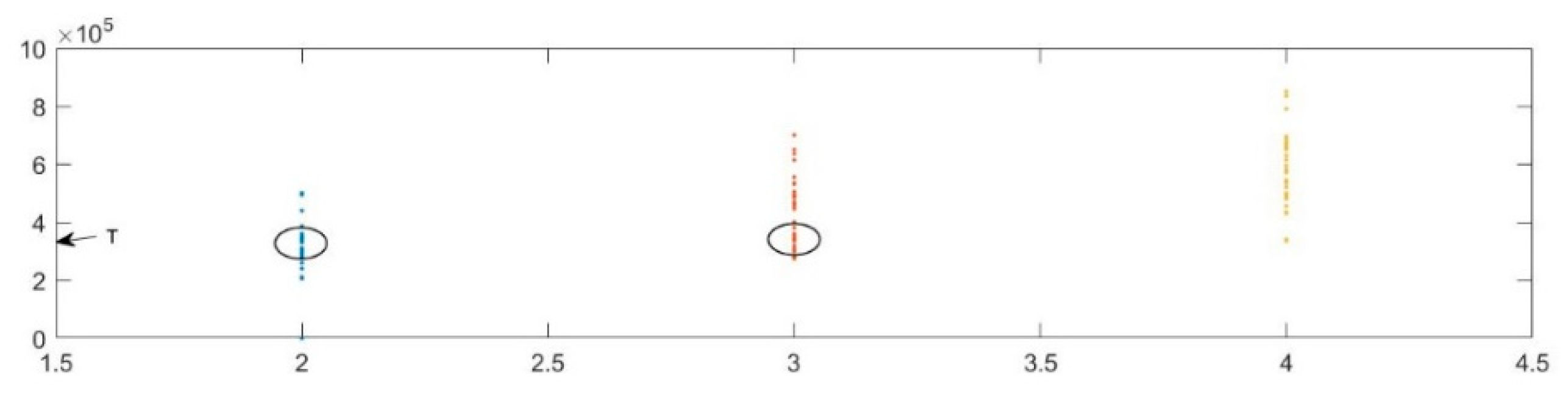
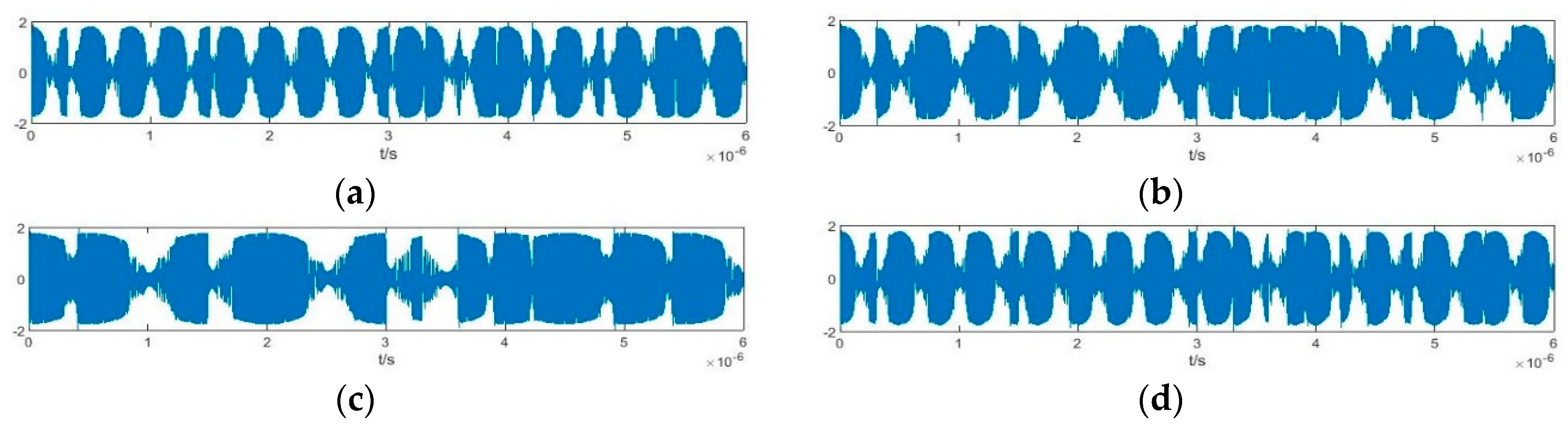
4.2. Semi-physical Simulation Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hannen, P. Radar and Electronic Warfare Principles for the Non-specialist. In Radar Electronic Warfare Principles for the Non-Specialist; Scitech Publishing: Raleigh, NC, USA, 2013. [Google Scholar]
- Golden, A., Jr. Radar Electronic Warfare; American Institute of Aeronautics and Astronautics (AIAA): Washington, DC, USA, 1987; ISBN 10 2514 4 403225. [Google Scholar]
- Hu, Y.; Sawan, M. A fully integrated low-power BPSK demodulator for implantable medical devices. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 2552–2562. [Google Scholar] [CrossRef]
- Nabovati, G.; Maymandi-Nejad, M. Ultra-low power BPSK demodulator for bio-implantable chips. IEICE Electron. Express 2010, 7, 1592–1596. [Google Scholar] [CrossRef][Green Version]
- Luo, Z.; Sonkusale, S. A Novel BPSK Demodulator for Biological Implants. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 1478–1484. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Luong, N.S.; Patzold, M. A method to estimate the path gains and propagation delays of underwater acoustic channels using the arrival phase information of the multipath components. AEU Int. J. Electron. Commun. 2017, 73, 129–138. [Google Scholar] [CrossRef]
- Jin, Y.; Ji, H. Cyclic Statistic Based Blind Parameter Estimation of BPSK and QPSK Signals. In Proceedings of the 2006 8th International Conference on Signal Processing, Guilin, China, 16–20 November 2006; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2006; Volume 1, ISBN 10 1109 2006 344452. [Google Scholar]
- Yang, W.; Yang, X.; Kuang, Y. Research on parameter estimation of MPSK signals based on the generalized second-order cyclic spectrum. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014. [Google Scholar] [CrossRef]
- Zhan, Y.; Duan, C. The application of stochastic resonance in parameter estimation for PSK signals. In Proceedings of the 2015 IEEE International Conference on Communication Software and Networks (ICCSN), Chengdu, China, 6–7 June 2015; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2015; pp. 166–172. [Google Scholar]
- Wang, Q.; Ge, Q. Blind estimation algorithm of parameters in PN sequence for DSSS-BPSK signals. In Proceedings of the 2012 International Conference on Wavelet Active Media Technology and Information Processing (ICWAMTIP), Chengdu, China, 17–19 December 2012; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2012; pp. 371–376. [Google Scholar]
- Guolin, L.; Min, H.; Ying, Z. PN Code Recognition and Parameter Estimation of PN-BPSK Signal Based on Synchronous Demodulation. In Proceedings of the 2007 8th International Conference on Electronic Measurement and Instruments, Xian, China, 16–18 August 2007; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2007; pp. 2–145. [Google Scholar]
- Gardner, W.; Spooner, C. Detection and source location of weak cyclostationary signals: Simplifications of the maximum-likelihood receiver. IEEE Trans. Commun. 1993, 41, 905–916. [Google Scholar] [CrossRef]
- Gardner, W.A.; Chen, C.-K. Signal-selective time-difference-of-arrival estimation for passive location of man-made signal sources in highly corruptive environments. I. Theory and method. IEEE Trans. Signal Process. 1992, 40, 1168–1184. [Google Scholar] [CrossRef]
- Akilli, M.; Yilmaz, N. Study of Weak Periodic Signals in the EEG Signals and Their Relationship with Postsynaptic Potentials. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1918–1925. [Google Scholar] [CrossRef] [PubMed]
- Vahedi, H.; Gharehpetian, G.B.; Karrari, M. Application of Duffing Oscillators for Passive Islanding Detection of Inverter-Based Distributed Generation Units. IEEE Trans. Power Deliv. 2012, 27, 1973–1983. [Google Scholar] [CrossRef]
- Rashtchi, V.; Nourazar, M. FPGA Implementation of a Real-Time Weak Signal Detector Using a Duffing Oscillator. Circuits Syst. Signal Process. 2015, 34, 3101–3119. [Google Scholar] [CrossRef]
- Patel, V.N.; Tandon, N.; Pandey, R.K. Defect detection in deep groove ball bearing in presence of external vibration using envelope analysis and Duffing oscillator. Measurement 2012, 45, 960–970. [Google Scholar] [CrossRef]
- Wang, G.Y.; Chen, D.J.; Lin, J.Y.; Chen, X. The application of chaotic oscillators to weak signal detection. IEEE Trans. Ind. Electron. 1999, 46, 440–444. [Google Scholar] [CrossRef]
- Liu, H.B.; Wu, D.W.; Yuan, Y.Y.; Yan, Z.J. New method for long-period DSSS/BPSK satellite signal carrier detection and power estimation. Syst. Eng. Electron. 2013, 7, 7. (In Chinese) [Google Scholar]
- Hu, J.; Wang, K. Carrier Detection Method of Binary-Phase-Shift-Keyed and Direct-Sequence-Spread-Spectrum Signals Based on Duffing Oscillator. Int. Conf. Telecommun. 2006, 1338–1341. [Google Scholar] [CrossRef]
- Zhang, S.; Rui, G.S. Chaotic detector for BPSK signals in very low SNR conditions. Int. J. Bifurc. Chaos 2012, 22, 1250144. [Google Scholar] [CrossRef]
- Fu, Y.Q.; Wu, D.M.; Zhang, L.; Li, X.Y. A circular zone partition method for identifying Duffing oscillator state transition and its application to BPSK signal demodulation. Sci. China Inf. Sci. 2011, 54, 1274–1282. [Google Scholar] [CrossRef]
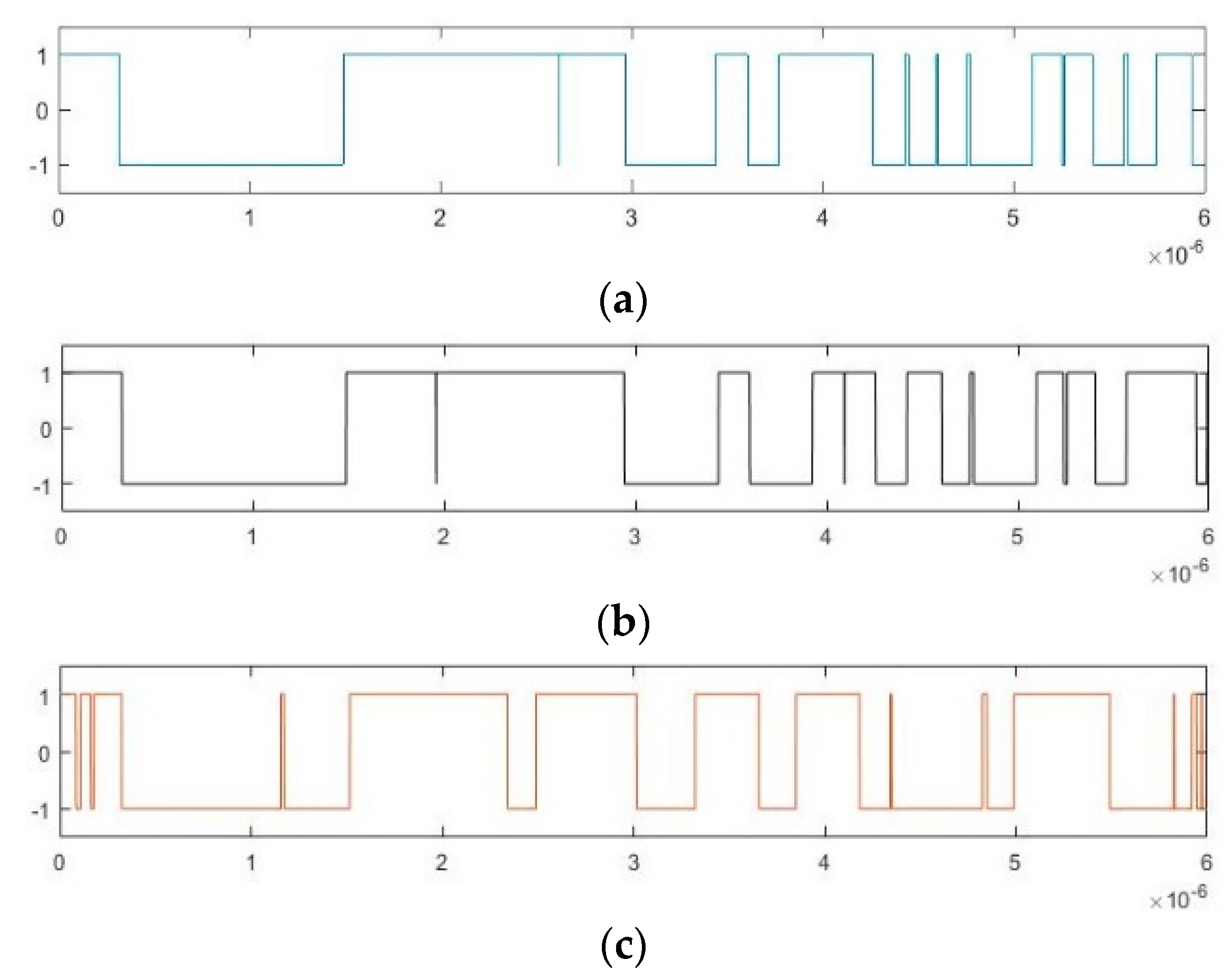
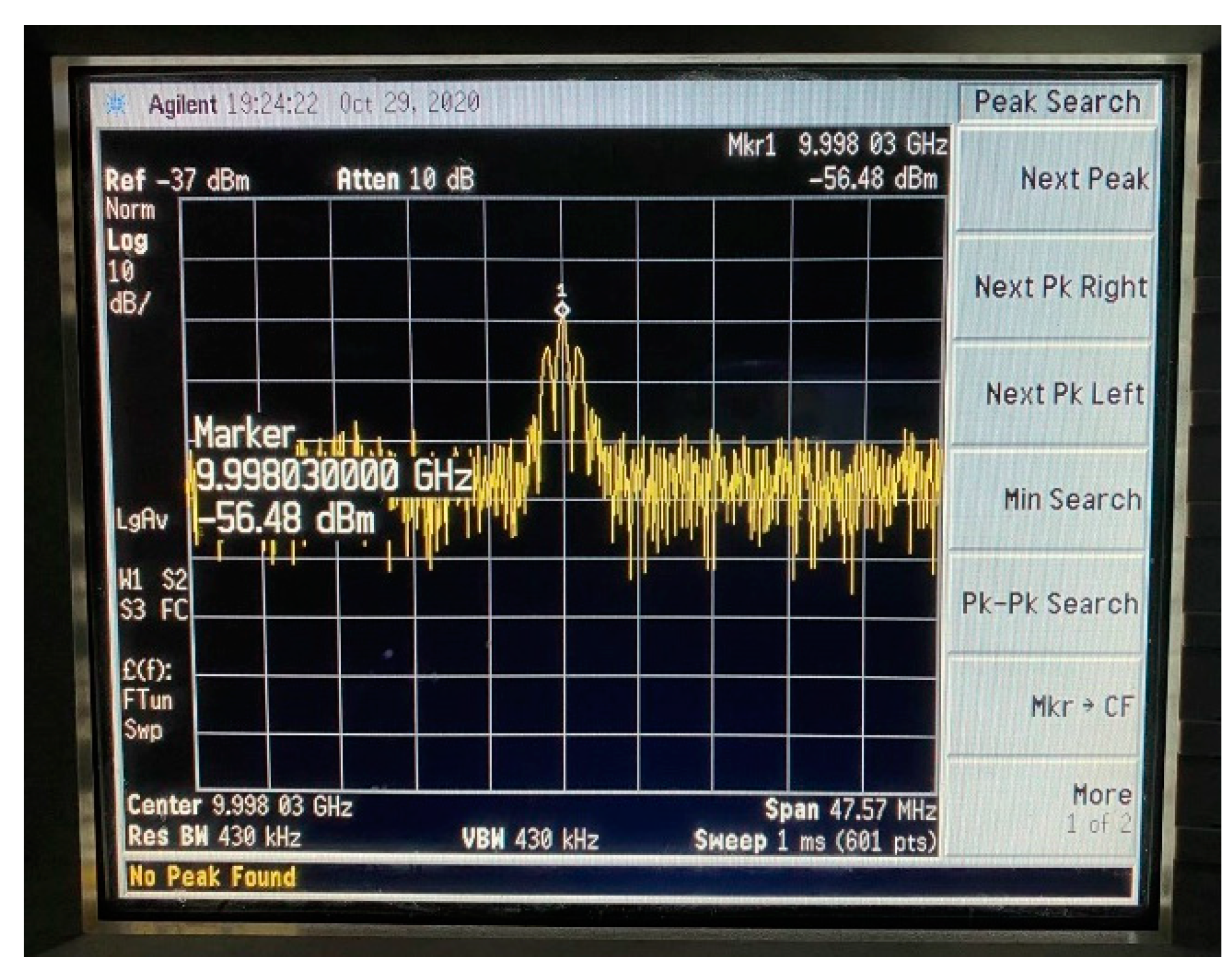
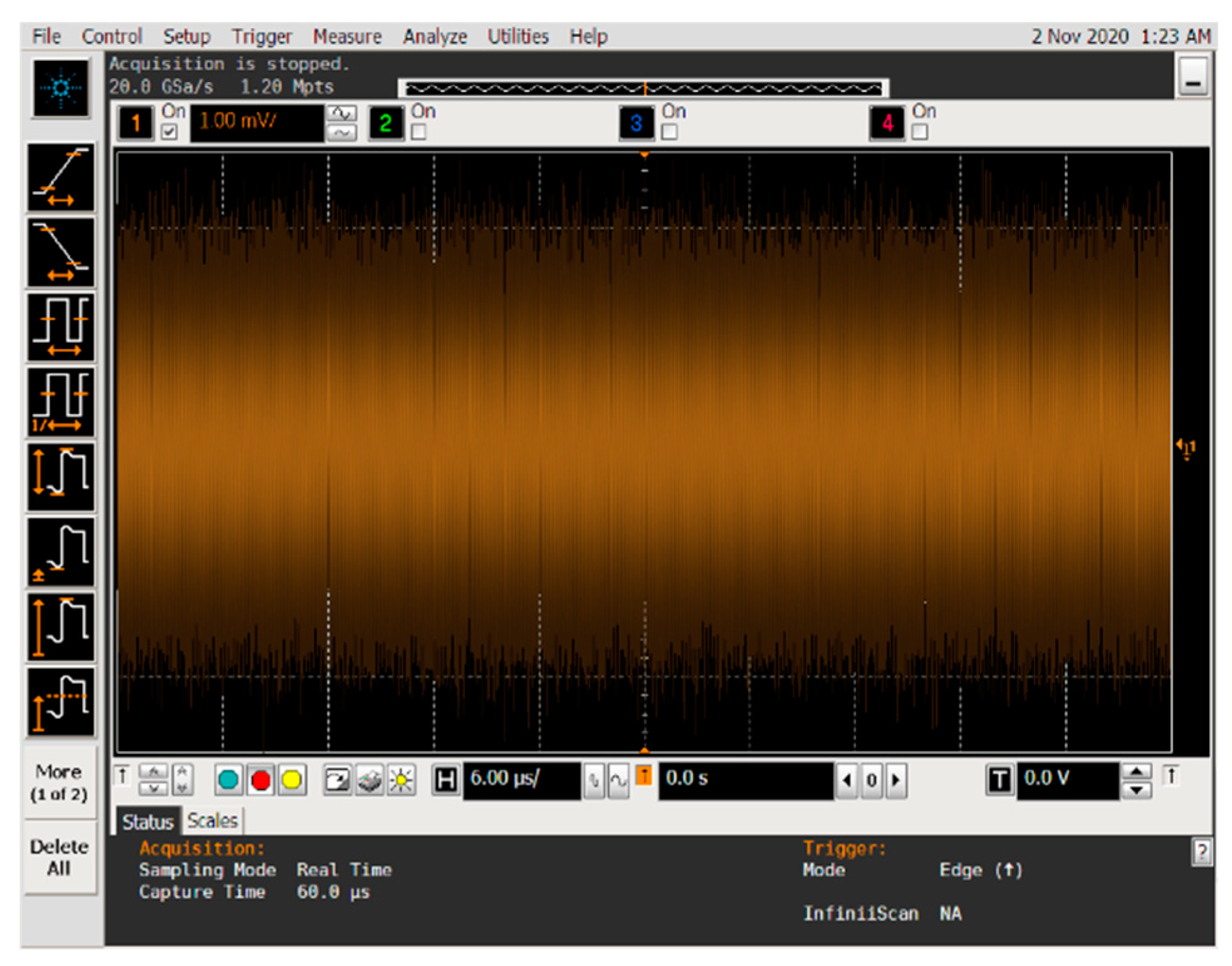
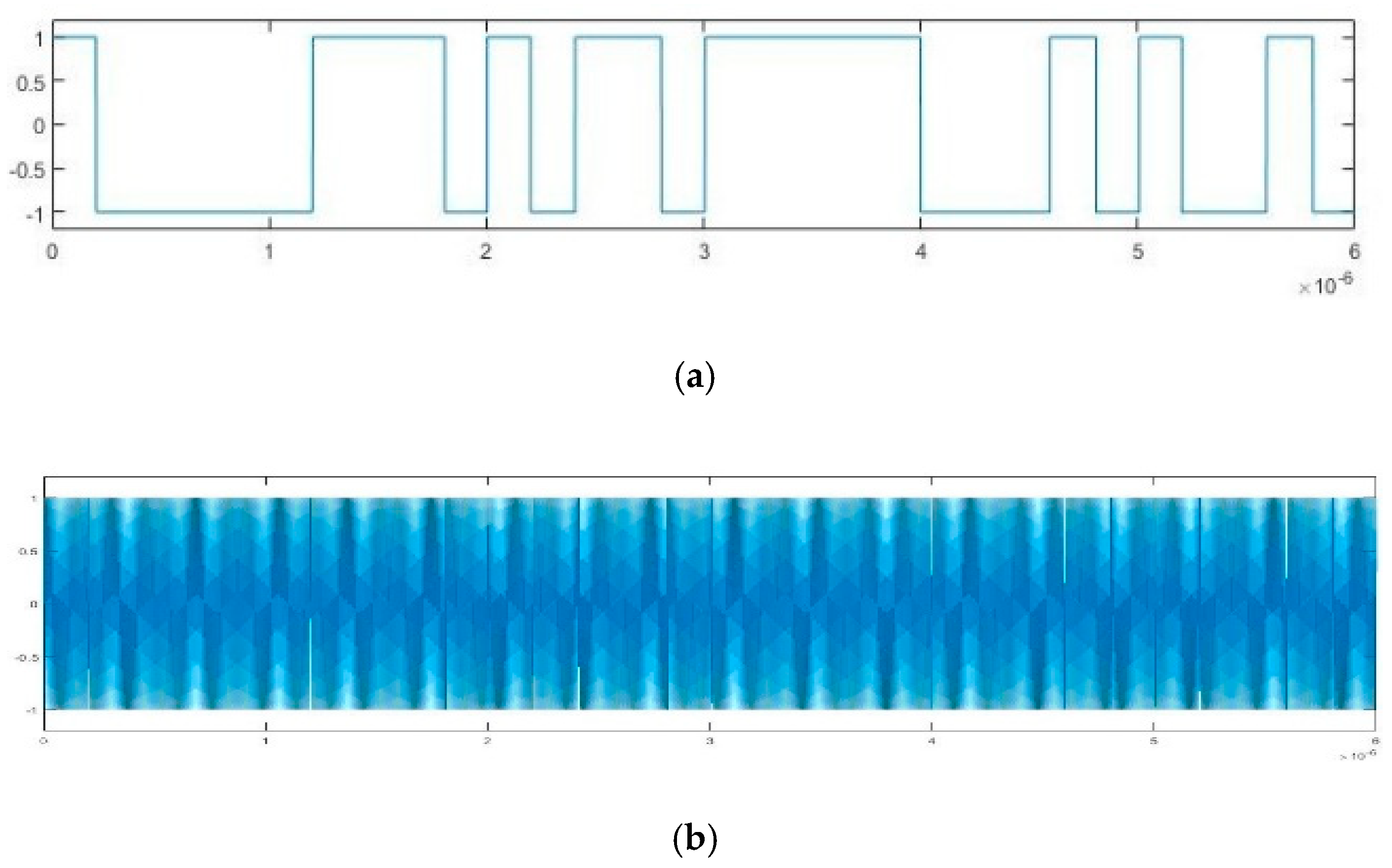
| sgn(cos(Δω + φ(t))) | φi = 0 | φi = π |
|---|---|---|
| t1 < t < t2 | 1 | −1 |
| t2 < t < t1 + 2π/|Δω| | −1 | 1 |
| Methods | Implied Periodicity | Pilot Frequency Array Synchronism | |
|---|---|---|---|
| Parameters | |||
| Duffing oscillator | a | 1 | 1 |
| b | 1 | 1 | |
| k | 0.5 | 0.5 | |
| Amplitude | 0.826 | 0.826 | |
| Frequency | 103 MHz, 98 MHz | 97 MHz, 98 MHz, 101 MHz, 103 MHz | |
| BPSK signal | Code Width | 30 ns | 30 ns |
| Amplitude | 0.6 | 0.6 | |
| Frequency | 100 MHz | 100 MHz |
| SNR/dB | Correlation Similarity Coefficients | ||
|---|---|---|---|
| Based on Implied Periodicity | Based on Array Synchronization | Based on Known Carrier Frequency | |
| −10 | 0.9627 | 0.9725 | 0.9740 |
| −20 | 0.9543 | 0.9703 | 0.9683 |
| −30 | 0.9470 | 0.9627 | 0.9604 |
| −35 | 0.9120 | 0.9156 | 0.9230 |
| −40 | 0.8205 | 0.8208 | 0.8231 |
| SNR/dB | Carrier Frequency Estimation Relative Error (%) | |
|---|---|---|
| Based on Implied Periodicity | Based on Array Synchronization | |
| −10 | 0.0101 | 0.0142 |
| −20 | 0.0112 | 0.0327 |
| −30 | 0.0355 | 0.0491 |
| −35 | 0.0828 | 0.0895 |
| −40 | 0.2470 | 0.2794 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Yan, X.; Zhu, Z.; Hao, X.; Li, P.; Yang, Q. Blind Estimation Methods for BPSK Signal Based on Duffing Oscillator. Sensors 2020, 20, 6412. https://doi.org/10.3390/s20226412
Wang K, Yan X, Zhu Z, Hao X, Li P, Yang Q. Blind Estimation Methods for BPSK Signal Based on Duffing Oscillator. Sensors. 2020; 20(22):6412. https://doi.org/10.3390/s20226412
Chicago/Turabian StyleWang, Ke, Xiaopeng Yan, Zhiqiang Zhu, Xinhong Hao, Ping Li, and Qian Yang. 2020. "Blind Estimation Methods for BPSK Signal Based on Duffing Oscillator" Sensors 20, no. 22: 6412. https://doi.org/10.3390/s20226412
APA StyleWang, K., Yan, X., Zhu, Z., Hao, X., Li, P., & Yang, Q. (2020). Blind Estimation Methods for BPSK Signal Based on Duffing Oscillator. Sensors, 20(22), 6412. https://doi.org/10.3390/s20226412





