Capacitive-Coupling Impedance Spectroscopy Using a Non-Sinusoidal Oscillator and Discrete-Time Fourier Transform: An Introductory Study
Abstract
1. Introduction
- (1)
- By coupling electrodes capacitively to the measured object and by incorporating the resulting couplings into an oscillation circuit, an alternating current is applicable inside the object covered with a thin insulating layer.
- (2)
- By measuring the amplitude and phase of the object’s current and those of the object’s potential difference resulting from oscillation, even with unknown coupling capacitance, the impedance of the object is measurable.
- (3)
- By estimating the impedance of the measured object from the amplitude and phase spectrum obtained from the waveform of a few oscillation cycles, the temporal resolution of IS is improved.
- (4)
- By making the oscillation waveform a non-sinusoidal wave, the fundamental frequency of oscillation and its higher harmonic waves are usable for the analysis. In this manner, the operation to switch frequency of a sinusoidal wave becomes unnecessary.
2. Approach of Capacitive-Coupling IS
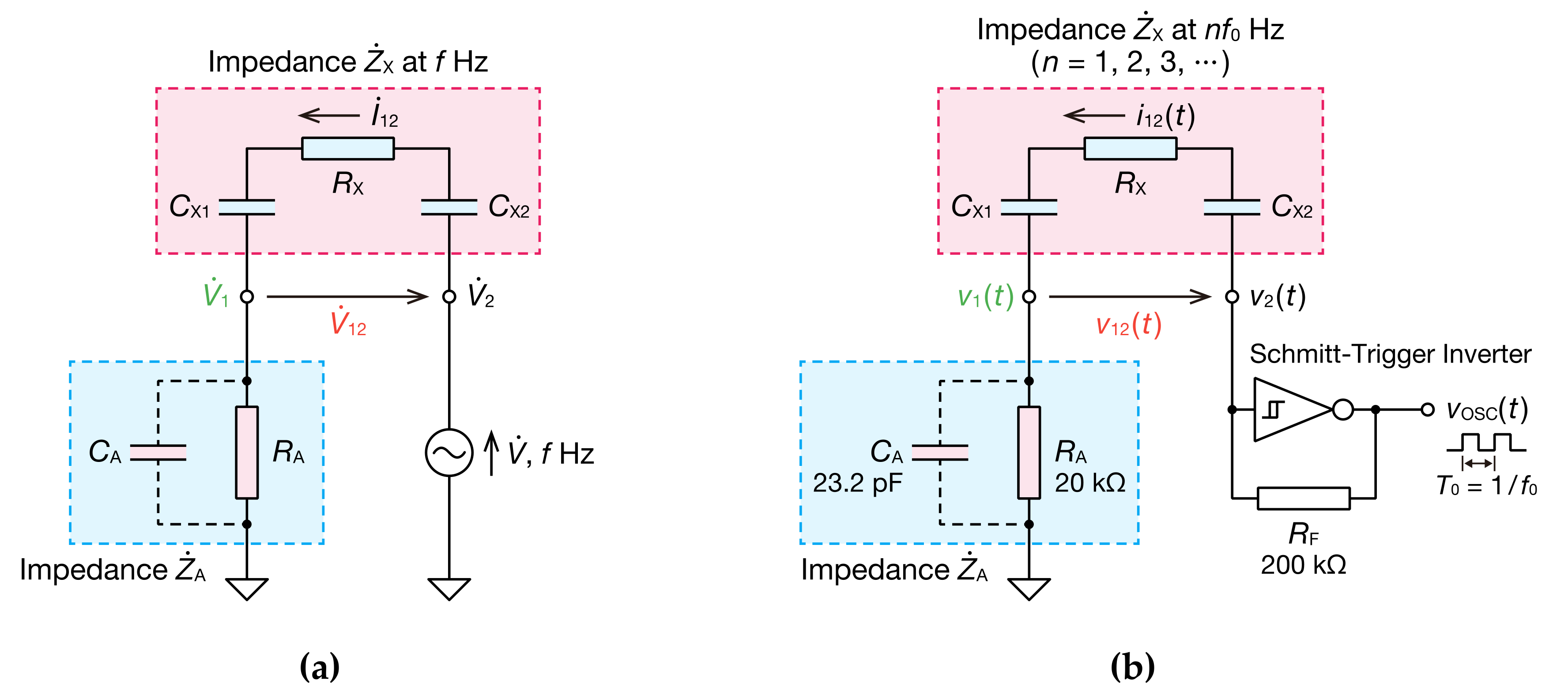
2.1. Non-Sinusoidal Oscillator Circuit with Capacitive Couplings
2.2. Determination of Unknown Capacitance and Resistance in Series Connection
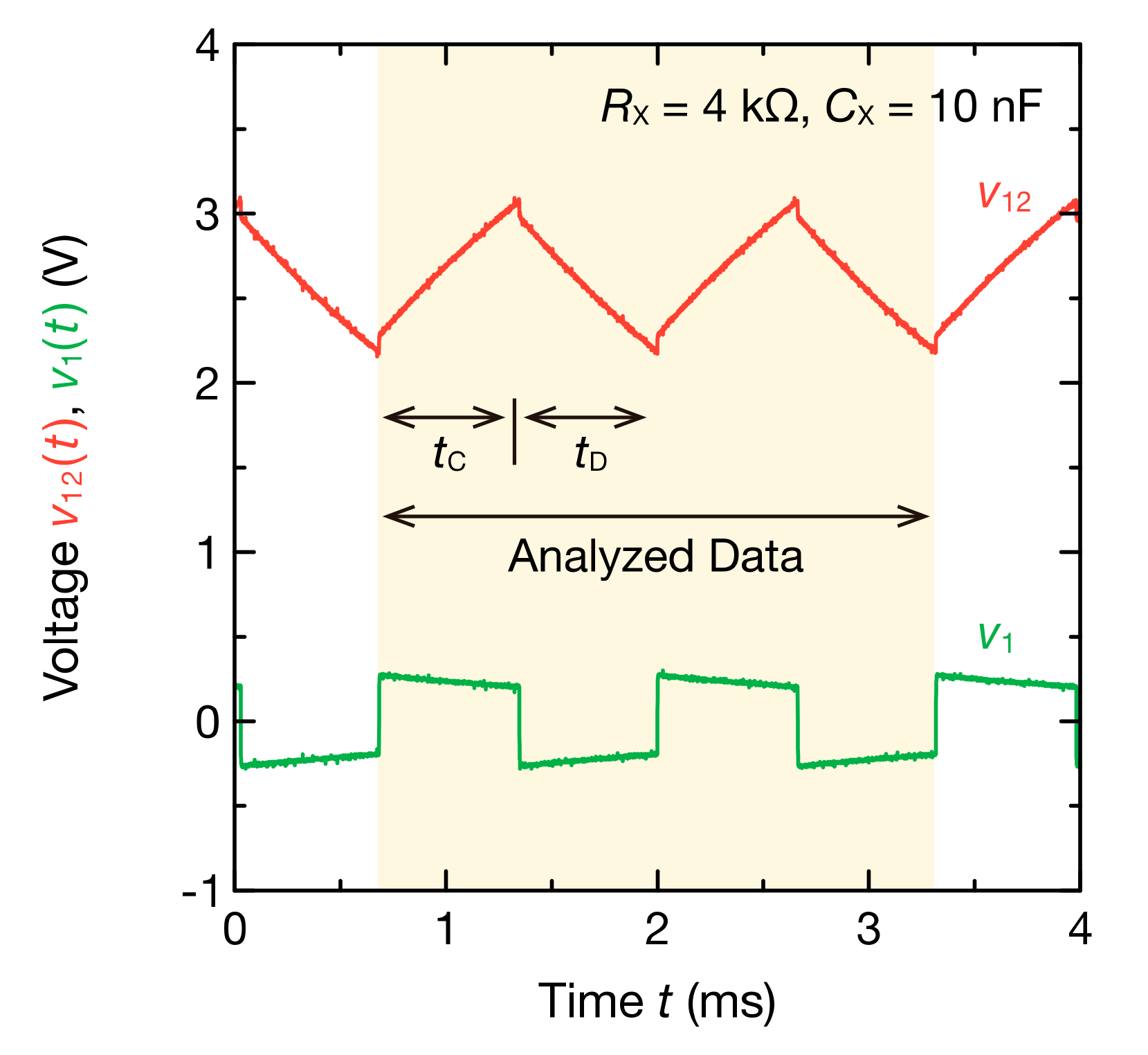
2.3. Experimental Method
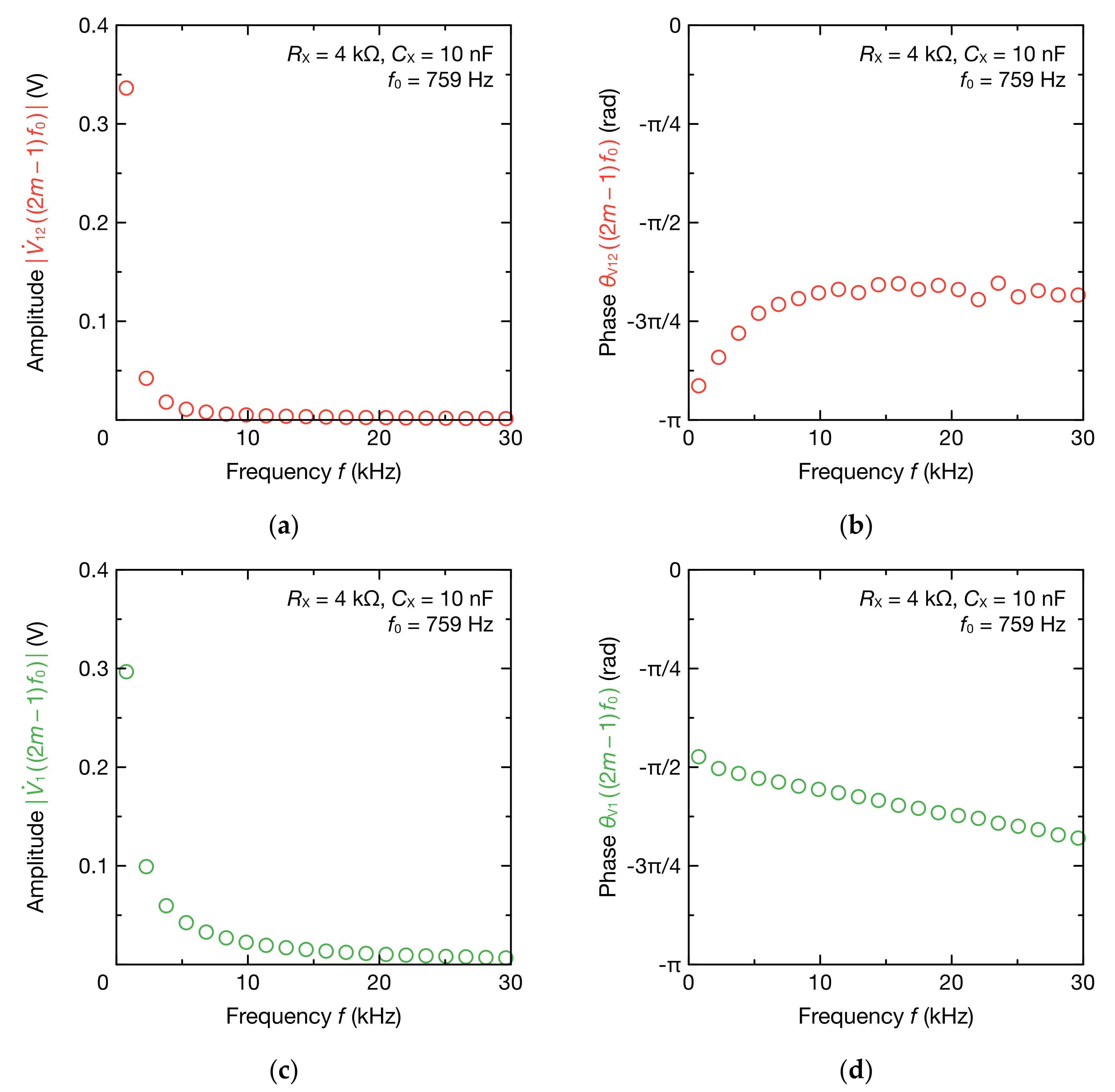
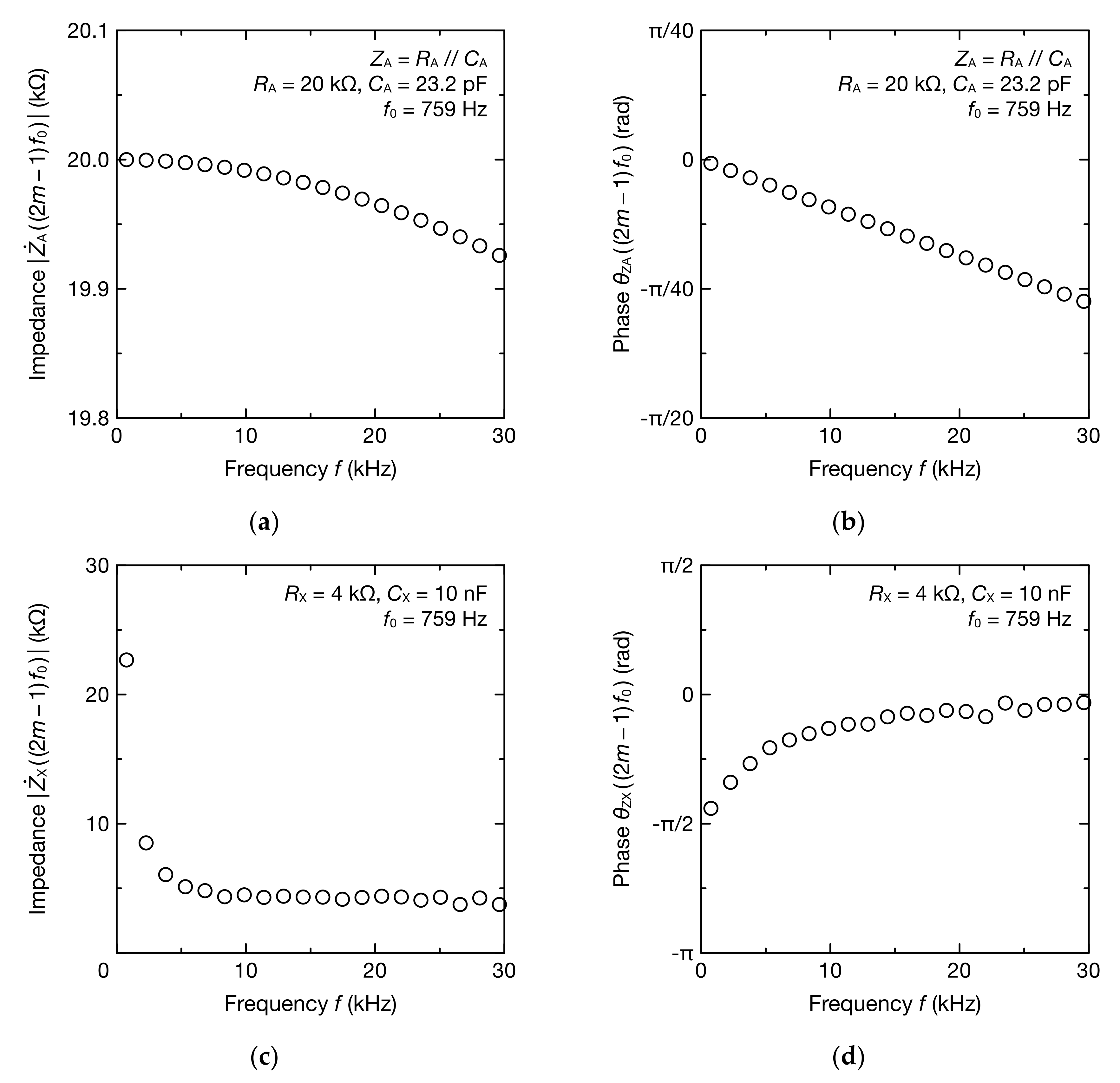
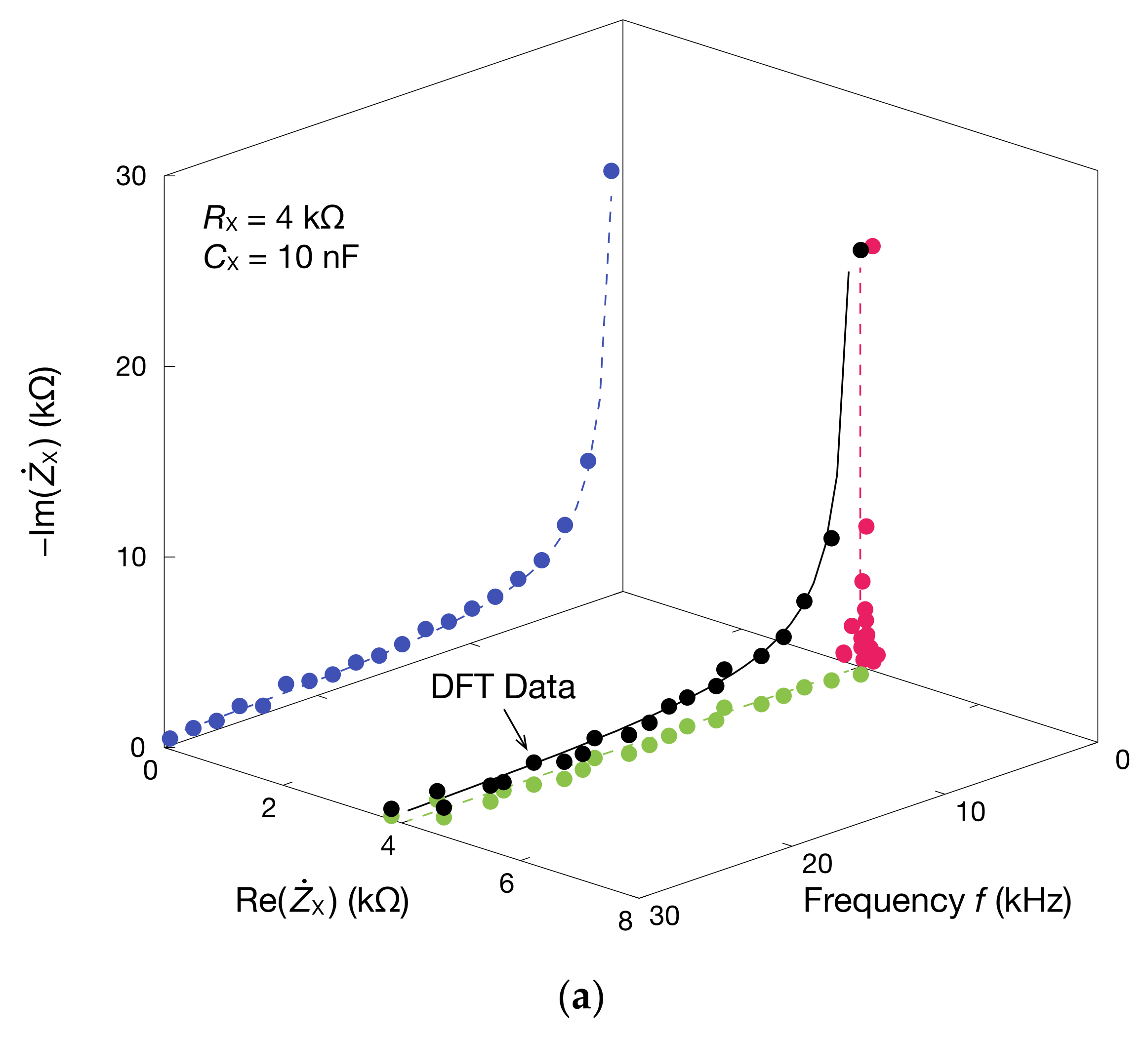
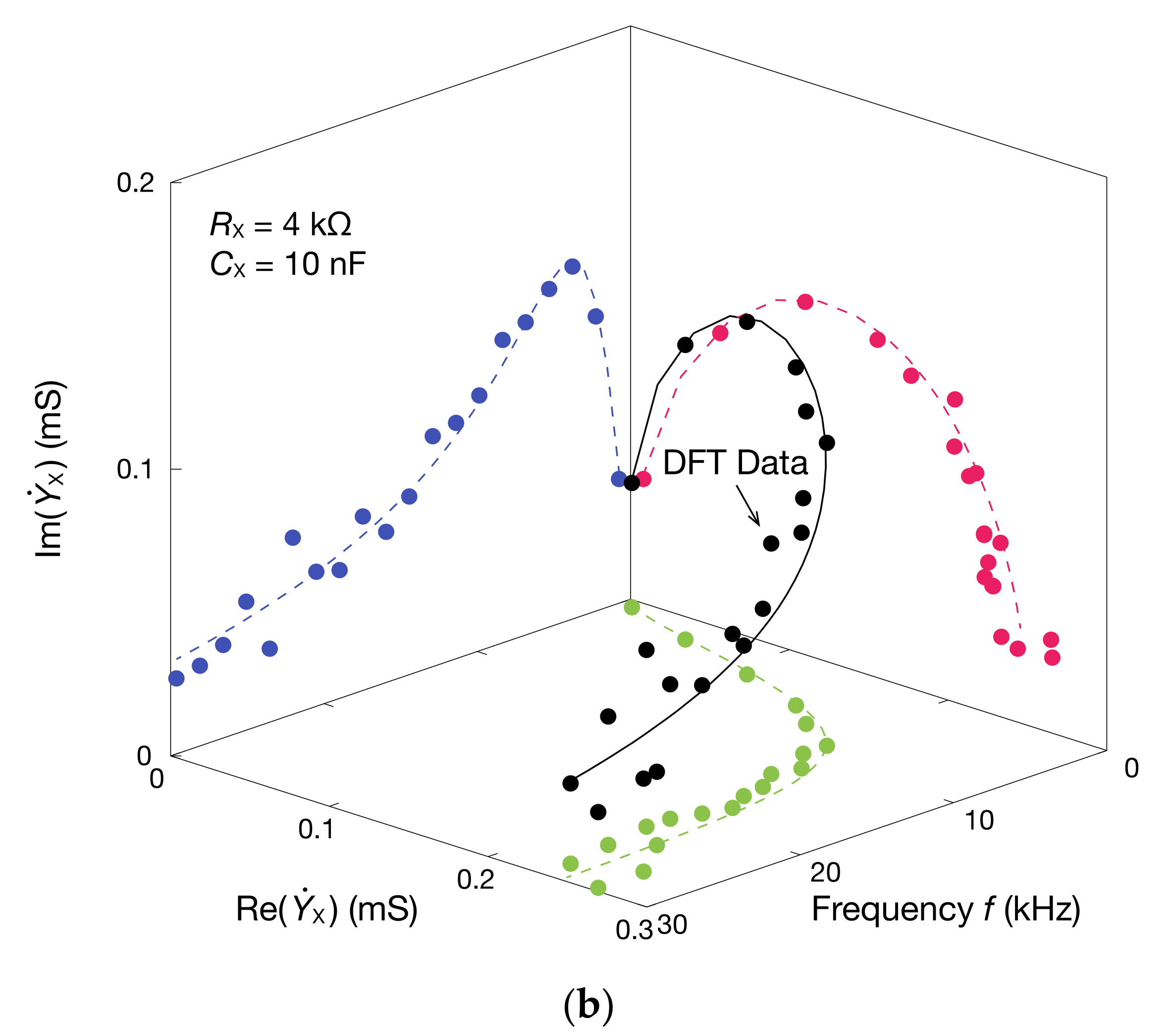
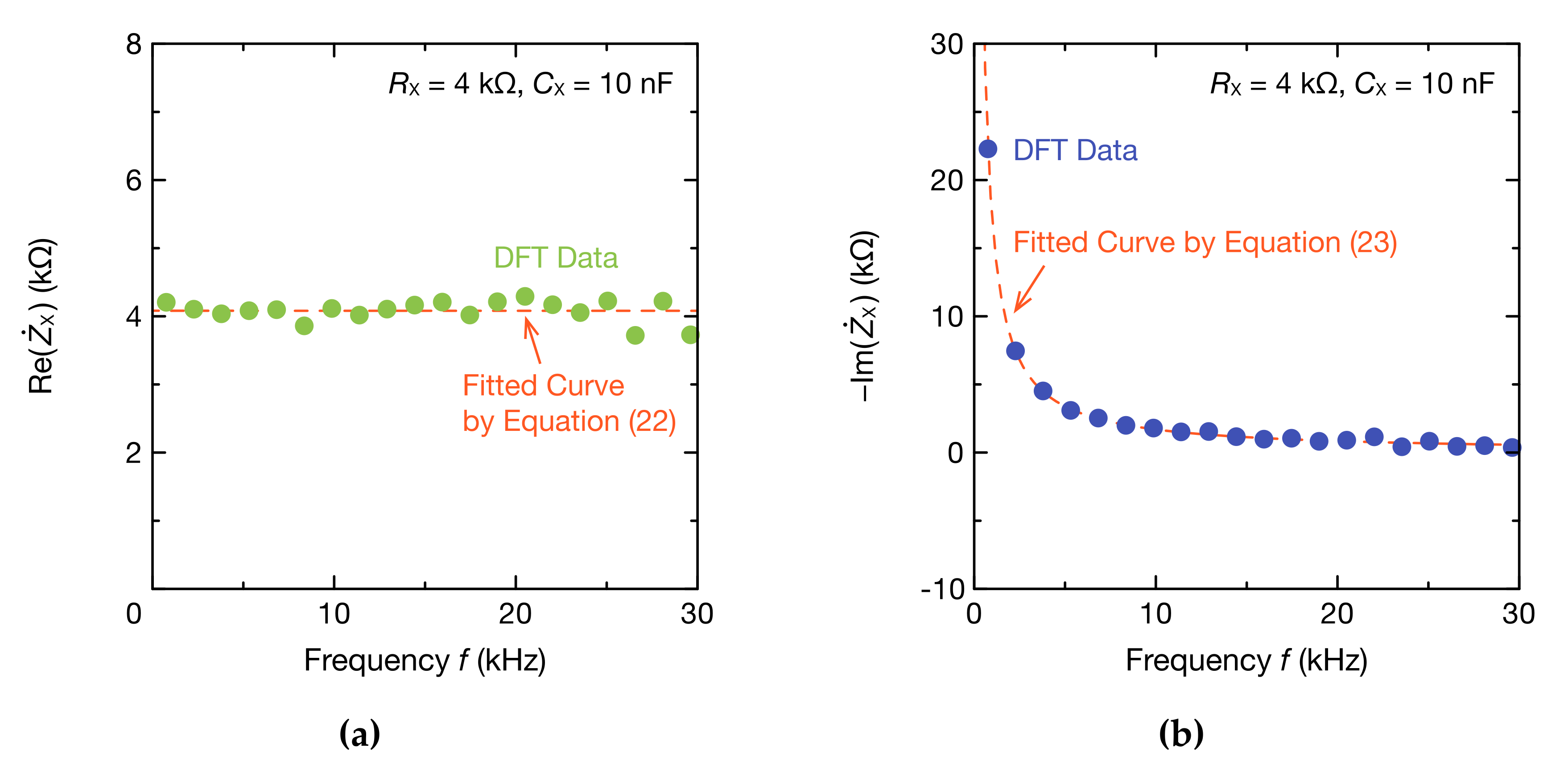
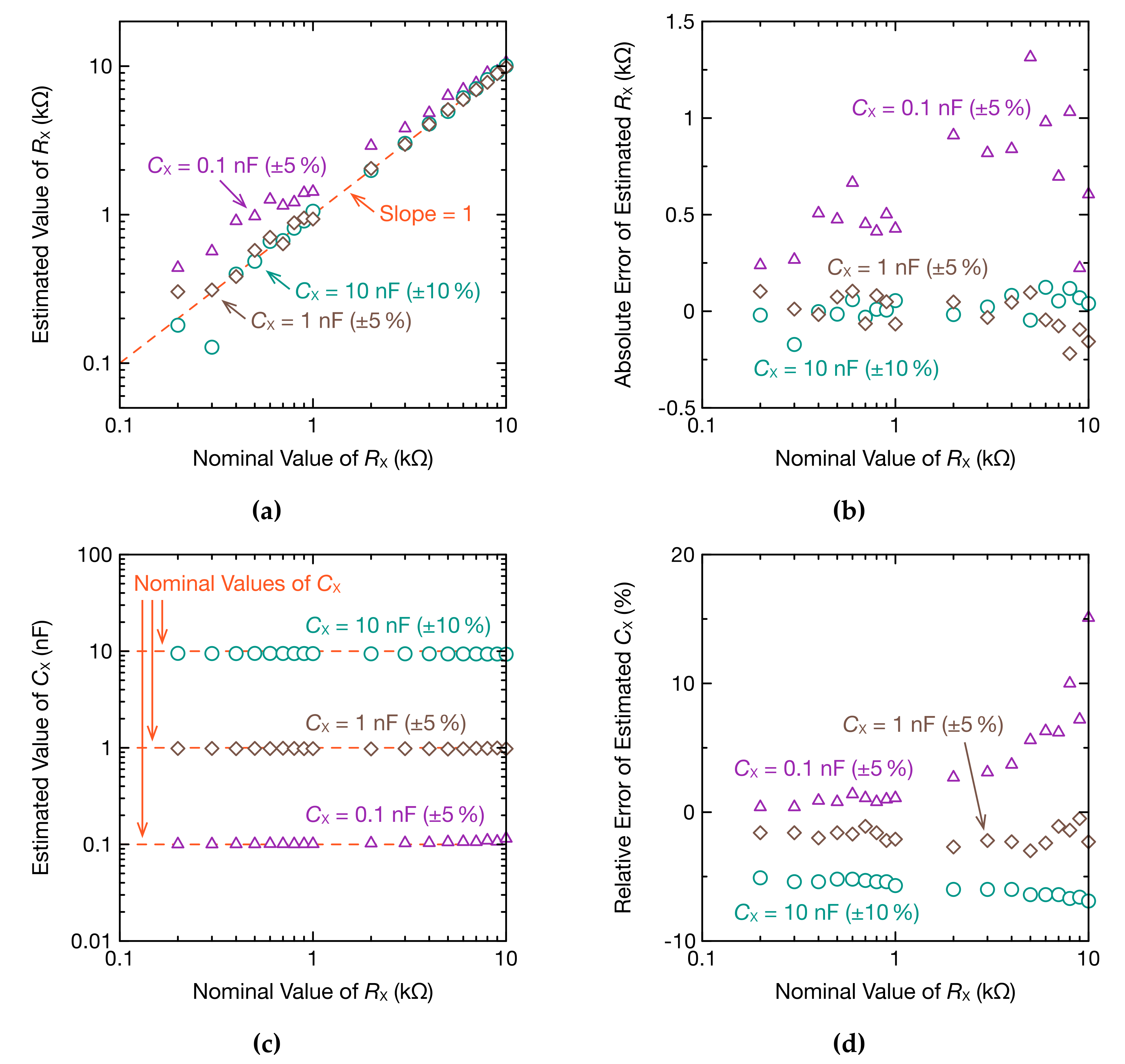
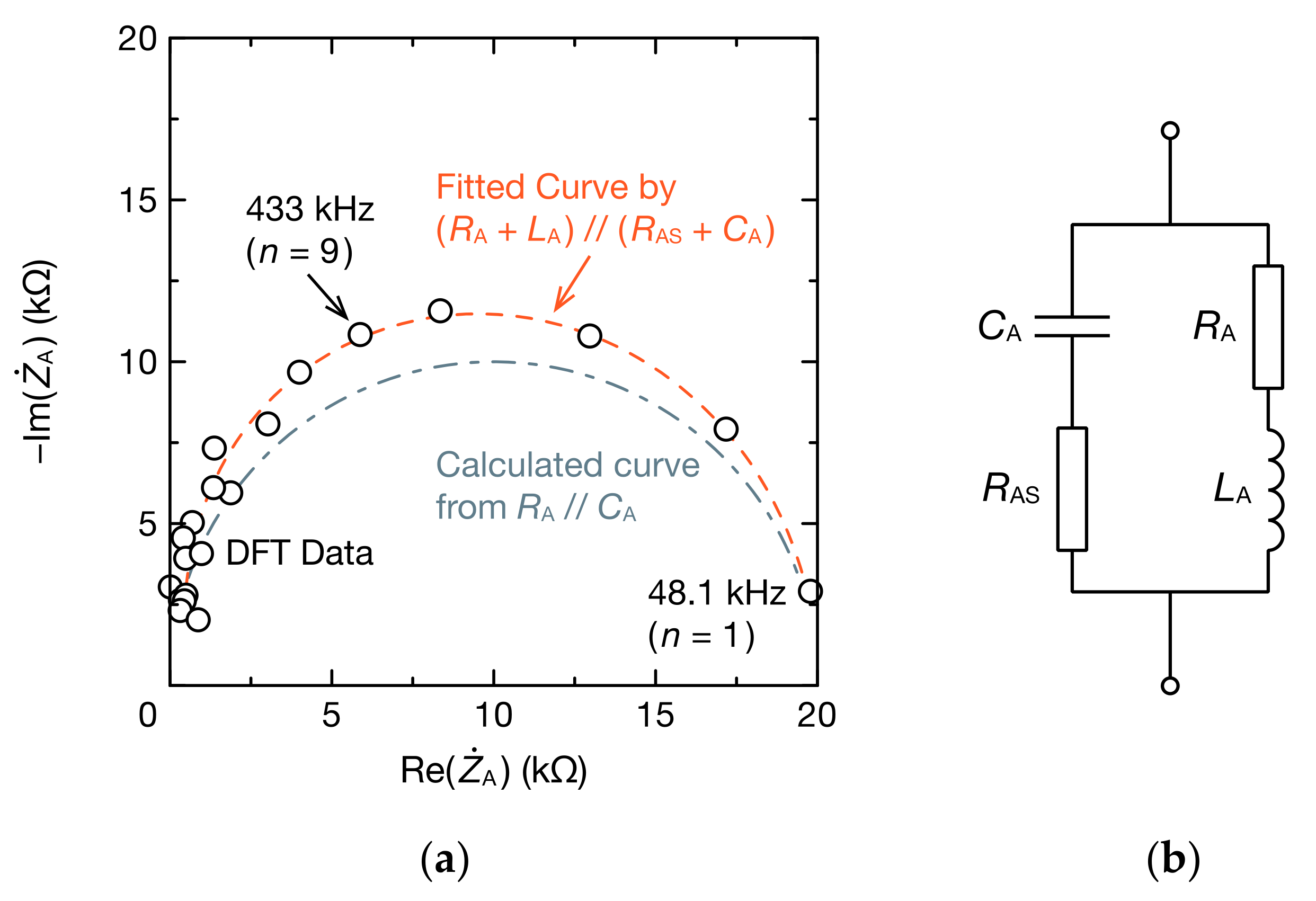
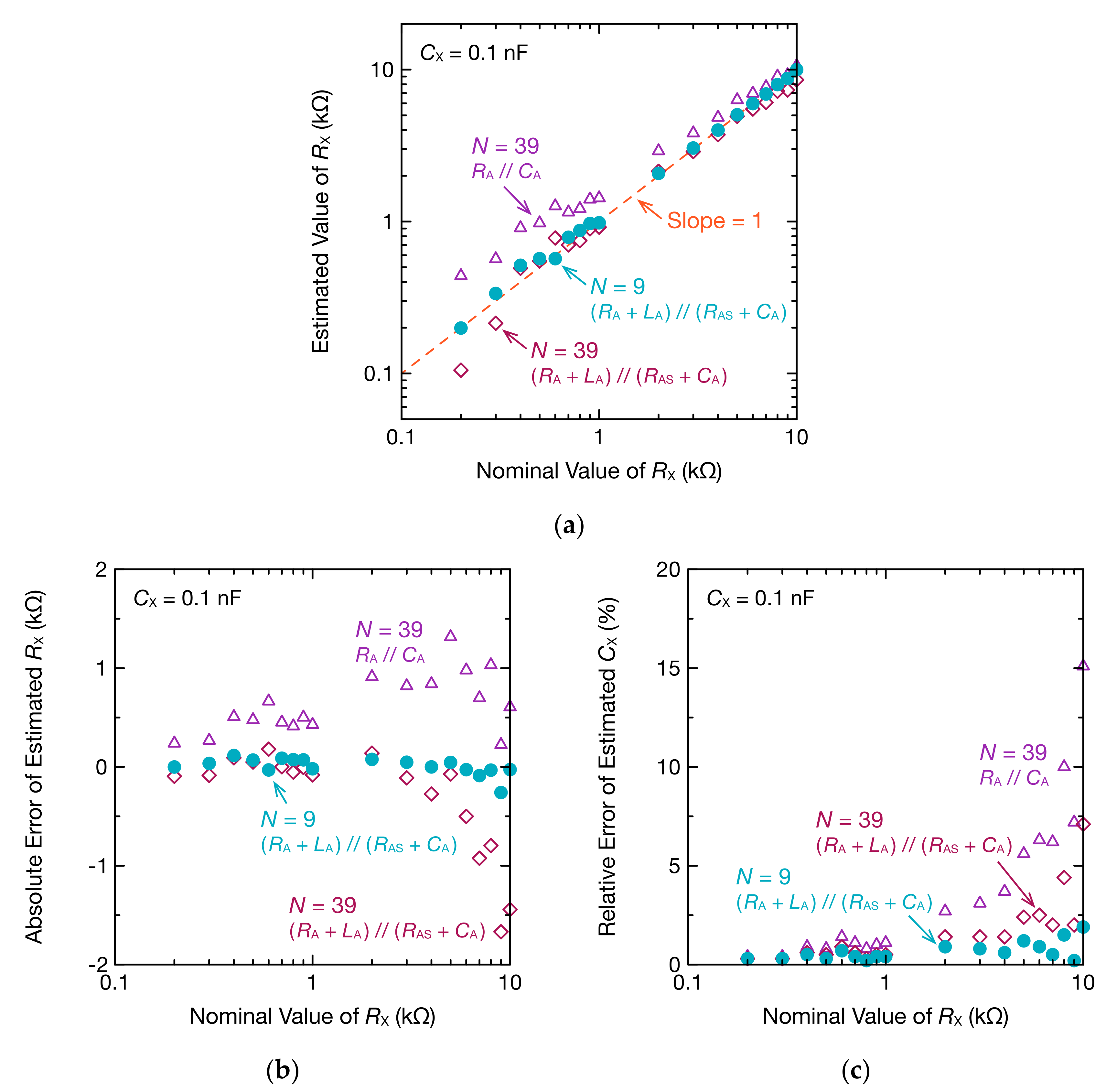
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brear, A.R.C.; Chown, A.L.; Burton, A.R.; Farnum, B.H. Electrochemical impedance spectroscopy of metal oxide electrodes for energy applications. ACS Appl. Energy Mater. 2020, 3, 66–98. [Google Scholar] [CrossRef]
- Encinas-Sánchez, V.; de Miguel, M.T.; Lasanta, M.I.; García-Martín, G.; Pérez, F.J. Electrochemical impedance spectroscopy (EIS): An efficient technique for monitoring corrosion processes in molten salt environments in CSP applications. Sol. Energy Mater. Sol. Cells 2019, 191, 157–163. [Google Scholar] [CrossRef]
- Itagaki, M.; Suzuki, S.; Shitanda, I.; Watanabe, K. Electrochemical impedance and complex capacitance to interpret electrochemical capacitor. Electrochemistry 2007, 75, 649–655. [Google Scholar] [CrossRef]
- Bonomo, M.; Naponiello, G.; Dini, D. Oxidative dissolution of NiO in aqueous electrolyte: An impedance study. J. Electroanal. Chem. 2018, 816, 205–214. [Google Scholar] [CrossRef]
- Fabregat-Santiago, F.; Garcia-Belmonte, G.; Mora-Seró, I.; Bisquert, J. Characterization of nanostructured hybrid and organic solar cells by impedance spectroscopy. Phys. Chem. Chem. Phys. 2011, 13, 9083–9118. [Google Scholar] [CrossRef] [PubMed]
- Balasubramani, V.; Chandraleka, S.; Subba Rao, T.; Sasikumar, R.; Kuppusamy, M.R.; Sridhar, T.M. Review—Recent advances in electrochemical impedance spectroscopy based toxic gas sensors using semiconducting metal oxides. J. Electrochem. Soc. 2020, 167, 037572. [Google Scholar] [CrossRef]
- Valiūnienė, A.; Rekertaitė, A.I.; Ramanavičienė, A.; Mikoliūnait, L.; Ramanavičius, A. Fast Fourier transformation electrochemical impedance spectroscopy for the investigation of inactivation of glucose biosensor based on graphite electrode modified by Prussian blue, polypyrrole and glucose oxidase. Colloids Surf. A Physicochem. Eng. Asp. 2017, 532, 165–171. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Takisawa, M.; Kiwa, T.; Yamada, H.; Tsukada, K. Analysis of response mechanism of a proton-pumping gate FET hydrogen gas sensor in air. Sens. Actuators B Chem. 2008, 133, 538–542. [Google Scholar] [CrossRef]
- Sekine, I. Recent evaluation of corrosion protective paint films by electrochemical methods. Prog. Org. Coat. 1997, 31, 73–80. [Google Scholar] [CrossRef]
- Bonora, P.L.; Deflorian, F.; Fedrizzi, L. Electrochemical impedance spectroscopy as a tool for investigating underpaint corrosion. Electrochim. Acta 1995, 41, 1073–1082. [Google Scholar] [CrossRef]
- Deflorian, F.; Fedrizzi, L.; Rossi, S.; Bonora, P.L. Organic coating capacitance measurement by EIS: Ideal and actual trends. Electrochim. Acta 1999, 44, 4243–4249. [Google Scholar] [CrossRef]
- Amirudin, A.; Thieny, D. Application of electrochemical impedance spectroscopy to study the degradation of polymer-coated metals. Prog. Org. Coat. 1995, 26, 1–28. [Google Scholar] [CrossRef]
- Mansfeld, F.; Tsai, C.H. Determination of coating deterioration with EIS: I. basic relationships. Corrosion 1991, 47, 958–963. [Google Scholar] [CrossRef]
- Mansfeld, F.; Tsai, C.H. Determination of coating deterioration with EIS: Part II. development of a method for field testing of protective coatings. Corrosion 1993, 49, 726–737. [Google Scholar]
- Rammelt, U.; Reinhard, G. Application of electrochemical impedance spectroscopy (EIS) for characterizing the corrosion-protective performance of organic coatings on metals. Prog. Org. Coat. 1992, 21, 205–226. [Google Scholar] [CrossRef]
- Kendig, M.; Scully, J. Basic aspects of electrochemical impedance application for the life prediction of organic coatings on metals. Corrosion 1990, 46, 22–29. [Google Scholar] [CrossRef]
- Walter, G.W. A review of impedance plot methods used for corrosion performance analysis of painted metals. Corros. Sci. 1986, 26, 681–703. [Google Scholar] [CrossRef]
- Lindqvist, S.A. Theory of dielectric properties of heterogeneous substances applied to water in a paint film. Corrosion 1985, 41, 69–75. [Google Scholar] [CrossRef]
- Grossi, M.; Riccò, B. Electrical impedance spectroscopy (EIS) for biological analysis and food characterization: A review. J. Sens. Sens. Syst. 2017, 6, 303–325. [Google Scholar] [CrossRef]
- Davies, S.J.; Davenport, A. The role of bioimpedance and biomarkers in helping to aid clinical decision-making of volume assessments in dialysis patients. Kidney Int. 2014, 86, 489–496. [Google Scholar] [CrossRef]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.-C.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part I: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.-C.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part II: Utilization in clinical practice. Clin. Nutr. 2004, 23, 1430–1453. [Google Scholar] [CrossRef] [PubMed]
- Jaffrin, M.Y.; Morel, H. Body fluid volumes measurements by impedance: A review of bioimpedance spectroscopy (BIS) and bioimpedance analysis (BIA) methods. Med. Eng. Phys. 2008, 30, 1257–1269. [Google Scholar] [CrossRef] [PubMed]
- Szuster, B.; Roj, Z.S.D.; Kowalski, P.; Sobotnicki, A.; Woloszyn, J. Idea and measurement methods used in bioimpedance spectroscopy. Adv. Intell. Syst. Comput. 2017, 623, 70–78. [Google Scholar]
- Demura, S.; Sato, S.; Kitabayashi, T. Percentage of total body fat as estimated by three automatic bioelectrical impedance analyzers. J. Physiol. Anthropol. Appl. Hum. Sci. 2004, 23, 93–99. [Google Scholar] [CrossRef]
- Cha, K.; Chertow, G.M.; Gonzalez, J.; Lazarus, J.M.; Wilmore, D.W. Multifrequency bioelectrical impedance estimates the distribution of body water. J. Appl. Physiol. 1995, 79, 1316–1319. [Google Scholar] [CrossRef]
- Piccoli, A. Bioelectric impedance measurement for fluid status assessment. Contrib. Nephrol. 2010, 164, 143–152. [Google Scholar]
- Piccoli, A.; Rossi, B.; Pillon, L.; Bucciante, G. A new method for monitoring body fluid variation by bioimpedance analysis: The RXc graph. Kidney Int. 1994, 46, 534–539. [Google Scholar] [CrossRef]
- Nwosu, A.C.; Mayland, C.R.; Mason, S.; Cox, T.F.; Varro, A.; Ellershaw, J. The association of hydration status with physical signs, symptoms and survival in advanced cancer—The use of bioelectrical impedance vector analysis (BIVA) technology to evaluate fluid volume in palliative care: An observational study. PLoS ONE 2016, 11, e0163114. [Google Scholar] [CrossRef]
- Toso, S.; Piccoli, A.; Gusella, M.; Menon, D.; Crepaldi, G.; Bononi, A.; Ferrazzi, E. Bioimpedance vector pattern in cancer patients without disease versus locally advanced or disseminated disease. Nutrition 2003, 19, 510–514. [Google Scholar] [CrossRef]
- Nescolarde, L.; Piccoli, A.; Román, A.; Núñez, A.; Morales, R.; Tamayo, J.; Doñate, T.; Rosell, J. Bioelectrical impedance vector analysis in haemodialysis patients: Relation between oedema and mortality. Physiol. Meas. 2004, 25, 1271–1280. [Google Scholar] [CrossRef]
- Piccoli, A.; Italian CAPD-BIA Study Group. Bioelectric impedance vector distribution in peritoneal dialysis patients with different hydration status. Kidney Int. 2004, 65, 1050–1063. [Google Scholar] [CrossRef]
- Pillon, L.; Piccoli, A.; Lowrie, E.G.; Lazarus, J.M.; Chertow, G.M. Vector length as a proxy for the adequacy of ultrafiltration in hemodialysis. Kidney Int. 2004, 66, 1266–1271. [Google Scholar] [CrossRef]
- Bozzetto, S.; Piccoli, A.; Montini, G. Bioelectrical impedance vector analysis to evaluate relative hydration status. Pediatr. Nephrol. 2010, 25, 329–334. [Google Scholar] [CrossRef]
- Codognotto, M.; Piazza, M.; Frigatti, P.; Piccoli, A. Influence of localized edema on whole-body and segmental bioelectrical impedance. Nutrition 2008, 24, 569–574. [Google Scholar] [CrossRef]
- Nwosu, A.C.; Morris, L.; Mayland, C.; Mason, S.; Pettitt, A.; Ellershaw, J. Longitudinal bioimpedance assessments to evaluate hydration in POEMS syndrome. BMJ Support. Palliat. Care 2016, 6, 369–372. [Google Scholar] [CrossRef]
- Stewart, G.N. The changes produced by the growth of bacteria in the molecular concentration and electrical conductivity of culture media. J. Exp. Med. 1899, 4, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Grossi, M.; Lazzarini, R.; Lanzoni, M.; Riccò, B. A novel technique to control ice-cream freezing by electrical characteristics analysis. J. Food Eng. 2011, 106, 347–354. [Google Scholar] [CrossRef]
- Pompei, A.; Grossi, M.; Lanzoni, M.; Perretti, G.; Lazzarini, R.; Riccò, B.; Matteuzzi, D. Feasibility of lactobacilli concentration detection in beer by automated impedance technique. MBAA Tech. Q. 2012, 49, 11–18. [Google Scholar] [CrossRef]
- Chuang, C.H.; Du, Y.C.; Wu, T.F.; Chen, C.H.; Lee, D.H.; Chen, S.M.; Huang, T.C.; Wu, H.P.; Shaikh, M.O. Immunosensor for the ultrasensitive and quantitative detection of bladder cancer in point of care testing. Biosens. Bioelectron. 2016, 84, 126–132. [Google Scholar] [CrossRef]
- Ma, H.; Wallbank, R.W.R.; Chaji, R.; Li, J.; Suzuki, Y.; Jiggins, C.; Nathan, A. An impedance-based integrated biosensor for suspended DNA characterization. Sci. Rep. 2013, 3, 2730. [Google Scholar] [CrossRef]
- van Grinsven, B.; Vandenryt, T.; Duchateau, S.; Gaulke, A.; Grieten, L.; Thoelen, R.; Ingebrandt, S.; De Ceuninck, W.; Wagner, P. Customized impedance spectroscopy device as possible sensor platform for biosensor applications. Phys. Status Solidi A 2010, 4, 919–923. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, Z.; Ying, Y. New trends in impedimetric biosensors for the detection of foodborne pathogenic bacteria. Sensors 2012, 12, 3449–3471. [Google Scholar] [CrossRef]
- Ibba, P.; Falco, A.; Abera, B.D.; Cantarella, G.; Petti, L.; Lugli, P. Bio-impedance and circuit parameters: An analysis for tracking fruit ripening. Postharvest Biol. Technol. 2020, 159, 110978. [Google Scholar] [CrossRef]
- Chowdhury, A.; Singh, P.; Bera, T.K.; Ghoshal, D.; Chakraborty, B. Electrical impedance spectroscopic study of mandarin orange during ripening. J. Food Meas. Charact. 2017, 11, 1654–1664. [Google Scholar] [CrossRef]
- Niu, J.; Lee, J.Y. A new approach for the determination of fish freshness by electrochemical impedance spectroscopy. J. Food Sci. 2000, 65, 780–785. [Google Scholar] [CrossRef]
- Breugelmans, T.; Tourwé, E.; Van Ingelgem, Y.; Wielant, J.; Hauffman, T.; Haubrand, R.; Pintelon, R.; Hubin, A. Odd random phase multisine EIS as a detection method for the onset of corrosion of coated steel. Electrochem. Commun. 2010, 12, 2–5. [Google Scholar] [CrossRef]
- Min, M.; Pliquett, U.; Nacke, T.; Barthel, A.; Annus, P.; Land, R. Broadband excitation for short-time impedance spectroscopy. Physiol. Meas. 2008, 29, 185–192. [Google Scholar] [CrossRef]
- Min, M.; Parve, T.; Ronk, A.; Annus, P.; Paavle, T. Synchronous sampling and demodulation in an instrument for multifrequency bioimpedance measurement. IEEE Trans. Instrum. Meas. 2007, 56, 1365–1372. [Google Scholar] [CrossRef]
- Darowicki, K.; Ślepski, P. Dynamic electrochemical impedance spectroscopy of the first order electrode reaction. J. Electroanal. Chem. 2003, 547, 1–8. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, H.; Luo, W.; Zhang, T.; Zhao, W. A Fast Time Domain Measuring Technique of Electrochemical Impedance Spectroscopy Based on FFT. In Proceedings of the 2018 Prognostics and System Health Management Conference, Chongqing, China, 26–28 October 2018; pp. 450–455. [Google Scholar]
- Zappen, H.; Ringbeck, F.; Sauer, D.U. Application of time-resolved multi-sine impedance spectroscopy for lithium-ion battery characterization. Batteries 2018, 4, 64. [Google Scholar] [CrossRef]
- Orlikowski, J.; Ryl, J.; Jarzynka, M.; Krakowiak, S.; Darowicki, K. Instantaneous impedance monitoring of aluminum alloy 7075 corrosion in borate buffer with admixed chloride ions. Corrosion 2015, 71, 828–838. [Google Scholar] [CrossRef]
- Valiūnienė, A.; Baltrūnas, G.; Valiūnas, R.; Popkirov, G. Investigation of the electroreduction of silver sulfite complexes by means of electrochemical FFT impedance spectroscopy. J. Hazard. Mater. 2010, 180, 259–263. [Google Scholar] [CrossRef]
- Carstensen, J.; Foca, E.; Keipert, S.; Föll, H.; Leisner, M.; Cojocaru, A. New modes of FFT impedance spectroscopy applied to semiconductor pore etching and materials characterization. Phys. Status Solidi (a) 2008, 205, 2485–2503. [Google Scholar] [CrossRef]
- Toyoda, K.; Tsenkova, R. Measurement of freezing process of agricultural products by impedance spectroscopy. IFAC Proc. Vol. 1998, 31, 89–94. [Google Scholar] [CrossRef]
- Niedzialkowski, P.; Slepski, P.; Wysocka, J.; Chamier-Cieminska, J.; Burczyk, L.; Sobaszek, M.; Wcislo, A.; Ossowski, T.; Bogdanowicz, R.; Ryl, J. Multisine impedimetric probing of biocatalytic reactions for label-free detection of DEFB1 gene: How to verify that your dog is not human? Sens. Actuators B Chem. 2020, 323, 128664. [Google Scholar] [CrossRef]
- Macdonald, J.R. Impedance spectroscopy and its use in analyzing the steady-state AC response of solid and liquid electrolytes. J. Electroanal. Chem. Interfacial Electrochem. 1987, 223, 25–50. [Google Scholar] [CrossRef]
- Kobayashi, K.; Suzuki, T.S. Development of impedance analysis software implementing a support function to find good initial guess using an interactive graphical user interface. Electrochemistry 2020, 88, 39–44. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaguchi, T.; Ueno, A. Capacitive-Coupling Impedance Spectroscopy Using a Non-Sinusoidal Oscillator and Discrete-Time Fourier Transform: An Introductory Study. Sensors 2020, 20, 6392. https://doi.org/10.3390/s20216392
Yamaguchi T, Ueno A. Capacitive-Coupling Impedance Spectroscopy Using a Non-Sinusoidal Oscillator and Discrete-Time Fourier Transform: An Introductory Study. Sensors. 2020; 20(21):6392. https://doi.org/10.3390/s20216392
Chicago/Turabian StyleYamaguchi, Tomiharu, and Akinori Ueno. 2020. "Capacitive-Coupling Impedance Spectroscopy Using a Non-Sinusoidal Oscillator and Discrete-Time Fourier Transform: An Introductory Study" Sensors 20, no. 21: 6392. https://doi.org/10.3390/s20216392
APA StyleYamaguchi, T., & Ueno, A. (2020). Capacitive-Coupling Impedance Spectroscopy Using a Non-Sinusoidal Oscillator and Discrete-Time Fourier Transform: An Introductory Study. Sensors, 20(21), 6392. https://doi.org/10.3390/s20216392




