Temperature Correction to Enhance Blood Glucose Monitoring Accuracy Using Electrical Impedance Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
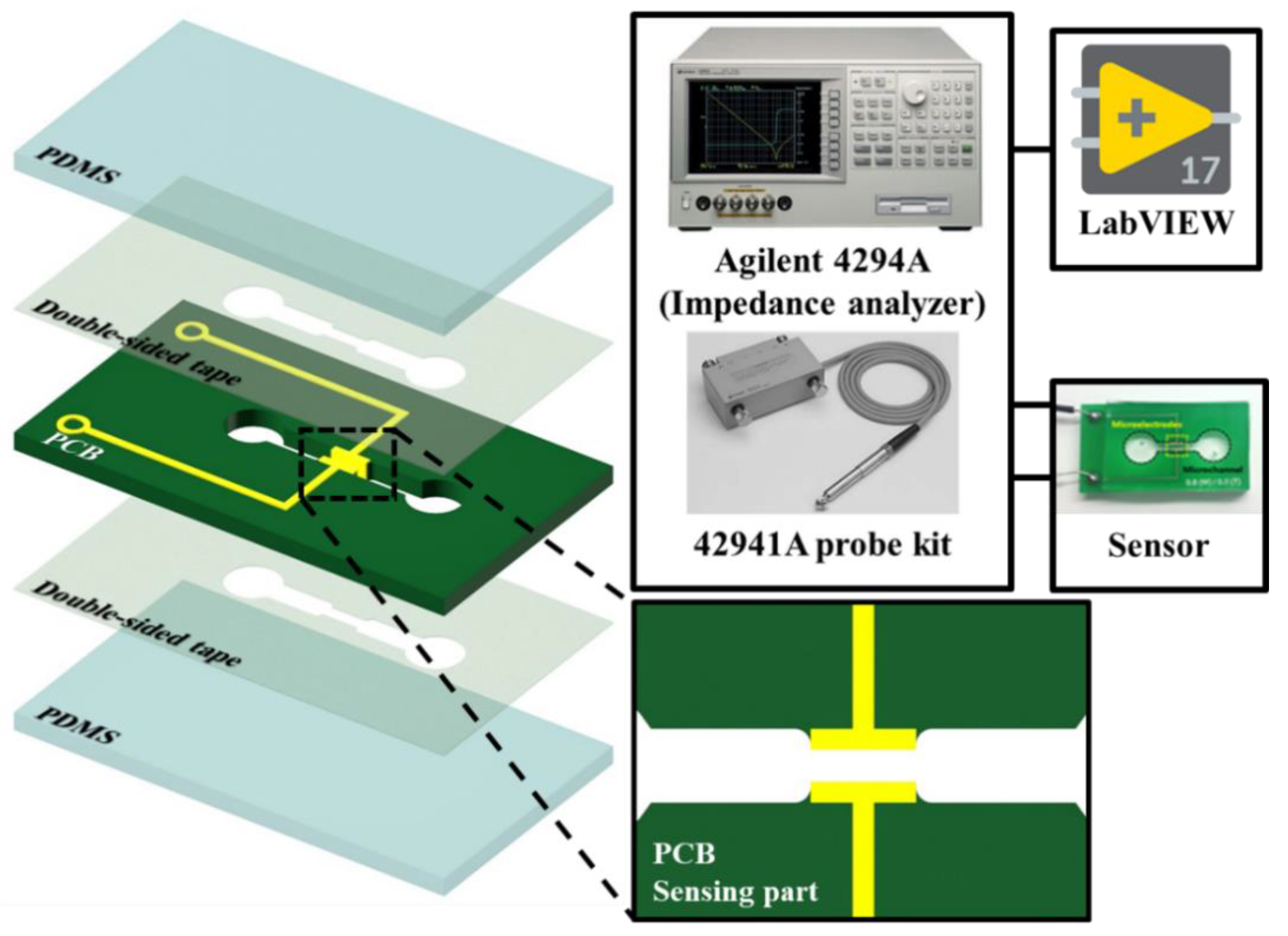
2.1. Impedance Sensor
2.2. Sample Preparation
2.3. Experimental Setup
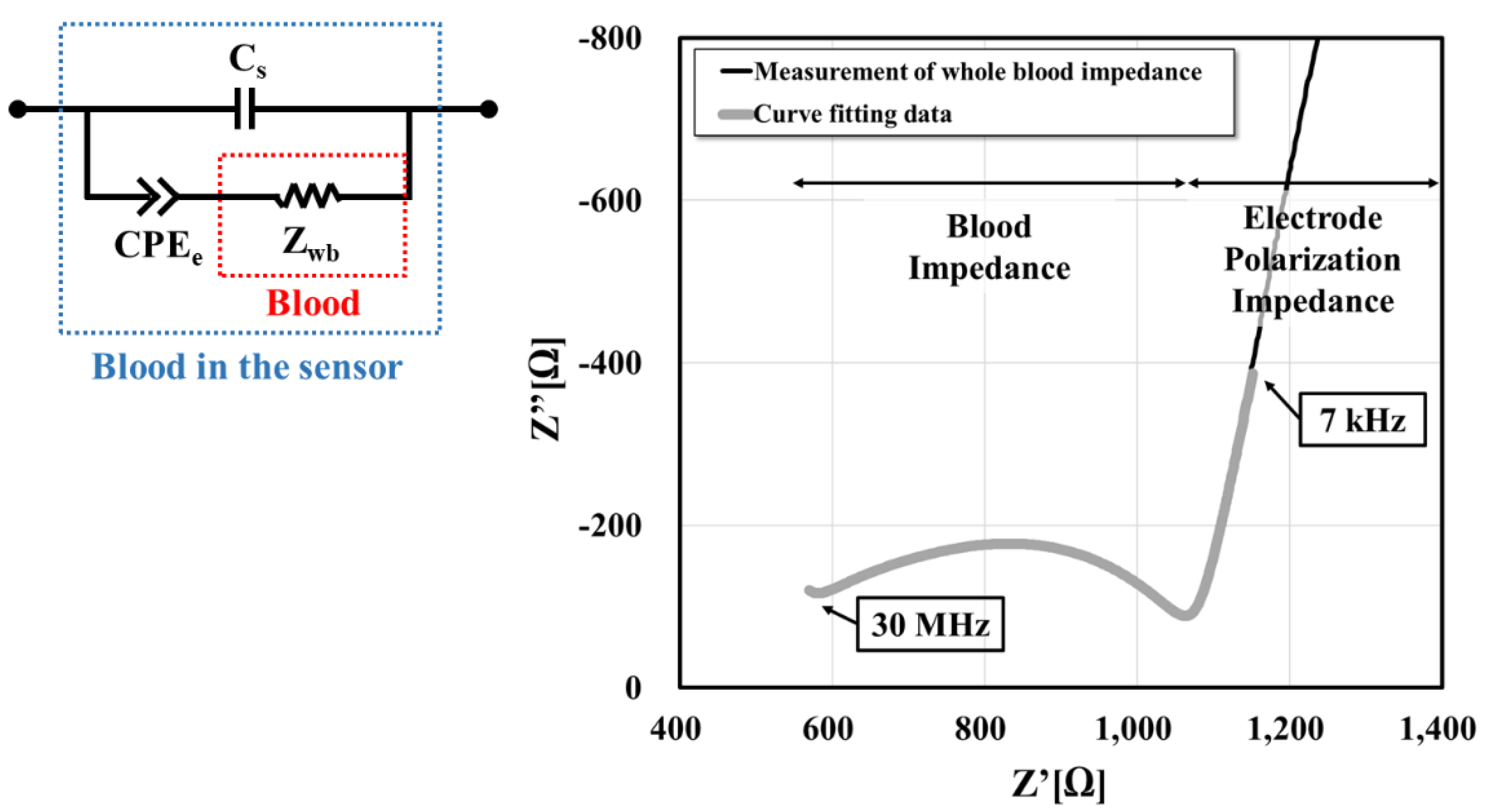
2.4. Extraction of Dielectric Properties
2.5. Temperature and Glucose Level Tests
2.6. Statistical Analysis
3. Results
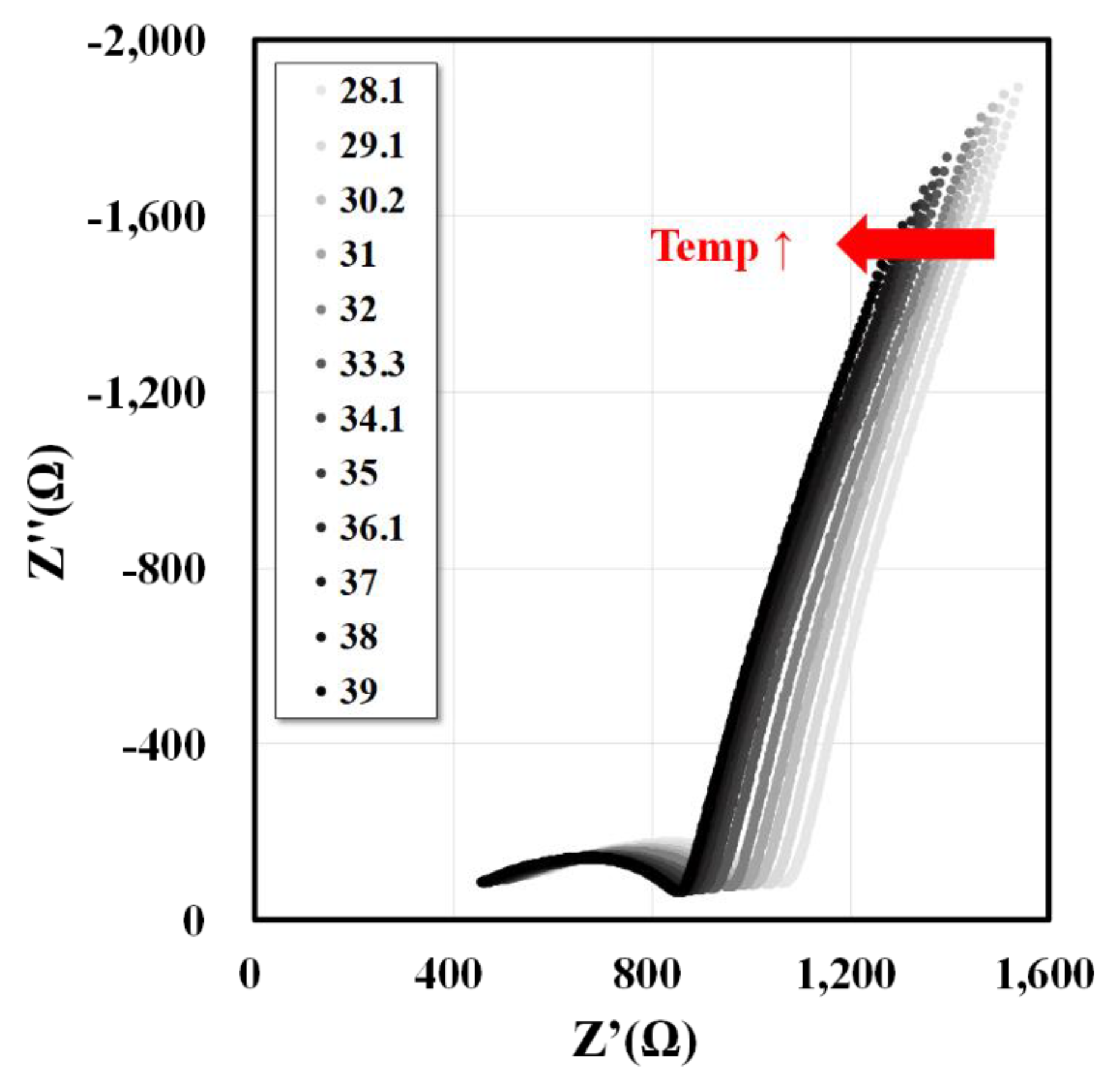
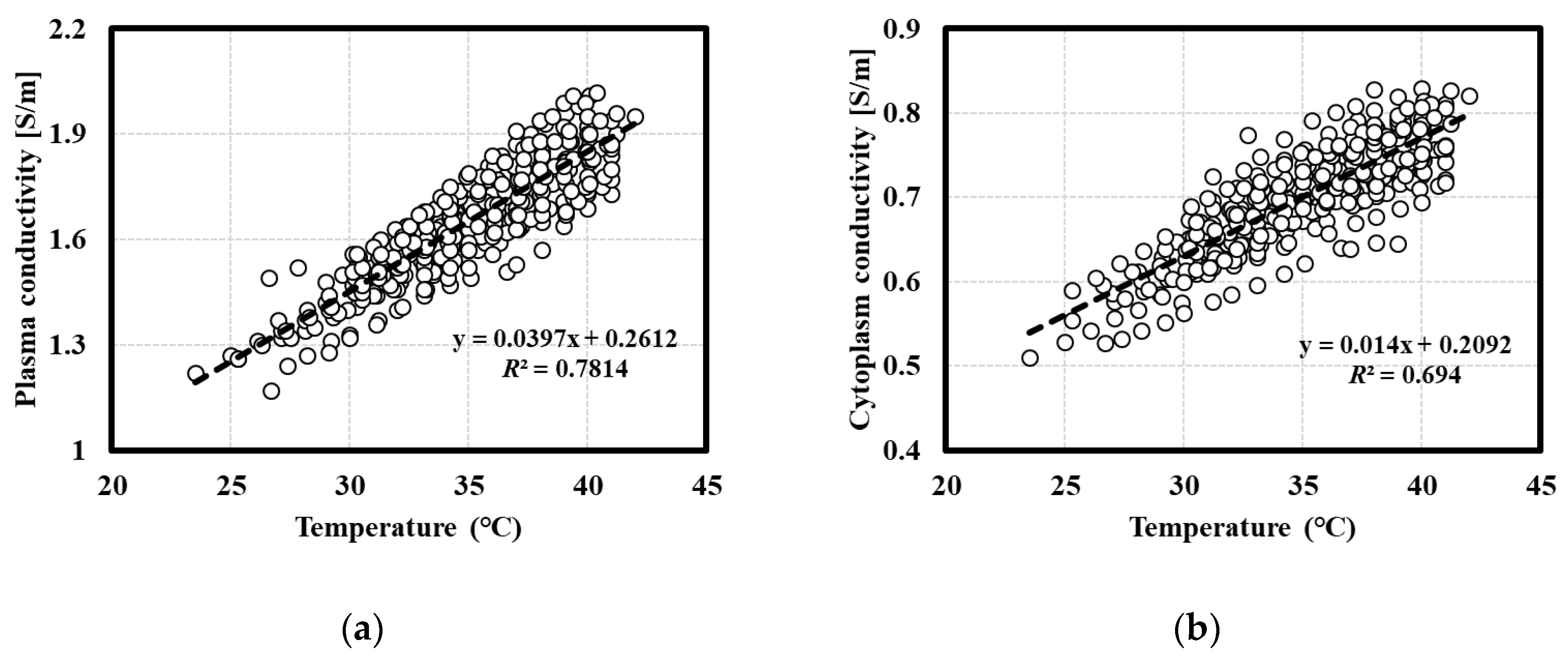
3.1. Temperature Dependence Test for the Electrical Properties of Whole Blood
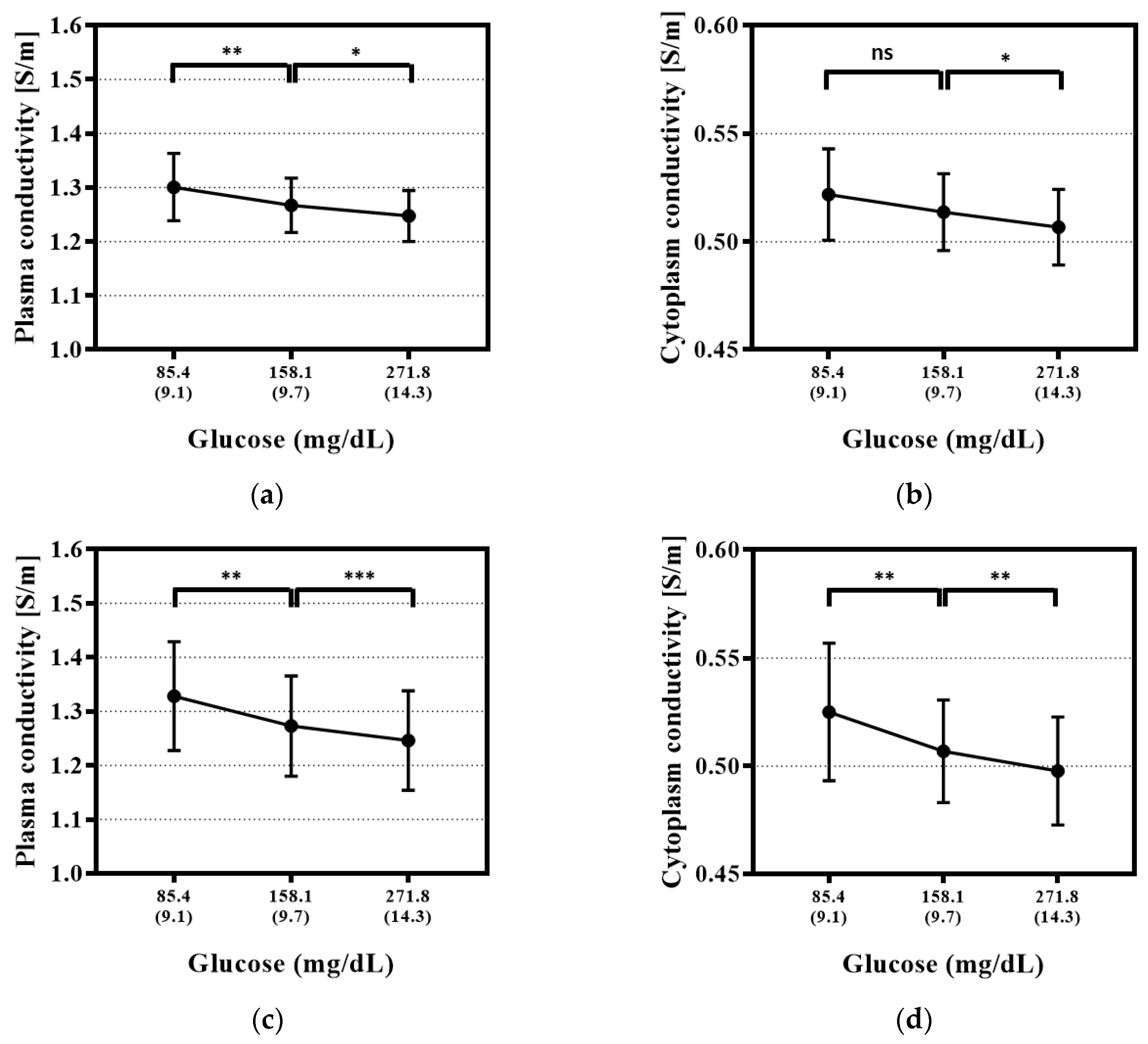
3.2. Glucose Level Dependence Test for the Electrical Properties of Whole Blood with Temperature Correction
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- WHO. Chronic Diseases and Their Common Risk Factors; World Health Organization: Geneva, Switzerland, 2005. [Google Scholar]
- Kim, B.-Y.; Won, J.C.; Lee, J.H.; Kim, H.-S.; Park, J.H.; Ha, K.H.; Won, K.C.; Kim, D.J.; Park, K.S. Diabetes Fact Sheets in Korea, 2018: An Appraisal of Current Status. Diabetes Metab. J. 2019, 43, 487–494. [Google Scholar] [CrossRef] [PubMed]
- Stone, J.Y.; Bailey, T.S. Benefits and limitations of continuous glucose monitoring in type 1 diabetes. Expert Rev. Endocrinol. Metab. 2020, 15, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Klonoff, D.C. Continuous Glucose Monitoring: Roadmap for 21st century diabetes therapy. Diabetes Care 2005, 28, 1231–1239. [Google Scholar] [CrossRef] [PubMed]
- Vashist, S.K. Non-invasive glucose monitoring technology in diabetes management: A review. Anal. Chim. Acta 2012, 750, 16–27. [Google Scholar] [CrossRef] [PubMed]
- Shokrekhodaei, M.; Quinones, S. Review of Non-Invasive Glucose Sensing Techniques: Optical, Electrical and Breath Acetone. Sensors 2020, 20, 1251. [Google Scholar] [CrossRef] [PubMed]
- Ahn, W.; Kim, J.-T. Blood Glucose Measurement Principles of Non-invasive Blood Glucose Meter: Focused on the Detection Methods of Blood Glucose. J. Biomed. Eng. Res. 2012, 33, 114–127. [Google Scholar] [CrossRef]
- Jang, C.; Park, J.-K.; Lee, H.-J.; Yun, G.-H.; Yook, J.-G. Temperature-Corrected Fluidic Glucose Sensor Based on Microwave Resonator. Sensors 2018, 18, 3850. [Google Scholar] [CrossRef]
- Caduff, A.; Mueller, M.; Megej, A.; Dewarrat, F.; Suri, R.E.; Klisic, J.; Donath, M.; Zakharov, P.; Schaub, D.; Stahel, W.A.; et al. Characteristics of a multisensor system for non invasive glucose monitoring with external validation and prospective evaluation. Biosens. Bioelectron. 2011, 26, 3794–3800. [Google Scholar] [CrossRef]
- Caduff, A.; Talary, M.S.; Zakharov, P. Cutaneous Blood Perfusion as a Perturbing Factor for Noninvasive Glucose Monitoring. Diabetes Technol. Ther. 2010, 12, 1–9. [Google Scholar] [CrossRef]
- Pfützner, A.; Caduff, A.; Larbig, M.; Schrepfer, T.; Forst, T. Impact of Posture and Fixation Technique on Impedance Spectroscopy Used for Continuous and Noninvasive Glucose Monitoring. Diabetes Technol. Ther. 2004, 6, 435–441. [Google Scholar] [CrossRef]
- Jaspard, F.; Nadi, M. Dielectric properties of blood: An investigation of temperature dependence. Physiol. Meas. 2002, 23, 547–554. [Google Scholar] [CrossRef] [PubMed]
- Mohapatra, S.N.; Hill, D.W. The changes in blood resistivity with haematocrit and temperature. Intensiv. Care Med. 1975, 1, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Tjin, S.C.; Xie, T.; Lam, Y.Z. Investigation into the effects of haematocrit and temperature on the resistivity of mammalian blood using a four-electrode probe. Med Biol. Eng. Comput. 1998, 36, 467–470. [Google Scholar] [CrossRef]
- Ley, S.; Schilling, S.; Fiser, O.; Vrba, J.; Sachs, J.; Helbig, M. Ultra-Wideband Temperature Dependent Dielectric Spectroscopy of Porcine Tissue and Blood in the Microwave Frequency Range. Sensors 2019, 19, 1707. [Google Scholar] [CrossRef]
- Huber, D.; Talary, M.S.; Dewarrat, F.; Caduff, A. The compensation of perturbing temperature fluctuation in glucose monitoring technologies based on impedance spectroscopy. Med Biol. Eng. Comput. 2007, 45, 863–876. [Google Scholar] [CrossRef]
- Forst, T.; Caduff, A.; Talary, M.; Weder, M.; Brändle, M.; Kann, P.; Flacke, F.; Friedrich, C.; Pfützner, A. Impact of Environmental Temperature on Skin Thickness and Microvascular Blood Flow in Subjects With and Without Diabetes. Diabetes Technol. Ther. 2006, 8, 94–101. [Google Scholar] [CrossRef]
- Gaw, R.L.; Cornish, B.H.; Thomas, B.J. The electrical impedance of pulsatile blood flowing through rigid tubes: An experimental investigation. In Proceedings of the 13th International Conference on Electrical Bioimpedance and the 8th Conference on Electrical Impedance Tomography, Graz, Austria, 29 August–2 September 2007; pp. 73–76. [Google Scholar]
- Gaw, R.L.; Cornish, B.H.; Thomas, B.J. The Electrical Impedance of Pulsatile Blood Flowing Through Rigid Tubes: A Theoretical Investigation. IEEE Trans. Biomed. Eng. 2008, 55, 721–727. [Google Scholar] [CrossRef]
- Visser, K.R. Electric conductivity of stationary and flowing human blood at low frequencies. Med Biol. Eng. Comput. 1992, 30, 636–640. [Google Scholar] [CrossRef]
- Jaspard, F.; Nadi, M.; Rouane, A. Dielectric properties of blood: An investigation of haematocrit dependence. Physiol. Meas. 2003, 24, 137–147. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Electrochemical Impedance Characterization of Blood Cell Suspensions. Part 2: Three-Phase Systems with Single-Shelled Particles. IEEE Trans. Biomed. Eng. 2020, 67, 1. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Electrochemical impedance spectroscopy of blood. Part 2: Numerical analysis of experimental dielectric spectra using the biconcave shape of human erythrocytes. Anal. Methods 2018, 10, 168–179. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Effects of Aggregation on Blood Sedimentation and Conductivity. PLoS ONE 2015, 10, e0129337. [Google Scholar] [CrossRef] [PubMed]
- Zhbanov, A.; Yang, S. Electrochemical impedance spectroscopy of blood for sensitive detection of blood hematocrit, sedimentation and dielectric properties. Anal. Methods 2017, 9, 3302–3313. [Google Scholar] [CrossRef]
- Wolf, M.; Gulich, R.; Lunkenheimer, P.; Loidl, A. Broadband dielectric spectroscopy on human blood. Biochim. Biophys. Acta (BBA) Gen. Subj. 2011, 1810, 727–740. [Google Scholar] [CrossRef] [PubMed]
- Abdalla, S.; Al-Ameer, S.S.; Al-Magaishi, S.H. Electrical properties with relaxation through human blood. Biomicrofluidics 2010, 4, 034101. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Electrochemical impedance spectroscopy of blood. Part 3: A study of the correlation between blood conductivity and sedimentation to shorten the erythrocyte sedimentation rate test. Anal. Methods 2018, 10, 180–189. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions; Courier Corporation: North Chelmsford, MA, USA, 2002. [Google Scholar]
- Trasatti, S. Atkins’ Physical Chemistry; Atkins, J., De paula, P., Eds.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Andrade, E.N.D.C. The Viscosity of Liquids. Nat. Cell Biol. 1930, 125, 582–584. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’connell, J.P. The Properties of Gases and Liquids; Mcgraw-hill: New York, NY, USA, 2001; Volume 5. [Google Scholar]
- Utracki†, L.A. Temperature dependence of liquid viscosity. J. Macromol. Sci. Part B 1974, 10, 477–505. [Google Scholar] [CrossRef]
- Viswanath, D.S.; Ghosh, T.K.; Prasad, D.H.; Dutt, N.V.; Rani, K.Y. Viscosity of Liquids: Theory, Estimation, Experiment, and Data; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- McCleskey, R.B. New Method for Electrical Conductivity Temperature Compensation. Environ. Sci. Technol. 2013, 47, 9874–9881. [Google Scholar] [CrossRef]
- McCleskey, R.B.; Nordstrom, D.K.; Ryan, J.N. Comparison of electrical conductivity calculation methods for natural waters. Limnol. Oceanogr. Methods 2012, 10, 952–967. [Google Scholar] [CrossRef]
- Sorensen, J.A.; Glass, G.E. Ion and temperature dependence of electrical conductance for natural waters. Anal. Chem. 1987, 59, 1594–1597. [Google Scholar] [CrossRef]
- Çinar, Y.; Şenyol, A.M.; Duman, K. Blood viscosity and blood pressure: Role of temperature and hyperglycemia. Am. J. Hypertens. 2001, 14, 433–438. [Google Scholar] [CrossRef]
- Bulavin, L.; Zabashta, Y.F.; Khlopov, A.M.; Khorol’Skii, A.V. Molecular mechanism of the viscosity of aqueous glucose solutions. Russ. J. Phys. Chem. A 2017, 91, 89–93. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.S.; Son, M.; Zhbanov, A.; Jung, Y.; Jung, M.H.; Eom, K.; Nam, S.H.; Park, J.; Yang, S. Temperature Correction to Enhance Blood Glucose Monitoring Accuracy Using Electrical Impedance Spectroscopy. Sensors 2020, 20, 6231. https://doi.org/10.3390/s20216231
Lee YS, Son M, Zhbanov A, Jung Y, Jung MH, Eom K, Nam SH, Park J, Yang S. Temperature Correction to Enhance Blood Glucose Monitoring Accuracy Using Electrical Impedance Spectroscopy. Sensors. 2020; 20(21):6231. https://doi.org/10.3390/s20216231
Chicago/Turabian StyleLee, Ye Sung, Minkook Son, Alexander Zhbanov, Yugyung Jung, Myoung Hoon Jung, Kunsun Eom, Sung Hyun Nam, Jongae Park, and Sung Yang. 2020. "Temperature Correction to Enhance Blood Glucose Monitoring Accuracy Using Electrical Impedance Spectroscopy" Sensors 20, no. 21: 6231. https://doi.org/10.3390/s20216231
APA StyleLee, Y. S., Son, M., Zhbanov, A., Jung, Y., Jung, M. H., Eom, K., Nam, S. H., Park, J., & Yang, S. (2020). Temperature Correction to Enhance Blood Glucose Monitoring Accuracy Using Electrical Impedance Spectroscopy. Sensors, 20(21), 6231. https://doi.org/10.3390/s20216231






