Micromagnetic Simulations of Submicron Vortex Structures for the Detection of Superparamagnetic Labels
Abstract
:1. Introduction
2. Simulation Methods and Parameters
2.1. Simulation Model
2.2. Material Parameters and Dimensions
3. Results
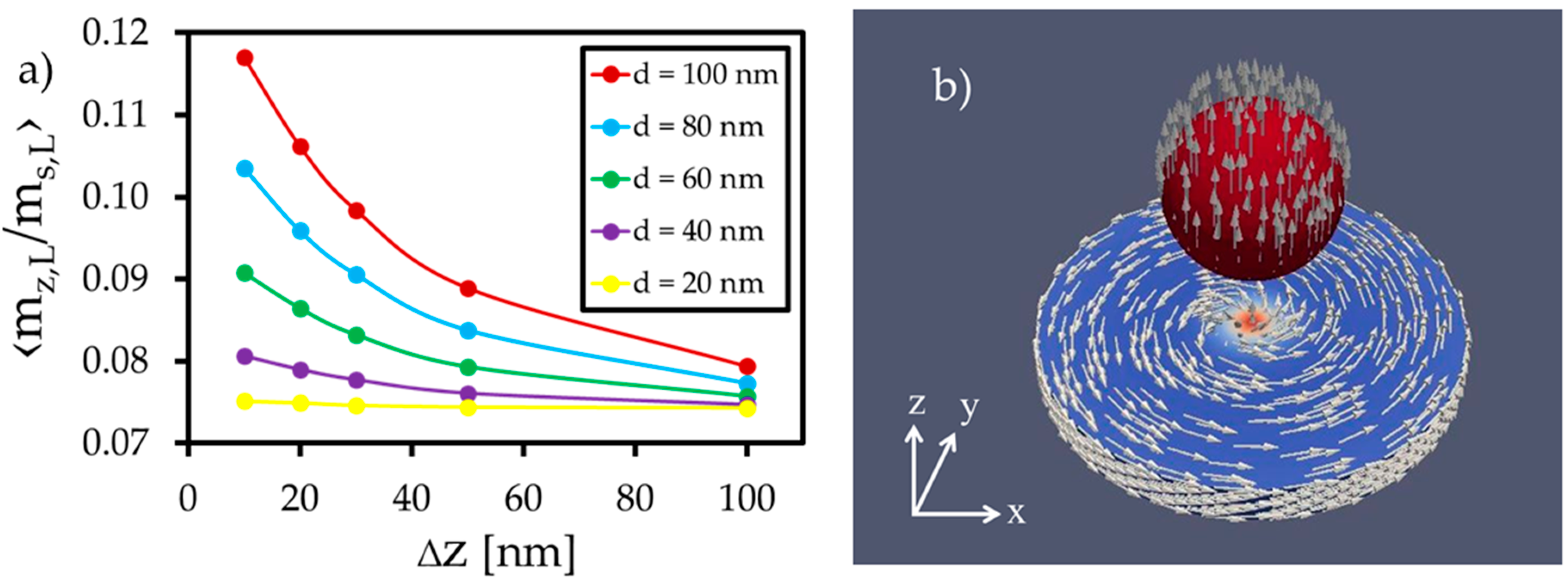
3.1. Change in the Free Layer’s Magnetization
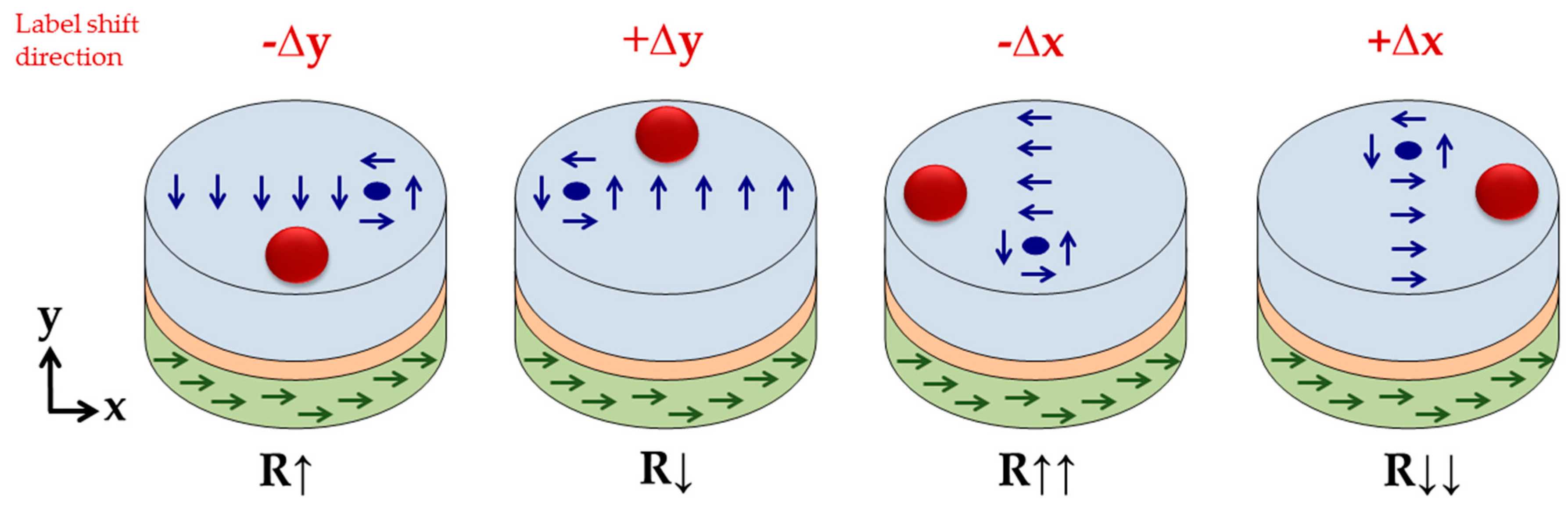
3.2. Resistance Changes due to the Label’s Stray Field
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Karnaushenko, D.; Makarov, D.; Stöber, M.; Karnaushenko, D.D.; Baunack, S.; Schmidt, O.G. Flexible Electronics: High-Performance Magnetic Sensorics for Printable and Flexible Electronics. Adv. Mater. 2015, 27, 955. [Google Scholar] [CrossRef]
- Simmons, L.P.; Welsh, J.S. Particle filter based finger tracking utilising magnetoresistive sensors. In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besancon, France, 8–11 July 2014; pp. 560–565. [Google Scholar]
- Caruso, L.; Wunderle, T.; Lewis, C.M.; Valadeiro, J.; Trauchessec, V.; Rosillo, J.T.; Amaral, J.P.; Ni, J.; Jendritza, P.; Fermon, C.; et al. In Vivo Magnetic Recording of Neuronal Activity. Neuron 2017, 95, 1283–1291.e4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, C.; Zhu, K.; Freitas, P.P.; Chang, J.-Y.; Davies, J.E.; Eames, P.; Freitas, P.P.; Kazakova, O.; Kim, C.; Leung, C.-W.; et al. Magnetoresistive Sensor Development Roadmap (Non-Recording Applications). IEEE Trans. Magn. 2019, 55, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.; Makarov, D.; Schmidt, O.G. Magnetic sensing platform technologies for biomedical applications. Lab A Chip 2017, 17, 1884–1912. [Google Scholar] [CrossRef] [PubMed]
- Gijs, M.A.M.; Lacharme, F.; Lehmann, U. Microfluidic Applications of Magnetic Particles for Biological Analysis and Catalysis. Chem. Rev. 2010, 110, 1518–1563. [Google Scholar] [CrossRef]
- Freitas, P.P.; Cardoso, F.A.; Martins, V.C.; Martins, S.A.M.; Loureiro, J.; Amaral, J.; Chaves, R.C.; Cardoso, S.; Fonseca, L.P.; Sebastião, A.M.; et al. Spintronic platforms for biomedical applications. Lab A Chip 2012, 12, 546–557. [Google Scholar] [CrossRef]
- Reiss, G.; Brueckl, H.; Huetten, A.; Schotter, J.; Brzeska, M.; Panhorst, M.; Sudfeld, D.; Becker, A.; Kamp, P.B.; Pühler, A.; et al. Magnetoresistive sensors and magnetic nanoparticles for biotechnology. J. Mater. Res. 2005, 20, 3294–3302. [Google Scholar] [CrossRef]
- Giouroudi, I.; Hristoforou, E. Perspective: Magnetoresistive sensors for biomedicine. J. Appl. Phys. 2018, 124, 30902. [Google Scholar] [CrossRef]
- Suess, D.; Bachleitner-Hofmann, A.; Satz, A.; Weitensfelder, H.; Vogler, C.; Bruckner, F.; Abert, C.; Prügl, K.; Zimmer, J.; Huber, C.; et al. Topologically protected vortex structures for low-noise magnetic sensors with high linear range. Nat. Electron. 2018, 1, 362–370. [Google Scholar] [CrossRef]
- Weitensfelder, H.; Brueckl, H.; Satz, A.; Pruegl, K.; Zimmer, J.; Luber, S.; Raberg, W.; Abert, C.; Bruckner, F.; Bachleitner-Hofmann, A.; et al. Comparison of Sensitivity and Low Frequency Noise Contributions in GMR and TMR Spin Valve Sensors with a Vortex State Free Layer. Phys. Rev. Appl. 2018, 10, 054056-1-6. [Google Scholar] [CrossRef] [Green Version]
- Shinjo, T. Magnetic Vortex Core Observation in Circular Dots of Permalloy. Science 2000, 289, 930–932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gloag, L.; Mehdipour, M.; Chen, D.; Tilley, R.D.; Gooding, J.J. Advances in the Application of Magnetic Nanoparticles for Sensing. Adv. Mater. 2019, 31, e1904385. [Google Scholar] [CrossRef] [PubMed]
- Papaefthymiou, G.C. Nanoparticle magnetism. Nano Today 2009, 4, 438–447. [Google Scholar] [CrossRef]
- Ennen, I.; Kappe, D.; Rempel, T.; Glenske, C.; Hütten, A. Giant Magnetoresistance: Basic Concepts, Microstructure, Magnetic Interactions and Applications. Sensors 2016, 16, 904. [Google Scholar] [CrossRef]
- Abert, C.; Ruggeri, M.; Bruckner, F.; Vogler, C.; Manchon, A.; Praetorius, D.; Suess, D. A self-consistent spin-diffusion model for micromagnetics. Sci. Rep. 2016, 6, 16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pietambaram, S.V.; Janesky, J.; Dave, R.W.; Sun, J.J.; Steiner, G.; Slaughter, J.M. Exchange coupling control and thermal endurance of synthetic antiferromagnet structures for MRAM. IEEE Trans. Magn. 2004, 40, 2619–2621. [Google Scholar] [CrossRef]
- Gilbert, T.L. A Phenomenological Theory of Damping in Ferromagnetic Materials. IEEE Trans. Magn. 2004, 40, 3443–3449. [Google Scholar] [CrossRef]
- Abert, C. Micromagnetics and spintronics: Models and numerical methods. Eur. Phys. J. B 2019, 92, 120. [Google Scholar] [CrossRef] [Green Version]
- Abert, C.; Exl, L.; Bruckner, F.; Drews, A.; Suess, D. magnum.fe: A micromagnetic finite-element simulation code based on FEniCS. J. Magn. Magn. Mater. 2013, 345, 29–35. [Google Scholar] [CrossRef] [Green Version]
- Akbarzadeh, A.; Samiei, M.; Davaran, S. Magnetic nanoparticles: Preparation, physical properties, and applications in biomedicine. Nanoscale Res. Lett. 2012, 7, 144. [Google Scholar] [CrossRef] [Green Version]
- Campos, E.A.; Pinto, D.V.B.S.; De Oliveira, J.I.S.; Mattos, E.D.C.; Dutra, R.D.C.L. Synthesis, Characterization and Applications of Iron Oxide Nanoparticles—a Short Review. J. Aerosp. Technol. Manag. 2015, 7, 267–276. [Google Scholar] [CrossRef] [Green Version]
- Tartaj, P.; del Puerto Morales, M.; Veintemillas-Verdaguer, S.; González-Carreño, T.; Serna, C. The preparation of magnetic nanoparticles for applications in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R182–R197. [Google Scholar] [CrossRef]
- Aftab, S.; Shah, S.A.; Nadhman, A.; Kurbanoglu, S.; Ozkan, S.A.; Dionysiou, D.D.; Shukla, S.S.; Aminabhavi, T.M. Nanomedicine: An effective tool in cancer therapy. Int. J. Pharm. 2018, 540, 132–149. [Google Scholar] [CrossRef] [PubMed]
- Arias, L.S.; Pessan, J.P.; Vieira, A.P.M.; De Lima, T.M.T.; Delbem, A.C.B.; Monteiro, D.R. Iron Oxide Nanoparticles for Biomedical Applications: A Perspective on Synthesis, Drugs, Antimicrobial Activity, and Toxicity. Antibiotics 2018, 7, 46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bilal, M.; Zhao, Y.; Rasheed, T.; Iqbal, H.M. Magnetic nanoparticles as versatile carriers for enzymes immobilization: A review. Int. J. Biol. Macromol. 2018, 120, 2530–2544. [Google Scholar] [CrossRef]
- Bulte, J.W. Superparamagnetic iron oxides as MPI tracers: A primer and review of early applications. Adv. Drug Deliv. Rev. 2019, 138, 293–301. [Google Scholar] [CrossRef]
- Wahajuddin, S.A. Superparamagnetic iron oxide nanoparticles: Magnetic nanoplatforms as drug carriers. Int. J. Nanomed. 2012, 7, 3445–3471. [Google Scholar] [CrossRef] [Green Version]
- Dadfar, S.M.; Camozzi, D.; Darguzyte, M.; Roemhild, K.; Varvarà, P.; Metselaar, J.; Banala, S.; Straub, M.; Güvener, N.; Engelmann, U.; et al. Size-isolation of superparamagnetic iron oxide nanoparticles improves MRI, MPI and hyperthermia performance. J. Nanobiotechnol. 2020, 18, 1–13. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Y.; Li, W.; Xie, Y.; Li, Y.; Wu, J.; Wang, S.; Tian, Y.; Tian, W.; Teng, Z.; et al. Synthesis of sub-100 nm biocompatible superparamagnetic Fe3O4 colloidal nanocrytal clusters as contrast agents for magnetic resonance imaging. RSC Adv. 2016, 6, 62550–62555. [Google Scholar] [CrossRef]
- Li, Q.; Kartikowati, C.W.; Horie, S.; Ogi, T.; Iwaki, T.; Okuyama, K. Correlation between particle size/domain structure and magnetic properties of highly cristalline Fe3O4 nanoparticles. Sci. Rep. 2017, 7, 1–7. [Google Scholar]
- Anthony, J.W.; Bideaux, R.A.; Bladh, K.W.; Nichols, M.C. Handbook of Mineralogy; Mineralogical Society of America: Chantilly, VA, USA, 2001; Volume 4, p. 333. [Google Scholar]
- Yamamuro, S.; Tanaka, T. Exchange-coupled Fe/Fe3O4 magnetic nanocomposite powder prepared by eutectoid decomposition of FeO. J. Ceram. Soc. Jpn. 2018, 126, 152–155. [Google Scholar] [CrossRef] [Green Version]
- Tondra, M.; Porter, M.; Lipert, R.J. Model for detection of immobilized superparamagnetic nanosphere assay labels using giant magnetoresistive sensors. J. Vac. Sci. Technol. A 2000, 18, 1125–1129. [Google Scholar] [CrossRef] [Green Version]
- Matthes, P.; Arekapudi, S.S.P.K.; Timmermann, F.; Albrecht, M. Magnetotransport Properties of Perpendicular [Pt/Co]/Cu/[Co/Pt] Pseudo-Spin-Valves. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Guslienko, K.Y. Magnetic Vortex State Stability, Reversal and Dynamics in Restricted Geometries. J. Nanosci. 2008, 8, 2745–2760. [Google Scholar] [CrossRef]
- Verba, R.V.; Navas, D.; Hierro-Rodriguez, A.; Bunyaev, S.A.; Ivanov, B.A.; Guslienko, K.Y.; Kakazei, G.N. Overcoming the Limits of Vortex Formation in Magnetic Nanodots by Coupling to Antidot Matrix. Phys. Rev. Appl. 2018, 10, 31002. [Google Scholar] [CrossRef] [Green Version]
- Goiriena-Goikoetxea, M.; Guslienko, K.Y.; Rouco, M.; Orue, I.; Berganza, E.; Jaafar, M.; Asenjo, A.; Fernández-Gubieda, M.L.; Barquín, L.F.; García-Arribas, A. Magnetization reversal in circular vortex dots of small radius. Nanoscale 2017, 9, 11269–11278. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Perez, M.J.; Müller, B.; Lin, J.; Rodríguez, L.A.; Snoeck, E.; Kleiner, R.; Sesé, J.; Koelle, D. Magnetic vortex nucleation and annihilation in bi-stable ultra-small ferromagnetic particles. Nanoscale 2020, 12, 2587–2595. [Google Scholar] [CrossRef]
- Metlov, K.L.; Lee, Y. Map of metastable states for thin circular magnetic nanocylinders. Appl. Phys. Lett. 2008, 92, 112506. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.X.; Morisako, A. Soft magnetic properties of FeCo films with high saturation magnetization. J. Appl. Phys. 2008, 103, 7E726. [Google Scholar] [CrossRef]
- Fujita, M.; Yamano, K.; Maeda, A.; Tanuma, T.; Kume, M. Exchange coupling in spin-valve structures containing amorphous CoFeB. J. Appl. Phys. 1997, 81, 4909–4911. [Google Scholar] [CrossRef]
- Abert, C.; Ruggeri, M.; Bruckner, F.; Vogler, C.; Hrkac, G.; Praetorius, D.; Suess, D. A three-dimensional spin-diffusion model for micromagnetics. Sci. Rep. 2015, 5, 14855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taslimi, H.; Sohi, M.H.; Mehrizi, S.; Saremi, M. Studies of the effects of addition of P and Cr on microstructure and electrical resistivity of nanocrystalline CoFe thin films. J. Mater. Sci. Mater. Electron. 2015, 26, 2962–2968. [Google Scholar] [CrossRef]
- Cecot, M.; Karwacki, Ł.; Skowroński, W.; Kanak, J.; Wrona, J.; Żywczak, A.; Yao, L.; Van Dijken, S.; Barnaś, J.; Stobiecki, T. Influence of intermixing at the Ta/CoFeB interface on spin Hall angle in Ta/CoFeB/MgO heterostructures. Sci. Rep. 2017, 7, 968. [Google Scholar] [CrossRef] [PubMed]
- Matula, R.A. Electrical resistivity of copper, gold, palladium, and silver. J. Phys. Chem. Ref. Data 1979, 8, 1147–1298. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Sun, S.; Wang, S.X. Spin valve biosensors: Signal dependence on nanoparticle position. J. Appl. Phys. 2006, 99, 8P107. [Google Scholar] [CrossRef]
- Wang, S.X.; Li, G. Advances in Giant Magnetoresistance Biosensors with Magnetic Nanoparticle Tags: Review and Outlook. IEEE Trans. Magn. 2008, 44, 1687–1702. [Google Scholar] [CrossRef]
- Devkota, J.; Kokkinis, G.; Berris, T.; Jamalieh, M.; Cardoso, S.; Srikanth, H.; Phan, M.-H.; Giouroudi, I. A novel approach for detection and quantification of magnetic nanomarkers using a spin valve GMR-integrated microfluidic sensor. RSC Adv. 2015, 5, 51169–51175. [Google Scholar] [CrossRef]
- Cubells-Beltrán, M.-D.; Reig, C.; Madrenas, J.; De Marcellis, A.; Santos, J.; Freitas, P.P.; Freitas, P.P. Integration of GMR Sensors with Different Technologies. Sensors 2016, 16, 939. [Google Scholar] [CrossRef] [PubMed]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wetterau, L.; Abert, C.; Suess, D.; Albrecht, M.; Witzigmann, B. Micromagnetic Simulations of Submicron Vortex Structures for the Detection of Superparamagnetic Labels. Sensors 2020, 20, 5819. https://doi.org/10.3390/s20205819
Wetterau L, Abert C, Suess D, Albrecht M, Witzigmann B. Micromagnetic Simulations of Submicron Vortex Structures for the Detection of Superparamagnetic Labels. Sensors. 2020; 20(20):5819. https://doi.org/10.3390/s20205819
Chicago/Turabian StyleWetterau, Lukas, Claas Abert, Dieter Suess, Manfred Albrecht, and Bernd Witzigmann. 2020. "Micromagnetic Simulations of Submicron Vortex Structures for the Detection of Superparamagnetic Labels" Sensors 20, no. 20: 5819. https://doi.org/10.3390/s20205819
APA StyleWetterau, L., Abert, C., Suess, D., Albrecht, M., & Witzigmann, B. (2020). Micromagnetic Simulations of Submicron Vortex Structures for the Detection of Superparamagnetic Labels. Sensors, 20(20), 5819. https://doi.org/10.3390/s20205819




