Lie Group Methods in Blind Signal Processing
Abstract
1. Introduction
2. Model Definition (ICA, ISA)
3. Geometry of ICA, ISA and Other BSP Models
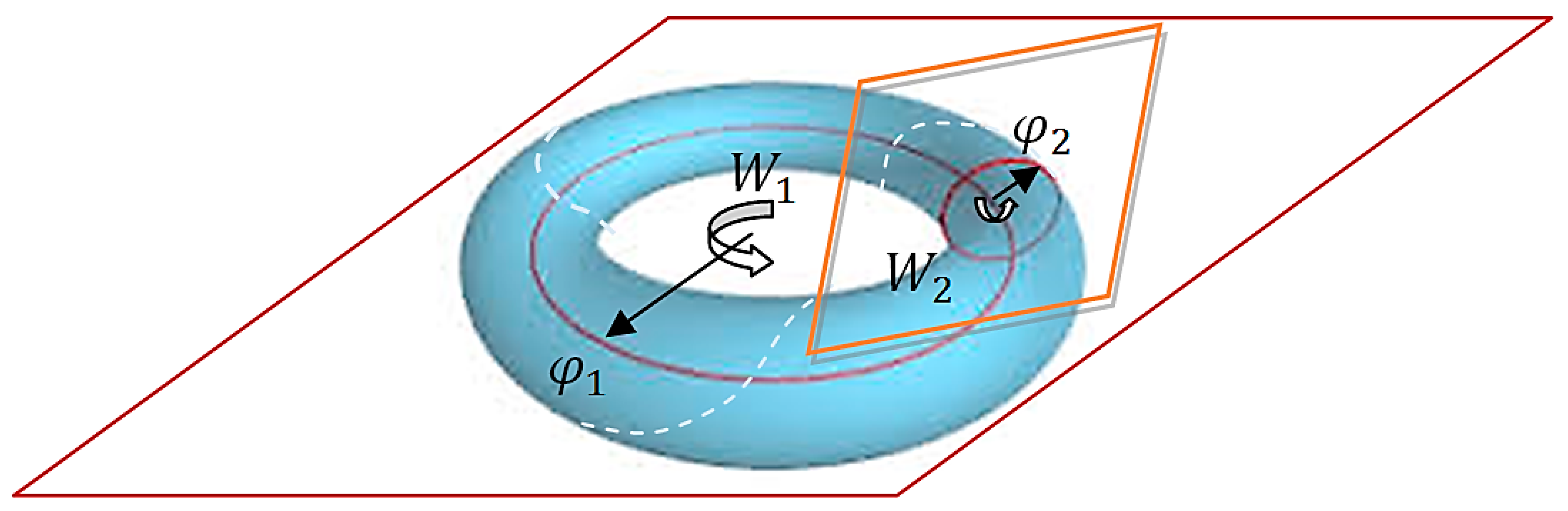
4. Lie Group Optimization Methods. One-Parameter Subalgebra and Toral Subalgebra
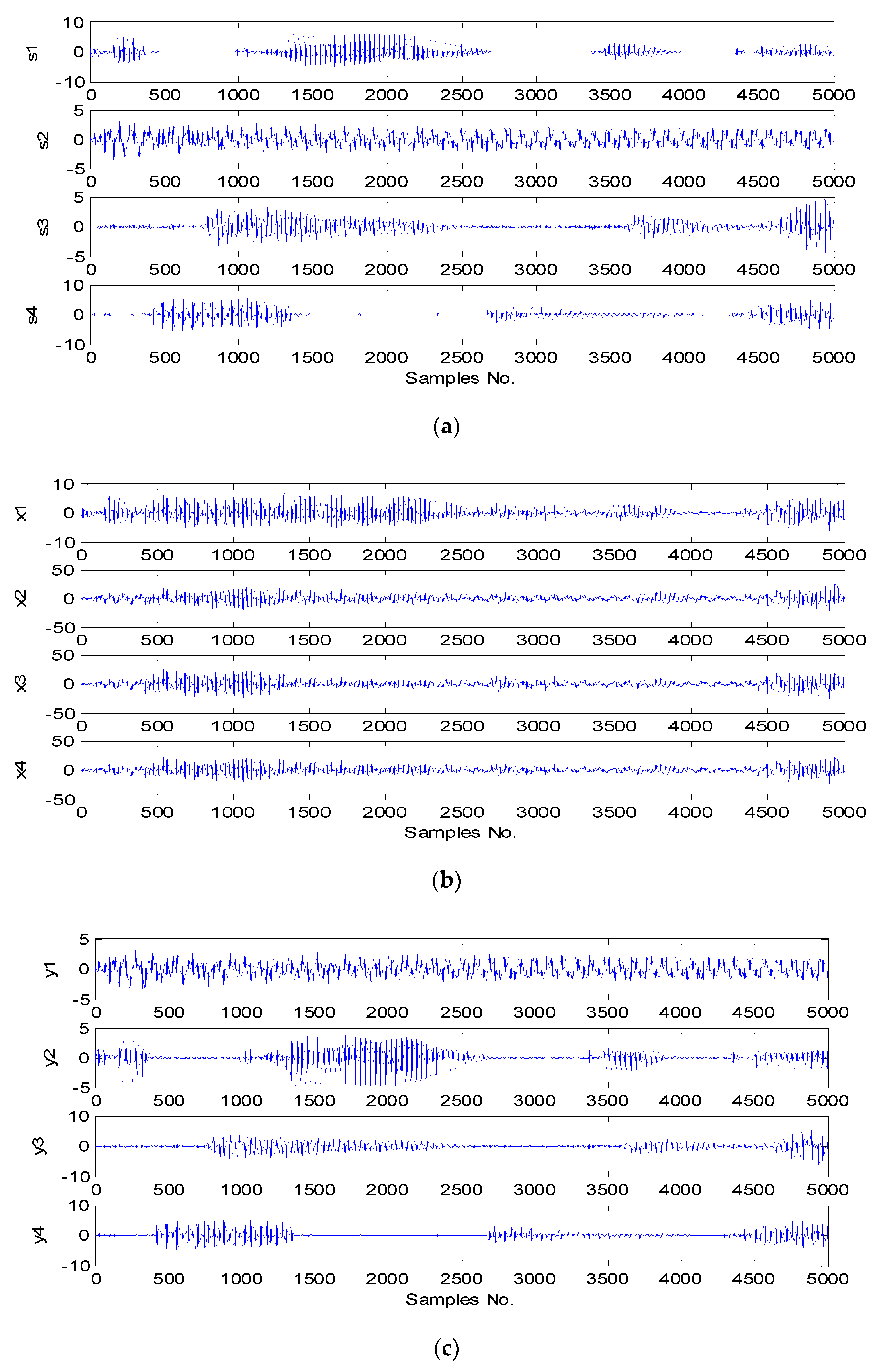
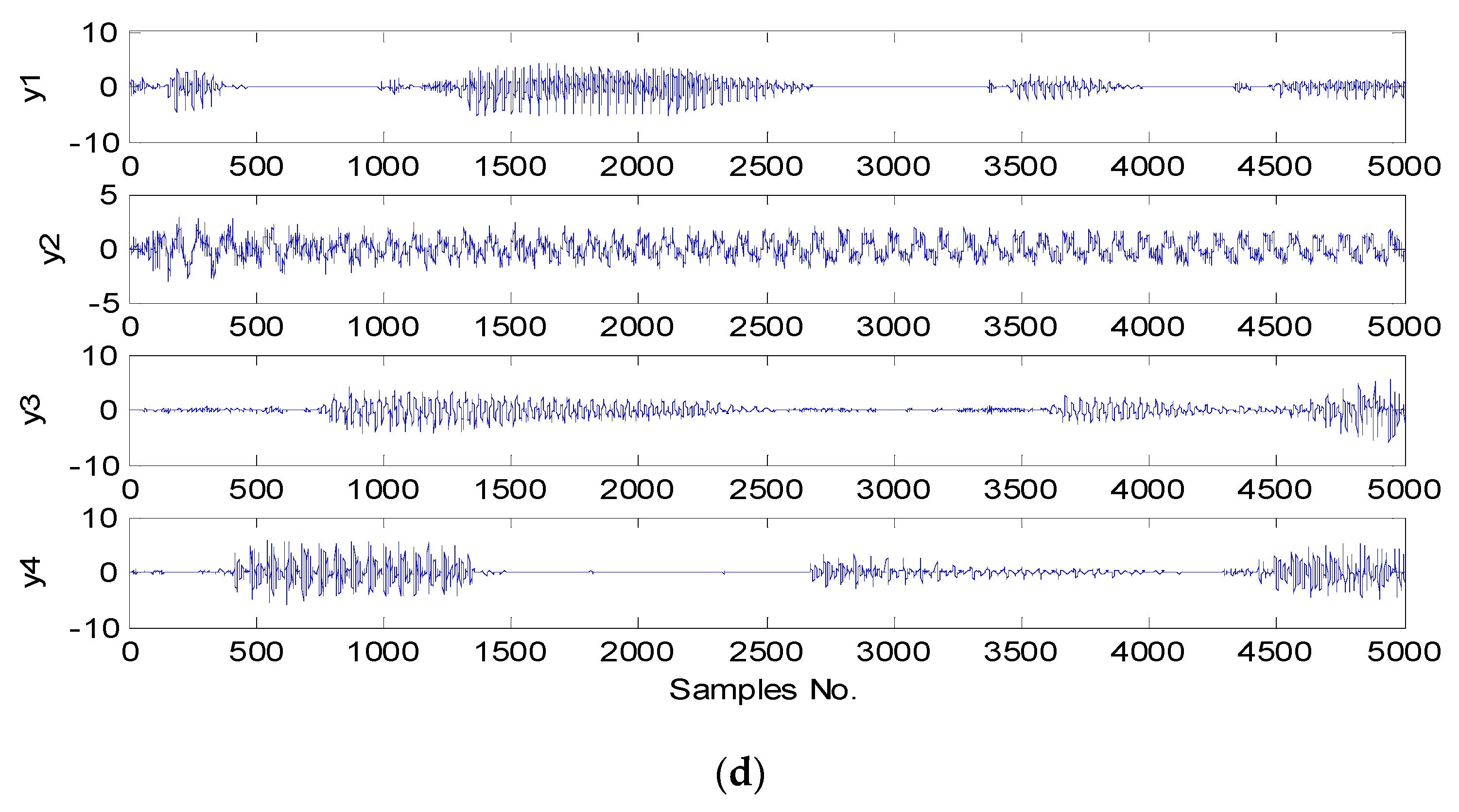
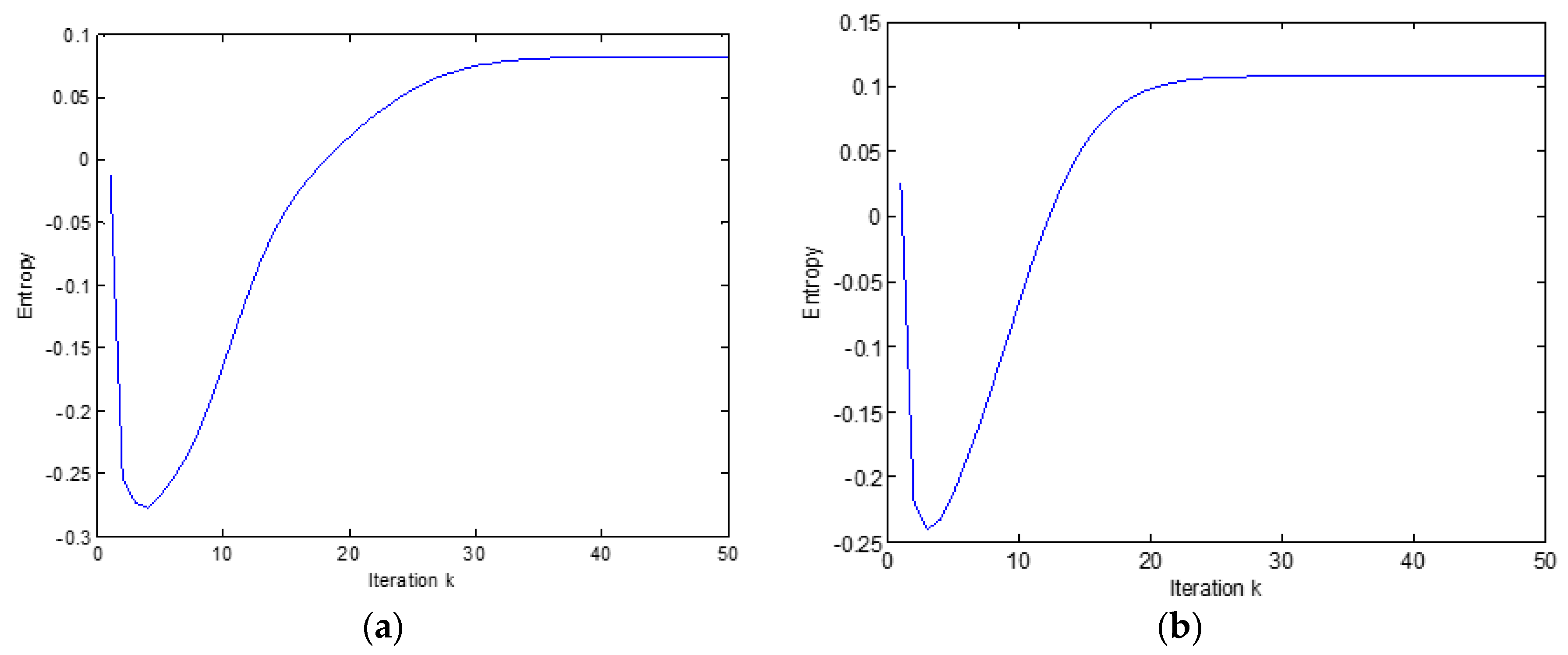
5. Experimental Results
- (1)
- algorithm SD unconstrained on the Euclidean space,
- (2)
- algorithm SD on the Euclidean space with constraint restoration,
- (3)
- algorithm SD on the Euclidean space with penalty function,
- (4)
- non-geodesic algorithm SD on Riemannian space,
- (5)
- geodesic algorithm SD on Riemannian space.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Lie Group and Lie Algebra
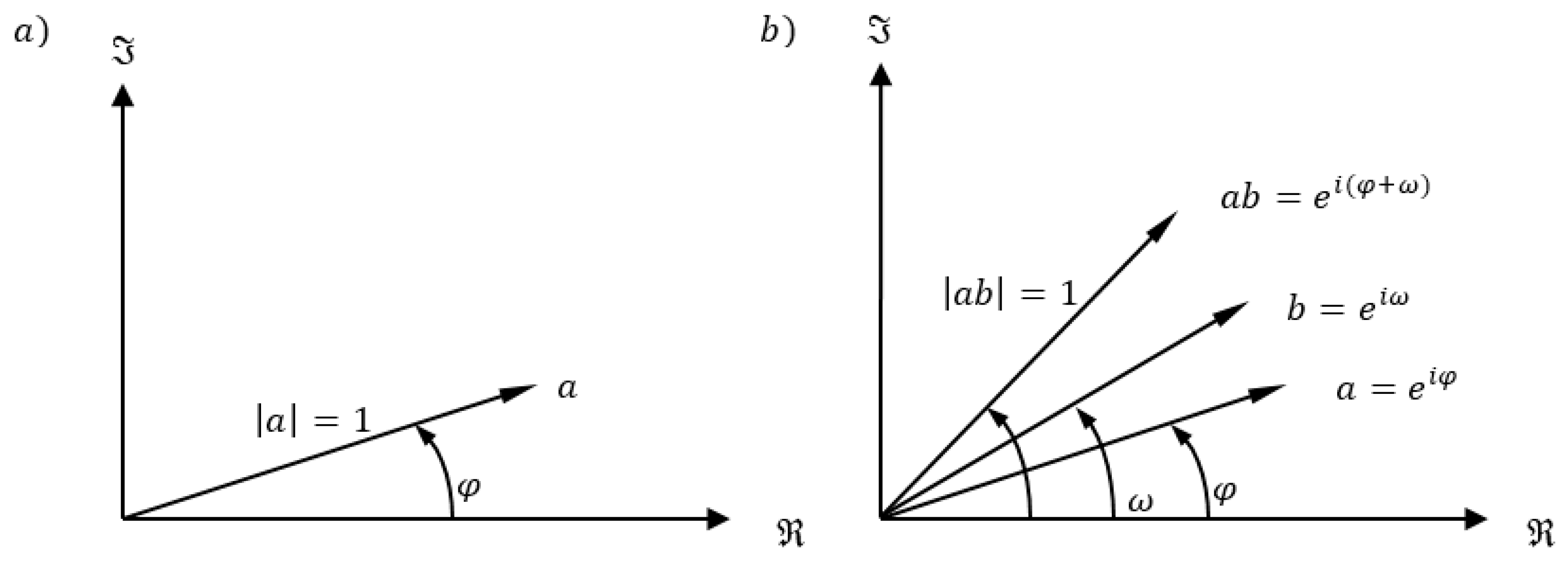
- Closure under group operation: if then
- Associativity:
- There exists a neutral element and an inverse element for every element of the group, such that:
References
- Fiori, S. Quasi-geodesic neural learning algorithms over the orthogonal group: A tutorial. J. Mach. Learn. Res. 2005, 6, 743–781. [Google Scholar]
- Georgiev, P.; Theis, F.; Cichocki, A.; Bakardjian, H. Sparse component analysis: A new tool for data mining. In Data Mining in Biomedicine; Springer: Boston, MA, USA, 2007; pp. 91–116. [Google Scholar]
- Hao, Y.; Song, L.; Cui, L.; Wang, H. A three-dimensional geometric features-based SCA algorithm for compound faults diagnosis. Measurement 2019, 134, 480–491. [Google Scholar] [CrossRef]
- Hao, Y.; Song, L.; Cui, L.; Wang, H. Underdetermined source separation of bearing faults based on optimized intrinsic characteristic-scale decomposition and local non-negative matrix factorization. IEEE Access 2019, 7, 11427–11435. [Google Scholar] [CrossRef]
- Kaselimi, M.; Doulamis, N.; Doulamis, A.; Voulodimos, A.; Protopapadakis, E. Bayesian-optimized Bidirectional LSTM Regression Model for Non-Intrusive Load Monitoring. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 2747–2751. [Google Scholar]
- Altrabalsi, H.; Stankovic, V.; Liao, J.; Stankovic, L. Low-complexity energy disaggregation using appliance load modelling. Aims Energy 2016, 4, 884–905. [Google Scholar] [CrossRef]
- Smith, S.T. Optimization techniques on Riemannian manifolds. Fields Inst. Commun. 1994, 3, 113–135. [Google Scholar]
- Plumbley, M.D. Geometrical methods for non-negative ICA: Manifolds, Lie groups and toral subalgebras. Neurocomputing 2005, 67, 161–197. [Google Scholar] [CrossRef]
- Plumbley, M.D. Lie group methods for optimization with orthogonality constraints. In Proceedings of the International Conference on Independent Component Analysis and Signal Separation, Granada, Spain, 22–24 September 2004; pp. 1245–1252. [Google Scholar]
- Plumbley, M.D. Algorithms for nonnegative independent component analysis. IEEE Trans. Neural Netw. 2003, 14, 534–543. [Google Scholar] [CrossRef] [PubMed]
- Plumbley, M.D. Optimization using Fourier expansion over a geodesic for non-negative ICA. In Proceedings of the International Conference on Independent Component Analysis and Signal Separation, Granada, Spain, 22–24 September 2004; pp. 49–56. [Google Scholar]
- Edelman, A.; Arias, T.A.; Smith, S.T. The geometry of algorithms with orthogonality constraints. Siam J. Matrix Anal. Appl. 1998, 20, 303–353. [Google Scholar] [CrossRef]
- Birtea, P.; Casu, I.; Comanescu, D. Steepest descent algorithm on orthogonal Stiefel manifolds. arXiv 2017, arXiv:1709.06295. [Google Scholar]
- Mika, D.; Kleczkowski, P. ICA-based single channel audio separation: New bases and measures of distance. Arch. Acoust. 2011, 36, 311–331. [Google Scholar] [CrossRef]
- Mika, D.; Kleczkowski, P. Automatic clustering of components for single channel ICA-based signal demixing. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Lisbon, Portugal, 13–16 June 2010; pp. 5350–5359. [Google Scholar]
- Hyvärinen, A.; Hoyer, P. Emergence of phase-and shift-invariant features by decomposition of natural images into independent feature subspaces. Neural Comput. 2000, 12, 1705–1720. [Google Scholar] [CrossRef] [PubMed]
- Selvana, S.E.; Amatob, U.; Qic, C.; Gallivanc, K.A.; Carforab, M.F.; Larobinad, M.; Alfanod, B. Unconstrained Optimizers for ICA Learning on Oblique Manifold Using Parzen Density Estimation; Tech. Rep. FSU11-05; Florida State University Department of Mathematics: Tallahassee, FL, USA, 2011. [Google Scholar]
- Hyvarinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Absil, P.-A.; Gallivan, K.A. Joint Diagonalization on the Oblique Manifold for Independent Component Analysis. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006. [Google Scholar]
- Selvan, S.E.; Amato, U.; Gallivan, K.A.; Qi, C.; Carfora, M.F.; Larobina, M.; Alfano, B. Descent algorithms on oblique manifold for source-adaptive ICA contrast. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1930–1947. [Google Scholar] [CrossRef] [PubMed]
- Nishimori, Y.; Akaho, S. Learning algorithms utilizing quasi-geodesic flows on the Stiefel manifold. Neurocomputing 2005, 67, 106–135. [Google Scholar] [CrossRef]
- Absil, P.-A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Absil, P.-A.; Mahony, R.; Sepulchre, R. Riemannian geometry of Grassmann manifolds with a view on algorithmic computation. Acta Appl. Math. 2004, 80, 199–220. [Google Scholar] [CrossRef]
- Comon, P.; Golub, G.H. Tracking a few extreme singular values and vectors in signal processing. Proc. IEEE 1990, 78, 1327–1343. [Google Scholar] [CrossRef]
- Demmel, J.W. Three methods for refining estimates of invariant subspaces. Computing 1987, 38, 43–57. [Google Scholar] [CrossRef]
- Nishimori, Y.; Akaho, S.; Abdallah, S.; Plumbley, M.D. Flag manifolds for subspace ICA problems. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP’07, Honolulu, HI, USA, 15–20 April 2007; pp. 1417–1420. [Google Scholar]
- Nishimori, Y.; Akaho, S.; Plumbley, M.D. Riemannian optimization method on the flag manifold for independent subspace analysis. In Proceedings of the International Conference on Independent Component Analysis and Signal Separation, Charleston, SC, USA, 5–8 March 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 295–302. [Google Scholar]
- Nishimori, Y.; Akaho, S.; Plumbley, M.D. Natural conjugate gradient on complex flag manifolds for complex independent subspace analysis. In Proceedings of the International Conference on Artificial Neural Networks, Prague, Czech Republic, 3–6 September 2008; pp. 165–174. [Google Scholar]
- Gallier, J.; Xu, D. Computing exponentials of skew-symmetric matrices and logarithms of orthogonal matrices. Int. J. Robot. Autom. 2003, 18, 10–20. [Google Scholar]
- Pecora, A.; Maiolo, L.; Minotti, A.; De Francesco, R.; De Francesco, E.; Leccese, F.; Cagnetti, M.; Ferrone, A. Strain gauge sensors based on thermoplastic nanocomposite for monitoring inflatable structures. In Proceedings of the 2014 IEEE Metrology for Aerospace (MetroAeroSpace), Benevento, Italy, 29–30 May 2014; pp. 84–88. [Google Scholar]
- Krantz, S.G. Function Theory of Several Complex Variables; American Mathematical Soc.: Providence, RI, USA, 2011. [Google Scholar]
- Cichocki, A.; Amari, S. Adaptive Blind Signal and Image Processing: Learning Algorithms and Applications; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]

 algorithm SD on the Euclidean space with constraint restoration (2). + algorithm SD on the Euclidean space with penalty function (3). o non-geodesic algorithm SD on Riemannian space (4).
algorithm SD on the Euclidean space with constraint restoration (2). + algorithm SD on the Euclidean space with penalty function (3). o non-geodesic algorithm SD on Riemannian space (4).  geodesic algorithm SD on Riemannian space (5).
geodesic algorithm SD on Riemannian space (5).
 algorithm SD on the Euclidean space with constraint restoration (2). + algorithm SD on the Euclidean space with penalty function (3). o non-geodesic algorithm SD on Riemannian space (4).
algorithm SD on the Euclidean space with constraint restoration (2). + algorithm SD on the Euclidean space with penalty function (3). o non-geodesic algorithm SD on Riemannian space (4).  geodesic algorithm SD on Riemannian space (5).
geodesic algorithm SD on Riemannian space (5).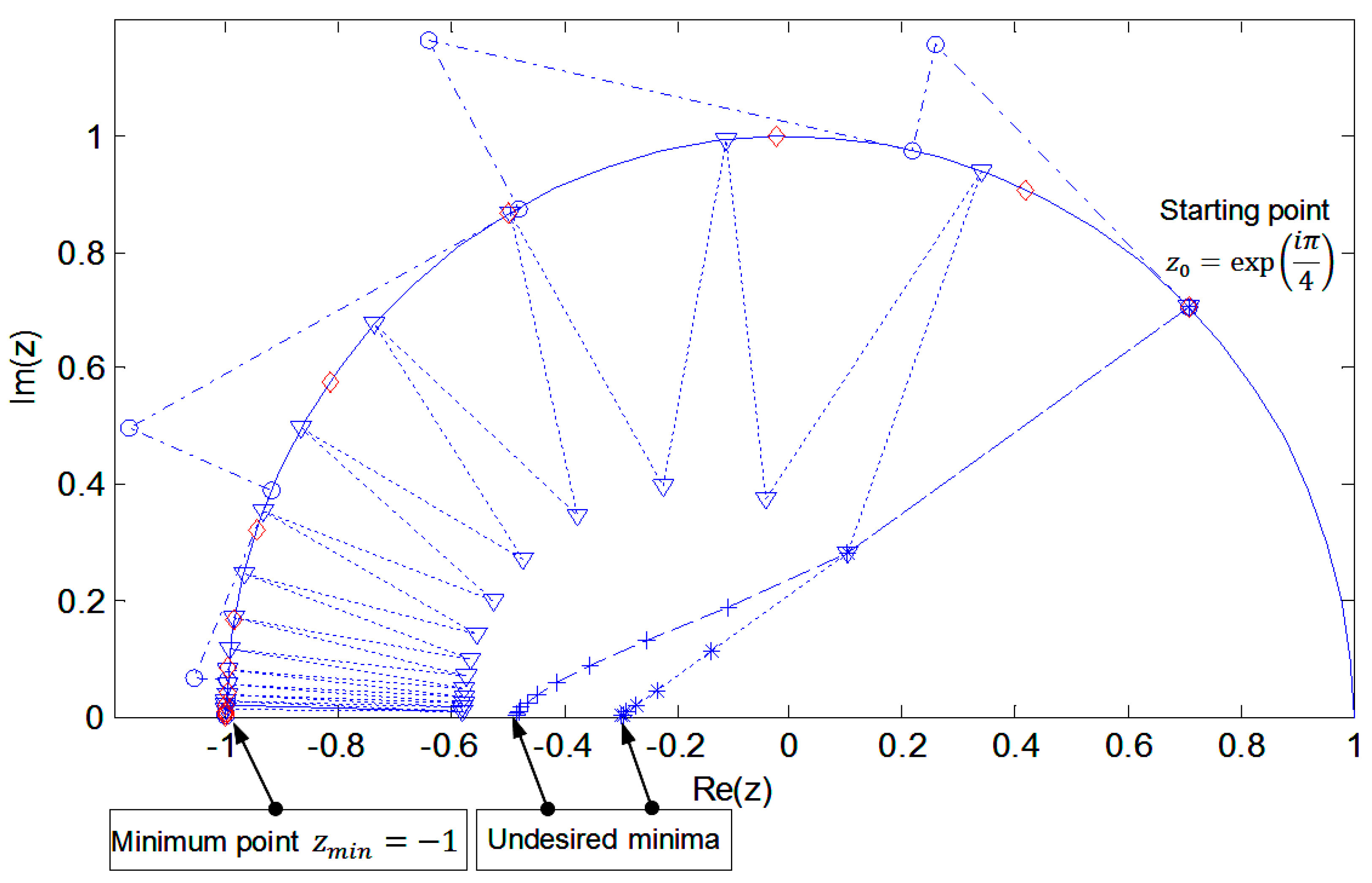
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mika, D.; Jozwik, J. Lie Group Methods in Blind Signal Processing. Sensors 2020, 20, 440. https://doi.org/10.3390/s20020440
Mika D, Jozwik J. Lie Group Methods in Blind Signal Processing. Sensors. 2020; 20(2):440. https://doi.org/10.3390/s20020440
Chicago/Turabian StyleMika, Dariusz, and Jerzy Jozwik. 2020. "Lie Group Methods in Blind Signal Processing" Sensors 20, no. 2: 440. https://doi.org/10.3390/s20020440
APA StyleMika, D., & Jozwik, J. (2020). Lie Group Methods in Blind Signal Processing. Sensors, 20(2), 440. https://doi.org/10.3390/s20020440





