1. Introduction
In order to improve spectral efficiency and meet the needs of users for massive connectivity, non-orthogonal multiple access (NOMA) has attracted great attention from many researchers [
1,
2]. NOMA is widely regarded as a promising multiple access technique for the fifth-generation mobile communication networks [
3]. The key idea of NOMA is that multiple users can be served by sharing the same physical resource over different power levels [
4]. More specifically, multiple users’ signals are transmitted by employing the superposition coding scheme at the transmitter and these users’ signals are decoded by applying successive interference cancellation at the receiver [
5]. To ensure user fairness, more transmit power is allocated to users with worse channel conditions, where NOMA is capable of providing services for multiple users.
Cooperative NOMA is a promising technology in the future wireless network, which has improved the spectral efficiency and enhanced the reliability of wireless network. The current research on cooperative NOMA is divided into two aspects. One aspect is that the nearby NOMA user with better channel conditions is viewed as user relaying to forward the information to the distant NOMA users [
6,
7,
8,
9,
10]. In Reference [
6], the authors initially have proposed cooperative NOMA scheme in which the nearby users with better channel conditions are regard as decode-and-forward (DF) relaying to improve the system reliability. From the perspective of energy efficiency, cooperative NOMA with simultaneous wireless information and power transfer (SWIPT) has been studied in Reference [
7], in which the nearby NOMA user plays the role of an energy harvesting DF relaying to assist distant NOMA user. The performance of integrating cooperative NOMA with full-duplex (FD) device-to-device (D2D) communication has been researched in Reference [
8], in which the NOMA-strong user is employed to assist the NOMA-weak user by FD D2D communications. Considering a two-user NOMA network, the best-near best-far user selection scheme has been developed to study the outage performance of NOMA-based cooperative relaying systems in Reference [
9], where the best cell-center user is selected to act as an energy harvesting relay to help a selected cell-edge user. The performance of cell-edge users in multiple-input single-output NOMA systems has been researched in Reference [
10] by using transmit antenna selection and SWIPT-based cooperative transmission, in which the cell-center user is considered as a hybrid time-switching/power-splitting energy harvesting relay. The other aspect is that the relay is introduced in the NOMA system, where the relay is an amplify-and-forward (AF) relay, DF relay, or an opportunistic relay [
11,
12,
13]. The outage performance of cooperative NOMA networks with SWIPT has been investigated in Reference [
11], where the DF relay is introduced to serve as an energy harvesting relay to deliver information to users. The two-stage DF and AF relay selection schemes for cooperative NOMA have been proposed in Reference [
12], and two optimal relay selection schemes for downlink cooperative NOMA system have been proposed in Reference [
13], in which one relay is chosen from multiple relays to communicate with the users.
The existing works on cooperative NOMA are analyzed under two conditions. The first condition is perfect channel state information (pCSI) [
14,
15]. Outage probability of a fixed gain NOMA based AF relaying system has been investigated under pCSI conditions over Nakagami-
m fading channels in Reference [
14]. The performance of a NOMA-based cooperative relaying system has been investigated under pCSI conditions over Rician fading channels in Reference [
15], and the exact expression of average achievable rate has been derived. The second condition is imperfect channel state information (ipCSI) [
16,
17]. The authors of Reference [
16] considered the ipCSI for a downlink relaying aided NOMA network, where the outage probability of the users has been evaluated in detail. The SWIPT in a multiple-input multiple-output AF relaying system has been investigated under ipCSI conditions in Reference [
17], where the relay is an energy harvesting relay and harvests the signal energy transmitted from the source.
The Nakagami-
m fading channel includes multiple types of channels, and both the Gaussian channel and the Rayleigh fading channel are its special cases. The authors of Reference [
18] have studied the performance of a NOMA based AF relaying network, in which NOMA is shown to outperform orthogonal multiple access (OMA) in terms of outage probability and ergodic sum rate and provides better spectral efficiency and user fairness over Nakagami-
m fading channels. Two NOMA transmission schemes based on different types of relaying in a cooperative NOMA system have been proposed in Reference [
19], in which the NOMA-DF scheme can achieve better performance than the NOMA-AF scheme in terms of outage probability and ergodic sum rate over Nakagami-
m fading channels. The authors in Reference [
20] have proposed a NOMA-based transmission scheme in cooperative spectrum-sharing networks, where the NOMA-based scheme is superior to the OMA-based scheme in terms of outage probability and system throughput and provides better spectrum utilization over Nakagami-
m fading channels. The outage performance of NOMA with fixed power allocation in a downlink NOMA system has been investigated in Reference [
21], where NOMA can provide higher individual rates than OMA for the users with larger channel gain over Nakagami-
m fading channels.
Most of the existing works about cooperative NOMA have been investigated under pCSI conditions over Rayleigh fading channels, but it is difficult to realize in practical wireless systems due to the existence of channel estimation errors. In addition, Nakagami-
m fading channel is used in many types of fading environments and it have better empirical data comparing with Rayleigh fading channel. The outage performance of cooperative NOMA with user relaying under Rayleigh fading has been studied in Reference [
22], but the influence of channel estimation errors on system performance over Nakagami-
m fading channels has not been taken into account. Motivated by these reasons, we develop this research work.
In this paper, we consider a downlink cooperative NOMA network with ipCSI over Nakagami-m fading channels. Two cooperative NOMA transmission scenarios are discussed: (1) The first scenario is that the base station (BS) sends information to distant user through with the aid of nearby user, which is taken as DF relaying; (2) The second scenario is that the BS can not only send information to distant user through nearby user, but also send information directly to distant user. The primary contributions of this paper are summarized as follows:
We propose a downlink cooperative NOMA network with ipCSI to investigate the effect of the channel estimation errors on system performance in practical wireless communication systems. We analyze the outage performance of NOMA users in two representative cooperative NOMA scenarios in terms of outage probability and diversity order over Nakagami-m fading channels.
We derive the closed-form expressions of outage probability for a pair of NOMA users in the two scenarios of both user relaying without direct link and user relaying with direct link. To better understand the outage behavior of the network, we derive the approximate expressions of outage probability for the pair of NOMA users at high SNR, where we attain the diversity orders of users.
The simulation results confirm the accuracy of our analysis results and the superiority of NOMA over OMA. We observe that there is the error floor for outage probability at high SNR as a result of channel estimation errors under ipCSI conditions. The outage behaviors of distant user with direct link outperforms distant user without direct link. Additionally, we further observe that the best user relaying location for cooperative NOMA networks should be close to the BS.
To understand NOMA networks investigated in this paper, we compare NOMA with conventional OMA in terms of the aim, solution, pros and cons in
Table 1.
The rest of the paper is organized as follows.
Section 2 describes the system model. In
Section 3, the exact and approximate expressions of outage probability for a pair of NOMA users are derived in two scenarios, and the corresponding diversity orders are analyzed. Numerical results are presented in
Section 4 for verifying the accuracy of our analysis.
Section 5 concludes the paper.
For the sake of clarity, the main notations and their descriptions are summarized in
Table 2.
2. System Model
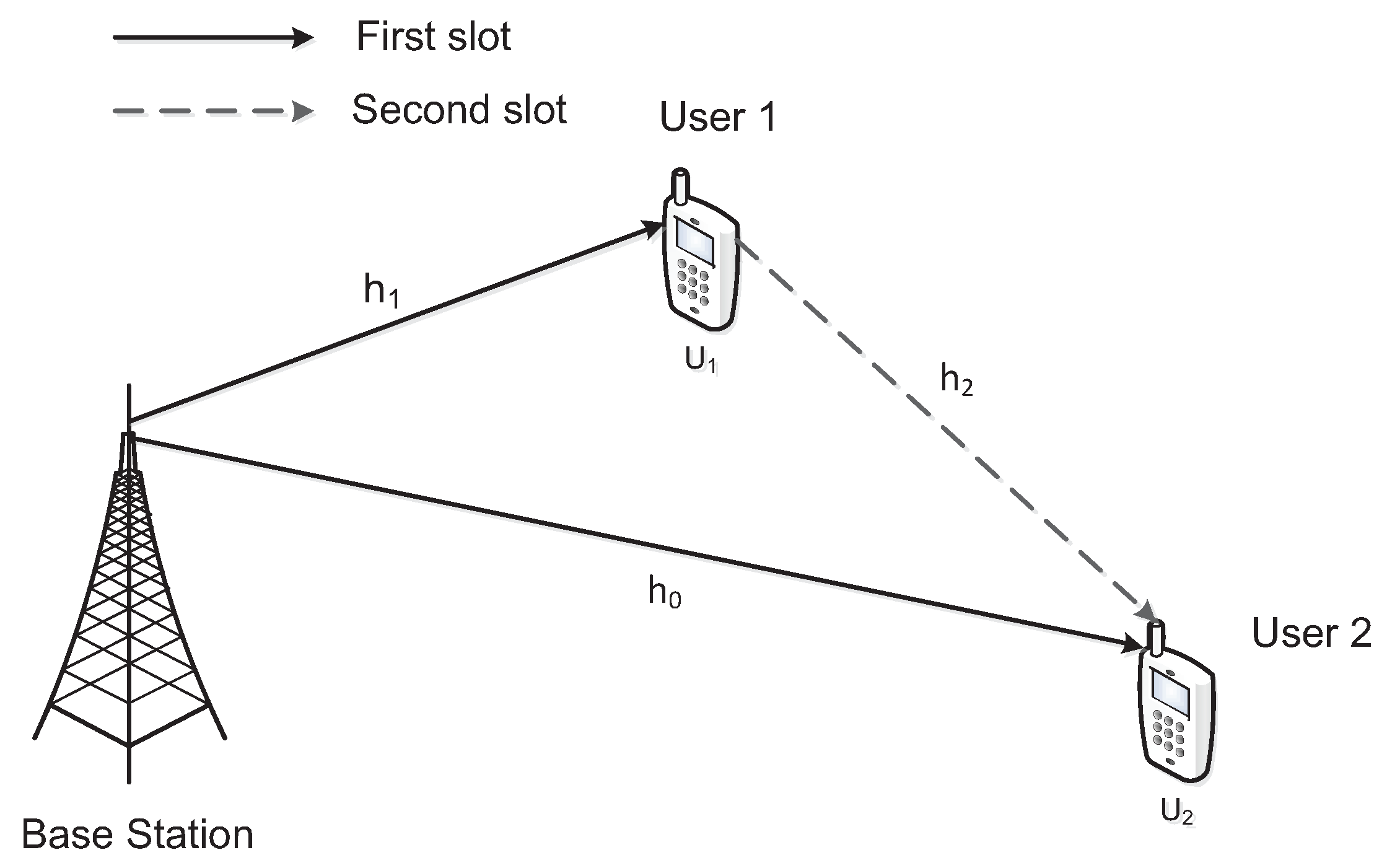
Consider a downlink cooperative NOMA network, which includes the BS, nearby user
, and distant user
in a cell, as shown in
Figure 1. The BS communicates with
by utilizing
as DF relay. The BS,
, and
are single-antenna devices and operate in half-duplex mode. Assuming that all wireless links suffer from Nakagami-
m fading and additive white Gaussian noise (AWGN) with zero mean and variance
. Because there are channel estimation errors in wireless networks with ipCSI, the channel coefficient is denoted by
with fading parameter
and link average power
and is modeled as
,
, where
denotes the estimated channel coefficient and
represents the channel estimation error which is subject to Gaussian distribution.
,
, and
denote the channel coefficient of
,
, and
links, respectively, and
,
, and
denote the corresponding estimated channel coefficients.
is assumed to be the distance between two nodes, and we have
, where
represents the path loss exponent. When
and
are statistically independent, we have estimated link average power
. Assuming that
represents the relative channel estimation error, we can obtain
and
.
The BS communicates with distant user
through direct link
and relaying link
in a cell. DF protocol is used for the relaying link where nearby user
acts as user relaying. Two consecutive slots are involved in the whole communication process. In the first slot, the BS transmits superposed signal
to relaying user
and distant user
according to the principle of NOMA, where
is the normalized transmission power at the BS,
and
are the normalized unit power signals of
and
, respectively, and
and
are the corresponding power allocation coefficients. Assuming that
and
. The received signals at
and
are given by
and
respectively, where
and
are AWGN at
and
respectively.
According to NOMA scheme, the nearby user with better channel conditions is allocated less transmit power to achieve fairness between users. Based on the assumption of power allocation coefficients, the signal of
is decoded firstly by exploiting successive interference cancellation from the received superposed signal at
, where
with more transmit power has less the inter-user interference. The received signal to interference and noise ratio (SINR) for
to decode signal
of
can be expressed as
where
is the transmit signal to noise ratio (SNR). Since imperfect successive interference cancellation (ipSIC) is performed, signal
is not completely canceled out from the received superposed signal of
after decoding it, there is residual interference (RI). The received SINR for
to decode its own signal
is given by
where
represents the impact level of RI.
only needs to treat signal
of
as noise to decode its own signal. The received SINR for
to decode its own signal
is given by
In the second slot, relaying user
forwards signal
decoded from the original superposed signal to
. The received signal at
for relaying link is written as
where
is the normalized transmission power at
. For simplicity, we set
. The received SINR for
to decode signal
for relaying link is given by
Hence
receives signals from two different links of direct link in the first slot and relaying link in the second slot. The total received signal at
is expressed as
The received SINR after selection combining (SC) at
is given by
4. Numerical Results
In this section, numerical results are presented to evaluate the outage performance of cooperative NOMA networks with ipCSI in terms of outage probability over Nakagami-
m fading channels. We use MATLAB programming software for simulation by setting reasonable parameters. The exact expressions for the outage probability are verified by utilizing Monte Carlo simulations. In addition, OMA is regarded as the benchmark to compare with NOMA. Considering that the BS,
, and
are located in a straight line. Without loss of generality, assuming that the distance between the BS and
is normalized to unity, i.e.,
, and we can obtain
, where
and
are the normalized distance between the BS and
, and between
and
, respectively. In the following simulations, we set the simulation parameters in
Table 3.
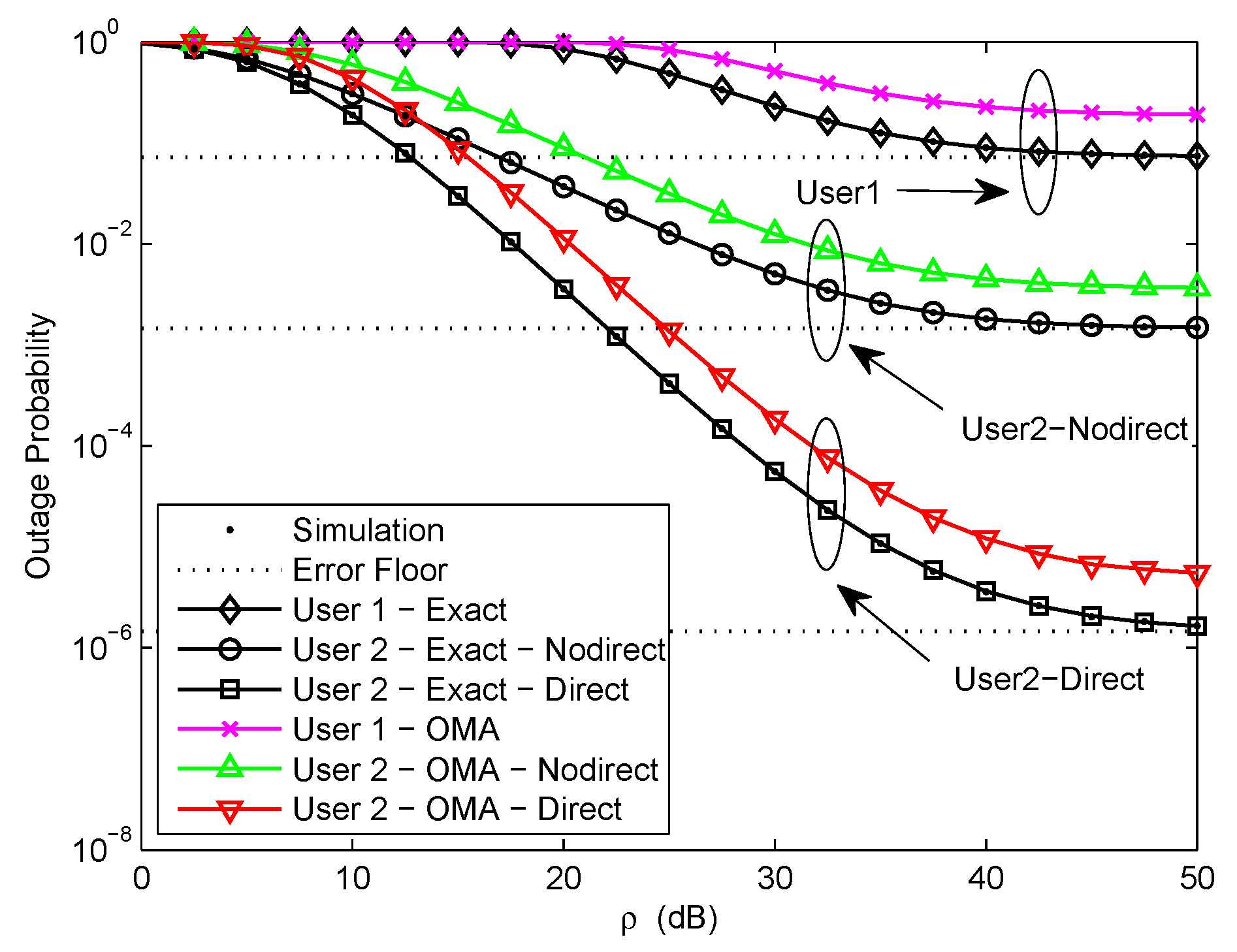
Figure 2 plots the outage probability of a pair of users for the two scenarios versus the transmit SNR. We assume
,
, and
. The target rate is set to be
,
bit per channel use (BPCU) for
and
, respectively. The exact outage probability curves of a pair of users for the two scenarios are plotted according to (
15), (
18), and (
34), respectively. We can easily observe that the exact outage probability curves and the Monte Carlo simulation results match well. It can be seen that the outage performance of NOMA outperforms OMA. It is the fact that the superposition coding scheme is performed at the transmitter in NOMA networks, multiple users can be served by sharing the same physical resource. To ensure user fairness, the target rate of OMA user is larger than that of NOMA user. The approximate outage probability curves of a pair of users for the two scenarios are plotted according to (
31), (
32), and (
48), respectively. It is observed that the outage probability decreases as the transmit SNR increases at low SNR and reaches a fixed value at high SNR. The error floor exists at high SNR owing to the channel estimation errors, which leads zero diversity order. Another important observation is that the outage probability of
with direct link in the second scenario is much better than that of
without direct link in the first scenario and the error floor gap is about 3 orders of magnitude. Because
only receives the signal from relaying link in the first scenario, but
receives the signals from relaying link and direct link in the second scenario, thus the reliability of the signal received by
in the second scenario has been improved.
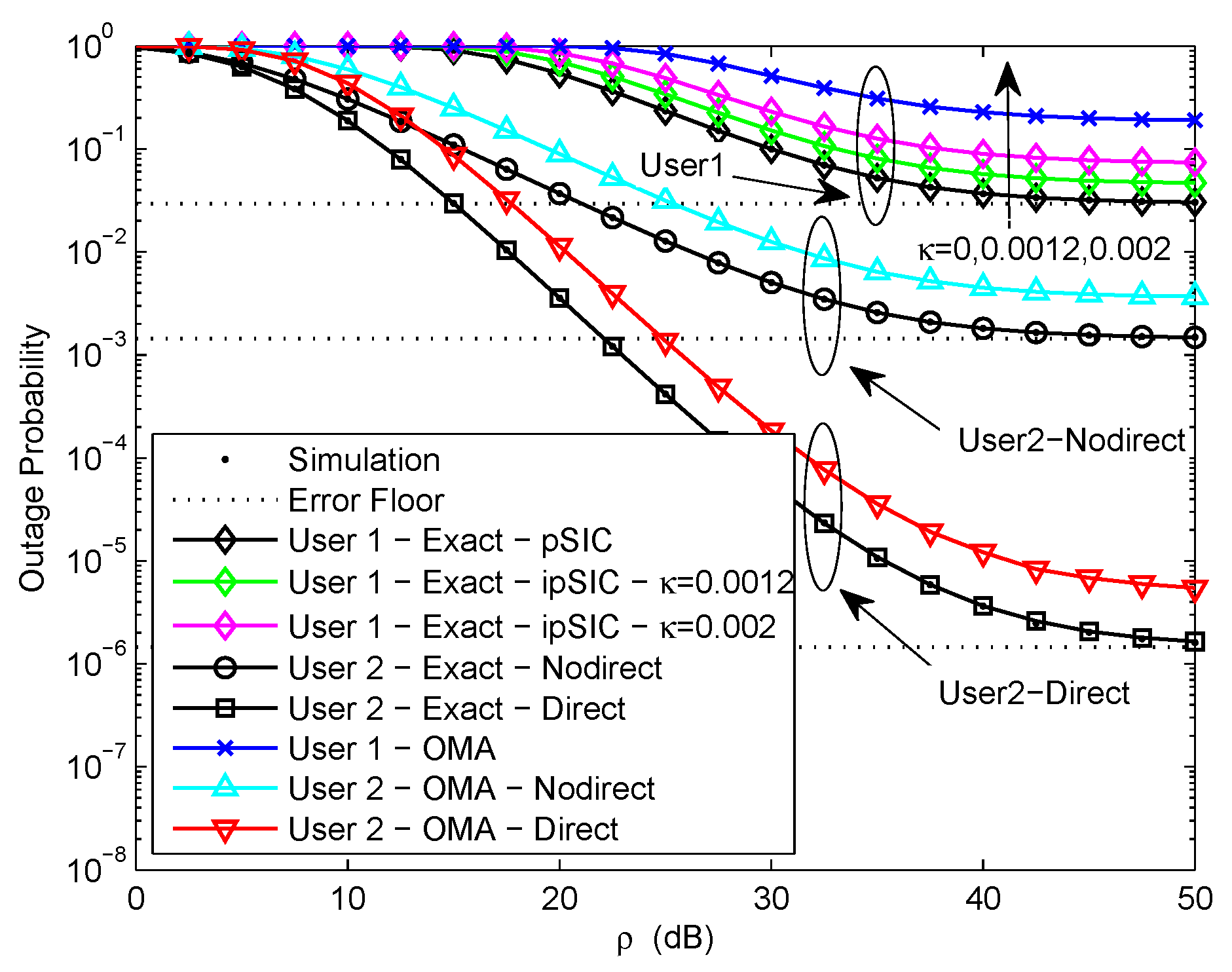
Figure 3 plots the outage probability of a pair of users for the two scenarios versus the transmit SNR with different levels of RI from 0 to 0.002. We assume
,
,
, and
. Obviously, the exact outage probability curves match perfectly with the Monte Carlo simulation results. We observe that NOMA is capable of achieving better outage performance than OMA. This is caused by the superposition coding scheme. Considering the impact of RI caused by ipSIC at user
, the outage probability of
with different levels of RI is plotted based on (
15). It can be observed that the RI-based exact outage probability curves of
reduce with the increase of the transmit SNR in low SNR region and an error floor appears in high SNR region. This is due to the existence of channel estimation errors, resulting in zero diversity order. More importantly, it is shown that the effect of RI on the outage performance of
is very obvious. The outage performance of
reduce significantly increasing the levels of RI from 0 to 0.002. This is because the larger the levels of RI, the greater the interference of
, hence the outage performance of
becomes worse. Therefore, it is extremely important to consider the effect of RI in practical ipSIC systems.
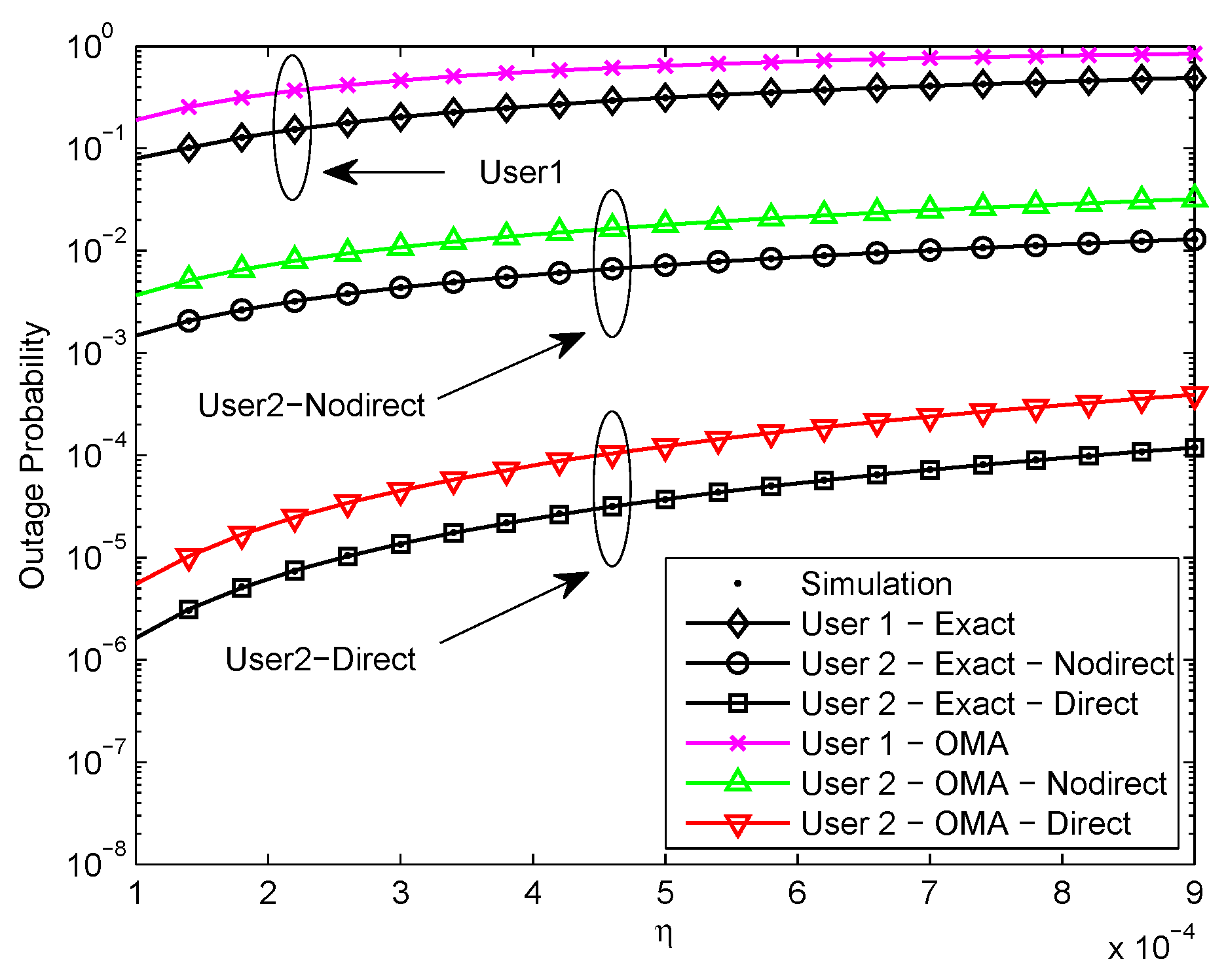
Figure 4 plots the outage probability of a pair of users for the two scenarios versus the relative channel estimation error. We assume
,
,
,
dB, and
. We can see that the exact outage probability curves and the Monte Carlo simulation results are in excellent agreement. One can observe that the outage performance of NOMA is superior to OMA. It is due to the superposition coding scheme. Moreover, it is observed that the outage probability increases as the relative channel estimation error increases due to the impact of error floor. In addition, it is worth noting that the outage performance of
with direct link in the second scenario exceeds
without direct link in the first scenario and the outage performance gap is about 3 orders of magnitude.It is that
only receives the signal from relaying link in the first scenario, but
receives the signals from two different paths in the second scenario, thus the performance of
in the second scenario is much better.
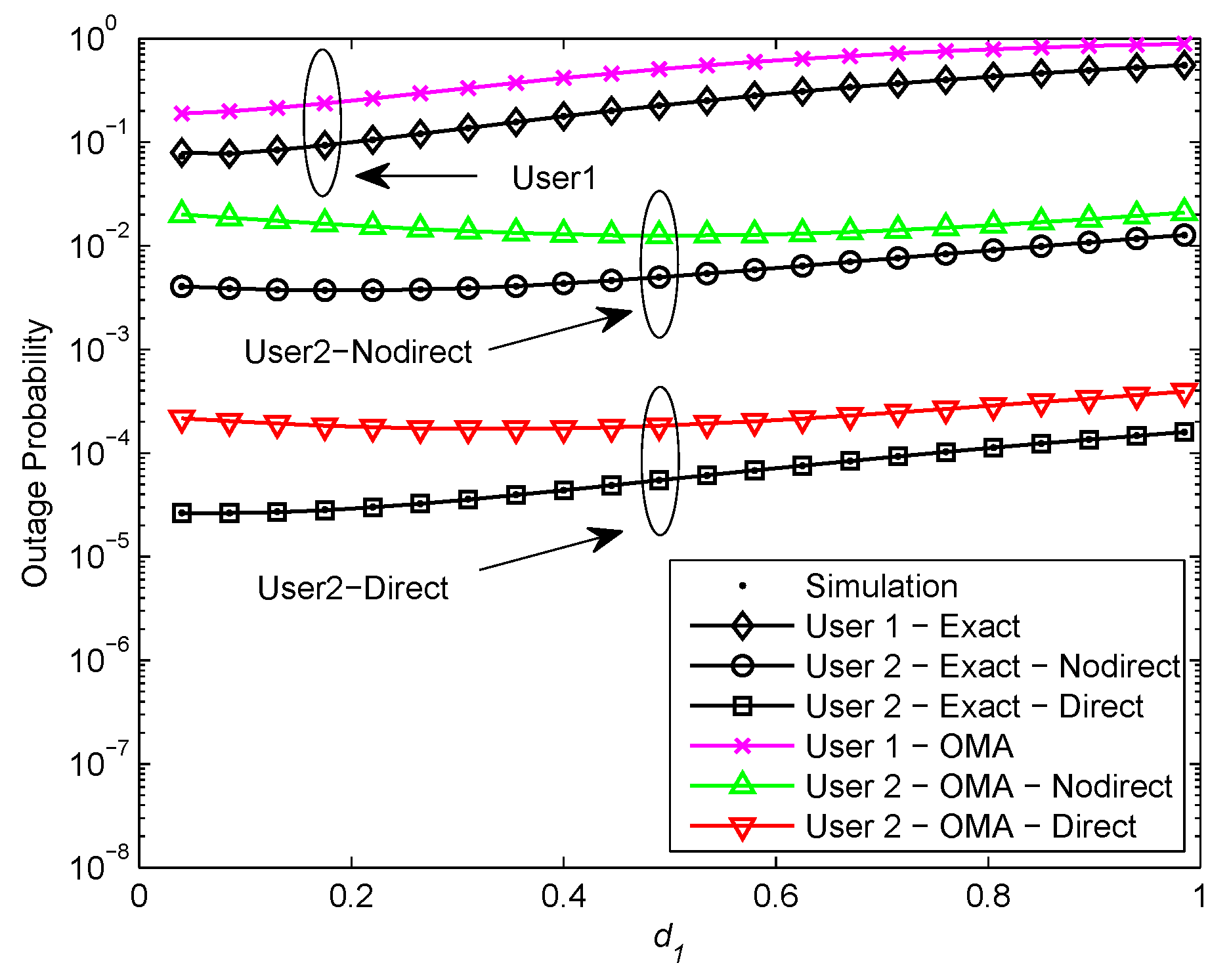
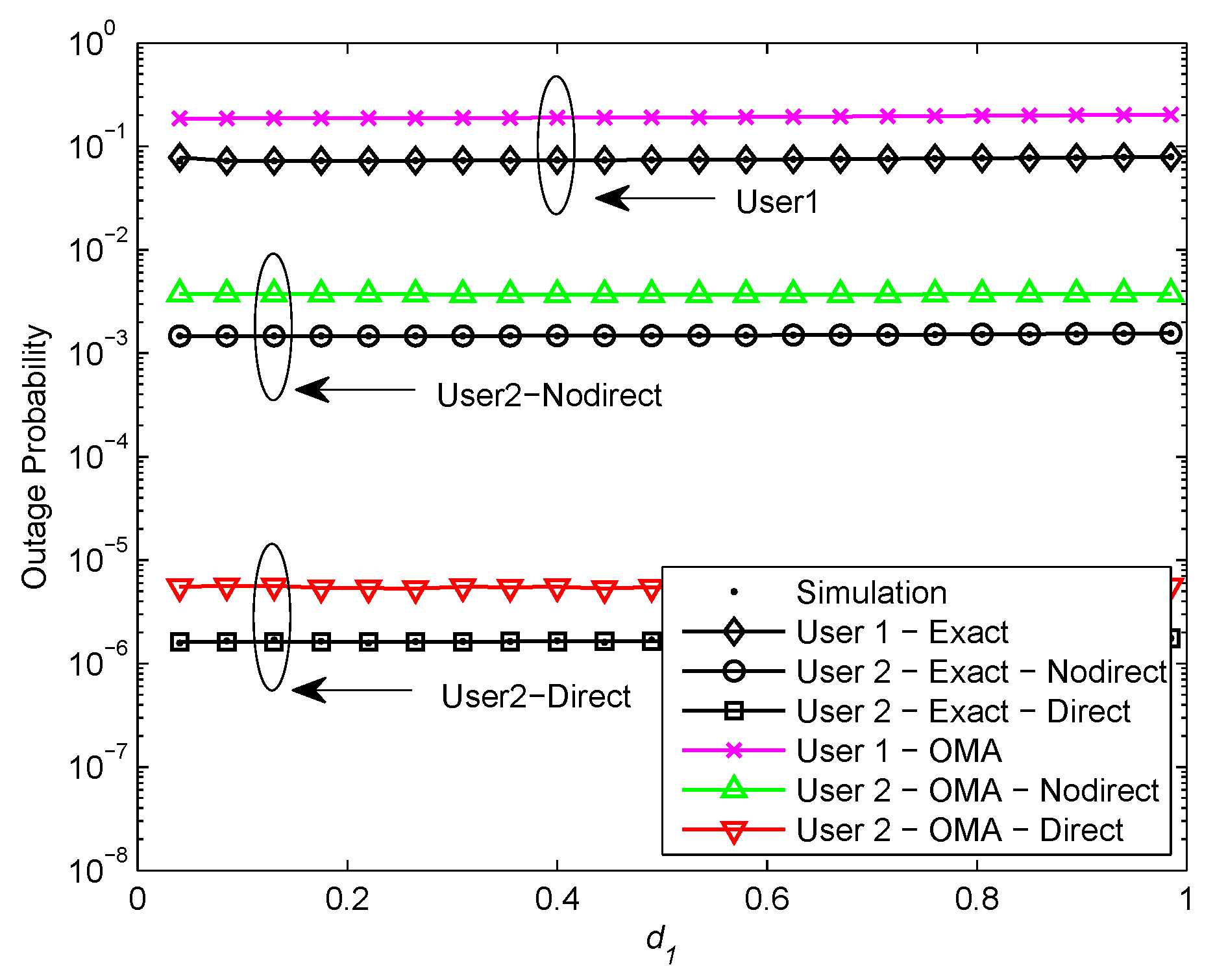
Figure 5 and
Figure 6 plot the outage probability of a pair of users for the two scenarios versus the normalized distance between BS and
for
and
dB, respectively. We assume
,
,
, and
. In
Figure 5, it is shown that the exact outage probability curves match precisely with the Monte Carlo simulation results. We observe that the optimal location for user relaying
is closer to the BS than
. The reason is that
with better channel condition is allocated less transmit power, the optimal location for
should be nearer to the BS in order to achieve high received SNR at
. Furthermore, it can be observed that the outage performance of NOMA exceeds OMA. That is owing to the superposition coding scheme. It is worth pointing out that the outage performance declines as
gets close to
and the outage performance gap between NOMA and OMA is no longer apparent. It is the fact that
with better channel condition is allocated less transmit power, the received SNR at
reduces as
gets close to
. Therefore, the user relaying location for cooperative NOMA networks should be near to the BS. Additionally, it is observed that the outage performance of
with direct link in the second scenario outperforms
without direct link in the first scenario and the outage performance gap is about 2 orders of magnitude. Since
in the second scenario has more paths to receive signals than
in the first scenario. In
Figure 6, it can be seen that the outage probability maintains constant as the user relaying location increases. This phenomenon can be explained that the outage probability achieves the error floor at high SNR which is independent of
and
.