1. Introduction
Grid-based environment modeling has become a popular perception paradigm since its first introduction in [
1]. Compared with object-based approaches such as [
2,
3], the grid-based method has several advantages since it is straightforward to integrate heterogeneous sensor information and it relaxes data-association problems which can be especially hard to handle in complex and dynamic environments. There exists a large literature regarding to grid-based environment modeling for robotics applications and for autonomous vehicles. In [
4], the authors have presented an occupancy-elevation grid mapping technique for autonomous navigation application. In [
5], the occupany grid is constructed to identify different shape of objects by applying sensor fusion. In [
6], the authors have presented a universal grid map library for grid construction. In [
7], the authors introduced an advanced occupancy grid approach to enable the robust separation of moving and stationary objects. In [
8], a generic architecture for perception in dynamic outdoor environment by applying grid-based SLAM (Simultaneous Localization and Mapping) is presented. In [
9], a grid-based approach is proposed for ADAS (Advanced Driving Assistance System) application. In [
10], a real-time algorithm for grid-based SLAM and detection of objects is presented.
Some works tried to integrate dynamic information into grids to get a more complete representation of the environment. In [
11], the space occupied by static and dynamic objects is distinguished by adopting a sequential fusion formalism. In [
12], the authors proposed a complete semantical occupancy grid mapping framework involving a new interpolation method to incorporate sensor readings in a Bayesian way. In [
13], a Bayesian filter approach was adopted to estimate the state of the occupancy grid with velocity information.
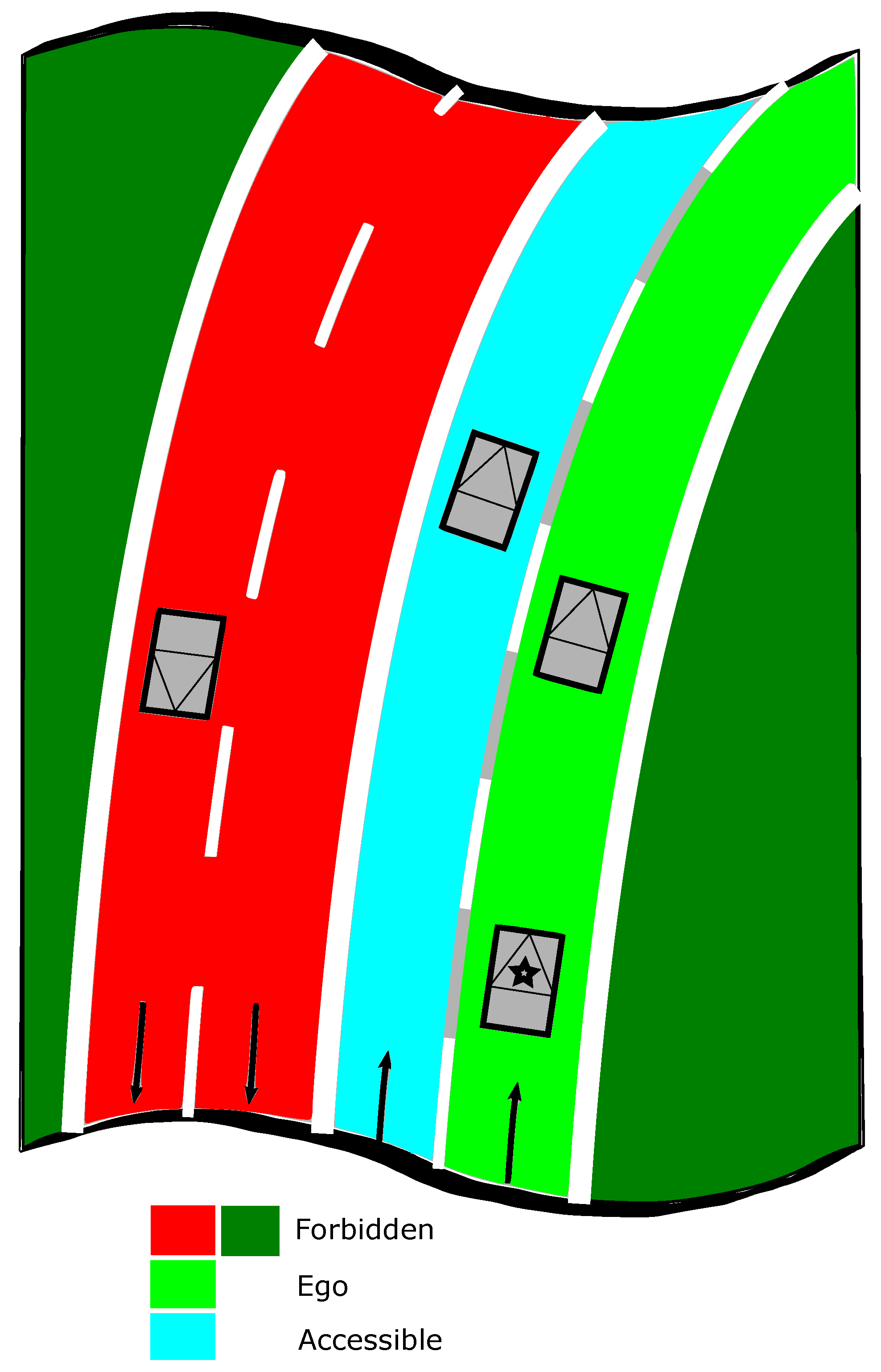
This paper deals with perception grids for the navigation of road vehicles. The road space is classically classified as occupied (by obstacles) or free. However, for autonomous navigation on public roads, this road space description is not sufficient as the host vehicles should be able to know which space is free to go with authorization. For this purpose, lane-level information should be provided. A vehicle typically has two options when facing a static obstacle in its own lane: (i) lane-keeping and stop or (ii) lane changing. For the second option, the host vehicle needs semantic road rules deduced from lane marking information to evaluate if the space is accessible or not. Thus, the road must be modeled semantically to represent the accessibility of the space.
Many lane detection methods have been proposed and developed using image processing. In [
14], a robust and real-time approach to detect lane markers was proposed. In [
15], the authors proposed a robust multilane detection and tracking method using LiDAR and mono-vision data. In [
16], based on spatiotemporal images, the authors proposed a method for lane detection, which proved to be more robust and efficient. In [
17], an implementation of semantic image segmentation to enhance LiDAR-based road and lane detection was presented. In [
18], using a proposed region of interest, the authors managed to reduce the calculation and high noise level for lane detection. Images are typically segmented into road, obstacles, sky, etc. These methods can be strongly influenced by weather conditions and by the quality of lane markings. Deep learning-based lane detection methods have shown superior performance over traditional methods. In [
19], the authors proposed a Dual-View Convolutional Neural Network framework. Reference [
20] extended the framework of deep neural network by accounting for the structural cues. In [
21], a unified end-to-end trainable multi-task network that jointly handles lane and road marking detection and recognition was proposed. The approach is guided by a vanishing point under adverse weather conditions. Reference [
22] proposed a sequential end-to-end transfer learning method to estimate left and right ego lanes directly and separately without any postprocessing. However, they usually perform well only when the road conditions are similar to those used in the training datasets.
We propose to tackle this problem by using geo-referenced maps. Prior map information has already been used for road object extraction, since it provides cues about the existence and location of on-road objects [
23,
24,
25]. In [
24], the authors used an open-source dataset for vehicle detection tasks with geographic information. In [
23], the authors have taken advantage of the maps for both localization and perception. With a map-aided pose estimation, they proposed an obstacle detection method based on the comparison between the image acquired by an on-board camera and the image extracted from a 3D model. Now we can have access to very detailed and accurate geo-referenced databases, which provide rich information for autonomous navigation. Using these maps, lane-level attributes describing the structure of the road is available. For this purpose, a localization system is mandatory. In [
26,
27], a prior map was considered to be a virtual sensor, providing information about the space occupied by infrastructures, buildings, etc. With an accurate pose estimation, the authors converted the extracted information into a local perception map. This perception map was then fused with a local occupancy grid generated from the on-board sensor data. In [
28], a holistic 3D scene understanding method was proposed based on geo-tagged images which allows joint reasoning about 3D object detection, pose estimation, semantic segmentation as well as depth reconstruction from a single image. Large-scale crowd-sourced maps were used to generate dense geographic, geometric and semantic priors. In [
29], an algorithm for road detection was proposed using Geographical Information Systems (GISs). The priors are obtained by building a road map using information such as the type of the road and the number of lanes, retrieved from a database and then by projecting the road map onto the vehicle frame.
Although geo-referenced maps provide valuable prior semantic information, a real difficulty remains in tackling the uncertainties coming from estimation errors on the pose of the vehicle and the errors on the map features arising from the mapping process. In this paper, we suppose that the prior map is very accurate in comparison with the localization errors thanks to the use of high-grade devices used in the data acquisition process and refined post-treatments. Localization is therefore the main source of uncertainty in this process.
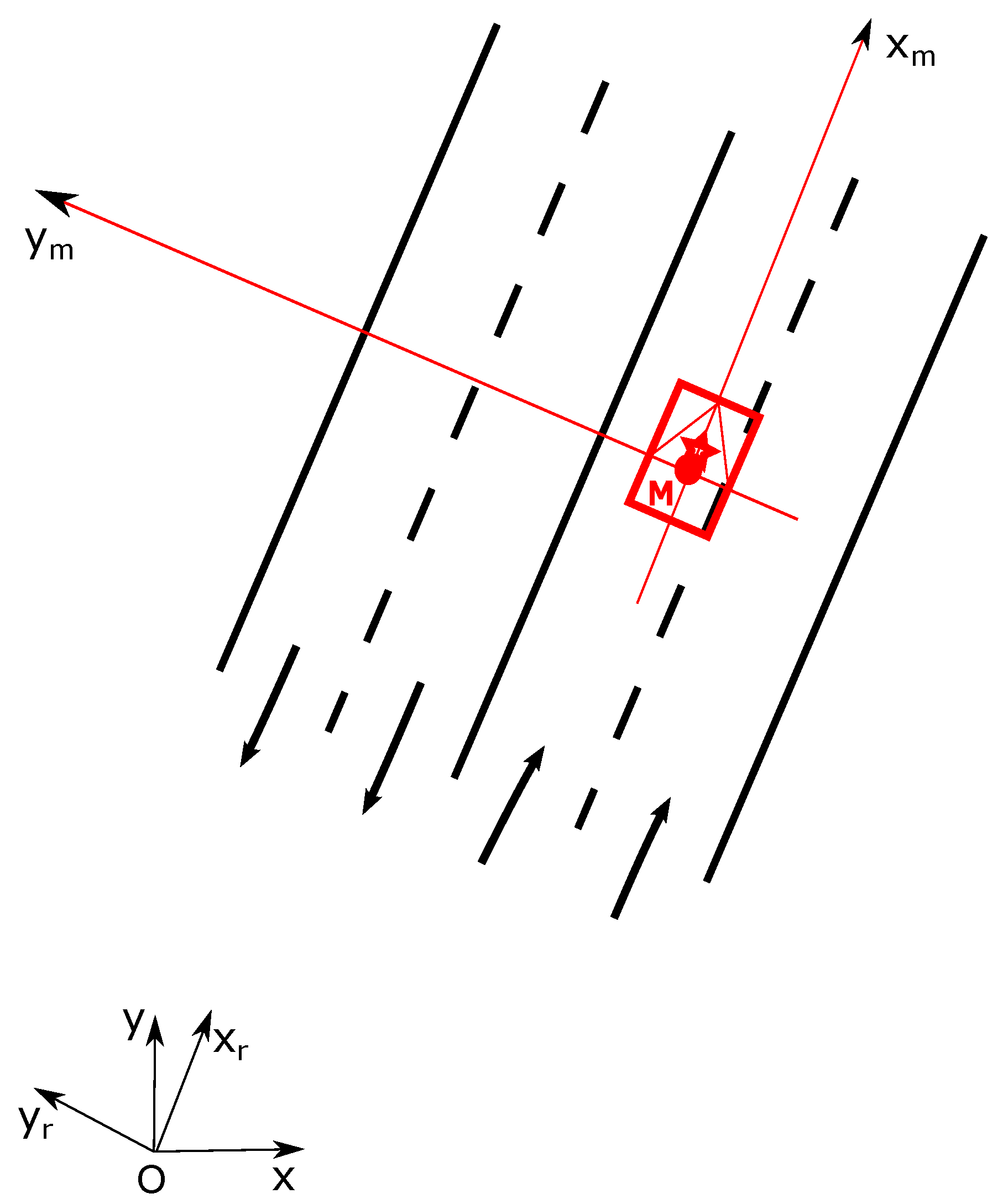
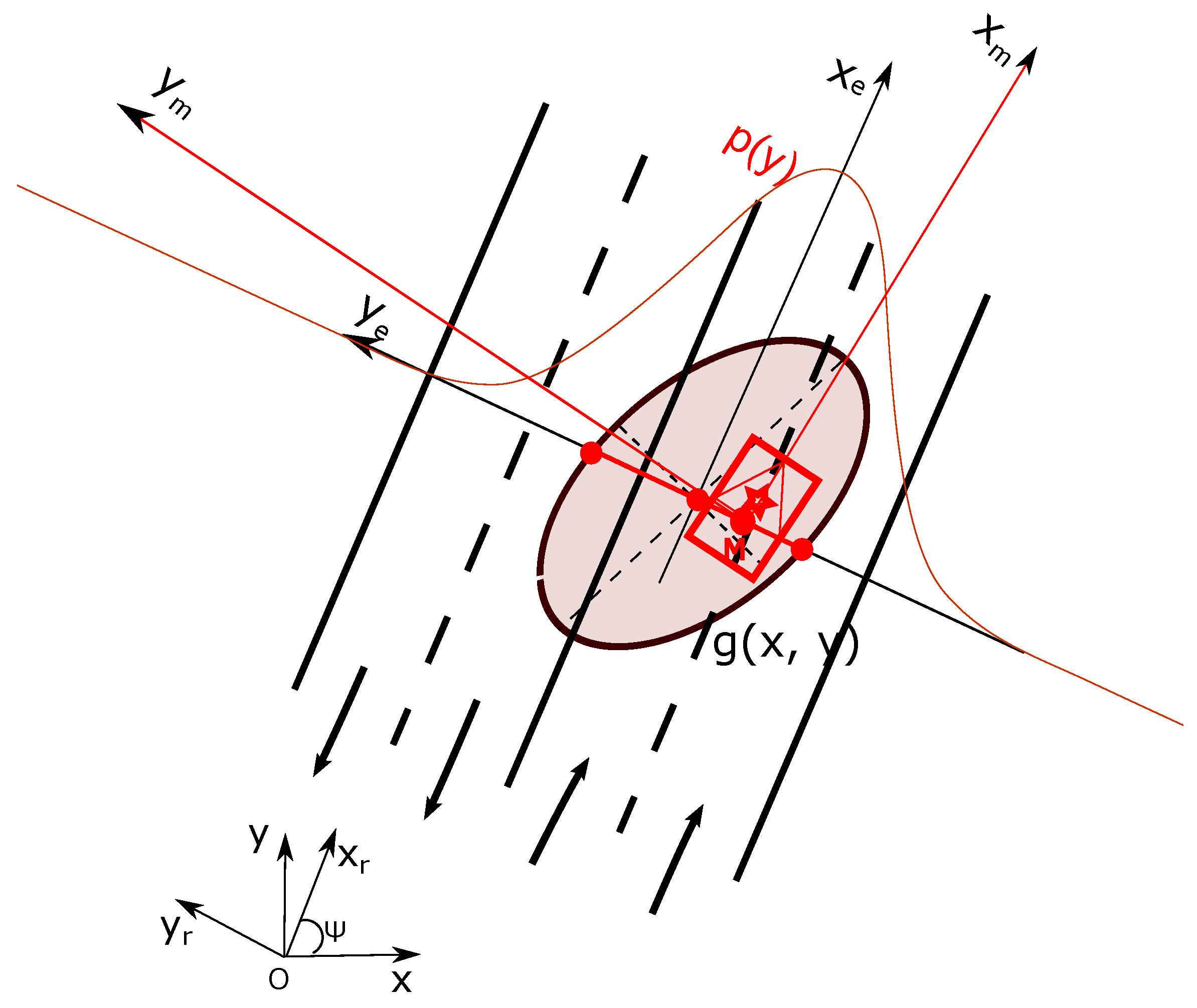
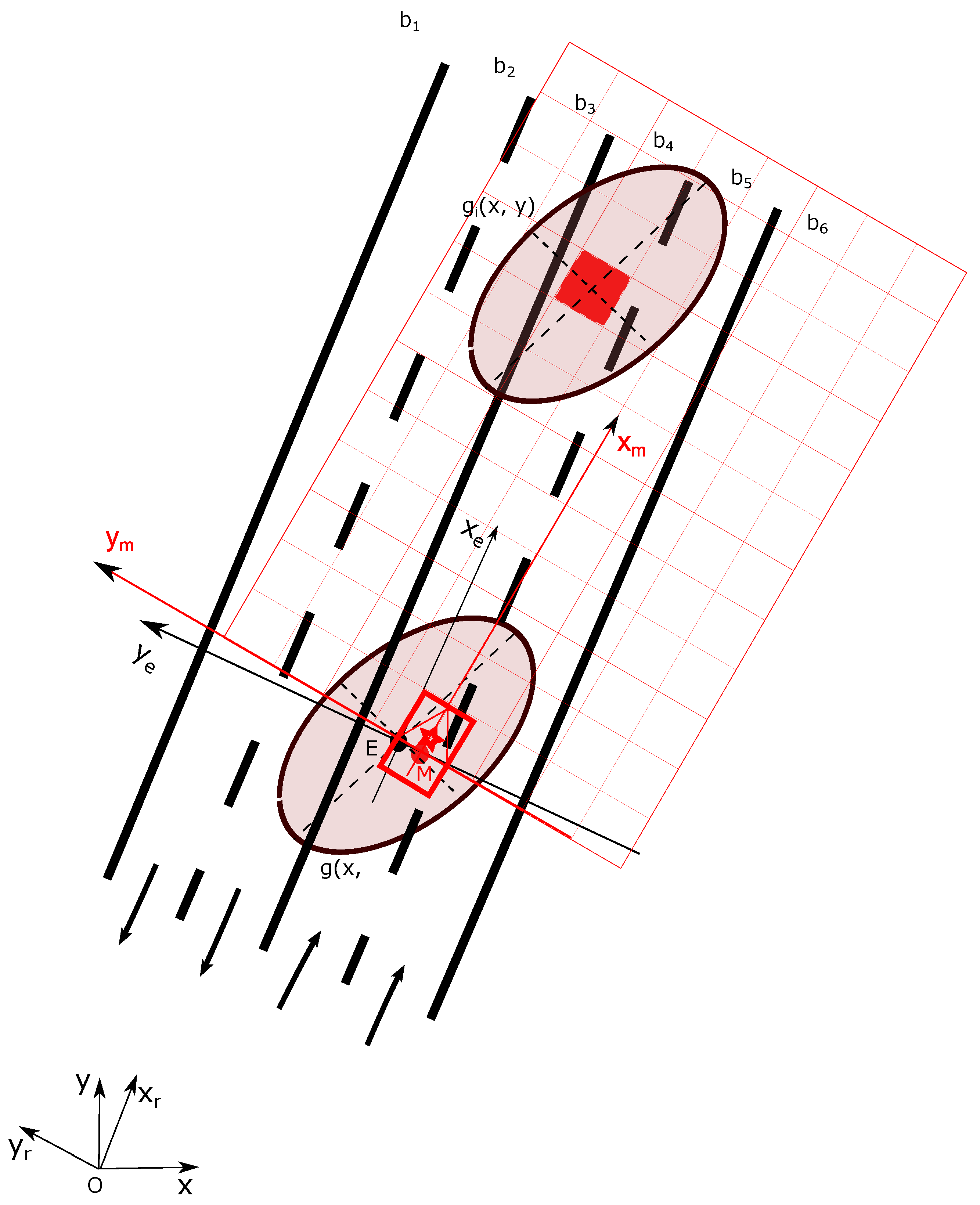
Based on this discussion, this work has the following contributions. We first propose a method to integrate semantic lane information from a prior map into grid–based environment models by taking into account explicitly the localization error of the vehicle. In previous work, we have presented some related results concerning the construction of grids based on prior maps[
30]. In this paper, we present extensive theoretical and experimental results to show further the interests of our approach. Secondly, an approach based on Dempster–Shafer theory is presented to fuse this semantic map with an occupancy map built from on-board sensing information.
The paper is organized as follows. In
Section 2, the approach to construct semantic lane grid based on prior map and uncertain pose is introduced. In
Section 3, the fusion of occupancy grid and semantic lane grid based on the Dempster–Shafer theory is presented. In
Section 4, real road results are reported and analyzed. Finally, in
Section 5, we draw conclusions.
4. Real Road Experiments and Results
4.1. Real Road Experiments
Real road experiments have been done with an experimental vehicle of the Heudiasyc Laboratory. The vehicle is shown in
Figure 9 and the sensor configuration is similar to [
35]. For semantic lane grid, the inputs of the algorithm are the map and the vehicle pose with its covariance matrix (provided by a localization system implementing a Kalman filter). We have used a high-definition map with negligible error level. In the map, the road is explicitly described with lane information, including lane markings and road boundary. The lane markings are distinguished in the map with different attributes which are important to determine the lane state. The vehicle pose comes from a GPS system with RTK corrections. This system can provide positioning with high accuracy in RTK-fixed operation mode.
We have used a LiDAR (SICK LDMRS) installed in the front of the vehicle to construct the occupancy grid. During the experiments, the LiDAR was triggered by the GPS receiver.
To qualitatively evaluate our result, we have adopted the approach proposed in [
36]. A wide-angle scene camera has been installed behind the windshield during the acquisition process in the experiment. The camera was also synchronized with the GPS receiver. The constructed lane grid is projected on the scene image captured by the camera to provide a qualitative evaluation indicator. This method enables the evaluation of the correspondence of the grids with regards to the observed scene. The calibration between the camera and the GPS antenna has been performed off-line. The retro-projection process consists in computing the 2D image coordinates corresponding to each grid cell vertex.
The system has been implemented on C++ with a Linux computer.
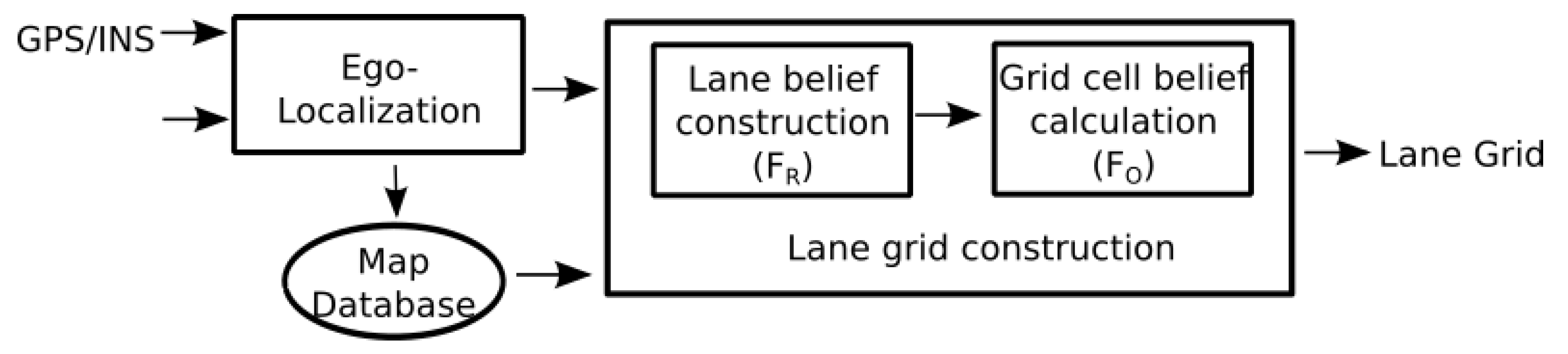
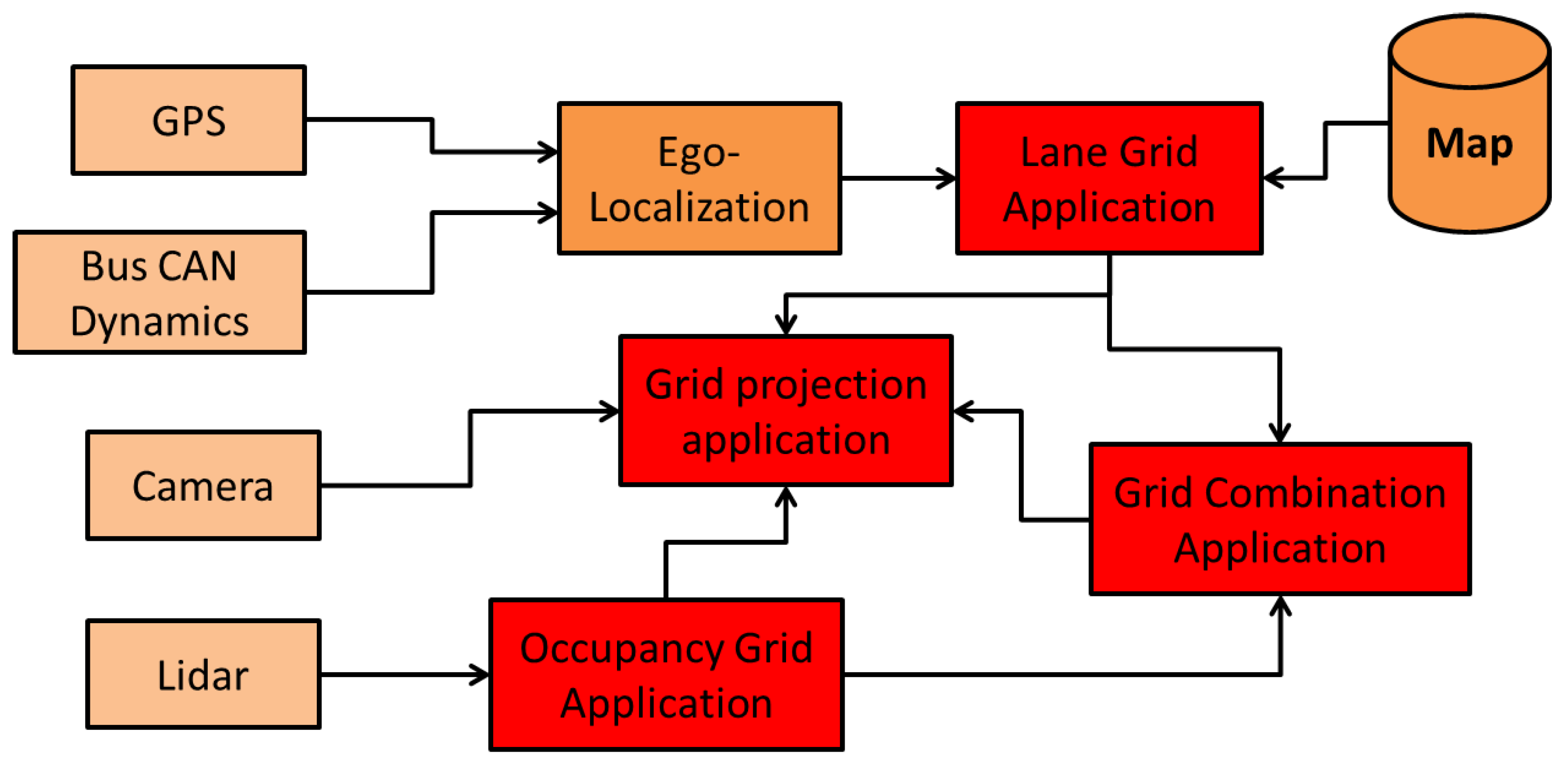
Figure 10 shows the system and its 9 components. The inputs are a GPS receiver, a CAN bus gateway of the vehicle to access to the speeds, a LiDAR driver and a camera for visualization. The output of a GPS receiver and CAN bus data (wheel speed and yaw rate) are used in the ego-localization process to estimate the absolute pose. The semantic lane grid is constructed in the Lane Grid Application component, where the estimated pose and the prior map are taken as inputs. The evaluation process takes place in the Grid projection application component. The lane grid is projected on the image coming from the scene camera. The component LiDAR acquires the data from the SICK LiDAR which is sent to the “Occupancy grid Application” to construct the occupancy grid in real time. This occupancy grid serves as input to the “Grid combination Application” with the lane grid from the “Lane Grid Application”. A qualitative evaluation is performed by projecting the combination grid onto the scene images.
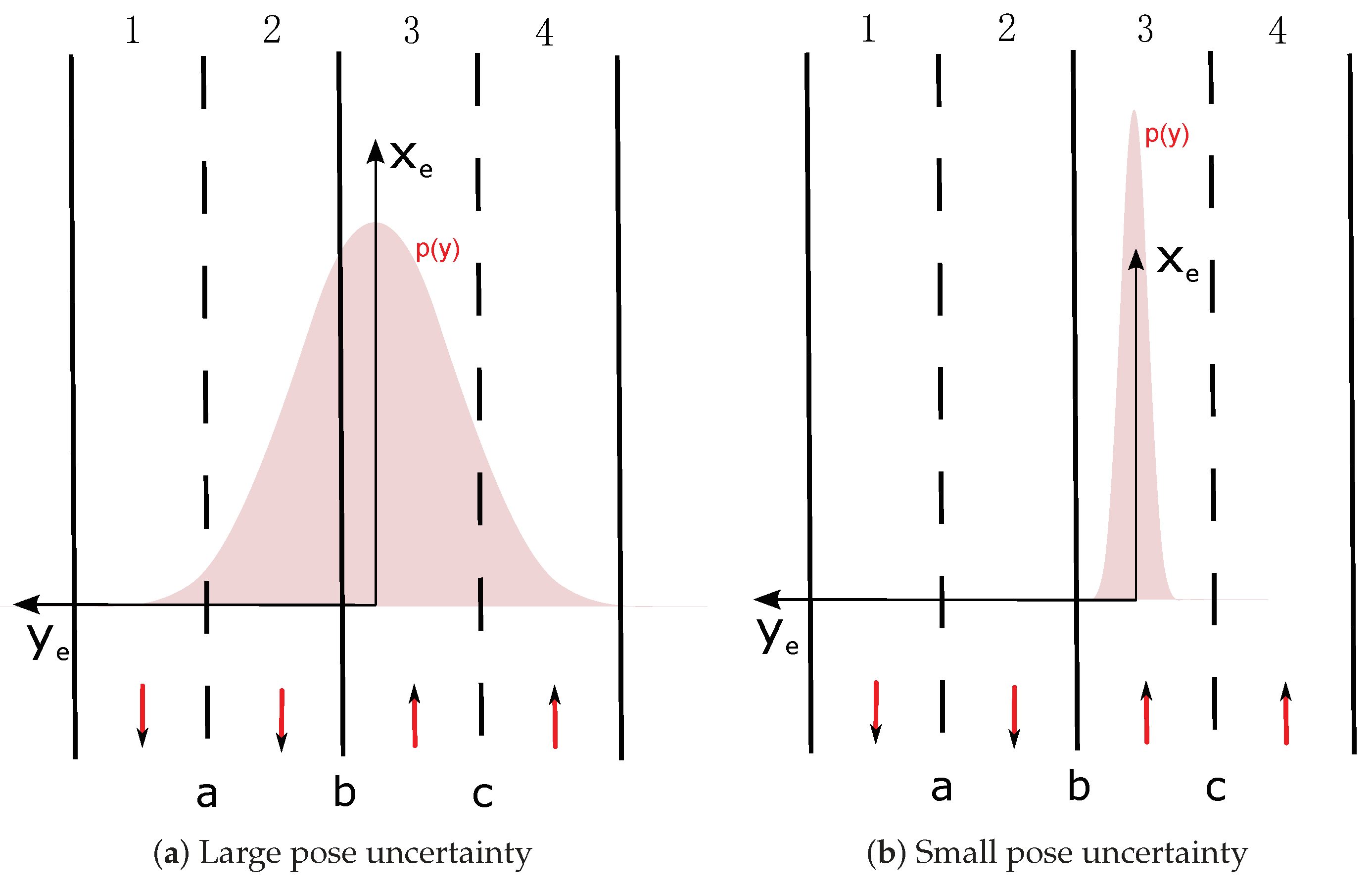
We show grids of m in length and width. The cells are with a size of m. In this part, grids constructed with two different levels of pose uncertainty are given. For notation purpose, we herein use as the 2D pose uncertainty. The grids are shown by visualization of a RGB image. The RGB image enables reflection of the belief level by the RGB color channel brightness. Brighter color reflects higher belief level.
4.2. Experimental Results
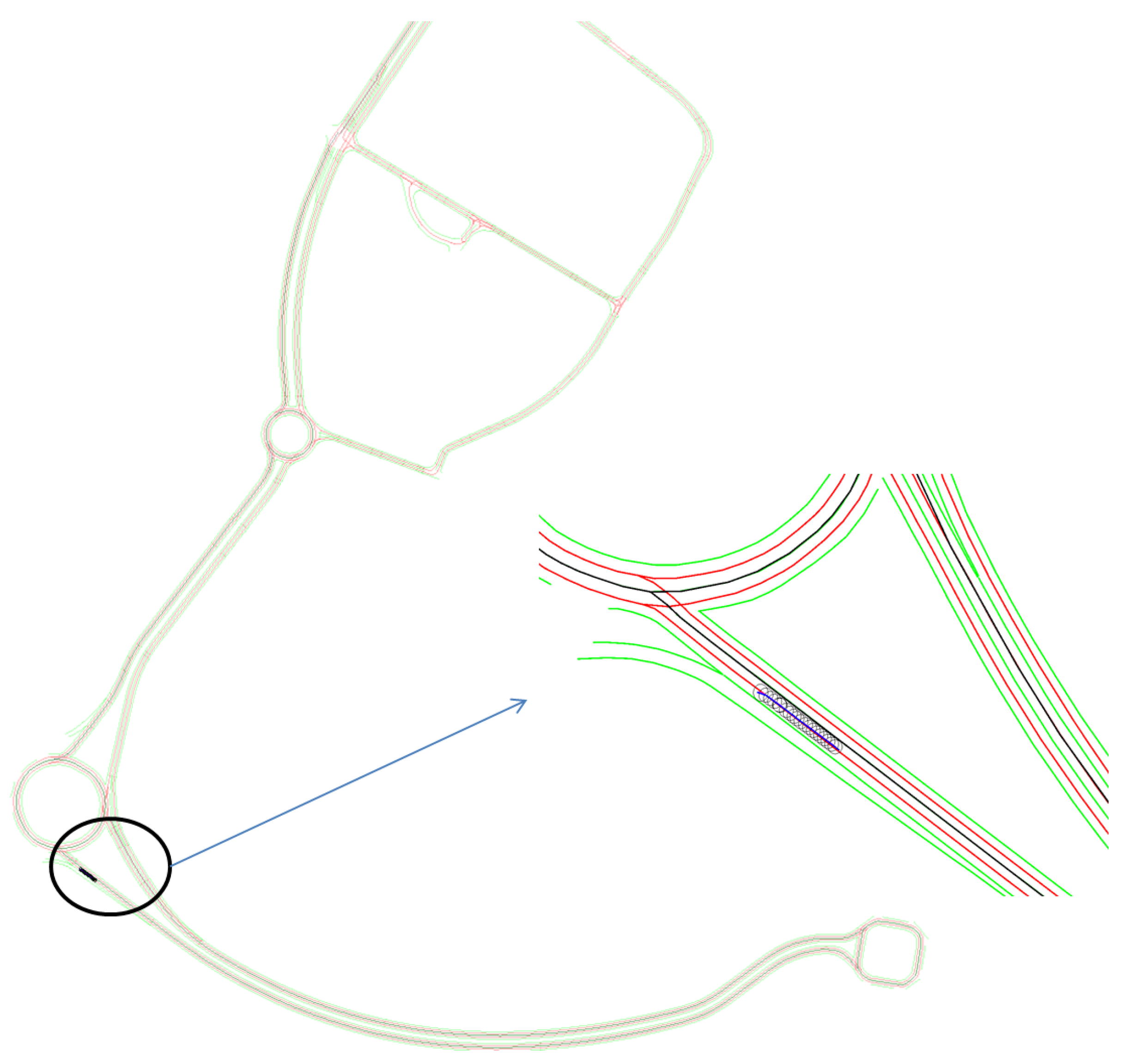
In this section, semantic lane grid results of both (probabilistic and evidential) approaches are given. For the purpose of demonstration, a projection of the host vehicle’s position on a prior map is displayed in
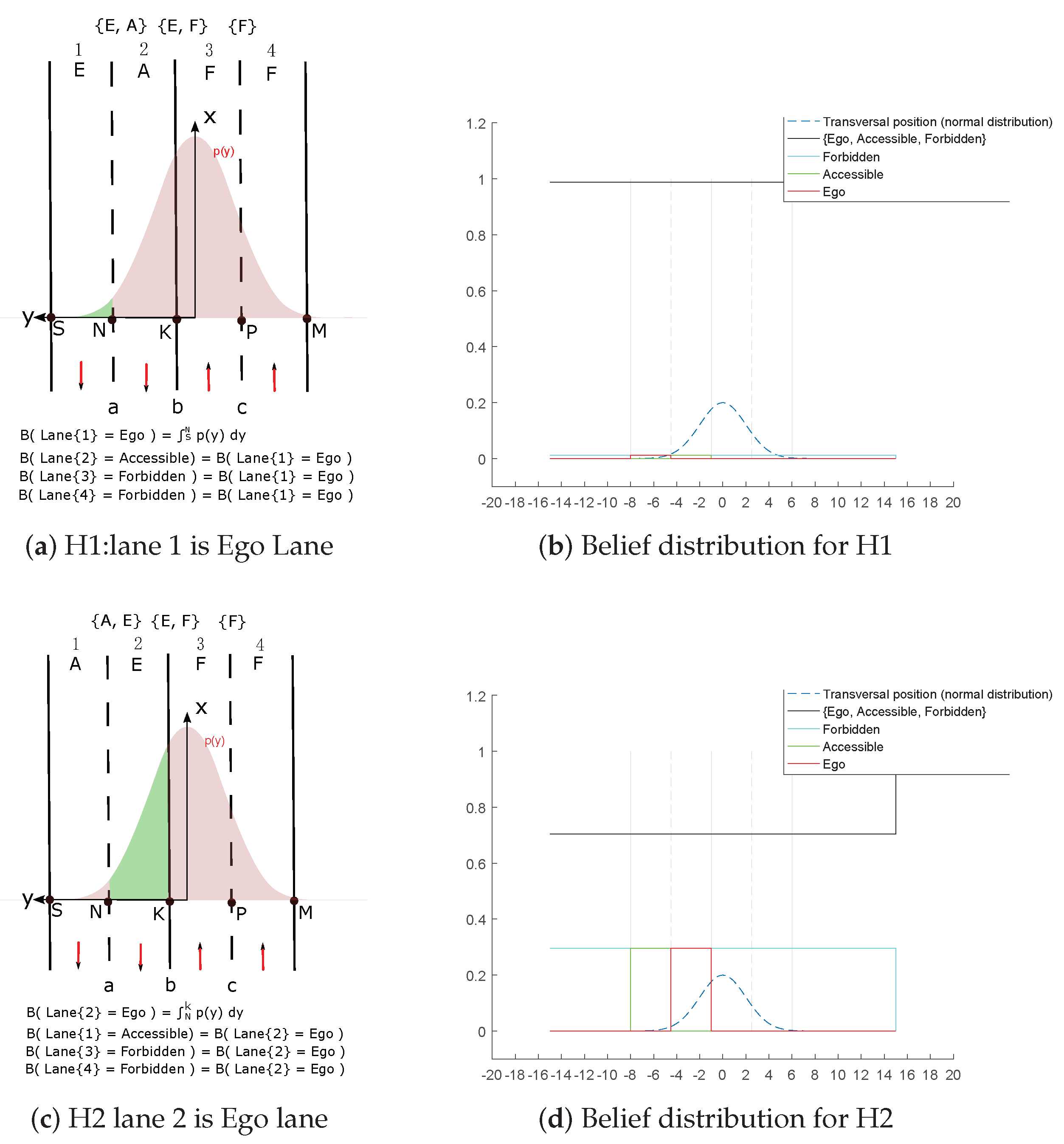
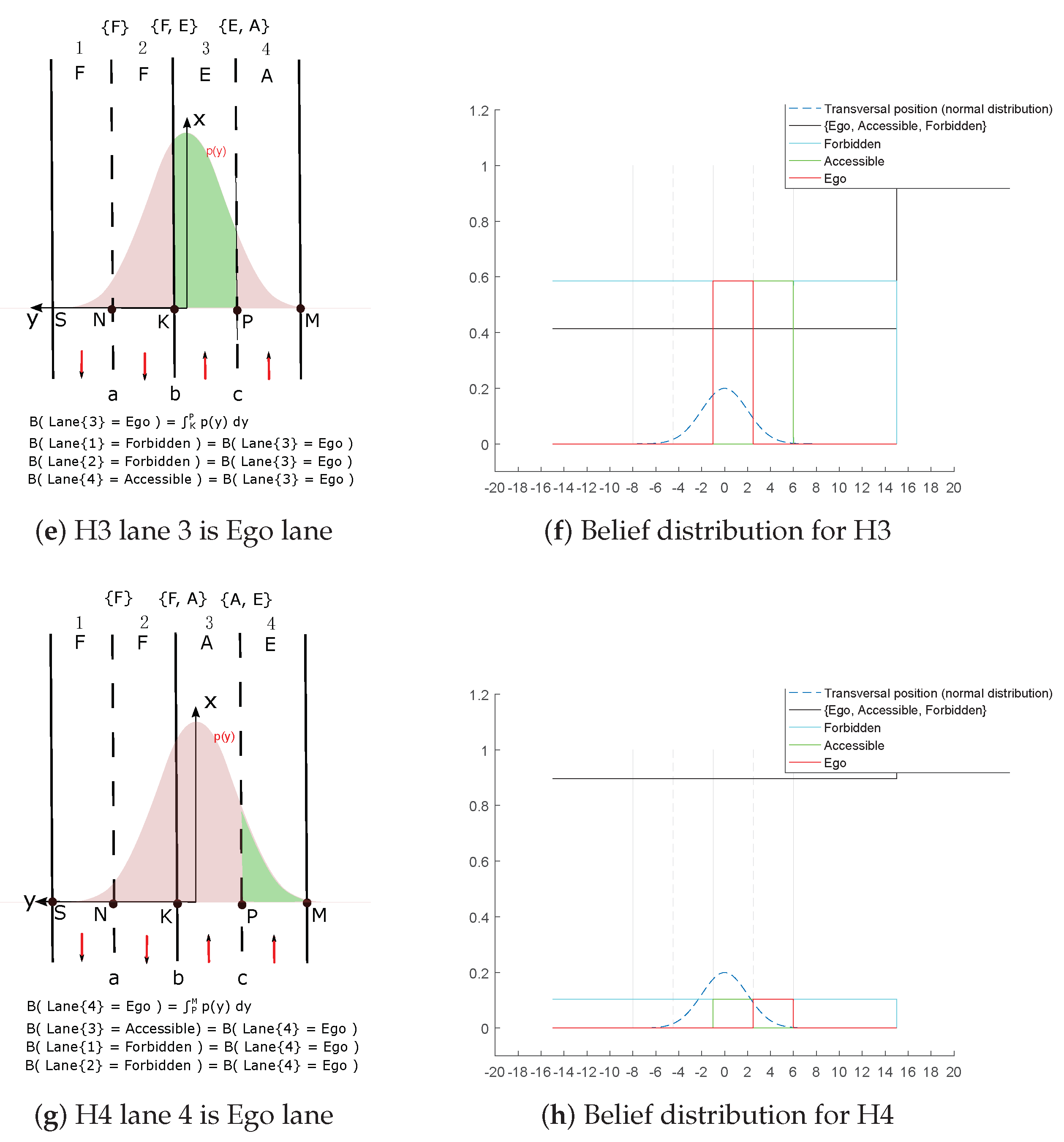
Figure 11. The bird view of the map is given with a zoom-out at the region where the host vehicle is located. In this situation, the host vehicle is running on a three-lane road. The vehicle is in the middle lane, whereas the lane on the right is for the purpose of entering the road, so this lane is not accessible. The lane on the left is a parallel lane with the same orientation than the current occupied lane, thus this lane is accessible.
4.2.1. Probabilistic Lane Grid Result
In
Figure 12, the probabilistic grids are shown with the pose uncertainty
, and in
Figure 13 shows the results with a larger pose uncertainty
. Corresponding to each uncertainty, the probability distribution of each lane state is shown separately. The combination of all states is also shown, as well as the retro-projection of the distribution on the scene image.
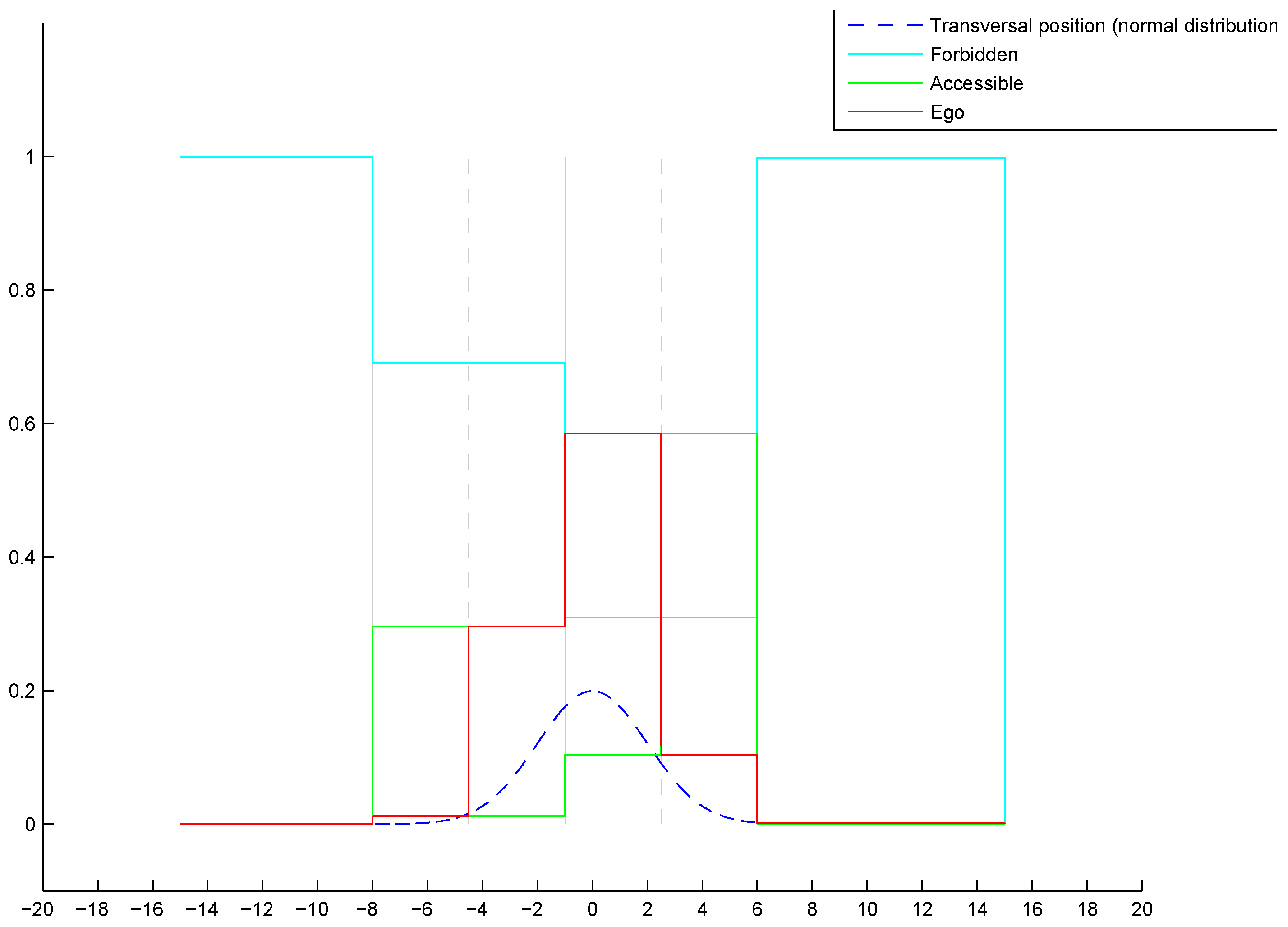
From these results, one can clearly remark that cells at farther distance have lower probability level according to the decreasing color level in the grid, especially in
Figure 13. The probability distribution extends to adjacent lanes, which means a dispersed probability. This is the consequence of uncertainty propagation. The combined probability shown in
Figure 12d and
Figure 13d further reflect this phenomenon. The lane cells that are located close to the host vehicle contain single state probability, whereas the probability distribution of the cells at farther distance can become very ambiguous and dispersed.
In
Figure 12e and
Figure 13e, the retro-projection of the constructed grids on the images provides a qualitative view of evaluation. The features reflecting the lanes are valid based on the correspondence between the grids and the image spaces.
4.2.2. Evidential Lane Grid Result
Figure 14 and
Figure 15 display respectively the resultant lane grids of the evidential approach with the small position uncertainty
and the large one
. In these two figures, the mass distributions are shown in the format of RGB images. From the color variance in the figure, one can clearly remark that grid cells have different mass level over distance change. Cells that are closer to the host vehicle tend to have higher level of mass in each state. This is due to the uncertainty of heading angle causing the farther cells to have larger uncertainty. The mass in the union of the states also demonstrate this effect. The mass in the union states are shown in
Figure 14d and
Figure 15d, and is displayed by the combination of colors: yellow, cyan and magenta colors represent respectively the mass in
,
and
. Moreover, one can remark from the retro-projection that the union of the masses focus mainly on the cells that are on the markings or close to the markings since the proposed operator takes full advantage of the property that the union of the masses should be assigned to union of the states that cannot be separated.
The difference between the resultant lane grids of the two different uncertainties is obvious. A larger pose uncertainty level results in less mass in the singleton states and more mass in the union states. The
mass level in
Figure 14a is clearly higher than in
Figure 15a, and in
Figure 15d clearly the union mass area (left to right:
,
,
) is larger than in
Figure 14d.
In
Figure 14f and
Figure 15f, the retro-projections of
,
, and
mass distributions are displayed. One can see that the lane information is correctly integrated in the grid. One should keep in mind that the road rules are implied in the cell states by different masses supporting each state.
Figure 14g and
Figure 15g show the retro-projection of the
,
,
,
and
masses. One can see these masses are concentrated over the markings. This is the advantage of the adopted operator.
The system has been tested of many roads and the reader can watch the following video online to get a better idea (
https://youtu.be/0fJp-d4K75s).
4.2.3. Comparison between Probabilistic and Evidential Lane Grids
Compared to probabilistic approach, the evidential approach provides more flexible way to handle uncertainty. It provides possibility to put belief into union states if, for example, the belief in each single state is not clear. The Unknown mass can explicitly quantify ignorance, which avoids putting prior information to the cases where no data support any state. In the evidential approach, the pignistic probability [
37] can be adopted to transform masses to probabilities. In
Figure 16a,c, we herein compare the pignistic probability grid and probabilistic decision grid. The ratio of identical decision between these two decision grids is
, which means the approach to handle uncertainty by evidential theory is valid.
Figure 16b illustrates the main difference of these two methods. This is the decision grid deduced by the maximum of evidence masses. The dark space is marked Unknown which means no decision of state is made over these spaces, because not enough information is provided. This is an important advantage over the probabilistic approach as this evidential decision grid enables the avoidance of risky trajectory with insufficient information provided.
4.2.4. Information Discussion
In this section, we give an analysis of the resultant lane grids by introducing the Specificity and Entropy. Together they give an evaluative view about the quality of the mass distribution of each cell in the lane grid. Average Specificity and Entropy values are calculated for eachlane grid [
38]. According to the definition of specificity and entropy, an informative and non-ambiguous mass function should have a high degree of specificity and a low degree of entropy.
Average Entropy and Specificity Variation Regarding to Position Uncertainty
Let study how these two measures evolve with regards to the position uncertainty. The study is simply conducted by adding random noises to a specific position of the host vehicle. This is a Monte-Carlo method. Every uncertainty level is sampled 1000 times and corresponding lane grids are constructed. The average entropy and specificity value are computed in each case.
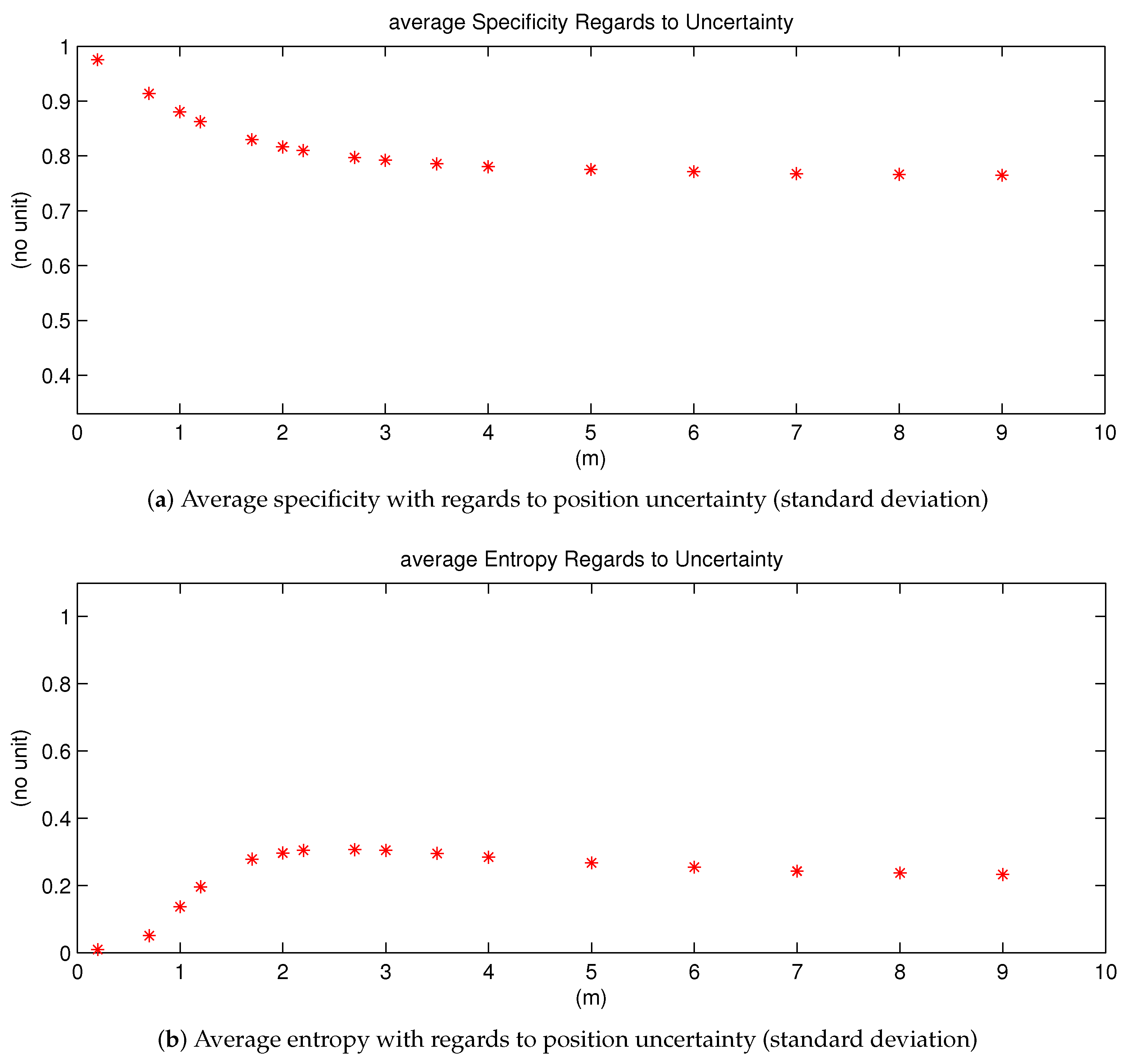
In
Figure 17, simulation results are shown, the x-axis of both images represent uncertainty variation.
Figure 17a shows the average specificity measure. One can remark that if the uncertainty level augments, the specificity measure gradually decreases, and at last converges to a constant value. This behavior demonstrates the fact that the specificity value should be smaller with a larger uncertainty level. Furthermore, we can deduce that if the position uncertainty becomes too large up to an inapplicable level, the average specificity value converges to a constant level, which is larger than the minimal value
. This is reasonable because there will be always certain quantity of mass in singleton states.
Similar to the Specificity measure, the Entropy measure shown in
Figure 17b eventually converges to a stable value as well. The explication is the same as for the Specificity measure. However, one can remark a difference: its value augments at first, then gradually decreases to the stable value, with regards to uncertainty level. With no uncertainty, the entropy value is 0 at first, then increasing uncertainty leads to dissonant mass thus larger entropy value. However, if the uncertainty continues to increase, according to the discounting process, more mass thus goes to ignorance and the mass in ignorance does not conflict with other states. Thus, finally the entropy measure goes down until convergence level.
The behaviors of the specificity and entropy demonstrate that the constructed lane grids become less informative with larger position uncertainty. This comportment means that the provided information from the constructed lane grids is consistent with input uncertainty. Thus, we can conclude that the proposed approach has well tackled the uncertainty.
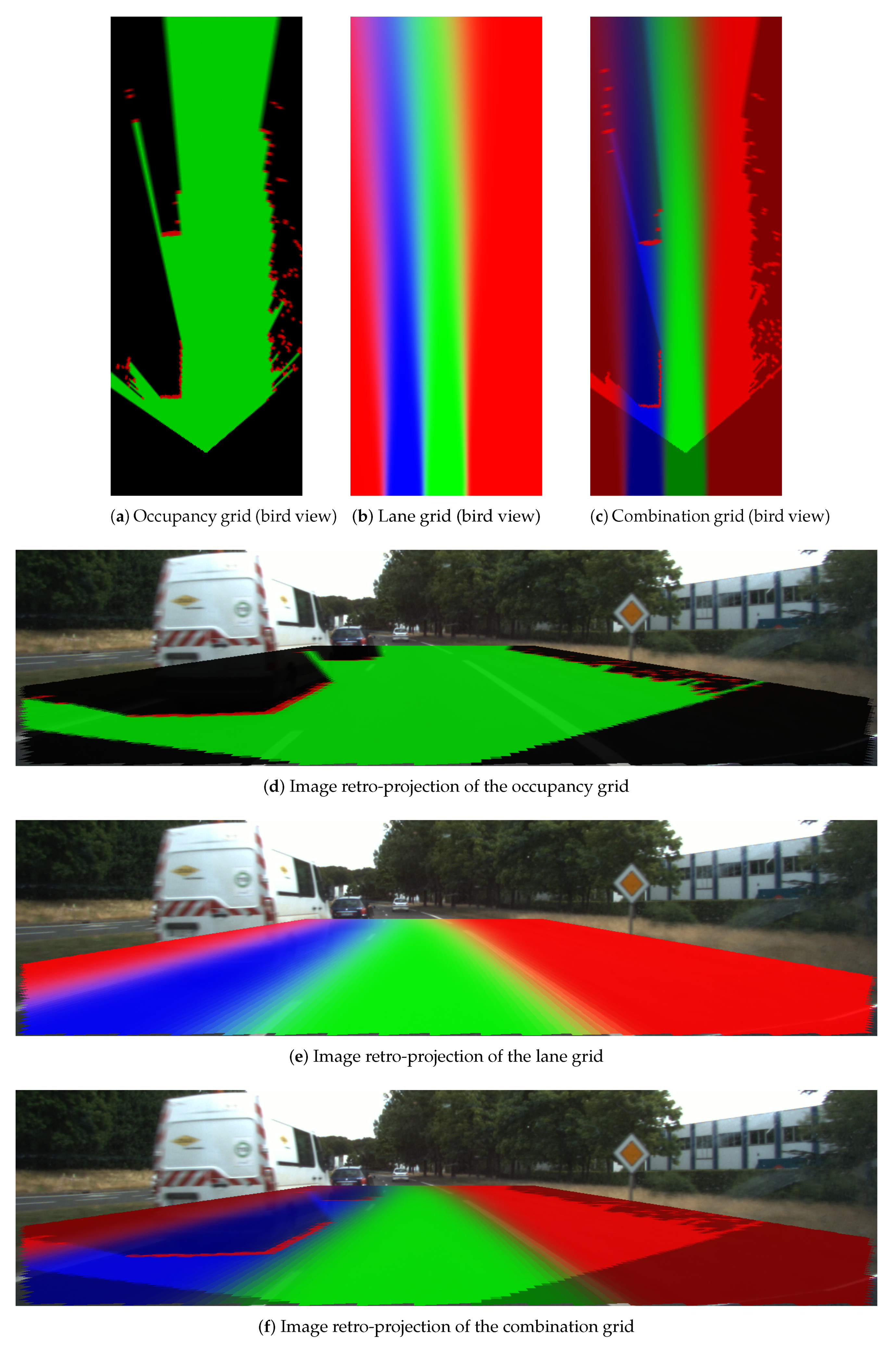
4.3. Combination Grid Results
Figure 18,
Figure 19 and
Figure 20 display three particular results. Bird views of the occupancy grids, lane grids, and combination grids are shown in the top row. They are front-looking grids, the vehicle being located at the bottom on the grids. More precisely, the grids have their origin exactly located at the middle of the rear axis of the car (and not at the front bumper as often made). This is to make them usable by a path planer.
The projection of the respective grids on the scene image are shown afterwards for a qualitative evaluation. Herein green, red, dark and blue colors are applied in these grids. The color code is identical as the one introduced for occupancy grids (green: free, red occupied) and lane grids. For the combination grid, since the frame of discernment is defined as = { }, we use for display the green color which represents the level, the blue color for the level, while the red color represents the sum of and levels. The state level shown in the combination grids are the pignistic probabilities calculated after the fusion process.
From the occupancy grid, one can remark from the projection on the scene image that the obstacle vehicle is correctly detected (even if there is a small calibration error on the reprojection). Moreover, the LiDAR is installed in the front of the host vehicle and this is the origin of the constructed occupancy grid. However, based on the approach introduced in
Section 2, the lane grids are constructed on local coordinates defined at the center of the vehicle’s rear axle, i.e., the origin
M. Herein, to compensate for this coordinate difference, a translation is performed for the occupancy grid. The resulting dark region at the bottom of the occupancy grid shows this translation. This area is an unperceived area (a dead zone), so total ignorance is assigned.
The lane grid shown in
Figure 18 is constructed by taking into account the pose uncertainty
. The effect of the uncertainty propagation can still be seen in the grid even if the angular uncertainty is small. The projection on the scene image shows that the semantic lane information is correctly modeled in the grid. One can also remark that the lanes (which are not straight in this experiment) are well characterized over a long distance ahead. In this particular situation, the characterization of the navigability of the lanes would be difficult to do with only on-board sensors like cameras. The advantage of using a localization system with a map is here clearly highlighted.
Figure 20 displays the result when the host vehicle was performing a lane changing from the left lane to the right lane. This lane change is particularly visible in the lane grid since the lanes are rotated on the left. In this kind of situation, one can remark from the mass level in the lane grid that the
and
states are uncertain (Green and blue color are not bright compared to the other two scene results), which is conform to the fact that the vehicle is running across to the dashed lane marking which separates the two lanes. The determination of the lane states in this kind of transition stage is very ambiguous and difficult to perform and the behavior of the perception system perfectly fits with reality.
Within the combination grid, the perception system handles obstacle information as well as semantic lane information in a unique representation of the world which is important for a path planning module as said before. Thus, we have kept the information in both the lane and lane. The obstacle information is drawn in red along with all the cells in the region.
Instead of storing the obstacle information and the semantic lane information in two separate grids, the combination process manages these two sources of information into a uniform frame which facilitates path planning afterwards. For the reinforcement of the grid application, the additional information makes it possible to find the path all along the ego lane for lane-keeping application, whereas the information can serve as a second choice when the ego lane is blocked.
The system has been tested on many roads and the reader can watch the video online (
https://youtu.be/0F078KJkSRo) of a 1.5 km long trial to evaluate the performance of the method.
4.4. Processing Time
The average time of execution is computed corresponding to the same grid resolutions as before. Each step in the approach is timed and the average time consumption is shown in
Table 1. The grid size is set to be (40 × 16 m) for all the shown results.
One can remark that the refinement and the fusion process add little processing time.
At 0.1 m resolution, we need more than a half of second to construct the combination grid, which is not compatible with a real time implementation. However, at 0.4 m, the average time consumption decreases to less than 0.1 s. This normally can meet the requirement of real-time applications. In fact, the shown results can be optimized through parallel programming, which has not been implemented in the current system.
5. Conclusions
A new grid-based approach to characterize the lane information, integrating semantic road rule into the grid cells has been proposed. Based on the Dempster–Shafer theory, a road rule is interpreted as semantic information of accessibility contained in the Semantic lane Grid. The , and propositions defined in the frame of discernment characterizes the road space into meaningful parts, and the boundaries of these meaningful parts contains the uncertain mass. We have proposed a multi-hypothesis model to take into account the host vehicle’s pose uncertainty relative to the road. Simulation results as well as real road experimental results have been reported.
A Dempster fusion process has been introduced to combine obstacle information and semantic lane information. They characterize the state of the same space with complementary aspects. The fusion process provides a more complete representation of the environment in a unique perception grid keeping the key information for path planning applications with a negligible additional processing time.
The results show interesting perspective in the domain of intelligent vehicle perception and navigation especially when HD maps will be available worldwide. Applying this resulting grid as an input to a path planner would be an interesting application of this work. New level of information can be added as an extension of this work, like emergency region, public transport region, etc. Moreover, an evaluation of this approach with a less accurate map would be interesting, since maps are often affected by errors. On the other hand, the hypothesis of an accurate prior map is not realistic, which is the main limitation of the proposed approach.