Does the Position of Foot-Mounted IMU Sensors Influence the Accuracy of Spatio-Temporal Parameters in Endurance Running?
Abstract
1. Introduction
2. Methods
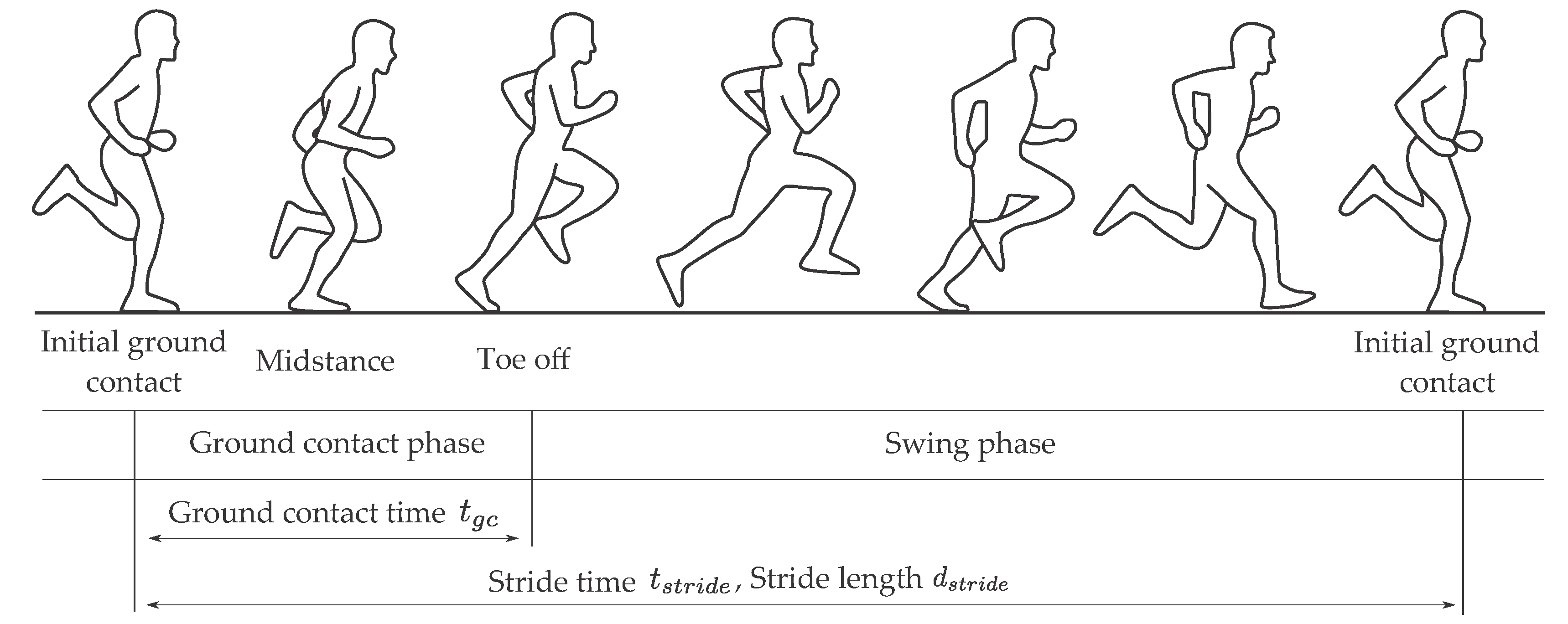
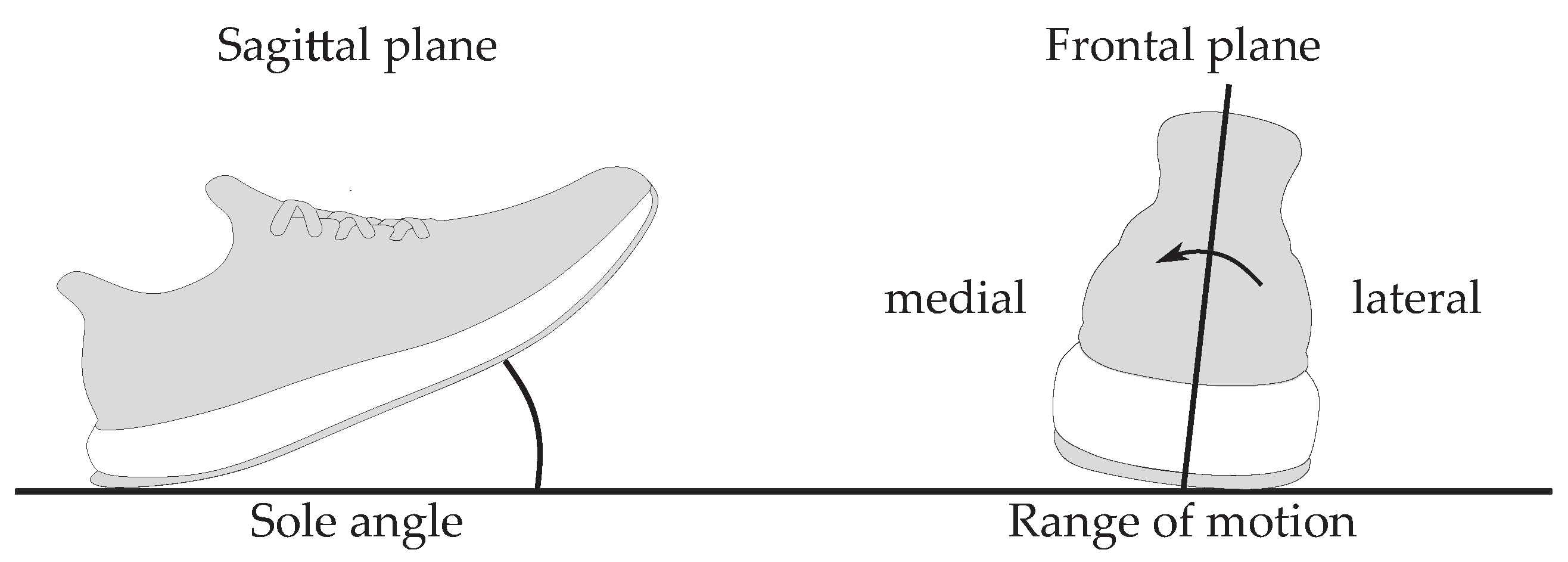
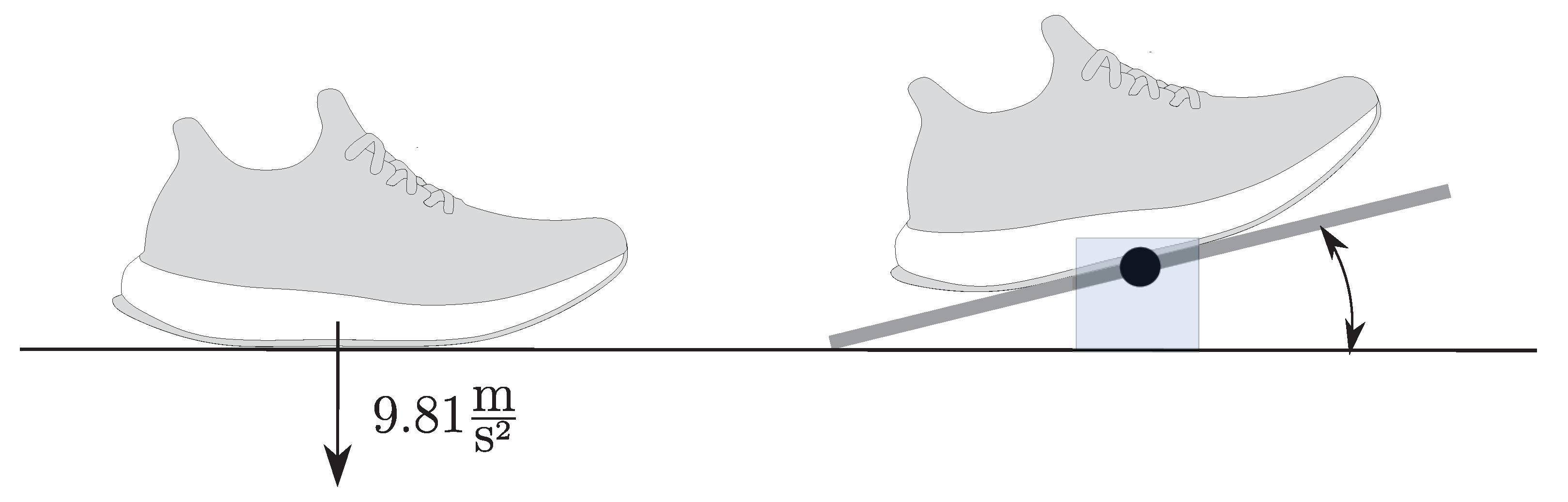
2.1. Definition of Spatio-Temporal Parameters
2.2. Data Set
- (1)
- Vector pair superior/inferior direction: The subjects were asked to stand still with both feet on the ground. Thus, the accelerometer of all sensors measured the gravitational acceleration in the sensor frame. The -axis was defined as the corresponding vector in the shoe frame.
- (2)
- Vector pair medial/lateral direction: The subjects rotated their feet on a balance board, which only allowed for a rotation in the shoe frame’s sagittal plane. A gyroscope in the shoe frame measures the angular rate of the rotation on the medial/lateral axis. The medial/lateral axis of the shoe frame corresponds to the principle component of the angular rate data during rotation in the sensor frame. The -axis was defined as the medial/lateral axis in the shoe frame.
2.3. Algorithm
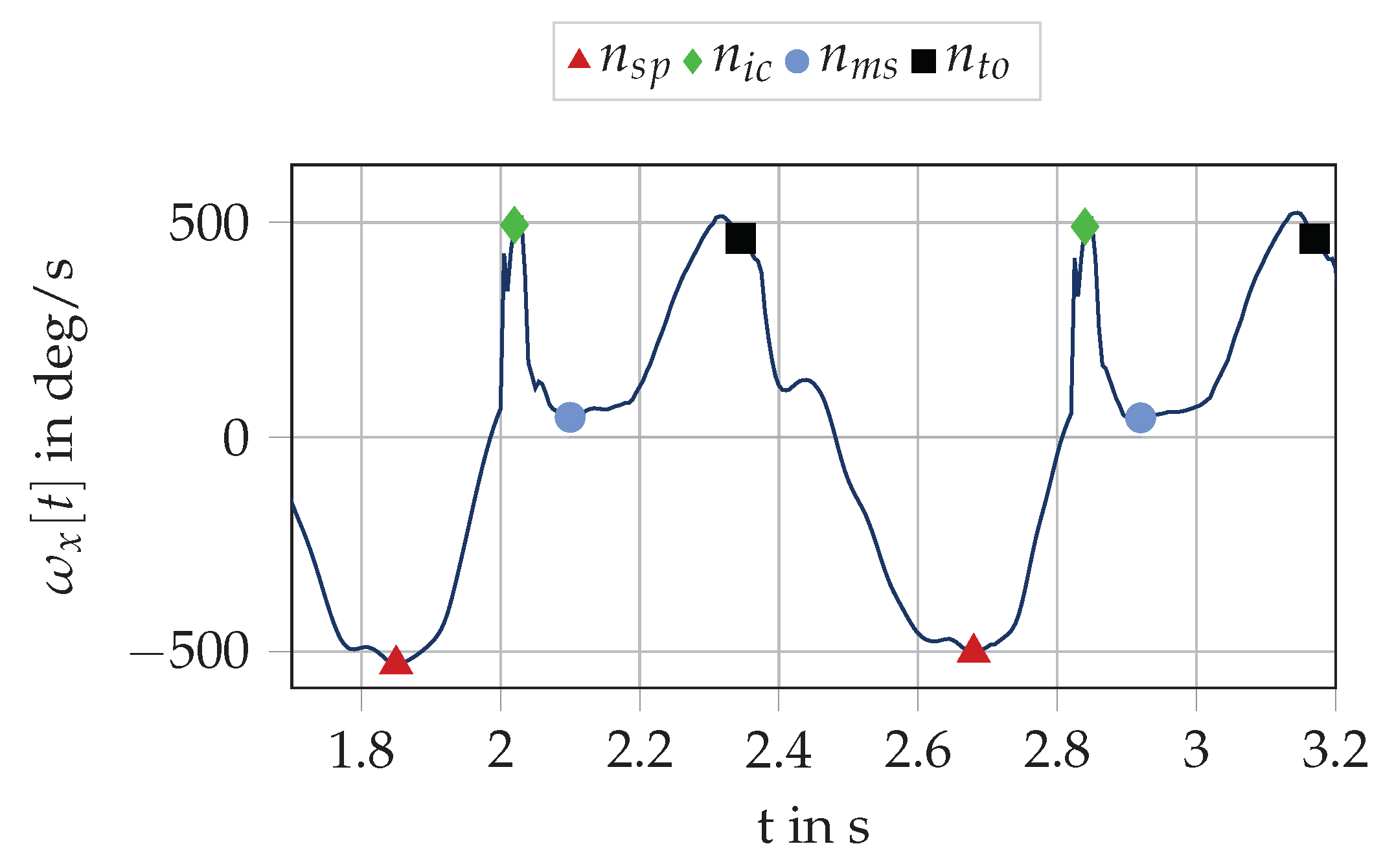
2.3.1. Stride Segmentation
2.3.2. Computation of Foot Trajectory
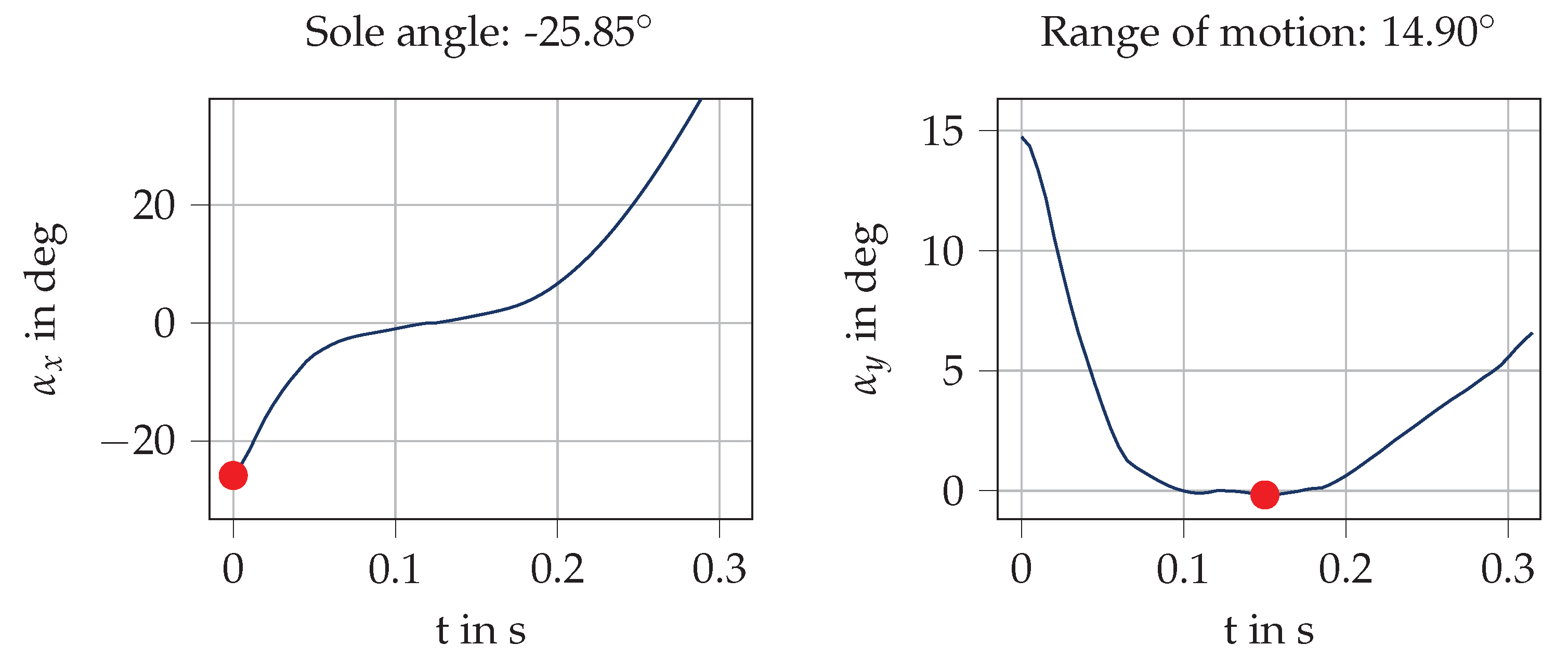
2.3.3. Parameter Computation
2.4. Evaluation
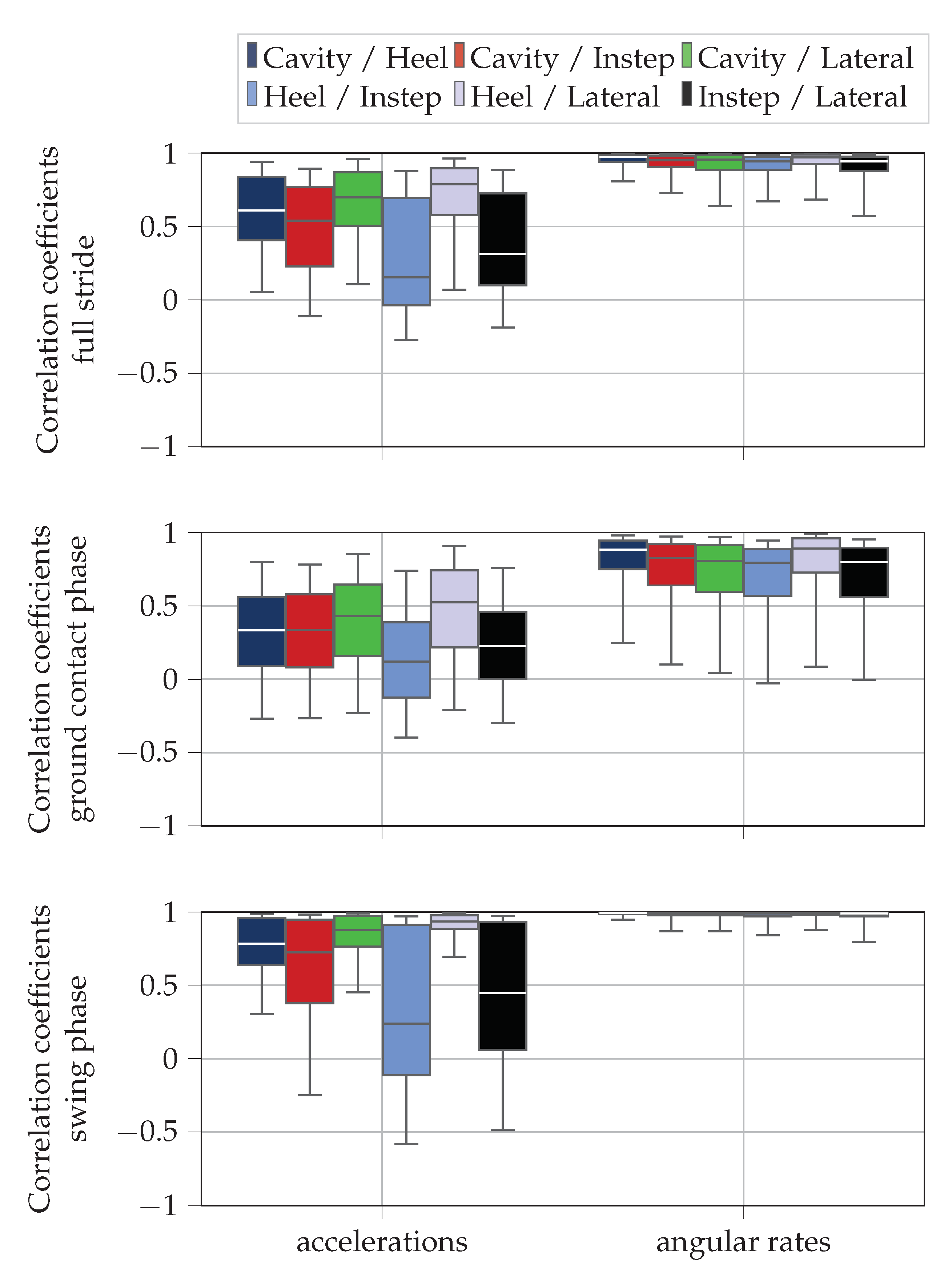
2.4.1. Evaluation of Raw Data Similarity
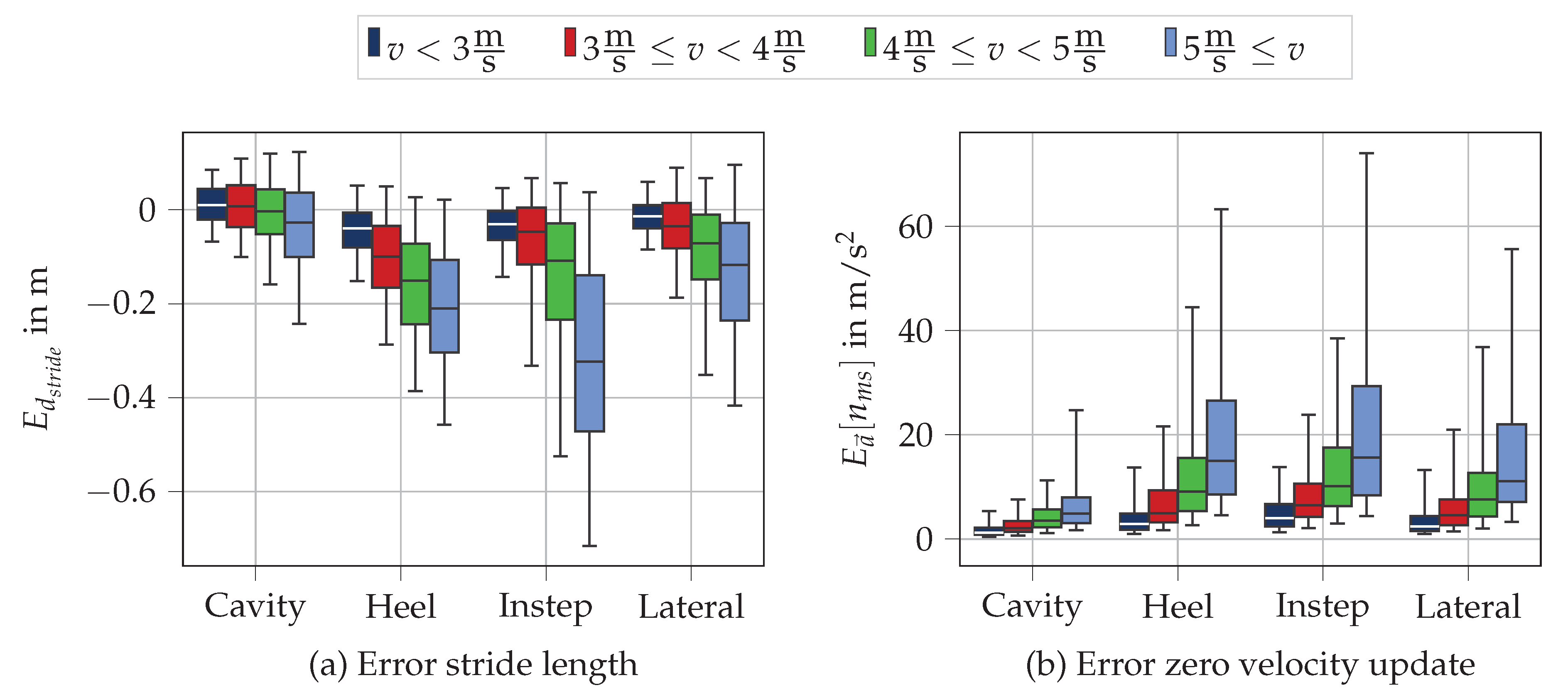
2.4.2. Evaluation of Spatio-Temporal Parameters
3. Results
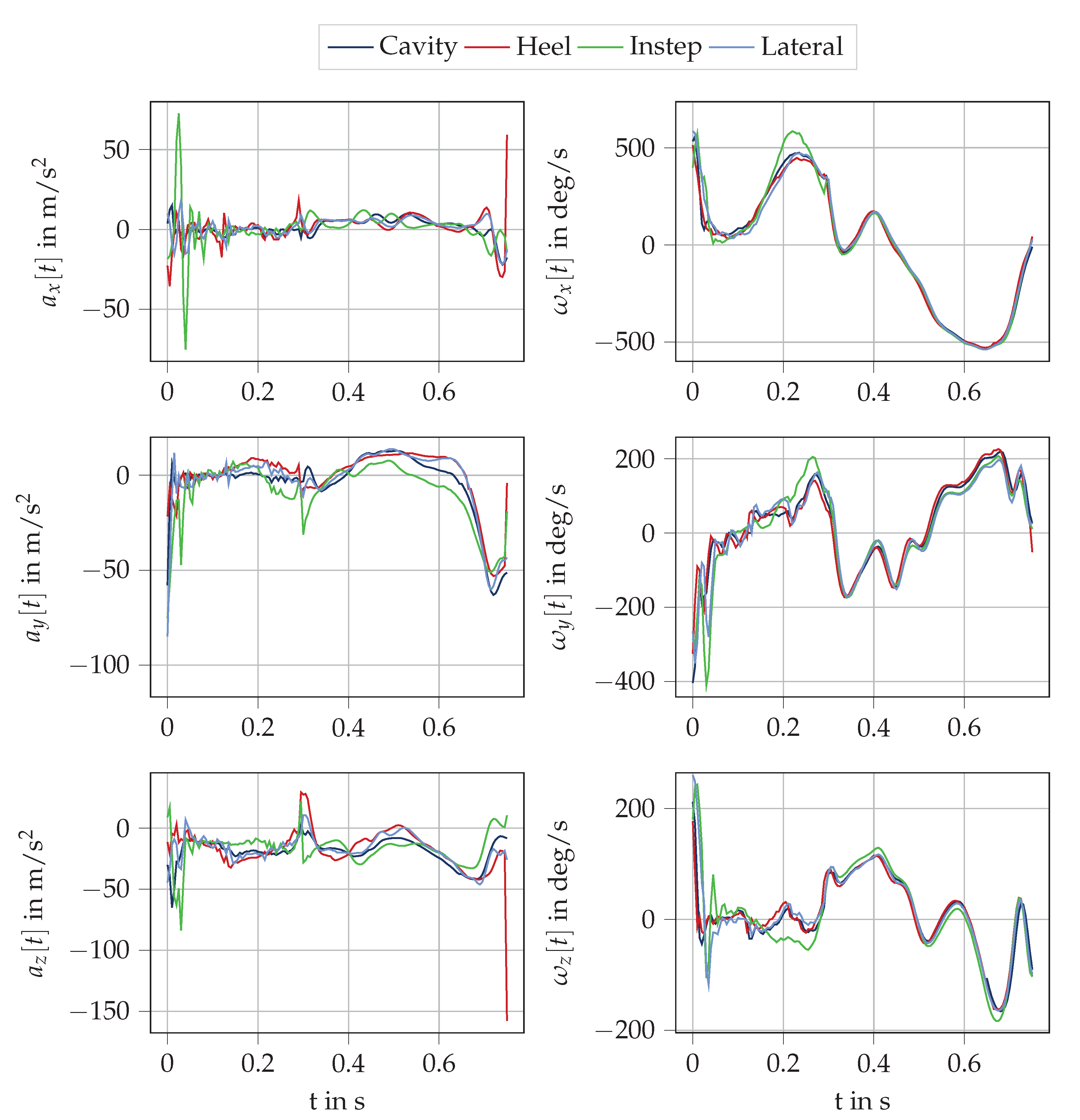
3.1. Results of Raw Data Similarity
3.2. Results of Spatio-Temporal Parameters
4. Discussion
4.1. Differences in Raw Data
4.2. Temporal Parameters
4.3. Spatial Parameters
4.4. General Aspects
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IMU | Inertial measurement unit |
| IC | Initial contact |
| TO | Toe off |
| MS | Midstance |
Appendix A. Trajectory Computation Plots
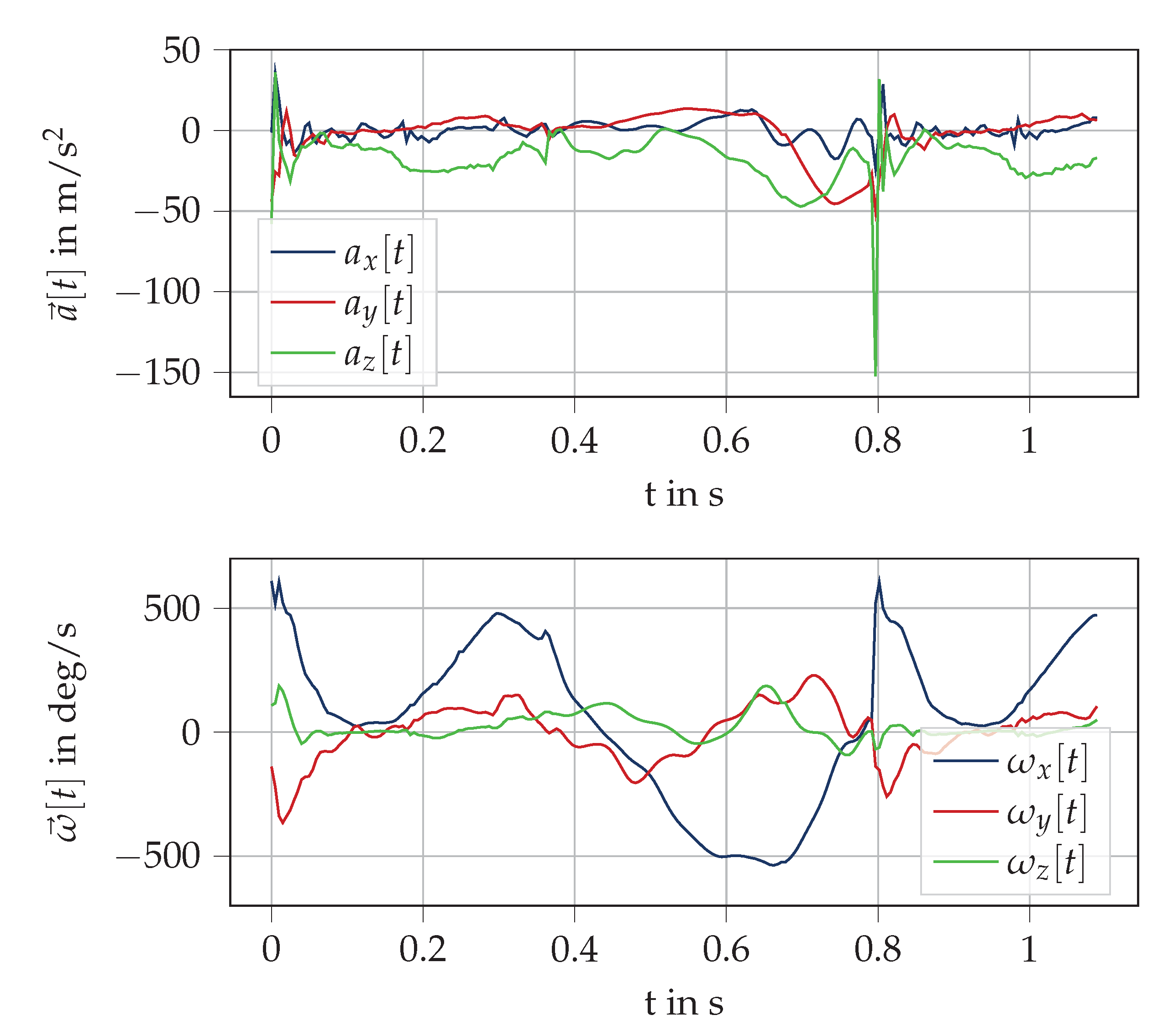

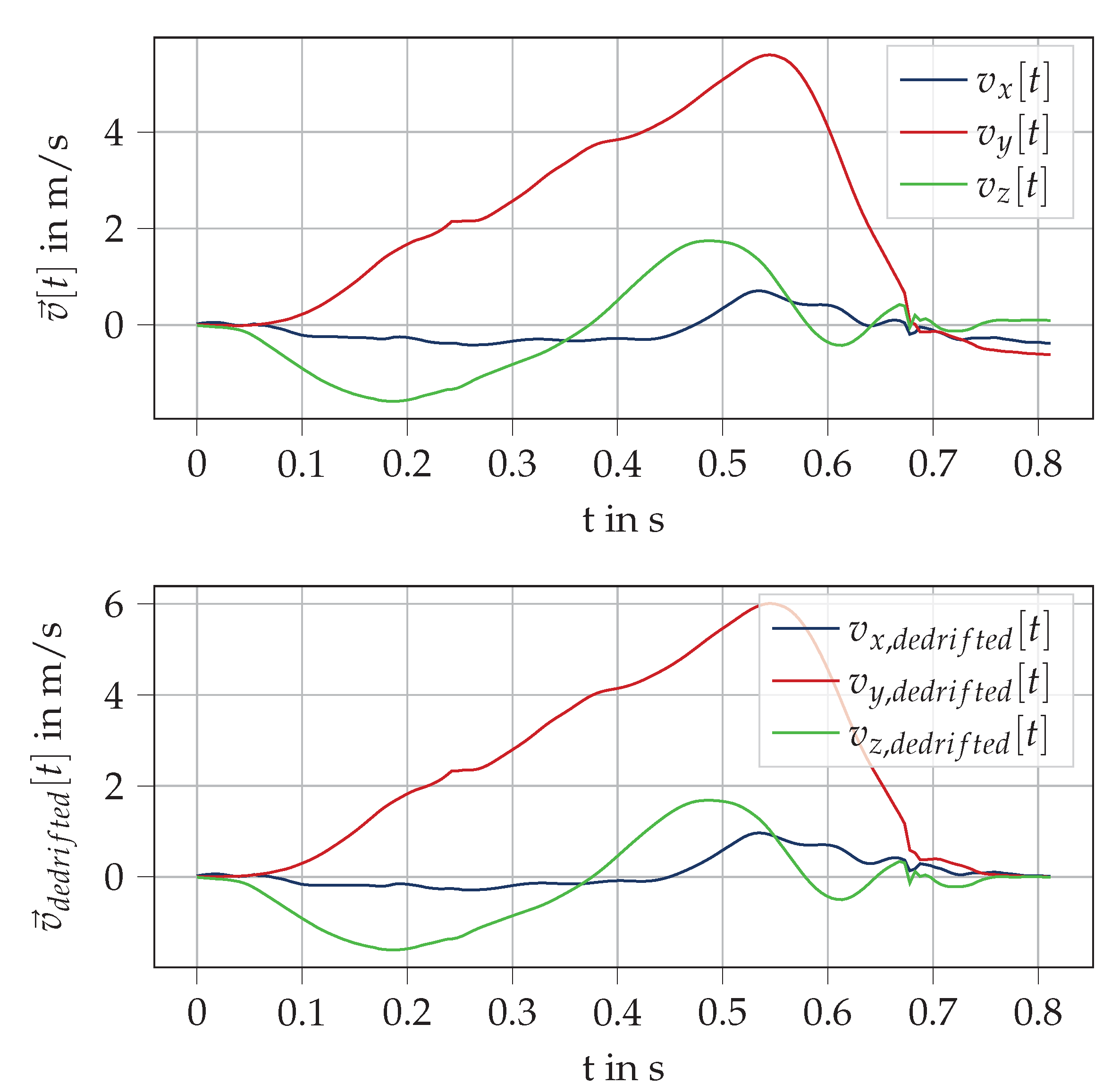
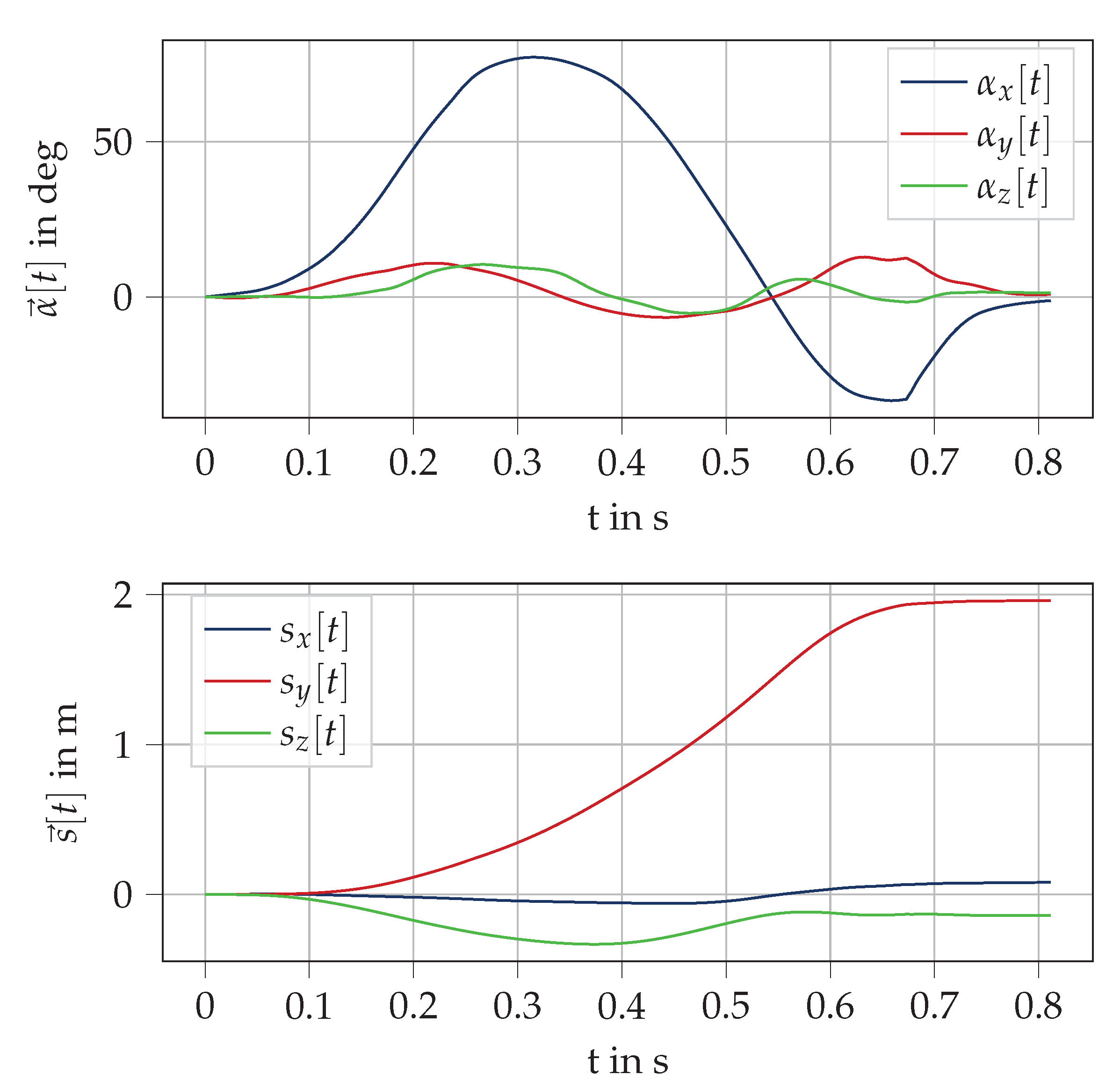
References
- Van Hooren, B.; Goudsmit, J.; Restrepo, J.; Vos, S. Real-time feedback by wearables in running: Current approaches, challenges and suggestions for improvements. J. Sports Sci. 2020, 38, 214–230. [Google Scholar] [CrossRef] [PubMed]
- Strohrmann, C.; Harms, H.; Tröster, G.; Hensler, S.; Müller, R. Out of the lab and into the woods: kinematic analysis in running using wearable sensors. In Proceedings of the 13th international conference on Ubiquitous computing, Beijing, China, 17–21 September 2011. [Google Scholar]
- Schutz, Y.; Herren, R. Assessment of speed of human locomotion using a differential satellite global positioning system. Med. Sci. Sport Exerc. 2000, 32, 642–646. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Yang, L.; Bie, R.; Yu, J.; Gao, Y.; Shen, Y.; Kos, A. An XGBoost-based physical fitness evaluation model using advanced feature selection and Bayesian hyper-parameter optimization for wearable running monitoring. Comput. Netw. 2019, 151, 166–180. [Google Scholar] [CrossRef]
- Strohrmann, C.; Harms, H.; Kappeler-Setz, C.; Troster, G. Monitoring kinematic changes with fatigue in running using body-worn sensors. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 983–990. [Google Scholar] [CrossRef]
- Schütte, K.H.; Maas, E.A.; Exadaktylos, V.; Berckmans, D.; Venter, R.E.; Vanwanseele, B. Wireless tri-axial trunk accelerometry detects deviations in dynamic center of mass motion due to running-induced fatigue. PLoS ONE 2015, 10, e0141957. [Google Scholar] [CrossRef]
- Benson, L.C.; Ahamed, N.U.; Kobsar, D.; Ferber, R. New considerations for collecting biomechanical data using wearable sensors: Number of level runs to define a stable running pattern with a single IMU. J. Biomech. 2019, 85, 187–192. [Google Scholar] [CrossRef]
- Meardon, S.A.; Hamill, J.; Derrick, T.R. Running injury and stride time variability over a prolonged run. Gait Posture 2011, 33, 36–40. [Google Scholar] [CrossRef]
- Norris, M.; Kenny, I.C.; Anderson, R. Comparison of accelerometry stride time calculation methods. J. Biomech. 2016, 49, 3031–3034. [Google Scholar] [CrossRef]
- Schmidt, M.; Rheinländer, C.; Nolte, K.F.; Wille, S.; Wehn, N.; Jaitner, T. IMU-based determination of stance duration during sprinting. Procedia Eng. 2016, 147, 747–752. [Google Scholar] [CrossRef]
- Shiang, T.Y.; Hsieh, T.Y.; Lee, Y.S.; Wu, C.C.; Yu, M.C.; Mei, C.H.; Tai, I.H. Determine the Foot Strike Pattern Using Inertial Sensors. J. Sens. 2016, 2016. [Google Scholar] [CrossRef]
- Falbriard, M.; Meyer, F.; Mariani, B.; Millet, G.P.; Aminian, K. Drift-Free Foot Orientation Estimation in Running Using Wearable IMU. Front. Bioeng. Biotechnol. 2020, 8, 65. [Google Scholar] [CrossRef] [PubMed]
- Lederer, P.; Blickhan, R.; Schlarb, H. Rearfoot Angle Velocities during Running - A Comparison between Optoelectronic and Gyroscopic Motion Analysis. In Proceedings of the 29th International Conference on Biomechanics in Sports (2011), Porto, Portugal, 27 June–1 July 2011. [Google Scholar]
- Koska, D.; Gaudel, J.; Hein, T.; Maiwald, C. Validation of an inertial measurement unit for the quantification of rearfoot kinematics during running. Gait Posture 2018, 64, 135–140. [Google Scholar] [CrossRef] [PubMed]
- Zrenner, M.; Gradl, S.; Jensen, U.; Ullrich, M.; Eskofier, B. Comparison of Different Algorithms for Calculating Velocity and Stride Length in Running Using Inertial Measurement Units. Sensors 2018, 18, 4194. [Google Scholar] [CrossRef] [PubMed]
- Falbriard, M.; Meyer, F.; Mariani, B.; Millet, G.P.; Aminian, K. Accurate estimation of running temporal parameters using foot-worn inertial sensors. Front. Physiol. 2018, 9, 610. [Google Scholar] [CrossRef] [PubMed]
- Bailey, G.; Harle, R. Assessment of foot kinematics during steady state running using a foot-mounted IMU. Procedia Eng. 2014, 72, 32–37. [Google Scholar] [CrossRef]
- Gradl, S.; Zrenner, M.; Schuldhaus, D.; Wirth, M.; Cegielny, T.; Zwick, C.; Eskofier, B.M. Movement Speed Estimation Based in Foot Acceleration Pattern. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018. [Google Scholar]
- Skog, I.; Nilsson, J.O.; Handel, P. Pedestrian tracking using an IMU array. In Proceedings of the 2014 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 6–7 January 2014. [Google Scholar]
- Peruzzi, A.; Della Croce, U.; Cereatti, A. Estimation of stride length in level walking using an inertial measurement unit attached to the foot: A validation of the zero velocity assumption during stance. J. Biomech. 2011, 44, 1991–1994. [Google Scholar] [CrossRef]
- Blank, P.; Kugler, P.; Schlarb, H.; Eskofier, B. A wearable sensor system for sports and fitness applications. In Proceedings of the 19th Annual Congress of the European College of Sport Science, Amsterdam, The Netherlands, 2–5 July 2014. [Google Scholar]
- Potter, M.V.; Ojeda, L.V.; Perkins, N.C.; Cain, S.M. Effect of IMU Design on IMU-Derived Stride Metrics for Running. Sensors 2019, 19, 2601. [Google Scholar] [CrossRef]
- Ferraris, F.; Grimaldi, U.; Parvis, M. Procedure for effortless in-field calibration of three-axial rate gyro and accelerometers. Sens. Mater. 1995, 7, 311–330. [Google Scholar]
- Wahba, G. A least squares estimate of satellite attitude. SIAM Rev. 1965, 7, 409. [Google Scholar] [CrossRef]
- Markley, F.L. Attitude determination using vector observations and the singular value decomposition. J. Astronaut. Sci. 1988, 36, 245–258. [Google Scholar]
- Michel, K.J.; Kleindienst, F.I.; Krabbe, B. Development of a lower extremity model for sport shoe research. Moment 2004, 1, 0–40. [Google Scholar]
- Maiwald, C.; Sterzing, T.; Mayer, T.; Milani, T. Detecting foot-to-ground contact from kinematic data in running. Footwear Sci. 2009, 1, 111–118. [Google Scholar] [CrossRef]
- Kugler, P.; Schlarb, H.; Blinn, J.; Picard, A.; Eskofier, B. A wireless trigger for synchronization of wearable sensors to external systems during recording of human gait. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012. [Google Scholar]
- Šprager, S.; Juric, M. Robust Stride Segmentation of Inertial Signals Based on Local Cyclicity Estimation. Sensors 2018, 18, 1091. [Google Scholar] [CrossRef] [PubMed]
- Skog, I.; Handel, P.; Nilsson, J.O.; Rantakokko, J. Zero-velocity detection—An algorithm evaluation. IEEE Trans. Biomed. Eng. 2010, 57, 2657–2666. [Google Scholar] [CrossRef]
- De Wit, B.; De Clercq, D.; Aerts, P. Biomechanical analysis of the stance phase during barefoot and shod running. J. Biomech. 2000, 33, 269–278. [Google Scholar] [CrossRef]
- Rampp, A.; Barth, J.; Schülein, S.; Gaßmann, K.G.; Klucken, J.; Eskofier, B.M. Inertial sensor-based stride parameter calculation from gait sequences in geriatric patients. IEEE Trans. Biomed. Eng. 2015, 62, 1089–1097. [Google Scholar] [CrossRef]
- Sola, J. Quaternion kinematics for the error-state Kalman filter. arXiv 2017, arXiv:1711.02508. [Google Scholar]
- Madgwick, S. An efficient orientation filter for inertial and inertial/magnetic sensor arrays. Report x-io Univ. Bristol (UK) 2010, 25, 113–118. [Google Scholar]
- Sedgwick, P. Pearson’s correlation coefficient. BMJ 2012, 345, e4483. [Google Scholar] [CrossRef]
- Mo, S.; Chow, D.H. Accuracy of three methods in gait event detection during overground running. Gait Posture 2018, 59, 93–98. [Google Scholar] [CrossRef]
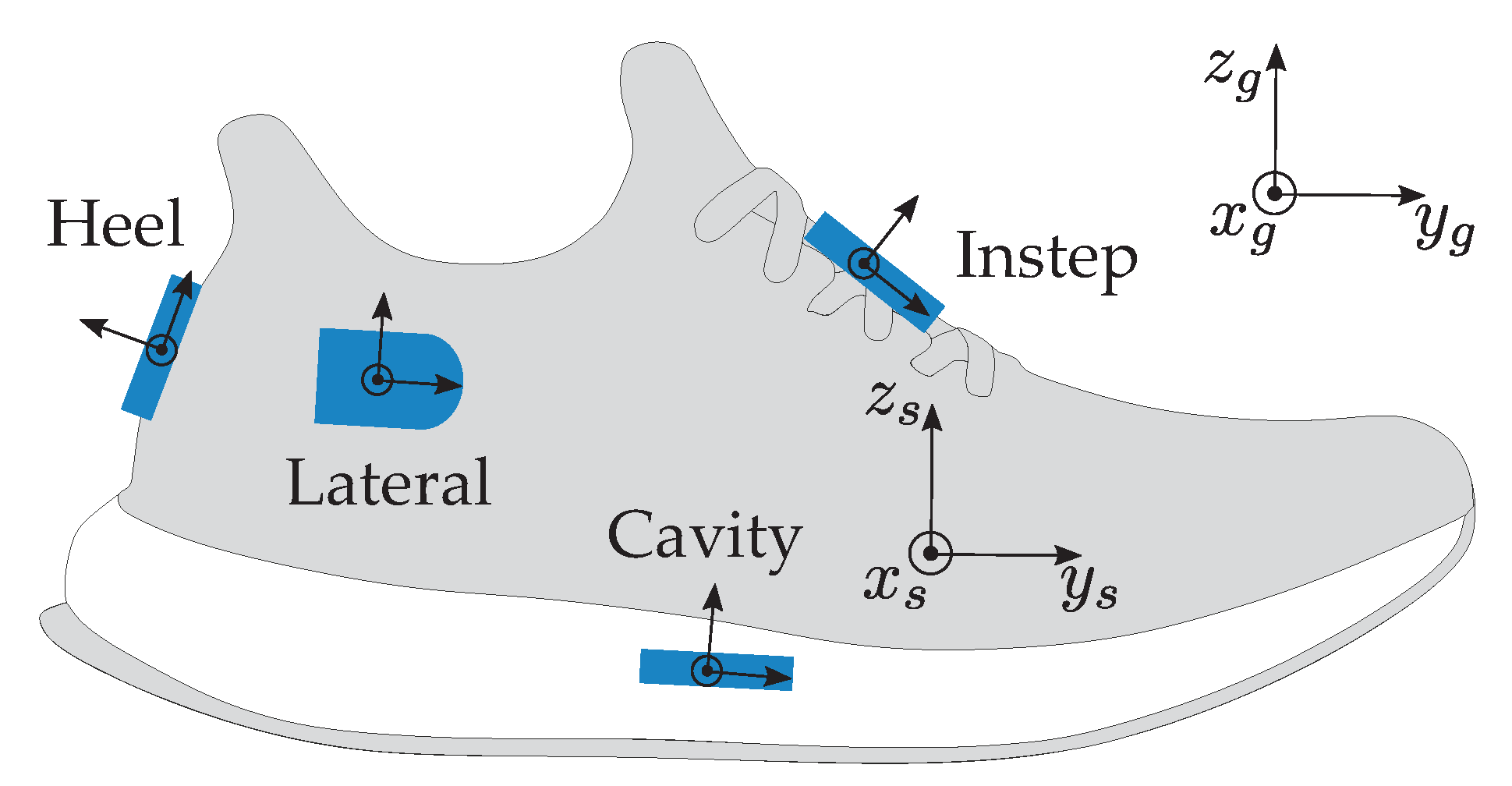
| Name | Mounting |
|---|---|
| Cavity | Cavity cut in the sole of the shoe under the arch |
| Instep | Mounted with suiting clip to laces of the shoe |
| Lateral | Mounted with tape laterally under ankle |
| Heel | Mounted with tape on heel cap |
| Velocity Range (m/s) | Number of Trials | Number of Strides |
|---|---|---|
| 2–3 | 10 | 962 |
| 3–4 | 10 | 558 |
| 4–5 | 15 | 544 |
| 5–6 | 15 | 362 |
| Cavity | Heel | Instep | Lateral | |||||
|---|---|---|---|---|---|---|---|---|
| Median | IQR | Median | IQR | Median | IQR | Median | IQR | |
| Stride time (ms) | −0.5 | 6.9 | 0.0 | 8.4 | 0.4 | 7.6 | 0.3 | 8.6 |
| Ground contact time (ms) | −11.0 | 37.6 | −1.3 | 29.5 | −22.6 | 37.5 | −1.7 | 29.0 |
| Sole angle () | 1.6 | 7.2 | −6.1 | 5.1 | 2.1 | 5.8 | −5.9 | 5.1 |
| Range of motion () | 0.0 | 2.8 | 1.2 | 2.9 | 2.3 | 3.3 | 1.4 | 3.0 |
| Stride length (cm) | 0.3 | 8.5 | −8.3 | 14.7 | −5.6 | 15.1 | −3.3 | 9.7 |
| Avg. stride velocity (m/s) | 0.0 | 0.1 | −0.1 | 0.2 | −0.1 | 0.2 | 0.0 | 0.1 |
| Cavity | Heel | Instep | Lateral | |||||
|---|---|---|---|---|---|---|---|---|
| Median | IQR | Median | IQR | Median | IQR | Median | IQR | |
| Sole angle () | 6.8 | 10.2 | −2.9 | 6.8 | 6.7 | 7.0 | −2.4 | 6.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zrenner, M.; Küderle, A.; Roth, N.; Jensen, U.; Dümler, B.; Eskofier, B.M. Does the Position of Foot-Mounted IMU Sensors Influence the Accuracy of Spatio-Temporal Parameters in Endurance Running? Sensors 2020, 20, 5705. https://doi.org/10.3390/s20195705
Zrenner M, Küderle A, Roth N, Jensen U, Dümler B, Eskofier BM. Does the Position of Foot-Mounted IMU Sensors Influence the Accuracy of Spatio-Temporal Parameters in Endurance Running? Sensors. 2020; 20(19):5705. https://doi.org/10.3390/s20195705
Chicago/Turabian StyleZrenner, Markus, Arne Küderle, Nils Roth, Ulf Jensen, Burkhard Dümler, and Bjoern M. Eskofier. 2020. "Does the Position of Foot-Mounted IMU Sensors Influence the Accuracy of Spatio-Temporal Parameters in Endurance Running?" Sensors 20, no. 19: 5705. https://doi.org/10.3390/s20195705
APA StyleZrenner, M., Küderle, A., Roth, N., Jensen, U., Dümler, B., & Eskofier, B. M. (2020). Does the Position of Foot-Mounted IMU Sensors Influence the Accuracy of Spatio-Temporal Parameters in Endurance Running? Sensors, 20(19), 5705. https://doi.org/10.3390/s20195705






