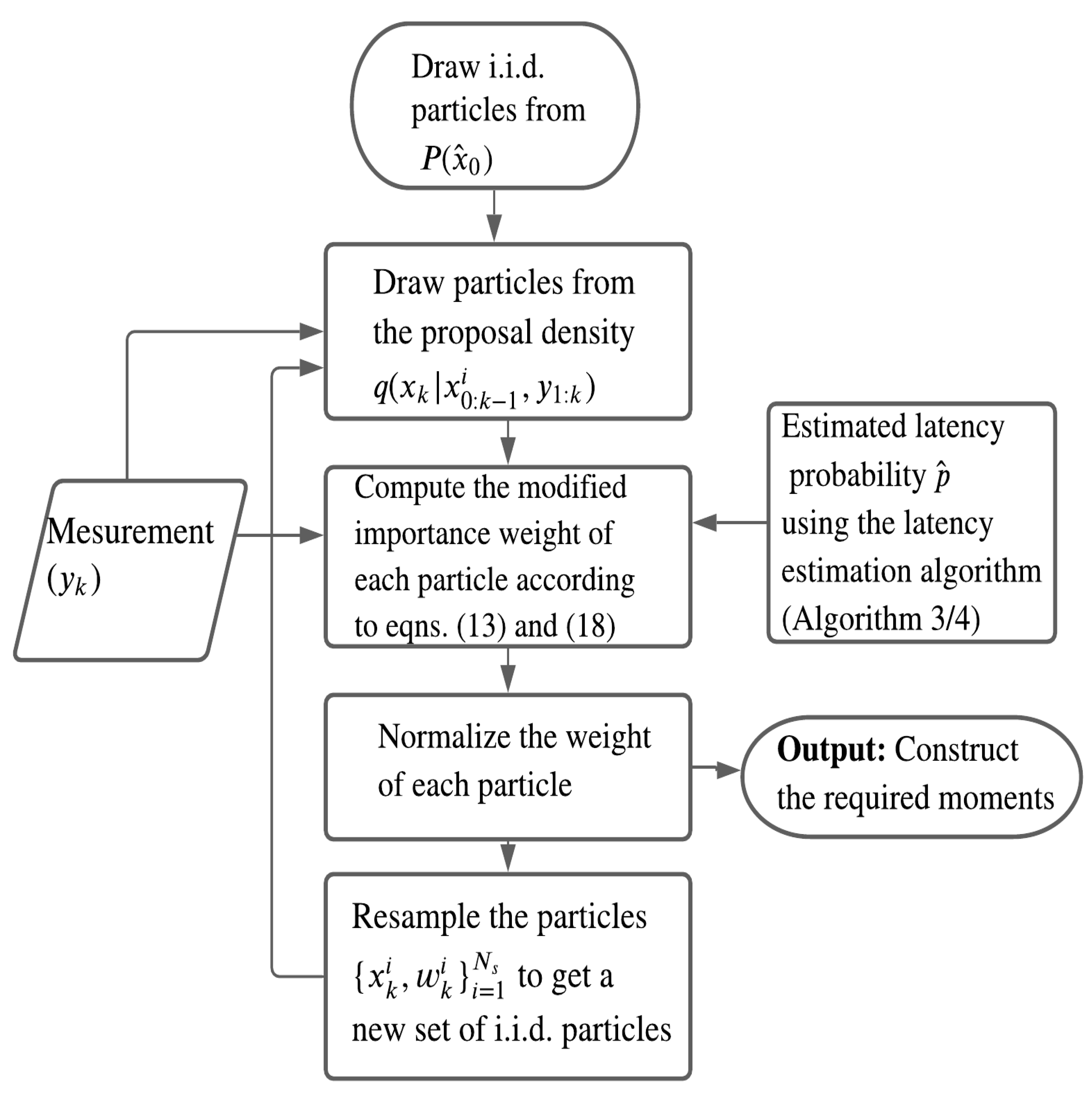
1. Introduction
State estimation for nonlinear discrete-time stochastic systems has received considerable attention from researchers because of its application in various fields of science, including navigation and localization [
1,
2], surveillance [
3], agriculture [
4], econometrics [
5], and meteorology [
6], for example. The Bayesian approach [
7] gives a recursive relationship for the computation of the posterior probability density functions (pdf) of the unobserved states. But the computation of the posterior pdf in case of a nonlinear system is often numerically intractable, and hence suboptimal approximations of these pdf are often used. The particle filter (PF) is a powerful sequential Monte Carlo method under the Bayesian framework to solve nonlinear and non-Gaussian estimation problems by approximating the posterior pdf empirically [
8]. The particle filter often outperforms other approximate Bayesian filters such as the extended Kalman filter (EKF) and the grid-based filters in solving nonlinear state estimation problems [
9]. However, most works on the EKF [
10] and as well as on the traditional PF [
8,
9,
11] typically assume that measurements are available at each time step without any delay. In practice, in many aerospace and underwater target tracking [
12], control [
13] and communication [
14] subsystems, random delays in receiving the measurements are inevitable. These delays, usually caused by the limitations of the network channel, need to be accounted for while designing the state estimator.
In the literature, the random delays have been addressed in the context of linear estimators [
15,
16,
17,
18,
19,
20]. A linear networked estimator is proposed in Reference [
21] to tackle irregularly-spaced and delayed measurements in a multisensor environment. On the other hand, the research on random delays and packet drops in nonlinear state estimation is limited. In Reference [
22] and Reference [
23], improved versions of the EKF and the unscented Kalman filter (UKF) are proposed for one-time step and two-time step randomly delayed measurements. In Reference [
24], quadrature filters have been modified to solve nonlinear filtering problem with one-step randomly delayed measurements. In Reference [
25], the cubature Kalman filter (CKF) [
26] is used to tackle one-step randomly delayed measurements for nonlinear systems. In Reference [
27], a methodology to solve nonlinear estimation problems with multi-step randomly delayed measurements is proposed. However, all these non-linear filters are restricted to Gaussian approximations. Moreover, they assume that the latency probability of delayed measurements is known. In Reference [
28] and Reference [
29], a modified PF that deals with one-step randomly delayed measurement with unknown latency probability and a PF for multi-step randomly delayed measurements with a known latency probability are presented, respectively. In References [
30,
31], the estimation of the unknown latency parameter with one-step randomly delayed measurements is addressed using data log-likelihood function within the Expectation-Maximization (EM) framework. However, none of these works considered the presence of random packet drops. Further,
filtering techniques are used to tackle network-induced delays and packet drops in References [
32,
33,
34].
The specific contributions of this paper to the state-of-the art, specifically over References [
28,
29,
30] are as follows: (i) We propose a new PF with an explicit expression for the importance weight for randomly delayed measurements of any number of time steps with an unknown latency probability and in the presence of packet drops. In Reference [
29], the design of a PF with multi-step randomly delayed measurements is addressed. However, the latency probability is assumed to be known and packet drop is not considered while deriving the expression for the importance weight. (ii) The latency parameter for the random delays and packet drops is assumed to be unknown and we present a method to estimate it both in offline and online manners by maximizing the likelihood function. The sequential Monte Carlo (SMC) method is used here to approximate the likelihood function in the presence of randomly delayed measurements of any number of time steps and packet drops. In References [
28,
30,
31] the latency probability for the measurements with random delays of maximum one step is estimated without considering packet drops. Moreover, while Gaussian approximation is used in the E-steps of the EM framework in References [
30,
31], the SMC approximation is used in Reference [
28], but only for measurements with random delays of maximum one time step and without considering any packet drops. (iii) Due to presence of random delays and packet drops, the measurement noise sequence at different time steps becomes correlated. This work first formulates the modified noise model and derives a general pdf for the modified noise. The proposed PF is then developed using the pdf of the modified measurement noise. In References [
25,
35], randomly delayed measurements with the correlated measurement noise for a nonlinear system is addressed. However, they have considered a maximum delay of one time step and used the Gaussian approximation to develop the filtering algorithm.
Finally, with the help of three numerical examples, the effectiveness and the superiority of the proposed PF are demonstrated in comparison with the state-of-the-art algorithms.
Table 1 lists the features of the previous works and of the proposed work.
The rest of this paper is organized as follows. The problem statement is defined in
Section 2. In
Section 3, the modified PF is proposed and its convergence is discussed.
Section 4 deals with the estimation of the unknown latency probability. In
Section 5, simulation results are presented to demonstrate the superiority of the proposed PF. Finally, in
Section 6, some conclusions are discussed.
2. Problem Statement
Consider a nonlinear dynamic system that can be described by the following equations:
where
denotes the state vector of the system and
is the measurement at any discrete time
, while
and
are mutually independent white noises with arbitrary but known pdf. Here, we consider the case where actual measurement received at a particular time step may be a randomly delayed measurement from a previous time step. This delay (in number of integer time steps) can be between 0 and
N at the
kth sampling instant. If any measurement gets delayed by more than
N steps, that measurement is discarded and no measurement is received at the estimator. Here,
N is the maximum (in number of integer time steps) delay that is determined as discussed in
Section 3.2 and
Section 3.3.
To model delayed measurements at the
kth instant, we choose the independent and identically distributed Bernoulli random numbers
that take values either 0 or 1 with an unknown probability
and
, where
p is the unknown latency parameter. If
is the measurement received at the
kth instant [
27], then
where
Here, is considered to be 1. A measurement received at the kth time instant is j step delayed if . Additionally, at time instant k, at most one of can be 1. If all are zeros, the estimator buffer keeps the measurement received at the previous step. This results in the loss of a measurement (packet drop) when that measurement is delayed by more than N steps due to buffer-size limitation.
Remark 1. Bernoulli random variable and its function are used to represent the real-time randomness of delays in measurements in practical systems [15]. Inclusion of the possibility that at a time step k no measurement may be received (when the delay is longer than N steps) corresponds to the practical limit on the buffer size in real systems. In our algorithm, if a received measurement matches with any of the measurements in the buffer, it is discarded. Remark 2. The latency parameter of received measurements, p, that is, the mean of random variable is unknown in real systems. Contrary to the assumption of single-step delay in Reference [28], the unknown latency probability in this paper is for arbitrary step delays along with the packet drops due to buffer limitation. Further, since both the ideal measurement and the measurement noise are modified in (
3),
needs to be rewritten for its subsequent use in characterizing the densities. Hereafter in this article,
and
will be written as
and
respectively, for brevity. Then, (3) can be restructured as
Here,
and
denote the ideal measurement parts (without any noise) of
from the non-delayed measurements
and the previous step measurement
, respectively, and are defined as
where
and
. Again,
is the additive measurement noise in (
3) defined as
where
is the noise received along with observation
and
.
Now, the objective is to develop a PF algorithm for the system in (
1) with measurement model (
3) that assumes the knowledge of latency probability
p. Additionally, we propose offline as well as online algorithms to estimate
p.
4. Identification of Latency Probability
In practice, when a set of randomly delayed measurements is given, we may not know channel properties and its random parameters. Hence, the latency probability that is required to design the filter may be unknown. Here, we use the ML criterion to identify the unknown latency probability for received measurements. This method involves the maximization of the joint density
of the received measurements, which is a function of latency parameter
p represented by [
28]
where
m is the number of measurements used for the identification of parameter
p and
is the estimated value of
p. Now, we assume that the first received measurement
is independent of parameter
p and is equal to
. Again, using the Bayes’ theorem the above joint pdf can be reformulated as
For computational simplicity the above maximization of likelihood is expressed in terms of the log-likelihood (LL). The LL of (
31) can be formulated as
where
is the LL function of the received measurements. Now, to solve the maximization problem of (
31), first the computation of likelihood
and then the maximization of
need to be carried out.
4.1. Computation of Likelihood Density
State likelihood can be used to compute
with the help of the SMC approximation [
41]. We can express the likelihood density
as the marginal density of a joint pdf that includes delayed measurement and previous states that are correlated using the Bayes’ theorem and Assumption 1 as follows:
Using Bayes’ rule, the joint state prior
can be decomposed as
Since the state vectors follow the first-order Markov property, using the chain rule and (
9), we can write the joint pdf as
where
and
are the unweighted particles and drawn from
and
, respectively. The accuracy of the SMC approximation in this case depends on the choice of the proposal density, the number of particles and the value of
N. This would be equivalent to that of the modified SIR as discussed in
Section 3.3. Now, substituting (
34) into (
33),
can be computed as
where
is given in (
18). Algorithm 2 illustrates the steps to compute the LL function.
| Algorithm 2. Computation of log-likelihood function. |
[] |
|
4.2. Maximization of Log-Likelihood Function
Substituting (
35) into (
32), we can rewrite the LL function in (
32) as
where
is independent of parameter
p and can be neglected in the maximization of the likelihood density. Equation (
36) can be maximized numerically over
.
There are two options for the numerical search of the latency parameter: offline and online identification. In the offline method, we can use more measurements for higher parameter estimation accuracy. A higher value of m and smaller steps () for p can yield a more accurate estimate of the latency probability, at the expense of higher computational burden. The offline algorithm can only be started after the first m measurements and it can be repeated with further measurements to improve the estimate. Algorithm 3 outlines the steps for offline identification.
In case of online identification, the latency probability is estimated at each time step and the estimated value of the parameter is used in the proposed PF algorithm. The running average of the estimated values at each step can be evaluated to improve the accuracy of the identified parameter. Algorithm 4 outlines the online method.
| Algorithm 3. Offline identification of latency probability. |
[] |
|
| Algorithm 4. Online identification of latency probability. |
[] |
Select the value for for - –
Set - –
for - –
- –
end for - –
Initialization:if - –
and
- –
Update:else - –
If - -
and
end for
|
4.3. Computational Complexity
Attributing to the use of numerical search method to maximize the likelihood, the estimation of latency parameter is a computationally involved process. However, once the latency parameter is estimated, the computational cost of the proposed PF algorithm is not substantially higher than that of the standard PF. In the offline mode of identification, the proposed particle filter will run
times slower than the standard PF, where
(
) is the step length used for the search algorithm. That is, if the standard PF is
[
42], then proposed PF in offline mode is
. Similarly, for online identification, the modified particle filter will be
, where
k is the time step.
5. Simulation Results
To demonstrate the superiority of the proposed PF over the standard PF and the state-of-the-art algorithms for randomly delayed measurements, three different types of filtering problems are simulated. Although any general proposal density [
39] can be chosen for the implementation of the proposed PF, in our simulations, the transitional prior density
is used as the proposal density for its simplicity. The latency probability of delayed measurements is first identified by maximizing (
36) over
with the help of the proposed PF algorithm. Subsequently, the estimated probability
p is used to implement the proposed PF for the given problems. To ensure a fair comparison of the proposed PF with the other state-of-the-art algorithms, two sets of simulation are carried out for each problem based on the measurement model used in the chosen filtering algorithm. In the first set of simulations, the proposed PF with estimated latency probability is compared against the standard PF and the cubature Kalman filter for the randomly delayed measurements (CKF-RD) [
27] by using the randomly delayed measurements with packet drops. The proposed PF with other than the true value of
N is also implemented to investigate the impact of selecting a wrong value for the maximum number of delay steps. The performances of all filters are compared in terms of the root mean square error (RMSE). Note that the proposed PF with the wrong value of
N and the CKF-RD are implemented with the true value of the latency probability. In the second set of simulations, the proposed PF with the estimated latency probability is compared against the PF for multi-step randomly delay measurements (PF-MD) [
29] by using the set of randomly delayed measurements with
no packet drops. To demonstrate the importance of the latency estimation, PF-MD is implemented with both the true latency probability and the incorrect latency probability. Further, recognizing the practical limitation on the buffer-length and to avoid the large convergence error as discussed in
Section 3.3, the true value of the maximum step delay is taken as
. However, the simulation work can be carried out with the larger value of
N as shown for Problem 1. For brevity, the case with the larger
N for other problems is not included in the paper.
MATLAB 2017a software is used to carry out the simulation work. No in-built subroutine for the PF is used and all the figures presented in this work are generated by running the standard instructions in MATLAB following the Algorithms 1–4. Both the truth and measurements are generated prior to filter implementation. The filtering algorithm uses the software generated measurement values for the PF to implement.
5.1. Problem 1
We consider a time-varying growth model that is widely used in literature because of its non-stationary property for validation of performances by nonlinear filters [
9,
23,
43,
44]. Nonlinear dynamics of the system are as follows:
where
and
are independent zero mean Gaussian processes with
and
, respectively. The initial state
, and the received measurements,
are generated by using (
37) and (
3) with
. The distribution of the initial estimated state
and the number of particles used for the simulation of this problem is,
.
Offline estimation of the latency probability is carried out by using Algorithm 3 with
and
. The latency probability (
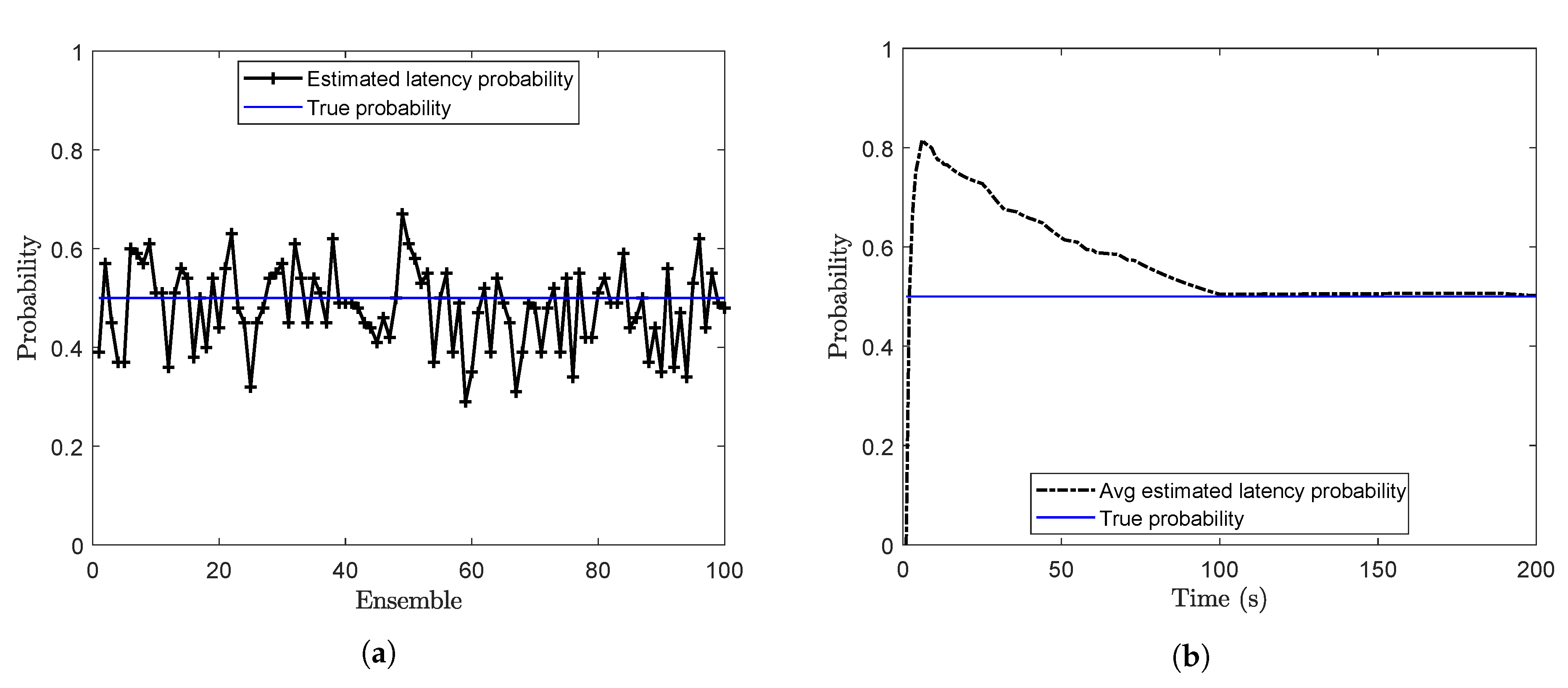
p) at the end of each ensemble is calculated and plotted in
Figure 2a. For this case, when the true value of
p is
, the mean of the estimated latency probability over 100 ensembles is calculated as
. Online estimates of the latency probability are shown in
Figure 2b. Here, the estimated probability at each time step is the running average of the estimated probabilities.
The proposed PF is implemented with
and
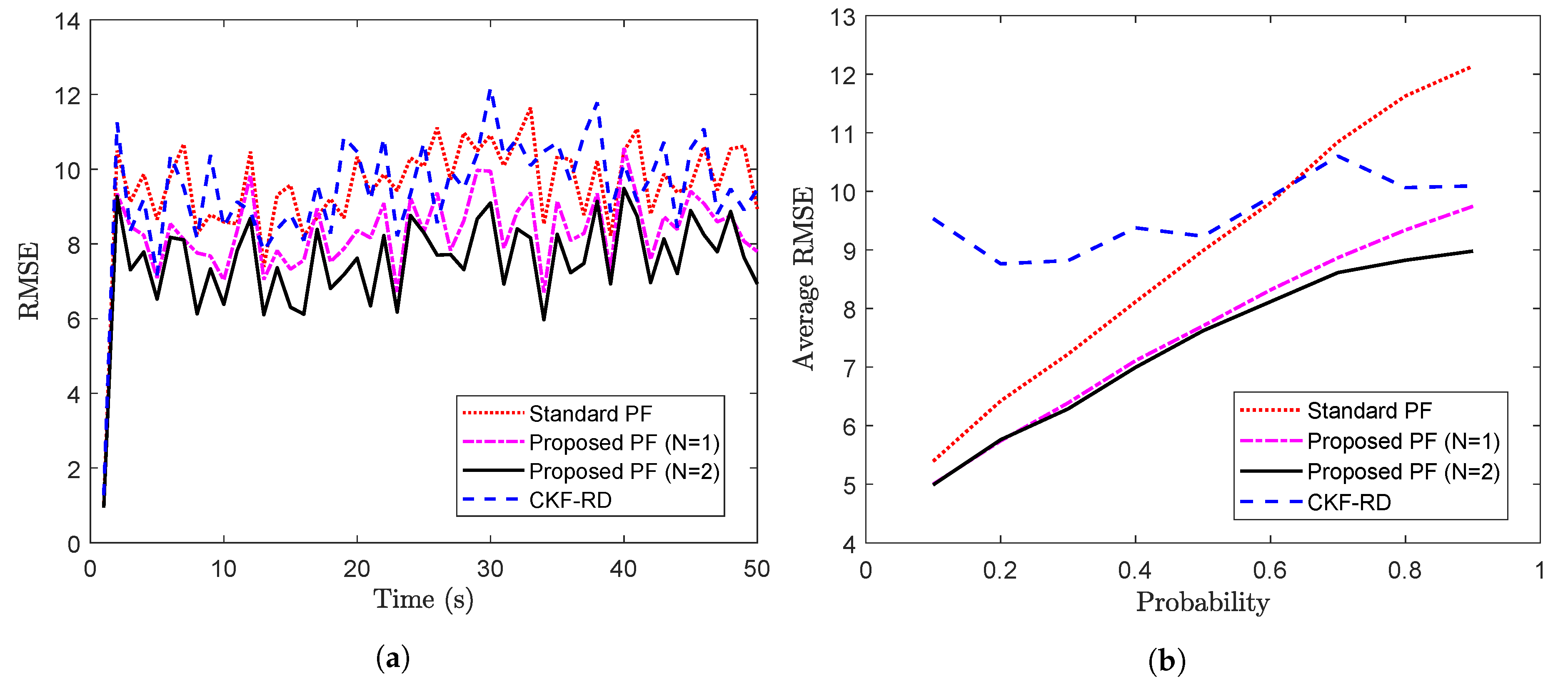
on the measurements as described above, and the results are compared against that of the CKF-RD and the standard PF. To compare the results, the RMSE calculated over 100 Monte Carlo (MC) runs are plotted over 50 time steps in
Figure 3a. It can been seen that the proposed PF with
outperforms the other three filters. Moreover, it is interesting to observe that the performance of the proposed PF with the wrong value of the maximum number of step delay (
) is closer to that of the proposed PF with
.
Further, the average RMSE calculated over 50 time steps for different values of true latency probability is shown in
Figure 3b. As expected, for a higher probability value where packet drop is more likely, filter designed for
performs better than the other filters.
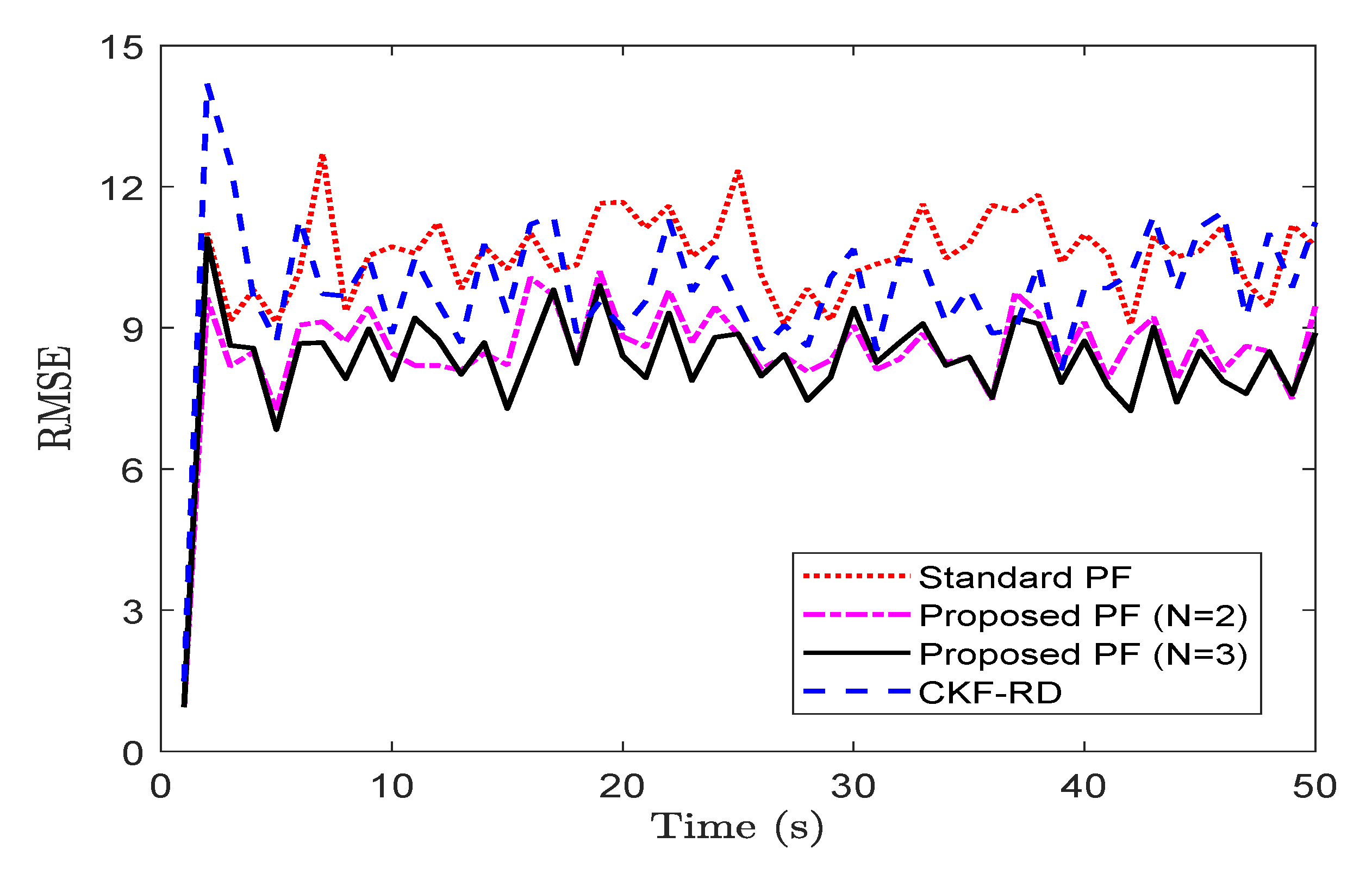
To observe the impact on the performance of the proposed filter when the maximum number of step delay is increased, we take a case of
.
Figure 4 shows the RMSE for the different filter while considering the true latency,
. The average RMSE of the proposed filter in
Figure 3a with
is
whereas that in
Figure 4 with
is
. The increase in the length of memory for the proposed filter explains the increase in the RMSE.
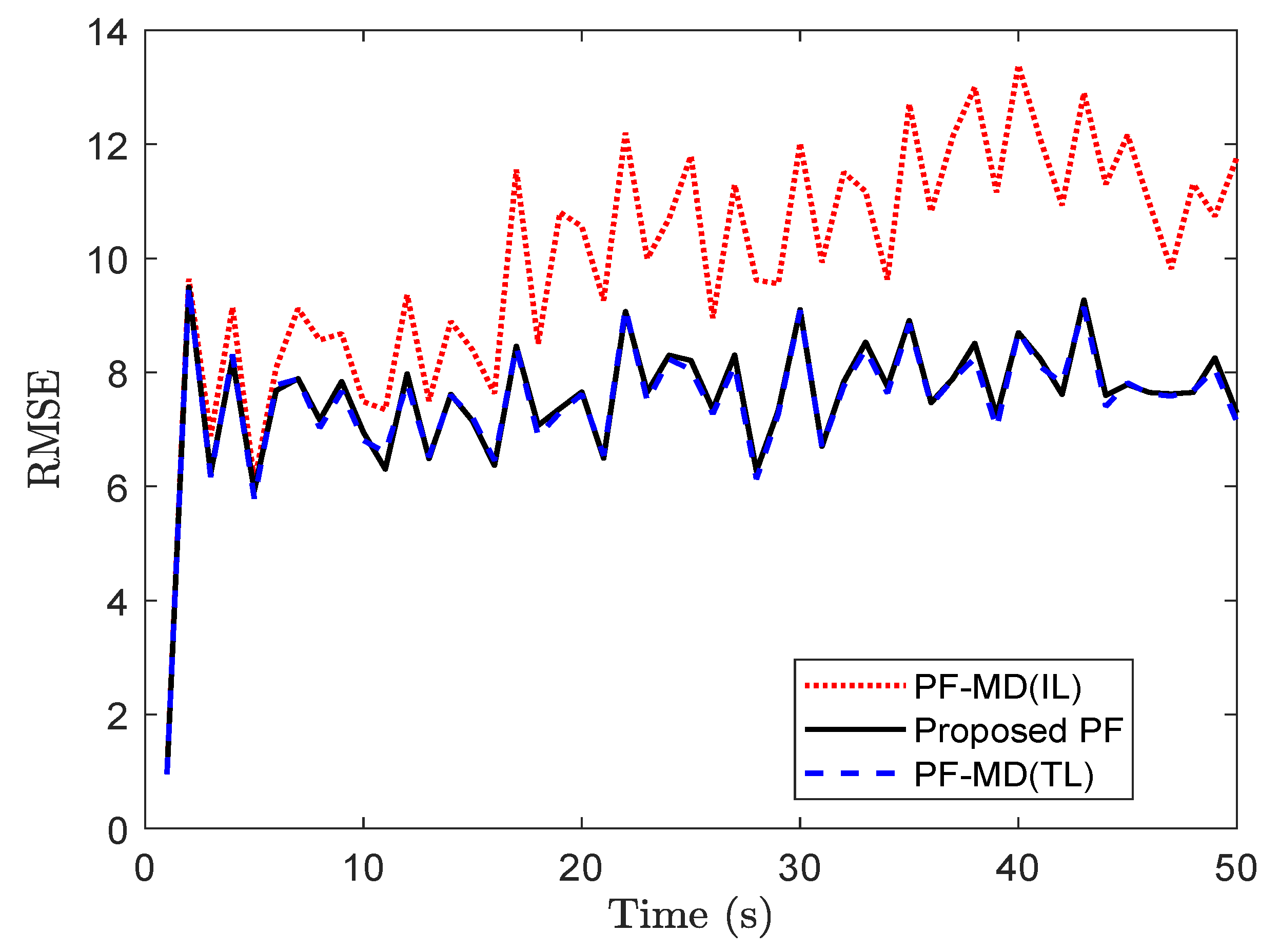
For simulation with the set of randomly delayed measurements without any packet drops, the RMSE value for PF-MD with the true latency (PF-MD(TL)), the proposed PF and PF-MD with the incorrect latency (PF-MD(IL)) are plotted in
Figure 5. It can be observed that the RMSE value of the proposed PF and PF-MD(TL) remain almost the same whereas the filtering performance of PF-MD degrades when the latency probability is unknown and considered an incorrect value.
Table 2 shows the comparison of the computational burden for the different filters. To make the computational comparison independent of the software and clock speed used for simulation, we have calculated the relative computational time for each filter. All computational time is calculated with respect to the computational time of the standard PF algorithm. Note that the given computational time for the proposed PF is after the estimation of the latency parameter. However, the estimation of the latency parameter requires
times running of the proposed PF algorithm.
5.2. Problem 2
Consider a ground surveillance problem where a moving target is tracked from a noisy sensor mounted on a moving platform at an approximately known altitude by using only bearing angle observations. This bearing-only tracking (BOT) problem has mainly two components, namely, the target kinematics and the tracking platform kinematics. A representative scenario is given in References [
3,
45]. The tracking platform motion may be represented by the following equations:
where
and
represent the X and Y coordinates of the tracking platform at
kth time-step, respectively.
and
are the known mean coordinates of the platform position and
and
are independent zero-mean Gaussian white noises with variances,
and
, respectively. The mean values for position coordinates (in meters) are
and
, where
T is sampling time for the discretization expressed in seconds (s).
The target moves in X direction according to following discrete state space relations.
where
with
and
denoting the position (in m) and velocity (in m/s), respectively, of the target.
is an independent zero-mean white Gaussian noise with variance
. The initial true states are assumed to be
.
The sensor measurement is given by
where
is the angle between the X axis and the line of sight from the sensor to target and
is independent Gaussian white noise with zero mean and variance
. For the implementation of CKF-RD, the measurement noise statistics, on account of the uncertainties in the position of the observer platform, need to be modified as given in Reference [
3].
The randomly delayed measurements with packet drops,
, are generated for 21s by using (
3) and (
39) with
. The number of particles used for approximating the pdf is
. At the beginning of simulation, the latency probability of received measurements is identified offline with
s,
, and
. Latency probability at the end of each ensemble is calculated. The mean value of estimated
p over 100 ensembles is calculated as
, whereas its true value is
. For online identification,
T is taken as
s and the running average of latency probability is calculated at each time step. The plots for the offline and online estimations are shown in the
Figure 6a,b, respectively.
Now, the proposed PF with
and
are implemented with the true and estimated latency probabilities, respectively. The results of CKF-RD and the standard PF for same set of delayed measurements are compared against that of proposed PF. The RMSE of four filters with the true latency probability
and sampling time
s, which have been calculated over 100 MC runs, are plotted in
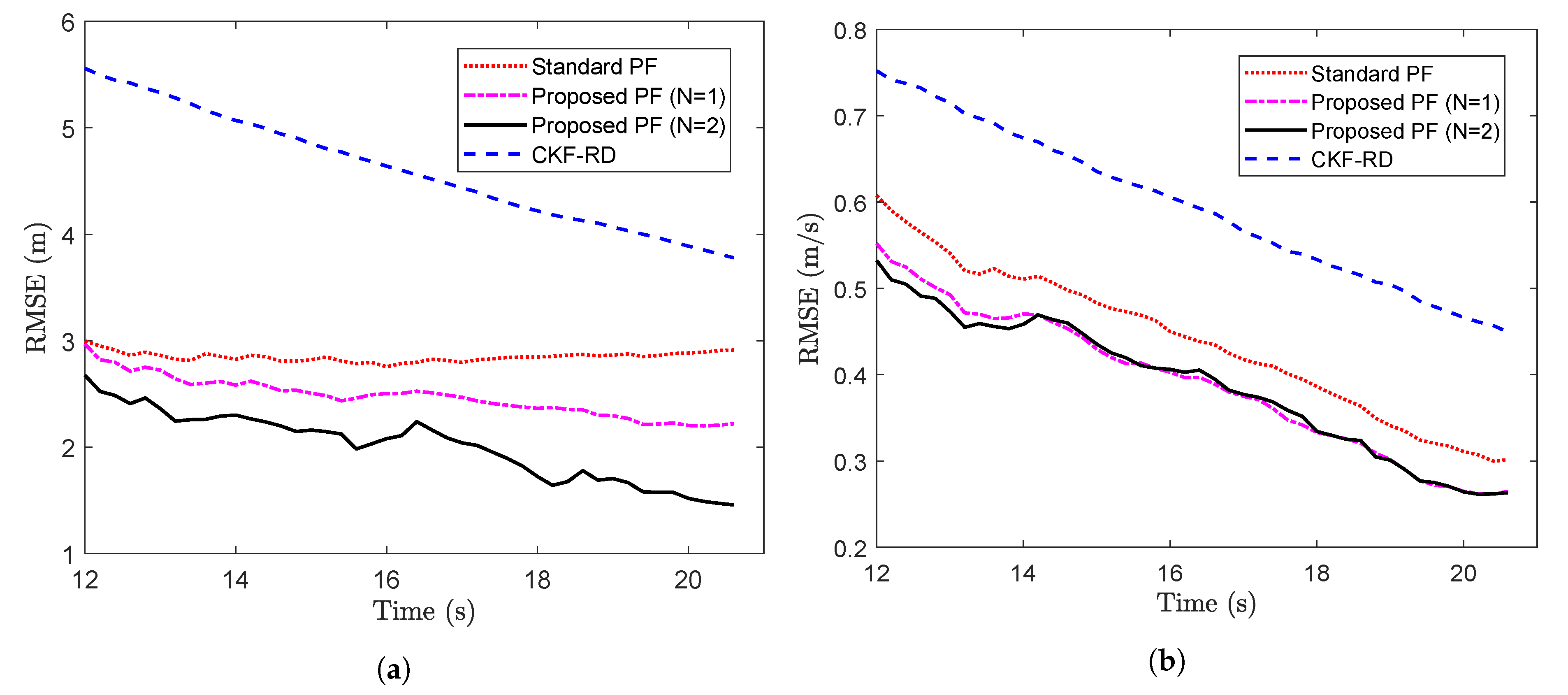
Figure 7a,b. From the plots, it can be seen that using a filter designed for delayed measurements is a better choice than a standard PF where the delays are not accounted.
Further, the average RMSE is calculated over 105 time steps for the different values of
p. The average RMSE for two states,
and
are plotted in
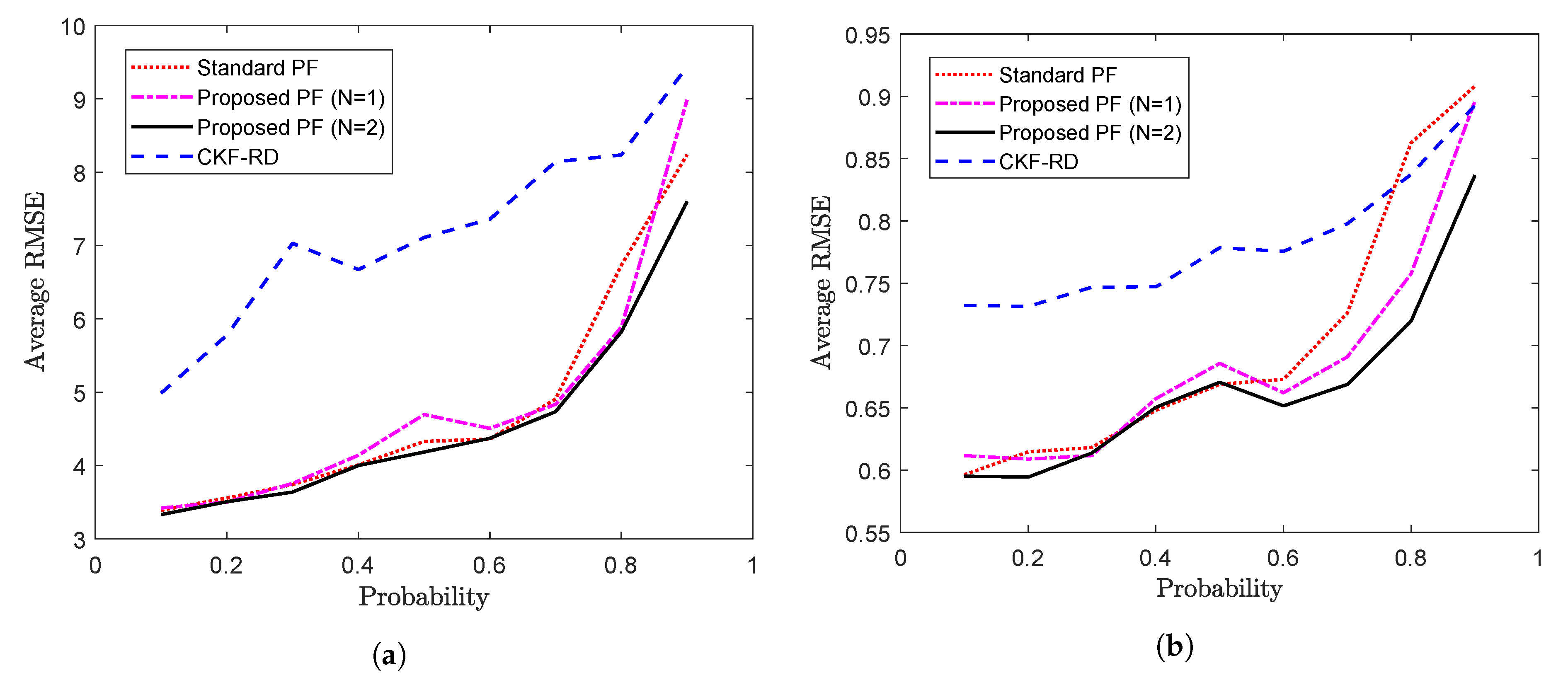
Figure 8a,b respectively. It can be seen that the difference in performance of the proposed PF and the standard PF becomes pronounced as the value of probability increases. However, at higher probabilities, the performance of the proposed filter also gets deteriorated on account of the higher rate of the packet loss.
To compare the performance of the proposed PF with the estimated latency, and PF-MD with the unknown latency, randomly delayed measurements with no packet drops are generated using the measurement model of Reference [
29]. The RMSE for three filters are plotted in
Figure 9. It can be observed that estimation of the latency affects the filtering process and the use of its incorrect value degrades the performance of a filter. The relative computational burden is given in the
Table 3.
5.3. Problem 3
Consider a coordinated turn model for an aerospace target tracking problem for an aircraft that executes a maneuvering turn in a two-dimensional plane with a fixed, but unknown turn rate
. This uses the bearing and the range measurement observed from a radar to estimate the kinematics of the target. The five-dimensional state vector for the kinematics of aircraft is considered as
, where
and
represent positions, and
and
represent velocities along the
X and
Y co-ordinates, respectively. The discrete-time state dynamics of the aircraft is given as [
46]:
where
T is the time between two successive measurements.
is a zero mean Gaussian noise with covariance
, where
and
are the noise intensity parameters, and
. The range,
r, and bearing,
are the measurement available for target tracking, which are being measured by a radar placed at the origin. The noise-corrupted measurements can be expressed as
where
is an independent zero-mean Gaussian noise with covariance
. Data for the different parameters used in this simulation are given in
Table 4. Initial values for the state and covariance are
m
m
and
, respectively.
The randomly delayed measurements with packet drops,
, are generated by using (
41) and (
3) with
and a probability,
. The number of particles used for approximating the pdf is
. In the beginning of simulation, the latency probability of received measurements is identified offline with
and
. The latency probability at the end of each ensemble is calculated and plotted in
Figure 10a. The mean value of the estimated probabilities
over 100 ensembles is calculated as 0.4864 against its true value 0.5.
Figure 10b shows the online estimation of latency probability.
To track the maneuvering target, the proposed PF with
and
(a wrong value of the maximum number of delay steps) are implemented. To demonstrate the superiority of the proposed PF, simulation results of the CKF-RD and the standard PF for the same set of measurements and with the true value of latency probability, are compared against that of the proposed PF. The RMSE of the position, velocity and turn rate are the performance metrics as defined in Reference [
46]. The RMSE of position, velocity and turn rate for the four filters with
, are plotted in
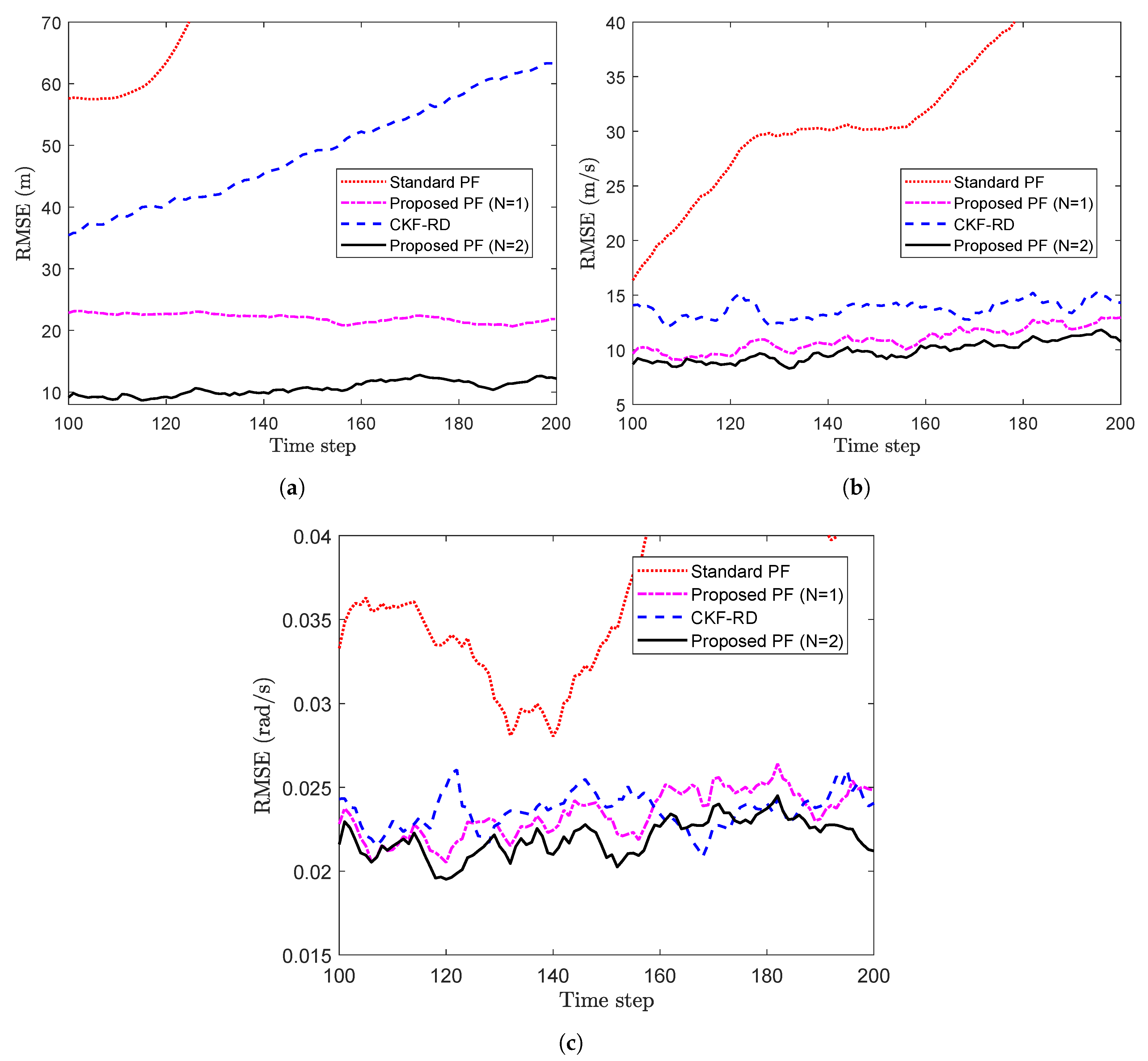
Figure 11a–c, respectively. Since the standard PF does not consider the correlation of current measurement with previously observed states due to random delays, it diverges, particularly in case of the RMSE in position. It can also be observed in the RMSE plots that the proposed PF with
, which has accounted at least partially for the presence of random delays, performs better than the standard PF. This is significant since the maximum number of delay steps will have to be decided by the user and setting
might still yield some benefit over assuming no delay. Note that the difference in RMSE of position between the proposed PF and the standard PF or, the CKF-RD is considerable and is worth the relatively higher computational cost paid to obtain it.
Further, to observe the impact of latency probability on the performances of the different filters, the time-averaged value of the RMSEs of the position, velocity and turn rate are plotted against different values of the
p in
Figure 12a–c, respectively. It can be seen that with high value of probability, that is, when the random delays are more likely, the standard PF and proposed PF with
become significantly less applicable than the proposed PF with
. It can also be observed that when the probability is high with insufficiently higher value of
N, the rate of packet drops increases and even the performance of the proposed PF (
) gets deteriorated.
The performance of the proposed PF and PF-MD is compared in terms of the RMSE in
Figure 13. To be in synchronization with the model of Reference [
29], the measurements used for the estimation are without any packet drops. It can be observed from the plot that without the knowledge of latency, the performance of PF-MD degrades considerably, which suggests estimation of the latency is needed as it is presented in the proposed PF.
Table 5 shows the relative computational burden for different filters.
6. Conclusions and Discussion
The standard PF loses its applicability if measurements are randomly delayed at the receiver. The random delays are possible in a system where the sensor and the receiver are connected through a network with bandwidth limitation.
In this paper, a recursion equation of the importance weight was developed to handle delays in measurements. A practical measurement model based on i.i.d. Bernoulli random variables, which includes the possibility of random delays in receiving the observations along with the packet drop situation if any measurement suffers a delay more than the data buffer length, was adopted. Moreover, the latency probability of the received measurements is usually unknown in practical cases. Hence, this paper presented a method to identify the latency probability in the randomly delayed measurement environment. Further, this paper explored the conditions to ensure the convergence of the proposed PF and the trade-off in selecting the maximum delay.
To validate the performance of the proposed filter and demonstrate its superiority, three numerical examples are simulated using the standard PF, the CKF-RD, the proposed PF with wrong selection of maximum delay and the proposed PF with the correct value of maximum delay. Simulation results show that a filter designed for the delayed measurements, even considering less delay than the actual, performs better than the standard PF. If the random delay is more likely in a system, number of the maximum possible delay should be chosen such that it strikes a balance between avoiding the information loss and minimizing the convergence error. Further, the proposed PF is compared with PF-MD, which is designed for the multi-step randomly delayed measurements without any packet drops and assumes that the latency probability is known. Simulation results showed that the performance of a filter depends on the correct value of latency and its estimation is necessary for the better accuracy of the filtering process.