Standing Wave Binding of Hemispherical Resonator Containing First–Third Harmonics of Mass Imperfection under Linear Vibration Excitation
Abstract
1. Introduction
2. Equations of Motion of Hemispherical Resonator with First–Third Harmonics of Mass Imperfection
2.1. Basic Structure of HRG
2.2. Establishment of Coordinate Systems of Hemispherical Resonator
2.3. Deformation Energy of Hemispherical Resonator
2.4. Second-Order Vibration Mode Function
2.5. Kinetic Energy of Hemispherical Resonator
2.6. Equations of Motion of Hemispherical Resonator Containing First–Third Harmonics of Mass Imperfection
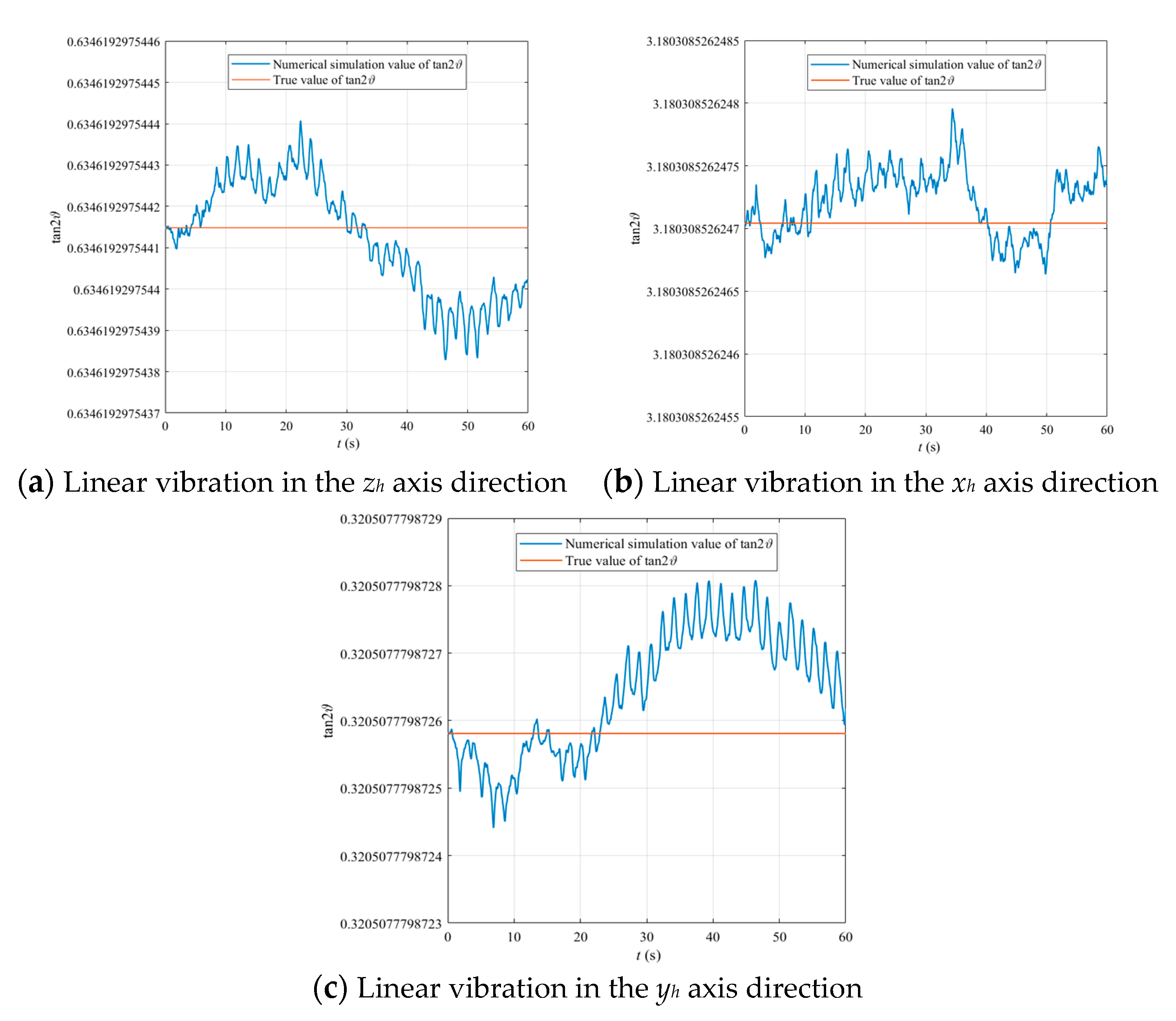
3. Effect of Linear Vibration on Standing Wave of Imperfect Hemispherical Resonator
3.1. Effect of Vertical Linear Vibration on Standing Wave of Imperfect Hemispherical Resonator
3.2. Effect of Horizonal Linear Vibration on Standing Wave of Imperfect Hemispherical Resonator
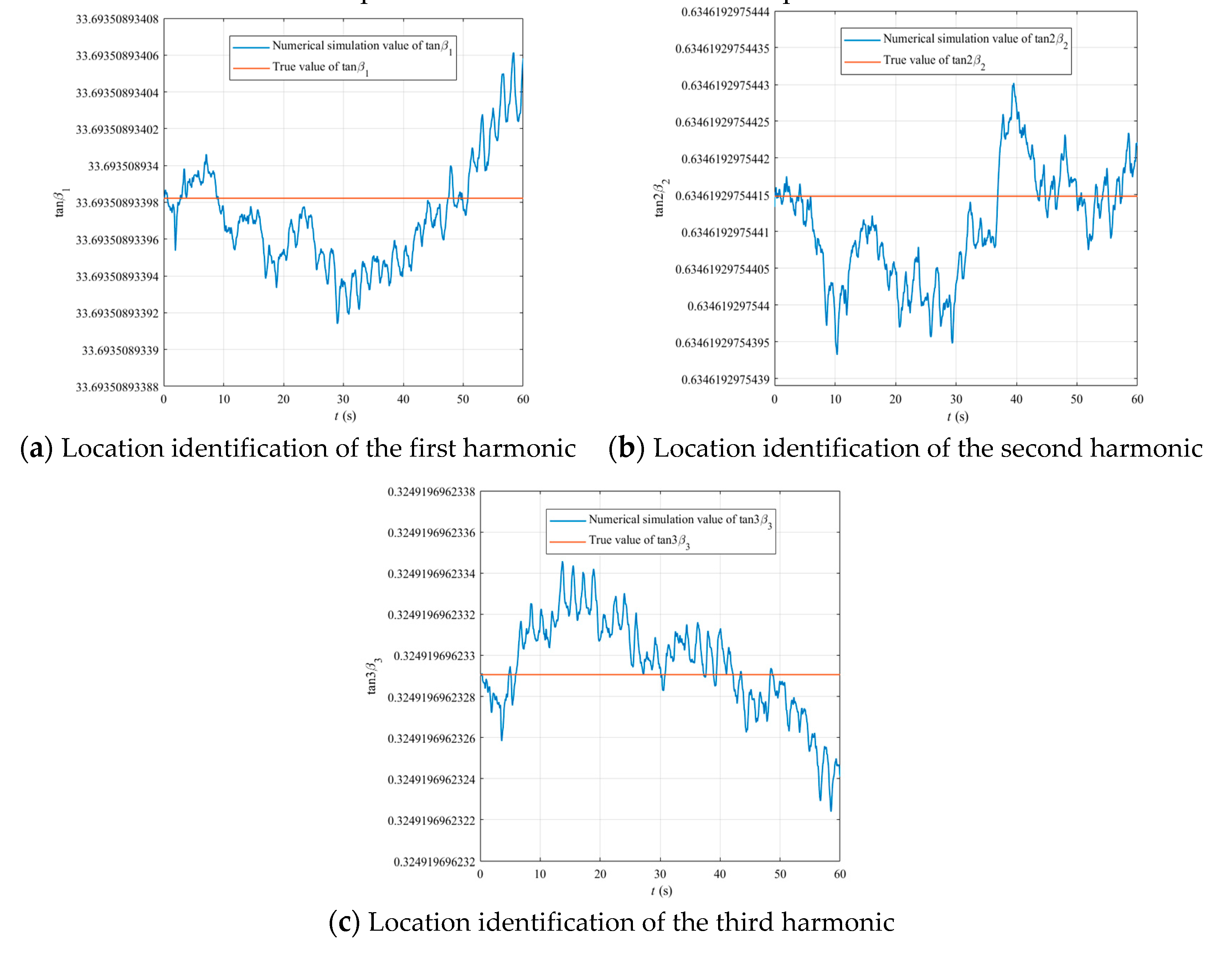
4. Identification of Location of First–Third Harmonics of Mass Imperfection by Linear Vibration
4.1. Identification for Location of the Second Harmonic of Mass Imperfection by Vertical Vibration
4.2. Calibration for Locations of the First and Third Harmonics of Mass Imperfection by Horizontal Vibration
5. Numerical Simulation Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rozelle, D.M. The Hemispherical Resonator Gyro: From Wineglass to the Planets. In Proceedings of the 19th AAS/AIAA Space Flight Mechanics Meeting, Savannah, GA, USA, 8–12 February 2009. [Google Scholar]
- Jeanroy, A.; Bouvet, A.; Remillieux, G. HRG and marine applications. Gyroscopy Navig. 2014, 5, 67–74. [Google Scholar] [CrossRef]
- Meyer, A.D.; Rozelle, D.M. Milli-HRG inertial navigation system. Gyroscopy Navig. 2012, 3, 24–29. [Google Scholar] [CrossRef]
- Emily, L.B.; Allan, Y.L. In-Flight Characterization of Cassini Inertial Reference Units, AIAA Guidance, Navigation and Control Conference and Exhibit; AIAA: Hilton Head, SC, USA, 2007. [Google Scholar]
- Lynch, D.D. Vibratory Gyro Analysis by the Method of Averaging. In Proceedings of the 2nd SAINT Petersburg International Conference on Gyroscopic Technology Navigation Part 1, Saint Petersburg, Russia, 24–25 May 1995; pp. 26–34. [Google Scholar]
- IEEE Standard Specification Format Guide and Test Procedure for Coriolis Vibratory Gyros. 2004. Available online: https://ieeexplore.ieee.org/servlet/opac?punumber=9606 (accessed on 8 April 2019).
- Loveday, P.W.; Rogers, C.A. The influence of control system design on the performance of vibratory gyroscopes. J. Sound Vib. 2002, 255, 417–432. [Google Scholar] [CrossRef]
- Fox, C.H.J. A simple theory for the analysis and correction of frequency splitting in slightly imperfect rings. J. Sound Vib. 1990, 142, 227–243. [Google Scholar] [CrossRef]
- Choi, S.Y.; Kim, J.H. Natural frequency split estimation for inextensional vibration of imperfect hemispherical shell. J. Sound Vib. 2011, 330, 2094–2106. [Google Scholar] [CrossRef]
- Basarab, M.A.; Lunin, B.S.; Matveev, V.A.; Chumankin, E.A. Balancing of hemispherical resonator gyros by chemical etching. Gyroscopy Navig. 2015, 6, 218–223. [Google Scholar] [CrossRef]
- Wang, Y.T.; Pan, Y.; Qu, T.L.; Yang, K.Y.; Luo, H. Decreasing Frequency Splits of Hemispherical Resonators by Chemical Etching. Sensors 2018, 18, 3772. [Google Scholar] [CrossRef] [PubMed]
- Gallacher, B.J.; Hedley, J.; Burdess, J.S.; Harris, A.J.; Rickard, A.; King, D.O. Electrostatic correction of structural imperfections present in a micro-ring gyroscope. J. Microelectromech. Syst. 2005, 14, 221–234. [Google Scholar] [CrossRef]
- Schwartz, D.; Dong, J.K.; M’Closkey, R.T. Frequency tuning of a disk resonator gyro via mass matrix perturbation. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; Volume 131, pp. 3740–3745. [Google Scholar]
- Xiao, D.; Yu, D.; Zhou, X.; Hou, Z.; He, H.; Wu, X. Frequency Tuning of a Disk Resonator Gyroscope via Stiffness Perturbation. IEEE Sens. J. 2017, 17, 4725–4734. [Google Scholar] [CrossRef]
- Senkal, D.; Ahamed, M.J.; Trusov, A.A.; Shkel, A.M. Achieving Sub-Hz Frequency Symmetry in Micro-Glassblown Wineglass Resonators. J. Microelectromech. Syst. 2014, 23, 30–38. [Google Scholar] [CrossRef]
- Matveev, V.A.; Lipatnikov, V.I.; Alekin, A.V.; Basarab, M.A. Solid Wave Gyroscope; National Defense Industry Press: Beijing, China, 2009. [Google Scholar]
- Shao, P.; Mayberry, C.L.; Gao, X.; Tavassoli, V.; Ayazi, F. A Polysilicon Micro-hemispherical Resonating Gyroscope. J. Microelectromech. Syst. 2014, 23, 762–764. [Google Scholar] [CrossRef]
- Xi, X.; Wu, Y.L.; Zhang, Y.M.; Wu, X.M.; Zheng, Y.; Wu, X.Z. A Simple Acoustic Method for Modal Parameter Measurement of the Resonator for Vibratory Shell Gyroscope. IEEE Sens. J. 2014, 14, 4069–4077. [Google Scholar]
- Hu, X.D.; Luo, J.K.; Yu, B.; Zhou, Q.; Lin, K.; Lei, T.; Fang, Z. Application of ion beam in the mass balancing of hemispherical resonator. In Proceedings of the Fifth Chinese Society of Inertial Technology Annual Conference Proceedings, Guilin, China, 13–17 October 2003; pp. 247–252. [Google Scholar]
- Wan, Q.; Gu, H.; Fan, B.; Zhao, H.; Xu, D.; Guo, S. A High Symmetry Polysilicon Micro Hemispherical Resonating Gyroscope with Spherical Electrodes. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Tao, Y.; Xi, X.; Xiao, D.; Tan, Y.; Cui, H.; Wu, X. Precision balance method for cupped wave gyro based on cup-bottom trimming. Chin. J. Mech. Eng. 2012, 25, 63–70. [Google Scholar] [CrossRef]
- Abdelmoneum, M.A.; Demirci, M.M.; Lin, Y.-W.; Nguyen, C.T.-C. Location-dependent frequency tuning of vibrating micromechanical resonators via laser trimming. In Proceedings of the 2004 IEEE International Frequency Control Symposium and Exposition, Montreal, QC, Canada, 23–27 August 2004; pp. 272–279. [Google Scholar]
- Kim, J.H.; Kim, J.H. Trimming of imperfect hemispherical shell including point mass distributions. Int. J. Mech. Sci. 2017, 131, 847–852. [Google Scholar] [CrossRef]
- Xi, X.; Qu, Y.L.; Wang, D.Y.; Wu, X.M.; Tao, Y.; Wu, X.Z. Investigation on standing wave vibration of the imperfect resonant shell for cylindrical gyro. Sens. Actuators A Phys. 2012, 179, 70–77. [Google Scholar] [CrossRef]
- Wang, X.; Wu, W.; Luo, B.; Fang, Z.; Li, Y.; Jiang, Q. Force to rebalance control of HRG and suppression of its errors on the basis of FPGA. Sensors 2011, 11, 11761–11773. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.Q.; Zhao, H.B. Influence of density error of hemispherical resonator on output accuracy of gyro. J. Chin. Inert Technol. 2011, 19, 364–368. (In Chinese) [Google Scholar]
- Tao, Y.; Xi, X.; Xiao, D.B.; Chen, Z.H.; Tan, Y.Q.; Wu, X.Z. A fast identification method for mode offset angle of cupped wave gyroscope. J. Vib. Eng. 2011, 24, 351–358. [Google Scholar]
- Huo, Y.; Ren, S.Q.; Yi, G.X.; Wang, C.H. Establishment of equations of motion of hemispherical resonator and analysis of frequency split caused by slight mass non-uniformity. Chin. J. Aeronaut. 2020, in press. [Google Scholar] [CrossRef]
- Xu, Z.L. Elasticity, 5th ed.; Higher Education Press: Beijing, China, 2016; pp. 174–193. (In Chinese) [Google Scholar]
- Liu, H.W. Shell Theory; Zhejiang University Press: Hangzhou, China, 1989; pp. 269–271. (In Chinese) [Google Scholar]
- Department of Engineering Mechanics, Tsinghua University. Mechanical Vibration; Mechanical Industry Press: Beijing, China, 1980; pp. 52–152. (In Chinese) [Google Scholar]
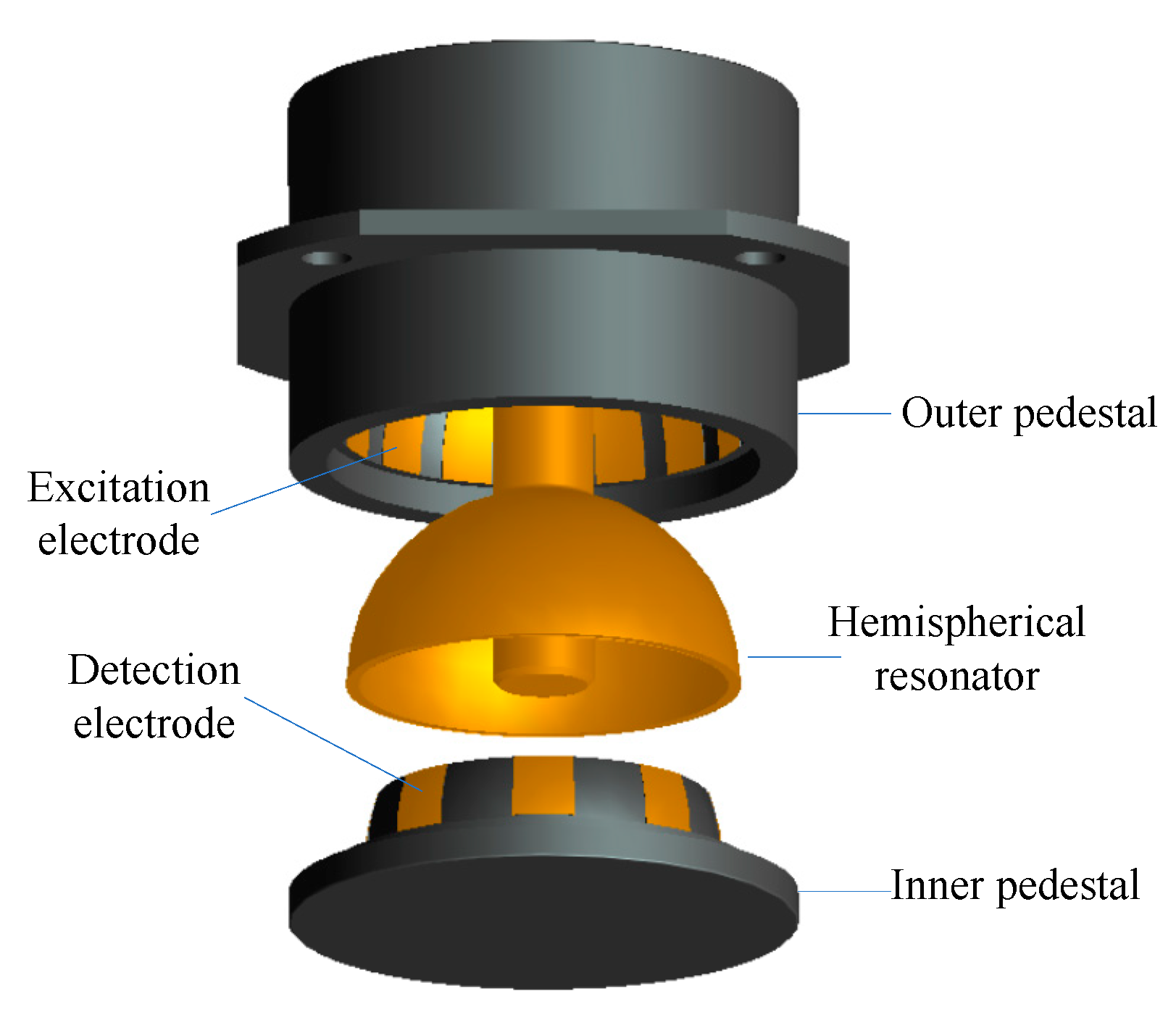
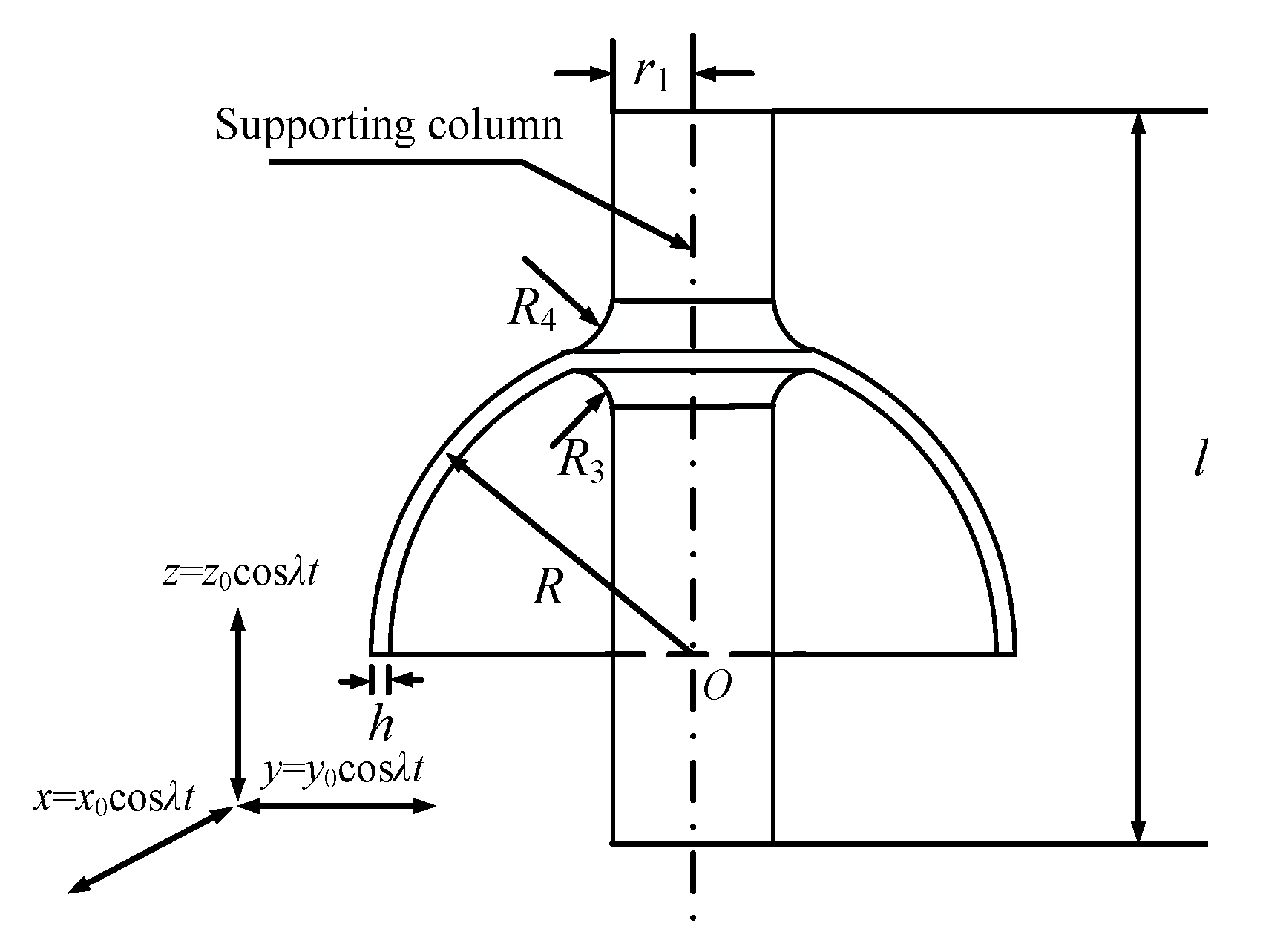

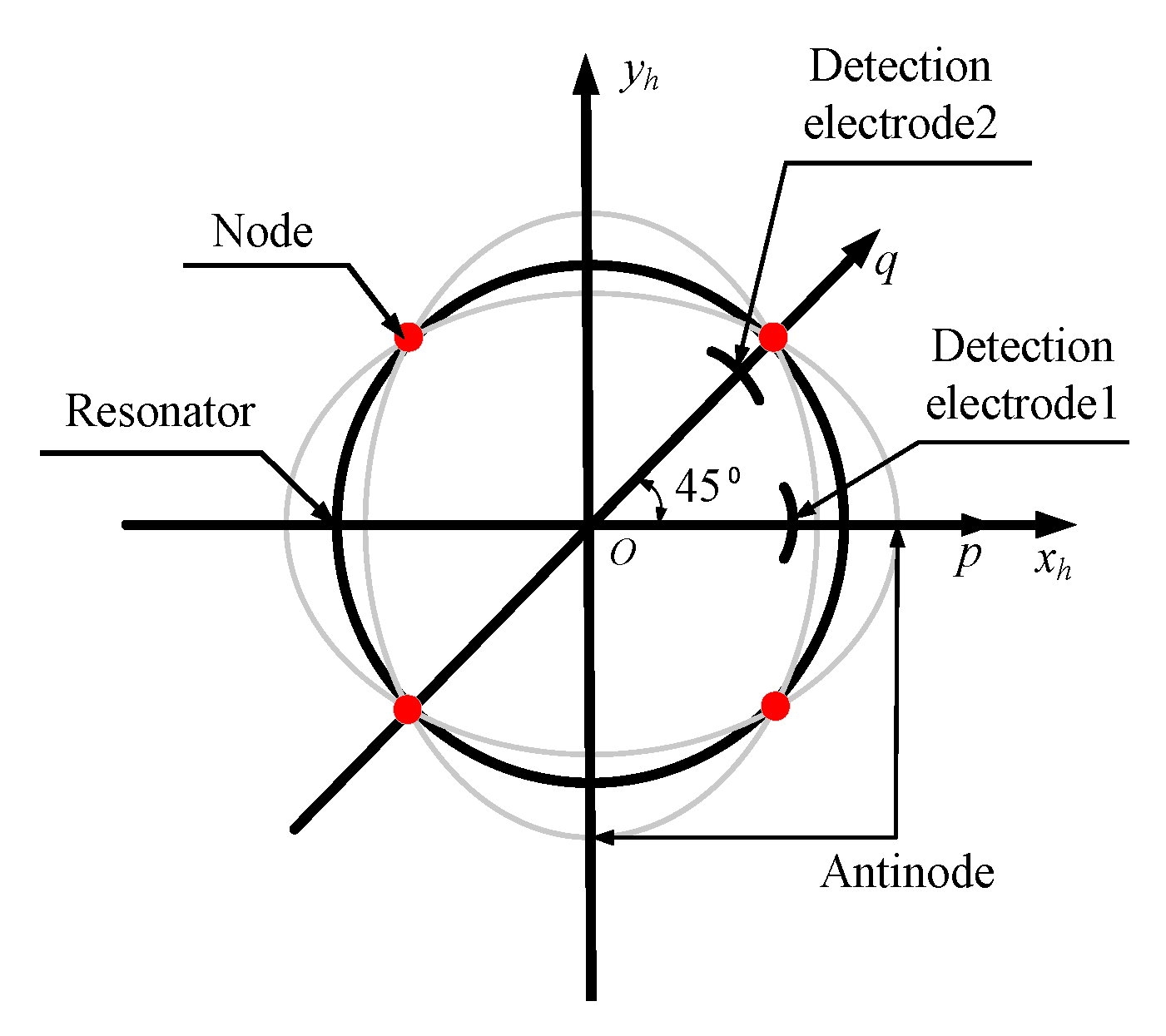
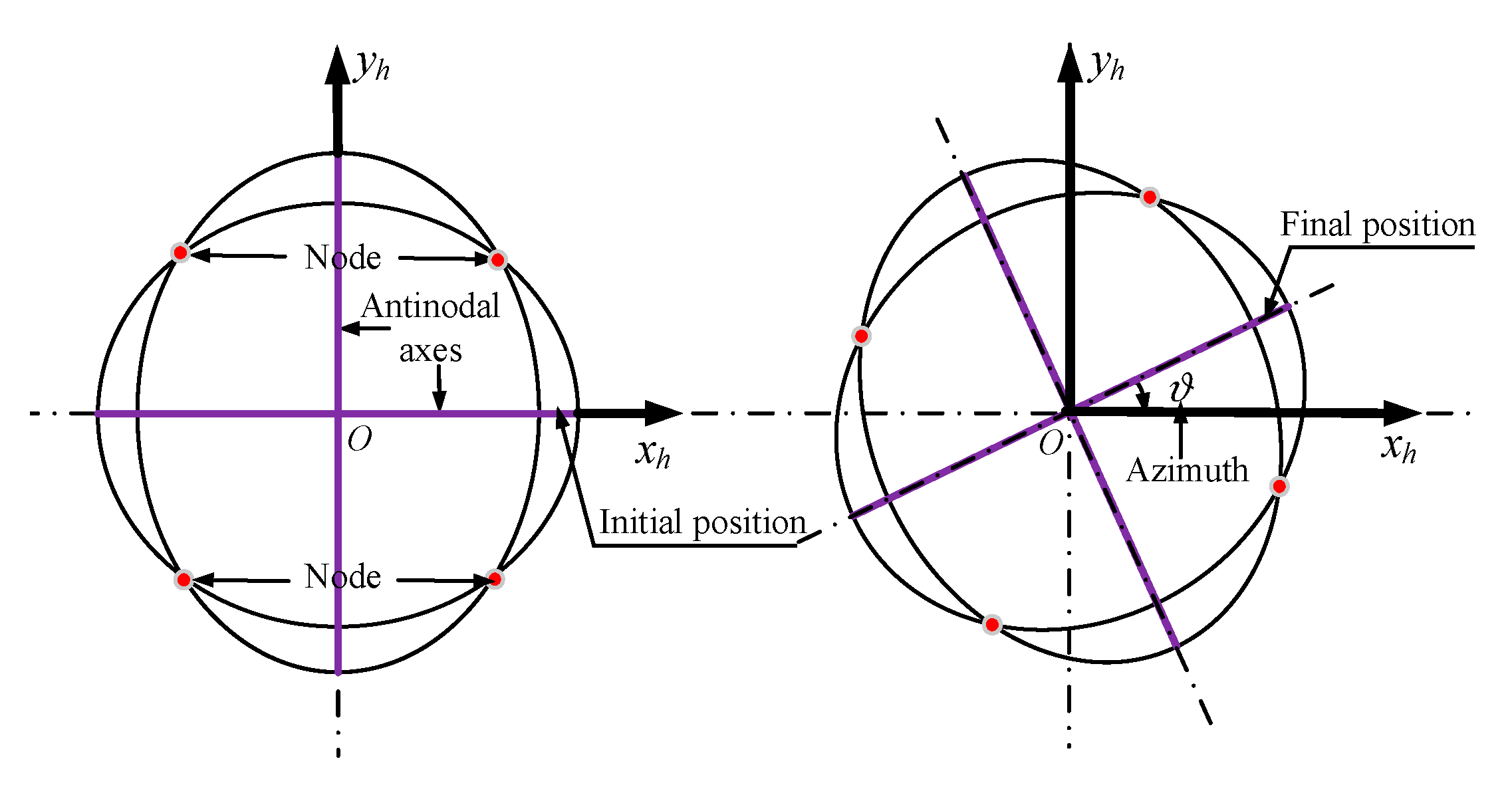
| Symbol | Name | Value | Symbol | Name | Value |
|---|---|---|---|---|---|
| ρ0 | Average density | 2500 kg/m3 | l | Length of supporting column | 60 mm |
| E | Young’s modulus | 76.7 GPa | r1 | Radius of supporting column | 6 mm |
| μ | Poisson’s ratio | 0.17 | R | Radius of mid-surface | 25 mm |
| Qf | Quality factor | 106 | R3 | Inner corner radius | 3 mm |
| h | Thickness | 1 mm | R4 | Outer corner radius | 3 mm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, Y.; Ren, S.; Wei, Z.; Yi, G. Standing Wave Binding of Hemispherical Resonator Containing First–Third Harmonics of Mass Imperfection under Linear Vibration Excitation. Sensors 2020, 20, 5454. https://doi.org/10.3390/s20195454
Huo Y, Ren S, Wei Z, Yi G. Standing Wave Binding of Hemispherical Resonator Containing First–Third Harmonics of Mass Imperfection under Linear Vibration Excitation. Sensors. 2020; 20(19):5454. https://doi.org/10.3390/s20195454
Chicago/Turabian StyleHuo, Yan, Shunqing Ren, Zhennan Wei, and Guoxing Yi. 2020. "Standing Wave Binding of Hemispherical Resonator Containing First–Third Harmonics of Mass Imperfection under Linear Vibration Excitation" Sensors 20, no. 19: 5454. https://doi.org/10.3390/s20195454
APA StyleHuo, Y., Ren, S., Wei, Z., & Yi, G. (2020). Standing Wave Binding of Hemispherical Resonator Containing First–Third Harmonics of Mass Imperfection under Linear Vibration Excitation. Sensors, 20(19), 5454. https://doi.org/10.3390/s20195454




